information Information Information Information 2078-2489 MDPI 10.3390/info3030256 information-03-00256 Review A Review on the Interpretability-Accuracy Trade-Off in Evolutionary Multi-Objective Fuzzy Systems (EMOFS) Shukla Praveen Kumar 1 * Tripathi Surya Prakash 2 Department of Information Technology, Babu Banarasi Das Northern India Institute of Technology, Lucknow 226001, India Department of Computer Science & Engineering, Institute of Engineering & Technology, Lucknow 226001, India; Email: tripathee_sp@yahoo.co.in Author to whom correspondence should be addressed; Email: praveenshuklak@rediffmail.com; Tel.: +91-993-625-9191; Fax: +91-0522-391-1047. 12 07 2012 09 2012 3 3 256 277 16 06 2012 21 06 2012 29 06 2012 © 2012 by the authors; licensee MDPI, Basel, Switzerland. 2012

This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).

Interpretability and accuracy are two important features of fuzzy systems which are conflicting in their nature. One can be improved at the cost of the other and this situation is identified as “Interpretability-Accuracy Trade-Off”. To deal with this trade-off Multi-Objective Evolutionary Algorithms (MOEA) are frequently applied in the design of fuzzy systems. Several novel MOEA have been proposed and invented for this purpose, more specifically, Non-Dominated Sorting Genetic Algorithms (NSGA-II), Strength Pareto Evolutionary Algorithm 2 (SPEA2), Fuzzy Genetics-Based Machine Learning (FGBML), (2 + 2) Pareto Archived Evolutionary Strategy ((2 + 2) PAES), (2 + 2) Memetic- Pareto Archived Evolutionary Strategy ((2 + 2) M-PAES), etc. This paper introduces and reviews the approaches to the issue of developing fuzzy systems using Evolutionary Multi-Objective Optimization (EMO) algorithms considering ‘Interpretability-Accuracy Trade-off’ and mainly focusing on the work in the last decade. Different research issues and challenges are also discussed.

Evolutionary Multi-Objective Fuzzy System (EMOFS) Evolutionary Multi-Objective Optimization (EMO) Genetic Fuzzy Systems (GFS) Interpretability-Accuracy Trade-Off Genetic Algorithm (GA) Multi-Objective Evolutionary Algorithms (MOEA) 1. Introduction

Interpretability [1,2,3] and accuracy [4] are the two important features of a fuzzy system developed for a specific application. The term ‘interpretability’ describes the capability of a model that allows a human being to understand its behavior by inspecting its functioning or its rule base. On the other hand, “accuracy” is the feature of the system that shows its capability to faithfully represent the real system. It can also be defined as the quantification of closeness between real system and its modeled fuzzy system.

Interpretability and accuracy are contradictory issues in the design of a fuzzy system. An increment in either feature can only be done at the cost of the other. This situation is called Interpretability-Accuracy (I-A) Trade-Off [5] and currently is a challenging research issue. Through this, various degrees of interpretability and accuracy of fuzzy systems are obtained and either one of them may be selected depending on the user’s needs and the requirements of application.

The identification of fuzzy systems from data samples for specific functions associates different tasks, like input selection, rule selection, rule generation, fuzzy partition, membership function tuning etc. These tasks can be implemented as an optimization or search process using Evolutionary Algorithms (EAs), more specifically Genetic Algorithms (GA) [6,7]. The above-discussed integration of GA in the design of Fuzzy Systems results in the evolution of a special research area called ‘Genetic Fuzzy Systems’ (GFS) [8,9,10,11]. Genetic fuzzy systems have been proven to be capable of building compact and transparent fuzzy models while maintaining a very good level of accuracy, [12,13].

To deal with Interpretability-Accuracy Trade-Off in Fuzzy Systems, Multi-Objective Evolutionary Algorithms (MOEAs) have been used, leading to the next generation of GFSs named Evolutionary Multi-Objective Fuzzy Systems (EMOFS) [14,15,16,17,18]. A list of references in this field has been given in [19]. A Multi-Objective Fuzzy Modeling is used in [20] to deal with Interpretability-Accuracy Trade-Off. These EMOFS may be any rule-based system [21], classification system [22], etc.

A recent discussion and review on the existing approaches of EMOFS has been given in [23]. A taxonomy on existing proposals in EMOFS has been carried out, focusing mainly on Interpretability-Accuracy Trade-Off, multi-objective control problems and fuzzy association rule mining. We have focused on only the first issue, Interpretability-Accuracy Trade-Off, in this paper. This paper continues the work of [23], mainly considering the issue of Trade-Off in EMOFS.

The paper is divided into four sections. In Section 2, EMO is introduced briefly. In Section 3, a vast discussion has been carried out on the application of EMO in the design of fuzzy systems covering the issues related to the interpretability as well as accuracy and their trade-off. In Section 4, the recent research issues related to EMOFS are discussed. Conclusions and the future scope are given in Section 5.

 2. Evolutionary Multi-Objective Optimization

Evolutionary algorithms are stochastic optimization techniques, which simulate the concept of natural evolution. Evolutionary approaches consist of methodologies, genetic algorithms, evolutionary programming and evolutionary strategies. These techniques have been proven to be a robust and powerful search mechanism. In Evolutionary Multi-Objective Optimization, the objectives conflict with each other. These approaches are capable of tackling the problems of (1) large, complex and high dimensional search space, and (2) multiple conflicting objectives. In these techniques, no optimal, ideal and single solution can be derived, instead, a set of solutions are produced because the improvement in one objective leads to degradation in the remaining objectives. These solutions are called Pareto-Optimal Solutions. These Pareto Optimal Solutions in terms of objective function are called Pareto Front.

For example, two objective maximization problems can be formulated as: maximize g (x) = (g1 (x), g2 (x)).

In Figure 1(a), solution X dominates Y or Y is dominated by X. It can be concluded that X is better than Y. But, X and Z are non-dominated by each other. A Pareto-Optimal Solution is a solution that is not dominated by any other solutions and Pareto Front (Figure 1(b)) of any problem is the set of all Pareto-Optimal Solutions in terms of objective functions.

(a) Dominated and non-dominated solutions; (b) Two-Objective Problem and Pareto Front.

Multi-objective optimization problems are solved by using evolutionary algorithms, like Genetic Algorithms (GA) and result in a new area called EMO [24,25,26,27,28,29]. The introduction and review of EMO is very well discussed in [30,31].

The conflicting nature of the objectives leads to many problems, like dominance resistance and speciation. In [32], two diversity management mechanisms are introduced using Non-Dominated Sorting Genetic Algorithms (NSGA-II). Handling large numbers of objectives in multi-objective optimization is a very critical research issue. To deal with this issue, an approach is discussed in [33]. A similar issue is discussed in [34] for handling many conflicting objectives using standard Pareto ranking and diversity promoting selection mechanism. Regarding the issue of constraint handling, an approach is developed for nonlinear constrained optimization-problems with fuzzy costs and constraints in [35].

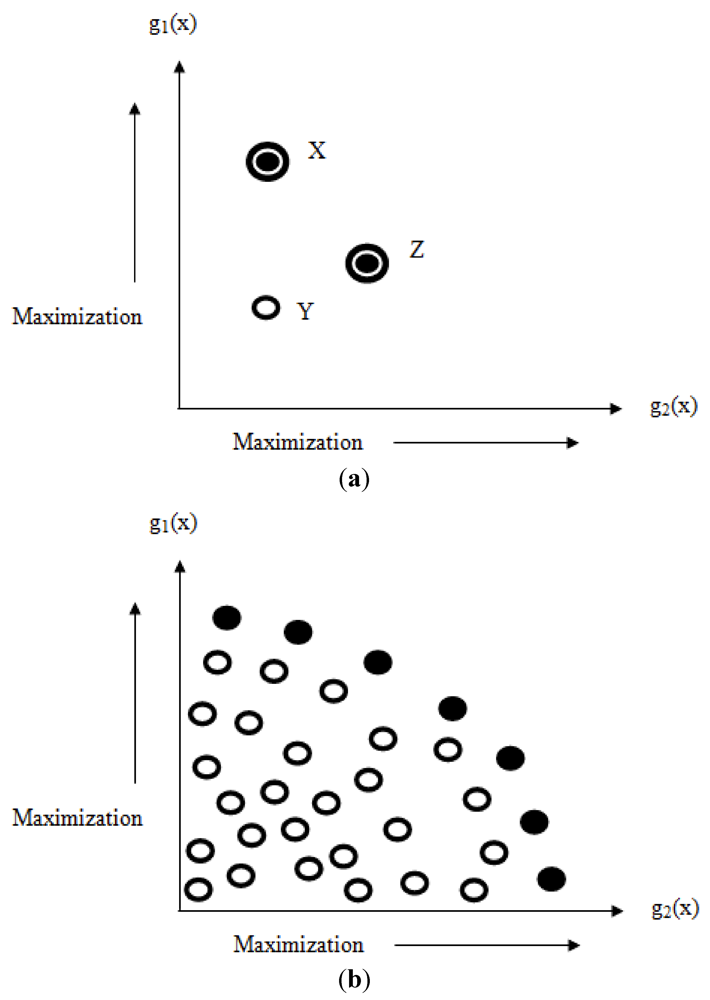
 3. Handling Interpretability-Accuracy Trade-Off using MOEAs in Fuzzy Systems

In the early 1990s, the work in the area of EMOFS was oriented towards the development of accurate fuzzy systems, with less concentration on interpretability. However, in the late 1990s, the interpretability became an important issue along with accuracy. Table 1 summarizes most of the work on the issues discussed above in the decade after 1990.

information-03-00256-t001_Table 1

Interpretability and Accuracy Related Work in the 1990s.

Approaches developed Focus References
Maximization of the number of correctly classified patterns along with minimization of the number of rules and fuzzy rule selection represented as a combinatorial optimization problem Accuracy improvement & complexity minimization [36]
Association of rule weights in rules also called certainty factor Accuracy improvement [37,38]
Multiple consequents in a rule Accuracy improvement [39]
Use of fine fuzzy partition (over-fitting), multiple fuzzy grid approach Accuracy Improvement [40]
Applying independent membership functions Accuracy & Scalability improvement [41]
Use of multi-dimensional fuzzy membership function Accuracy and scalability improvement [42,43]
Use of tree-type fuzzy partitions Accuracy & Scalability Improvement [44,45]
Scalability and hierarchical fuzzy systems Accuracy & Scalability Improvement [46]
Use of don’t care conditions/ scalability improvement/input selection for each rule (rule wise input selection) Complexity minimization [47]
3.1. MOEAs with Two Objectives

Many non-dominated fuzzy systems can be obtained along the trade-off surface (Figure 2) by a single run of a MOEA, in which the user can select one, depending on the situation and requirements.

The most commonly used MOEAs are NSGA-II [48], Strength Pareto Evolutionary Algorithm (SPEA) [49], Strength Pareto Evolutionary Algorithm 2 (SPEA2) [50] and Pareto Archived Evolutionary Strategy (PAES) [51].

Pareto front non-dominated fuzzy systems.

During the search for non-dominated fuzzy systems in an EMO environment, accuracy and complexity are the two important factors to be considered with the objectives of accuracy maximization and interpretability maximization (complexity minimization). Initially, an aggregation approach is used for this purpose.

After that the MOEAs are well adapted for this issue and it is represented as,

To obtain these objectives, several criteria, like number of selected fuzzy rules, number of correctly classified rules, tuning of membership, granularity of the uniform partition, etc., are considered.

A two objective approach, considering maximization of the number of correctly classified training patterns and minimization of the number of selected fuzzy rules, is proposed in [52]. In this, a hybrid algorithm is also proposed by the integration of a learning method of classification rules and a multi-objective genetic algorithm.

A multi-objective genetic procedure has been proposed in [53] with the objectives of feature selection and granularity learning. The approach is used in a fuzzy rule-based classification system to automatically learn the knowledge base.

Interpretability-accuracy trade-off analysis was done in [54] with the objectives of classification accuracy and number of rules. The approach is discussed for a classification problem. Initially, this approach introduces the extraction of rules from numerical data using a heuristic rule criterion approach.

In [55], a multi-objective genetic algorithm (MOGA) is used to obtain Fuzzy Rule Based Systems with a better trade-off between interpretability and accuracy in linguistic fuzzy modeling. A new post-processing approach is developed to get the desired goal which is based on the selection of rules along with the tuning of membership functions. The developed approach uses MOEA, SPEAII.

A Pareto based multi-objective evolutionary approach has been proposed in [56] to generate a set of Mamdani fuzzy systems from numerical data. A variant of (2 + 2) Pareto Archived Evolutionary Strategy has been used for this approach. The objectives concerned are root mean squared error for accuracy and sum of conditions which compose the antecedents of rules for complexity. Finally, the goal is to find the right trade-off between accuracy and complexity.

A rule selection and a tuning of the membership functions of an initial set of candidate linguistic fuzzy rules were performed in [57] by minimizing the number of rules and the system error in a multi-objective environment. This leads to improvement in the complex trade-off between accuracy and interpretability.

A new post processing method is developed in [58] for maintaining a good interpretability-accuracy trade-off in linguistic fuzzy systems, which performs rule selection and membership function tuning by focusing on the Pareto zone having most accurate solutions but the least number of possible rules. SPEA2 algorithm has been utilized for this approach.

A multi-objective genetic algorithm is proposed in [59] to generate Mamdani Fuzzy Rule Based Systems with trade-off between complexity and accuracy. In this approach, both rule base and granularity of the uniform partitions defined on the input and output variables are learned concurrently.

A brief review on the state of the art on the use of multi-objective genetic algorithms to obtain the compact fuzzy rule-based systems under rule selection and parameter tuning has been done in [60]. A linguistic model with improved accuracy and smallest number of possible rules are proposed.

A set of linguistic fuzzy rule-based systems with different trade-offs between accuracy and interpretability has been generated in [61] using multi-objective evolutionary approach. Accuracy is measured by approximation error and interpretability is quantified by rule base complexity. It learns rule base and parameters of the membership functions of associated linguistic labels concurrently. A modeling linguistic 2-tuple representation has been used and it uses (2 + 2) Pareto Achieved Evolutionary Strategies (PAES), Non-Dominated Sorting Genetic Algorithms (NSGA-II) and evolutionary driven single objective Evolutionary Algorithm (EA).

A multi-objective evolutionary algorithm for tuning fuzzy rule-based systems has been proposed in [62], considering the two objectives, accuracy and interpretability. An interpretability index is proposed based on the three metrics, membership displacements, membership function symmetry, and membership function area similarity.

A Mamdani fuzzy rule-based system with different good trade-offs between complexity and accuracy has been developed by using multi-objective evolutionary algorithm in [63]. In this approach, both rule base and granularity of uniform partitions defined on the input and output variables are learned concurrently.

Six different MOEA are used to obtain simpler and still accurate linguistic fuzzy models by performing rule selection and tuning of membership functions in [64,65]. These algorithms are NSGA-II [48], SPEA2 [49], SPEA2ACC [66], SPEA2ACC2, NSGA-IIA, NSGA-IIU. These algorithms use two objectives, systems error and number of rules. A new post processing approach has been developed in [66] which considers the selection of rules together with the tuning of membership functions to get the right trade-off between accuracy and interpretability.

A deep-tuned fuzzy rule-based classifier system (FRBCS) from examples has been designed in [67]. The approach is based on rule learning and membership function tuning. The algorithm used in this approach is SPEA2, generating interpretable and accurate systems.

A method for generating single granularity based fuzzy classification rules and lateral tuning of membership functions has been proposed in [68] in a multi-objective genetic fuzzy environment. The NSGA-II algorithm is used in the practical implementation of this method.

A multi-objective evolutionary framework applied to regression problem has been proposed in [69]. In this framework, a two-level rule selection (2LRS) and learning of membership function parameters are introduced. Also, different trade-offs between accuracy and Rule Base (RB) complexity were obtained for a Mamdani Fuzzy Rule Based Systems.

A post processing approach is developed to reduce complexity of data-driven linguistic fuzzy models in [70]. The purpose is to get sufficient accuracy and better fuzzy linguistic performance with respect to their initial values. The basis of this approach lies on rule selection by formulating the bi-objective problem with objective accuracy and interpretability. Data sets from the KEEL project repository are used for evaluating this approach.

In [71], a multi-objective evolutionary algorithm is proposed to deal with two conflicting issues, complexity of the problem and the approximation error. The proposal focuses on the function of approximation problems.

The Pareto optimum set of fuzzy systems with different I-A trade-off has been generated in [72] using a multi-objective evolutionary approach. The two objectives taken in this approach are fuzzy rule parameter optimization and identification of system structure in terms of number of membership functions and fuzzy rules. The modification of NSGA-II algorithm is presented for modeling of a fuzzy system for function approximation from a set of training data.

The MOEA for searching the Pareto optimal fuzzy rules are discussed in [73] to get the Pareto optimal fuzzy system.

An approach for an evolutionary training set selection in the framework of multi-objective evolutionary learning of Mamdani fuzzy rule-based systems (MFRBS) has been proposed in [74,75]. A modified version of PAES (2 + 2) M-PAES is used in this approach. The objectives are system accuracy and rule base complexity. The rule base and parameters of membership functions are concurrently learned, and selected reduced training sets are used to compute the fitness of each individual, which leads to saving considerable execution time.

A MOEA has been proposed in [76] for improving the complexity in accuracy–complexity trade-off using adaptive defuzzification.

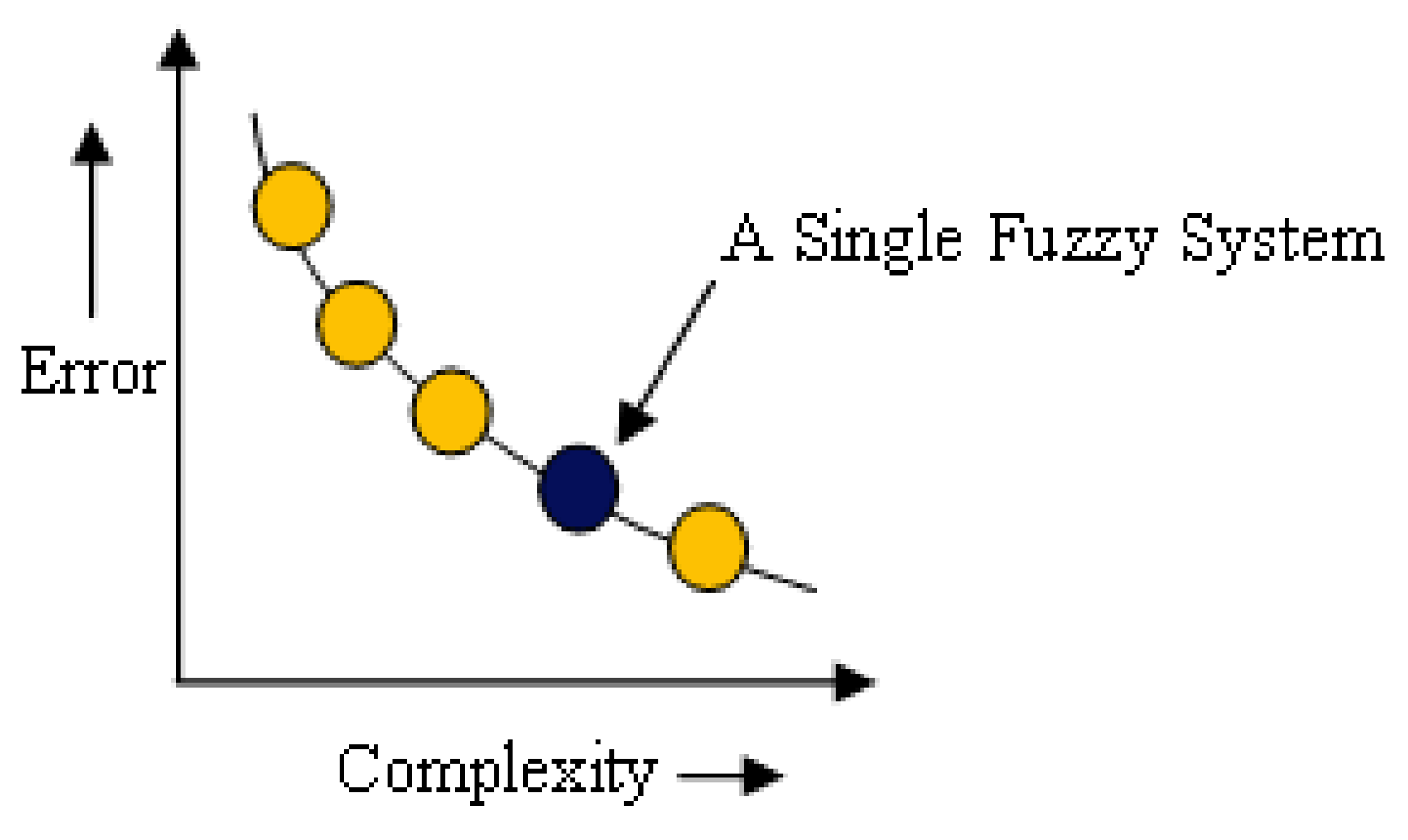
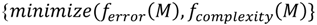
3.2. MOEA with Three Objectives

Several approaches have used three objectives to deal with the interpretability and accuracy trade-off issue in developing fuzzy systems.

A three-objective approach is proposed in [77] for the extraction of interpretable fuzzy rules from numerical data. The objectives are maximization of the number of correctly classified training patterns, minimization of the number of selected fuzzy rules and minimization of the total number of antecedent conditions (total rule length). The approach is developed for high-dimensional pattern classification problems. Also, a hybrid fuzzy GBML algorithm has been proposed for getting non-dominated rule sets from proposed three objective optimization problems.

In [78], the fuzzy modeling is presented as a multi-objective problem, taking consideration of the goals, accuracy, interpretability and autonomy. It is assumed to handle all these issues via a single objective ε-constrained decision-making problem the solution of which is provided by a hierarchical evolutionary process. The resulting fuzzy models are discussed as a classification problem.

A rule selection criterion for prescreening a candidate as fuzzy has been proposed in [79]. This task is completed in two steps. In the first step, candidate rules are generated by two rule evaluation measures, which are confidence and support, and in a second step multi-objective evolutionary algorithms are used for rule selection. The objectives of multi-objective optimization are classification error for measuring accuracy, the number of rules and conditions within a fuzzy classification rule system to measure its comprehensibility or complexity, respectively.

A multi-objective evolutionary algorithm (MOEA) is proposed in [80] to generate a Mamdani fuzzy rule-based system with a different accuracy-complexity trade-off. It is done by concurrently learning the granularities of input and output partitions, membership function parameters and rules. The concept of virtual and concrete partition is introduced as well. The proposed MOEA is tested over three real world regression problems.

The NSGA-II algorithm has been used to create multiple Pareto optimal fuzzy systems in [81]. The three objectives used are the precision performance, number of fuzzy rules and number of fuzzy sets. A modified fuzzy clustering algorithm is used to identify the antecedents of the fuzzy rule, while the consequents are designed separately to reduce the computational burden.

An approach for improving the interpretability of linguistic fuzzy rule-based systems has been proposed in [82]. In this approach, adaptive defuzzification improves the system accuracy. The proposed approach is based on the three objectives, (i) reduction in the number of total rules which considers that rules with weights close to zero should be removed; (ii) reduction in rules which have rule weights one and do not need any weight; and (iii) reduction of rules which are triggered jointly. Also, MOEA is utilized to get a set of solutions with a trade-off between accuracy and complexity.

A three-objective evolutionary algorithm has been proposed in [83,84] to generate a set of Mamdani FRBS with different trade-offs among accuracy, complexity and partition integrity. Accuracy is measured in terms of mean squared error, complexity is estimated by the number of conditions in the antecedents of the rules and integrity is defined by a proposed index. In this approach, Rule Base and MF parameters are learned concurrently.

A multi-objective genetic fuzzy system has been proposed in [85] to learn the granularities of the fuzzy partitions, tune the membership functions and learn the fuzzy rules. The fuzzy model is initialized by an integrated approach of the Wang-Mendal (WM) method and decision-tree algorithms. Also, dynamic constraints are proposed to improve the accuracy by 3-parameter MF tuning.

HILK (Highly Interpretable Linguistic Knowledge) in [86] is a fuzzy modeling approach dedicated to design the interpretable FRBS. It is integrated with a three-objective evolutionary algorithm (HILKMO) for performing genetic feature selection and fuzzy partition learning.

An index is proposed to preserve the semantic interpretability of linguistic fuzzy models in [87,88]. Also, a post processing multi-objective evolutionary algorithm is proposed which performs rule selection and tuning of fuzzy rule-based systems with three objectives: accuracy maximization, semantic interpretability maximization and complexity minimization.

Three types of interpretability measures are introduced in [89], which include semantic quality measures, rule base quality measures and model dimension measures. Also, a new alteration measure is proposed for fuzzy partition tuning.

A Pareto Multi-Objective Cooperative Co-Evolutionary Algorithm (PMOCCA) is proposed in [90] for constructing interpretable and precise fuzzy systems. PMOCCA is used to optimize the number of rules, antecedents of the rules and parameters of antecedents simultaneously. The initial fuzzy system is initialized by the fuzzy clustering algorithm.

A multi-objective fuzzy genetics-based machine-learning (GBML) algorithm is developed for fuzzy rule-based classifiers for examining the Interpretability-Accuracy Trade-Off in [91]. This approach is the amalgam of the Michigan and Pittsburgh approach. The accuracy is measured by correctly classified training patterns and the complexity is measured by the number of fuzzy rules and/or total number of antecedent conditions of fuzzy rules.

 3.3. Improving the Search Ability of the MOEAs

The capability of MOEA to find a variety of FRBS with different trade-offs between complexity and interpretability is called search ability. The improvement in the search ability of any MOEA is a critical research issue.

In [92] the search ability of NSGA-II algorithm was improved by solving the issues of removal of overlapping solutions, recombination of similar patterns and selection of extreme and similar patterns.

An improvement in the search ability has been proposed in [93] by using multiple weighted sums with different weight vectors instead of original objectives in a fuzzy classifier. The idea is implemented on the classification problem.

In MOGFS approaches, a set of non-dominated solutions has been generated, which makes it very difficult to choose one. A double cross-validation approach is used to do this task in [94] for a fuzzy classifier.

The comparison between GBML and Genetic Rule Selection has been done in [95] in terms of their search ability to efficiently find compact fuzzy rule-based classification systems with high accuracy.

The search ability of MOEA in Pareto-optimal or near Pareto optimal fuzzy rule-based systems for classification problems has been discussed in [96,97]. NSGA-II (Non-dominated Sorting Genetic Algorithm) and MOEA/D (Multi-Objective Evolutionary Algorithm based on Decomposition) [98] are used in MoFGBML (Muti-objective Fuzzy Genetics Based Machine Learning) algorithm under various settings of computational load, finer fuzzy partitions and granularity of fuzzy partition.

 3.4. MOEA to Design Ensemble Classifiers

The design of reliable classifiers by integrating multiple classifiers into a single one resulted in the development of ensemble classifiers. The generation of ensemble classifiers with high diversity using MOEA is an important research issue.

In [99], a MOEA is examined to develop an ensemble classifier by different non-dominated fuzzy rule-based classifiers with different accuracy-complexity trade-off. Accuracy is measured by the number of correctly classified training patterns while its complexity is measured by the number of fuzzy rules and the total number of antecedents’ conditions.

Three objective-based multi-objective formulations of fuzzy rule selection have been discussed in [100] for a fuzzy rule-based ensemble classifier design. The multi-objective interpretation of the fuzzy rule selection is discussed with two objectives, accuracy maximization and complexity minimization. A number of non-dominated rule sets for fuzzy classifiers are produced along with an interpretability-accuracy trade-off curve.

3.5. MOEA for Scaling Functions and Fine Fuzzy Partition

Optimization of scalarizing functions and fine fuzzy partitions in EMOFRBS is a crucial research issue.

An approach to optimize scalarizing functions using EMO has been developed in [101]. The effectiveness of the approach is achieved by the computational experiments using NSGA-II.

The fine fuzzy partitions are used in the evolutionary multi-objective optimization for designing the fuzzy rule-based classifiers in [102]. It is concluded that the application of fine fuzzy partition enhances the number of obtained non-dominated fuzzy rule-based classifiers. The relationship between granularity of fuzzy partitions and number of antecedent conditions are examined.

3.6. Approaches Related to User Preferences

User preferences [103] can be integrated in the MOEA for searching the Pareto optimal fuzzy systems.

An iterative fuzzy modeling has been performed in [104] by MOEA with user’s preferences. User preferences are represented by several satisfaction level functions, which can be interactively modified by users. In [105,106], the user preference is integrated with a multi-objective genetic fuzzy rule selection. A preference function is proposed based on the satisfactory function of six objectives: average confidence, average coverage, number of used attributes, maximum number of used granularity, classification accuracy and number of rules.

3.7. Approaches Related to High Dimensional Problems

High dimensionality in fuzzy systems can be handled by using Evolutionary Multi-Objective Optimization (EMO), and it is an important research issue. High dimensional and large data sets lead to expansion in search space and affect the performance of evolutionary algorithms in the form of solution quality and convergence.

A MOEA is proposed for knowledge extraction from numerical data for high dimensional pattern classification problems with many continuous attributes in [107]. The three objective rule selection problem is discussed. The objectives are the number of correctly classified training patterns by the rule set, the number of rules and the total length of rules. Many rule sets with different accuracy-complexity trade-off have been generated.

In [108], an approach is proposed to deal with high-dimensional and large data sets in a multi-objective evolutionary framework for Mamdani Fuzzy Rule Based Systems (MFRBS). The proposed algorithm is based on a co-evolutionary approach that allows concurrent evolutionary training set selection (TSS) and multi-objective evolutionary learning of the RB and membership function parameters. The approach is tested on the high dimensional and large regression data sets.

A MOEA has been proposed in [109] for the learning of linguistic Knowledge Base (KB) in high dimensional regression problems. This approach is based on embedded genetic database learning involving variables, granularities and slight fuzzy partition displacement.

 3.8. Semantic Co-intension Approach

Explicit semantics (fuzzy sets, operators, inference engine) and implicit semantics (knowledge gathered by user) are compared using a co-intension approach called Semantic Co-intension. A novel index has been proposed in [110] for designing highly interpretable rule-based classifiers, based on Semantic Co-intension.

 3.9. Context Adaptation

Context adaptation is the approach to develop context-free models for creating context adapted FRBS so as to increase the accuracy. In [111], a novel index based on fuzzy ordering relations has been proposed for the quantification of interpretability. This proposed index and mean square error are used as the goal of the MOEA.

3.10. EMO Approaches for Data Mining Applications

The EMO has been used in developing data mining approaches addressing different issues, like sub-group discovery, rule mining etc.

A three-objective based multi-objective genetic rule selection has been introduced in [112] for pattern classification problems and it finds Pareto optimal rules and Pareto optimal rule sets in a data mining application. Similar work has been done in [113,114] introducing the concept of rule discovery and selection in an EMO based environment.

In [115], a non-dominated MOEA is proposed for extracting fuzzy rules in subgroup discovery (NMEEF-SD). The approach is based on the NSGA-II. In [116], a post processing approach for improving the results of algorithm NMEEF-SD in a sub group discovery is proposed. It allows the partitions to be adapted in the context of variables.

3.11. Other Specific Applications Developed Using EMO

Using EMO in fuzzy systems, several applications have been developed.

A genetic fuzzy framework has been proposed for financial prediction in [117] in multi-objective evolutionary algorithms. In this contribution, the relationship between predictive capability and interpretability of FRBS obtained by MOEA is studied.

A fine tuned fuzzy logic controller for heating, ventilating and air conditioning systems has been developed using multi-objective evolutionary algorithms in [118]. The two objectives considered are maximizing system performance and minimizing number of rules obtained. The proposed algorithm is based on SPEA2 algorithm.

The accuracy-complexity relationship has been analyzed in [119] for fish habitat modeling using a Genetic Takagi-Sugeno Fuzzy Model called Fuzzy Habitat Preference Model (FHPM).

 4. Burning Research Issues

Several research issues have been identified in EMOFS while considering the issue of Interpretability-Accuracy Trade-Off. Some of these are listed below:

Formulation and quantification of interpretability along with the identification of its global definition [2,20,120,121,122,123] in EMO framework is an important research issue because interpretability is the subjective feature of any system, which is not easy to quantify.

Improvement in the interpretability of a system by selecting parameters like number of inputs, number of rules, rule length, fuzzy partition granularity, membership function separability, linguistic modifiers, linguistic hedges etc. Choosing these parameters may be considered in order to develop new interpretability indexes.

Handling Interpretability-Accuracy (I-A) Trade–Off using EMO [5,72,124] is a critical issue because interpretability and accuracy are the features conflicting with each other. One can be improved at the cost of the other, which leads to generation of multiple sets of solutions instead of any single solution.

An increment in the number of objectives degrades the performance of any EMO algorithm. Hence, improvement of the performance of MOEA when the numbers of objectives are high is a big research line. It helps to deal with the High Dimensional Problems [125], leading to the development of Hierarchical Fuzzy Systems.

Integration of user preferences [103,104,105,106,126] that facilitate to focus on a specific zone of Pareto Front to get the desired solution moreefficiently.

Handling large and multi-dimensional data sets [127] by EMO algorithms.

Improvement in the search ability [92,93,94,95,96,97,98] of the MOEA and dealing with exponentially increased solutions approximating the Pareto Front.

Generation of mechanisms for interpretable explanations for fuzzy reasoning and inference mechanism, quantification of explanation ability of FRBS [128].

 5. Conclusion and Future Scope

The EMO algorithms applied in developing Fuzzy Systems need improvement in order to deal with problems like high dimensionality, exponentially populated solutions, Interpretability-Accuracy Trade-Off, quantification of interpretability and explanation ability of the fuzzy systems, etc. This paper introduces and reviews such problems and their recent solutions in the capacity of different EMO algorithms, listed in Table 2.

information-03-00256-t002_Table 2

Evolutionary Multi-Objective Optimization (EMO) Algorithms used in Multi-objective Fuzzy Systems.

S. No. EMO Used References
1 SPEA2 [55,57,58,60,62,65,85,88,109,117,118]
2 NSGA-II [55,56,57,60,61,65,68,72,76,81,85,89,92,93,96,101,105,106,107,110,111,112,115,117]
3 SPEA2ACC [64,65,66]
4 (2 + 2) PAES [56,61,63]
5 (2 + 2) M-PAES [59,69,74,75,82,83,84,108]
6 HILK EMO [86,110]
7 Fuzzy GBML [94,95,97,102]
8 PMOCCA [90]

Many types of problems are also considered for fuzzy systems with their multi-objective development, listed in Table 3.

information-03-00256-t003_Table 3

Types of problems identified and discussed in the literature.

S. No. Type of the problem identified References
1 Classification of Problems [52,53,54,67,68,77,78,79,90,91,92,93,94,95,96,97,99,100,101,102,104,105,106,107,110,112,113,114,115,116,117]
2 Regression [69,85,87,88,109]
3 Linguistic FRBS [55,56,57,58,59,60,61,62,63,64,65,74,75,76,80,82,83,86,89,108,111,118]
4 Function Approximation Problems [71,72]
5 TS Type FRBS [119]

In the future, the authors are interested to develop efficient and robust MOEA, applicable for the development of accurate and interpretable fuzzy systems. Focus would also be dedicated to invent new indexes for measuring the interpretability of EMOFS and new EMO approaches for managing Interpretability-Accuracy Trade-off.

References Cassilas J. Cordon O. Herrera F. Interpretability Improvements in Linguistic Fuzzy Modeling Springer Heidelberg, Germany 2003 Gacto M.J. Alcala R. Herrera F. Interpretability of linguistic fuzzy rule based systems: An overview of interpretability measures Inf. Sci. 2011 181 4340 4360 10.1016/j.ins.2011.02.021 Alonso J.M. Magdalena L. An experimental study on the interpretability of fuzzy systems Proceedings of International Fuzzy Systems Association World Congress and 2009 European Society of Fuzzy Logic and Technology Conference (IFSA-EUSFLAT) Lisbon, Portugal 20–24 July 2009 125 130 Cassilas J. Cordon O. Herrera F. Magdalena L. Accuracy Improvements in Linguistic Fuzzy Modeling Springer New York, NY, USA 2003 Shukla P.K. Tripathi S.P. A Survey on Interpretability-Accuracy (I-A) Trade-Off in Evolutionary Fuzzy Systems Proceedings of 2011 5th International Conference on Genetic and Evolutionary Computing Kinmen, Taiwan/Xiamen, China 29 August–1 September 2011 97 101 Goldberg D.E. Genetic Algorithms in Search Optimization and Machine Learning Addison-Wesley Boston, MA, USA 1989 Davis L. Handbook of Genetic Algorithms Van Nostrand Reinhold New York, NY, USA 1991 Cordon O. Herrera F. Hoffmann F. Magdalena L. Genetic Fuzzy System: Evolutionary Tuning and Learning of the Fuzzy Knowledge Bases Advances in Fuzzy Systems—Applications and Theory, World Scientific London, UK 2001 19 Cordon O. Gomide F. Herrera F. Hoffmann F. Magdalena L. Ten years of genetic fuzzy systems: Current framework and new trends Fuzzy Sets Syst. 2004 41 5 31 Herrera F. Genetic Fuzzy Systems: Taxonomy, current research trends and prospects Evol. Intell. 2008 1 27 46 10.1007/s12065-007-0001-5 Herrera F. Genetic Fuzzy Systems: Status, critical considerations and future directions Int. J. Comput. Intell. Res. 2005 1 59 67 Roubos H. Setnes M. Compact and transparent fuzzy models and classifiers through iterative complexity reduction IEEE Trans. Fuzzy Syst. 2001 9 516 524 10.1109/91.940965 Chang X. Lilly J.H. Evolutionary design of fuzzy classifier from data IEEE Trans. Syst. Man Cybern. Part B Cybern. 2004 34 1894 1906 10.1109/TSMCB.2004.831160 Ishibuchi H. Tsukamoto N. Nojima Y. Evolutionary Many Objective Optimization: A Short Review Proceedings of IEEE World Congress on Evolutionary Computation (CEC 2008) Hong Kong, China 1–6 June 2008 2424 2431 Ishibuchi H. Multi-Objective Genetic Fuzzy Systems: Review and Future Research Directions Proceedings of 2007 FUZZ-IEEE London, UK 23–26 July 2007 913 918 Ishibuchi H. Tsukamoto N. Nojima Y. Evolutionary Many Objective Optimization Proceedings of 3rd International Workshop on Genetic and Evolutionary Fuzzy Systems 2008 Witten-Bommerholz, Germany 2008 47 52 Ishibuchi H. Yamamoto T. Fuzzy Rule selection by multi-objective genetic local search algorithms and rule evaluation measures in data mining Fuzzy Sets Syst. 2004 141 59 88 10.1016/S0165-0114(03)00114-3 Ducange P. Marcelloni F. Multi-Objective Evolutionary Fuzzy Systems Springer-Verlag Berlin/Heidelberg, Germany 2011 83 90 Cococcioni M. The evolutionary multi objective optimization of fuzzy rule based systems bibliography page (accessed on 4 March 2012) Available online:http://www2.ing.unipi.it/~r000439/emofrbss.html Cannone R. Alonso J.M. Magdalena L. An Empirical Study on Interpretability Indexes through Multi-Objective Evolutionary Algorithms Springer-Verlag Berlin/Heidelberg, Germany 2011 131 138 Ishibuchi H. Evolutionary Multi-Objective Design of Fuzzy Rule-Based Systems Proceedings of 2007 IEEE Symposium on Foundations of Computational Intelligence (FOCI 2007) Honolulu, HI, USA 1–5 April 2007 9 16 Ishibuchi H. Nojima Y. Kuwajima I. Evolutionary multi-objective design of fuzzy rule based classifiers Stud. Comput. Intell. 2008 115 641 685 10.1007/978-3-540-78293-3_15 Fazzolari M. Alcala R. Nojima Y. Ishibuchi H. Herrera F. A review of the application of Multi-Objective Evolutionary Fuzzy systems: Current status and further directions IEEE Trans. Fuzzy Syst. 2012 10.1109/TFUZZ.2012.2201338 Deb K. Multi-Objective Optimization Using Evolutionary Algorithms John Wiley & Sons Chichester, UK 2001 Coello Coello C.A. van Veldhuizen D.A. Lamont G.B. Evolutionary Algorithms for Solving Multi-Objective Problems Kluwer Academic Publishers Boston, MA, USA 2002 Coello Coello C.A. Lamont G.B. Applications of Multi-Objective Evolutionary Algorithms World Scientific Hackensack, NJ, USA 2004 Jin Y. Multi-Objective Machine Learning Springer-Verlag Berlin, Germany 2006 Tan K.C. Khor E.F. Lee T.H. Multi-Objective Evolutionary Algorithms and Applications Springer-Verlag Berlin, Germany 2005 Abraham A. Jain L.C. Goldberg R. Evolutionary Multi-objective Optimization: Theoretical Advances and Applications Springer Berlin, Germany 2005 Konak A. Coit D.W. Smith A.E. Multi-objective optimization using genetic algorithms: A tutorial Reliab. Eng. Syst. Saf. 2006 91 992 1007 10.1016/j.ress.2005.11.018 Zhou A. Ou B.-Y. Li H. Zhao S.Z. Suganthan P.N. Multi-objective evolutionary algorithms: A survey of the state of the art Swarm Evol. Comput. 2011 1 32 49 10.1016/j.swevo.2011.03.001 Adra S.F. Fleming P.J. Diversity management in Evolutionary computation IEEE Trans. Evol. Comput. 2011 15 183 195 10.1109/TEVC.2010.2058117 Zou X. Chen Y. Liu M. Kang L. A new evolutionary algorithm for solving many objective optimization problems IEEE Trans. Syst. Man Cybern. B Cybern. 2008 38 1402 1412 10.1109/TSMCB.2008.926329 Purshouse R.C. Fleming P.J. On the Evolutionary optimization of many conflicting objectives IEEE Trans. Evol. Comput. 2007 22 770 784 10.1109/TEVC.2007.910138 Jimenez F. Cadenas J.M. Sanchz G. Gomez-Skarmeta A.F. Verdegay J.L. Multi-objective evolutionary computation and fuzzy optimization Int. J. Approx. Reason. 2006 43 59 75 10.1016/j.ijar.2006.02.001 Ishibuchi H. Nozaki K. Yamamoto N. Tanaka H. Selecting fuzzy if then rules for classification problems using genetic algorithms IEEE Trans. Fuzzy Syst. 1995 3 260 270 10.1109/91.413232 Nauck D. Kruse R. How the Learning of the Rule Weight Affects the Interpretability of the Fuzzy Systems Proceedings of 1998 IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 1998) Anchorage, AK, USA 1998 2 1235 1240 Ishibuchi H. Nakashima T. Effect of the rule weights in fuzzy rule-based classification systems IEEE Trans. Fuzzy Syst. 2001 9 506 515 10.1109/91.940964 Cordon O. Del Jesus M.J. Herrera F. A proposal on reasoning methods in fuzzy rule-based classification systems Int. J. Approx. Reason. 1999 20 21 45 Ishibuchi H. Nozaki K. Tanaka H. Distributed representation of fuzzy rules and its application to pattern classification Fuzzy Sets Syst. 1992 52 21 32 10.1016/0165-0114(92)90032-Y Abe S. Lan M.S. A method for fuzzy rules extraction directly from numerical data and its application to pattern classification IEEE Trans. Fuzzy Syst. 1995 3 18 28 10.1109/91.366565 Abe S. Thawonmas R. Kobayashi Y. Feature selection by analyzing classification regions approximated by ellipsoids IEEE Trans. SMC C Appl. Rev. 1998 28 282 287 Abe S. Thawonmas R. Kayama M. A fuzzy classifier with ellipsoidal regions for diagnosis problems IEEE Trans. SMC C Appl. Rev. 1999 29 140 149 Yuan Y. Shaw M.J. Induction of Fuzzy decision trees Fuzzy Sets Syst. 1995 69 125 139 10.1016/0165-0114(94)00229-Z Janikow C.Z. Fuzzy decision trees: Issues and methods IEEE Trans. SMC B Cybern. 1998 28 1 14 10.1109/3477.658573 Shimojima K. Fukada T. Hasegawa Y. Self-tuning fuzzy modeling with adaptive membership function, rules and hierarchical structure based on genetic algorithm Fuzzy Sets Syst. 1995 71 295 309 10.1016/0165-0114(94)00280-K Ishibuchi H. Nakashima T. Murata T. Performance evaluation of fuzzy classifier systems for multidimensional pattern classification problems IEEE Trans. SMC B Cybern. 1999 29 601 618 10.1109/3477.790443 Deb K. Pratap A. Agarwal S. Meyarivan T. A fast and elitist multi-objective genetic algorithm: NSGA-II IEEE Trans. Evol. Comput. 2002 6 182 197 10.1109/4235.996017 Zitzler E. Thiele L. Multi-objective evolutionary algorithms: A comparative case study and the strength Pareto approach IEEE Trans. Evol. Comput. 1999 3 257 271 10.1109/4235.797969 Zitzler E. Laumanns M. Thiele L. SPEA2: Improving the Strength Pareto Evolutionary Algorithms TIK-Report 103, Computer Engineering and Networks Laboratory (TIK) Swiss Federal Institute of Technology (ETH) Zurich, Switzerland 2001 Cococcioni M. Ducange P. Lazzerini B. Marcelloni F. A pareto based multiobjective evolutionary approach to the identification of Mamdani fuzzy systems Soft Comput. 2007 11 1013 1031 10.1007/s00500-007-0150-6 Ishibuchi H. Murata T. Turksen I.B. Single objective and two objective genetic algorithms for selecting linguistic rules for pattern classification problems Fuzzy Sets Syst. 1997 89 135 150 10.1016/S0165-0114(96)00098-X Cordon O. Herrera F. Del Jesus M.J. Villar P. A Multi-Objective Genetic Algorithm for Feature Selection and Granularity Learning in Fuzzy Rule Based Classification Systems Proceedings of 9th International Fuzzy Systems Associations (IFSA) World Congress 2001 Vancouver, Canada 25–28 July 2001 1253 1258 Ishibuchi H. Nojima Y. Accuracy-Complexity Trade-off Algorithms by Multi-Objective Rule Selection Proceedings of 2005 Workshop on Computational Intelligence in Data Mining Houston, TX, USA 2005 39 48 Alcala R. Gacto M.J. Herrera F. A Multi-objective genetic algorithm for tuning and Rule selection to obtain accurate and compact linguistic fuzzy rule-based systems Int. J. Uncertain. Fussiness Knowl. Based Syst. 2007 15 539 557 10.1142/S0218488507004868 Cococcioni M. Ducange P. Lazzerini B. Marcelloni F. A Pareto based multi-objective evolutionary approach to the identification of Mamdani fuzzy systems Soft Comput. 2007 11 1013 1031 10.1007/s00500-007-0150-6 Alcala R. A-Fdez J. Gacto M.J. Herrera F. A Multi-Objective Evolutionary Algorithm for Rule-Selection and Tuning on Fuzzy Rule based Systems Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2007) London, UK 23–26 July 2007 1367 1372 Gacto M.J. Alcala R. Herrera F. An Improved Multi-Objective Genetic Algorithm for Tuning Linguistic Fuzzy Systems Proceedings of Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU’08) Málaga, Spain 22–27 June 2008 1121 1128 Anotonelli M. Ducange P. Lazzerini B. Marcelloni F. A Multi-Objective Genetic Approach to Concurrently Learn Partition Granularity and Rule Bases of Mamdani Fuzzy Systems Proceedings of 8th International Conference on Hybrid Intelligent Systems 2008 Barcelona, Spain 10–12 September 2008 278 283 Alcala R. Alcala-Fdez J. Gacto M.J. Herrera F. On the usefulness of MOEAs for getting compact FRBSs under parameter tuning and rule selection Stud. Comput. Intell. 2008 98 91 107 10.1007/978-3-540-77467-9_5 Alcala R. Ducange P. Herrera F. Lazzerini B. Marcelloni F. A Multi-objective evolutionary approach to concurrently learn rule and databases of linguistic fuzzy rule based systems IEEE Trans. Fuzzy Syst. 2009 17 1106 1121 10.1109/TFUZZ.2009.2023113 Gacto M.J. Alcala R. Herrera F. A Multi-Objective Evolutionary Algorithm for Tuning Fuzzy Rule Based Systems with Measures for Preserving Interpretability Proceedings of International Fuzzy Systems Association World Congress and 2009 European Society of Fuzzy Logic and Technology Conference (IFSA-EUSFLAT 2009) Lisbon, Portugal 20–24 July 2009 1146 1151 Antonelli M. Ducange P. Lazzerini B. Marcelloni F. Learning concurrently partition granularities and rule bases of Mamdani fuzzy systems in a multi-objective evolutionary framework Int. J. Approx. Reason. 2009 50 1066 1080 10.1016/j.ijar.2009.04.004 Gacto M.J. Alcala R. Herrera F. Multi-Objective Genetic Fuzzy Systems: On the Necessity of Including Expert Knowledge in the MOEA Design Process Proceedings of Information Processing and Management of Uncertainty in Knowledge-Based Systems (IPMU 2008) Malaga, Spain 22-27 June 2008 1446 1453 Gacto M.J. Alcala R. Herrera F. Adaptation and application of multi-objective evolutionary algorithms for rule reduction and parameter tuning of fuzzy rule based systems Soft Comput. 2009 13 419 436 10.1007/s00500-008-0359-z Alcala R. Gacto M.J. Herrera F. A multi-objective genetic algorithm for tuning and rule selection to obtain accurate and compact linguistic fuzzy rule-based systems Int. J. Uncertain. Fuzziness Knowl. Based Syst. 2007 15 539 557 10.1142/S0218488507004868 Di Nuovo A.G. Catania V. Linguistic Modifiers to Improve the Accuracy-Interpretability Trade-off in Multi-Objective Genetic Design of Fuzzy Rule Based Classifier Systems Proceedings of 2009 9th International Conference on Intelligent Systems Design and Applications Pisa, Italy 30 November–2 December 2009 128 133 Alcala R. Nojima Y. Herrera F. Ishibuchi H. Multi-objective genetic fuzzy rule selection of single granularity-based fuzzy classification rules and its interaction with lateral tuning of membership functions Soft Comput. 2011 15 2303 2318 10.1007/s00500-010-0671-2 Antonelli M. Ducange P. Lazzerini B. Marcelloni F. Multi-objective Evolutionary Generation of Mamdani Fuzzy Rule Based Systems based on Rule and Condition Selection Proceedings of 5th IEEE International Workshop on Genetic and Evolutionary Fuzzy Systems 2011 Paris, France 11–15 April 2011 47 53 Galende-Hernández M. Sainz-Palmero G.I. Fuente-Aparicio M.J. Complexity reduction and interpretability improvement for fuzzy rule systems based on simple interpretability measures and indices by bi-objective evolutionary rule selection Soft Comput. 2012 16 451 470 10.1007/s00500-011-0748-6 Gonzalez J. Rojas I. Pomares H. Rojas F. Palomares J.M. Multi-objective evolution of fuzzy systems Soft Comput. 2006 10 735 748 10.1007/s00500-005-0003-0 Gonzalez J. Rojas I. Pomares H. Herrera L.J. Guillen A. Palomares J.M. Rojas F. Improving the accuracy while preserving the interpretability of fuzzy function approximators by means of Multi-objective evolutionary algorithms Int. J. Approx. Reason. 2007 44 32 44 10.1016/j.ijar.2006.02.006 Ishibuchi H. Evolutionary Multi-objective Optimization for Fuzzy knowledge Extraction Proceedings of 2007 International Symposium on Advanced Intelligent Systems Sokcho, Korea 5–8 September 2007 58 63 Antonelli M. Ducange P. Marcelloni F. Exploiting a Coevolutionary Approach to Concurrently Select Training Instances and Learn Rule Bases of Mamdani Fuzzy Systems Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2010) Barcelona, Spain 18–23 July 2010 1 7 Antonelli M. Ducange P. Marcelloni F. Genetic Training instance selection in multi-objective evolutionary fuzzy systems: A Co-evolutionary approach IEEE Trans. Fuzzy Syst. 2012 20 276 290 10.1109/TFUZZ.2011.2173582 Marquez A.A. Marquez F.A. Peregrin A. A Multi-Objective evolutionary algorithm with an interpretability improvement mechanism for linguistic fuzzy systems with adaptive defuzzification Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2010) Barcelona, Spain 18–23 July 2010 1 7 Ishibuchi H. Nakashima T. Murata T. Three-objectives genetics-based machine learning for linguistic rule extraction Inf. Sci. 2001 136 109 133 10.1016/S0020-0255(01)00144-X Delgado M.R. Zuben F.V. Gomide F. Multi-Objective Decision Making: Towards Improvement of Accuracy, Interpretability and Design Autonomy in Hierarchical Genetic Fuzzy Systems Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2002) Honolulu, HI, USA 12–17 May 2002 1222 1227 Ishibuchi H. Yamamoto T. Fuzzy rule selection by multi-objective genetic local search algorithms and rule evaluation measures in data mining Fuzzy Sets Syst. 2004 141 59 88 10.1016/S0165-0114(03)00114-3 Antonelli M. Ducange P. Lazzrini B. Mareclloni F. Multi-objective evolutionary learning of granularity, membership function parameters and rules of Mamdani fuzzy systems Evol. Intell. 2009 2 21 37 10.1007/s12065-009-0022-3 Xing Z.-Y. Zhang Y. Hou Y.-L. Cai G.-Q. Multi-objective Fuzzy Modeling using NSGA-II Proceedings of 2008 IEEE Conference on Cybernetics and Intelligent Systems Chengdu, China 21–24 September 2008 119 124 Marquez A.A. Marquez F.A. Peregrin A. A mechanism to improve the interpretability of linguistic fuzzy systems with adaptive defuzzification based on the use of a multi-objective evolutionary algorithms Int. J. Comput. Intell. Syst. 2012 5 297 321 Antonelli M. Ducange P. Lazzerini B. Marcelloni F. Learning knowledge bases of multi-objective evolutionary fuzzy systems by simultaneously optimizing accuracy, complexity and partition integrity Soft Comput. 2011 15 2335 2354 10.1007/s00500-010-0665-0 Antonelli M. Ducange P. Lazzerini B. A Three-Objective Evolutionary Approach to Gene Rate Mamdani Fuzzy Rule Based Systems Springer-Verlag Berlin/Heidelberg, Germany 2009 613 620 Pulkkinen P. Koivisto H. A dynamically constrained multiobjective genetic fuzzy systems for regression problems IEEE Trans. Fuzzy Syst. 2010 18 161 167 10.1109/TFUZZ.2009.2038712 Alonso J.M. Magdalena L. Cordon O. Embedding HILK in a Three Objective Evolutionary Algorithm with the Aim of Modeling Highly Interpretable Fuzzy Rule-based Classifiers Proceedings of 4th International Workshop on Genetic and Evolutionary Fuzzy Systems 2010 Asturias, Spain 17–19 March 2010 15 20 Gacto M.J. Alcala R. Herrera F. Analysis of the performance of a semantic interpretability-based tuning and rule selection of fuzzy rule-based systems by means of a multi-objective evolutionary algorithm Proceedings of the 23rd International Conference on Industrial Engineering and Other Applications of Applied Intelligent Systems (IEA/AIE’10) Cordoba, Spain 1–4 June 2010 228 238 Gacto M.J. Alcala R. Herrera F. Integration of Index to preserve the semantic interpretability in the Multi-objective evolutionary rule selection and tuning of linguistic fuzzy systems IEEE Trans. Fuzzy Syst. 2010 18 515 531 10.1109/TFUZZ.2010.2041008 Gonzalez M. Cassilas J. Morell C. Dealing with Three Uncorrelated Criteria by Multi-Objective Genetic Fuzzy Systems Proceedings of 5th International Workshop on Genetic and Evolutionary Fuzzy Systems 2011 Paris, France 11–15 April 2011 39 46 Zhang Y. Wu X.-B. Xing Z.-Y. Hu W.-L. On generating interpretable and precise fuzzy systems based on pareto multi-objective cooperating co-evolutionary algorithm Appl. Soft Comput. 2011 11 1289 1294 Ishibuchi H. Nojima Y. Analysis of interpretability-accuracy trade-off of fuzzy systems by multi-objective fuzzy genetics-based machine learning Int. J. Approx. Reason. 2007 44 4 31 10.1016/j.ijar.2006.01.004 Nakukawa K. Nojima Y. Ishibuchi H. Modification of evolutionary Multi objective optimization Algorithms for Multi-objective Design of Fuzzy Rule-Based Classification Systems Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2005) Reno, NV, USA 22–25 May 2005 809 814 Ishibuchi H. Nakashima Y. Nojima Y. Simple Changes in Problem Formulations make a Difference in Multi-objective Genetic Fuzzy Systems Proceedings of 4th International Workshop on Genetic and Evolutionary Fuzzy Systems 2010 Mieres, Spain 17–19 March 2010 3 8 Ishibuchi H. Nakashima Y. Nojima Y. Double Cross Validation for Performance Evaluation of Multi-objective Genetic Fuzzy Systems Proceedings of 5th International Workshop on Genetic and Evolutionary Fuzzy Systems 2011 Paris, France 11–15 April 2011 31 38 Nojima Y. Ishibuchi H. Kuwajima I. Comparison of Search Ability between Genetic Fuzzy Rule Selection and Fuzzy Genetics based Machine Learning Proceedings of 2006 International Symposium on Evolving Fuzzy Systems Ambelside, UK 7–9 September 2006 125 130 Ishibuchi H. Nakashima Y. Nojima Y. Search Ability of Evolutionary Multi-objective Optimization Algorithms for Multi-objective Fuzzy Genetics based Machine Learning Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2009) Jeju Island, Korea 20–24 August 2009 1724 1729 Ishibuchi H. Nakashima Y. Nojima Y. Performance evaluation of evolutionary Multi-objective optimization algorithms for Multi-objective fuzzy genetics based machine learning Soft Comput. 2011 15 2415 2434 10.1007/s00500-010-0669-9 Zhang Q. Li H. MOEA/D: A Multi-objective evolutionary algorithm based on decomposition IEEE Trans. Evol. Comput. 2007 11 712 731 10.1109/TEVC.2007.892759 Ishibuchi H. Nojima Y. Evolutionary Multi-objective optimization for the design of fuzzy rule based ensemble classifiers Int. J. Hybrid Intell. Syst. 2006 3 129 145 Ishibuchi H. Nojima Y. Fuzzy ensemble design thorough multi-objective fuzzy rule selection Stud. Comput. Intell. 2006 16 507 530 10.1007/3-540-33019-4_22 Ishibuchi H. Nojima Y. Optimization of scalarizing functions through evolutionary Multi-objective optimization Proceedings of the 4th International Conference on Evolutionary Multi-criterion Optimization (EMO’07) Matsishima, Japan 5-8 March 2007 51 65 Ishibuchi H. Nakashima Y. Nojima Y. Effects of Fine Fuzzy Partitions on the Generalization Ability of Evolutionary Multi-objective Fuzzy Rule based Classifiers Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2010) Barcelona, Spain 18–23 July 2010 1 8 Branke J. Deb K. Integrating User Preferences into Evolutionary Multi-objective Optimization Knowledge Incorporation in Evolutionary Computation Jin Y. Springer Berlin, Germany 2004 167 Nojima Y. Ishibuchi H. Interactive Fuzzy Modeling by Evolutionary Multi-objective Optimization with User Preferences Proceedings of International Fuzzy Systems Association World Congress and 2009 European Society of Fuzzy Logic and Technology Conference (IFSA-EUSFLAT 2009) Lisbon, Portugal 20–24 July 2009 1839 1844 Nojima Y. Ishibuchi H. Incorporation of User Preference into Multi-objective Genetic Fuzzy rule Selection for Pattern Classification Problems Proceedings of 14th International Symposium on Artificial Life and Robotics 2009 Ooita, Japan 5–7 February 2009 186 189 Nojima Y. Ishibuchi H. Interactive Genetic Fuzzy rule Selection through Evolutionary Multi-objective Optimization with User Preference Proceedings of 2009 IEEE Symposium on Computational Intelligence in Multicriteria Decision-Making City, Country 30 March–2 April 2009 141 148 Ishibuchi H. Namba S. Evolutionary Multi-Objective Knowledge Extraction for High Dimensional Pattern Classification Problems Springer Heidelberg, Germany 2004 3242 1123 1132 Antonelli M. Ducange P. Marcelloni F. A New Approach to Handle High Dimensional and Large Data Sets in Multi-objective Evolutionary Fuzzy Systems Proceedings of IEEE International Conference on Fuzzy Systems (FUZZ-IEEE 2011) Taipei, Taiwan 29 June 2011 1286 1293 Alcala R. Gacto M.J. Herrera F. A fast and scalable multi-objective genetic fuzzy system for linguistic fuzzy modeling in high dimensional regression problems IEEE Trans. Fuzzy Syst. 2011 19 666 681 10.1109/TFUZZ.2011.2131657 Cannone R. Alonso J.M. Magdalena L. Multi-objective Design of Highly Interpretable Fuzzy Rule Based Classifiers with Semantic Co-Intention Proceedings of 5th International Workshop on Genetic and Evolutionary Fuzzy Systems 2011 Paris, France 11–15 April 2011 1 8 Botta A. Lazzerini B. Marcelloni F. Stefanescu D.C. Context adaptation of fuzzy systems through a multi-objective evolutionary approach based on a novel interpretability index Soft Comput. 2009 13 437 449 10.1007/s00500-008-0360-6 Ishibuchi H. Kuwajima I. Nojima Y. Relation between Pareto-optimal Fuzzy Rules and Pareto Optimal Fuzzy Rule Sets Proceedings of 2007 IEEE Symposium on Computational Intelligence in Multicriteria Decision Making (MCDM) Honolulu, HI, USA 1–5 April 2007 42 49 Ishibuchi H. Kuwajima I. Nojima Y. Evolutionary multi-objective rule selection for classification rule mining Stud. Comput. Intell. 2008 98 47 70 10.1007/978-3-540-77467-9_3 Ishibuchi H. Kuwajima I. Nojima Y. Multi-objective classification rule mining Multi-Objective Problem Solving from Nature World Scientific Ackensack, NJ, USA 2008 219 240 Carmona C.J. Gonzalez P. Del Jesus M.J. Herrera F. NMEEF-SD: Non-dominated multi-objective evolutionary algorithm for extracting fuzzy rules in subgroup discovery IEEE Trans. Fuzzy Syst. 2010 18 958 970 10.1109/TFUZZ.2010.2060200 Carmona C.J. Gonzalaez R. Gacto M.J. del Jesus M.J. Genetic lateral tuning for subgroup discovery with fuzzy rules using the algorithm NMEEF-SD Int. J. Comput. Intell. Syst. 2012 5 2012 Ghandar A. Michalewicz Z. An Experimental Study of Multi-objective Evolutionary Algorithms for Balancing Interpretability and Accuracy in Fuzzy Rule base Classifiers for Financial Prediction Proceedings of IEEE Symposium on Computational Intelligence for Financial Engineering and Economics 2011 Paris, France 11–15 April 2011 1 6 Gacto M.J. Alcala R. Herrera F. A multi-objective evolutionary algorithm for an effective tuning of fuzzy logic controllers in heating, ventilating and air conditioning system Appl. Intell. 2012 36 330 347 10.1007/s10489-010-0264-x Fukuda S. Nakajima J. de Beats B. Wargeman W. Mukai T. Mouton A.M. Onikura N. A Discussion on the Accuracy-Complexity Relationship in Modeling Fish Habitat Preference Using Genetic Takagi-Sugeno Fuzzy Systems Proceedings of 5th International Workshop on Genetic and Evolutionary Fuzzy Systems 2011 Paris, France 11–15 April 2011 81 86 Mencar C. Castiello C. Cannone R. Fanelli A.M. Interpretability assessment of fuzzy knowledge bases: A cointension based approach Int. J. Approx. Reason. 2011 52 501 518 10.1016/j.ijar.2010.11.007 Mencar C. Fanelli A.M. Interpretability constraints for fuzzy information granulation Inf. Sci. 2008 178 4585 4618 10.1016/j.ins.2008.08.015 Mikut R. Jakel J. Groll L. Interpretability issues in data based learning of fuzzy systems Fuzzy Sets Syst. 2005 150 179 197 10.1016/j.fss.2004.06.006 Alonso J.M. Magdalena L. Special issues on interpretable fuzzy systems Inf. Sci. 2011 181 4331 4339 10.1016/j.ins.2011.07.001 Alcala R. Alcala-Fdez J. Cassilas J. Cordon O. Herrera F. Hybrid learning models to get the interpretability—accuracy trade-off in fuzzy modeling Soft Comput. 2006 10 717 734 10.1007/s00500-005-0002-1 Jin Y. Fuzzy modeling of high dimensional systems: Complexity reduction and interpretability improvement IEEE Trans. Fuzzy Syst. 2000 8 212 221 10.1109/91.842154 Deb K. Sundar J. Reference Point Based Multi-objective optimization Using Evolutionary Algorithms Proceedings of Genetic and Evolutionary Computation Conference (GECCO 2006) Seattle, DC, USA 8–12 July 2006 635 642 Cano J.R. Herrera F. Lozano M. Stratification for scaling up evolutionary prototype selection Pattern Recognit. Lett. 2005 26 953 963 10.1016/j.patrec.2004.09.043 Ishibuchi H. Nojima Y. Toward Quantification Definition of Explanation Ability of Fuzzy Rule Based Classifiers Proceedings ofFUZZ-IEEE 2011 Taipei, Taiwan 27–30 June 2011 549 556