A New Prospect Projection Multi-Criteria Decision-Making Method for Interval-Valued Intuitionistic Fuzzy Numbers
Abstract
:1. Introduction
2. Preliminaries
2.1. IVIFS
- (i)
- If , then is smaller than , denoted by ;
- (ii)
- If , then:
- If , then is smaller than , denoted by ;
- If , then and represent the same information, denoted by .
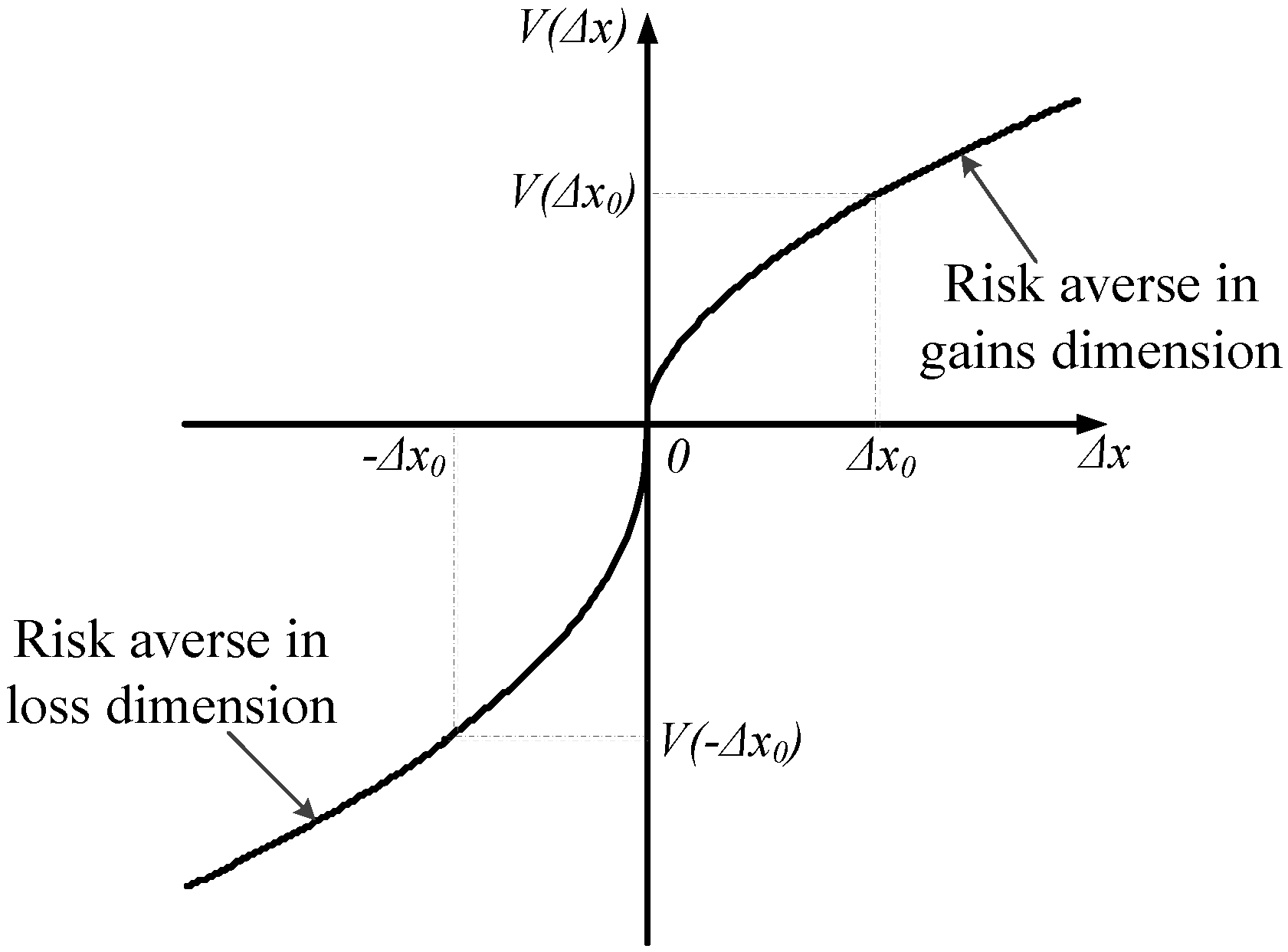
2.2. Prospect Theory
- (i)
- Reference dependence: the DM normally perceives outcomes as gains or losses relative to a reference point [26]. Correspondingly, the value function is divided into two parts by the reference point, i.e., the gain dimension () and the loss dimension ().
- (ii)
- Diminishing sensitivity: the risk attitude of DMs for relative gains (outcomes above the reference point) is risk-averse whereas it tends to be risk-seeking for relative losses (outcomes below the reference point) [49]. Consequently, the value function is concave in the gain dimension and convex in the loss dimension, which is represented by the parameters and .
- (iii)
- Loss aversion: the DM is more sensitive to losses than to absolutely commensurate gains [50]. Accordingly, the value function in the loss dimension is steeper than in the gain dimension, i.e., the loss-aversion coefficient .
3. Prospect Projection Method for Interval-Valued Intuitionistic Fuzzy MCDM
3.1. Constructing the Prospect Decision Matrices
3.2. Determining the Criteria Weights
3.2.1. Determining the Subjective Weights
- A weak ranking: ;
- A strict ranking: ;
- A ranking with multiples: ;
- A ranking of differences: ;
- An interval form: .
3.2.2. Determining the Objective Weights
3.2.3. An Optimization Weighting Model Integrating Subjective and Objective Factors
- (i)
- Model (9) not only captures the subjective considerations of DM and the objective information to maintain fairness but can also overcome the sole consideration of either subjective or objective influence. In addition, the proposed model sufficiently considers the risk attitudes of the DM that are overlooked in previous studies.
- (ii)
- In this optimization model, different can be used to indicate the varied attitudes of the DM. For example, if , then the DM will focus more on the objective weights than the subjective weights; if , then the DM will argue that the subjective and objective factors are equally important; and if , then the DM will focus considerable attention to the subjective preference. During the real decision process, the DM can opt for a suitable according to his/her preference
- (iii)
- The relative importance of the subjective and objective factors can be determined by the DM's knowledge or experience on the problem domain. If there is no significant evidence to show the inequality of two factors, the relative importance can be set to be equal. To maintain fairness, we assume the subjective and objective factors are equally important throughout the rest of this paper.
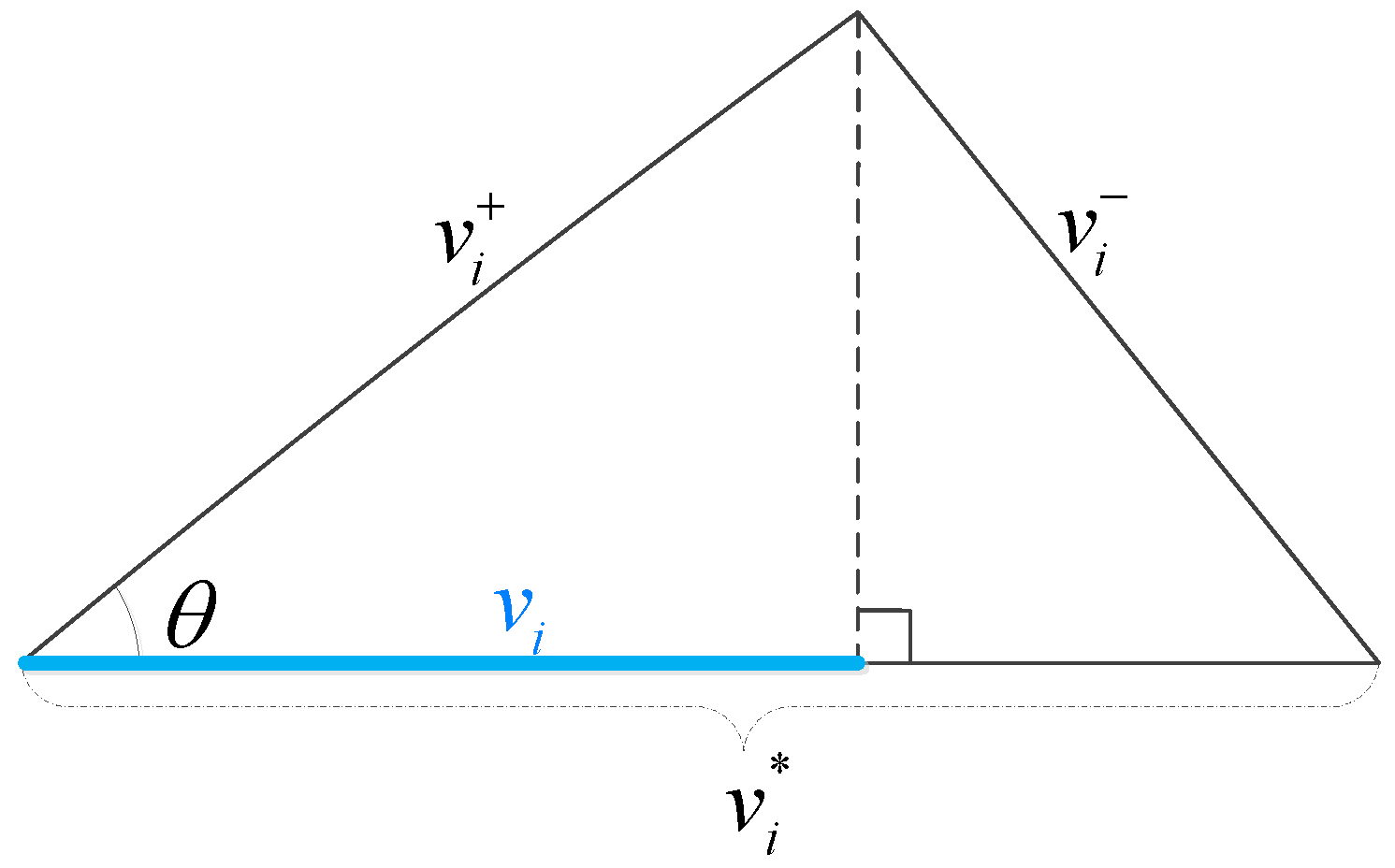
3.3. Assessing the Ranking Order of Alternatives
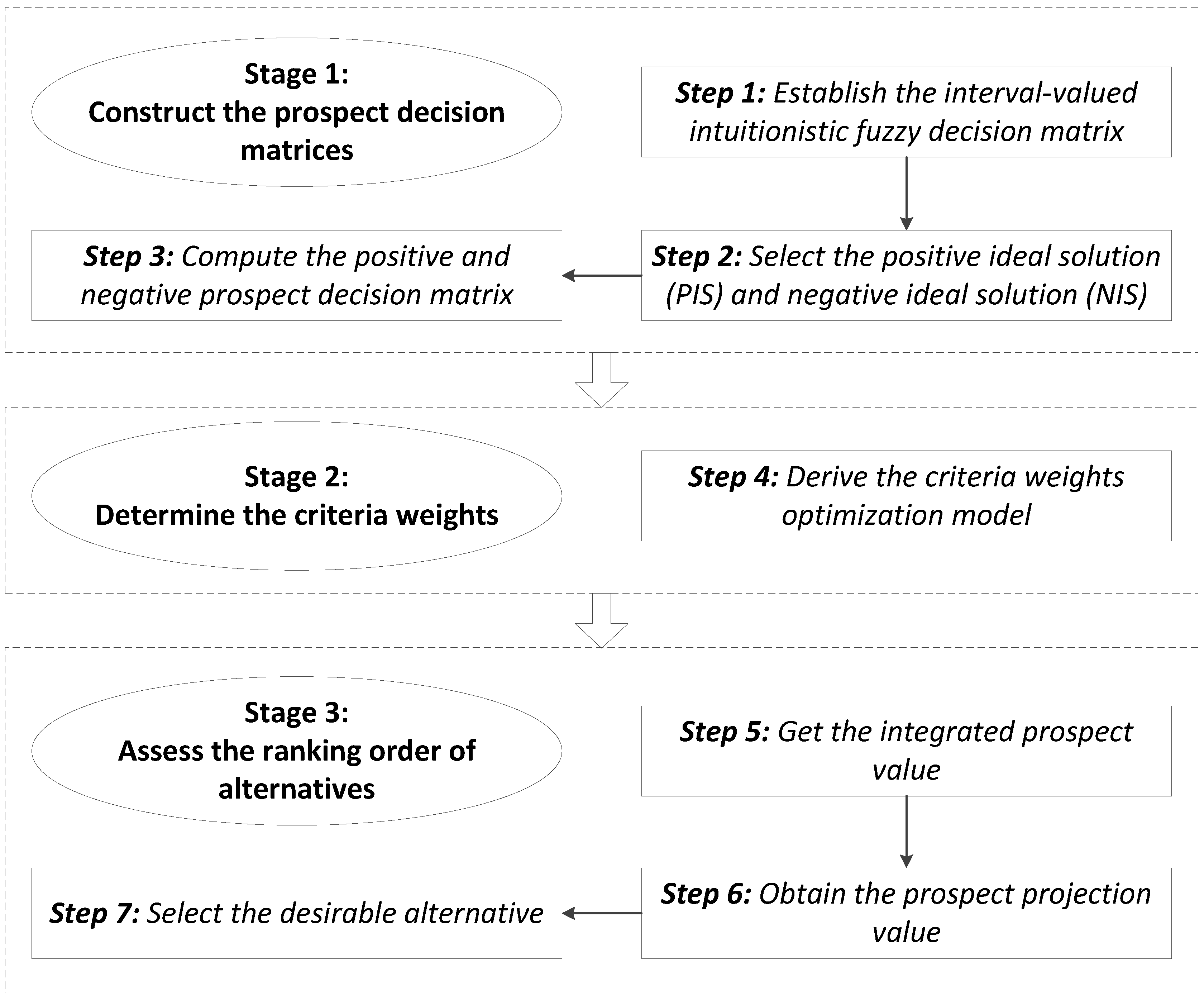
3.4. Procedure of the Proposed Method
- Step 1.
- Obtain the interval-valued intuitionistic fuzzy decision matrix according to the MCDM problem.
- Step 2.
- Select the positive ideal solution and negative ideal solution via Equation (4).
- Step 3.
- Compute the positive prospect matrix using Equation (5) and negative prospect matrix using Equation (6).
- Step 4.
- Calculate the criteria weights according to model (9) when the weight information is incompletely known or model (13) when the weight information is completely unknown.
- Step 5.
- Obtain the integrated prospect value of the ith alternative via Equation (14).
- Step 6.
- Derive the prospect projection value of the ith alternative using Equation (15).
- Step 7.
- Rank the prospect projection values in descending order; consequently, the optimal alternative(s) (e.g., the one(s) with the greatest value) is (are) selected.
4. Illustrative Examples
4.1. Numerical Example and Discussion
4.1.1. Numerical Example
- Step 1.
- Select the PIS and NIS via Equation (4):
- Step 2.
- Compute the positive and negative prospect matrix using Equations (5) and (6):
- Step 3.
- Derive the criteria weights based on model (9):
- Step 4.
- Calculate the prospect projection value of each alternative according to Equation (15):
- Step 5.
- Based on the prospect projection value, the ranking of the alternatives is as follows:
4.1.2. Sensitivity Analysis of the Parameters in the Prospect Value Function
4.2. Application to Evaluate the Hydrogen Production Technologies
- Step 1.
- Select the PIS and NIS via Equation (4):
- Step 2.
- Compute the positive and negative prospect matrix using Equations (5) and (6):
- Step 3.
- Calculate the prospect projection value of each alternative according to Equation (15):
- Step 4.
- Based on the prospect projection value, the ranking of the alternatives is as follows:
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ahn, B.S. Extreme point-based multi-attribute decision analysis with incomplete information. Eur. J. Oper. Res. 2015, 240, 748–755. [Google Scholar] [CrossRef]
- Chen, T.Y. A prioritized aggregation operator-based approach to multiple criteria decision making using interval-valued intuitionistic fuzzy sets: A comparative perspective. Inf. Sci. 2014, 281, 97–112. [Google Scholar] [CrossRef]
- Deng, X.Y.; Zheng, X.; Su, X.Y.; Chan, F.T.S.; Hu, Y.; Sadiq, R.; Deng, Y. An evidential game theory framework in multi-criteria decision making process. Appl. Math. Comput. 2014, 244, 783–793. [Google Scholar] [CrossRef]
- Fan, Z.P.; Zhang, X.; Liu, Y.; Zhang, Y. A method for stochastic multiple attribute decision making based on concepts of ideal and anti-ideal points. Appl. Math. Comput. 2013, 219, 11438–11450. [Google Scholar] [CrossRef]
- Krohling, R.A.; De Souza, T.T.M. Combining prospect theory and fuzzy numbers to multi-criteria decision making. Expert Syst. Appl. 2012, 39, 11487–11493. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T.; Gargov, G. Interval-valued intuitionistic fuzzy sets. Fuzzy Sets Syst. 1989, 31, 343–349. [Google Scholar] [CrossRef]
- Garg, H. A new generalized improved score function of interval-valued intuitionistic fuzzy sets and applications in expert systems. Appl. Soft Comput. 2016, 38, 988–999. [Google Scholar] [CrossRef]
- Hajiagha, S.H.R.; Mahdiraji, H.A.; Hashemi, S.S.; Zavadskas, E.K. Evolving a linear programming technique for MAGDM problems with interval valued intuitionistic fuzzy information. Expert Syst. Appl. 2015, 42, 9318–9325. [Google Scholar] [CrossRef]
- Hashemi, S.S.; Hajiagha, S.H.R.; Zavadskas, E.K.; Mahdiraji, H.A. Multicriteria group decision making with ELECTRE III method based on interval-valued intuitionistic fuzzy information. Appl. Math. Model. 2016, 40, 1554–1564. [Google Scholar] [CrossRef]
- Meng, F.Y.; Tan, C.Q.; Zhang, Q. The induced generalized interval-valued intuitionistic fuzzy hybrid Shapley averaging operator and its application in decision making. Knowl. Based Syst. 2013, 42, 9–19. [Google Scholar] [CrossRef]
- Nguyen, H. A new interval-valued knowledge measure for interval-valued intuitionistic fuzzy sets and application in decision making. Expert Syst. Appl. 2016, 56, 143–155. [Google Scholar] [CrossRef]
- Wei, G.W.; Wang, H.J.; Lin, R. Application of correlation coefficient to interval-valued intuitionistic fuzzy multiple attribute decision-making with incomplete weight information. Knowl. Inf. Syst. 2011, 26, 337–349. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria fuzzy decision-making method based on a novel accuracy function under interval-valued intuitionistic fuzzy environment. Expert Syst. Appl. 2009, 36, 6899–6902. [Google Scholar] [CrossRef]
- Wu, H.; Su, X.Q. Interval-valued intuitionistic fuzzy prioritized hybrid weighted aggregation operator and its application in decision making. J. Intell. Fuzzy Syst. 2015, 29, 1697–1709. [Google Scholar] [CrossRef]
- Dymova, L.; Sevastjanov, P.; Tikhonenko, A. Two-criteria method for comparing real-valued and interval-valued intuitionistic fuzzy values. Knowl. Based Syst. 2013, 45, 166–173. [Google Scholar] [CrossRef]
- Hong, D.H.; Choi, C.H. Multicriteria fuzzy decision-making problems based on vague set theory. Fuzzy Sets Syst. 2000, 114, 103–113. [Google Scholar] [CrossRef]
- Park, D.G.; Kwun, Y.C.; Park, J.H.; Park, I.Y. Correlation coefficient of interval-valued intuitionistic fuzzy sets and its application to multiple attribute group decision making problem. Math. Comput. Model. 2009, 50, 1279–1293. [Google Scholar] [CrossRef]
- Yu, D.J.; Wu, Y.Y.; Lu, T. Interval-valued intuitionistic fuzzy prioritized operators and their application in group decision making. Knowl. Based Syst. 2012, 30, 57–66. [Google Scholar] [CrossRef]
- Qi, X.W.; Liang, C.Y.; Zhang, J.L. Generalized cross-entropy based group decision making with unknown expert and attribute weights under interval-valued intuitionistic fuzzy environment. Comput. Ind. Eng. 2015, 79, 52–64. [Google Scholar] [CrossRef]
- Ye, J. Multicriteria fuzzy decision-making method using entropy weights-based correlation coefficients of interval-valued intuitionistic fuzzy sets. Appl. Math. Model. 2010, 34, 3864–3870. [Google Scholar] [CrossRef]
- Ye, J. Fuzzy cross entropy of interval-valued intuitionistic fuzzy sets and its optimal decision-making method based on the weights of alternatives. Expert Syst. Appl. 2011, 38, 6179–6183. [Google Scholar] [CrossRef]
- Zhang, Q.S.; Xing, H.Y.; Liu, F.C.; Ye, J.; Tang, P. Some new entropy measures for interval-valued intuitionistic fuzzy sets based on distances and their relationships with similarity and inclusion measures. Inf. Sci. 2014, 283, 55–69. [Google Scholar] [CrossRef]
- Driesen, B.; Perea, A.; Peters, H. On loss aversion in bimatrix games. Theory Decis. 2010, 68, 367–391. [Google Scholar] [CrossRef]
- Ho, H.P.; Chang, C.T.; Ku, C.Y. House selection via the internet by considering homebuyers’ risk attitudes with S-shaped utility functions. Eur. J. Oper. Res. 2015, 241, 188–201. [Google Scholar] [CrossRef]
- Kahneman, D.; Tversky, A. Prospect theory: An analysis of decision under risk. Econometrica 1979, 47, 263–292. [Google Scholar] [CrossRef]
- Köszegi, B.; Rabin, M. Reference-dependent risk attitudes. Am. Econ. Rev. 2007, 97, 1047–1073. [Google Scholar] [CrossRef]
- Nwogugu, M. A further critique of cumulative prospect theory and related approaches. Appl. Math. Comput. 2006, 179, 451–465. [Google Scholar] [CrossRef]
- Walker, S.G.B.; Hipel, K.W.; Inohara, T. Attitudes and preferences: Approaches to representing decision maker desires. Appl. Math. Comput. 2012, 218, 6637–6647. [Google Scholar]
- Allais, M. Le comportement de l’homme rationnel devant le risque: Critique des postulats et axiomes de l’ecole americaine. Econometrica 1953, 21, 503–546. [Google Scholar] [CrossRef]
- Ellsberg, D. Risk, ambiguity and the savage axioms. Q. J. Econ. 1961, 75, 643–669. [Google Scholar] [CrossRef]
- Nusrat, E.; Yamada, K. A descriptive decision-making model under uncertainty: Combination of Dempster-Shafer theory and prospect theory. Int. J. Uncertain. Fuzz. 2013, 21, 79–102. [Google Scholar] [CrossRef]
- Abdellaoui, M.; Bleichrodt, H.; Kammoun, H. Do financial professionals behave according to prospect theory? An experimental study. Theory Decis. 2013, 74, 411–429. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, Z.P.; Zhang, Y. Risk decision analysis in emergency response: A method based on cumulative prospect theory. Comput. Oper. Res. 2014, 42, 75–82. [Google Scholar] [CrossRef]
- Raue, M.; Streicher, B.; Lermer, E.; Frey, D. How far does it feel? Construal level and decisions under risk. J. Appl. Res. Mem. Cognit. 2015, 4, 256–264. [Google Scholar] [CrossRef]
- Abdellaoui, M.; Kemel, E. Eliciting prospect theory when consequences are measured in time units: “Time is not money”. Manag. Sci. 2014, 60, 1844–1859. [Google Scholar] [CrossRef]
- Sadiq, R.; Tesfamariam, S. Environmental decision-making under uncertainty using intuitionistic fuzzy analytic hierarchy process (IF-AHP). Stoch. Environ. Res. Risk Assess. 2009, 23, 75–91. [Google Scholar] [CrossRef]
- Izadikhah, M. Group decision making process for supplier selection with TOPSIS method under interval-valued intuitionistic fuzzy numbers. Adv. Fuzzy Syst. 2012, 2012, 1–14. [Google Scholar] [CrossRef]
- Chen, T.Y. An interval-valued intuitionistic fuzzy LINMAP method with inclusion comparison possibilities and hybrid averaging operations for multiple criteria group decision making. Knowl. Based Syst. 2013, 45, 134–146. [Google Scholar] [CrossRef]
- Wang, Z.J.; Li, K.W.; Wang, W.Z. An approach to multiattribute decision making with interval-valued intuitionistic fuzzy assessments and incomplete weights. Inf. Sci. 2009, 179, 3026–3040. [Google Scholar] [CrossRef]
- Wei, G.W. Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting. Knowl. Based Syst. 2008, 21, 833–836. [Google Scholar] [CrossRef]
- Park, J.H.; Park, I.Y.; Kwun, Y.C.; Tan, X.G. Extension of the TOPSIS method for decision making problems under interval-valued intuitionistic fuzzy environment. Appl. Math. Model. 2011, 35, 2544–2556. [Google Scholar] [CrossRef]
- Wan, S.P.; Li, D.F. Fuzzy mathematical programming approach to heterogeneous multiattribute decision-making with interval-valued intuitionistic fuzzy truth degrees. Inf. Sci. 2015, 325, 484–503. [Google Scholar] [CrossRef]
- Aggarwal, M. Compensative weighted averaging aggregation operators. Appl. Soft Comput. 2015, 28, 368–378. [Google Scholar] [CrossRef]
- Xu, Z.S. Methods for aggregating interval-valued intuitionistic fuzzy information and their application to decision making. Control Decis. 2007, 2, 215–219. [Google Scholar]
- Xu, Z.S.; Yager, R.R. Intuitionistic and interval-valued intutionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group. Fuzzy Optim. Decis. Mak. 2009, 8, 123–139. [Google Scholar] [CrossRef]
- Park, J.H.; Lim, K.M.; Park, J.S.; Kwun, Y.C. Distances between interval-valued intuitionistic fuzzy sets. J. Phys. Conf. Ser. 2008, 96, 012089. [Google Scholar] [CrossRef]
- Grzegorzewski, P. Distance between intuitionistic fuzzy sets and/or interval-valued fuzzy sets on the hausdorff metric. Fuzzy Sets Syst. 2004, 148, 319–328. [Google Scholar] [CrossRef]
- Köbberling, V.; Wakker, P.P. An index of loss aversion. J. Econ. Theory 2005, 122, 119–131. [Google Scholar] [CrossRef]
- Abdellaoui, M.; Bleichrodt, H.; Paraschiv, C. Loss aversion under prospect theory: A parameter-free measurement. Manag. Sci. 2007, 53, 1659–1674. [Google Scholar] [CrossRef] [Green Version]
- Yu, H.L.; Liu, P.D.; Jin, F. Research on the stochastic hybrid multi-attribute decision making method based on prospect theory. Sci. Iran. 2014, 21, 1105–1119. [Google Scholar]
- Horng, M.H.; Liou, R.J. Multilevel minimum cross entropy threshold selection based on the firefly algorithm. Expert Syst. Appl. 2011, 38, 14805–14811. [Google Scholar] [CrossRef]
- Abdellaoui, M. Parameter-free elicitation of utility and probability weighting functions. Manag. Sci. 2000, 46, 1497–1512. [Google Scholar] [CrossRef]
- Guiso, L.; Paiella, M. Risk aversion, wealth, and background risk. J. Eur. Econ. Assoc. 2008, 6, 1109–1150. [Google Scholar] [CrossRef]
- Merigó, J.M.; Gil-Lafuente, A.M. The induced generalized OWA operator. Inf. Sci. 2009, 179, 729–741. [Google Scholar] [CrossRef]
- Yu, D.J. Hydrogen Production technologies evaluation based on interval-valued intuitionistic fuzzy multiattribute decision making method. J. Appl. Math. 2014, 2014, 751249. [Google Scholar] [CrossRef]


| ([0.4, 0.5], [0.3, 0.4]) | ([0.4, 0.6], [0.2, 0.4]) | ([0.3, 0.4], [0.4, 0.5]) | ([0.5, 0.6], [0.1, 0.3]) | |
| ([0.5, 0.6], [0.2, 0.3]) | ([0.6, 0.7], [0.2, 0.3]) | ([0.5, 0.6], [0.3, 0.4]) | ([0.4, 0.7], [0.1, 0.2]) | |
| ([0.3, 0.5], [0.3, 0.4]) | ([0.1, 0.3], [0.5, 0.6]) | ([0.2, 0.5], [0.4, 0.5]) | ([0.2, 0.3], [0.4, 0.6]) | |
| ([0.2, 0.5], [0.3, 0.4]) | ([0.4, 0.7], [0.1, 0.2]) | ([0.4, 0.5], [0.3, 0.5]) | ([0.5, 0.8], [0.1, 0.2]) | |
| ([0.3, 0.4], [0.1, 0.3]) | ([0.7, 0.8], [0.1, 0.2]) | ([0.5, 0.6], [0.2, 0.4]) | ([0.6, 0.7], [0.1, 0.2]) |
| The Prospect Projection Value | Ordering | |||||||
|---|---|---|---|---|---|---|---|---|
| 0.12 | 0.15 | 1.1 | 0.927 | 0.951 | 0.903 | 0.937 | 0.949 | |
| 0.25 | 0.30 | 1.5 | 0.854 | 0.901 | 0.809 | 0.872 | 0.896 | |
| 0.45 | 0.52 | 1.8 | 0.753 | 0.828 | 0.682 | 0.781 | 0.821 | |
| 0.67 | 0.87 | 2.1 | 0.654 | 0.753 | 0.566 | 0.690 | 0.745 | |
| 0.89 | 0.92 | 2.3 | 0.570 | 0.677 | 0.470 | 0.613 | 0.688 | |
| 0.93 | 0.95 | 5.0 | 0.550 | 0.663 | 0.451 | 0.589 | 0.667 | |
| 0.97 | 0.99 | 7.0 | 0.534 | 0.645 | 0.435 | 0.572 | 0.651 | |
| ([0.1, 0.2], [0.0, 0.0]) | ([0.1, 0.3], [0.5, 0.7]) | ([0.1, 0.2], [0.6, 0.7]) | ([0.0, 0.0], [0.7, 0.8]) | |
| ([0.2, 0.3], [0.1, 0.2]) | ([0.3, 0.4], [0.2, 0.3]) | ([0.2, 0.3], [0.3, 0.5]) | ([0.1, 0.2], [0.4, 0.5]) | |
| ([0.3, 0.5], [0.2, 0.3]) | ([0.1, 0.3], [0.4, 0.6]) | ([0.3, 0.4], [0.4, 0.6]) | ([0.2, 0.4], [0.3, 0.6]) |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, J.; Liu, H. A New Prospect Projection Multi-Criteria Decision-Making Method for Interval-Valued Intuitionistic Fuzzy Numbers. Information 2016, 7, 64. https://doi.org/10.3390/info7040064
Gao J, Liu H. A New Prospect Projection Multi-Criteria Decision-Making Method for Interval-Valued Intuitionistic Fuzzy Numbers. Information. 2016; 7(4):64. https://doi.org/10.3390/info7040064
Chicago/Turabian StyleGao, Jianwei, and Huihui Liu. 2016. "A New Prospect Projection Multi-Criteria Decision-Making Method for Interval-Valued Intuitionistic Fuzzy Numbers" Information 7, no. 4: 64. https://doi.org/10.3390/info7040064






