The Genetic Codes: Mathematical Formulae and an Inverse Symmetry-Information Relationship
Abstract
:1. Introduction
2. Formulae for the Standard Genetic Code and Its Variants
- The Vertebrate Mitochondrial Code
- The Thraustochytrium Mitochondrial Code
- The Standard Genetic Code
- The Bacterial, Archeal and plant Plastid Code
- The Scenedesmus Oblicus Mitochondrial Code and Alternative Yeast Nuclear Code
- The Pashysolen Tannophilus Nuclear Code
- The Mold, Protozoan, and Coelenterate Mitochondrial Code and the Mycoplasma/Spirolasma Code
- The Invertebrate Mitochondrial Code
- The Echinoderm and Flatworm Mitochondrial Code
- The Euploid Nuclear Code
- The Ascidian Mitochondrial Code
- The Chlorophycean Mitochondrial Code
- The Trematode Mitochondrial Code
- The Pterobranchia Mitochondrial Code
- The Candidate Division SR1 and Gracilibacteria Code
- The Ciliate Dascladacean and Hexamita Nuclear Code
- The Alternative Flatworm Mitochondrial Code
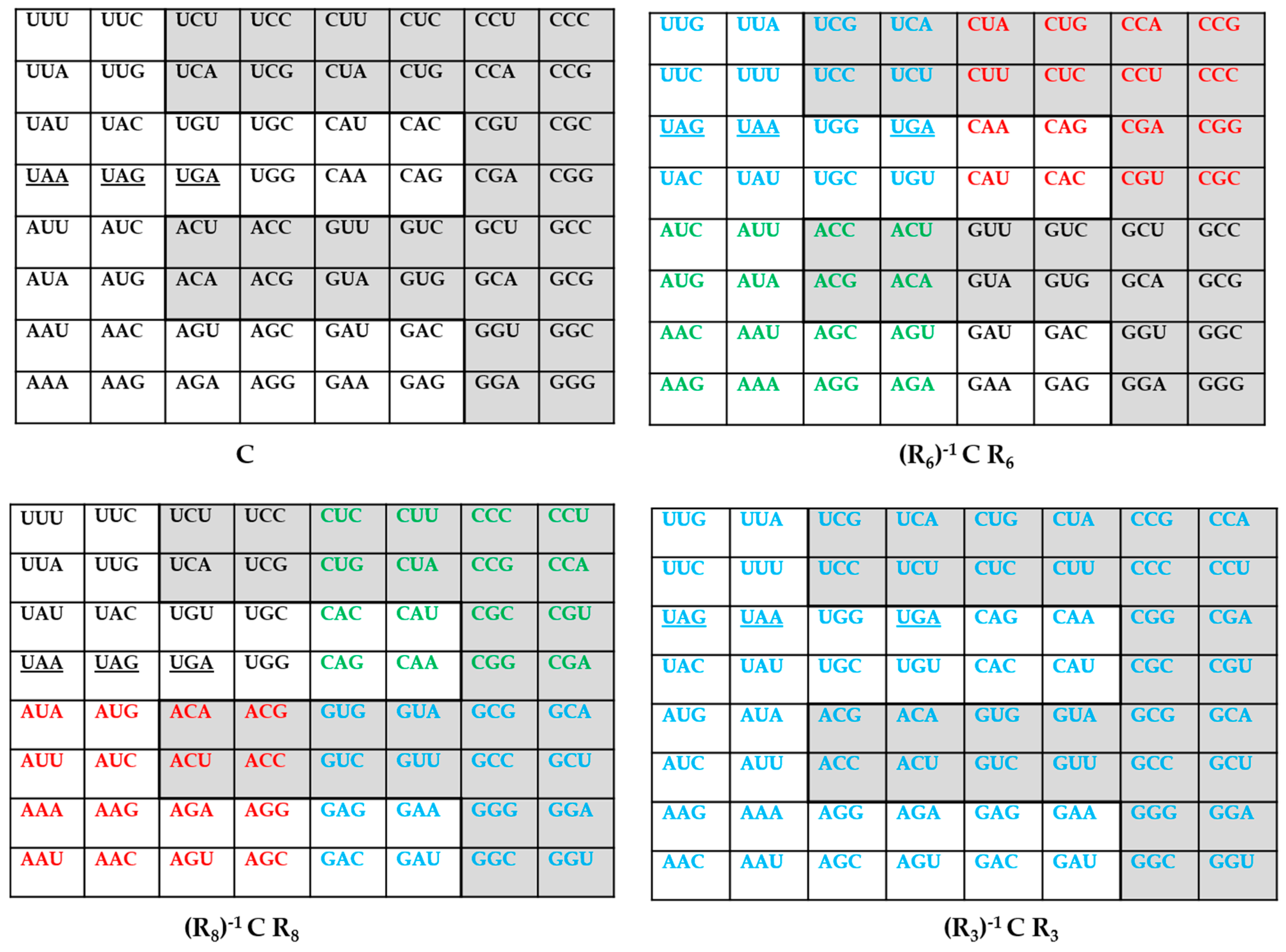
3. The Genetic Codes via q-Deformations
4. An Inverse Symmetry-Information Relationship in the Genetic Codes
5. Summary and Concluding Remarks
Acknowledgments
Conflicts of Interest
References
- Watson, J.D.; Crick, F.H.C. A Structure for deoxyribose nucleic acid. Nature 1953, 171, 737–738. [Google Scholar] [CrossRef] [PubMed]
- Nirenberg, M.; Leder, P.; Bernfield, M.; Brimacombe, R.; Trupin, J.; Rottman, F.; O’Neal, C. RNA codewords and protein synthesis, VII. On the general nature of the RNA code. Proc. Natl. Acad. Sci. USA 1965, 53, 1161–1168. [Google Scholar] [CrossRef] [PubMed]
- Négadi, T. The genetic code multiplet structure, in one number. Symmetry Cult. Sci. 2007, 18, 149–160. [Google Scholar] [CrossRef]
- Négadi, T. The genetic code via Gödel encoding. Open Phys. Chem. J. 2008, 2, 1–5. [Google Scholar] [CrossRef]
- Négadi, T. A taylor-made arithmetic model of the genetic code and applications. Symmetry Cult. Sci. 2009, 20, 51–76. [Google Scholar]
- Négadi, T. A Mathematical model of the genetic code(s) based on Fibonacci numbers and their q-analogues. NeuroQuantology 2015, 13, 259–272. [Google Scholar] [CrossRef]
- Négadi, T. Semi-phenomenological classification models of the genetic code(s) using q-deformed numbers. Symmetry Cult. Sci. 2016, 27, 81–94. [Google Scholar]
- The Genetic Codes. Available online: https://www.ncbi.nlm.nih.gov/Taxonomy/Utils/wprintgc.cgi (accessed on 12 August 2016).
- Gavaudan, P. The genetic code and the origin of life. In Chemical Evolution and the Origin of Life; Buvet, R., Ponnamperuma, C., Eds.; North-Holland Publishing Company: Amsterdam, The Netherlands, 1971; pp. 432–445. [Google Scholar]
- Záhonová, K.; Kostygov, A.Y.; Ševčíková, T.; Yurchenko, V.; Eliás, M. An unprecedented non-canonical nuclear genetic code with all three termination codons reassigned as sense codons. Curr. Biol. 2016, 26, 2364–2369. [Google Scholar] [CrossRef] [PubMed]
- Heaphy, S.M.; Mariotti, M.; Gladyshev, V.N.; Atkins, J.F.; Baranov, P.V. Novel ciliate genetic code variants including the reassignment of all three stop codons to sense codons in Condylostoma magnum. Mol. Biol. Evol. 2016, 33, 2885–2889. [Google Scholar] [CrossRef] [PubMed]
- Meaning and Structure in Biology and Physics: Some Outstanding Questions. Available online: http://www.fdavidpeat.com/bibliography/essays/bermuda.htm (accessed on 26 October 2016).
- Bateson, G. Steps to an Ecology of Mind; Jason Aronson Inc.: Northvale, NJ, USA; London, UK, 1987. [Google Scholar]
- Muller, S.J. Asymmetry: The Foundation of Information; Springer: Berlin/Heidelberg, Germany, 2007; pp. 96–97. [Google Scholar]
- Schutzenberger, M.P.; Gavaudan, P.; Besson, J. Sur l’existence d’une certain correlation entre le poids moléculaire des acides aminés et le nombre de triplets intervenant dans leur codage. C. R. Acad. Sci. (Paris) 1969, 268, 1342–1344. [Google Scholar]
- Biro, J.C. Does codon bias have an evolutionary origin? Theor. Biol. Model. 2008, 5, 1–16. [Google Scholar] [CrossRef] [PubMed]
- Drake, J.W. A constant rate of spontaneous mutation in DNA-based microbes. Proc. Natl. Acad. Sci. USA 1991, 88, 7160–7164. [Google Scholar] [CrossRef] [PubMed]
- Huang, S. Inverse relationship between genetic diversity and epigenetic complexity. In Cancer Epigenetics; Nature Proceedings; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]
- Rumer, Y.B. About the codon’s systematization in the genetic code. Proc. Akad. Sci. USSR 1966, 167, 1393–1394. [Google Scholar]
- Négadi, T. Symmetry groups for the Rumer-Konopel’chenko-Shcherbak “bisections” of the Genetic Code and applications. Intern. Electron. J. Mol. Des. 2004, 3, 247–270. [Google Scholar]
- Négadi, T.; Kibler, M. A q-deformed Aufbau Prinzip. J. Phys. A Math. Gen. 1992, 25, L157–L160. [Google Scholar] [CrossRef]
- Sviratcheva, K.D.; Bahri, C.; Georgieva, A.I.; Draayer, J.P. Physical significance of q deformation and many-body interactions in nuclei. Phys. Rev. Lett. 2004, 93, 152501. [Google Scholar] [CrossRef]
- Frappat, L.; Sorba, P.; Sciarrino, A. A model of the genetic code. Int. J. Mod. Phys. 2000, B14, 2485. [Google Scholar] [CrossRef]
- Frappat, L.; Sorba, P.; Sciarrino, A. Quantum groups and the genetic code. Theor. Math. Phys. 2001, 128, 756–859. [Google Scholar] [CrossRef]
- Jestin, J.L. Degeneracy in the genetic code and its symmetries by base substitutions. C. R. Biol. 2006, 329, 168–171. [Google Scholar] [CrossRef] [PubMed]
- Jestin, J.L.; Soulé, C. Symmetries by base substitutions in the genetic code predict 2’ or 3’aminoacylation of tRNAs. J. Theor. Biol. 2007, 247, 391–394. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.J.; Lehmann, J. About a symmetry of the genetic code. J. Theor. Biol. 1997, 189, 171–174. [Google Scholar] [CrossRef] [PubMed]
- Hornos, J.E.M.; Braggion, L.; Magini, M.; Forger, M. Symmetry preservation in the evolution of the genetic code. Life 2004, 56, 125–130. [Google Scholar] [CrossRef]
- Gonzalez, D.L. Can the genetic code be mathematically described? Med. Sci. Monit. 2004, 10, 11–17. [Google Scholar]
- Bashford, J.D.; Tsohantjis, I.; Jarvis, P.D. A supersymmetric model for the evolution of the genetic code. Proc. Natl. Acad. Sci. USA 1998, 95, 987–992. [Google Scholar] [CrossRef] [PubMed]
- Antoneli, F.; Forger, F.; Hornos, J.E.M. The search for symmetries in the genetic code: Finite groups. Mod. Phys.Lett. 2004, B18, 971. [Google Scholar] [CrossRef]
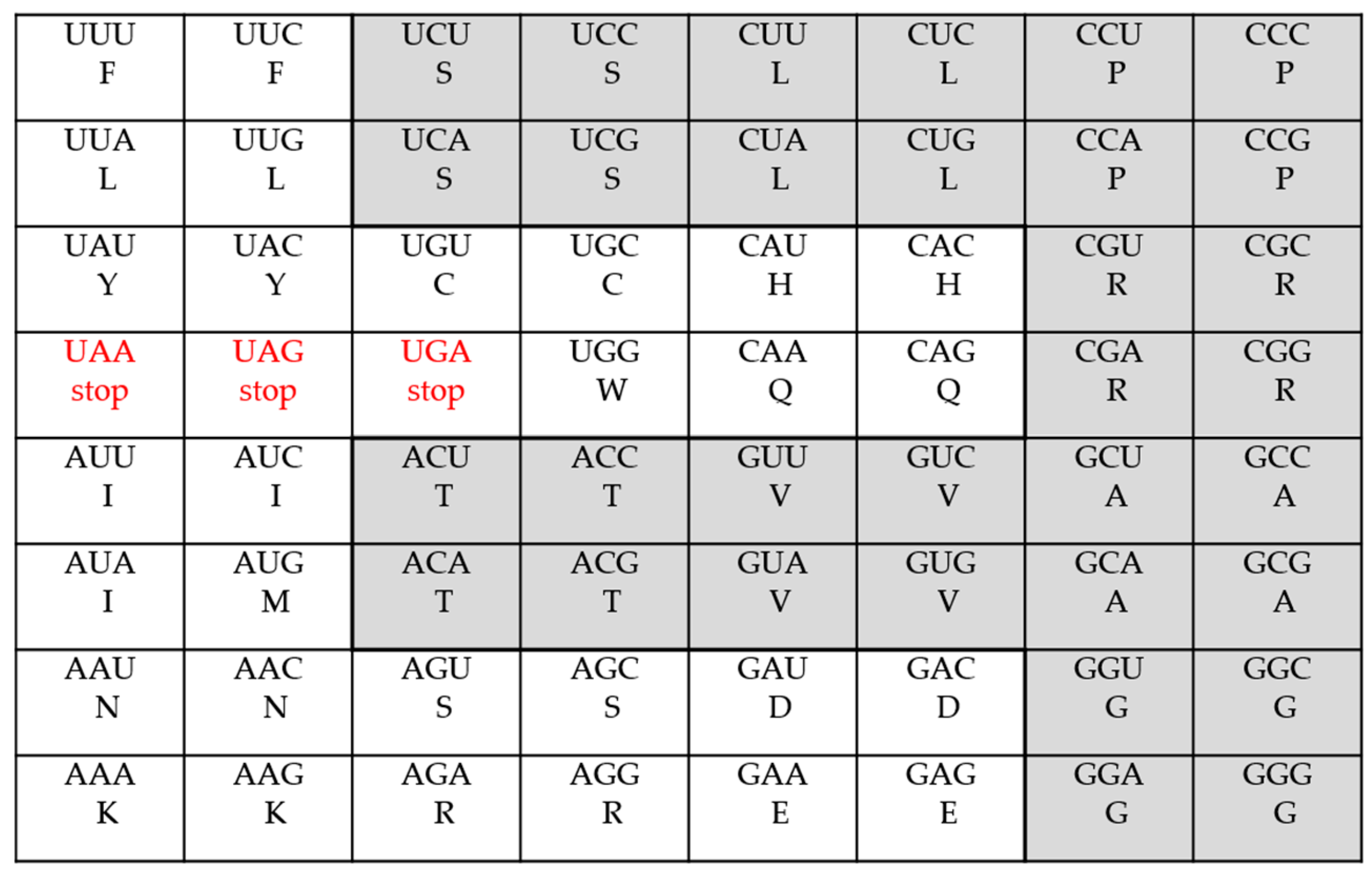
| The Various Genetic Codes | Multiplets | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | # Stops | |
| The Vertebrate Mitochondrial Code | 12 | 6 | 2 | 4 | |||||
| The Thraustochytrium Mitochondrial Code | 2 | 9 | 1 | 5 | 1 | 2 | 4 | ||
| The Standard Code | 2 | 9 | 1 | 5 | 3 | 3 | |||
| The Bacterial, Archeal and plant Plastid Code | 2 | 9 | 1 | 5 | 3 | 3 | |||
| The Alternative Yeast Nuclear Code | 2 | 9 | 1 | 5 | 1 | 1 | 1 | 3 | |
| The Scenedesmus obliqus Mitochondrial Code | 2 | 9 | 1 | 5 | 1 | 1 | 1 | 3 | |
| The Pachysolen tannophilus Nuclear Code | 2 | 9 | 1 | 4 | 2 | 2 | 3 | ||
| The Yeast Mitochondrial Code (see below) | 13 | 5 | 1 | 1 | 2 | ||||
| The Mold, Protozoan, and Coelenterate Mitochondrial Code and the Mycolasma/Spirolasma Code | 1 | 10 | 1 | 5 | 3 | 2 | |||
| The Invertebrate Mitochondrial Code | 12 | 6 | 1 | 1 | 2 | ||||
| The Echinoderm and Flatworm Mitochondrial Code | 2 | 8 | 2 | 6 | 1 | 1 | 2 | ||
| The Euploid Nuclear Code | 2 | 8 | 2 | 5 | 3 | 2 | |||
| The Ascidian Mitochondrial Code | 12 | 5 | 3 | 2 | |||||
| The Chlorophycean Mitochondrial Code | 2 | 9 | 1 | 5 | 2 | 1 | 2 | ||
| The Trematode Mitochondrial Code | 1 | 10 | 1 | 6 | 1 | 1 | 2 | ||
| The Pterobranchia Mitochondrial Code | 1 | 9 | 2 | 6 | 1 | 1 | 2 | ||
| The Candidate Division SR1 and Gracilibacteria Code | 2 | 9 | 1 | 4 | 1 | 3 | 2 | ||
| The Ciliate, Dasycladacean and Hexamita Nuclear Code | 2 | 8 | 1 | 6 | 3 | 1 | |||
| The Alternative Flatworm Mitochondrial Code | 2 | 7 | 3 | 6 | 1 | 1 | 1 | ||
| The Various Genetic Codes | The Modifications |
|---|---|
| The Vertebrate Mitochondrial Code | AGA→stop, AGG→stop, AUA→M, UGA→W |
| The Thraustochytrium Mitochondrial Code | UUA→stop |
| The Bacterial, Archeal and plant Plastid Code | Same as the Standard Genetic Code |
| The Alternative Yeast Nuclear Code | CUG → S |
| The Scenedesmus obliqus Mitochondrial Code | UCA → stop, UAG → L |
| The Pachysolen tannophilus Nuclear Code | CUG → A |
| The Yeast Mitochondrial Code (see below) | AUA → M, {CUU, CUC, CUA, CUG} → T, {CGA, CGC} → absent ([8]) |
| The Mold, Protozoan, and Coelenterate Mitochondrial Code and the Mycolasma/Spirolasma Code | UGA → W |
| The Invertebrate Mitochondrial Code | {AGA, AGG} → S, AUA → M, UGA → W |
| The Echinoderm and Flatworm Mitochondrial Code | AAA → N, {AGA, AGG} → S, UGA → W |
| The Euploid Nuclear Code | UGA → C |
| The Ascidian Mitochondrial Code | {AGA, AGG} → G, AUA → M, UGA → W |
| The Chlorophycean Mitochondrial Code | UAG → L |
| The Trematode Mitochondrial Code | UGA → W, AUA → M, {AGA, AGG} → S, AAA → N |
| The Pterobranchia Mitochondrial Code | AGA → S, AGA → K, UGA → W |
| The Candidate Division SR1 and Gracilibacteria Code | UGA → G |
| The Ciliate, Dasycladacean and Hexamita Nuclear Code | {UAA, UAG} →Q |
| The Alternative Flatworm Mitochondrial Code | AAA →N, {AGA, AGG} → S, UAA → Y, UGA → W |
© 2016 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Négadi, T. The Genetic Codes: Mathematical Formulae and an Inverse Symmetry-Information Relationship. Information 2017, 8, 6. https://doi.org/10.3390/info8010006
Négadi T. The Genetic Codes: Mathematical Formulae and an Inverse Symmetry-Information Relationship. Information. 2017; 8(1):6. https://doi.org/10.3390/info8010006
Chicago/Turabian StyleNégadi, Tidjani. 2017. "The Genetic Codes: Mathematical Formulae and an Inverse Symmetry-Information Relationship" Information 8, no. 1: 6. https://doi.org/10.3390/info8010006





