NS-Cross Entropy-Based MAGDM under Single-Valued Neutrosophic Set Environment
Abstract
:1. Introduction
- i.
- ii.
- iii.
- i.
- Is it possible to define a new cross entropy measure that is free from asymmetrical phenomena and undefined behavior?
- ii.
- Is it possible to define a new weighted cross entropy measure that is free from the asymmetrical phenomena and undefined behavior?
- iii.
- Is it possible to develop a new MAGDM strategy based on the proposed cross entropy measure in single-valued neutrosophic set environment, which is free from the asymmetrical phenomena and undefined behavior?
- iv.
- Is it possible to develop a new MAGDM strategy based on the proposed weighted cross entropy measure in the single-valued neutrosophic set environment that is free from the asymmetrical phenomena and undefined behavior?
- v.
- How do we assign unknown weight of attributes?
- vi.
- How do we assign unknown weight of decision-makers?
- To define a new cross entropy measure and prove its basic properties, which are free from asymmetrical phenomena and undefined behavior.
- To define a new weighted cross measure and prove its basic properties, which are free from asymmetrical phenomena and undefined behavior.
- To develop a new MAGDM strategy based on weighted cross entropy measure under single-valued neutrosophic set environment.
- To develop a technique to incorporate unknown weight of attributes and unknown weight of decision-makers in the proposed NS-cross entropy-based MAGDM under single-valued neutrosophic environment.
- We define a new NS-cross entropy measure and prove its basic properties. It is straightforward symmetric and it has no undefined behavior.
- We define a new weighted NS-cross entropy measure in the single-valued neutrosophic set environment and prove its basic properties. It is straightforward symmetric and it has no undefined behavior.
- In this paper, we develop a new MAGDM strategy based on weighted NS cross entropy to solve MAGDM problems with unknown weight of the attributes and unknown weight of decision-makers.
- Techniques to determine unknown weight of attributes and unknown weight of decisions makers are proposed in the study.
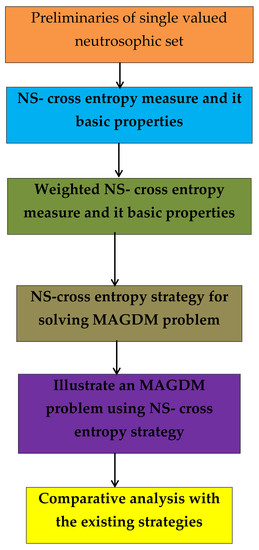
2. Preliminaries
3. NS-Cross Entropy Measure
- i.
- .
- ii.
- if and only if , ,
- iii.
- iv.
- i.
- ii.
- , if and only if , ,
- iii.
- iv.
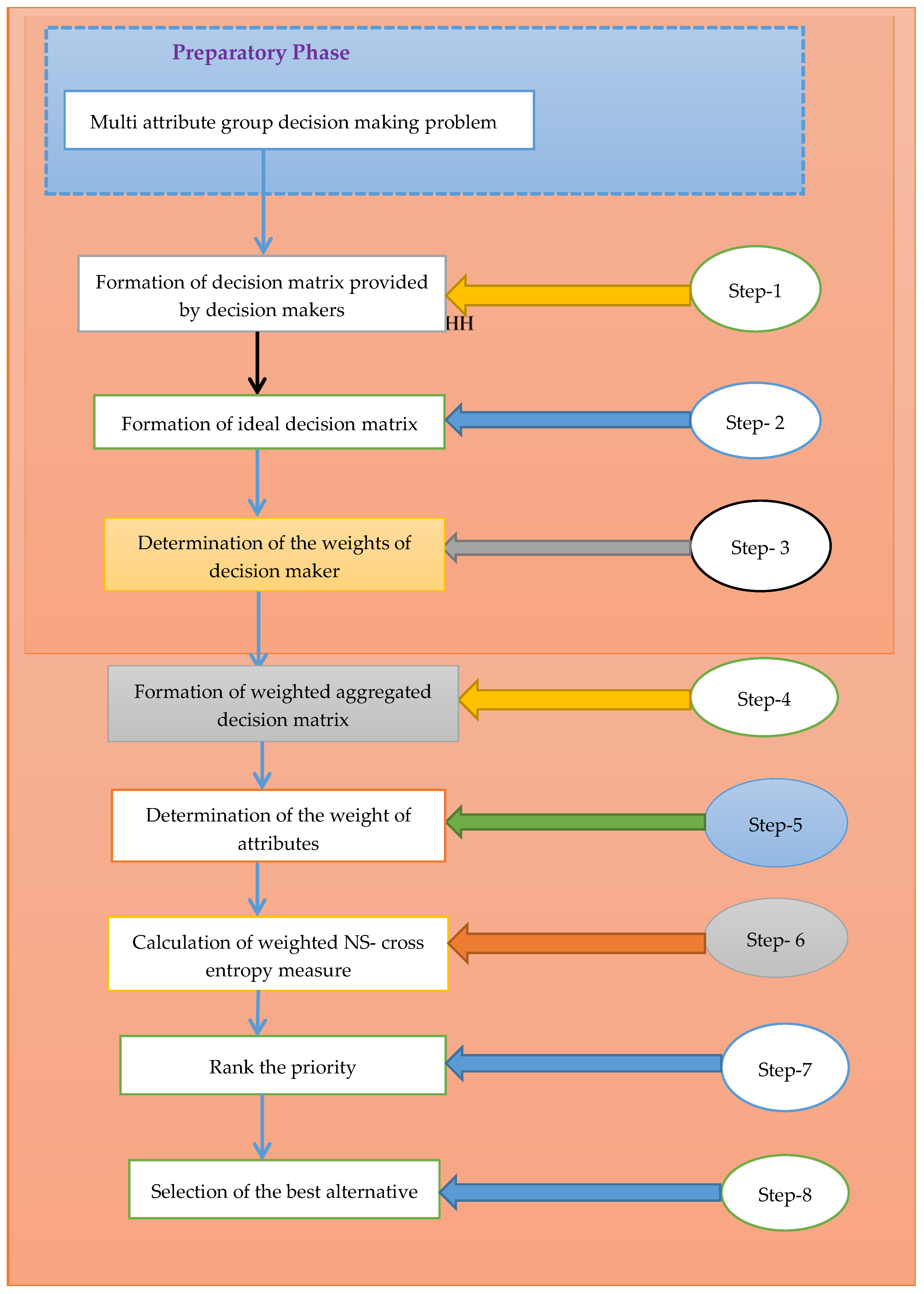
4. MAGDM Strategy Using Proposed Ns-Cross Entropy Measure under SVNS Environment
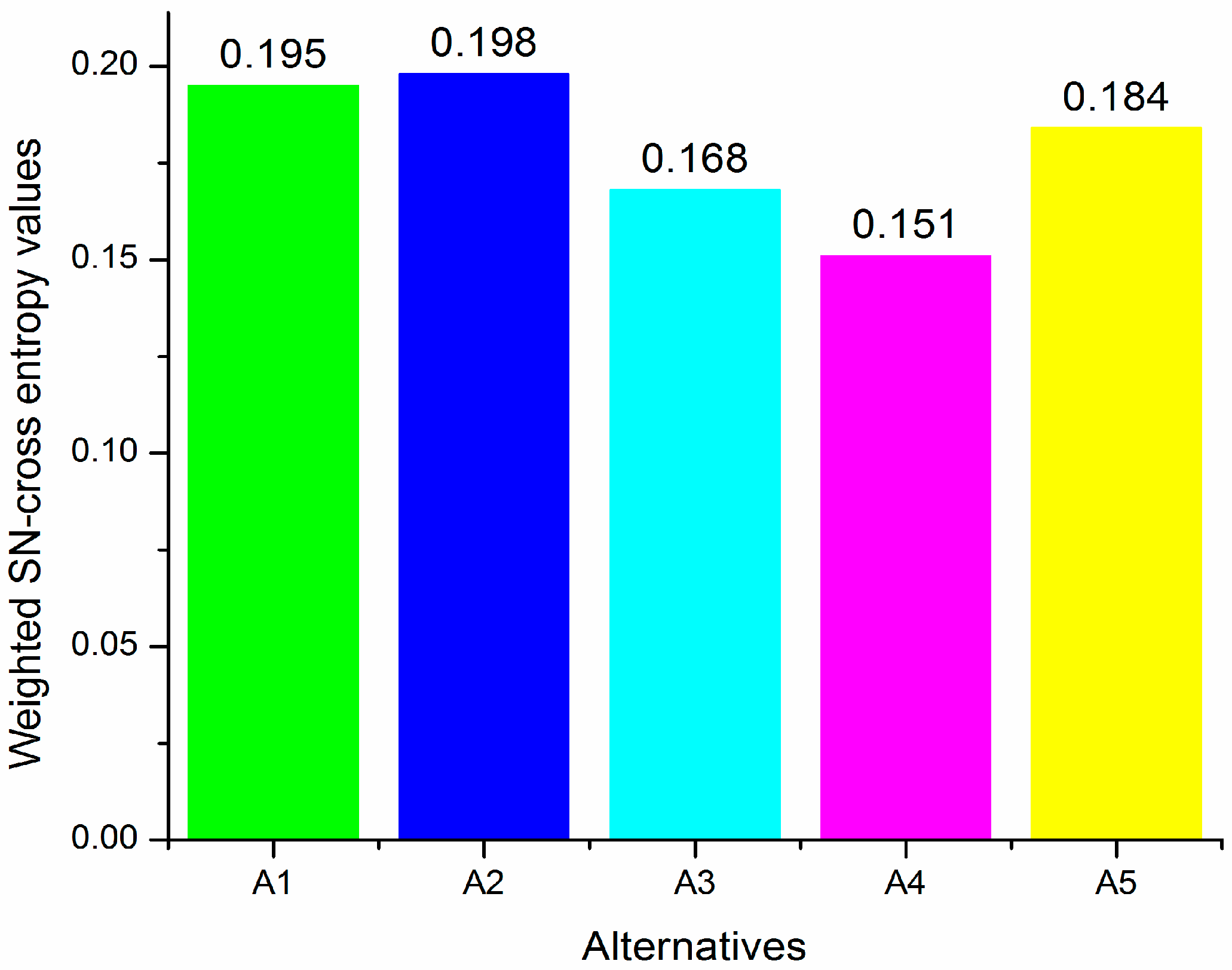
5. Illustrative Example
- (1)
- Automobile company (A1)
- (2)
- Military manufacturing enterprise (A2)
- (3)
- TV media company (A3)
- (4)
- Food enterprises (A4)
- (5)
- Computer software company (A5)
- (1)
- Social and political factor (G1)
- (2)
- The environmental factor (G2)
- (3)
- Investment risk factor (G3)
- (4)
- The enterprise growth factor (G4).
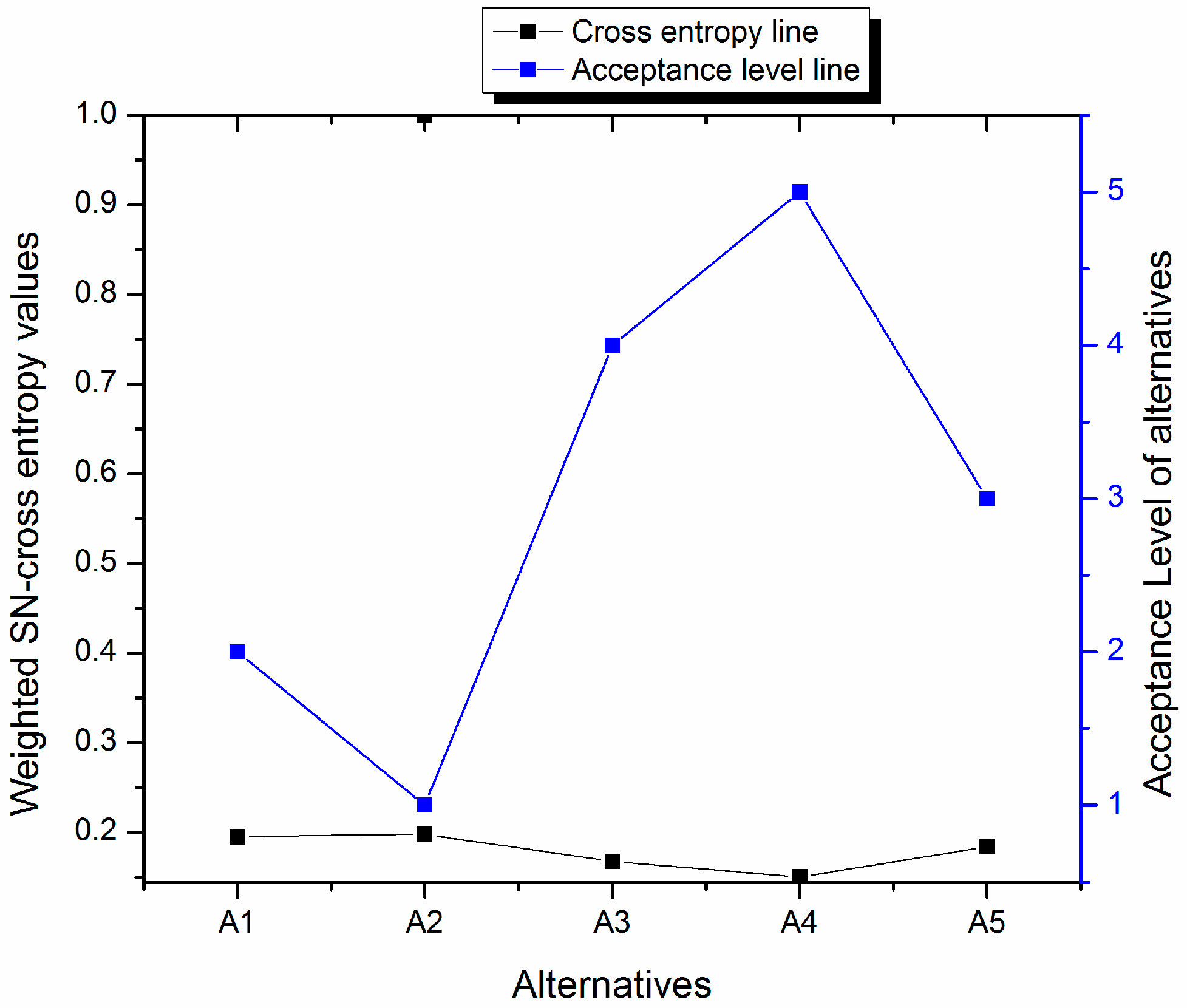
6. Comparative Study and Discussion
- i.
- ii.
- Ye [144] proposed cross entropy that does not satisfy the symmetrical property straightforward and is undefined for some situations but the proposed strategy satisfies symmetric property and is free from undefined phenomenon.
- iii.
- iv.
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–356. [Google Scholar] [CrossRef]
- Bellman, R.; Zadeh, L.A. Decision-making in A fuzzy environment. Manag. Sci. 1970, 17, 141–164. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Pramanik, S.; Mukhopadhyaya, D. Grey relational analysis-based intuitionistic fuzzy multi-criteria group decision-making approach for teacher selection in higher education. Int. J. Comput. Appl. 2011, 34, 21–29. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S. Intuitionistic fuzzy multi criteria group decision making approach to quality-brick selection problem. J. Appl. Quant. Methods 2014, 9, 35–50. [Google Scholar]
- Dey, P.P.; Pramanik, S.; Giri, B.C. Multi-criteria group decision making in intuitionistic fuzzy environment based on grey relational analysis for weaver selection in Khadi institution. J. Appl. Quant. Methods 2015, 10, 1–14. [Google Scholar]
- Ye, J. Multicriteria fuzzy decision-making method based on the intuitionistic fuzzy cross-entropy. In Proceedings of the International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2009; Volume 1, pp. 59–61. [Google Scholar]
- Chen, S.M.; Chang, C.H. A novel similarity measure between Atanassov’s intuitionistic fuzzy sets based on transformation techniques with applications to pattern recognition. Inf. Sci. 2015, 291, 96–114. [Google Scholar] [CrossRef]
- Chen, S.M.; Cheng, S.H.; Chiou, C.H. Fuzzy multi-attribute group decision making based on intuitionistic fuzzy sets and evidential reasoning methodology. Inf. Fusion 2016, 27, 215–227. [Google Scholar] [CrossRef]
- Wang, J.Q.; Han, Z.Q.; Zhang, H.Y. Multi-criteria group decision making method based on intuitionistic interval fuzzy information. Group Decis. Negot. 2014, 23, 715–733. [Google Scholar] [CrossRef]
- Yue, Z.L. TOPSIS-based group decision-making methodology in intuitionistic fuzzy setting. Inf. Sci. 2014, 277, 141–153. [Google Scholar] [CrossRef]
- He, X.; Liu, W.F. An intuitionistic fuzzy multi-attribute decision-making method with preference on alternatives. Oper. Res. Manag. Sci. 2013, 22, 36–40. [Google Scholar]
- Zadeh, L.A. Probability Measures of Fuzzy Events. J. Math. Anal. Appl. 1968, 23, 421–427. [Google Scholar] [CrossRef]
- Burillo, P.; Bustince, H. Entropy on intuitionistic fuzzy sets and on interval-valued fuzzy sets. Fuzzy Sets Systs. 1996, 78, 305–316. [Google Scholar] [CrossRef]
- Szmidt, E.; Kacprzyk, J. Entropy for intuitionistic fuzzy sets. Fuzzy Sets Syst. 2001, 118, 467–477. [Google Scholar] [CrossRef]
- Wei, C.P.; Wang, P.; Zhang, Y.Z. Entropy, similarity measure of interval-valued intuitionistic fuzzy sets and their applications. Inf. Sci. 2011, 181, 4273–4286. [Google Scholar] [CrossRef]
- Li, X.Y. Interval-valued intuitionistic fuzzy continuous cross entropy and its application in multi-attribute decision-making. Comput. Eng. Appl. 2013, 49, 234–237. [Google Scholar]
- Shang, X.G.; Jiang, W.S. A note on fuzzy information measures. Pattern Recognit. Lett. 1997, 18, 425–432. [Google Scholar] [CrossRef]
- Vlachos, I.K.; Sergiadis, G.D. Intuitionistic fuzzy information applications to pattern recognition. Pattern Recognit. Lett. 2007, 28, 197–206. [Google Scholar] [CrossRef]
- Ye, J. Fuzzy cross entropy of interval-valued intuitionistic fuzzy sets and its optimal decision-making method based on the weights of alternatives. Expert Syst. Appl. 2011, 38, 6179–6183. [Google Scholar] [CrossRef]
- Xia, M.M.; Xu, Z.S. Entropy/cross entropy-based group decision making under intuitionistic fuzzy environment. Inf. Fusion 2012, 13, 31–47. [Google Scholar] [CrossRef]
- Tong, X.; Yu, L. A novel MADM approach based on fuzzy cross entropy with interval-valued intuitionistic fuzzy sets. Math. Probl. Eng. 2015, 2015, 965040. [Google Scholar] [CrossRef]
- Smarandache, F. Neutrosophy, Neutrosophic Probability, Set, and Logic, 4th ed.; American Research Press: Rehoboth, DE, USA, 1998. [Google Scholar]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistruct. 2010, 4, 410–413. [Google Scholar]
- Pramanik, S.; Biswas, P.; Giri, B.C. Hybrid vector similarity measures and their applications to multi-attribute decision making under neutrosophic environment. Neural Comput. Appl. 2017, 28, 1163–1176. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Entropy based grey relational analysis method for multi-attribute decision making under single valued neutrosophic assessments. Neutrosoph. Sets Syst. 2014, 2, 102–110. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. A new methodology for neutrosophic multi-attribute decision making with unknown weight information. Neutrosoph. Sets Syst. 2014, 3, 42–52. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. TOPSIS method for multi-attribute group decision-making under single valued neutrosophic environment. Neural Comput. Appl. 2016, 27, 727–737. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Aggregation of triangular fuzzy neutrosophic set information and its application to multi-attribute decision making. Neutrosoph. Sets Syst. 2016, 12, 20–40. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Value and ambiguity index based ranking method of single-valued trapezoidal neutrosophic numbers and its application to multi-attribute decision making. Neutrosoph. Sets Syst. 2016, 12, 127–138. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Multi-attribute group decision making based on expected value of neutrosophic trapezoidal numbers. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium; Volume II, in press.
- Biswas, P.; Pramanik, S.; Giri, B.C. Non-linear programming approach for single-valued neutrosophic TOPSIS method. New Math. Nat. Comput. 2017, in press. [Google Scholar]
- Deli, I.; Subas, Y. A ranking method of single valued neutrosophic numbers and its applications to multi-attribute decision making problems. Int. J. Mach. Learn. Cybern. 2017, 8, 1309–1322. [Google Scholar] [CrossRef]
- Ji, P.; Wang, J.Q.; Zhang, H.Y. Frank prioritized Bonferroni mean operator with single-valued neutrosophic sets and its application in selecting third-party logistics providers. Neural Comput. Appl. 2016. [Google Scholar] [CrossRef]
- Kharal, A. A neutrosophic multi-criteria decision making method. New Math. Nat. Comput. 2014, 10, 143–162. [Google Scholar] [CrossRef]
- Liang, R.X.; Wang, J.Q.; Li, L. Multi-criteria group decision making method based on interdependent inputs of single valued trapezoidal neutrosophic information. Neural Comput. Appl. 2016, 1–20. [Google Scholar] [CrossRef]
- Liang, R.X.; Wang, J.Q.; Zhang, H.Y. A multi-criteria decision-making method based on single-valued trapezoidal neutrosophic preference relations with complete weight information. Neural Comput. Appl. 2017, 1–16. [Google Scholar] [CrossRef]
- Liu, P.; Chu, Y.; Li, Y.; Chen, Y. Some generalized neutrosophic number Hamacher aggregation operators and their application to group decision making. Int. J. Fuzzy Syst. 2014, 16, 242–255. [Google Scholar]
- Liu, P.D.; Li, H.G. Multiple attribute decision-making method based on some normal neutrosophic Bonferroni mean operators. Neural Comput. Appl. 2017, 28, 179–194. [Google Scholar] [CrossRef]
- Liu, P.; Wang, Y. Multiple attribute decision-making method based on single-valued neutrosophic normalized weighted Bonferroni mean. Neural Comput. Appl. 2014, 25, 2001–2010. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J.Q.; Wang, J.; Zhang, H.Y.; Chen, X.H. Simplified neutrosophic sets and their applications in multi-criteria group decision-making problems. Int. J. Syst. Sci. 2016, 47, 2342–2358. [Google Scholar] [CrossRef]
- Peng, J.; Wang, J.; Zhang, H.; Chen, X. An outranking approach for multi-criteria decision-making problems with simplified neutrosophic sets. Appl. Soft Comput. 2014, 25, 336–346. [Google Scholar] [CrossRef]
- Zavadskas, E.K.; Baušys, R.; Lazauskas, M. Sustainable assessment of alternative sites for the construction of a waste incineration plant by applying WASPAS method with single-valued neutrosophic set. Sustainability 2015, 7, 15923–15936. [Google Scholar] [CrossRef]
- Pramanik, S.; Dalapati, S.; Roy, T.K. Logistics center location selection approach based on neutrosophic multi-criteria decision making. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; Volume 1, pp. 161–174. [Google Scholar]
- Sahin, R.; Karabacak, M. A multi attribute decision making method based on inclusion measure for interval neutrosophic sets. Int. J. Eng. Appl. Sci. 2014, 2, 13–15. [Google Scholar]
- Sahin, R.; Kucuk, A. Subsethood measure for single valued neutrosophic sets. J. Intell. Fuzzy Syst. 2015, 29, 525–530. [Google Scholar] [CrossRef]
- Sahin, R.; Liu, P. Maximizing deviation method for neutrosophic multiple attribute decision making with incomplete weight information. Neural Comput. Appl. 2016, 27, 2017–2029. [Google Scholar] [CrossRef]
- Sodenkamp, M. Models, Strategies and Applications of Group Multiple-Criteria Decision Analysis in Complex and Uncertain Systems. Ph.D. Dissertation, University of Paderborn, Paderborn, Germany, 2013. [Google Scholar]
- Ye, J. Multicriteria decision-making method using the correlation coefficient under single-valued neutrosophic environment. Int. J. Gen. Syst. 2013, 42, 386–394. [Google Scholar] [CrossRef]
- Jiang, W.; Shou, Y. A Novel single-valued neutrosophic set similarity measure and its application in multi criteria decision-making. Symmetry 2017, 9, 127. [Google Scholar] [CrossRef]
- Ye, J. A multi criteria decision-making method using aggregation operators for simplified neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 2459–2466. [Google Scholar]
- Xu, D.S.; Wei, C.; Wei, G.W. TODIM method for single-valued neutrosophic multiple attribute decision making. Information 2017, 8, 125. [Google Scholar] [CrossRef]
- Ye, J. Bidirectional projection method for multiple attribute group decision making with neutrosophic number. Neural Comput. Appl. 2017, 28, 1021–1029. [Google Scholar] [CrossRef]
- Ye, J. Projection and bidirectional projection measures of single valued neutrosophic sets and their decision—Making method for mechanical design scheme. J. Exp. Theor. Artif. Intell. 2017, 29, 731–740. [Google Scholar] [CrossRef]
- Pramanik, S.; Roy, T.K. Neutrosophic game theoretic approach to Indo-Pak conflict over Jammu-Kashmir. Neutrosoph. Sets Syst. 2014, 2, 82–101. [Google Scholar]
- Mondal, K.; Pramanik, S. Multi-criteria group decision making approach for teacher recruitment in higher education under simplified Neutrosophic environment. Neutrosoph. Sets Syst. 2014, 6, 28–34. [Google Scholar]
- Mondal, K.; Pramanik, S. Neutrosophic decision making model of school choice. Neutrosoph. Sets Syst. 2015, 7, 62–68. [Google Scholar]
- Cheng, H.D.; Guo, Y. A new neutrosophic approach to image thresholding. New Math. Nat. Comput. 2008, 4, 291–308. [Google Scholar] [CrossRef]
- Guo, Y.; Cheng, H.D. New neutrosophic approach to image segmentation. Pattern Recognit. 2009, 42, 587–595. [Google Scholar] [CrossRef]
- Guo, Y.; Sengur, A.; Ye, J. A novel image thresholding algorithm based on neutrosophic similarity score. Measurement 2014, 58, 175–186. [Google Scholar] [CrossRef]
- Ye, J. Single valued neutrosophic minimum spanning tree and its clustering method. J. Intell. Syst. 2014, 23, 311–324. [Google Scholar] [CrossRef]
- Ye, J. Clustering strategies using distance-based similarity measures of single-valued neutrosophic sets. J. Intell. Syst. 2014, 23, 379–389. [Google Scholar]
- Mondal, K.; Pramanik, S. A study on problems of Hijras in West Bengal based on neutrosophic cognitive maps. Neutrosoph. Sets Syst. 2014, 5, 21–26. [Google Scholar]
- Pramanik, S.; Chakrabarti, S. A study on problems of construction workers in West Bengal based on neutrosophic cognitive maps. Int. J. Innov. Res. Sci. Eng. Technol. 2013, 2, 6387–6394. [Google Scholar]
- Maji, P.K. Neutrosophic soft set. Ann. Fuzzy Math. Inform. 2012, 5, 157–168. [Google Scholar]
- Maji, P.K. Neutrosophic soft set approach to a decision-making problem. Ann. Fuzzy Math. Inform. 2013, 3, 313–319. [Google Scholar]
- Sahin, R.; Kucuk, A. Generalized neutrosophic soft set and its integration to decision-making problem. Appl. Math. Inf. Sci. 2014, 8, 2751–2759. [Google Scholar] [CrossRef]
- Dey, P.P.; Pramanik, S.; Giri, B.C. Neutrosophic soft multi-attribute decision making based on grey relational projection method. Neutrosoph. Sets Syst. 2016, 11, 98–106. [Google Scholar]
- Dey, P.P.; Pramanik, S.; Giri, B.C. Neutrosophic soft multi-attribute group decision making based on grey relational analysis method. J. New Results Sci. 2016, 10, 25–37. [Google Scholar]
- Dey, P.P.; Pramanik, S.; Giri, B.C. Generalized neutrosophic soft multi-attribute group decision making based on TOPSIS. Crit. Rev. 2015, 11, 41–55. [Google Scholar]
- Pramanik, S.; Dalapati, S. GRA based multi criteria decision making in generalized neutrosophic soft set environment. Glob. J. Eng. Sci. Res. Manag. 2016, 3, 153–169. [Google Scholar]
- Das, S.; Kumar, S.; Kar, S.; Pal, T. Group decision making using neutrosophic soft matrix: An algorithmic approach. J. King Saud Univ. Comput. Inf. Sci. 2017. [Google Scholar] [CrossRef]
- Şahin, M.; Alkhazaleh, S.; Uluçay, V. Neutrosophic soft expert sets. Appl. Math. 2015, 6, 116–127. [Google Scholar] [CrossRef]
- Pramanik, S.; Dey, P.P.; Giri, B.C. TOPSIS for single valued neutrosophic soft expert set based multi-attribute decision making problems. Neutrosoph. Sets Syst. 2015, 10, 88–95. [Google Scholar]
- Broumi, S.; Smarandache, F. Single valued neutrosophic soft expert sets and their application in decision making. J. New Theory 2015, 3, 67–88. [Google Scholar]
- Ali, M.; Smarandache, F. Complex neutrosophic set. Neural Comput. Appl. 2017, 28, 1817–1831. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F.; Dhar, M. Rough neutrosophic sets. Ital. J. Pure Appl. Math. 2014, 32, 493–502. [Google Scholar]
- Broumi, S.; Smarandache, F.; Dhar, M. Rough neutrosophic sets. Neutrosoph. Sets Syst. 2014, 3, 60–66. [Google Scholar]
- Yang, H.L.; Zhang, C.L.; Guo, Z.L.; Liu, Y.L.; Liao, X. A hybrid model of single valued neutrosophic sets and rough sets: Single valued neutrosophic rough set model. Soft Comput. 2016, 21, 6253–6267. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S. Rough neutrosophic multi-attribute decision-making based on grey relational analysis. Neutrosoph. Sets Syst. 2015, 7, 8–17. [Google Scholar]
- Mondal, K.; Pramanik, S. Rough neutrosophic multi-attribute decision-making based on rough accuracy score function. Neutrosoph. Sets Syst. 2015, 8, 14–21. [Google Scholar]
- Mondal, K.; Pramanik, S.; Smarandache, F. Several trigonometric Hamming similarity measures of rough neutrosophic sets and their applications in decision making. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; Volume 1, pp. 93–103. [Google Scholar]
- Mondal, K.; Pramanik, S.; Smarandache, F. Multi-attribute decision making based on rough neutrosophic variational coefficient similarity measure. Neutrosoph. Sets Syst. 2016, 13, 3–17. [Google Scholar]
- Mondal, K.; Pramanik, S.; Smarandache, F. Rough neutrosophic TOPSIS for multi-attribute group decision making. Neutr. Sets Syst. 2016, 13, 105–117. [Google Scholar]
- Pramanik, S.; Roy, R.; Roy, T.K.; Smarandache, F. Multi criteria decision making using correlation coefficient under rough neutrosophic environment. Neutrosoph. Sets Syst. 2017, 17, 29–36. [Google Scholar]
- Pramanik, S.; Roy, R.; Roy, T.K. Multi criteria decision making based on projection and bidirectional projection measures of rough neutrosophic sets. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2017; Volume II. [Google Scholar]
- Mondal, K.; Pramanik, S. Tri-complex rough neutrosophic similarity measure and its application in multi-attribute decision making. Crit. Rev. 2015, 11, 26–40. [Google Scholar]
- Mondal, K.; Pramanik, S.; Smarandache, F. Rough neutrosophic hyper-complex set and its application to multi-attribute decision making. Crit. Rev. 2016, 13, 111–126. [Google Scholar]
- Wang, J.Q.; Li, X.E. TODIM method with multi-valued neutrosophic sets. Control Decis. 2015, 30, 1139–1142. [Google Scholar]
- Peng, J.J.; Wang, J.Q.; Wu, X.H.; Wang, J.; Chen, X.H. Multi-valued neutrosophic sets and power aggregation operators with their applications in multi-criteria group decision-making problems. Int. J. Comput. Intell. Syst. 2015, 8, 345–363. [Google Scholar] [CrossRef]
- Peng, J.J.; Wang, J. Multi-valued neutrosophic sets and its application in multi-criteria decision-making problems. Neutrosoph. Sets Syst. 2015, 10, 3–17. [Google Scholar] [CrossRef]
- Ye, J. Multiple-attribute decision-making method under a single-valued neutrosophic hesitant fuzzy environment. J. Intell. Syst. 2015, 24, 23–36. [Google Scholar] [CrossRef]
- Sahin, R.; Liu, P. Correlation coefficient of single-valued neutrosophic hesitant fuzzy sets and its applications in decision making. Neural Comput Appl. 2017, 28, 1387–1395. [Google Scholar] [CrossRef]
- Liu, P.; Zhang, L. The extended VIKOR method for multiple criteria decision making problem based on neutrosophic hesitant fuzzy set. arXiv, 2015; arXiv:1512.0139. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. Some distance measures of single valued neutrosophic hesitant fuzzy sets and their applications to multiple attribute decision making. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; pp. 55–63. [Google Scholar]
- Biswas, P.; Pramanik, S.; Giri, B.C. GRA method of multiple attribute decision making with single valued neutrosophic hesitant fuzzy set information. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; pp. 55–63. [Google Scholar]
- Sahin, R.; Liu, P. Distance and similarity measure for multiple attribute with single–valued neutrosophic hesitant fuzzy information. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; pp. 35–54. [Google Scholar]
- Deli, I.; Ali, M.; Smarandache, F. Bipolar neutrosophic sets and their applications based on multi criteria decision making problems. In Proceedings of the 2015 International Conference on Advanced Mechatronic Systems (ICAMechS), Beijing, China, 22–24 August 2015; pp. 249–254. [Google Scholar] [CrossRef]
- Dey, P.P.; Pramanik, S.; Giri, B.C. TOPSIS for solving multi-attribute decision making problems under bi-polar neutrosophic environment. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; pp. 65–77. [Google Scholar]
- Pramanik, S.; Dey, P.P.; Giri, B.C.; Smarandache, F. Bipolar neutrosophic projection based models for solving multi-attribute decision making problems. Neutrosoph. Sets Syst. 2017, 15, 70–79. [Google Scholar]
- Uluçay, V.; Deli, I.; Şahin, M. Similarity measures of bipolar neutrosophic sets and their application to multiple criteria decision making. Neural Comput. Appl. 2016, 1–10. [Google Scholar] [CrossRef]
- Sahin, M.; Deli, I.; Ulucay, V. Jaccard vector similarity measure of bipolar neutrosophic set based on multi-criteria decision making. In Proceedings of the International Conference on Natural Science and Engineering (ICNASE’16), Kilis, Turkey, 19–20 March 2016. [Google Scholar]
- Deli, I.; Subas, Y.A. Multiple criteria decision making method on single valued bipolar neutrosophic set based on correlation coefficient similarity measure. In Proceedings of the International Conference on Mathematics and Mathematics Education (ICMME 2016), Elazg, Turkey, 12–14 May 2016. [Google Scholar]
- Ali, M.; Deli, I.; Smarandache, F. The theory of neutrosophic cubic sets and their applications in pattern recognition. J. Intell. Fuzzy Syst. 2016, 30, 1957–1963. [Google Scholar] [CrossRef]
- Jun, Y.B.; Smarandache, F.; Kim, C.S. Neutrosophic cubic sets. New Math. Nat. Comput. 2017, 13, 41–54. [Google Scholar] [CrossRef]
- Banerjee, D.; Giri, B.C.; Pramanik, S.; Smarandache, F. GRA for multi attribute decision making in neutrosophic cubic set environment. Neutrosoph. Sets Syst. 2017, 15, 60–69. [Google Scholar]
- Pramanik, S.; Dalapati, S.; Alam, S.; Roy, T.K. NC-TODIM-based MAGDM under a neutrosophic cubic set environment. Information 2017, 8, 149. [Google Scholar] [CrossRef]
- Pramanik, S.; Dalapati, S.; Alam, S.; Roy, T.K.; Smarandache, F. Neutrosophic cubic MCGDM method based on similarity measure. Neutrosoph. Sets Syst. 2017, 16, 44–56. [Google Scholar]
- Lu, Z.; Ye, J. Cosine measures of neutrosophic cubic sets for multiple attribute decision-making. Symmetry 2017, 9, 121. [Google Scholar]
- Pramanik, S.; Dey, P.P.; Giri, B.C.; Smarandache, F. An Extended TOPSIS for Multi-Attribute Decision Making Problems with Neutrosophic Cubic Information. Neutrosoph. Sets Syst. 2017, 17, 20–28. [Google Scholar]
- Zhan, J.; Khan, M.; Gulistan, M. Applications of neutrosophic cubic sets in multi-criteria decision-making. Int. J. Uncertain. Quantif. 2017, 7, 377–394. [Google Scholar] [CrossRef]
- Ye, J. Linguistic neutrosophic cubic numbers and their multiple attribute decision-making method. Information 2017, 8, 110. [Google Scholar] [CrossRef]
- Pramanik, S.; Dalapati, S.; Alam, S.; Roy, T.K. TODIM method for group decision making under bipolar neutrosophic set environment. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2017; Volume II. [Google Scholar]
- Chinnadurai, V.; Swaminathan, A.; Anu, B. Some properties of neutrosophic cubic soft set. Int. J. Comput. Res. Dev. 2016, 1, 113–119. [Google Scholar]
- Pramanik, S.; Dalapati, S.; Alam, S.; Roy, T.K. Some operations and properties of neutrosophic cubic soft set. Glob. J. Res. Rev. 2017, 4, 1–8. [Google Scholar] [CrossRef]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Interval Neutrosophic Sets and Logic: Theory and Applications in Computing; Hexis: Phoenix, AZ, USA, 2005. [Google Scholar]
- Deli, I. Interval-valued neutrosophic soft sets and its decision making. Int. J. Mach. Learn. Cybern. 2017, 8, 665. [Google Scholar] [CrossRef]
- Ali, M.; Dat, L.Q.; Son, L.H.; Smarandache, F. Interval complex neutrosophic set: Formulation and applications in decision-making. Int. J. Fuzzy Syst. 2017, 1–14. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F. Interval neutrosophic rough set. Neutrosoph. Sets Syst. 2015, 7, 23–31. [Google Scholar] [CrossRef]
- Pramanik, S.; Mondal, K. Interval neutrosophic multi-attribute decision-making based on grey relational analysis. Neutrosoph. Sets Syst. 2015, 9, 13–22. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S. Decision making based on some similarity measures under interval rough neutrosophic environment. Neutrosoph. Sets Syst. 2015, 10, 46–57. [Google Scholar] [CrossRef]
- Ye, J. Correlation coefficients of interval neutrosophic hesitant fuzzy sets and its application in a multiple attribute decision making method. Informatica 2016, 27, 179–202. [Google Scholar] [CrossRef]
- Biswas, P.; Pramanik, S.; Giri, B.C. Cosine similarity measure based multi-attribute decision-making with trapezoidal fuzzy neutrosophic numbers. Neutrosoph. Sets Syst. 2015, 8, 47–57. [Google Scholar]
- Ye, J. Trapezoidal neutrosophic set and its application to multiple attribute decision-making. Neural Comput. Appl. 2015, 26, 1157–1166. [Google Scholar] [CrossRef]
- Liu, P.D.; Teng, F. Multiple attribute decision making method based on normal neutrosophic generalized weighted power averaging operator. Int. J. Mach. Learn. Cybern. 2015, 1–13. [Google Scholar] [CrossRef]
- Ye, J. An extended TOPSIS method for multiple attribute group decision making based on single valued neutrosophic linguistic numbers. J. Intell. Fuzzy Syst. 2015, 28, 247–255. [Google Scholar]
- Ye, J. Some aggregation operators of interval neutrosophic linguistic numbers for multiple attribute decision making. J. Intell. Fuzzy Syst. 2014, 27, 2231–2241. [Google Scholar]
- Ma, Y.X.; Wang, J.Q.; Wang, J.; Wu, X.H. An interval neutrosophic linguistic multi-criteria group decision-making method and its application in selecting medical treatment options. Neural Comput. Appl. 2017, 28, 2745–2765. [Google Scholar] [CrossRef]
- Tian, Z.P.; Wang, J.; Zhang, H.Y.; Chen, X.H.; Wang, J.Q. Simplified neutrosophic linguistic normalized weighted Bonferroni mean operator and its application to multi-criteria decision making problems. Filomat 2015, 30, 3339–3360. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F. Single valued neutrosophic trapezoid linguistic aggregation operators based on multi-attribute decision making. Bull. Pure Appl. Sci. Math. Stat. 2014, 33, 135–155. [Google Scholar] [CrossRef]
- Broumi, S.; Smarandache, F. An extended TOPSIS method for multiple attribute decision making based on interval neutrosophic uncertain linguistic variables. Neutrosoph. Sets Syst. 2015, 8, 22–31. [Google Scholar]
- Ye, J. Multiple attribute group decision making based on interval neutrosophic uncertain linguistic variables. Int. J. Mach. Learn. Cybern. 2017, 8, 837–848. [Google Scholar] [CrossRef]
- Dey, P.P.; Pramanik, S.; Giri, B.C. An extended grey relational analysis based multiple attribute decision making in interval neutrosophic uncertain linguistic setting. Neutrosoph. Sets Syst. 2016, 11, 21–30. [Google Scholar]
- Deli, I.; Broumi, S.; Smarandache, F. On neutrosophic refined sets and their applications in medical diagnosis. J. New Theory 2015, 6, 88–98. [Google Scholar]
- Broumi, S.; Deli, I. Correlation measure for neutrosophic refined sets and its application in medical diagnosis. Palest. J. Math. 2016, 5, 135–143. [Google Scholar]
- Pramanik, S.; Banerjee, D.; Giri, B.C. TOPSIS approach for multi attribute group decision making in refined neutrosophic environment. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium, 2016; pp. 79–91. [Google Scholar]
- Pramanik, S.; Banerjee, D.; Giri, B.C. Multi–criteria group decision making model in neutrosophic refined set and its application. Glob. J. Eng. Sci. Res. Manag. 2016, 3, 12–18. [Google Scholar] [CrossRef]
- Mondal, K.; Pramanik, S. Neutrosophic refined similarity measure based on tangent function and its application to multi-attribute decision making. J. New Theory 2015, 8, 41–50. [Google Scholar]
- Mondal, K.; Pramanik, S. Neutrosophic refined similarity measure based on cotangent function and its application to multi-attribute decision making. Glob. J. Adv. Res. 2015, 2, 486–494. [Google Scholar]
- Mondal, K.; Pramanik, S.; Giri, B.C. Multi-criteria group decision making based on linguistic refined neutrosophic strategy. In New Trends in Neutrosophic Theory and Applications; Smarandache, F., Pramanik, S., Eds.; Pons Editions: Brussels, Belgium; Volume II, in press.
- Şubaş, Y.; Deli, I. Bipolar neutrosophic refined sets and their applications in medical diagnosis. In Proceedings of the International Conference on Natural Science and Engineering (ICNASE’16), Kilis, Turkey, 19–20 March 2016; pp. 1121–1132. [Google Scholar]
- Ye, J. Correlation coefficient between dynamic single valued neutrosophic multisets and its multiple attribute decision-making method. Information 2017, 8, 41. [Google Scholar] [CrossRef]
- Majumdar, P.; Samanta, S.K. On similarity and entropy of neutrosophic sets. J. Intell. Fuzzy Syst. 2014, 26, 1245–1252. [Google Scholar]
- Ye, J. Single valued neutrosophic cross-entropy for multi criteria decision making problems. Appl. Math. Model. 2013, 38, 1170–1175. [Google Scholar] [CrossRef]
- Ye, J. Improved cross entropy measures of single valued neutrosophic sets and interval neutrosophic sets and their multi criteria decision making methods. Cybern. Inf. Technol. 2015, 15, 13–26. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pramanik, S.; Dalapati, S.; Alam, S.; Smarandache, F.; Roy, T.K. NS-Cross Entropy-Based MAGDM under Single-Valued Neutrosophic Set Environment. Information 2018, 9, 37. https://doi.org/10.3390/info9020037
Pramanik S, Dalapati S, Alam S, Smarandache F, Roy TK. NS-Cross Entropy-Based MAGDM under Single-Valued Neutrosophic Set Environment. Information. 2018; 9(2):37. https://doi.org/10.3390/info9020037
Chicago/Turabian StylePramanik, Surapati, Shyamal Dalapati, Shariful Alam, Florentin Smarandache, and Tapan Kumar Roy. 2018. "NS-Cross Entropy-Based MAGDM under Single-Valued Neutrosophic Set Environment" Information 9, no. 2: 37. https://doi.org/10.3390/info9020037