Distributed State Estimation under State Inequality Constraints with Random Communication over Multi-Agent Networks
Abstract
:1. Introduction
2. Problem Formulation
2.1. Preliminaries
- (i)
- , for all ;
- (ii)
- , for all x and z;
- (iii)
- , for any .
2.2. Problem Formulation
3. Distributed Algorithms
3.1. Random Sleep Algorithm
| Algorithm 1 KCF with constraints via RS (RSKCF) |
At time k, a prior information Initialization , ; Random Sleep on Measurement Collection Random Sleep on Consensus Projection |
3.2. Stochastic Event-Triggered Scheme
| Algorithm 2 KCF with constraints via stochastic event-triggered scheme |
Initialization ; Local Estimation Consensus Projection |
4. Performance Analysis
4.1. Random Sleep Scheme
4.2. Event-Triggered Scheme
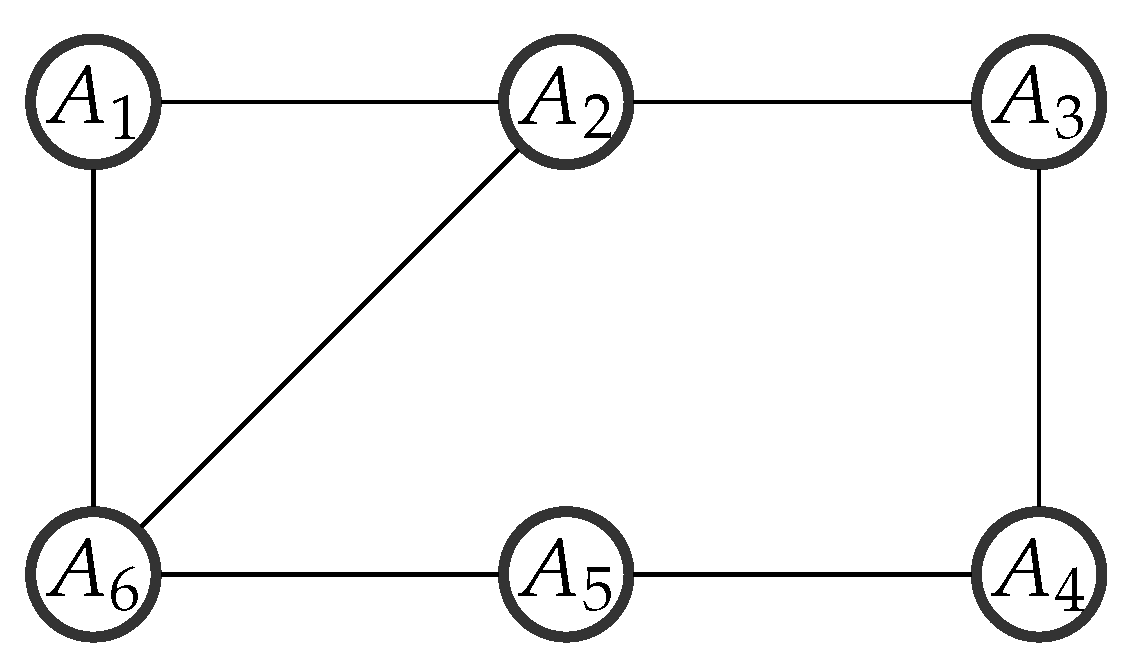
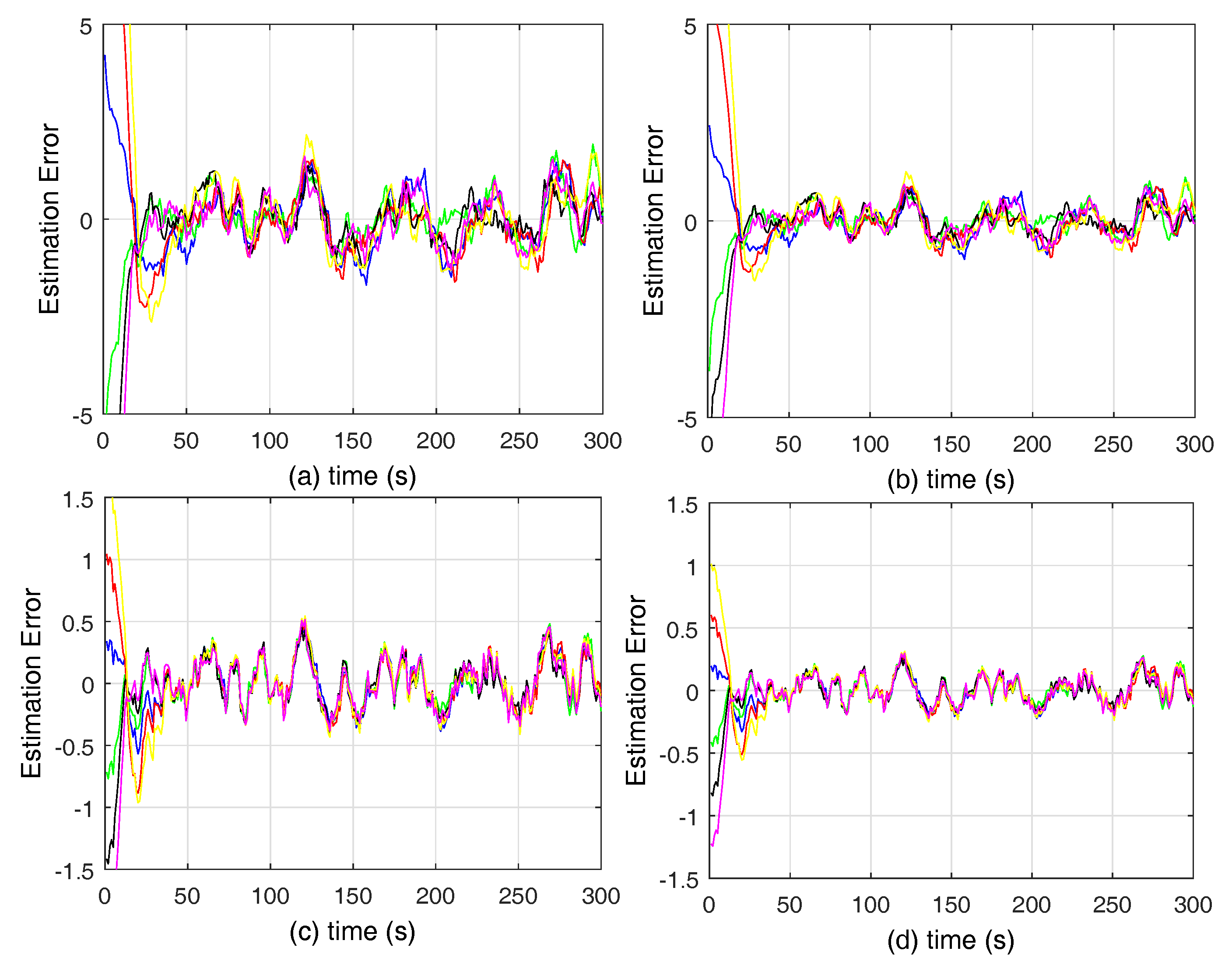
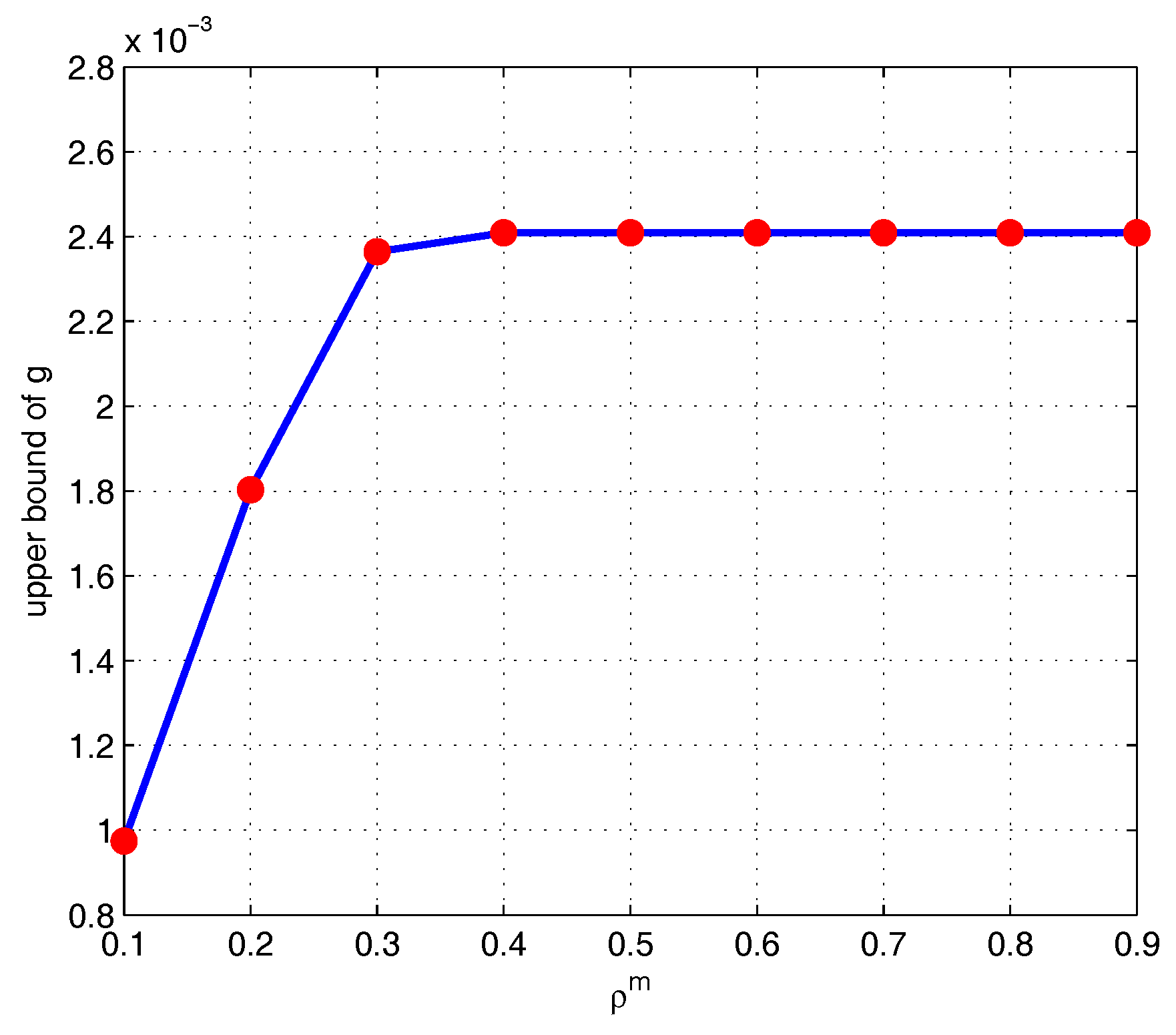
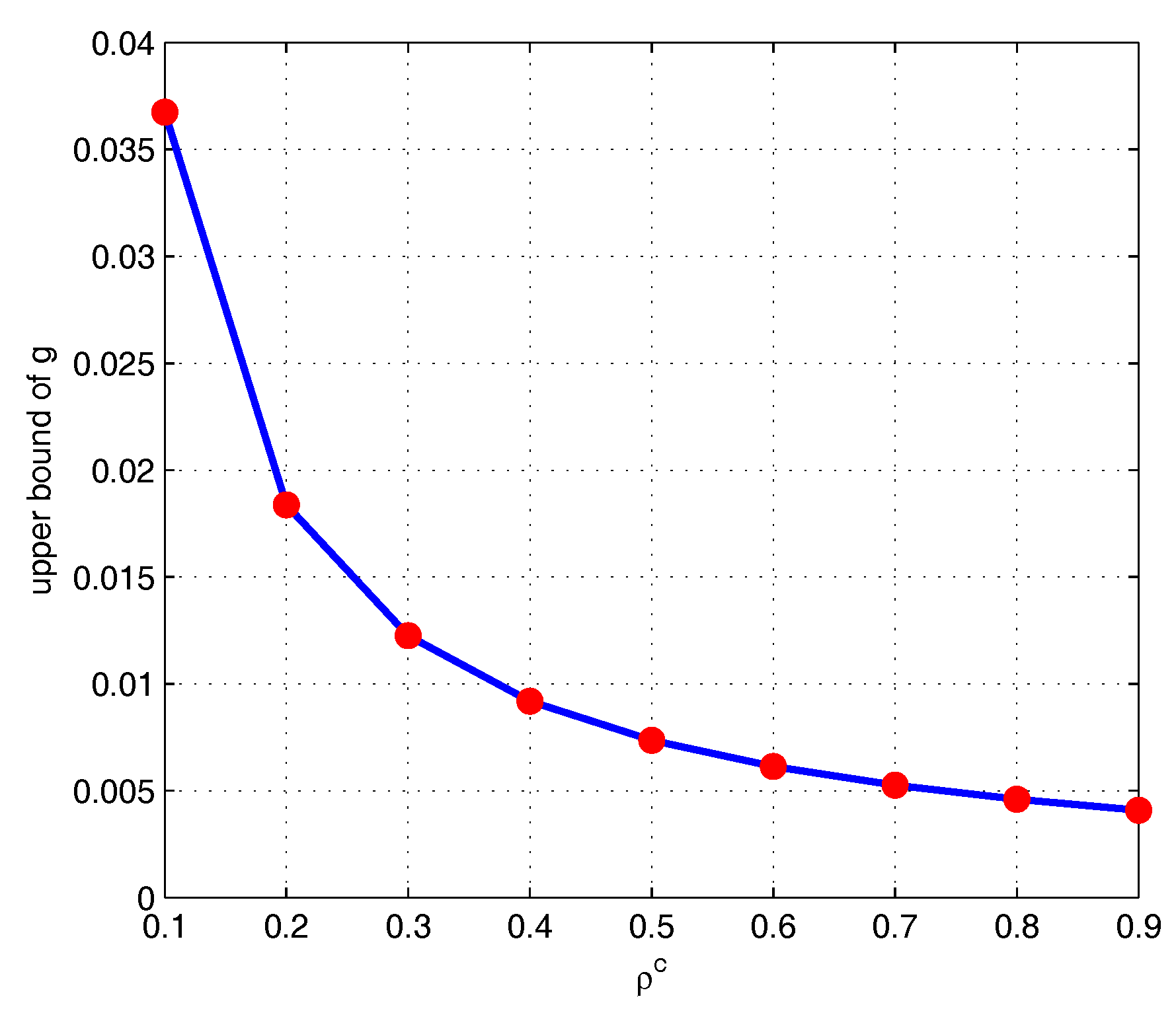
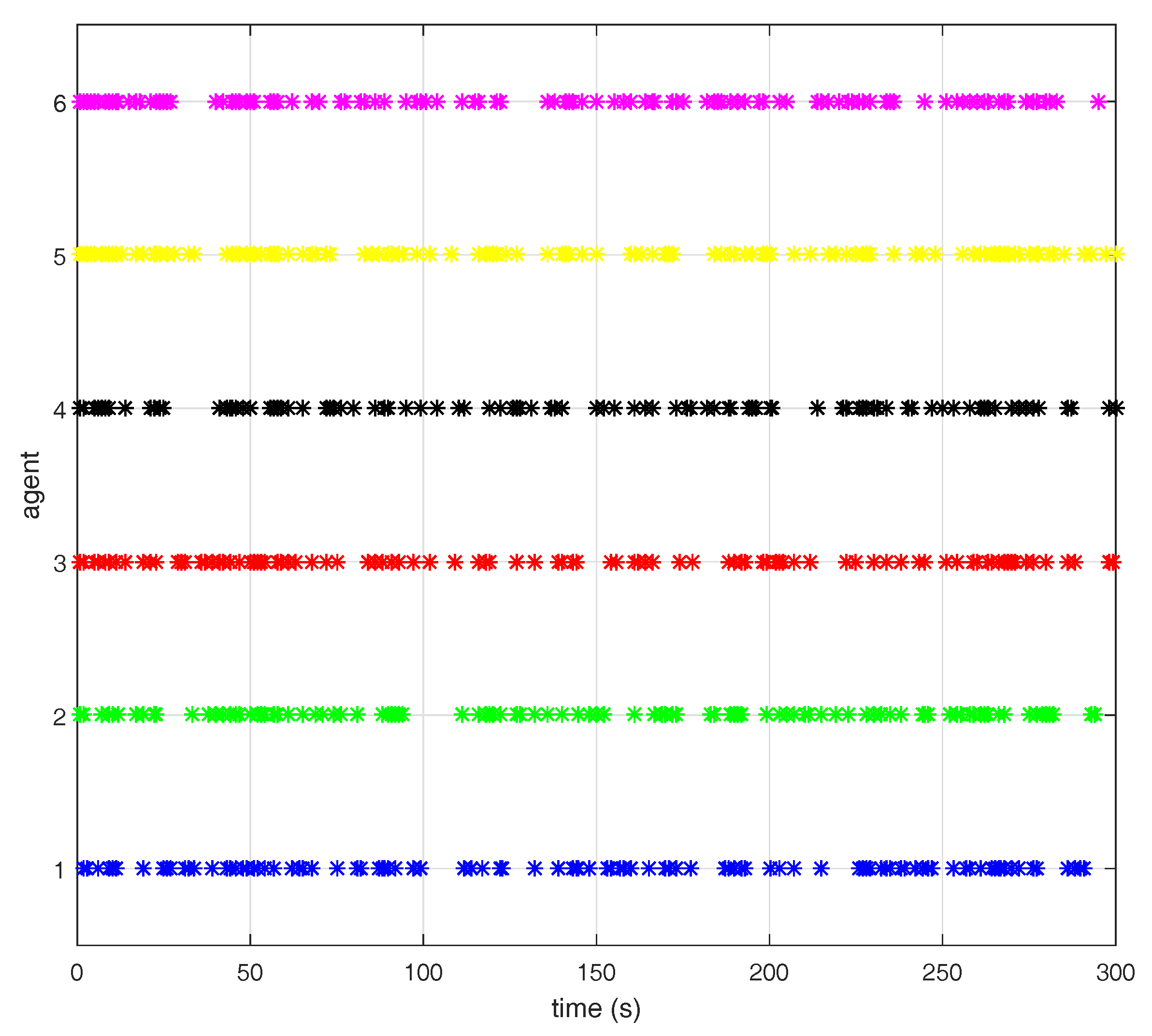
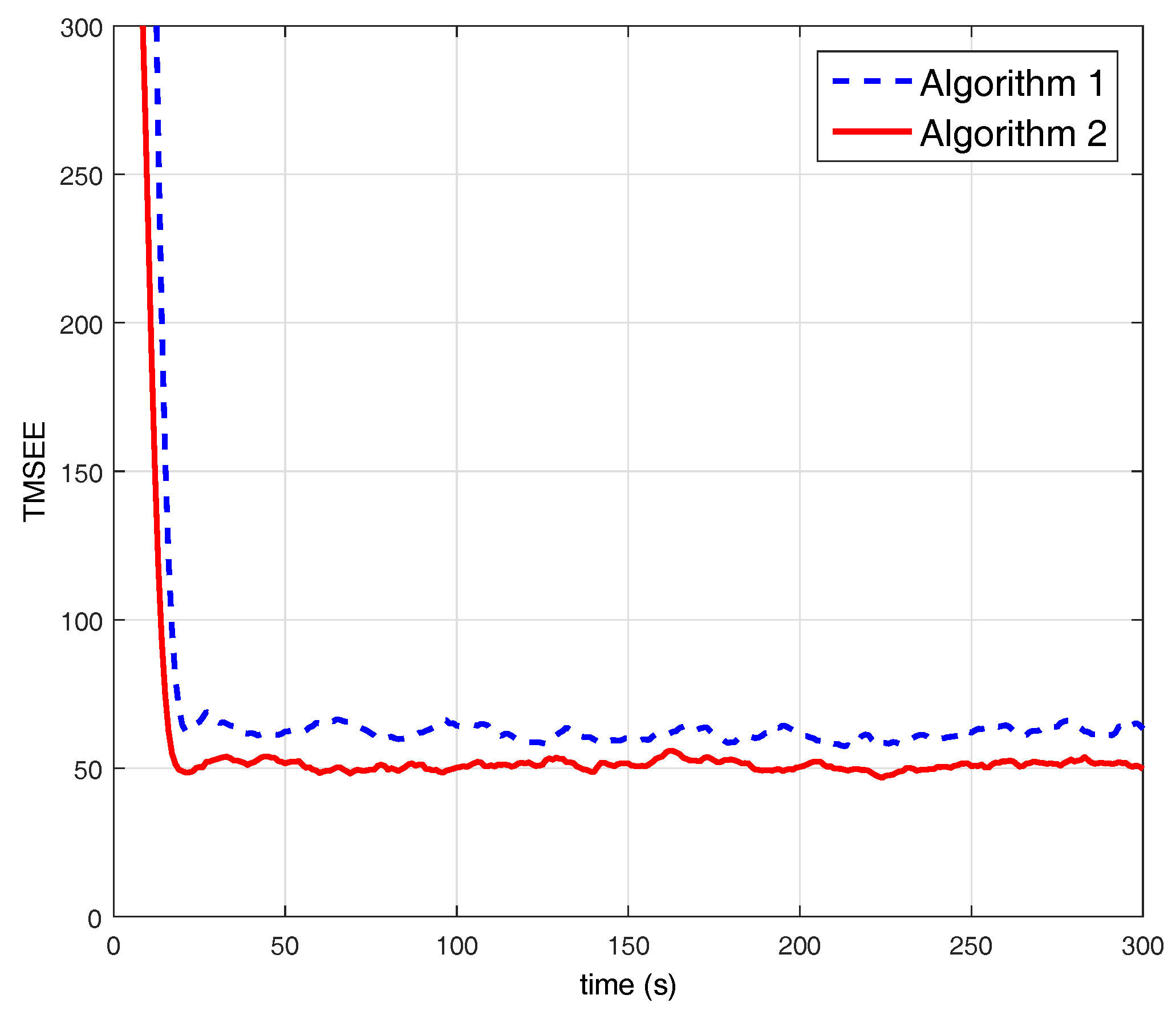
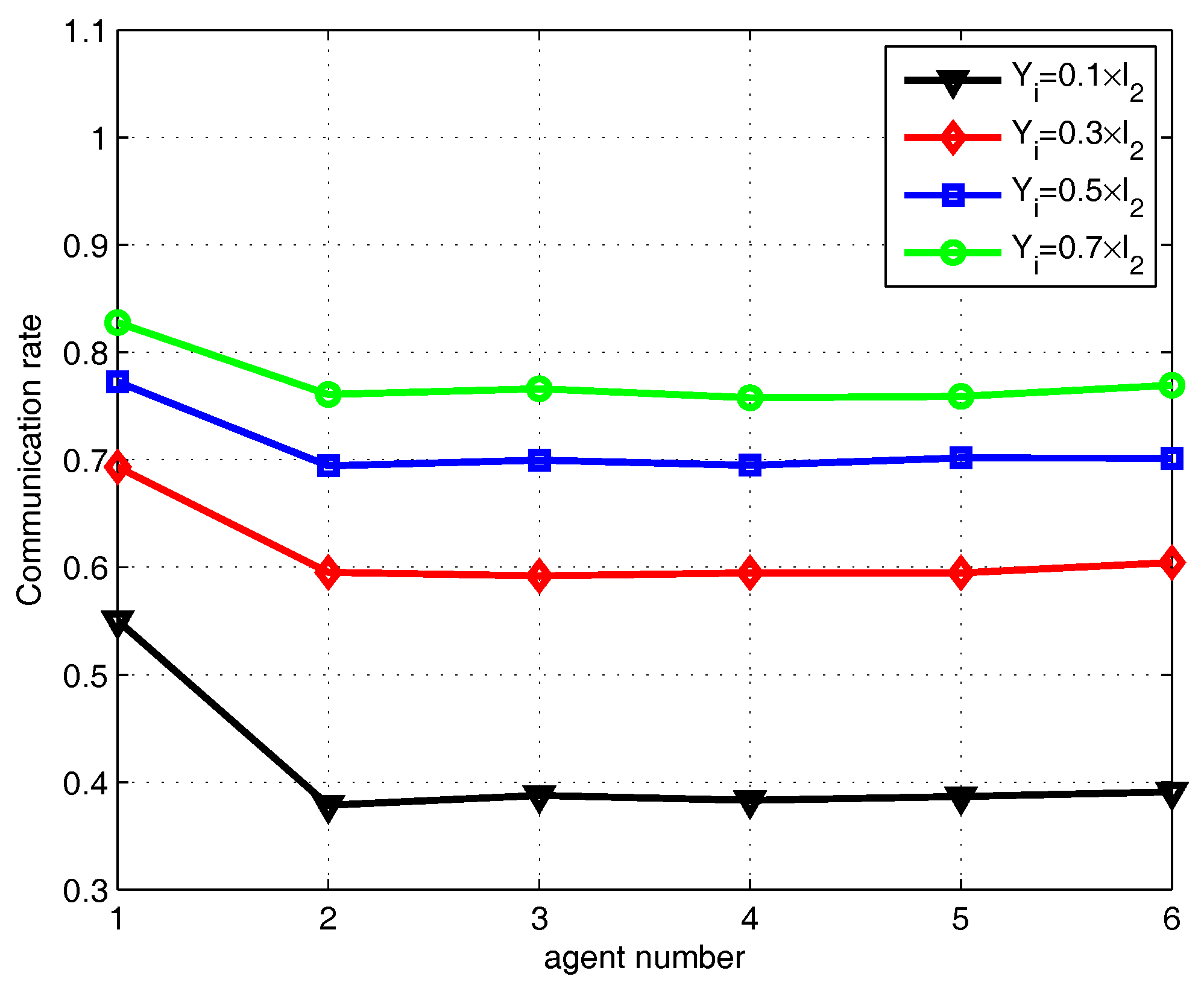
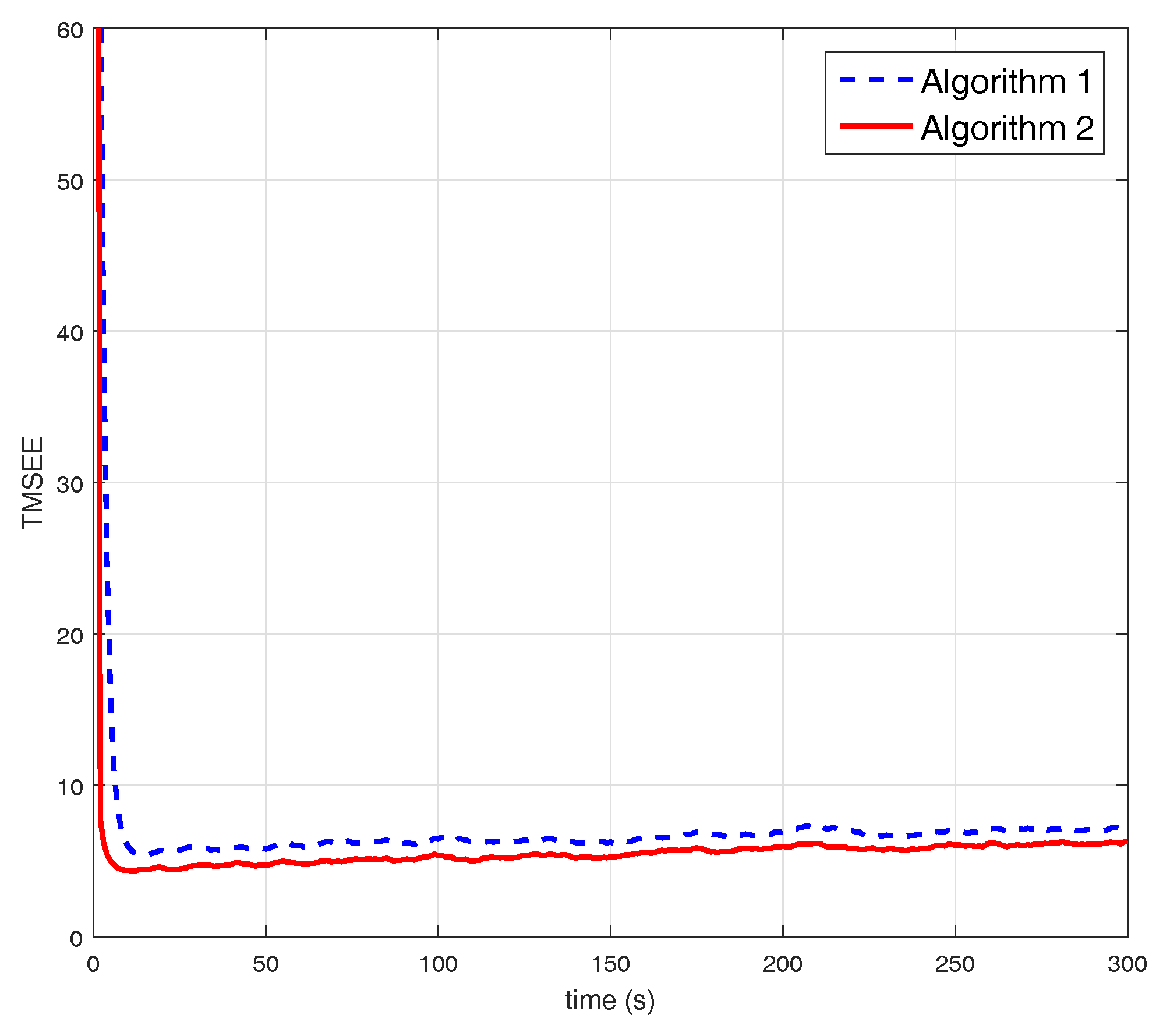
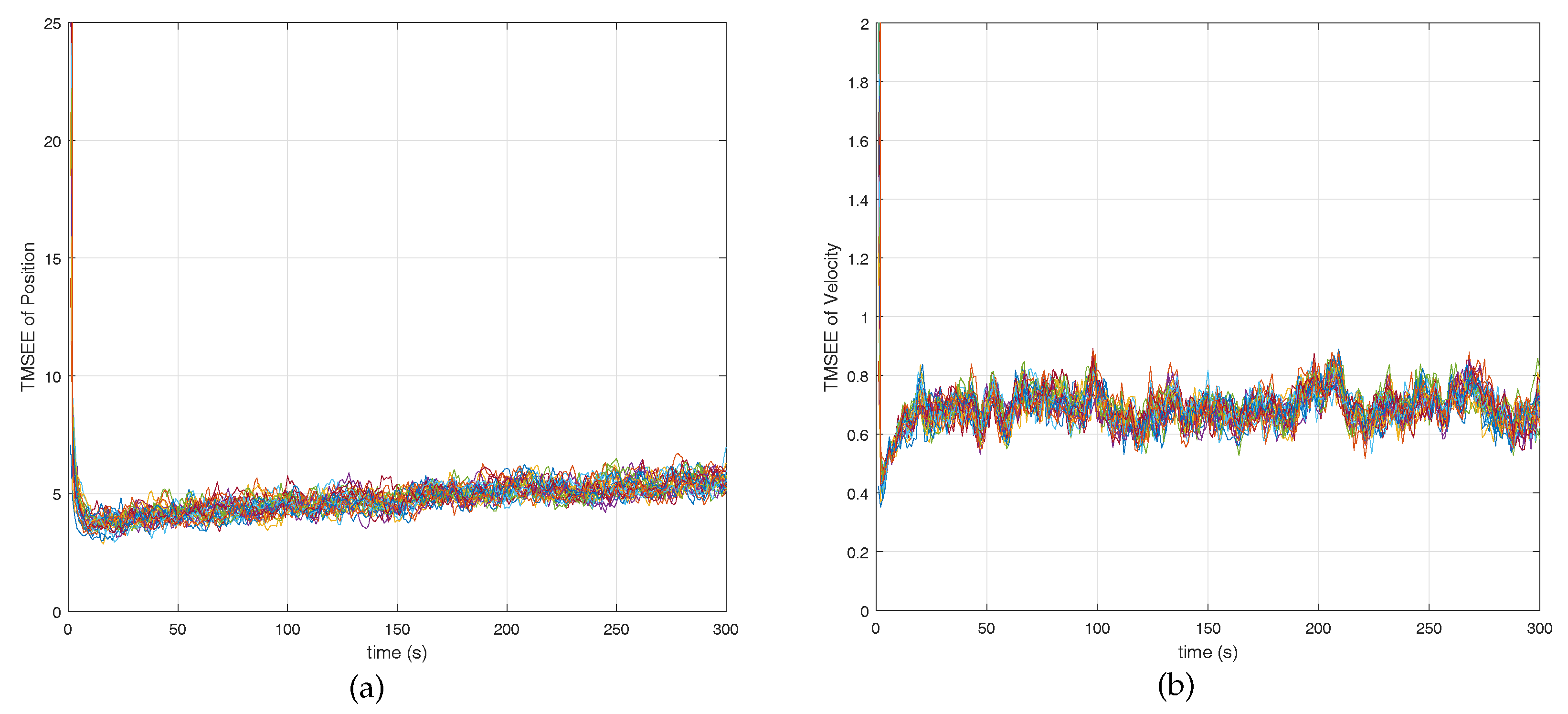
5. Simulations
6. Discussion
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Proof of Lemma 5
References
- Olfati-Saber, R. Distributed Kalman filtering for sensor networks. In Proceedings of the IEEE Conference on Decision and Control, New Orleans, LA, USA, 12–14 December 2007; pp. 5492–5498. [Google Scholar]
- Olfati-Saber, R. Kalman-consensus filter: Optimality, stability, and performance. In Proceedings of the Joint IEEE Conference on Decision and Control and Chinese Control Conference, Shanghai, China, 15–18 Decmber 2009; pp. 7036–7042. [Google Scholar]
- Cattivelli, F.; Sayed, A. Diffusion strategies for distributed Kalman filtering and smoothing. IEEE Trans. Autom. Control 2010, 55, 2069–2084. [Google Scholar] [CrossRef]
- Hu, J.; Xie, L.; Zhang, C. Diffusion Kalman Filtering Based on Covariance Intersection. IEEE Trans. Signal Process. 2012, 60, 891–902. [Google Scholar] [CrossRef]
- Yang, W.; Chen, G.; Wang, X.; Shi, L. Stochastic sensor activation for distributed state estimation over a sensor network. Automatica 2014, 50, 2070–2076. [Google Scholar] [CrossRef]
- Stanković, S.; Stanković, M.; Stipanović, D. Consensus based overlapping decentralized estimation with missing observations and communication faults. Automatica 2009, 45, 1397–1406. [Google Scholar] [CrossRef]
- Zhou, Z.; Fang, H.; Hong, Y. Distributed estimation for moving target based on state-consensus strategy. IEEE Trans. Autom. Control 2013, 58, 2096–2101. [Google Scholar] [CrossRef]
- Hu, C.; Qin, W.; He, B.; Liu, G. Distributed H∞ estimation for moving target under switching multi-agent network. Kybernetika 2014, 51, 814–819. [Google Scholar]
- Yang, W.; Yang, C.; Shi, H.; Shi, L.; Chen, G. Stochastic link activation for distributed filtering under sensor power constraint. Automatica 2017, 75, 109–118. [Google Scholar] [CrossRef]
- Ji, H.; Lewis, F.L.; Hou, Z.; Mikulski, D. Distributed information-weighted Kalman consensus filter for sensor networks. Automatica 2017, 77, 18–30. [Google Scholar] [CrossRef]
- Hu, C.; Qin, W.; Li, Z.; He, B.; Liu, G. Consensus-based state estimation for multi-agent systems with constraint information. Kybernetika 2017, 53, 545–561. [Google Scholar] [CrossRef]
- Das, S.; Moura, J.M. Distributed Kalman filtering with dynamic observations consensus. IEEE Trans. Signal Process. 2015, 63, 4458–4473. [Google Scholar]
- Das, S.; Moura, J.M. Consensus+ innovations distributed Kalman filter with optimized gains. IEEE Trans. Signal Process. 2017, 65, 467–481. [Google Scholar] [CrossRef]
- Dong, H.; Wang, Z.; Gao, H. Distributed Filtering for a Class of Time-Varying Systems Over Sensor Networks With Quantization Errors and Successive Packet Dropouts. IEEE Trans. Signal Process. 2012, 60, 3164–3173. [Google Scholar] [CrossRef]
- Lou, Y.; Shi, G.; Johansson, K.; Henrik, K.; Hong, Y. Convergence of random sleep algorithms for optimal consensus. Syst. Control Lett. 2013, 62, 1196–1202. [Google Scholar] [CrossRef]
- Yi, P.; Hong, Y. Stochastic sub-gradient algorithm for distributed optimization with random sleep scheme. Control Theory Technol. 2015, 13, 333–347. [Google Scholar] [CrossRef]
- Wu, J.; Jia, Q.; Johansson, K.; Shi, L. Event-based sensor data scheduling: Trade-off between communication rate and estimation quality. IEEE Trans. Autom. Control 2013, 58, 1041–1046. [Google Scholar] [CrossRef]
- Han, D.; Mo, Y.; Wu, J.; Weerakkody, S.; Sinopoli, B.; Shi, L. Stochastic event-triggered sensor schedule for remote state estimation. IEEE Trans. Autom. Control 2015, 60, 2661–2675. [Google Scholar] [CrossRef]
- Julier, S.; LaViola, J. On Kalman filtering with nonlinear equality constraints. IEEE Trans. Signal Process. 2007, 55, 2774–2784. [Google Scholar] [CrossRef]
- Simon, D.; Chia, T.L. Kalman filtering with state equality constraints. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 128–136. [Google Scholar] [CrossRef]
- Ko, S.; Bitmead, R. State estimation for linear systems with state equality constraints. Automatica 2007, 43, 1363–1368. [Google Scholar] [CrossRef]
- Rao, C.; Rawlings, J.; Lee, J. Constrained linear state estimation—A moving horizon approach. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 1619–1628. [Google Scholar] [CrossRef]
- Simon, D. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Nedić, A.; Ozdaglar, A.; Parrilo, P. Constrained consensus and optimization in multi-agent networks. IEEE Trans. Autom. Control 2010, 55, 922–938. [Google Scholar] [CrossRef]
- Bell, B.; Burke, J.; Pillonetto, G. An inequality constrained nonlinear Kalman-Bucy smoother by interior point likelihood maximization. Automatica 2009, 45, 25–33. [Google Scholar] [CrossRef]
- Simon, D.; Simon, D. Kalman filtering with inequality constraints for turbofan engine health estimation. IEE Proc. Control Theory Appl. 2006, 153, 371–378. [Google Scholar] [CrossRef]
- Goodwin, G.; Seron, M.; Doná, J.D. Constrained Control and Estimation: An Optimisation Approach; Springer: New York, NY, USA, 2006. [Google Scholar]
- Godsil, C.; Royle, G. Algebraic Graph Theory; Springer: New York, NY, USA, 2001. [Google Scholar]
- Sinopoli, B.; Schenato, L.; Franceschetti, M.; Poolla, K.; Jordan, M.I.; Sastry, S.S. Kalman filtering with intermittent observations. IEEE Trans. Autom. Control 2004, 49, 1453–1464. [Google Scholar] [CrossRef]
- Agniel, R.; Jury, E. Almost sure boundedness of randomly sampled systems. SIAM J. Control 1971, 9, 372–384. [Google Scholar] [CrossRef]
- Tarn, T.; Rasis, Y. Observers for nonlinear stochastic systems. IEEE Trans. Autom. Control 1976, 21, 441–448. [Google Scholar] [CrossRef]
- Reif, K.; Günther, S.; Yaz, E.; Unbehauen, R. Stochastic stability of the discrete-time extended Kalman filter. IEEE Trans. Autom. Control 1999, 44, 714–728. [Google Scholar] [CrossRef]
- Yang, C.; Blasch, E. Kalman filtering with nonlinear state constraints. IEEE Trans. Aerosp. Electron. Syst. 2009, 45, 70–84. [Google Scholar] [CrossRef]
- Liu, Q.; Wang, Z.; He, X.; Zhou, D. Event-based distributed filtering with stochastic measurement fading. IEEE Trans. Ind. Inform. 2015, 11, 1643–1652. [Google Scholar] [CrossRef]
- Meng, X.; Chen, T. Optimality and stability of event triggered consensus state estimation for wireless sensor networks. In Proceedings of the American Control Conference, Portland, OR, USA, 4–6 June 2014; pp. 3565–3570. [Google Scholar]
- Gutiérrez Cosio, C.; García Magariño, I. A metrics suite for the communication of multi-agent systems. J. Phys. Agents 2009, 3, 7–14. [Google Scholar] [CrossRef]
- Ding, L.; Zheng, W.X.; Guo, G. Network-based practical set consensus of multi-agent systems subject to input saturation. Automatica 2018, 89, 316–324. [Google Scholar] [CrossRef]
- Lakhlef, H.; Bouabdallah, A.; Raynal, M.; Bourgeois, J. Agent-based broadcast protocols for wireless heterogeneous node networks. Comput. Commun. 2018, 115, 51–63. [Google Scholar] [CrossRef]
- García-Magariño, I.; Gutiérrez, C. Agent-oriented modeling and development of a system for crisis management. Expert Syst. Appl. 2013, 40, 6580–6592. [Google Scholar] [CrossRef]
- Lewis, F.; Xie, L.; Popa, D. Optimal and Robust Estimation: With an Introduction to Stochastic Control Theory; CRC Press: Boca Raton, FL, USA, 2008. [Google Scholar]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, C.; Li, Z.; Lin, H.; He, B.; Liu, G. Distributed State Estimation under State Inequality Constraints with Random Communication over Multi-Agent Networks. Information 2018, 9, 64. https://doi.org/10.3390/info9030064
Hu C, Li Z, Lin H, He B, Liu G. Distributed State Estimation under State Inequality Constraints with Random Communication over Multi-Agent Networks. Information. 2018; 9(3):64. https://doi.org/10.3390/info9030064
Chicago/Turabian StyleHu, Chen, Zhenhua Li, Haoshen Lin, Bing He, and Gang Liu. 2018. "Distributed State Estimation under State Inequality Constraints with Random Communication over Multi-Agent Networks" Information 9, no. 3: 64. https://doi.org/10.3390/info9030064



