Steady-State Anderson Accelerated Coupling of Lattice Boltzmann and Navier–Stokes Solvers
Abstract
:1. Introduction
2. Materials and Methods
2.1. Navier–Stokes
| Algorithm 1 Navier–Stokes time stepping scheme |
| while do set boundary conditions assemble right hand side of Poisson equation solve Poisson equation () do time step for velocities () end while |
2.2. Lattice Boltzmann
2.3. Coupling Strategies
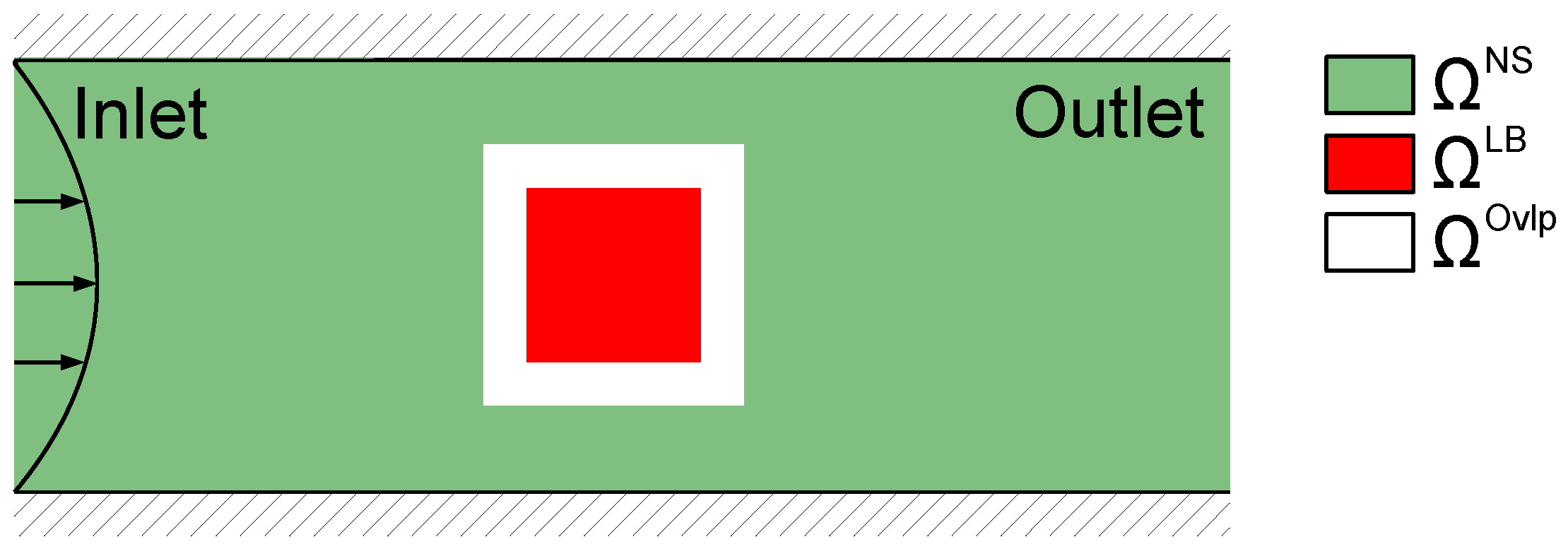
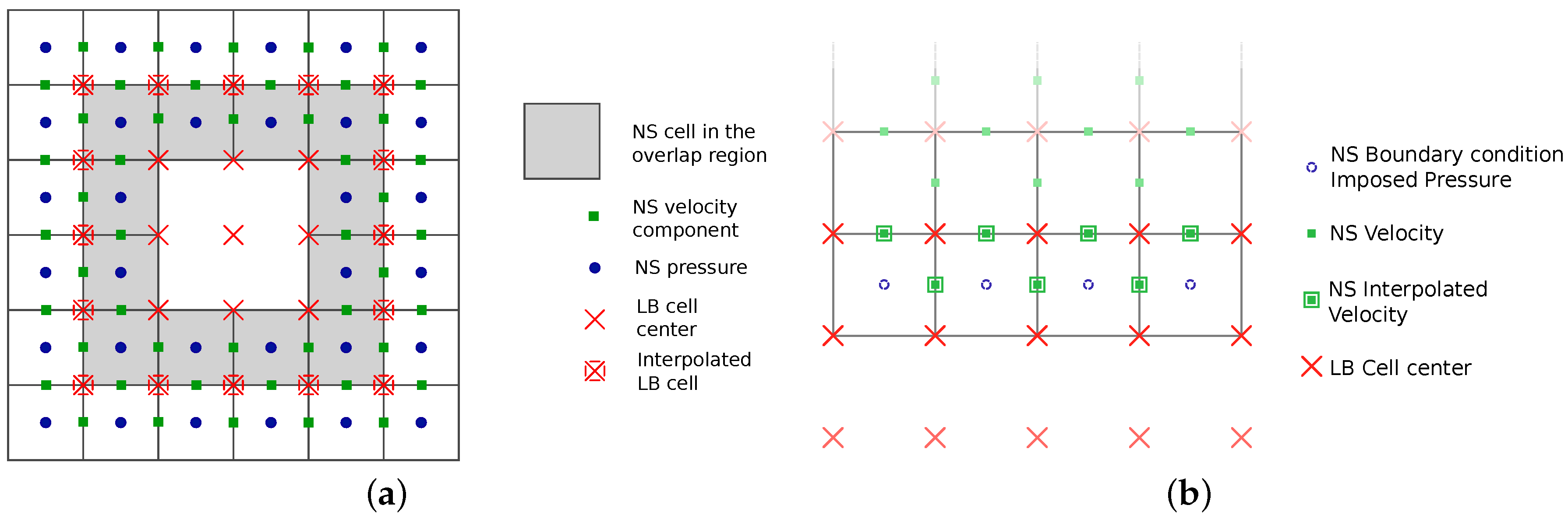
2.3.1. Spatial Coupling: General Methodology
Domain Decomposition, Interpolation and Unit Conversion
From Lattice Boltzmann to Navier–Stokes
From Navier–Stokes to Lattice Boltzmann
2.3.2. Sequential Coupling
| Algorithm 2 Sequential Schwarz coupling |
| while global solution not converged do while LB not at steady-state do solve LB end while send data from LB to NS and init boundaries while NS not at steady-state do solve NS end while send data from NS to LB and init boundaries end while |
2.3.3. Parallel Coupling
| Algorithm 3 Parallel Schwarz coupling |
| while global solution not converged do send data from LB/NS to NS/LB and init boundaries while LB and NS not at steady-state do solve LB and NS simultaneously end while end while |
2.3.4. Anderson Accelerated Coupling
| Algorithm 4 Parallel Anderson accelerated coupling |
| while global solution not converged do send data from LB/NS to NS/LB and init boundaries while LB and NS not at steady-state do solve LB and NS simultaneously end while perform Anderson acceleration with LB and NS data end while |
| Algorithm 5 Anderson acceleration in pseudocode |
| , initial value , , and while fixed-point iteration (global solution) not converged do // send data from LB/NS to NS/LB and solve LB/NS simultaneously and // perform Anderson acceleration with with decompose solve the first k lines of end while |
3. Results
3.1. Implementation
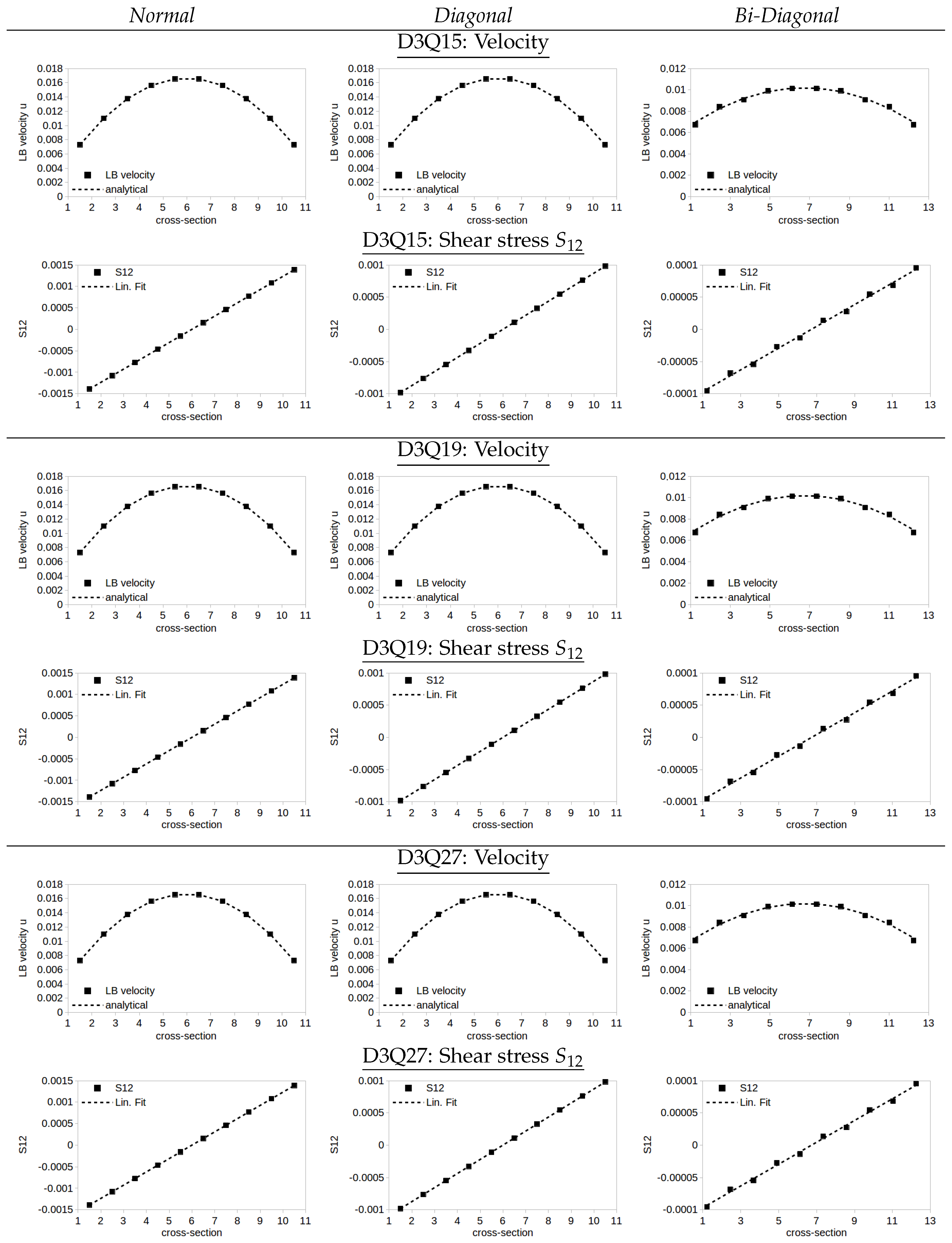
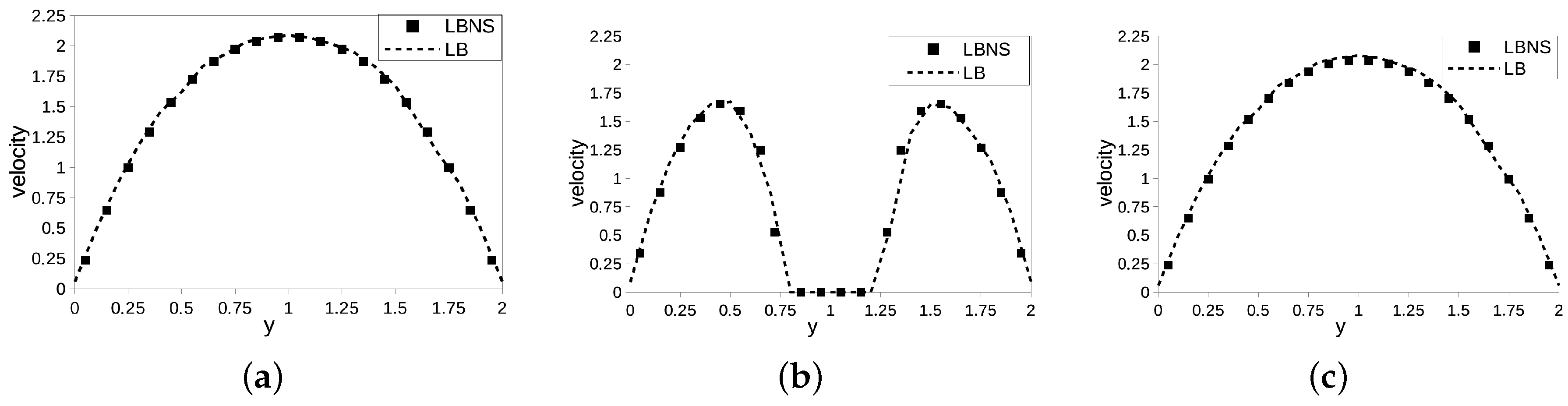
3.2. Validation: Optimization-Based LB Boundary Conditions
- Normal: the LB grid is aligned with the plates and the main flow direction, cf. Figure 3a. The main flow direction is thus given by .
- Diagonal: the LB grid is rotated away from the main flow axis and kept aligned with the plates, cf. Figure 3b. The main flow direction is hence parallel to .
- Bi-Diagonal: the LB grid is rotated such that only one corner is placed on each boundary plane, cf. Figure 3c. The main flow direction is aligned with , the normal of the plates is given by .
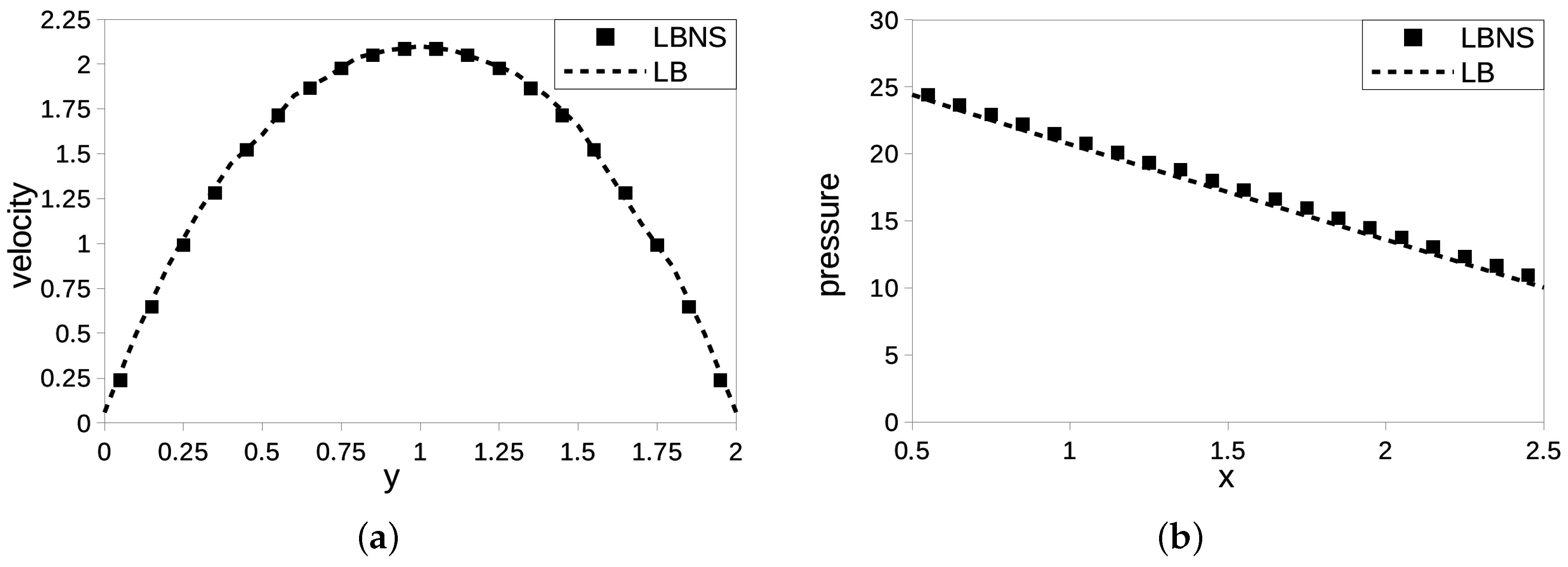
3.3. LBNS Validation: Plane Channel
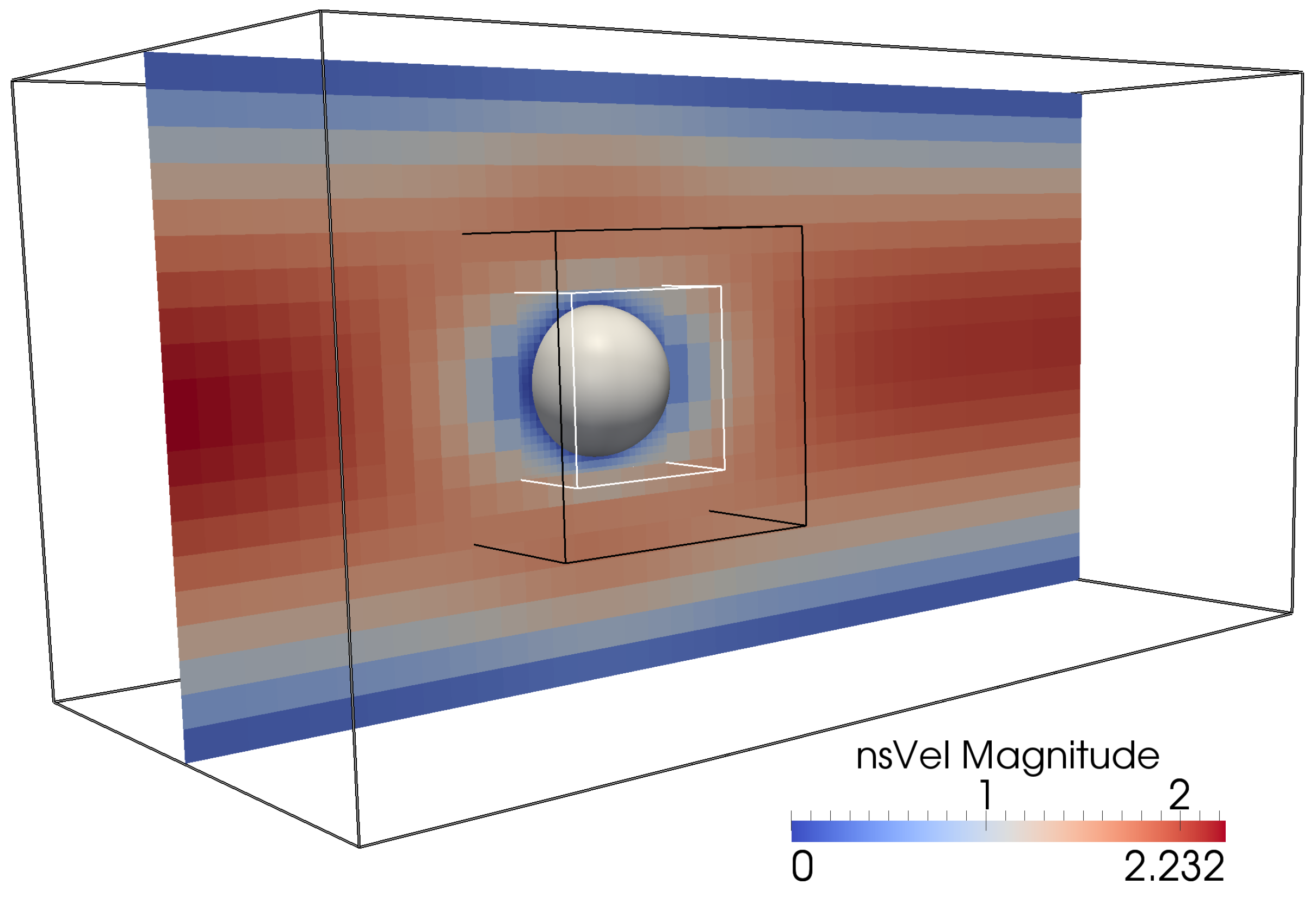
3.4. LBNS: Flow Past Spherical Obstacle
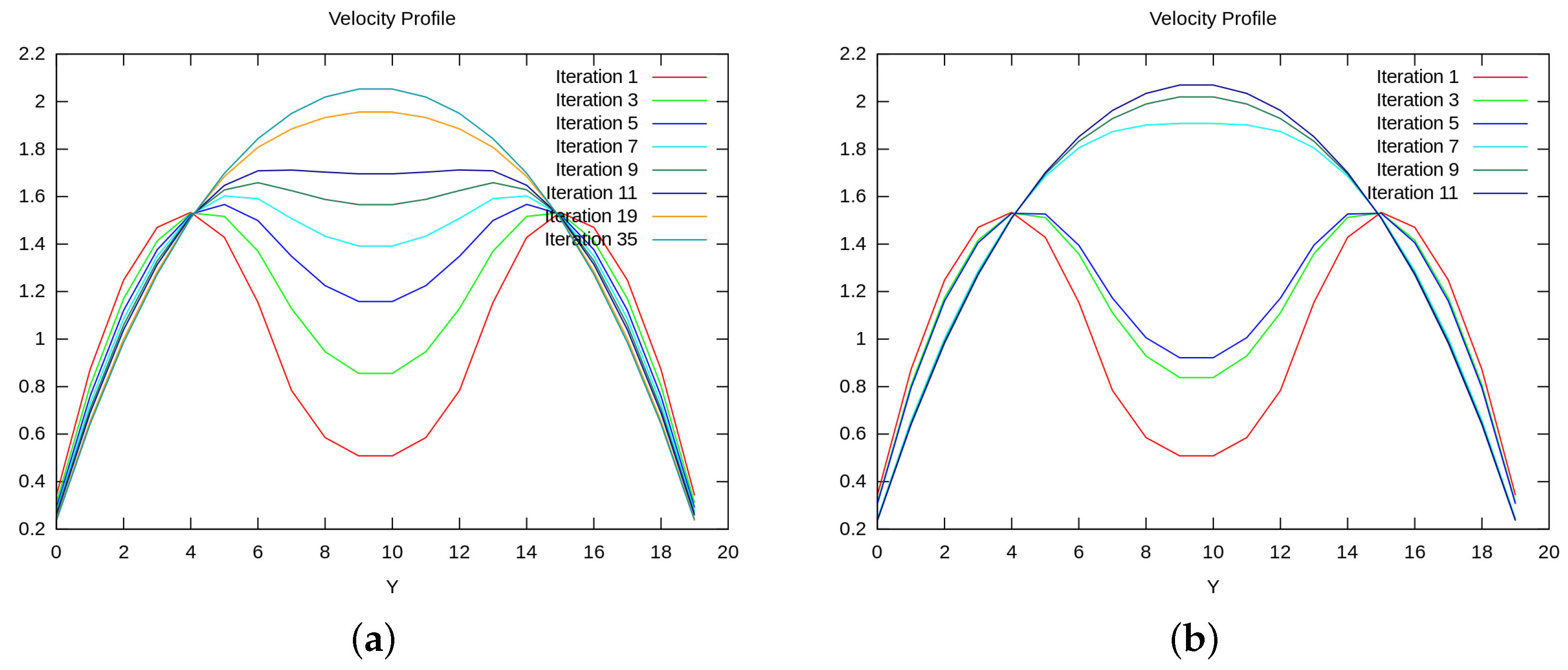
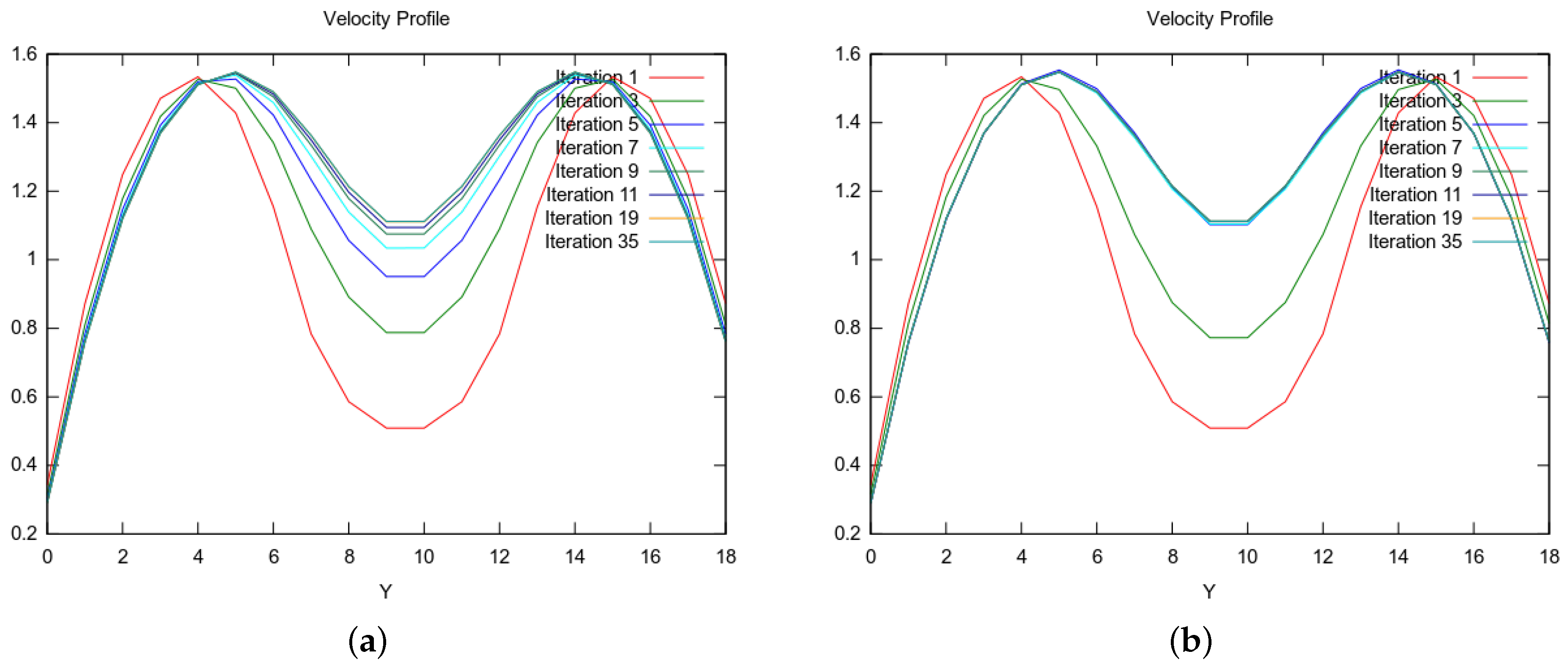
3.5. Anderson Acceleration: Parameter Study
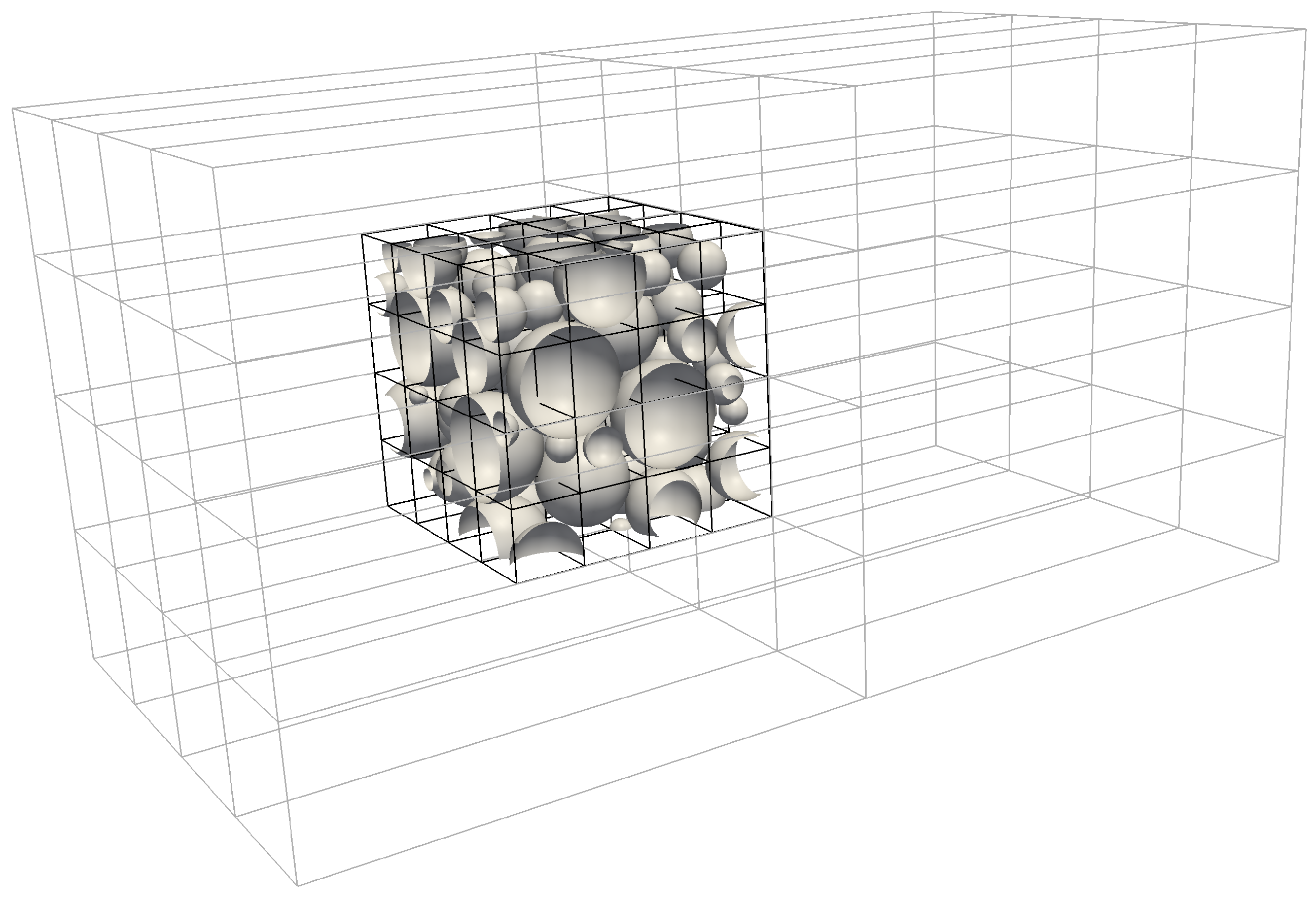
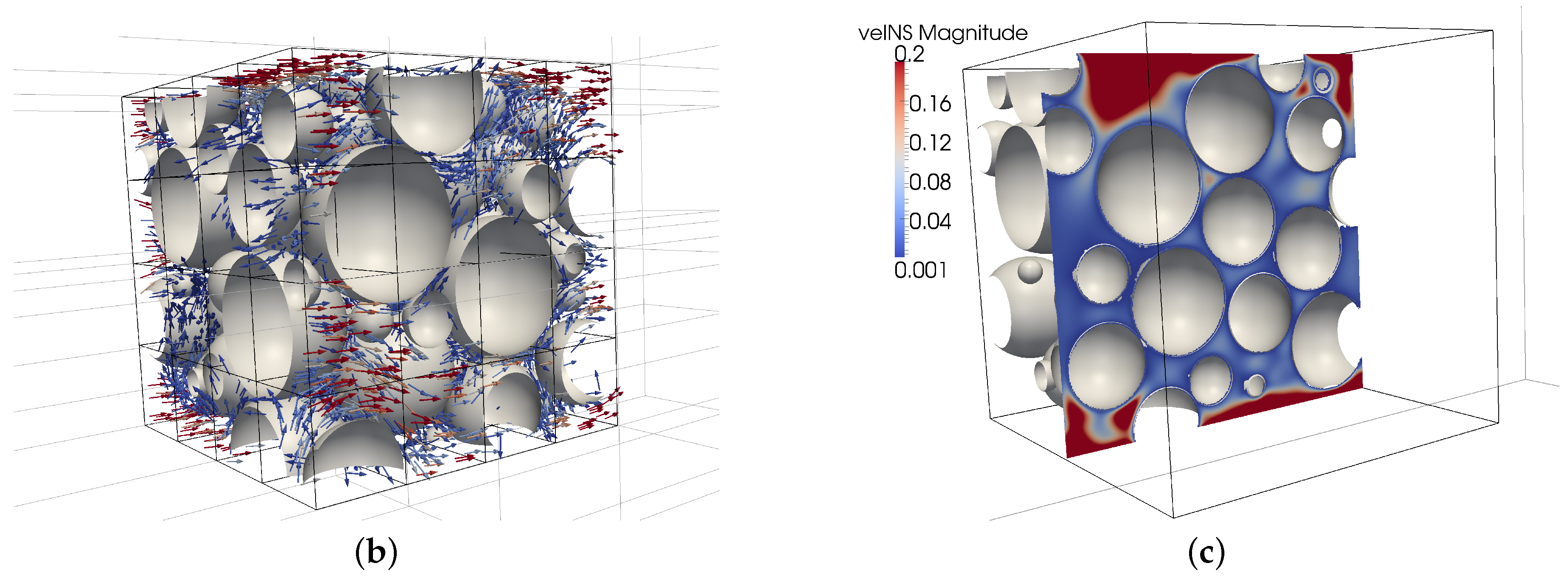
3.6. LBNS Showcase: Flow in Porous Structures
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LB | Lattice Boltzmann |
| NS | Navier–Stokes |
| PDE | Partial differential equation |
| HPC | High-performance computing |
| BGK | Bhatnagar-Gross-Krook |
| MCMD | multiple component multiple data |
References
- Ferziger, J.; Perić, M. Computational Methods for Fluid Dynamics, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Fletcher, C. Computational Techniques for Fluid Dynamics, Volume 2: Specific Techniques for Different Flow Categories, 2nd ed.; Springer: Berlin, Germany, 1997. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation for Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Wolf-Gladrow, D. Lattice-Gas Cellular Automata and Lattice Boltzmann Models—An Introduction; Springer: Berlin, Germany, 2000. [Google Scholar]
- Geller, S.; Krafczyk, M.; Tölke, J.; Turek, S.; Hron, J. Benchmark computations based on lattice-Boltzmann, finite element and finite volume methods for laminar flows. Comput. Fluids 2006, 35, 888–897. [Google Scholar] [CrossRef]
- Mehl, M.; Neckel, T.; Neumann, P. Navier–Stokes and Lattice-Boltzmann on octree-like grids in the Peano framework. Int. J. Numer. Methods Fluids 2010, 65, 67–86. [Google Scholar] [CrossRef]
- Junk, M.; Klar, A.; Luo, L.S. Asymptotic analysis of the lattice Boltzmann equation. J. Comput. Phys. 2005, 210, 676–704. [Google Scholar] [CrossRef]
- Chen, L.; He, Y.L.; Kang, Q.; Tao, W.Q. Coupled numerical approach combining finite volume and lattice Boltzmann methods for multi-scale multi-physicochemical processes. J. Comput. Phys. 2013, 255, 83–105. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B.; Albuquerque, P. Spatial Coupling of a Lattice Boltzmann fluid model with a Finite Difference Navier–Stokes solver. 2005; arXiv:physics/0511243. Available online: http://xxx.lanl.gov/abs/physics/0511243 (accessed on 11 October 2016). [Google Scholar]
- Neumann, P. Hybrid Multiscale Simulation Approaches for Micro- and Nanoflows. Ph.D. Thesis, Technische Universität München, Institut für Informatik, Munich, Germany, 2013. [Google Scholar]
- Neumann, P.; Bungartz, H.-J.; Mehl, M.; Neckel, T.; Weinzierl, T. A Coupled Approach for Fluid Dynamic Problems Using the PDE Framework Peano. Commun. Comput. Phys. 2012, 12, 65–84. [Google Scholar] [CrossRef]
- Yeshala, N. A Coupled Lattice-Boltzmann–Navier–Stokes Methodology for Drag Reduction. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, 2010. [Google Scholar]
- Albuquerque, P.; Alemani, D.; Chopard, B.; Leone, P. Coupling a Lattice Boltzmann and a Finite Difference Scheme. In Computational Science–ICCS 2004; Springer: Berlin/Heidelberg, Germany, 2004; pp. 540–547. [Google Scholar]
- Albuquerque, P.; Alemani, D.; Chopard, B.; Leone, P. A Hybrid Lattice Boltzmann Finite Difference Scheme for the Diffusion Equation. Int. J. Mult. Comp. Eng. 2006, 4, 209–219. [Google Scholar]
- Neumann, P. On transient hybrid Lattice Boltzmann–Navier–Stokes flow simulations. J. Comput. Sci. 2016, in press. [Google Scholar] [CrossRef]
- Degroote, J.; Bathe, K.; Vierendeels, J. Performance of a new partitioned procedure versus a monolithic procedure in fluid-structure interaction. Comput. Struct. 2009, 87, 793–801. [Google Scholar] [CrossRef]
- Lott, P.; Walker, H.; Woodward, C.; Yang, U. An accelerated Picard method for nonlinear systems related to variably saturated flow. Adv. Water Resour. 2012, 38, 92–101. [Google Scholar] [CrossRef]
- Ni, P. Anderson Acceleration of Fixed-Point Iteration with Applications to Electronic Structure Computations. Ph.D. Thesis, Worcester Polytechnic Institute, Worcester, MA, USA, 2009. [Google Scholar]
- Anderson, D.G. Iterative procedures for nonlinear integral equations. J. ACM 1965, 12, 547–560. [Google Scholar] [CrossRef]
- Fang, H.; Saad, Y. Two classes of multisecant methods for nonlinear acceleration. Numer. Linear Algebra Appl. 2009, 16, 197–221. [Google Scholar] [CrossRef]
- Walker, H.; Ni, P. Anderson acceleration for fixed-point iterations. SIAM J. Numer. Anal. 2011, 49, 1715–1735. [Google Scholar] [CrossRef]
- Shan, X. Lattice Boltzmann in micro- and nano-flow simulations. IMA J. Appl. Math. 2011, 76, 650–660. [Google Scholar] [CrossRef]
- Meng, J.; Zhang, Y.; Shan, X. Multiscale lattice Boltzmann approach to modeling gas flows. Phys. Rev. E 2011, 83, 046701. [Google Scholar] [CrossRef] [PubMed]
- Dünweg, B.; Schiller, U.; Ladd, A. Statistical Mechanics of the Fluctuating Lattice Boltzmann Equation. Phys. Rev. E 2007, 76, 036704. [Google Scholar] [CrossRef] [PubMed]
- Griebel, M.; Dornseifer, T.; Neunhoeffer, T. Numerical Simulation in Fluid Dynamics. A Practical Introduction; SIAM: Philadelphia, PA, USA, 1997. [Google Scholar]
- Bhatnagar, P.; Gross, E.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T. The Mathematical Theory of Nonuniform Gases; Cambridge University Press: London, UK, 1970. [Google Scholar]
- Zou, Q.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar] [CrossRef]
- Latt, J.; Chopard, B.; Malaspinas, O.; Deville, M.; Michler, A. Straight velocity boundaries in the lattice Boltzmann method. Phys. Rev. E 2008, 77. [Google Scholar] [CrossRef] [PubMed]
- Chikatamarla, S.; Ansumali, S.; Karlin, I. Grad’s approximation for missing data in lattice Boltzmann simulations. Europhys. Lett. 2006, 74, 215–221. [Google Scholar] [CrossRef]
- Schwarz, H. Ueber einen Grenzübergang durch alternierendes Verfahren. Vierteljahrsschrift der Naturforschenden Gesellschaft Zürich 1870, 15, 272–286. (In German) [Google Scholar]
- Uekermann, B.; Bungartz, H.-J.; Gatzhammer, B.; Mehl, M. A parallel, black-box coupling algorithm for fluid-structure interaction. In Proceedings of the 5th International Conference on Computational Methods for Coupled Problems in Science and Engineering, Ibiza, Spain, 17–19 June 2013; pp. 1–12.
- Atanasov, A. Software Idioms for Component-Based and Topology-Aware Simulation Assembly and Data Exchange in High Performance Computing and Visualisation Environments. Ph.D. Thesis, Technische Universität München, Institut für Informatik, Munich, Germany, 2014. [Google Scholar]
- Atanasov, A.; Bungartz, H.-J.; Unterweger, K.; Weinzierl, T.; Wittmann, R. A Case Study on Multi-Component Multi-Cluster Interaction with an AMR Solver. In Proceedings of the Third International Workshop on Domain-Specific Languages and High-Level Frameworks for High Performance Computing (WOLFHPC 2013), Denver, CO, USA, 18 November 2013.
- Balay, S.; Adams, M.F.; Brown, J.; Brune, P.; Buschelman, K.; Eijkhout, V.; Gropp, W.D.; Kaushik, D.; Knepley, M.G.; McInnes, L.C.; et al. PETSc Web Page. Available online: http://www.mcs.anl.gov/petsc (accessed on 17 November 2014).
- Bungartz, H.-J.; Lindner, F.; Gatzhammer, B.; Mehl, M.; Scheufele, K.; Shukaev, A.; Uekermann, B. preCICE—A Fully Parallel Library for Multi-Physics Surface Coupling. Comput. Fluids 2016, in press. [Google Scholar] [CrossRef]
- Khirevich, S.; Ginzburg, I.; Tallarek, U. Coarse- and fine-grid numerical behavior of MRT/TRT lattice-Boltzmann schemes in regular and random sphere packings. J. Comput. Phys. 2014, 281, 708–742. [Google Scholar] [CrossRef]
- Grucelski, A.; Pozorski, J. Lattice Boltzmann simulations of flow past a circular cylinder and in simple porous media. Comput. Fluids 2013, 71, 406–416. [Google Scholar] [CrossRef]



| Primary | Secondary | Norm. | Iterations till | Iterations till |
|---|---|---|---|---|
| (//) | (//) | |||
| , | no | 15 / 13 / 15 | 23 / 21 / 23 | |
| , | yes | 14 / 15 / 14 | 20 / 23 / 20 | |
| , , | - | yes | 15 / 15 / 15 | 22 / 23 / 22 |
| , | yes | 14 / 17 / 14 | 22 / 24 / 22 |
| Ratio | dim() | dim() | Norm. | Iterations till | Iterations till |
|---|---|---|---|---|---|
| (//) | (//) | ||||
| 1 | 10080 | 460 | no | 9 / 9 / 9 | 12 / 13 / 12 |
| 1 | 10080 | 460 | yes | 8 / 10 / 8 | 12 / 13 / 16 |
| 2 | 34980 | 460 | no | 10 / 7 / 10 | 13 / 11 / 13 |
| 2 | 34980 | 460 | yes | 8 / 10 / 8 | 12 / 14 / 13 |
| 4 | 129780 | 460 | no | 11 / 7 / 10 | 14 / 13 / 17 |
| 4 | 129780 | 460 | yes | 8 / 11 / 8 | 13 / 15 / 17 |
| 8 | 499380 | 460 | no | 11 / 7 / 11 | 16 / 14 / 16 |
| 8 | 499380 | 460 | yes | 8 / 11 / 8 | 14 / 15 / 14 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atanasov, A.; Uekermann, B.; Pachajoa Mejía, C.A.; Bungartz, H.-J.; Neumann, P. Steady-State Anderson Accelerated Coupling of Lattice Boltzmann and Navier–Stokes Solvers. Computation 2016, 4, 38. https://doi.org/10.3390/computation4040038
Atanasov A, Uekermann B, Pachajoa Mejía CA, Bungartz H-J, Neumann P. Steady-State Anderson Accelerated Coupling of Lattice Boltzmann and Navier–Stokes Solvers. Computation. 2016; 4(4):38. https://doi.org/10.3390/computation4040038
Chicago/Turabian StyleAtanasov, Atanas, Benjamin Uekermann, Carlos A. Pachajoa Mejía, Hans-Joachim Bungartz, and Philipp Neumann. 2016. "Steady-State Anderson Accelerated Coupling of Lattice Boltzmann and Navier–Stokes Solvers" Computation 4, no. 4: 38. https://doi.org/10.3390/computation4040038





