A Non-Isothermal Chemical Lattice Boltzmann Model Incorporating Thermal Reaction Kinetics and Enthalpy Changes
Abstract
:1. Introduction
2. Chemical Lattice Boltzmann Algorithm
2.1. Single-Phase Fluid
2.2. Thermohydrodynamics
2.3. Dissolved Chemical Species
2.4. Isothermal Reactive LBM
2.4.1. Single Reaction Benchmark Test
2.4.2. Pattern Formation in the Gray–Scott System
2.5. Thermal Reactive LBM
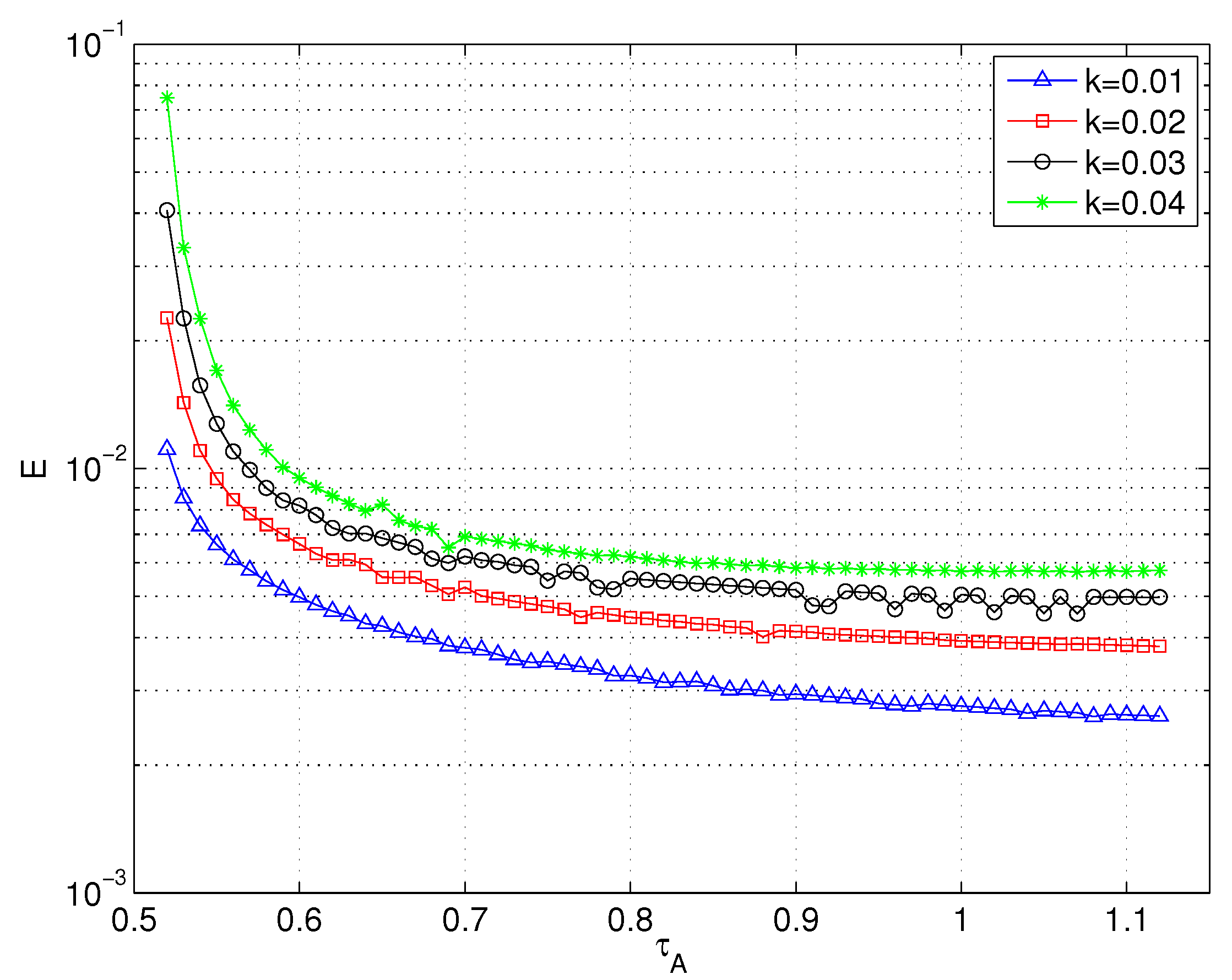
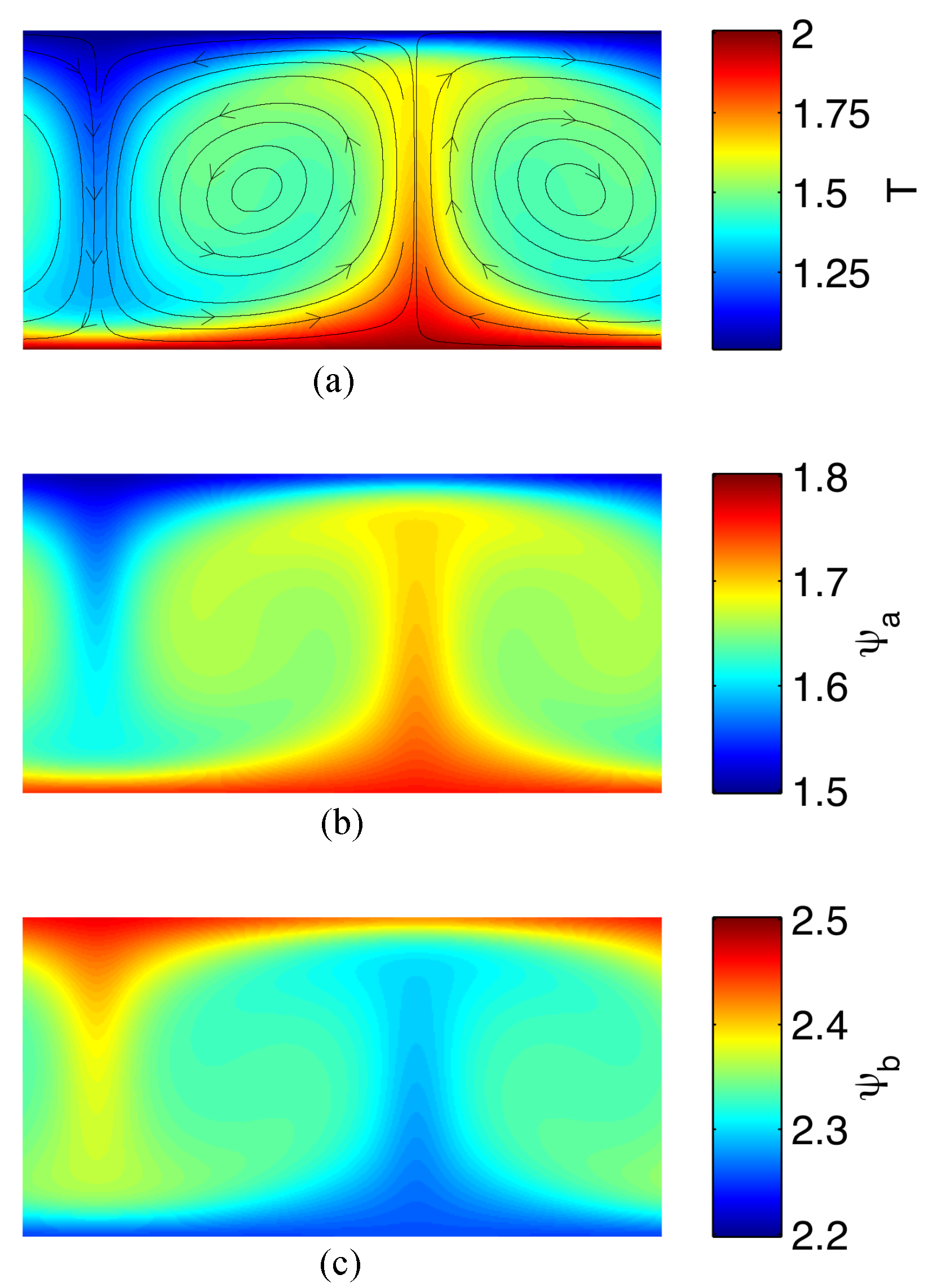
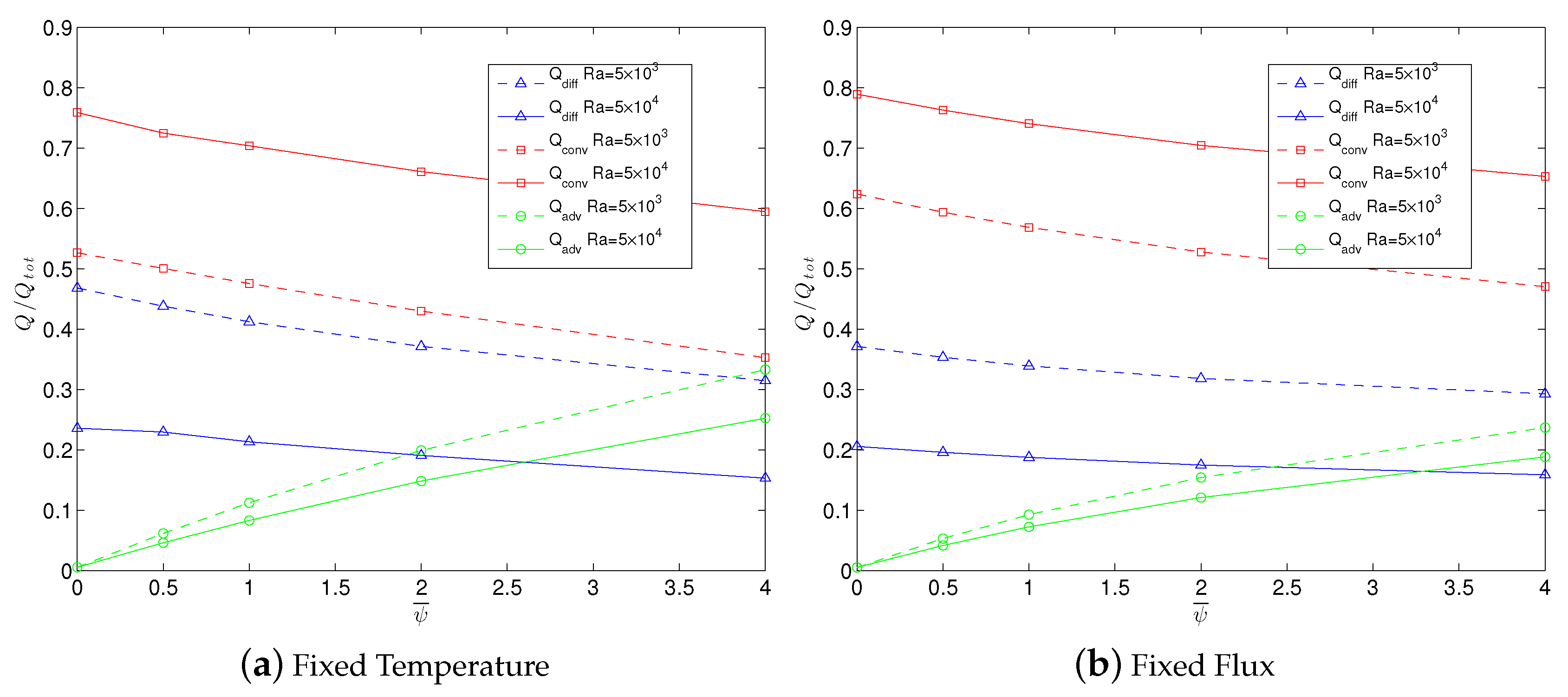
2.5.1. Reversibility and Heat Transport Enhancement
3. Conclusions
4. Further Work
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LBM | Lattice Boltzmann method |
| LGCA | Lattice gas cellular automata |
| CFD | Computational fluid dynamics |
| MEP | Maximum entropy production |
| RLBM | Reactive lattice Boltzmann method |
| TRLBM | Thermal reactive lattice Boltzmann method |
| GSRDS | Gray–Scott reaction diffusion system |
| BC | Boundary condition |
References
- Frisch, U.; Hasslacher, B.; Pomeau, Y. Lattice-gas automata for the navier-stokes equation. Phys. Rev. Lett. 1986, 56, 1505–1508. [Google Scholar] [CrossRef] [PubMed]
- McNamara, G.R.; Zanetti, G. Use of the boltzmann equation to simulate lattice-gas automata. Phys. Rev. Lett. 1988, 61, 2332–2335. [Google Scholar] [CrossRef] [PubMed]
- Qian, Y.H.; D’Humières, D.; Lallemand, P. Lattice bgk models for navier-stokes equation. EPL (Europhys. Lett.) 1992, 17, 479. [Google Scholar] [CrossRef]
- Bagnoli, F.; Rechtman, R. Thermodynamic entropy and chaos in a discrete hydrodynamical system. Phys. Rev. E 2009, 79. [Google Scholar] [CrossRef] [PubMed]
- Boghosian, B.M. Lattice gases and cellular automata. Future Gener. Comput. Syst. 1999, 16, 171–185. [Google Scholar] [CrossRef]
- Aidun, C.K.; Clausen, J.R. Lattice-Boltzmann method for complex flows. Annu. Rev. Fluid Mech. 2010, 42, 439–472. [Google Scholar] [CrossRef]
- Chen, S.; Doolen, G.D. Lattice Boltzmann Method for Fluid Flows. Annu. Rev. Fluid Mech. 1998, 30, 329–364. [Google Scholar] [CrossRef]
- D’Humières, D. Multiple–relaxation–time lattice Boltzmann models in three dimensions. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2002, 360, 437–451. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.S.; Krafczyk, M.; Shyy, W. Lattice Boltzmann Method for Computational Fluid Dynamics. In Encyclopedia of Aerospace Engineering; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2010. [Google Scholar]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Numerical Mathematics and Scientific Computation, Clarendon Press: Wotton-under-Edge, Glos, UK, 2001. [Google Scholar]
- Sofonea, V.; Sekerka, R.F. Viscosity of finite difference lattice Boltzmann models. J. Comput. Phys. 2003, 184, 422–434. [Google Scholar] [CrossRef]
- Dorschner, B.; Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Grid refinement for entropic lattice Boltzmann models. Phys. Rev. E 2016, 94, 053311. [Google Scholar] [CrossRef] [PubMed]
- Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Multispeed entropic lattice Boltzmann model for thermal flows. Phys. Rev. E 2014, 90, 043306. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Chen, S.; Doolen, G.D. A Novel Thermal Model for the Lattice Boltzmann Method in Incompressible Limit. J. Comput. Phys. 1998, 146, 282–300. [Google Scholar] [CrossRef]
- Karlin, I.V.; Sichau, D.; Chikatamarla, S.S. Consistent two-population lattice Boltzmann model for thermal flows. Phys. Rev. E 2013, 88, 063310. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.H.; Lin, K.H.; Mai, H.C.; Lin, C.A. Thermal boundary conditions for thermal lattice Boltzmann simulations. Comput. Math. Appl. 2010, 59, 2178–2193. [Google Scholar] [CrossRef]
- Pareschi, G.; Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Conjugate heat transfer with the entropic lattice Boltzmann method. Phys. Rev. E 2016, 94, 013305. [Google Scholar] [CrossRef] [PubMed]
- Peng, Y.; Shu, C.; Chew, Y.T. Simplified thermal lattice Boltzmann model for incompressible thermal flows. Phys. Rev. E 2003, 68, 026701. [Google Scholar] [CrossRef] [PubMed]
- Arcidiacono, S.; Karlin, I.; Mantzaras, J.; Frouzakis, C. Lattice Boltzmann model for the simulation of multicomponent mixtures. Phys. Rev. E 2007, 76, 046703. [Google Scholar] [CrossRef] [PubMed]
- Gunstensen, A.; Rothman, D.; Zaleski, S. Lattice Boltzmann model of immiscible fluids. Phys. Rev. A 1991, 43, 4320–4327. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.S.; Girimaji, S. Lattice Boltzmann model for binary mixtures. Phys. Rev. E 2002, 66, 035301. [Google Scholar] [CrossRef] [PubMed]
- Stiebler, M.; Tölke, J.; Krafczyk, M. Advection-diffusion lattice Boltzmann scheme for hierarchical grids. Comput. Math. Appl. 2008, 55, 1576–1584. [Google Scholar] [CrossRef]
- Ayodele, S.G.; Varnik, F.; Raabe, D. Lattice Boltzmann study of pattern formation in reaction-diffusion systems. Phys. Rev. E 2011, 83, 016702. [Google Scholar] [CrossRef] [PubMed]
- Ayodele, S.G.; Raabe, D.; Varnik, F. Lattice Boltzmann modeling of advection-diffusion-reaction equations: Pattern formation under uniform differential advection. Commun. Comput. Phys. 2013, 13, 741–756. [Google Scholar] [CrossRef]
- Dawson, S.; Chen, S.; Doolen, G.D. Lattice Boltzmann computations for reaction-diffusion equations. J. Chem. Phys. 1993, 98, 1514–1523. [Google Scholar] [CrossRef]
- Kang, J.; Prasianakis, N.I.; Mantzaras, J. Thermal multicomponent lattice Boltzmann model for catalytic reactive flows. Phys. Rev. E 2014, 89, 063310. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Yan, G. Lattice Boltzmann model for the bimolecular autocatalytic reaction–diffusion equation. Appl. Math. Model. 2014, 38, 5796–5810. [Google Scholar] [CrossRef]
- Chen, S.; Liu, Z.; Tian, Z.; Shi, B.; Zheng, C. A simple lattice Boltzmann scheme for combustion simulation. Comput. Math. Appl. 2008, 55, 1424–1432. [Google Scholar] [CrossRef]
- Chiavazzo, E.; Karlin, I.V.; Gorban, A.N.; Boulouchos, K. Combustion simulation via lattice Boltzmann and reduced chemical kinetics. J. Stat. Mech. Theory Exp. 2009, 2009, P06013. [Google Scholar] [CrossRef]
- Chiavazzo, E.; Karlin, I.V.; Gorban, A.N.; Boulouchos, K. Coupling of the model reduction technique with the lattice Boltzmann method for combustion simulations. Combust. Flame 2010, 157, 1833–1849. [Google Scholar] [CrossRef]
- Yamamoto, K.; He, X.; Doolen, G.D. Simulation of Combustion Field with Lattice Boltzmann Method. J. Stat. Phys. 2002, 107, 367–383. [Google Scholar] [CrossRef]
- Dellar, P.J. An interpretation and derivation of the lattice Boltzmann method using Strang splitting. Comput. Math. Appl. 2013, 65, 129–141. [Google Scholar] [CrossRef]
- He, X.; Luo, L.S. Theory of the lattice Boltzmann method: From the Boltzmann equation to the lattice Boltzmann equation. Phys. Rev. E 1997, 56, 6811–6817. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Geller, S.; Krafczyk, M.; Tolke, J.; Turek, S.; Hron, J. Benchmark computations based on lattice-Boltzmann, finite element and finite volume methods for laminar flows. Comput. Fluids 2006, 35, 888–897. [Google Scholar] [CrossRef]
- Karlin, I.V.; Bösch, F.; Chikatamarla, S.S. Gibbs’ principle for the lattice-kinetic theory of fluid dynamics. Phys. Rev. E 2014, 90, 031302. [Google Scholar] [CrossRef] [PubMed]
- Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Lattice Kinetic Theory in a Comoving Galilean Reference Frame. Phys. Rev. Lett. 2016, 117, 010604. [Google Scholar] [CrossRef] [PubMed]
- Frapolli, N.; Chikatamarla, S.S.; Karlin, I.V. Entropic lattice Boltzmann model for compressible flows. Phys. Rev. E 2015, 92, 061301. [Google Scholar] [CrossRef] [PubMed]
- Geier, M.; Schönherr, M.; Pasquali, A.; Krafczyk, M. The cumulant lattice Boltzmann equation in three dimensions: Theory and validation. Comput. Math. Appl. 2015, 70, 507–547. [Google Scholar] [CrossRef]
- Shi, Y.; Zhao, T.S.; Guo, Z.L. Thermal lattice Bhatnagar-Gross-Krook model for flows with viscous heat dissipation in the incompressible limit. Phys. Rev. E 2004, 70, 066310. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Ohashi, H.; Akiyama, M. Two-Parameter Thermal Lattice BGK Model with a Controllable Prandtl Number. J. Sci. Comput. 1997, 12, 169–185. [Google Scholar] [CrossRef]
- Chen, H.; Teixeira, C. H-theorem and origins of instability in thermal lattice Boltzmann models. Comput. Phys. Commun. 2000, 129, 21–31. [Google Scholar] [CrossRef]
- Teixeira, C.; Chen, H.; Freed, D.M. Multi-speed thermal lattice Boltzmann method stabilization via equilibrium under-relaxation. Comput. Phys. Commun. 2000, 129, 207–226. [Google Scholar] [CrossRef]
- Peng, Y.; Shu, C.; Chew, Y. A 3D incompressible thermal lattice Boltzmann model and its application to simulate natural convection in a cubic cavity. J. Comput. Phys. 2004, 193, 260–274. [Google Scholar] [CrossRef]
- Shan, X. Simulation of Rayleigh-Bénard convection using a lattice Boltzmann method. Phys. Rev. E 1997, 55, 2780–2788. [Google Scholar] [CrossRef]
- D’Orazio, A.; Corcione, M.; Celata, G.P. Application to natural convection enclosed flows of a lattice Boltzmann BGK model coupled with a general purpose thermal boundary condition. Int. J. Therm. Sci. 2004, 43, 575–586. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, T. Lattice Boltzmann simulation of natural convection with temperature-dependent viscosity in a porous cavity. Prog. Comput. Fluid Dyn. Int. J. 2005, 5, 110–117. [Google Scholar] [CrossRef]
- Kao, P.H.; Yang, R.J. Simulating oscillatory flows in Rayleigh Bénard convection using the lattice Boltzmann method. Int. J. Heat Mass Transf. 2007, 50, 3315–3328. [Google Scholar] [CrossRef]
- Rong, F.; Guo, Z.; Zhang, T.; Shi, B. Numerical study of Bénard convection with temperature-dependent viscosity in a porous cavity via lattice Boltzmann method. Int. J. Mod. Phys. C 2010, 21, 1407–1419. [Google Scholar] [CrossRef]
- Watanabe, T. Flow pattern and heat transfer rate in Rayleigh Bénard convection. Phys. Fluids 2004, 16, 972–978. [Google Scholar] [CrossRef]
- Chen, S.; Krafczyk, M. Entropy generation in turbulent natural convection due to internal heat generation. Int. J. Therm. Sci. 2009, 48, 1978–1987. [Google Scholar] [CrossRef]
- Chen, S.; Tölke, J.; Krafczyk, M. Simple lattice Boltzmann subgrid-scale model for convectional flows with high Rayleigh numbers within an enclosed circular annular cavity. Phys. Rev. E 2009, 80, 026702. [Google Scholar] [CrossRef] [PubMed]
- Dixit, H.; Babu, V. Simulation of high Rayleigh number natural convection in a square cavity using the lattice Boltzmann method. Int. J. Heat Mass Transf. 2006, 49, 727–739. [Google Scholar] [CrossRef]
- Van Treeck, C.; Rank, E.; Krafczyk, M.; Tölke, J.; Nachtwey, B. Extension of a hybrid thermal LBE scheme for large-eddy simulations of turbulent convective flows. Comput. Fluids 2006, 35, 863–871. [Google Scholar] [CrossRef]
- D’Orazio, A.; Succi, S. Simulating two-dimensional thermal channel flows by means of a lattice Boltzmann method with new boundary conditions. Future Gener. Comput. Syst. 2004, 20, 935–944. [Google Scholar] [CrossRef]
- Tian, Z.W.; Zou, C.; Liu, H.; Liu, Z.; Guo, Z.; Zheng, C. Thermal lattice boltzmann model with viscous heat dissipation in the incompressible limit. Int. J. Mod. Phys. C 2006, 17, 1131–1139. [Google Scholar] [CrossRef]
- Chang, Q.; Alexander, J.I.D. Application of the lattice Boltzmann method to two-phase Rayleigh-Bénard convection with a deformable interface. J. Comput. Phys. 2006, 212, 473–489. [Google Scholar] [CrossRef]
- Chen, S.; Tölke, J.; Krafczyk, M. Simulation of buoyancy-driven flows in a vertical cylinder using a simple lattice Boltzmann model. Phys. Rev. E 2009, 79, 016704. [Google Scholar] [CrossRef] [PubMed]
- Huber, C.; Parmigiani, A.; Chopard, B.; Manga, M.; Bachmann, O. Lattice Boltzmann model for melting with natural convection. Int. J. Heat Fluid Flow 2008, 29, 1469–1480. [Google Scholar] [CrossRef]
- Inamuro, T. Lattice Boltzmann methods for viscous fluid flows and for two-phase fluid flows. Fluid Dyn. Res. 2006, 38, 641–659. [Google Scholar] [CrossRef]
- Inamuro, T.; Yoshino, M.; Inoue, H.; Mizuno, R.; Ogino, F. A Lattice Boltzmann Method for a Binary Miscible Fluid Mixture and Its Application to a Heat-Transfer Problem. J. Comput. Phys. 2002, 179, 201–215. [Google Scholar] [CrossRef]
- Safari, H.; Rahimian, M.H.; Krafczyk, M. Extended lattice Boltzmann method for numerical simulation of thermal phase change in two-phase fluid flow. Phys. Rev. E 2013, 88, 013304. [Google Scholar] [CrossRef] [PubMed]
- Safari, H.; Rahimian, M.H.; Krafczyk, M. Consistent simulation of droplet evaporation based on the phase-field multiphase lattice Boltzmann method. Phys. Rev. E 2014, 90, 033305. [Google Scholar] [CrossRef] [PubMed]
- Yuan, P.; Schaefer, L. A thermal lattice Boltzmann two-phase flow model and its application to heat transfer problems part 1. Theoretical foundation. J. Fluids Eng. 2006, 128, 142–150. [Google Scholar] [CrossRef]
- Yuan, P.; Schaefer, L. A thermal lattice Boltzmann two-phase flow model and its application to heat transfer problems part 2. Integration and validation. J. Fluids Eng. 2006, 128, 151–156. [Google Scholar] [CrossRef]
- Bartlett, S.; Bullock, S. Natural convection of a two-dimensional Boussinesq fluid does not maximize entropy production. Phys. Rev. E 2014, 90, 023014. [Google Scholar] [CrossRef] [PubMed]
- Bartlett, S.; Virgo, N. Maximum Entropy Production Is Not a Steady State Attractor for 2D Fluid Convection. Entropy 2016, 18, 431. [Google Scholar] [CrossRef]
- Weaver, I.; Dyke, J.G.; Oliver, K. Can the Principle of Maximum Entropy Production be Used to Predict the Steady States of a Rayleigh-Bénard Convective System? In Beyond the Second Law: Entropy Production and Non-Equilibrium Systems; Springer: Berlin/Heidelberg, Germany, 2014; pp. 277–290. [Google Scholar]
- Dyke, J.; Kleidon, A. The Maximum Entropy Production Principle: Its Theoretical Foundations and Applications to the Earth System. Entropy 2010, 12, 613–630. [Google Scholar] [CrossRef]
- Martyushev, L.; Seleznev, V. Maximum entropy production principle in physics, chemistry and biology. Phys. Rep. 2006, 426, 1–45. [Google Scholar] [CrossRef]
- Bradford, R. An investigation into the maximum entropy production principle in chaotic Rayleigh Bénard convection. Phys. A Stat. Mech. Its Appl. 2013, 392, 6273–6283. [Google Scholar] [CrossRef]
- Ozawa, H.; Shimokawa, S.; Sakuma, H. Thermodynamics of fluid turbulence: A unified approach to the maximum transport properties. Phys. Rev. E 2001, 64, 026303. [Google Scholar] [CrossRef] [PubMed]
- Kleidon, A. The atmospheric circulation and states of maximum entropy production. Geophys. Res. Lett. 2003, 30, 1–4. [Google Scholar] [CrossRef]
- Lorenz, R.D. The two-box model of climate: limitations and applications to planetary habitability and maximum entropy production studies. Philos. Trans. R. Soc. Lond. B Biol. Sci 2010, 365, 1349–1354. [Google Scholar] [CrossRef] [PubMed]
- Paltridge, G. The steady-state format of global climate. Q. J. R. Meteorol. Soc. 1978, 104, 927–945. [Google Scholar] [CrossRef]
- Bartlett, S. Why is Life? An Assessment of the Thermodynamic Properties Of Dissipative, Pattern-Forming Systems. Ph.D. Thesis, University of Southampton, Southampton, UK, 2014. [Google Scholar]
- Di Rienzo, A.F.; Asinari, P.; Chiavazzo, E.; Prasianakis, N.I.; Mantzaras, J. Lattice Boltzmann model for reactive flow simulations. EPL (Europhys. Lett.) 2012, 98. [Google Scholar] [CrossRef]
- Filippova, O.; Hänel, D. A Novel Lattice BGK Approach for Low Mach Number Combustion. J. Comput. Phys. 2000, 158, 139–160. [Google Scholar] [CrossRef]
- Succi, S.; Bella, G.; Papetti, F. Lattice kinetic theory for numerical combustion. J. Sci. Comput. 1997, 12, 395–408. [Google Scholar] [CrossRef]
- Mishra, S.K.; De, A. Coupling of reaction and hydrodynamics around a reacting block modeled by Lattice Boltzmann Method (LBM). Comput. Fluids 2013, 71, 91–97. [Google Scholar] [CrossRef]
- Kang, Q.; Zhang, D.; Chen, S.; He, X. Lattice Boltzmann simulation of chemical dissolution in porous media. Phys. Rev. E 2002, 65, 036318. [Google Scholar] [CrossRef] [PubMed]
- Kang, Q.; Zhang, D.; Chen, S. Simulation of dissolution and precipitation in porous media. J. Geophys. Res. Solid Earth 2003, 108. [Google Scholar] [CrossRef]
- Kang, Q.; Lichtner, P.C.; Zhang, D. Lattice Boltzmann pore-scale model for multicomponent reactive transport in porous media. J. Geophys. Res. Solid Earth 2006, 111, 1–9. [Google Scholar] [CrossRef]
- Verhaeghe, F.; Arnout, S.; Blanpain, B.; Wollants, P. Lattice-Boltzmann modeling of dissolution phenomena. Phys. Rev. E 2006, 73, 036316. [Google Scholar] [CrossRef] [PubMed]
- Succi, S.; Gabrielli, A.; Smith, G.; Kaxiras, E. Chemical efficiency of reactive microflows with heterogeneous catalysis: A lattice Boltzmann study. Eur. Phys. J. Appl. Phys. 2001, 16, 71–84. [Google Scholar] [CrossRef]
- Succi, S.; Smith, G.; Kaxiras, E. Lattice Boltzmann Simulation of Reactive Microflows over Catalytic Surfaces. J. Stat. Phys. 2002, 107, 343–366. [Google Scholar] [CrossRef]
- Gray, P.; Scott, S. Sustained oscillations and other exotic patterns of behavior in isothermal reactions. J. Phys. Chem. 1985, 89, 22–32. [Google Scholar] [CrossRef]
- Mahara, H.; Suzuki, K.; Jahan, R.A.; Yamaguchi, T. Coexisting stable patterns in a reaction-diffusion system with reversible Gray-Scott dynamics. Phys. Rev. E 2008, 78, 066210. [Google Scholar] [CrossRef] [PubMed]
- Pearson, J.E. Complex patterns in a simple system. Science 1993, 261, 189–192. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.J.; McCormick, W.D.; Ouyang, Q.; Swinney, H.L. Pattern Formation by Interacting Chemical Fronts. Science 1993, 261, 192–194. [Google Scholar] [CrossRef] [PubMed]
- Nishiura, Y.; Ueyama, D. Spatio-temporal chaos for the Gray-Scott model. Phys. D Nonlinear Phenom. 2001, 150, 137–162. [Google Scholar] [CrossRef]
- Nishiura, Y.; Ueyama, D. A skeleton structure of self-replicating dynamics. Phys. D Nonlinear Phenom. 1999, 130, 73–104. [Google Scholar] [CrossRef]
- Virgo, N. Thermodynamics and the Structure of Living Systems. Ph.D. Thesis, University of Sussex, Brighton, UK, 2011. [Google Scholar]
- Froese, T.; Virgo, N.; Ikegami, T. Motility at the origin of life: Its characterization and a model. Artif. Life 2014, 20, 55–76. [Google Scholar] [CrossRef] [PubMed]
- Froese, T.; Ikegami, T.; Virgo, N. The behavior-based hypercycle: From parasitic reaction to symbiotic behavior. Artif. Life 2012, 13, 457–464. [Google Scholar]
- Epstein, I.R.; Xu, B. Reaction-diffusion processes at the nano- and microscales. Nat. Nanotechnol. 2016, 11, 312–319. [Google Scholar] [CrossRef] [PubMed]
- Turing, A.M. The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B 1952, 237, 37–72. [Google Scholar] [CrossRef]
- Lee, K.; McCormick, W.; Pearson, J.E.; Swinney, H. Experimental observation of self-replicating spots in a reaction-diffusion system. Nature 1994, 369, 215–218. [Google Scholar] [CrossRef]
- Lee, K.; Swinney, H. Lamellar structures and self-replicating spots in a reaction-diffusion system. Phys. Rev. E 1995, 51. [Google Scholar] [CrossRef]
- Andres, J.T.H.; Cardoso, S.S.S. Convection and reaction in a diffusive boundary layer in a porous medium: Nonlinear dynamics. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 037113. [Google Scholar] [CrossRef] [PubMed]
- Rogers, M.C.; Morris, S.W. The heads and tails of buoyant autocatalytic balls. Chaos Interdiscip. J. Nonlinear Sci. 2012, 22, 037110. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J. Lattice Boltzmann method for microfluidics: Models and applications. Microfluid. Nanofluid. 2011, 10, 1–28. [Google Scholar] [CrossRef]
- Chen, L.; Kang, Q.; He, Y.L.; Tao, W.Q. Pore-scale simulation of coupled multiple physicochemical thermal processes in micro reactor for hydrogen production using lattice Boltzmann method. Int. J. Hydrogen Energy 2012, 37, 13943–13957. [Google Scholar] [CrossRef]
- Bartlett, S.; Bullock, S. Emergence of competition between different dissipative structures for the same free energy source. In Proceedings of the European Conference on Artificial Life, York, UK, 20–24 July 2015; MIT Press: Cambridge, MA, USA, 2015; pp. 415–422. [Google Scholar]
- Bartlett, S.; Bullock, S. A Precarious Existence: Thermal Homeostasis of Simple Dissipative Structures. In Proceedings of the 15th International Conference on the Synthesis and Simulation of Living Systems, Cancún, Mexico, 4–8 July 2016; MIT Press: Cambridge, MA, USA, 2016; pp. 608–615. [Google Scholar]


© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bartlett, S. A Non-Isothermal Chemical Lattice Boltzmann Model Incorporating Thermal Reaction Kinetics and Enthalpy Changes. Computation 2017, 5, 37. https://doi.org/10.3390/computation5030037
Bartlett S. A Non-Isothermal Chemical Lattice Boltzmann Model Incorporating Thermal Reaction Kinetics and Enthalpy Changes. Computation. 2017; 5(3):37. https://doi.org/10.3390/computation5030037
Chicago/Turabian StyleBartlett, Stuart. 2017. "A Non-Isothermal Chemical Lattice Boltzmann Model Incorporating Thermal Reaction Kinetics and Enthalpy Changes" Computation 5, no. 3: 37. https://doi.org/10.3390/computation5030037




