Meta-Chirality: Fundamentals, Construction and Applications
Abstract
:1. Introduction
2. Fundamentals of Chiral Media
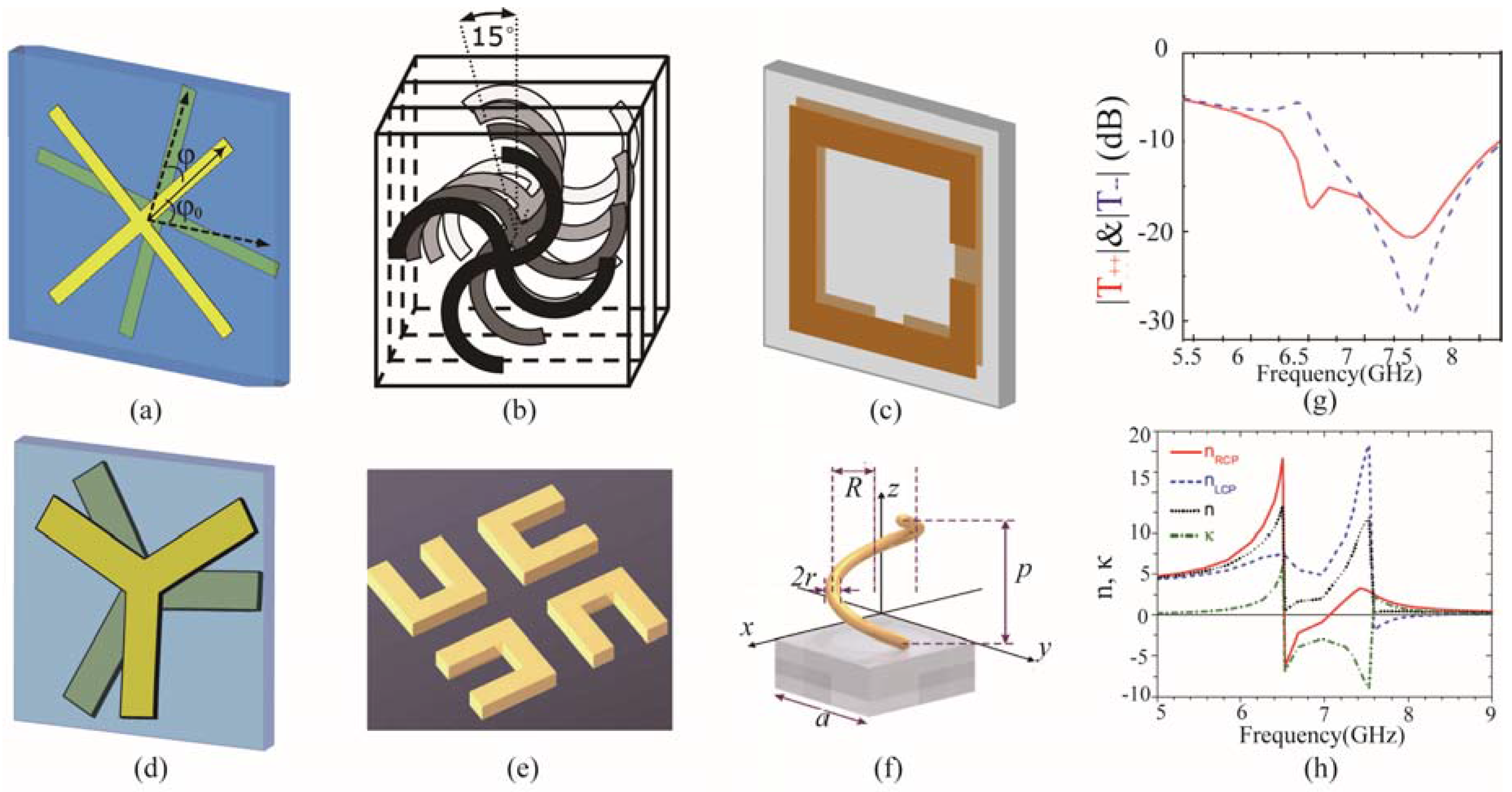
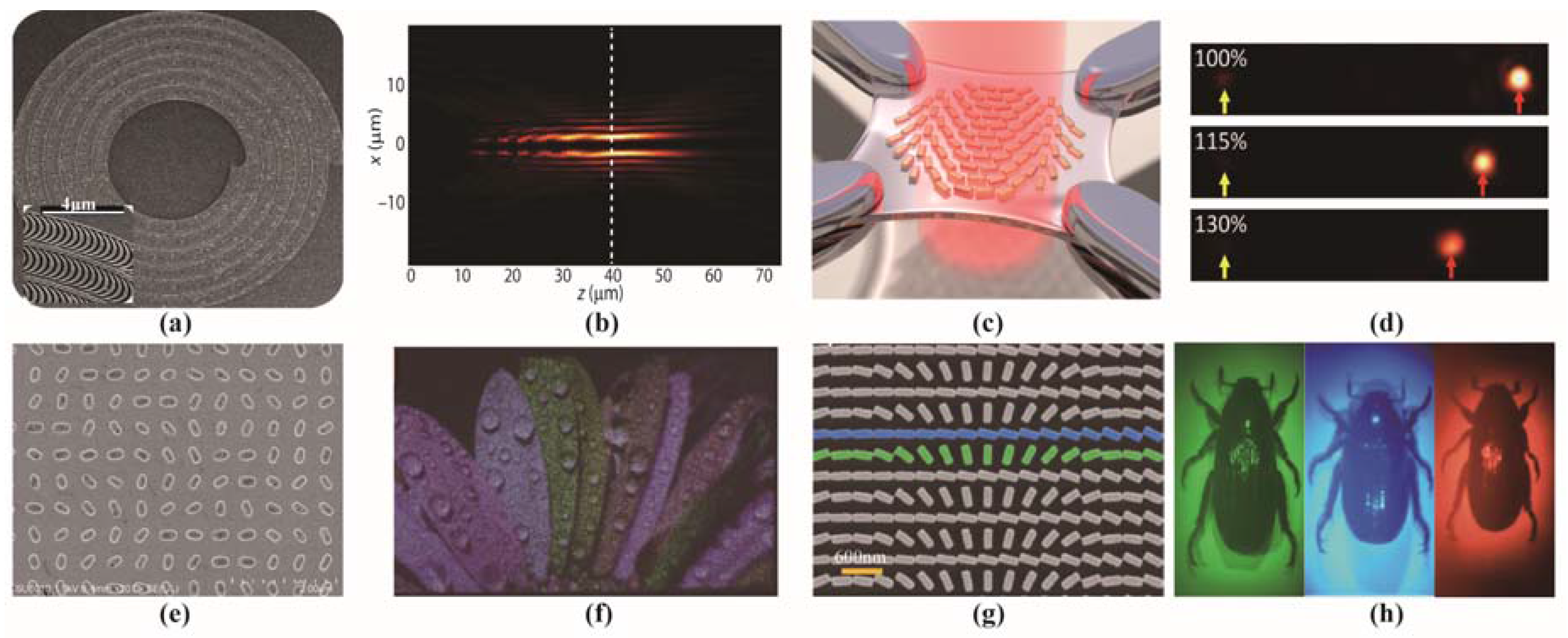
3. Construction of Chiral Metamaterials
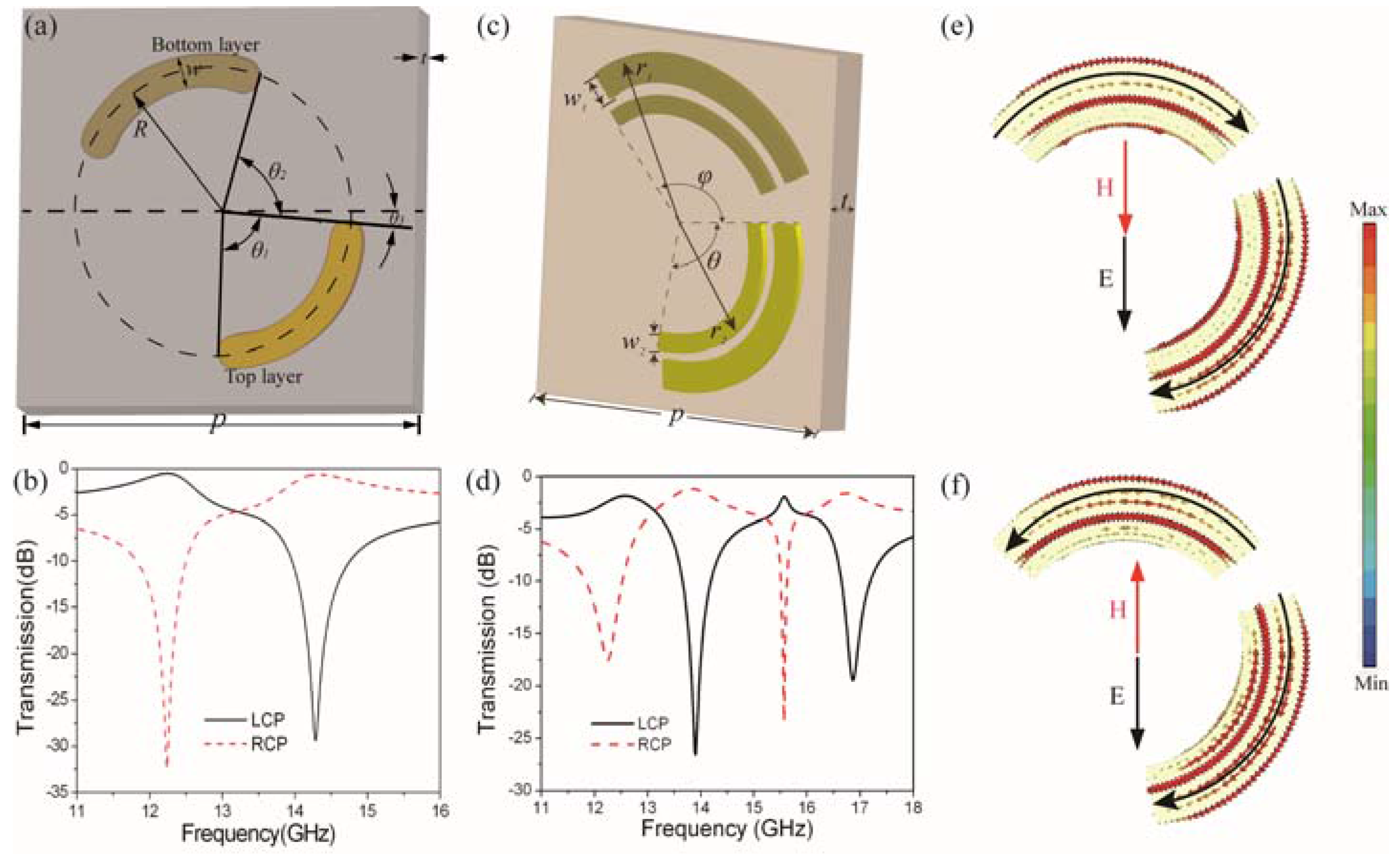
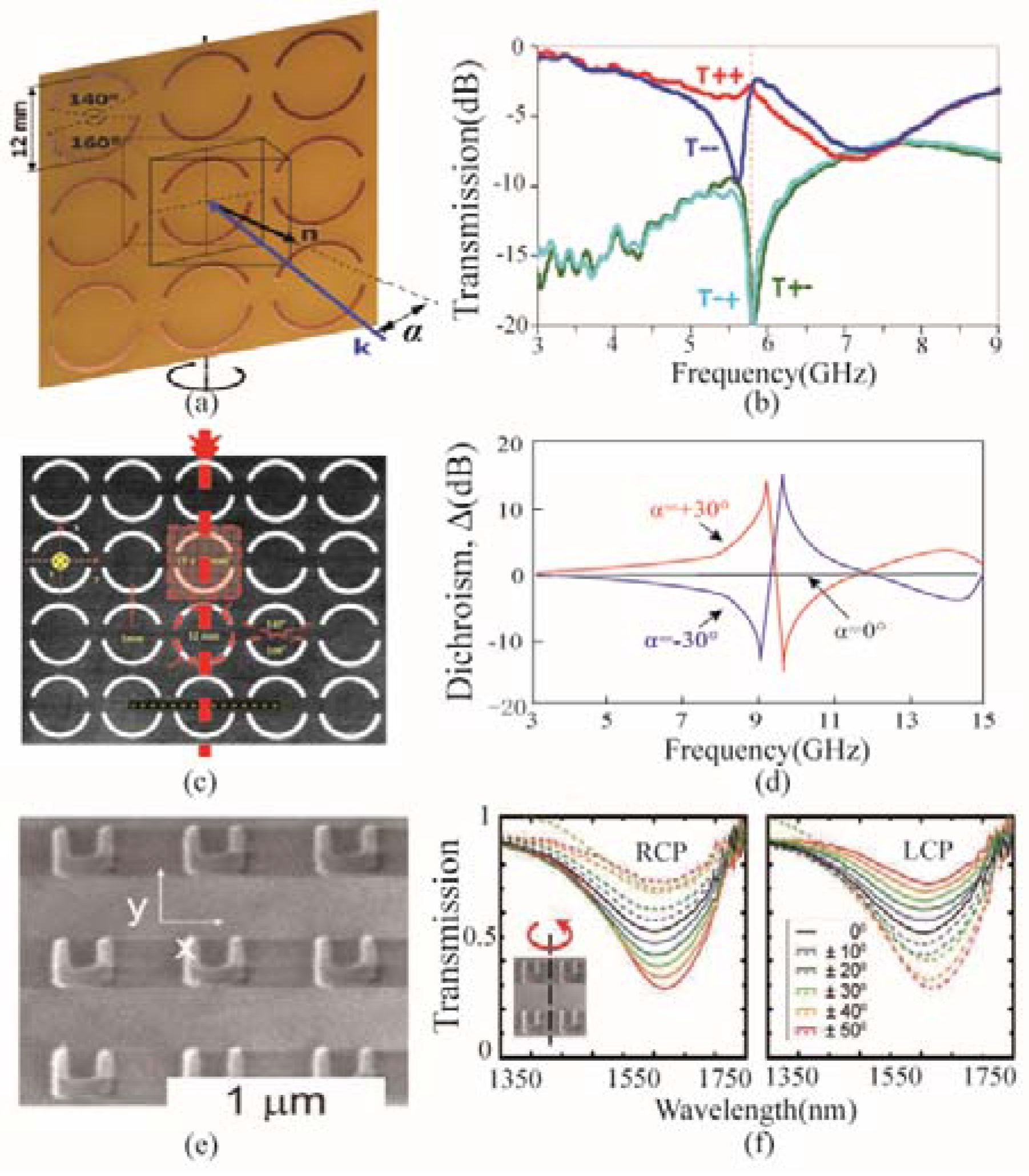
4. Extrinsic Chirality in Planar Metamaterials
5. Chiral Metamaterials for Absorption
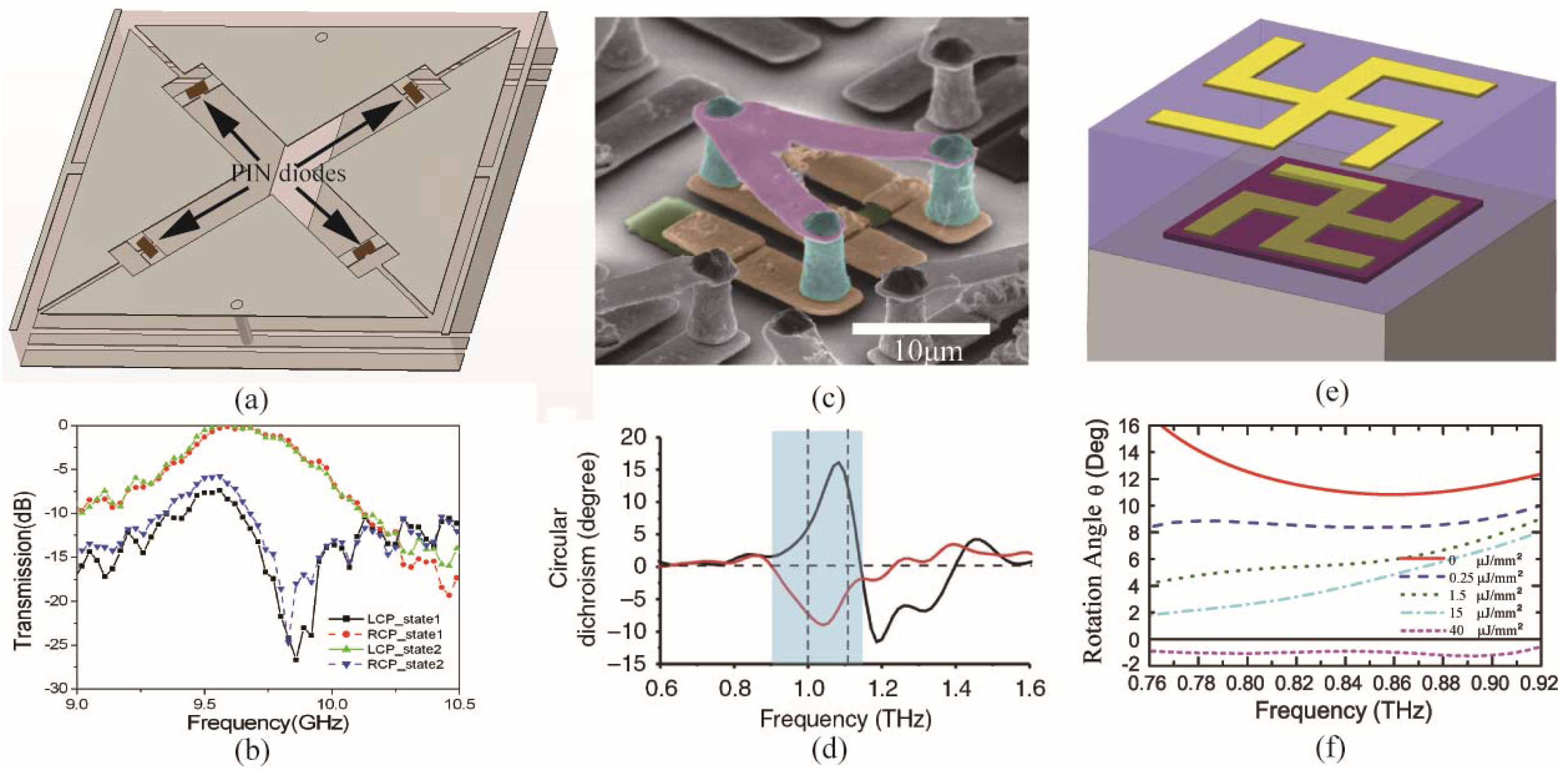
6. Reconfigurable Chiral Metamaterials
7. Conclusions and Outlook
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Barron, L.D. Molecular Light Scattering and Optical Activity; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Wang, Z.; Cheng, F.; Winsor, T.; Liu, Y. Optical chiral metamaterials: A review of the fundamentals, fabrication methods and applications. Nanotechnology 2016, 27, 412001. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 2000, 85, 3966–3969. [Google Scholar] [CrossRef] [PubMed]
- Shelby, R.; Smith, D.; Schultz, S. Experimental verification of a negative index of refraction. Science 2001, 292, 77–79. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Padilla, W.; Vier, D.; Nemat-Nasser, S.; Schultz, S. Composite medium with simultaneously negative permeability and permittivity. Phys. Rev. Lett. 2000, 84, 4184–4187. [Google Scholar] [CrossRef] [PubMed]
- Parazzoli, C.G.; Greegor, R.B.; Li, K.; Koltenbah, B.E.C.; Tanielian, M. Experimental verification and simulation of negative index of refraction using Snell’s law. Phys. Rev. Lett. 2003, 90, 107401. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.R.; Pendry, J.B.; Wiltshire, M.C.K. Metamaterials and negative refractive index. Science 2004, 305, 788–792. [Google Scholar] [CrossRef] [PubMed]
- Lezec, H.J.; Dionne, J.A.; Atwater, H.A. Negative Refraction at Visible Frequencies. Science 2007, 316, 430. [Google Scholar] [CrossRef] [PubMed]
- Soukoulis, C.M.; Linden, S.; Wegener, M. Negative Refractive Index at Optical Wavelengths. Science 2007, 315, 47. [Google Scholar] [CrossRef] [PubMed]
- Veselago, V.G. The electrodynamics of substances with simultaneously negative values of ε and μ. Sov. Phys. USPEKHI 1968, 10, 509–514. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Teperik, T.V.; Garcia de Abajo, F.J.; Borisov, A.G.; Abdelsalam, M.; Bartlett, P.N.; Sugawara, Y.; Baumberg, J.J. Omnidirectional absorption in nanostructured metal surfaces. Nat. Photon. 2008, 2, 299–301. [Google Scholar] [CrossRef]
- Tao, H.; Bingham, C.M.; Strikwerda, A.C.; Pilon, D.; Shrekenhamer, D.; Landy, N.I.; Fan, K.; Zhang, X.; Padilla, W.J.; Averitt, R.D. Highly flexible wide angle of incidence terahertz metamaterial absorber: Design, fabrication, and characterization. Phys. Rev. B 2008, 78, 241103. [Google Scholar] [CrossRef]
- Ye, Y.Q.; Jin, Y.; He, S. Omnidirectional, polarization-insensitive and broadband thin absorber in the terahertz regime. J. Opt. Soc. Am. B-Opt. Phys. 2010, 27, 498–504. [Google Scholar] [CrossRef]
- Wang, M.; Huang, C.; Pu, M.; Hu, C.; Pan, W.; Zhao, Z.; Luo, X. Electric-controlled scanning Luneburg lens based on metamaterials. Appl. Phys. A 2013, 111, 445–450. [Google Scholar] [CrossRef]
- Lal, N.N.; Soares, B.F.; Sinha, J.K.; Huang, F.; Mahajan, S.; Bartlett, P.N.; Greenham, N.C.; Baumberg, J.J. Enhancing solar cells with localized plasmons in nanovoids. Opt. Express 2011, 19, 11256–11263. [Google Scholar] [CrossRef] [PubMed]
- Pu, M.; Hu, C.; Wang, M.; Huang, C.; Zhao, Z.; Wang, C.; Feng, Q.; Luo, X. Design principles for infrared wide-angle perfect absorber based on plasmonic structure. Opt. Express 2011, 19, 17413–17420. [Google Scholar] [CrossRef] [PubMed]
- Zürcher, J.F. A meander-line polarizer covering the full E-band (60-90GHz). Microw. Opt. Technol. Lett. 1998, 18, 320–323. [Google Scholar] [CrossRef]
- Schau, P.; Fu, L.; Frenner, K.; Schäferling, M.; Schweizer, H.; Giessen, H.; Venancio, L.M.G.; Osten, W. Polarization scramblers with plasmonic meander-type metamaterials. Opt. Express 2012, 20, 22700. [Google Scholar] [CrossRef] [PubMed]
- Dietlein, C.; Luukanen, A.; Popovi, Z.; Grossman, E. A W-Band Polarization Converter and Isolator. IEEE Trans. Antennas Propag. 2007, 55, 1804–1809. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.R.; Chen, H.-T. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef] [PubMed]
- Ekinci, Y.; Solak, H.H.; David, C.; Sigg, H. Bilayer Al wire-grids as broadband and high-performance polarizers. Opt. Express 2006, 14, 2323–2334. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Huang, C.; Pu, M.; Hu, C.; Feng, Q.; Luo, X. Single-layer circular polarizer using metamaterial and its application in antenna. Microw. Opt. Technol. Lett. 2012, 54, 1770–1774. [Google Scholar] [CrossRef]
- Pu, M.; Chen, P.; Wang, Y.; Zhao, Z.; Huang, C.; Wang, C.; Ma, X.; Luo, X. Anisotropic meta-mirror for achromatic electromagnetic polarization manipulation. Appl. Phys. Lett. 2013, 102, 131906. [Google Scholar] [CrossRef]
- Guo, Y.; Wang, Y.; Pu, M.; Zhao, Z.; Wu, X.; Ma, X.; Wang, C.; Yan, L.; Luo, X. Dispersion management of anisotropic metamirror for super-octave bandwidth polarization conversion. Sci. Rep. 2015, 5, 8434. [Google Scholar] [CrossRef] [PubMed]
- Ren, L.S.; Jiao, Y.C.; Li, F.; Zhao, J.J.; Zhao, G. A Dual-Layer T-Shaped Element for Broadband Circularly Polarized Reflectarray with Linearly Polarized Feed. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 407–410. [Google Scholar]
- Guo, Y.; Pu, M.; Ma, X.; Li, X.; Luo, X. Advances of dispersion-engineered metamaterials. Opto-Electron. Eng. 2017, 44, 3–22. [Google Scholar]
- Luo, X.; Ishihara, T. Surface plasmon resonant interference nanolithography technique. Appl. Phys. Lett. 2004, 84, 4780–4782. [Google Scholar] [CrossRef]
- Luo, X.; Ishihara, T. Subwavelength photolithography based on surface-plasmon polariton resonance. Opt. Express 2004, 12, 3055–3065. [Google Scholar] [CrossRef] [PubMed]
- Fang, N.; Lee, H.; Sun, C.; Zhang, X. Sub-diffraction-limited optical imaging with a silver superlens. Science 2005, 308, 534–537. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Lee, H.; Xiong, Y.; Sun, C.; Zhang, X. Far-field optical hyperlens magnifying sub-diffraction-limited objects. Science 2007, 315, 1686. [Google Scholar] [CrossRef] [PubMed]
- Xu, T.; Agrawal, A.; Abashin, M.; Chau, K.J.; Lezec, H.J. All-angle negative refraction and active flat lensing of ultraviolet light. Nature 2013, 497, 470–474. [Google Scholar] [CrossRef] [PubMed]
- Pu, M.; Ma, X.; Li, X.; Guo, Y.; Luo, X. Merging plasmonics and metamaterials by two-dimensional subwavelength structures. J. Mater. Chem. C 2017, 5, 4361–4378. [Google Scholar] [CrossRef]
- Luo, X. Principles of electromagnetic waves in metasurfaces. Sci. China-Phys. Mech. Astron. 2015, 58, 594201. [Google Scholar] [CrossRef]
- Zhao, Z.; Pu, M.; Wang, Y.; Luo, X. The generalized laws of refraction and reflection. Opto-Electron. Eng. 2017, 44, 129–139. [Google Scholar]
- Decker, M.; Ruther, M.; Kriegler, C.E.; Zhou, J.; Soukoulis, C.M.; Linden, S.; Wegener, M. Strong optical activity from twisted-cross photonic metamaterials. Opt. Lett. 2009, 34, 2501–2503. [Google Scholar] [CrossRef] [PubMed]
- Kenanakis, G.; Zhao, R.; Stavrinidis, A.; Konstantinidis, G.; Katsarakis, N.; Kafesaki, M.; Soukoulis, C.M.; Economou, E.N. Flexible chiral metamaterials in the terahertz regime: A comparative study of various designs. Opt. Mater. Express 2012, 2, 1702–1712. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, L.; Zhou, J.; Koschny, T.; Soukoulis, C.M. Conjugated gammadion chiral metamaterial with uniaxial optical activity and negative refractive index. Phys. Rev. B 2011, 83, 035105. [Google Scholar] [CrossRef]
- Plum, E.; Fedotov, V.A.; Schwanecke, A.S.; Zheludev, N.I.; Chen, Y. Giant optical gyrotropy due to electromagnetic coupling. Appl. Phys. Lett. 2007, 90, 223113. [Google Scholar] [CrossRef]
- Huang, W.; Zhang, Y.; Tang, X.; Cai, L.S.; Zhao, J.; Zhou, L.; Wang, Q.; Huang, C.; Zhu, Y. Optical properties of a planar metamaterial with chiral symmetry breaking. Opt. Lett. 2011, 36, 3359–3361. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Huang, C.; Pu, M.; Hu, C.; Feng, Q.; Luo, X. Multi-band circular polarizer using planar spiral metamaterial structure. Opt. Express 2012, 20, 16050–16058. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Huang, C.; Pan, W.; Zhao, B.; Cui, J.; Luo, X. A dual circularly polarized horn antenna in Ku-band based on chiral metamaterial. IEEE Trans. Antennas Propag. 2014, 62, 2307–2311. [Google Scholar] [CrossRef]
- Ma, X.; Huang, C.; Pu, M.; Wang, Y.; Zhao, Z.; Wang, C.; Luo, X. Dual-band asymmetry chiral metamaterial based on planar spiral structure. Appl. Phys. Lett. 2012, 101, 161901. [Google Scholar] [CrossRef]
- Cui, Y.; Kang, L.; Lan, S.; Rodrigues, S.; Cai, W. Giant chiral optical response from a twisted-arc metamaterial. Nano Lett. 2014, 14, 1021–1025. [Google Scholar] [CrossRef] [PubMed]
- Rodrigues, S.P.; Lan, S.; Kang, L.; Cui, Y.; Cai, W. Nonlinear Imaging and Spectroscopy of Chiral Metamaterials. Adv. Mater. 2014, 26, 6157–6162. [Google Scholar] [CrossRef] [PubMed]
- Mutlu, M.; Ozbay, E. A transparent 90° polarization rotator by combining chirality and electromagnetic wave tunneling. Appl. Phys. Lett. 2012, 100, 051909. [Google Scholar] [CrossRef]
- Mutlu, M.; Akosman, A.E.; Serebryannikov, A.E.; Ozbay, E. Asymmetric chiral metamaterial circular polarizer based on four U-shaped split ring resonators. Opt. Lett. 2011, 36, 1653–1655. [Google Scholar] [CrossRef] [PubMed]
- Decker, M.; Zhao, R.; Soukoulis, C.M.; Linden, S.; Wegener, M. Twisted split-ring-resonator photonic metamaterial with huge optical activity. Opt. Lett. 2010, 35, 1593–1595. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Zhou, J.; Koschny, T.; Soukoulis, C.M. Nonplanar chiral metamaterials with negative index. Appl. Phys. Lett. 2009, 94, 151112. [Google Scholar] [CrossRef]
- Li, Z.; Zhao, R.; Koschny, T.; Kafesaki, M.; Alici, K.B.; Colak, E.; Caglayan, H.; Ozbay, E.; Soukoulis, C.M. Chiral metamaterials with negative refractive index based on four “U” split ring resonators. Appl. Phys. Lett. 2010, 97, 081901. [Google Scholar] [CrossRef]
- Novitsky, A.V.; Galynsky, V.M.; Zhukovsky, S.V. Asymmetric transmission in planar chiral split-ring metamaterials: Microscopic Lorentz-theory approach. Phys. Rev. B 2012, 86, 075138. [Google Scholar] [CrossRef]
- Ma, X.; Huang, C.; Pu, M.; Pan, W.; Wang, Y.; Luo, X. Circular dichroism and optical rotation in twisted Y-shaped chiral metamaterial. Appl. Phys. Express 2013, 6, 022001. [Google Scholar] [CrossRef]
- Wongkasem, N.; Akyurtlu, A.; Marx, K.A.; Dong, Q.; Li, J.; Goodhue, W.D. Development of Chiral Negative Refractive Index Metamaterials for the Terahertz Frequency Regime. IEEE Trans. Antennas Propag. 2007, 55, 3052–3062. [Google Scholar] [CrossRef]
- Gansel, J.K.; Thiel, M.; Rill, M.S.; Decker, M.; Bade, K.; Saile, V.; von Freymann, G.; Linden, S.; Wegener, M. Gold helix photonic metamaterial as broadband circular polarizer. Science 2009, 325, 1513–1515. [Google Scholar] [CrossRef] [PubMed]
- Gansel, J.K.; Wegener, M.; Burger, S.; Linden, S. Gold helix photonic metamaterials: A numerical parameter study. Opt. Express 2010, 18, 1059–1069. [Google Scholar] [CrossRef] [PubMed]
- Mark, A.G.; Gibbs, J.G.; Lee, T.C.; Fischer, P. Hybrid nanocolloids with programmed three-dimensional shape and material composition. Nat. Mater. 2013, 12, 802–807. [Google Scholar] [CrossRef] [PubMed]
- Frank, B.; Yin, X.; Schäferling, M.; Zhao, J.; Hein, S.M.; Braun, P.V.; Giessen, H. Large-Area 3D Chiral Plasmonic Structures. ACS Nano 2013, 7, 6321–6329. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Tasco, V.; Todisco, F.; Cuscunà, M.; Benedetti, A.; Sanvitto, D.; Passaseo, A. Triple-helical nanowires by tomographic rotatory growth for chiral photonics. Nat. Commun. 2015, 6, 6484. [Google Scholar] [CrossRef] [PubMed]
- Pendry, J.B. A Chiral Route to Negative Refraction. Science 2004, 306, 1353–1355. [Google Scholar] [CrossRef] [PubMed]
- Monzon, C.; Forester, D. Negative refraction and focusing of circularly polarized waves in optically active media. Phys. Rev. Lett. 2005, 95. [Google Scholar] [CrossRef] [PubMed]
- Ding, Y.; Zhang, G.; Cheng, Y. Giant optical activity and negative refractive index in the terahertz region using complementary chiral metamaterials. Phys. Scr. 2012, 85, 065405. [Google Scholar] [CrossRef]
- Sabah, C.; Roskos, H.G. Design of a terahertz polarization rotator based on a periodic sequence of chiral metamaterial and dielectric slabs. Prog. Electromagn. Res. 2012, 124, 301–314. [Google Scholar] [CrossRef]
- Singh, R.; Plum, E.; Menzel, C.; Rockstuhl, C.; Azad, A.K.; Cheville, R.A.; Lederer, F.; Zhang, W.; Zheludev, N.I. Terahertz metamaterial with asymmetric transmission. Phys. Rev. B 2009, 80, 153104. [Google Scholar] [CrossRef]
- Cheng, H.; Chen, S.; Yu, P.; Li, J.; Deng, L.; Tian, J. Mid-infrared tunable optical polarization converter composed of asymmetric graphene nanocrosses. Opt. Lett. 2013, 38, 1567–1569. [Google Scholar] [CrossRef] [PubMed]
- Krasavin, A.V.; Schwanecke, A.S.; Zheludev, N.I. Extraordinary properties of light transmission through a small chiral hole in a metallic screen. J. Opt. -Pure Appl. Opt. 2006, 8, S98–S105. [Google Scholar] [CrossRef]
- Christofi, A.; Stefanou, N.; Gantzounis, G.; Papanikolaou, N. Giant Optical Activity of Helical Architectures of Plasmonic Nanorods. J. Phys. Chem. C 2012, 116, 16674–16679. [Google Scholar] [CrossRef]
- Du, L.; Kou, S.S.; Balaur, E.; Cadusch, J.J.; Roberts, A.; Abbey, B.; Yuan, X.C.; Tang, D.; Lin, J. Broadband chirality-coded meta-aperture for photon-spin resolving. Nat. Commun. 2015, 6, 10051. [Google Scholar] [CrossRef] [PubMed]
- Esposito, M.; Tasco, V.; Todisco, F.; Benedetti, A.; Sanvitto, D.; Passaseo, A. Three dimensional chiral metamaterial nanospirals in the visible range by vertically compensated focused ion beam induced-deposition. Adv. Opt. Mater. 2014, 2, 154–161. [Google Scholar] [CrossRef]
- Post, E.J. Formal Structure of Electromagnetics: General Covariance and Electromagnetics; Dover Publications: Mineola, NY, USA, 1997. [Google Scholar]
- Xie, X.; Simon, J.D. Picosecond circular dichroism spectroscopy: A Jones matrix analysis. J. Opt. Soc. Am. B 1990, 7, 1673–1684. [Google Scholar] [CrossRef]
- Menzel, C.; Rockstuhl, C.; Paul, T.; Lederer, F. Retrieving effective parameters for quasiplanar chiral metamaterials. Appl. Phys. Lett. 2008, 93, 233106. [Google Scholar] [CrossRef]
- Zhao, R.; Koschny, T.; Soukoulis, C.M. Chiral metamaterials: Retrieval of the effective parameters with and without substrate. Opt. Express 2010, 18, 14553–14567. [Google Scholar] [CrossRef] [PubMed]
- Kwon, D.H.; Werner, D.H.; Kildishev, A.V.; Shalaev, V.M. Material parameter retrieval procedure for general bi-isotropic metamaterials and its application to optical chiral negative-index metamaterial design. Opt. Express 2008, 16, 11822–11829. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Dong, J.; Wang, B.; Koschny, T.; Kafesaki, M.; Soukoulis, C.M. Negative refractive index due to chirality. Phys. Rev. B 2009, 79, 121104. [Google Scholar] [CrossRef]
- Plum, E.; Zhou, J.; Dong, J.; Fedotov, V.A.; Koschny, T.; Soukoulis, C.M.; Zheludev, N.I. Metamaterial with negative index due to chirality. Phys. Rev. B 2009, 79. [Google Scholar] [CrossRef]
- Huang, C.; Ma, X.; Pu, M.; Yi, G.; Wang, Y.; Luo, X. Dual-band 90° polarization rotator using twisted split ring resonators array. Opt. Commun. 2013, 291, 345–348. [Google Scholar] [CrossRef]
- Liu, N.; Giessen, H. Three-dimensional optical metamaterials as model systems for longitudinal and transverse magnetic coupling. Opt. Express 2008, 16, 21233–21238. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Li, H.; Yu, X.; Li, F.; Chen, H.; Chan, C.T. Metallic Helix Array as a Broadband Wave Plate. Phys. Rev. Lett. 2011, 107, 177401. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Yang, Z.; Zhao, M.; Wu, L.; Lu, Z.; Cheng, Y.; Gong, R.; Zheng, Y.; Duan, J. Similar structures, different characteristics: Circular dichroism of metallic helix arrays with single-, double-, and triple-helical structures. J. Opt. Soc. Am. A 2013, 30, 677–681. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Yang, Z.; Wang, J.; Zhao, M. Broadband terahertz circular polarizers with single- and double-helical array metamaterials. J. Opt. Soc. Am. A 2011, 28, 19–23. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.; Yang, Z.; Li, S.; Zhao, M. Higher extinction ratio circular polarizers with hetero-structured double-helical metamaterials. Opt. Express 2011, 19, 10886–10894. [Google Scholar] [CrossRef] [PubMed]
- Plum, E.; Fedotov, V.A.; Zheludev, N.I. Optical activity in extrinsically chiral metamaterial. Appl. Phys. Lett. 2008, 93, 191911. [Google Scholar] [CrossRef]
- Plum, E.; Fedotov, V.A.; Zheludev, N.I. Extrinsic electromagnetic chirality in metamaterials. J. Opt. Pure Appl. Opt. 2009, 11, 074009. [Google Scholar] [CrossRef]
- Plum, E.; Liu, X.X.; Fedotov, V.A.; Chen, Y.; Tsai, D.P.; Zheludev, N.I. Metamaterials: Optical activity without chirality. Phys. Rev. Lett. 2009, 102, 113902. [Google Scholar] [CrossRef] [PubMed]
- Sersic, I.; van de Haar, M.A.; Arango, F.B.; Koenderink, A.F. Ubiquity of Optical Activity in Planar Metamaterial Scatterers. Phys. Rev. Lett. 2012, 108, 223903. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Pu, M.; Li, X.; Huang, C.; Wang, Y.; Pan, W.; Zhao, B.; Cui, J.; Wang, C.; Zhao, Z.; et al. A planar chiral meta-surface for optical vortex generation and focusing. Sci. Rep. 2015, 5, 10365. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Chen, W.T.; Devlin, R.C.; Oh, J.; Zhu, A.Y.; Capasso, F. Metalenses at visible wavelengths: Diffraction-limited focusing and subwavelength resolution imaging. Science 2016, 352, 1190. [Google Scholar] [CrossRef] [PubMed]
- Pu, M.; Zhao, Z.; Wang, Y.; Li, X.; Ma, X.; Hu, C.; Wang, C.; Huang, C.; Luo, X. Spatially and spectrally engineered spin-orbit interaction for achromatic virtual shaping. Sci. Rep. 2015, 5, 9822. [Google Scholar] [CrossRef] [PubMed]
- Luo, J.; Zeng, B.; Wang, C.; Gao, P.; Liu, K.; Pu, M.; Jin, J.; Zhao, Z.; Li, X.; Yu, H.; et al. Fabrication of anisotropically arrayed nano-slots metasurfaces using reflective plasmonic lithography. Nanoscale 2015, 7, 18805–18812. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Li, X.; Chen, L.; Pu, M.; Jin, J.; Hong, M.; Luo, X. Orbital angular momentum multiplexing and demultiplexing by a single metasurface. Adv. Opt. Mater. 2017, 5, 1600502. [Google Scholar] [CrossRef]
- Lin, D.; Fan, P.; Hasman, E.; Brongersma, M.L. Dielectric gradient metasurface optical elements. Science 2014, 345, 298–302. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Kats, M.A.; Genevet, P.; Capasso, F. Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science 2015, 347, 1342–1345. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Ma, X.; Luo, X. Principles and applications of metasurfaces with phase modulation. Opto-Electron. Eng. 2017, 44, 255–275. [Google Scholar]
- Pu, M.; Li, X.; Ma, X.; Wang, Y.; Zhao, Z.; Wang, C.; Hu, C.; Gao, P.; Huang, C.; Ren, H.; et al. Catenary optics for achromatic generation of perfect optical angular momentum. Sci. Adv. 2015, 1, e1500396. [Google Scholar] [CrossRef] [PubMed]
- Ee, H.S.; Agarwal, R. Tunable Metasurface and Flat Optical Zoom Lens on a Stretchable Substrate. Nano Lett. 2016, 16, 2818–2823. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Chen, L.; Li, Y.; Zhang, X.; Pu, M.; Zhao, Z.; Ma, X.; Wang, Y.; Hong, M.; Luo, X. Multicolor 3D meta-holography by broadband plasmonic modulation. Sci. Adv. 2016, 2, e1601102. [Google Scholar] [CrossRef] [PubMed]
- Khorasaninejad, M.; Chen, W.T.; Zhu, A.Y.; Oh, J.; Devlin, R.C.; Rousso, D.; Capasso, F. Multispectral Chiral Imaging with a Metalens. Nano Lett. 2016, 16, 4595–4600. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Coppens, Z.J.; Besteiro, L.V.; Wang, W.; Govorov, A.O.; Valentine, J. Circularly polarized light detection with hot electrons in chiral plasmonic metamaterials. Proceeding of the Frontiers in Optics 2015, San Jose, CA, USA, 18–22 October 2015; OSA Publishing: Washington, DC, USA, 2015. [Google Scholar]
- Wang, Z.; Jia, H.; Yao, K.; Cai, W.; Chen, H.; Liu, Y. Circular Dichroism Metamirrors with Near-Perfect Extinction. ACS Photonics 2016, 3, 2096–2101. [Google Scholar] [CrossRef]
- Tehrani, K.N.; Abdolali, A.; Zarifi, D.; Hojjat-Kashani, F. Application of chiral layers and metamaterials for the reduction of radar cross section. Prog. Electromagn. Res. 2013, 137, 759–773. [Google Scholar] [CrossRef]
- Lv, T.T.; Zhu, Z.; Shi, J.H.; Guan, C.Y.; Wang, Z.P.; Cui, T.J. Optically controlled background-free terahertz switching in chiral metamaterial. Opt. Lett. 2014, 39, 3066–3069. [Google Scholar] [CrossRef] [PubMed]
- Kenanakis, G.; Zhao, R.; Katsarakis, N.; Kafesaki, M.; Soukoulis, C.M.; Economou, E.N. Optically controllable THz chiral metamaterials. Opt. Express 2014, 22, 12149–12159. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Rogers, E.T.F.; Gholipour, B.; Wang, C.M.; Yuan, G.; Teng, J.; Zheludev, N.I. Optically reconfigurable metasurfaces and photonic devices based on phase change materials. Nat. Photonics 2016, 10, 60–65. [Google Scholar] [CrossRef]
- Kan, T.; Isozaki, A.; Kanda, N.; Nemoto, N.; Konishi, K.; Takahashi, H.; Kuwata-Gonokami, M.; Matsumoto, K.; Shimoyama, I. Enantiomeric switching of chiral metamaterial for terahertz polarization modulation employing vertically deformable MEMS spirals. Nat. Commun. 2015, 6, 8422. [Google Scholar] [CrossRef] [PubMed]
- Ma, X.; Pan, W.; Huang, C.; Pu, M.; Wang, Y.; Zhao, B.; Cui, J.; Wang, C.; Luo, X. An active metamaterial for polarization manipulating. Adv. Opt. Mater. 2014, 2, 945–949. [Google Scholar] [CrossRef]
- Huang, C.; Pan, W.; Luo, X. Low–Loss circularly polarized transmitarray for beam steering application. IEEE Trans. Antennas Propag. 2016, 64, 4471–4476. [Google Scholar] [CrossRef]
- Cui, J.; Huang, C.; Pan, W.; Pu, M.; Guo, Y.; Luo, X. Dynamical manipulation of electromagnetic polarization using anisotropic meta-mirror. Sci. Rep. 2016, 6, 30771. [Google Scholar] [CrossRef] [PubMed]
- Yin, X.; Schäferling, M.; Michel, A.K.U.; Tittl, A.; Wuttig, M.; Taubner, T.; Giessen, H. Active Chiral Plasmonics. Nano Lett. 2015, 15, 4255–4260. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zhou, J.; Park, Y.S.; Rho, J.; Singh, R.; Nam, S.; Azad, A.K.; Chen, H.T.; Yin, X.; Taylor, A.J.; et al. Photoinduced handedness switching in terahertz chiral metamolecules. Nat. Commun. 2012, 3, 942. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Chowdhury, D.R.; Zhao, R.; Azad, A.K.; Chen, H.T.; Soukoulis, C.M.; Taylor, A.J.; O’Hara, J.F. Terahertz chiral metamaterials with giant and dynamically tunable optical activity. Phys. Rev. B 2012, 86, 035448. [Google Scholar] [CrossRef]
- Kuzyk, A.; Schreiber, R.; Fan, Z.; Pardatscher, G.; Roller, E.M.; Hogele, A.; Simmel, F.C.; Govorov, A.O.; Liedl, T. DNA-based self-assembly of chiral plasmonic nanostructures with tailored optical response. Nature 2012, 483, 311–314. [Google Scholar] [CrossRef] [PubMed]
- Kuzyk, A.; Schreiber, R.; Zhang, H.; Govorov, A.O.; Liedl, T.; Liu, N. Reconfigurable 3D plasmonic metamolecules. Nat. Mater. 2014, 13, 862–866. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.; Asenjo-Garcia, A.; Liu, Q.; Jiang, Q.; García De Abajo, F.J.; Liu, N.; Ding, B. Three-dimensional plasmonic chiral tetramers assembled by DNA origami. Nano Lett. 2013, 13, 2128–2133. [Google Scholar] [CrossRef] [PubMed]
- Hur, K.; Francescato, Y.; Giannini, V.; Maier, S.A.; Hennig, R.G.; Wiesner, U. Three-dimensionally isotropic negative refractive index materials from block copolymer self-Assembled chiral gyroid networks. Angew. Chem. Int. Ed. 2011, 50, 11985–11989. [Google Scholar] [CrossRef] [PubMed]
- Mamonov, E.; Kolmychek, I.; Murzina, T.; Maydykovsky, A.; Aktsipetrov, O.; Valev, V.; Verbiest, T.; Silhanek, A.; Moshchalkov, V. Circular dichroism in optical second harmonic generated in reflection from chiral G-shaped metamaterials. J. Phys. Conf. Ser. 2012, 352, 012029. [Google Scholar] [CrossRef]
- Valev, V.K.; Baumberg, J.J.; Clercq, B.D.; Braz, N.; Zheng, X.; Osley, E.J.; Vandendriessche, S.; Hojeij, M.; Blejean, C.; Mertens, J.; et al. Nonlinear superchiral meta-surfaces: Tuning chirality and disentangling non-reciprocity at the nanoscale. Adv. Mater. 2014, 26, 4074–4081. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Mutlu, M. Highly asymmetric transmission of linearly polarized waves realized with a multilayered structure including chiral metamaterials. J. Phys. Appl. Phys. 2014, 47, 075107. [Google Scholar] [CrossRef]
- Zhao, R.; Zhou, J.; Koschny, T.; Economou, E.N.; Soukoulis, C.M. Repulsive Casimir Force in Chiral Metamaterials. Phys. Rev. Lett. 2009, 103, 103602. [Google Scholar] [CrossRef] [PubMed]
- Zhao, R.; Koschny, T.; Economou, E.; Soukoulis, C. Comparison of chiral metamaterial designs for repulsive Casimir force. Phys. Rev. B 2010, 81, 235126. [Google Scholar] [CrossRef]
- Tang, Y.; Cohen, A.E. Enhanced enantioselectivity in excitation of chiral molecules by superchiral light. Science 2011, 332, 333–336. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, X.; Pu, M.; Li, X.; Guo, Y.; Gao, P.; Luo, X. Meta-Chirality: Fundamentals, Construction and Applications. Nanomaterials 2017, 7, 116. https://doi.org/10.3390/nano7050116
Ma X, Pu M, Li X, Guo Y, Gao P, Luo X. Meta-Chirality: Fundamentals, Construction and Applications. Nanomaterials. 2017; 7(5):116. https://doi.org/10.3390/nano7050116
Chicago/Turabian StyleMa, Xiaoliang, Mingbo Pu, Xiong Li, Yinghui Guo, Ping Gao, and Xiangang Luo. 2017. "Meta-Chirality: Fundamentals, Construction and Applications" Nanomaterials 7, no. 5: 116. https://doi.org/10.3390/nano7050116





