Strategies to Ascertain the Sign of the Spatial Curvature
Abstract
:1. Introduction
2. Cosmological Consequences of the Second Law
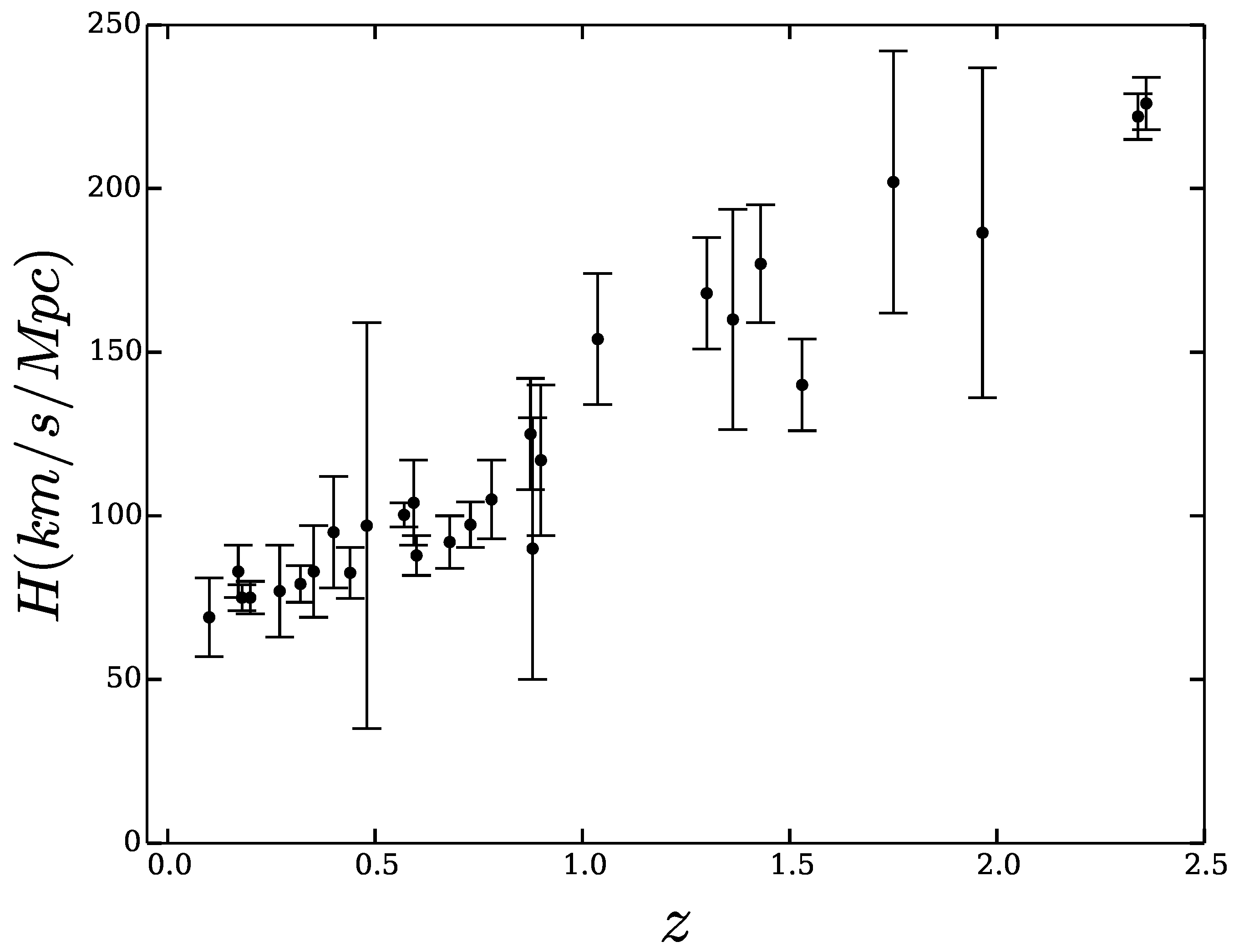
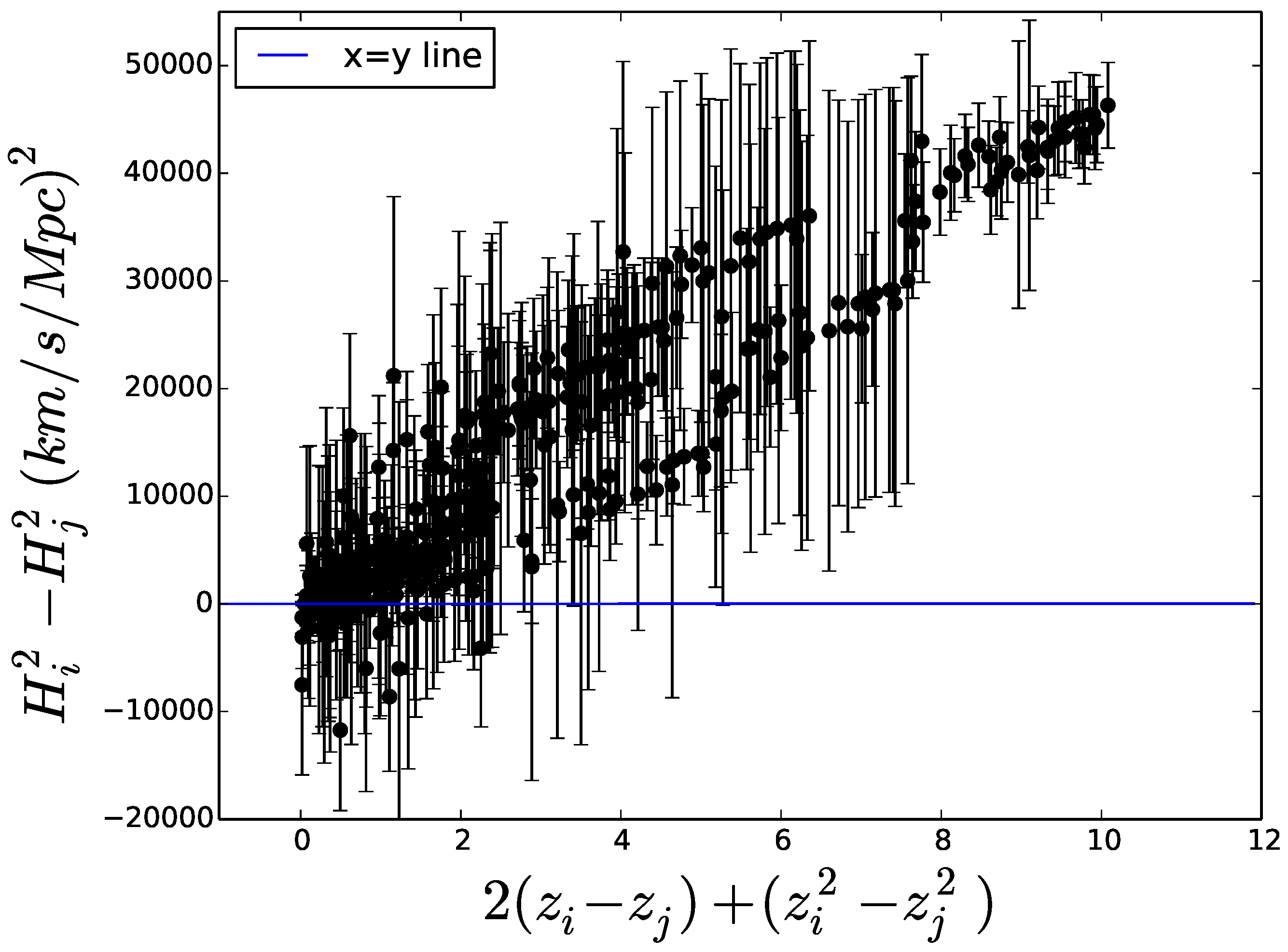
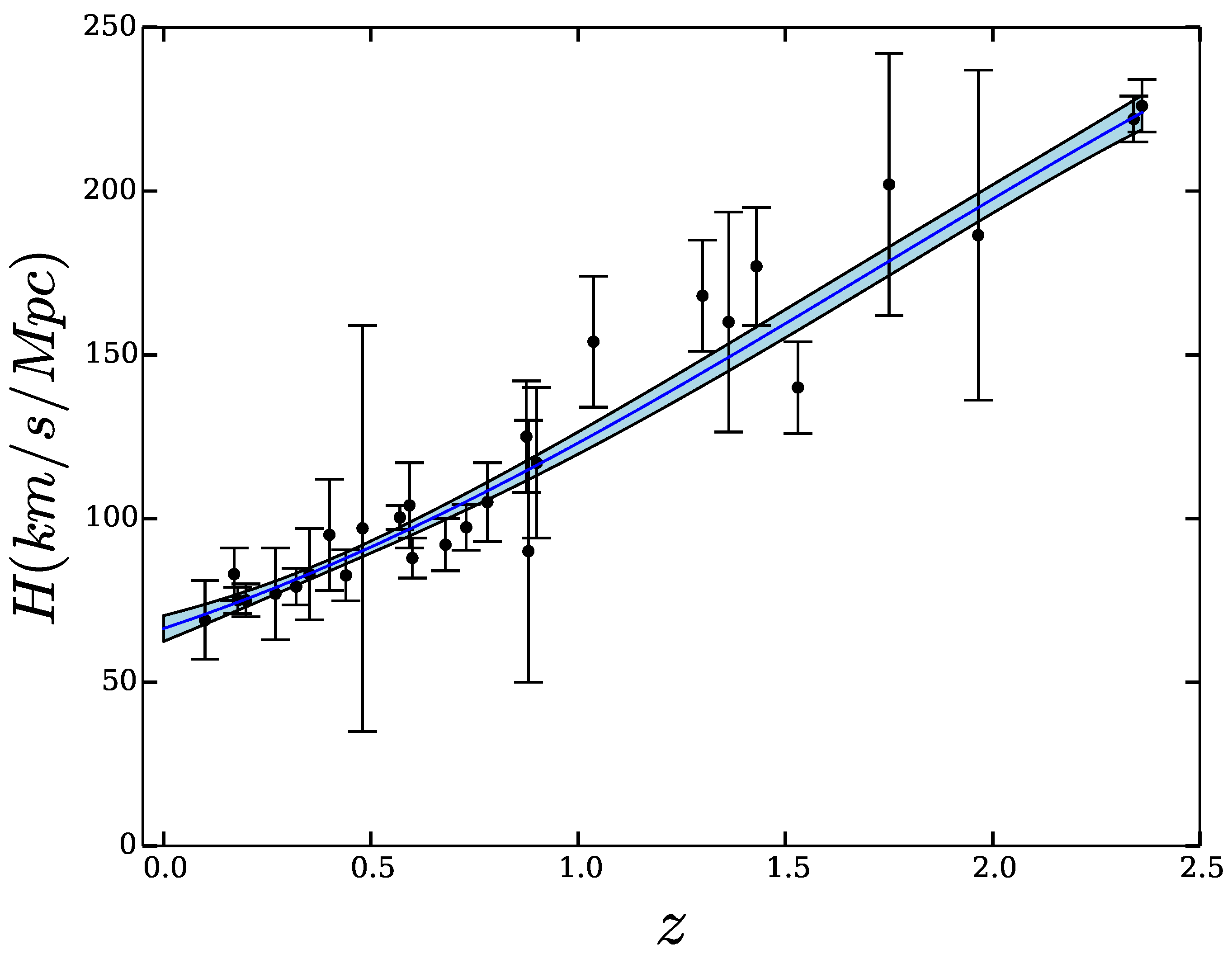
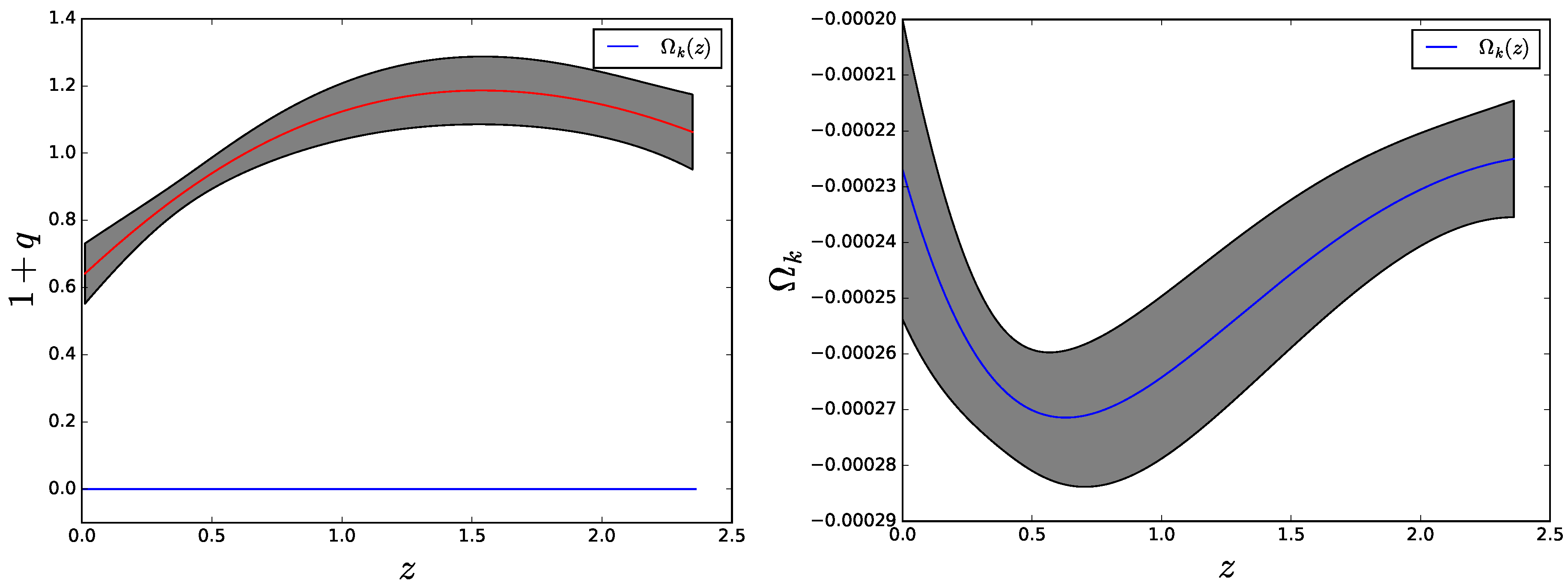
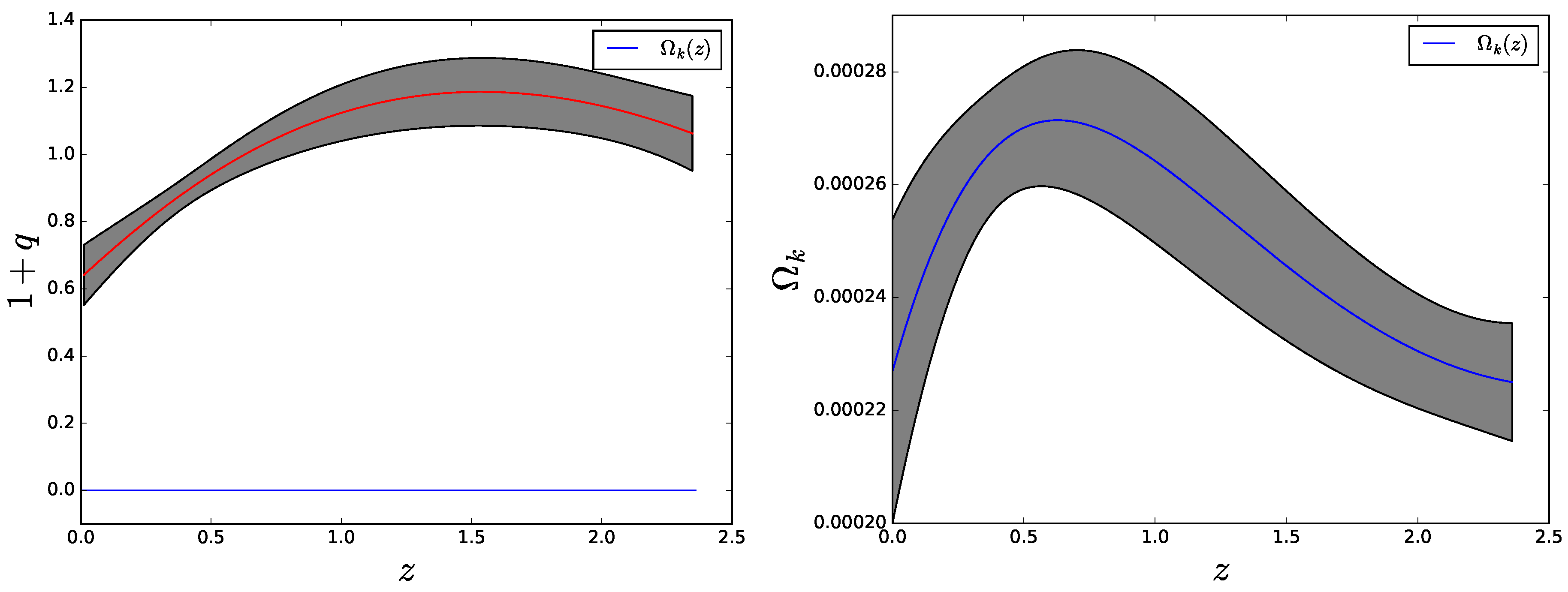
3. The Jerk Parameter
4. Concluding Remarks
Author Contributions
Conflicts of Interest
References
- Bekenstein, J.D. Generalized second law of thermodynamics in black-hole physics. Phys. Rev. D 1974, 9, 3292–3300. [Google Scholar] [CrossRef]
- Bekenstein, J.D. Statistical Black Hole Thermodynamics. Phys. Rev. D 1975, 12, 3077–3085. [Google Scholar] [CrossRef]
- Sorkin, R.D.; Wald, R.M.; Jiu, Z.Z. Entropy of Self-Gravitating Radiation. Gen. Relativ. Gravit. 1981, 13, 1127–1146. [Google Scholar] [CrossRef]
- Pavón, D.; Landsberg, P.T. Heat capacity of a self-gravitating radiation sphere. Gen. Relativ. Gravit. 1988, 20, 457–461. [Google Scholar] [CrossRef]
- Ferreira, P.C.; Pavón, D. Thermodynamics of nonsingular bouncing universes. Eur. Phys. J. C 2016, 76, 37. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and World-Structure. Astrophys. J. 1935, 82, 284–301. [Google Scholar] [CrossRef]
- Robertson, H.P. Kinematics and World-Structure III. Astrophys. J. 1936, 83, 257–271. [Google Scholar] [CrossRef]
- Walker, A.G. On Milne’s theory of world-structure. Proc. Lond. Math. Soc. 1936, s2-42, 90–127. [Google Scholar] [CrossRef]
- Clarkson, C.; Basset, B.; Lu, T.H.-C. A general test of the Copernican principle Phys. Rev. Lett. 2008, 101, 011301. [Google Scholar] [CrossRef] [PubMed]
- Zhang, P.; Stebbins, A. Confirmation of the Copernican principle through the anisotropic kinetic Sunyaev Zel’dovich effect. Phil. Trans. R. Soc. A 2011, 369, 5138–5145. [Google Scholar] [CrossRef] [PubMed]
- Bentivegna, E.; Bruni, M. Effects of Nonlinear Inhomogeneity on the Cosmic Expansion with Numerical Relativity. Phys. Rev. Lett. 2016, 116, 251302. [Google Scholar] [CrossRef] [PubMed]
- Saadeh, D.; Feeney, S.M.; Pontzen, A.; Peiris, H.V.; McEwen, J.D. How Isotropic is the Universe? Phys. Rev. Lett. 2016, 117, 131302. [Google Scholar] [CrossRef] [PubMed]
- Komatsu, E.; Smith, K.M.; Dunkley, J.; Bennett, C.L.; Gold, B.; Hinshaw, G.; Jarosik, N.; Larson, D.; Nolta, M.R.; Page, L.; et al. Seven-year Wilkinson Microwave Anisotropy Probe (WMAP) Observations: Cosmological Interpretation. Astrophys. J. Suppl. Ser. 2011, 192, 18. [Google Scholar] [CrossRef]
- Ade, P.R.; Aghanim, N.; Armitage-Caplan, C.; Arnaud, M.; Ashdown, M.; Atrio-Barandela, F.; Aumont, J.; Baccigalupi, C.; Banday, A.J.; Barreiro, R.B.; et al. Planck 2013 results. XVI. Cosmological parameters. Astron. Astrophys. 2014, 571, A16. [Google Scholar]
- Hawking, S.W. Black hole explosions? Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Jacobson, T. Thermodynamics of Spacetime: The Einstein Equation of State. Phys. Rev. Lett. 1995, 75, 1260–1263. [Google Scholar] [CrossRef] [PubMed]
- Padmanabhan, T. Gravity and the thermodynamics of horizons. Phys. Rep. 2005, 406, 49–125. [Google Scholar] [CrossRef]
- Radicella, N.; Pavón, D. A thermodynamic motivation for dark energy. Gen. Relativ. Grav. 2012, 44, 685–702. [Google Scholar] [CrossRef]
- Pavón, D.; Radicella, N. Does the entropy of the Universe tend to a maximum? Gen. Relativ. Grav. 2013, 45, 63–68. [Google Scholar] [CrossRef]
- Bak, D.; Rey, S.-J. Cosmic holography. Class. Quantum Grav. 2000, 17, L83. [Google Scholar] [CrossRef]
- Egan, C.; Lineweaver, C.L. A Larger Estimate of the Entropy of the Universe. Astrophys. J. 2010, 710, 1825–1834. [Google Scholar] [CrossRef]
- Wang, B.; Gong, Y.; Abdalla, E. Thermodynamics of an accelerated expanding universe. Phys. Rev. D 2006, 74, 083520. [Google Scholar] [CrossRef]
- Frautschi, S. Entropy in an Expanding Universe. Science 1982, 217, 593–599. [Google Scholar] [CrossRef] [PubMed]
- Farook, O.; Madiyar, F.R.; Crandall, S.; Ratra, B. Hubble Parameter Measurement Constraints on the Redshift of the Deceleration-Acceleration Transition, Dynamical Dark Energy, and Space Curvature. 2016; arXiv:1607.03537. [Google Scholar]
- Cyburt, R.H.; Fields, B.D.; Olive, K.; Yeh, T.H. Big bang nucleosynthesis: Present status. Rev. Mod. Phys. 2016, 88, 015004. [Google Scholar] [CrossRef]
- Simon, J.; Verde, L.; Jiménez, R. Constraints on the redshift dependence of the dark energy potential. Phys. Rev. D 2005, 71, 123001. [Google Scholar] [CrossRef]
- Moresco, M.; Cimatti, A.; Jimenez, R.; Pozzetti, L.; Zamorani, G.; Bolzonella, M.; Dunlop, J.; Lamareille, F.; Mignoli, M.; Pearce, H.; et al. Improved constraints on the expansion rate of the Universe up to z ∼ 1.1 from the spectroscopic evolution of cosmic chronometers. J. Cosmol. Astropart. Phys. 2012, 2012, 006. [Google Scholar] [CrossRef] [PubMed]
- Cuesta, A.J.; Vargas-Magaña, M.; Beutler, F.; Bolton, A.S.; Brownstein, J.R.; Eisenstein, D.J.; Gil-Marín, H.; Ho, S.; McBride, C.K.; Maraston, C.; et al. The clustering of galaxies in the SDSS-III Baryon Oscillation Spectroscopic Survey: Baryon acoustic oscillations in the correlation function of LOWZ and CMASS galaxies in Data Release 12. Mont. Not. R. Astron. Soc. 2016, 457, 1770–1785. [Google Scholar] [CrossRef] [Green Version]
- Blake, C.; Brough, S.; Colless, M.; Contreras, C.; Couch, W.; Croom, S.; Croton, D.; Davis, T.M.; Drinkwater, M.J.; Forster, K.; et al. The WiggleZ Dark Energy Survey: Joint measurements of the expansion and growth history at z < 1. Mon. Not. R. Astron. Soc. 2012, 425, 405–141. [Google Scholar]
- Stern, D.; Jimenez, R.; Verde, L.; Kamionkowski, M.; Adam, S. Cosmic Chronometers: Constraining the Equation of State of Dark Energy. I: H(z) Measurements. J. Cosmol. Astropart. Phys. 2010, 2010, 008. [Google Scholar] [CrossRef]
- Moresco, M. Raising the bar: New constraints on the Hubble parameter with cosmic chronometers at z∼2. Mon. Not. R. Astron. Soc. 2015, 450, L16–L20. [Google Scholar] [CrossRef]
- Delubac, T.; Bautista, J.E.; Busca, N.G.; Rich, J.; Kirkby, D.; Bailey, S.; Font-Ribera, A.; Slosar, A.; Lee, K.-G.; Pieri, M.M.; et al. aryon acoustic oscillations in the Lyα forest of BOSS DR11 quasars. Astron. Astrophys. 2015, 574, A59. [Google Scholar] [CrossRef] [Green Version]
- Font-Ribera, A.; Kirkby, D.; Busca, N.; Miralda-Escudé, J.; Ross, N.P.; Slosar, A.; Rich, J.; Aubourg, E.; Bailey, S.; Bhardwaj, V.; et al. Quasar-Lyman α forest cross-correlation from BOSS DR11: Baryon Acoustic Oscillations. J. Cosmol. Astropart. Phys. 2014, 2014, 027. [Google Scholar] [CrossRef]
- Seikel, M.; Clarkson, C.; Smith, M. Reconstruction of dark energy and expansion dynamics using Gaussian processes. J. Cosmol. Astropart. Phys. 2012, 2012, 036. [Google Scholar] [CrossRef]
- Sandage, A. The Change of Redshift and Apparent Luminosity of Galaxies due to the Deceleration of Selected Expanding Universes. Astrophys. J. 1962, 136, 319–333. [Google Scholar] [CrossRef]
- Loeb, A. The Change of Redshift and Apparent Luminosity of Galaxies due to the Deceleration of Selected Expanding Universes. Astrophys. J. 1998, 499, L111–L114. [Google Scholar] [CrossRef] [Green Version]
- Vittie, G.C.M. Cosmological Theory, 2nd ed.; Wiley: New York, NY, USA, 1949. [Google Scholar]
- Spectrograph CODEX. Available online: http://www.iac.es/proyecto/codex/ (accessed on 22 November 2016).
- The European Extremely Large Telescope. Available online: http://www.eso.org/public/teles-instr/e-elt/ (accessed on 22 November 2016).
- Klockner, H.R.; Obreschkow, D.; Martins, C.; Raccanelli, A.; Champion, D.; Roy, A.; Lobanov, A.; Wagner, J.; Keller, R. Real time cosmology-A direct measure of the expansion rate of the Universe with the SKA. Proc. Sci. 2015, AASKA14, 027. [Google Scholar]
- Parkers 21 cm Multibeam Project. Available online: http://www.atnf.csiro.au/research/multibeam/ (accessed on 22 November 2016).
- The Canadian Hydrogen Intensity Mapping Experiment. Available online: chime.phas.ubc.ca/ (accessed on 22 November 2016).
- Yu, H.R.; Zhang, T.J.; Pen, U.L. Method for Direct Measurement of Cosmic Acceleration by 21-cm Absorption Systems. Phys. Rev. Lett. 2014, 113, 041303. [Google Scholar] [CrossRef] [PubMed]
- Liske, J.; Grazian, A.; Vanzella, E.; Dessauges, M.; Viel, M.; Pasquini, L.; Haehnelt, M.; Cristiani, S.; Pepe, F.; Avila, G.; et al. Cosmic dynamics in the era of Extremely Large Telescopes. Mon. Not. R. Astron. Soc. 2008, 386, 1192–1218. [Google Scholar] [CrossRef]
- Bochner, B.; Pappas, D.; Dong, M. Testing Lambda and the Limits of. Cosmography with the Union2.1. Supernova Compilation. Astrophys. J. 2015, 814, 7. [Google Scholar] [CrossRef]
- Daly, R.; Djorgovski, S.G.; Freeman, K.A.; Mory, M.P.; O’Dea, C.P.; Kharb, P.; Baum, S. Improved Constraints on the Acceleration History of the Universe and the Properties of the Dark Energ. Astrophys. J. 2008, 677, 1–11. [Google Scholar] [CrossRef]
- Perlmutter, S.; Aldering, G.; Della Valle, M.; Deustua, S.; Ellis, R.S.; Fabbro, S.; Fruchter, A.; Goldhaber, G.; Groom, D.E.; Hook, I.M.; et al. Discovery of a supernova explosion at half the age of the Universe. Nature 1998, 391, 51–54. [Google Scholar] [CrossRef] [Green Version]
- Riess, A.G.; Kirshner, R.P.; Schmidt, B.P.; Jha, S.; Challis, P.; Garnavich, P.M.; Esin, A.A.; Carpenter, C.; Grashius, R.; Schild, R.E.; et al. BV RI light curves for 22 type Ia supernovae. Astron. J. 1999, 117, 707–724. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferreira, P.C.; Pavón, D. Strategies to Ascertain the Sign of the Spatial Curvature. Universe 2016, 2, 27. https://doi.org/10.3390/universe2040027
Ferreira PC, Pavón D. Strategies to Ascertain the Sign of the Spatial Curvature. Universe. 2016; 2(4):27. https://doi.org/10.3390/universe2040027
Chicago/Turabian StyleFerreira, Pedro C., and Diego Pavón. 2016. "Strategies to Ascertain the Sign of the Spatial Curvature" Universe 2, no. 4: 27. https://doi.org/10.3390/universe2040027






