1. Introduction
The ground state of Yang-Mills (YM) theories plays a critical role in both Particle Physics and Cosmology. In particular, the gluon condensate in Quantum Chromo Dynamics (QCD) largely determines non-trivial properties of the topological QCD vacuum and is responsible, e.g., for the color confinement effects and hadron mass generation which can be understood beyond the Perturbation Theory (PT) only (for a comprehensive review on the QCD vacuum, see, e.g., Refs. [
1,
2,
3,
4] and references therein). The gluon condensate directly influences properties of the quark-gluon plasma and its hadronisation, as well as dynamics of the QCD phase transition. On the other hand, YM condensates have various implications in the cosmological evolution ranging from the Cosmic Inflation [
5,
6,
7] to the phenomenon of late-time acceleration and the Dark Energy (DE) [
8,
9,
10] (see also Refs. [
11,
12,
13,
14,
15,
16]).
Currently, the Cosmological Constant (CC) with the vacuum equation of state
is a preferred scenario for the late-time acceleration epoch supported by a wealth of recent observations provided that
(see, e.g., Refs. [
17,
18]). Despite of many DE/CC models existing in the literature, there is not a compelling resolution of the CC problem i.e., why the CC term is small and positive as well as why the CC term is non-zeroth and exists at all (for the existing proposals in connection to the hierarchy and origin problems of the Standard Model (SM) see, e.g., Refs. [
19,
20,
21]). From the Quantum Field Theory (QFT) viewpoint, the ground state energy density of the universe should account for a bulk of various contributions from existing quantum fields at energy scales ranging from the Quantum Gravity (Planck) scale,
GeV, down to the QCD confinement scale,
GeV. Of course, in absence of a workable version of quantum gravity the CC problem is not fully defined yet so in what follows non-quantum-gravitational aspects of this problem. Indeed, even such relatively well-known vacuum subsystems of the SM as the Higgs and quark-gluon condensates (which supposedly have nothing to do with quantum gravity) exceed by far the observed cosmological constant which is often considered as a severe problem [
22,
23] (for recent reviews on this topic, see, e.g., Refs. [
24,
25,
26] and references therein). Also it is well known, that an every field in the universe forms a divergent perturbative vacuum contribution, which is usually cut off at the Planck scale. The cancellation of these contributions may need the introduction of additional bosonic and fermionic fields putting important constraints for the particle spectrum [
27,
28,
29].
In this work, we discuss a well-defined part of the CC problem connected with formation of big non-perturbative vacuum contributions on the hadronic scale after the QCD phase transition, assuming that the contributions from higher scales are already compensated. In the case of confined QCD with color
gauge symmetry, there is a rather unique (negative-valued) contribution to the ground state energy of the universe originating from the non-perturbative quantum fluctuations of the quark and gluon fields [
1,
2,
30,
31],
. Given the fact that the CC term observed in astrophysical measurements is very small (and positive-valued),
one must eliminate the QCD vacuum contribution,
, with an unprecedented accuracy over forty decimal digits. A dynamical mechanism for such a gross cancellation of vacua terms is yet theoretically unknown although several possible scenarios elaborating on the cosmological role of the QCD condensates have been discussed so far, e.g., in Refs. [
9,
24,
32,
33,
34,
35,
36]. This work is devoted to making a further step in exploring the possibility for vacua cancellations in quantum YM theories with a non-trivial ground state. Clearly, in order to cancel the QCD vacuum contribution,
, formed during the QCD phase transition epoch, a positive contribution to the vacuum energy density should be formed at the same QCD energy scale
. Where could such an extra contribution originate from?
Here we suggest a new scenario of compensation realized by means of a hidden (mirror) sector of particles [
37] which correspond to the extra non-Abelian gauge group and whose possible interaction with the visible SM sectors is strongly suppressed.
In particular, a class of models known as Neutral Naturalness theories has been proposed in the literature [
38,
39,
40] as a promising solution of the naturalness problem in the SM protecting the weak scale from large radiative corrections. Various phenomenological implications of such a “Mirror World” concept have been discussed, e.g., in Ref. [
41]. In particular, the mirror color
gauge group is typically assumed to be a symmetry describing the confined phase in full analogy with ordinary QCD revealing interesting signatures at the Large Hadron Collider due to, e.g., a mixing of mirror glueballs with the Higgs boson [
42].
Quite naturally, the quantum vacua contributions from the “Mirror World” should contribute to the CC on the same footing as known vacua since “mirror” particles are expected to gravitate in the same way as the usual ones. We argue that mirror QCD (mQCD) sector, if exists, should affect the cosmological expansion, in particular, via an extra non-trivial “mirror gluon” contribution into the ground state energy of the universe. In particular, an invisible QCD sector reconstructing Dark Energy was suggested in Refs. [
10,
43] while a unified description of Dark Matter and Dark Energy originating from invisible QCD dynamics was proposed in Refs. [
44,
45]. Below, we will demonstrate that under certain conditions the mirror gluon condensate can contribute to the energy density of the universe with positive sign and thus may, in principle, eliminate the negative QCD vacuum effect yielding a vanishingly small CC term. Attributing the positive vacuum energy contribution to the mQCD sector non-interacting with quarks and gluons in ordinary QCD, one may therefore resolve the issue of why such a positive-valued condensate energy density does not emerge in QCD hadron physics and affects the CC-term only. Then the observed CC can, in principle, be formed as a remnant of the gluon condensate cancellation in expanding universe (e.g., due to an uncompensated quantum gravity correction to the QCD ground state energy) [
9], which appears to be remarkably consistent with the observed CC and with the Zeldovich scaling relation [
46]. The exact compensation of the QCD vacuum effect by means of the mirror gluon condensate is therefore the central point to the observable smallness of the CC.
2. QCD and Mirror QCD Vacua Compensation
The condensate in QCD is formed by the contributions of gluon and quark non-perturbative quantum fluctuations
Usually, the dominant gluon contribution is given by means of the trace anomaly relation in QCD
which to one-loop order reads [
1,
2]
where
is the first (one-loop) coefficient of the negative perturbative
-function in
gluodynamics with three light flavors
with
being the QCD scale parameter (the normalization of
corresponds to Ref. [
47]). The formation of the chromomagnetic gluon condensate
is typically considered at characteristic momentum scales
inverse to the correlation length
, i.e.,
GeV [
1,
2], where the perturbative QCD still provides a realistic estimate. This validates the use of one-loop approximated expression (
4).
One would like to explain why such a big negative contribution (
2), which is responsible for a variety of well-known phenomena in hadron physics and is rather unique for QCD, does not affect the cosmological expansion at late times. Provided that the observed CC-term density
is tiny compared to the QCD vacuum density (
4), the latter should be almost totally eliminated during the QCD phase transition epoch. Which mechanism could be responsible for that?
A mirror copy of QCD may generate a similar gluon contribution to the trace anomaly proportional to the corresponding
-function in mQCD,
In mQCD framework mirror quarks can be much heavier than in ordinary QCD [
40]. Applying the idea, that mQCD is similar in main features to usual QCD, this means, that in mQCD the vacuum is formed only by mirror gluon contribution with pure gluonic
-function, as long as the heavy quark condensates [
48] are compensated by quark part of
-function, i.e.,
A possible cancellation of QCD and mQCD vacuum may ensure a required smallness of the observable CC density
which means that the corresponding mirror gluon condensate should provide a positive contribution to the vacuum density, i.e.,
. We suppose, that mQCD gluon condensate can compensate both gluon and quark condensates of usual QCD.
Adopting the traditional hypothesis that the mQCD sector of mirror quarks and gluons is confined but is not (or very weakly) interacting with the observed SM sectors [
42] and considering only chromomagnetic condensates, the compensation condition (
9) can be satisfied if and only if the mQCD
-function is positive, i.e.,
which is not realized in the perturbative mQCD regime due to Equation (
5). It is, however, possible to achieve the positivity of the non-perturbative
-function provided that at the characteristic scale of the QCD gluon condensate formation,
, the mQCD sector is in deeply non-perturbative regime. The latter condition can be satisfied if the mQCD scale parameter is large, i.e.,
such that the mirror gluon condensate would be in deeply non-perturbative regime by the moment in the cosmological evolution when its density gets precisely cancelled with the QCD contribution. Note that the compensation conditions for the QCD and mQCD contributions (
9) and (
10), if indeed realized in nature, may be one of the most important implications of the mirror QCD in Cosmology yielding a vanishing CC-term and thus providing a dynamical way to resolve the CC problem.
Can the sign of the
-function in mQCD become positive in the non-perturbative regime? In order to answer this question, one has to employ a proper formalism which extends the effective action approach in a gauge theory beyond the perturbativity domain. Indeed, the compensation (
9) emerges as a long-distance phenomenon and thus should hold beyond the PT.
3. Effective Yang-Mills tHeory in Expanding Universe
The effective action of the quantum YM gauge
(
) theory consistently incorporating the vacuum polarisation effects and leading to the trace anomaly can be properly generalised to the FLRW background as follows [
49,
50] (see also Ref. [
10])
where the YM field and the corresponding stress tensor are defined as usual
with internal (in adjoint representation)
and Lorentz
indices and the gauge coupling
satisfying the RG evolution equation [
49,
50]
Depending on the sign of the invariant J, one distinguishes the chromoelectric and chromomagnetic YM fields.
The effective YM equation of motion in a non-trivial background metric reads
and can be employed beyond the PT as long as the non-perturbative
-function is known. Note, this equation is the exact equation of the Einstein-YM theory as it does not imply any approximations. Remarkably enough, this equation has a simple manifestly non-perturbative and exact ground-state solution with positive
-function
which is a complete analog of similar solution (see Ref. [
50], Equations (13) and (17)) found in the Euclidian case with the negative coupling and the
-function corresponding to the ferromagnetic vacuum. It is also a non-perturbative analog of the perturbative solution [
5,
32] eliminating the traceless part of the energy-momentum tensor
which then takes the following form
We have explicitly checked that the exact partial solution (
15) of the YM equation (
14) naturally corresponds to the minimum of the non-perturbative effective YM Lagrangian (
12). It holds strictly beyond the Perturbation Theory, just like the YM trace anomaly itself. Thus, the exact solution (
15) corresponds to the physical quantum ground state of an effective YM theory.
It is important to point out following Ref. [
50], that the Equations (
15)–(
16) were obtained in the pure YM case when the interaction with other fields can be neglected. In particular, we neglect the mQCD quark current in the right hand side of Equation (
14). Let us also stress that we consider the effective YM Lagrangian (
12) and energy-momentum tensor (16) as a classical model [
50] which possesses well-known properties of the full quantum theory such as (i) local gauge invariance; (ii) RG evolution and asymptotic freedom; (iii) correct quantum vacuum configurations; and (iv) trace anomaly given by the last term in Equation (16). These provide a sufficient motivation and physics interest in cosmological aspects of the considering effective model.
As the solution (
15) leads to the energy-momentum tensor of vacuum type (
16), it immediately follows from the Friedmann equations that the corresponding energy density is constant
thus, the contribution of the YM fields has a cosmological constant form. In particular, this can be realised if
. Indeed, the solution (
15) fixes the invariant
J to its constant initial value
Such solutions were also considered in Refs. [
5,
32,
50] in connection with the spontaneous vacuum magnetisation and in the domain concept of the QCD vacuum [
51] (see also the recent paper [
52] and references therein).
Further, we will apply the solution (
15) and (
18) to the the mQCD theory in the non-perturbative regime. The energy-momentum tensor in this case becomes constant as expected
where
. The coupling
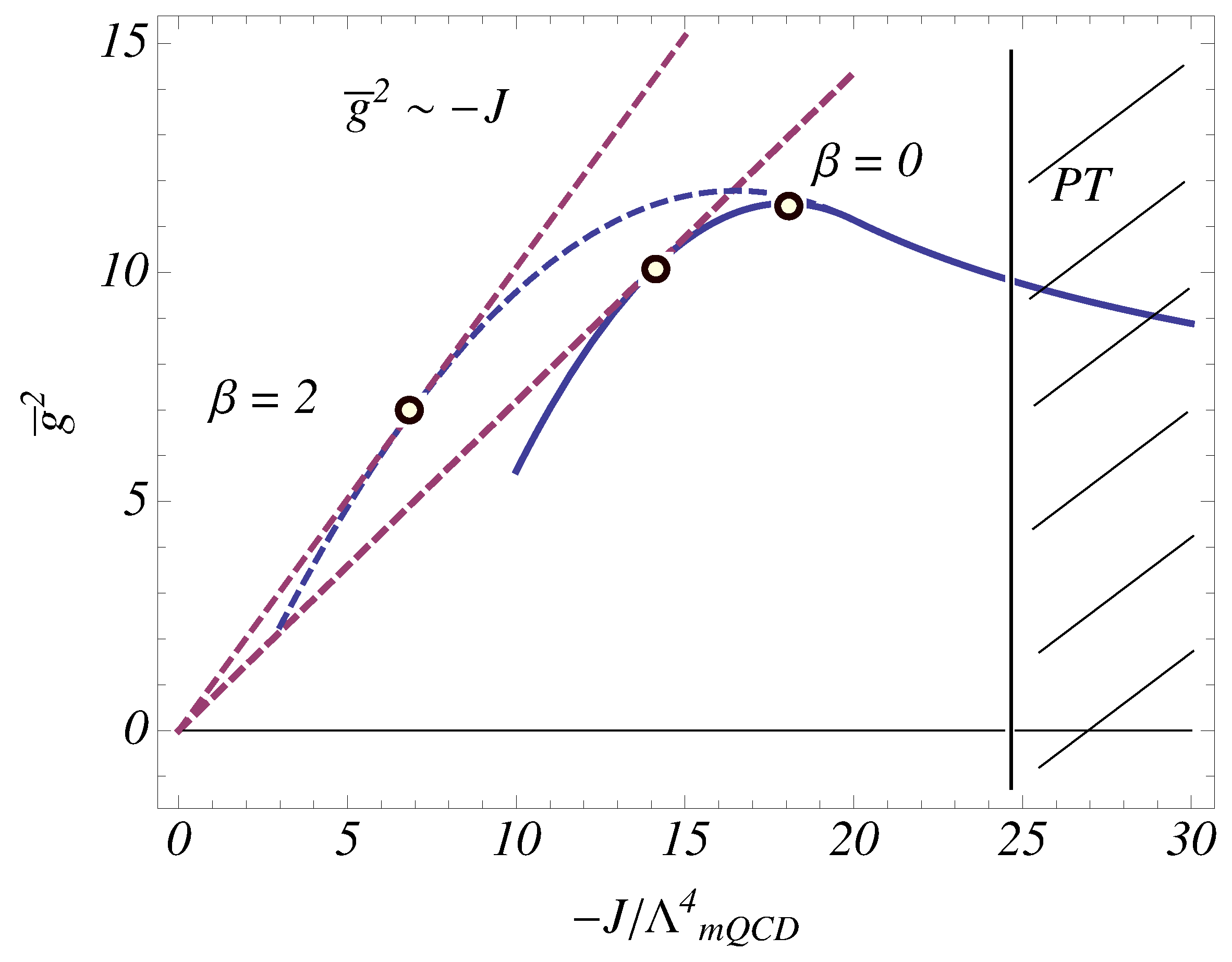
touches the linear function
at the point
(indeed, it has the same value and derivative). And vice versa, if
touches
at some point
, then
, which means that Equation (
15) is satisfied at
. Indeed, the existence of such a contact point is a necessary and sufficient condition for the solution (
15) with fixed
. This allows us to constrain generic non-perturbative behavior of the corresponding
. An illustration of the corresponding infrared behavior of the mQCD coupling in consistency with both the non-perturbative asymptotics for the
-function (
15) and the conventional perturbative regime of asymptotic freedom (
5) is shown in
Figure 1. A desirable non-monotonic shape of the coupling was earlier discussed in the case of usual QCD [
53,
54].
From Equation (
17) one notices that the mQCD gauge field gives a constant vacuum contribution to the energy-momentum tensor in the Einstein equations. Since the QCD and mQCD contributions to the ground-state energy density have opposite signs there is a compelling possibility that they can, in principle, cancel each other at some moment
in the cosmological history provided that
in the infrared regime of mQCD. We argue that this relation can be reached at some
around the QCD phase transition epoch as long as the mQCD energy scale
is much larger than that in QCD
such that at the cancellation time
their
-functions have different signs. Keeping
in both QCD and mQCD, we arrive at the following form of the compensation condition (
9)
which means, that mQCD condensate has to be chromomagnetic.
After such a compensation is achieved, only a very small
contribution, which could be formed by other vacuum sources
and possibly by a non-compensated part of mQCD and QCD vacua contributions
, remains. Of course, a fine-tuning is unavoidable to match the observations, although would not be entirely unreasonable due to the same order magnitude of the QCD and mQCD contributions. Such a vacua alignment, if realised in Nature, can be suggested, e.g., by macroscopic cancellation of trace anomalies in gauge theories inspired by the phenomenologically well-known color confinement phenomenon. Then the standard Friedmann equation in the non-stationary FLRW universe
determines the cosmological evolution,
, driven by the gluon and mirror gluon condensate densities (compensating each other exactly or in part), the matter contribution,
, and other possible vacua contributions of a different kind,
.
Let us notice for completeness, that Equation (
15) allows for a more specific solution apart from constant fields (
18). This another solution appears, if the non-perturbative
-function becomes constant satisfying Equation (
15) in some finite domain which corresponds to the strong coupling regime (saturated behaviour). In this case, Equation (
15) can be substituted into the RG equation
(
is a numerical parameter) which implies that the mQCD coupling is proportional to
J in the infrared limit, e.g.,
Such behaviour clearly guarantees a constant vacuum energy (see Equation (
16)) as well as a possibility for the QCD/mQCD vacua compensation. According to Equation (
24) the gauge coupling squared has to approach the linear
asymptotics in the non-perturbative regime (note, for the constant field solution (
18)
has to satisfy a much less restrictive constraint and just touches the linear asymptotics
at a fixed point).
So, within the QCD/mQCD vacua compensation hypothesis, both vacua subsystems should be generated in early universe at close (but different) energy scales and then get compensated during the cosmological QCD phase transition epoch. As was shown above, this can be realised in a deeply non-perturbative regime for the mirror gluon condensate which asymptotically acquires the same absolute value of energy density and opposite sign compared to the QCD gluon one, such that they almost exactly eliminate each other at macroscopically large space-time separations.
4. Summary
The only non-perturbative strongly-coupled vacuum system known in the Standard Model is the QCD ground state. One of the basic aspects of the Cosmological Constant problem related to the fact that neither perturbative (e.g., Higgs) nor non-perturbative (such as QCD) quantum vacua affect the cosmological expansion remains unexplored. While perturbative (weakly-coupled) quantum vacua should be treated elsewhere, e.g., in a proper theory of Quantum Gravity etc., the low-energy strongly-coupled vacua such that in QCD are the most problematic ones since they do not affect the Cosmological Constant but a priori they have nothing to do with quantum dynamics at the Planck scale. The absence of vacuum contributions of the color (quark and gluon) fields at macroscopic distances in QCD is tightly related with the confinement phenomenon, i.e., with the fact that no colored particles can propagate through macroscopic spacetime separations.
Note, we do not attempt to resolve the Cosmological Constant problem but consider a small but essential part of it connected with the QCD vacuum (provided that all perturbative vacua are eliminated by some other mechanism, see, e.g., Refs. [
27,
28,
29]). Namely, in this Letter, we discuss a plausible hypothesis of a partial or exact cancellation of averaged vacuum densities between QCD and a mirror high-scale copy of QCD in the confined regime corresponding to large separations (while locally such a compensation may not hold).
In this work, we do not propose any dynamical mechanism for such a compensation between QCD and mirror QCD vacua as this task would require a more detailed knowledge of their real-time dynamics, unavailable at the current state of this research field. Instead, for the first time we derive simple and generic conditions under which their contributions to the Cosmological Constant are mutually eliminated, if at all realised in Nature (for earlier works on this topic, see Refs. [
9,
32]). These conditions are based upon our main new finding that the
-function of an effective Yang-Mills theory has opposite signs in its perturbative and non-perturbative regimes. By an appropriate fine-tuning of QCD and mirror QCD vacua parameters whose dynamical reasons are unknown, the compensation can be provided by a partial non-perturbative solution of the Yang-Mills equation of motion corresponding to a positive constant
-function in deeply infrared regime of mirror QCD.