Non-Linear Stationary Solutions in Realistic Models for Analog Black-Hole Lasers
Abstract
:1. Introduction
2. Gravitational Analogues in Bose–Einstein Condensates
2.1. Effective One-Dimensional Configurations
2.2. Gross–Pitaevskii and Bogoliubov—De Gennes Equations
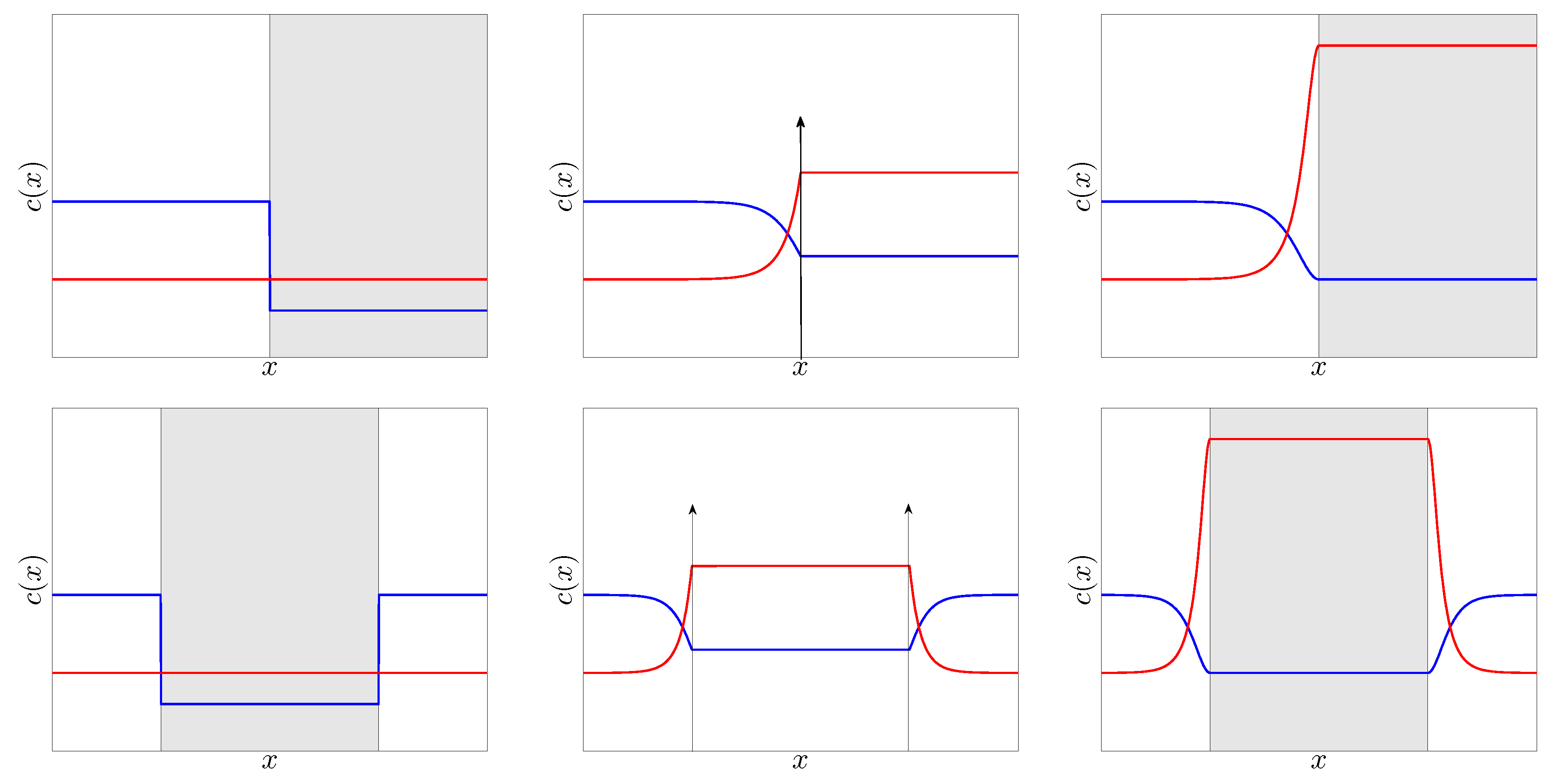
2.3. Analog Configurations
2.4. Solutions of the Homogeneous Gross—Pitaevskii Equation
3. General Relation between Black Holes and Black-Hole Lasers
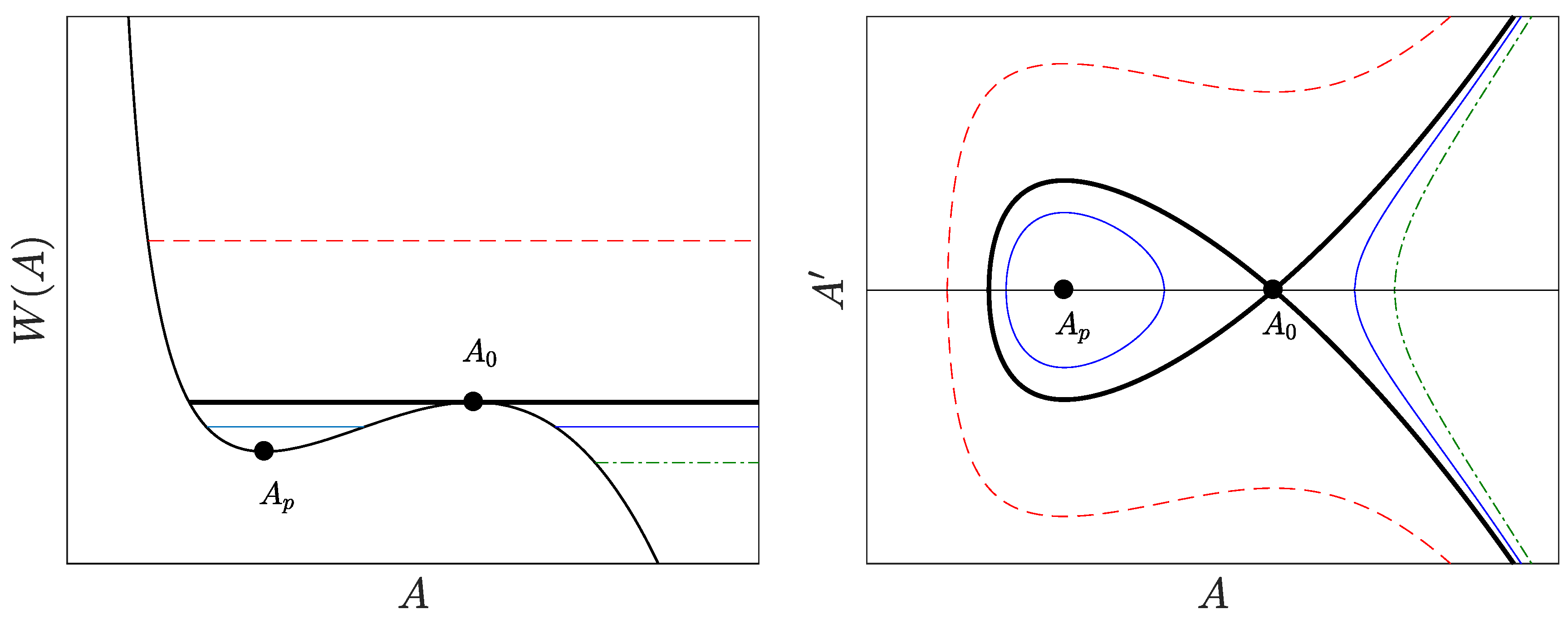
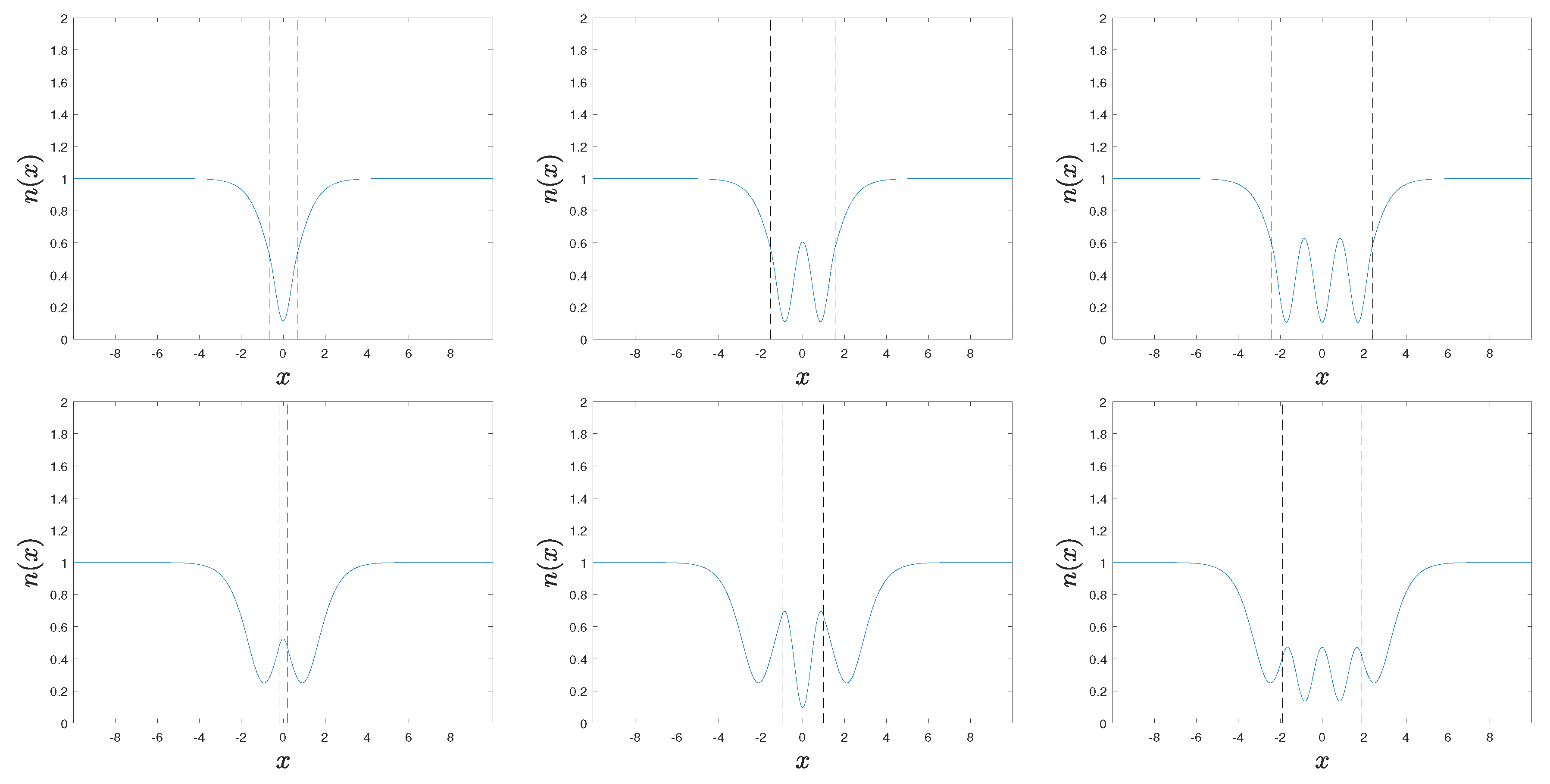
4. Attractive Square Well
4.1. General Structure
4.2. Homogeneous Plane Wave
4.3. Asymptotic Shadow Solitons
4.4. Asymptotic Solitons
4.4.1. Symmetric Solutions
Incomplete-Soliton Solutions
Complete-Soliton Solutions
4.4.2. Asymmetric Solutions
5. Double Delta-Barrier
5.1. General Structure
5.2. Symmetric Solutions
5.2.1. Solutions
5.2.2. Solutions
5.2.3. Solutions
5.3. Asymmetric Solutions
5.3.1. Solutions
5.3.2. Solutions
6. Conclusions and Outlook
Acknowledgments
Conflicts of Interest
Appendix A. Elliptic Functions
Appendix B. Computation of the Non-Linear Solutions of the Attractive Square Well
Appendix B.1. Homogeneous Plane Wave
Appendix B.2. Subsonic Shadow Solitons
Appendix B.3. Subsonic Solitons
Appendix B.3.1. Symmetric Solutions
Incomplete-Soliton Solutions
Complete-Soliton Solutions
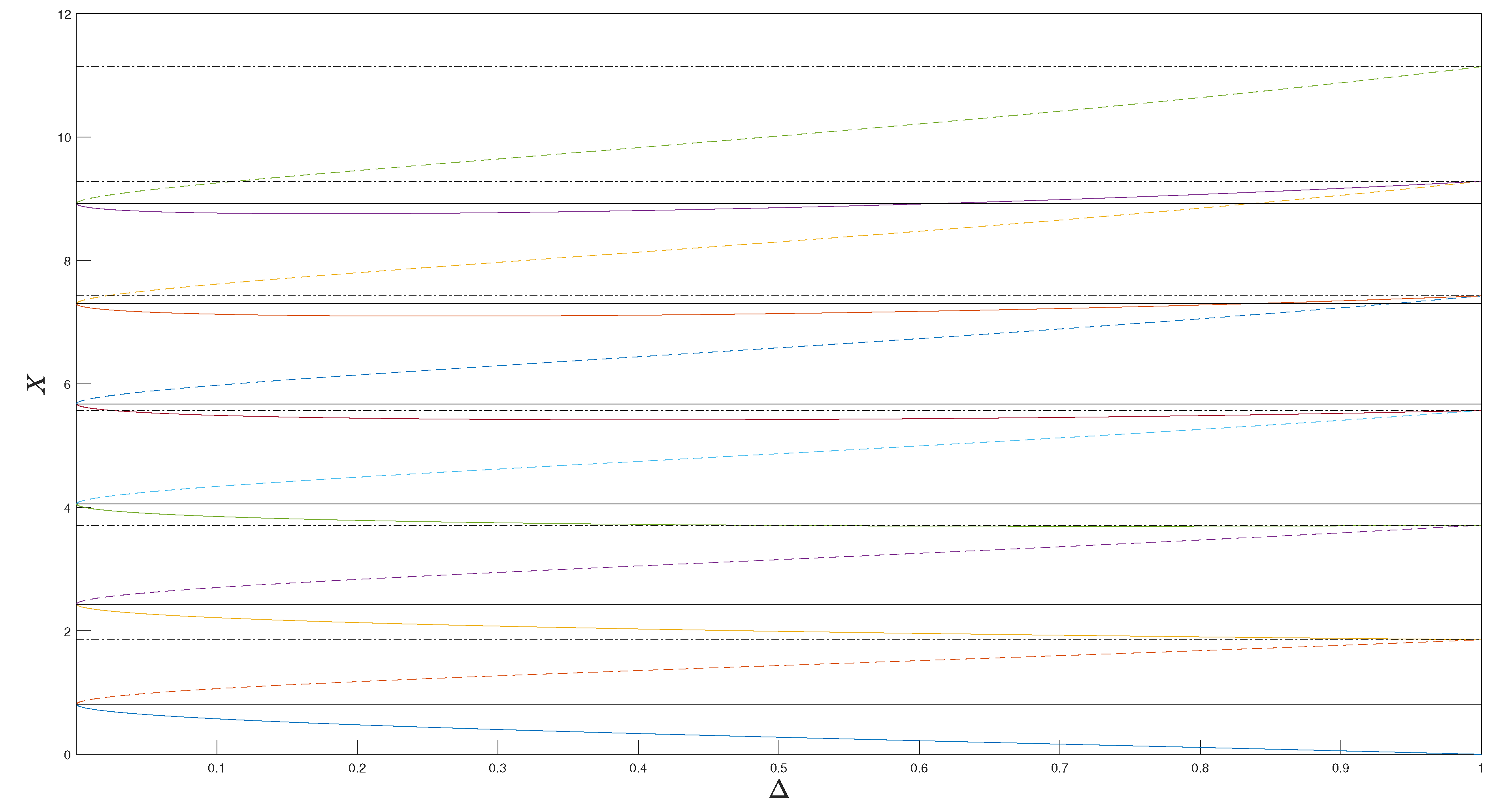
Appendix B.3.2. Asymmetric Solutions
Appendix C. Computation of the Non-Linear Solutions of the Double Delta-Barrier
Appendix C.1. Symmetric Solutions
Appendix C.1.1. S+ Solutions
Appendix C.1.2. S− Solutions
Appendix C.1.3. SD Solutions
Appendix C.2. Asymmetric Solutions
Appendix C.2.1. AC Solutions
Appendix C.2.2. AD Solutions
References
- Hawking, S.W. Black-hole evaporation. Nature 1974, 248, 30–31. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220. [Google Scholar] [CrossRef]
- Corley, S.; Jacobson, T. Black hole lasers. Phys. Rev. D 1999, 59, 124011. [Google Scholar] [CrossRef]
- Unruh, W.G. Experimental Black-Hole Evaporation? Phys. Rev. Lett. 1981, 46, 1351–1353. [Google Scholar] [CrossRef]
- Giovanazzi, S. Hawking Radiation in Sonic Black Holes. Phys. Rev. Lett. 2005, 94, 061302. [Google Scholar] [CrossRef] [PubMed]
- Horstmann, B.; Reznik, B.; Fagnocchi, S.; Cirac, J.I. Hawking Radiation from an Acoustic Black Hole on an Ion Ring. Phys. Rev. Lett. 2010, 104, 250403. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, H.S.; Gerace, D.; Carusotto, I.; Sanvitto, D.; Galopin, E.; Lemaître, A.; Sagnes, I.; Bloch, J.; Amo, A. Acoustic Black Hole in a Stationary Hydrodynamic Flow of Microcavity Polaritons. Phys. Rev. Lett. 2015, 114, 036402. [Google Scholar] [CrossRef] [PubMed]
- Euvé, L.-P.; Michel, F.; Parentani, R.; Philbin, T.G.; Rousseaux, G. Observation of Noise Correlated by the Hawking Effect in a Water Tank. Phys. Rev. Lett. 2016, 117, 121301. [Google Scholar] [CrossRef] [PubMed]
- Garay, L.J.; Anglin, J.R.; Cirac, J.I.; Zoller, P. Sonic Analog of Gravitational Black Holes in Bose-Einstein Condensates. Phys. Rev. Lett. 2000, 85, 4643–4647. [Google Scholar] [CrossRef] [PubMed]
- Leonhardt, U.; Kiss, T.; Öhberg, P. Theory of elementary excitations in unstable Bose-Einstein condensates and the instability of sonic horizons. Phys. Rev. A 2003, 67, 033602. [Google Scholar] [CrossRef]
- Leonhardt, U.; Kiss, T.; Öhberg, P. Bogoliubov theory of the Hawking effect in Bose-Einstein condensates. J. Opt. B 2003, 5, S42. [Google Scholar] [CrossRef]
- Balbinot, R.; Fabbri, A.; Fagnocchi, S.; Recati, A.; Carusotto, I. Nonlocal density correlations as a signature of Hawking radiation from acoustic black holes. Phys. Rev. A 2008, 78, 021603. [Google Scholar] [CrossRef]
- Carusotto, I.; Fagnocchi, S.; Recati, A.; Balbinot, R.; Fabbri, A. Numerical observation of Hawking radiation from acoustic black holes in atomic Bose–Einstein condensates. New J. Phys. 2008, 10, 103001. [Google Scholar] [CrossRef]
- Recati, A.; Pavloff, N.; Carusotto, I. Bogoliubov theory of acoustic Hawking radiation in Bose-Einstein condensates. Phys. Rev. A 2009, 80, 043603. [Google Scholar] [CrossRef]
- Macher, J.; Parentani, R. Black/white hole radiation from dispersive theories. Phys. Rev. D 2009, 79, 124008. [Google Scholar] [CrossRef]
- Coutant, A.; Parentani, R. Black hole lasers, a mode analysis. Phys. Rev. D 2010, 81, 084042. [Google Scholar] [CrossRef]
- De Nova, J.R.M.; Sols, F.; Zapata, I. Violation of Cauchy-Schwarz inequalities by spontaneous Hawking radiation in resonant boson structures. Phys. Rev. A 2014, 89, 043808. [Google Scholar] [CrossRef]
- Finazzi, S.; Carusotto, I. Entangled phonons in atomic Bose-Einstein condensates. Phys. Rev. A 2014, 90, 033607. [Google Scholar] [CrossRef]
- Busch, X.; Parentani, R. Quantum entanglement in analogue Hawking radiation: When is the final state nonseparable? Phys. Rev. D 2014, 89, 105024. [Google Scholar] [CrossRef]
- De Nova, J.R.M.; Guéry-Odelin, D.; Sols, F.; Zapata, I. Birth of a quasi-stationary black hole in an outcoupled Bose–Einstein condensate. New J. Phys. 2014, 16, 123033. [Google Scholar] [CrossRef]
- De Nova, J.R.M.; Sols, F.; Zapata, I. Entanglement and violation of classical inequalities in the Hawking radiation of flowing atom condensates. New J. Phys. 2015, 17, 105003. [Google Scholar] [CrossRef]
- Michel, F.; Parentani, R.; Zegers, R. No-hair theorems for analogue black holes. Phys. Rev. D 2016, 93, 065039. [Google Scholar] [CrossRef]
- Michel, F.; Coupechoux, J.-F.; Parentani, R. Phonon spectrum and correlations in a transonic flow of an atomic Bose gas. Phys. Rev. D 2016, 94, 084027. [Google Scholar] [CrossRef]
- Barceló, C.; Cano, A.; Garay, L.J.; Jannes, G. Stability analysis of sonic horizons in Bose-Einstein condensates. Phys. Rev. D 2006, 74, 024008. [Google Scholar] [CrossRef]
- Jain, P.; Bradley, A.; Gardiner, C. Quantum de Laval nozzle: Stability and quantum dynamics of sonic horizons in a toroidally trapped Bose gas containing a superflow. Phys. Rev. A 2007, 76, 023617. [Google Scholar] [CrossRef]
- Finazzi, S.; Parentani, R. Black hole lasers in Bose–Einstein condensates. New J. Phys. 2010, 12, 095015. [Google Scholar] [CrossRef]
- Michel, F.; Parentani, R. Saturation of black hole lasers in Bose-Einstein condensates. Phys. Rev. D 2013, 88, 125012. [Google Scholar] [CrossRef]
- Michel, F.; Parentani, R. Nonlinear effects in time-dependent transonic flows: An analysis of analog black hole stability. Phys. Rev. A 2015, 91, 053603. [Google Scholar] [CrossRef]
- De Nova, J.R.M.; Finazzi, S.; Carusotto, I. Time-dependent study of a black-hole laser in a flowing atomic condensate. Phys. Rev. A 2016, 94, 043616. [Google Scholar] [CrossRef]
- Lahav, O.; Itah, A.; Blumkin, A.; Gordon, C.; Rinott, S.; Zayats, A.; Steinhauer, J. Realization of a Sonic Black Hole Analog in a Bose-Einstein Condensate. Phys. Rev. Lett. 2010, 105, 240401. [Google Scholar] [CrossRef] [PubMed]
- Steinhauer, J. Observation of self-amplifying Hawking radiation in an analogue black-hole laser. Nat. Phys. 2014, 10, 864–869. [Google Scholar] [CrossRef]
- Tettamanti, M.; Cacciatori, S.L.; Parola, A.; Carusotto, I. Numerical study of a recent black-hole lasing experiment. Europhys. Lett. 2016, 114, 60011. [Google Scholar] [CrossRef]
- Wang, Y.-H.; Jacobson, T.; Edwards, M.; Clark, C.W. Mechanism of stimulated Hawking radiation in a laboratory Bose-Einstein condensate. arXiv 2016. [Google Scholar]
- Steinhauer, J.; de Nova, J.R.M. Self-amplifying Hawking radiation and its background: A numerical study. Phys. Rev. A 2017, 95, 033604. [Google Scholar] [CrossRef]
- Steinhauer, J. Observation of quantum Hawking radiation and its entanglement in an analogue black hole. Nat. Phys. 2016, 12, 959–965. [Google Scholar] [CrossRef]
- Kamchatnov, A.M.; Pavloff, N. Generation of dispersive shock waves by the flow of a Bose-Einstein condensate past a narrow obstacle. Phys. Rev. A 2012, 85, 033603. [Google Scholar] [CrossRef]
- Larré, P.E.; Recati, A.; Carusotto, I.; Pavloff, N. Quantum fluctuations around black hole horizons in Bose-Einstein condensates. Phys. Rev. A 2012, 85, 013621. [Google Scholar] [CrossRef]
- Leboeuf, P.; Pavloff, N. Bose-Einstein beams: Coherent propagation through a guide. Phys. Rev. A 2001, 64, 033602. [Google Scholar] [CrossRef]
- Zapata, I.; Albert, M.; Parentani, R.; Sols, F. Resonant Hawking radiation in Bose–Einstein condensates. New J. Phys. 2011, 13, 063048. [Google Scholar] [CrossRef]
- Macher, J.; Parentani, R. Black-hole radiation in Bose-Einstein condensates. Phys. Rev. A 2009, 80, 043601. [Google Scholar] [CrossRef]
- De Nova, J.R.M.; Zapata, I.; Sols, F. Violation of classical inequalities by resonant Hawking radiation in a sonic black hole. Phys. Scr. 2015, 2015, 014035. [Google Scholar] [CrossRef]
- Menotti, C.; Stringari, S. Collective oscillations of a one-dimensional trapped Bose-Einstein gas. Phys. Rev. A 2002, 66, 043610. [Google Scholar] [CrossRef]
- Fetter, A.; Walecka, J. Quantum Theory of Many-Particle Systems; Dover Books on Physics (Dover Publications): Mineola, NY, USA, 2003. [Google Scholar]
- Dickhoff, W.; Van Neck, D. Many-Body Theory Exposed!: Propagator Description of Quantum Mechanics in Many-Body Systems; World Scientific: Singapore, 2005. [Google Scholar]
- Pitaevskii, L.; Stringari, S. Bose-Einstein Condensation and Superfluidity; Clarendon Press: Oxford, UK, 2016. [Google Scholar]
- Pethick, C.J.; Smith, H. Bose-Einstein Condensation in Dilute Gases; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Carusotto, I.; Hu, S.X.; Collins, L.A.; Smerzi, A. Bogoliubov-Čerenkov Radiation in a Bose-Einstein Condensate Flowing against an Obstacle. Phys. Rev. Lett. 2006, 97, 260403. [Google Scholar] [CrossRef] [PubMed]
- Busch, T.; Anglin, J.R. Motion of Dark Solitons in Trapped Bose-Einstein Condensates. Phys. Rev. Lett. 2000, 84, 2298–2301. [Google Scholar] [CrossRef] [PubMed]
- Seaman, B.T.; Krämer, M.; Anderson, D.Z.; Holland, M.J. Atomtronics: Ultracold-atom analogs of electronic devices. Phys. Rev. A 2007, 75, 023615. [Google Scholar] [CrossRef]
- Labouvie, R.; Santra, B.; Heun, S.; Wimberger, S.; Ott, H. Negative Differential Conductivity in an Interacting Quantum Gas. Phys. Rev. Lett. 2015, 115, 050601. [Google Scholar] [CrossRef] [PubMed]
- Abramowitz, M.; Stegun, I.A.; Romer, R.H. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Am. J. Phys. 1988, 56. [Google Scholar] [CrossRef]
- Byrd, P.F.; Friedman, M.D. Handbook of Elliptic Integrals for Engineers and Scientists; Springer: Berlin/Heidelberg, Germany, 1971. [Google Scholar]





© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De Nova, J.R.M. Non-Linear Stationary Solutions in Realistic Models for Analog Black-Hole Lasers. Universe 2017, 3, 54. https://doi.org/10.3390/universe3030054
De Nova JRM. Non-Linear Stationary Solutions in Realistic Models for Analog Black-Hole Lasers. Universe. 2017; 3(3):54. https://doi.org/10.3390/universe3030054
Chicago/Turabian StyleDe Nova, Juan Ramón Muñoz. 2017. "Non-Linear Stationary Solutions in Realistic Models for Analog Black-Hole Lasers" Universe 3, no. 3: 54. https://doi.org/10.3390/universe3030054




