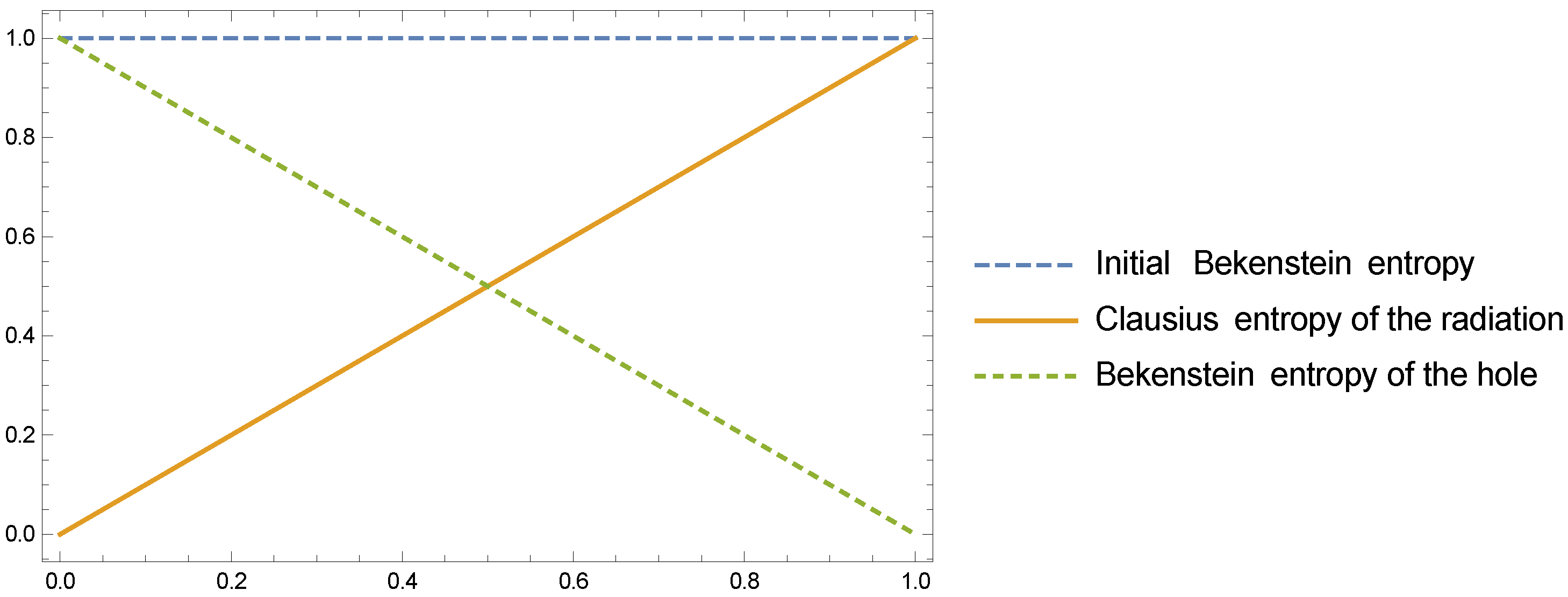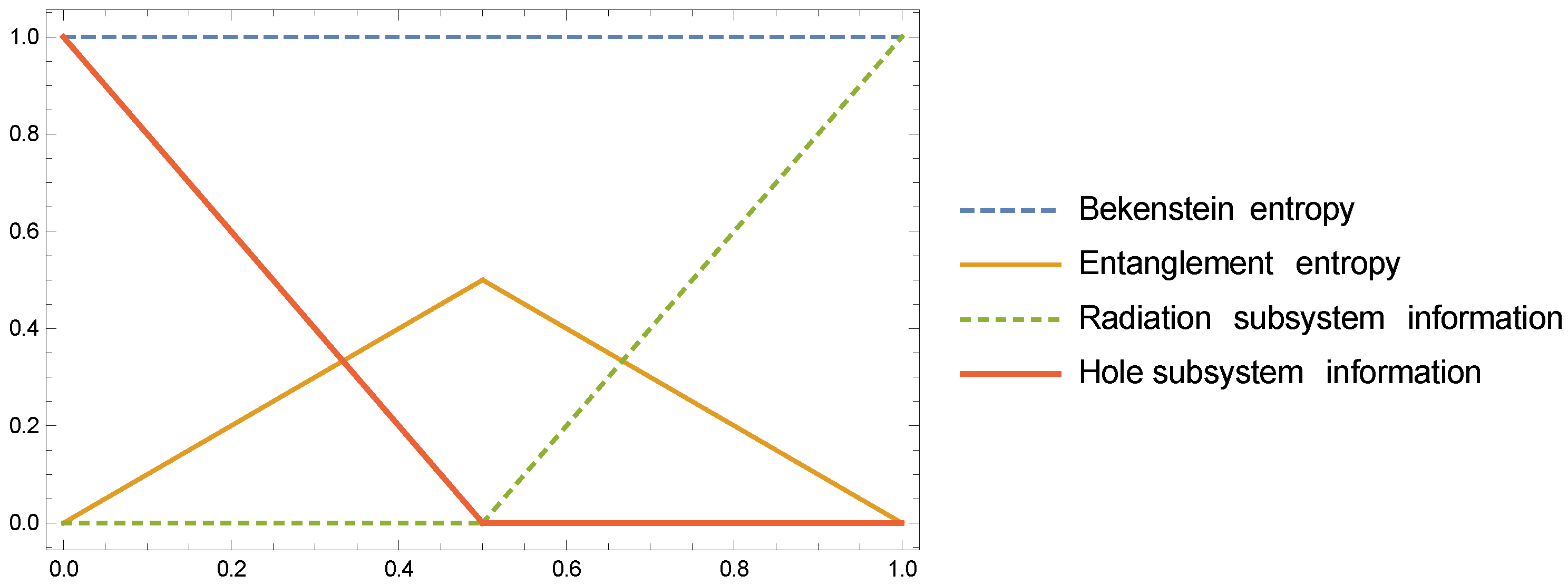1. Introduction
Hawking’s 1976 calculation [
1] of the thermal emission from a black hole is often interpreted in terms of Clausius entropy, indicating that, starting from a star in some unknown pure state, after it collapses to a black hole and subsequently evaporates, the system will (at the final stage) be in a mixed state, with corresponding loss of information. This argument gave rise to the so-called black hole information paradox, and there exist many very different proposals mooted to resolve it. For example, the information is irremediably lost, or it is stored in remnants or baby universes, or perhaps one has to appeal to the existence of new physical phenomena such as firewalls, fuzzballs, gravastars, etc. Most of the current ideas are based on the maintenance of unitary, as in standard quantum mechanics, but in some situations this assumption gives rise to non-standard physical effects—as in the case of the Page proposal [
2], which motivated, in part, the idea of firewalls [
3].
In order to obtain a better understanding of this problem, we first considered a standard unitary process, standard thermodynamic burning, in order to show the exact quantity of entropy exchanged between the burning matter and the electromagnetic field, which (given unitarity) must be compensated for with information hidden in correlations between the photons involved in the process [
4]. We have used this quite standard result as a starting point to understand what happens with the entropy/information budget in general relativistic black hole evaporation. In this context, we have constructed a specific model in which we have seen that there is no paradoxical behaviour [
5]. So, we claim that maybe the evaporation process is relatively benign.
2. Entropy/Information in Blackbody Radiation
We begin by considering the standard thermodynamics process of burning matter, where it is well known that the underlying theory is unitary—at least as long as one uses standard quantum mechanics. Unitarity implies strict conservation of the von Neumann entropy. We will use this fact to correctly understand entropy budget when we calculate the entropy associated with the blackbody radiation.
1The application of standard statistical mechanics to a furnace with a small hole leads to the notion of blackbody radiation. The reasoning that then gives rise to the Planck spectrum implies some coarse graining (that is, we choose to measure some aspects of the emitted photons and ignore others). In this process, every photon that escapes from the furnace transfers an amount of entropy to the radiation field given by
where
is the energy of the photon and
T is the temperature of the furnace. This is simply the Clausius definition of entropy. For convenience, from now on, this single-photon definition of entropy will be measured in terms of bits, converted from “physical” entropy by means of the relation.
Now take into account the effect of coarse graining the entropy, considering it in terms of the von Neumann entropy, which is conserved under the evolution of the system. The information hidden in the correlations hidden by the coarse graining process is simply
After these preliminary definitions, the next step is to calculate the average energy per photon in blackbody radiation (using the Planck distribution). We see
where
is the Riemann zeta function. From this expression, it is straightforward to calculate, using the definitions of Equations (
1) and (
2), the average entropy per blackbody photon. We find
The standard deviation, (simply coming from the fact that the Planck spectrum has a finite width), is
Overall, the average entropy per photon in blackbody radiation is [
4]:
This expression is relevant when the only thing that we know about the photon is that it was emitted as part of some blackbody spectrum from a furnace at some (possibly unknown) temperature. The result depends only on the shape of the Planck spectrum, the Clausius notion of entropy, and quite ordinary thermodynamic reasoning.
Since we know that the underlying physics is unitary, this entropy must be compensated with an equal quantity of information. That information would be hidden in the photon–photon correlations that we did not take into account in our coarse graining procedure. The fact that even a standard unitary burning process has a precisely quantifiable entropy/information budget should not really come as a surprise, but it certainly does not seem to be a well-appreciated facet of quantum statistical mechanics.
4. Bipartite Entanglement
The specific model considered by Page [
2] was a global system comprised of one subsystem that corresponds to the Hawking radiation and another subsystem that corresponds to the black hole, for which Hilbert spaces are given, respectively, by
and
. In this bipartite system, initially, before the evaporation of the black hole starts, there is not yet any Hawking radiation. Then, the Hilbert space
is trivial, but the Hilbert space
is enormous. (However, note that one has to assume that the total system is in a pure state to apply Page’s argument.) As the subsystem entropy is given by the minimum Hilbert space dimension, one has
, where the subscript indicates the initial state,
.
In the opposite way, once the evaporation is completed, there will be no black hole, so, its Hilbert space dimension is trivial, and it is the Hawking radiation subspace which has an enormous Hilbert space dimension, giving , where now the subscript indicates the final state, considered when .
In order to calculate the entropy at intermediate states, it is necessary to consider that the evolution is unitary, thus the total Hilbert space dimension is constant
. Under these conditions, the average subsystem entropy will be given in terms of
It is easy to find the maximum value of the average subsystem entropy, which is reached when
, at which stage it takes the value
This time at which the black hole has lost half of its entropy is called the “Page time”. It is possible to represent the shape of the evolution of this subsystem entropy, as it can be seen in
Figure 2. The so-called “Page curve” [
2] is the “entanglement entropy” curve.
Page also calculated the (averaged) asymmetric subsystem information given by the expressions [
2]
which are also represented in
Figure 2. These are the curves labelled “radiation subsystem information” and “hole subsystem information". In order to get a better understanding of the information budget, we have calculated the mutual entropy of the subsystems, given by
In this bipartite system, it can be expressed as
We have found that when we apply the “average subsystem” process to the mutual information, and combine it with the asymmetric subsystem information, we have that the “sum rule” is satisfied:
This sum rule is represented in
Figure 3.
The Page curve underlies much of the present discussion about the “information paradox”. The main result implies that the black hole subsystem is maximally entangled with the radiation subsystem. However, at the same time, if we sub-divide the Hawking radiation subsystem between early and late radiation (respectively, before and after Page time), these two subsystems would be also maximally entangled between them, and also with the black hole subsystem. The problem lies in the fact that, due to the monogamy of entanglement, this is not possible, and it was one of the motivations for the proposal of firewalls [
3]. Nevertheless, we argue that this model misses much of the relevant physics.
There are some unacceptable aspects of the standard argument. For instance, the standard argument assumes that the initial black hole (after formation but before any radiation is emitted) is in a pure state, so that the initial subsystem entropy vanishes. That assertion is in tension with the idea of relating the initial von Neumann entropy with the Bekenstein entropy of the black hole. That the Bekenstein entropy is a coarse-grained von Neumann entropy characterizing the number of ways in which the black hole could have formed is an old idea going back to the 1970s. Quantitatively, this idea was first formalized by Bombelli et al. [
11], and few years later was independently explored by Srednicki [
12], both groups calculating the scaling of entanglement entropy with area (see, also, the reviews [
13,
14], and the recent article on coarse-graining [
15]). We propose that these problematic issues may be related to the consideration of an over-simplified (black hole)+(radiation) “closed box” system, ignoring the environment. That is, we argue that we should instead consider a tripartite system, in which we explicitly add the rest of the universe, (the environment), expecting a much better physically more reasonable behaviour for the entropy budget.
5. Tripartite Entanglement
We now consider a tripartite system which consists of three subsystems, associated to the black hole, the Hawking radiation, and rest of the universe (environment), respectively. So the Hilbert space now is split in the form:
. Since we assume that the entire Universe is in a pure state (
), now the entropy of the subsystems is given by
,
, and
. In this case
3, the initial subsystem entropies, (before the evaporation starts, when
), are
and
. It is important to realise that after black hole formation but before evaporation starts one has
.
Starting from any stellar object, collapse and horizon formation (be it an apparent horizon, trapping horizon, event horizon, or some notion of approximate horizon) is an extremely dramatic coarse-graining process. We emphasize (since we have seen this point causes some considerable confusion) that the end result of the collapse process is that the entropy of the newly formed black hole is the Bekenstein entropy associated with the horizon. Indeed, the Bekenstein entropy is the entropy associated with all possible ways in which the black hole could have been formed; not the entropy of the original stellar object that underwent collapse; that stellar entropy is unknown and unknowable after black hole formation, this merely being one side effect of the “no hair” theorems.
(Indeed, if one denies the applicability of Bekenstein entropy to the newly created black hole, then it is absolutely no surprise that one rapidly ties oneself up in logical knots when considering the Hawking emission process.)
More precisely: One can either appeal to Bekenstein’s original papers to get (entropy) ∝ (area), and then fix the normalization constant using Hawking’s original papers [
16,
17]. Alternatively, if one insists on working only with von Neumann entropy, then one can use Srednicki’s calculation showing that generically (entropy) ∝ (area) for any surface we cannot look behind [
12], and again fix the normalization constant using Hawking’s original papers [
17]. (See also Bombelli et al. calculations of the von Neumann entropy implied by the existence of a horizon [
11].)
The final entropies, when the black hole is completely evaporated () are and . We assume that the evolution is unitary, so the total Hilbert space is preserved. The environment does not participate directly in the evaporation process, since the role of the environment is merely to allow the initial black hole to have a non-zero entropy. After , the environment evolves separately, that is, the unitary time evolution operator is the tensor product of a unitary operator corresponding to the environment and another unitary operator corresponding to the black hole and Hawking radiation subsystems, . Thus, the total Hilbert space of the environment and the total Hilbert space of the other two subsystems are independently preserved during the evaporation process, and we can express the conservation of the Hilbert space dimension as and .
We have computed the average entropy of the black hole and Hawking radiation subsystems, taking as an additional assumption that (throughout the evolution) the Bekenstein entropy can be interpreted as the entanglement entropy of the black hole,
We have also obtained the sum of both averaged entropies. After some calculation
This sum rule is represented in
Figure 4. In the same way, we have obtained the average entropy of the environment subsystem. It is important to note that this entropy only corresponds to that part of the universe which is entangled with the other subsystems, it is not the entropy of the rest of the universe. Calculation yields
In this tripartite system, the mutual information between the Hawking radiation subsystem and the black hole subsystem is more interesting, and is given by the expression
It is possible to calculate the average mutual information, and one finally finds [
5] that it is always less than
nat during the whole evaporation process,
It is also interesting to note that if the environment becomes arbitrarily large, which is certainly possible in this tripartite system without any loss of generality, then it can be seen that the previous sum in Equation (
21) becomes exact
and the mutual entropy is also exactly zero [
5]
6. Discussion
First of all, we have obtained the numerical value of the entropy per photon emitted in black body radiation, which, because the process is unitary, must be compensated by an equal “hidden information” in the correlations. As is well known, there is no “information puzzle” in a standard thermodynamic process, but we note that due to the coarse-graining [
15], a specifically quantifiable amount of entropy/information is nevertheless exchanged in the process [
4].
From this starting point, we have applied these ideas to the consideration of general relativistic black holes, calculating both the classical thermodynamic entropy and the Bekenstein entropy, and seeing that they compensate perfectly. Once we have calculated the classical entropy, we then calculate the quantum (entanglement) entropy, considering a model based on a tripartite system. The result obtained is completely in agreement with the classical expected results, at least to within 1 nat. In contrast, the result previously obtained by Page, by considering a bipartite model that does not interact with the environment, gives rise to not well-understood physics.
From our analysis, it can be seen that although when we restrict attention to any particular subsystem we perceive an amount of entanglement entropy, (a loss of information), there exists a complementary amount of entropy/information that is codified in the correlations between the subsystems. Then, assuming the unitarity of the evolution of the (black hole) + (Hawking radiation) subsystem, and working within the standard Page-like average-subsystem framework, we showed that it seems that there is no pressing need for any unusual physical effect to enter into the process. This implies a continuous purification of the Hawking radiation, and could lead to a completely non-controversial and quite standard physical picture for the evaporation of a black hole. (Here, we are taking into account only the semiclassical process of Hawking radiation, until a deeper understanding of the underlying micro-physics of quantum gravity phenomena might be found.)