The Black Hole Radiation in Massive Gravity
Abstract
:1. Introduction
2. Massive Gravity Formulation
3. The Stückelberg Trick: The Two Points of View
3.1. Stückelberg Fields Appearing in the Dynamical Metric
3.2. Stückelberg Fields Appearing in the Fiducial Metric
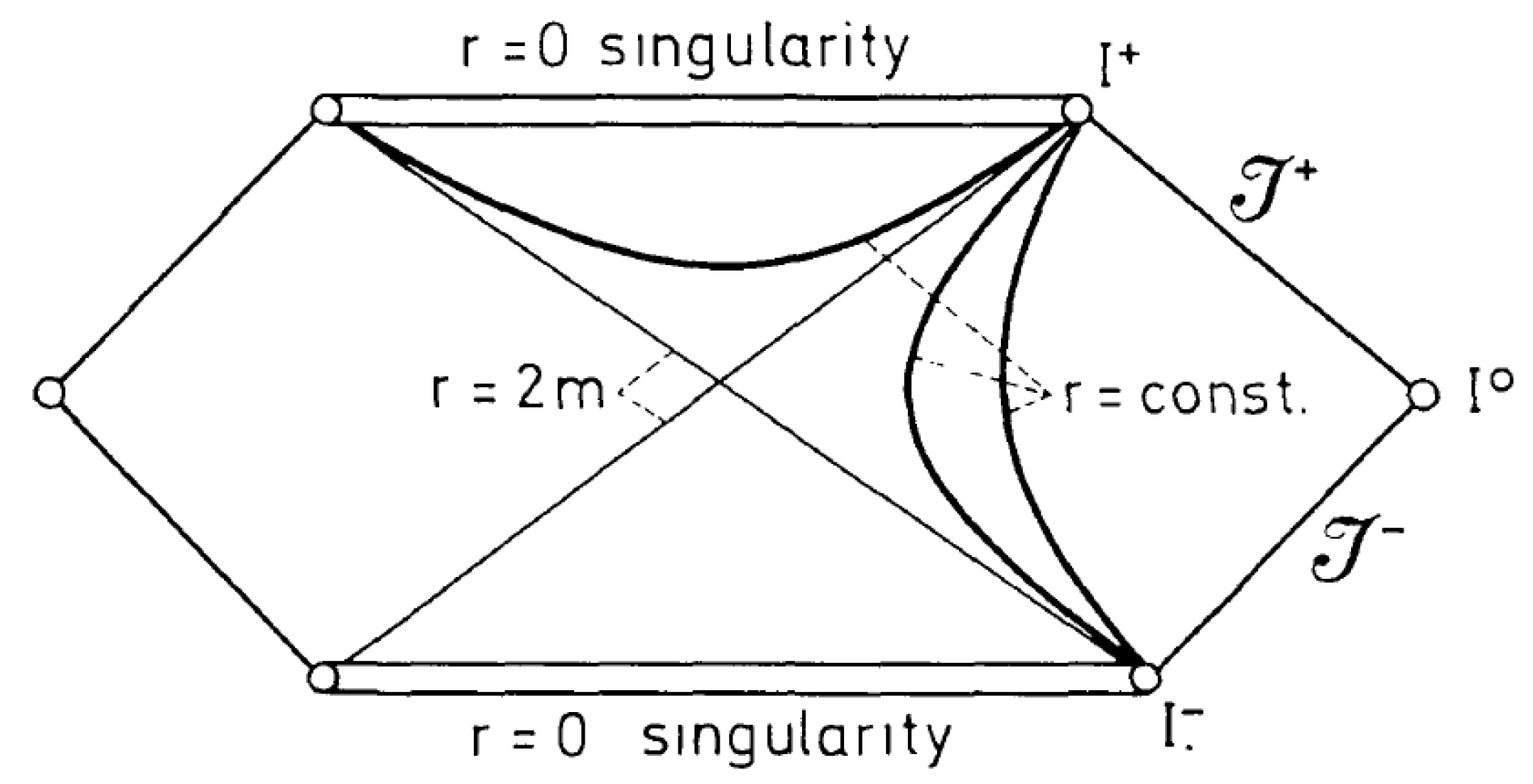
4. The Schwarzschild de-Sitter Solution in dRGT
5. The Particle Creation Process
5.1. Observers Defining the Time in Agreement with
5.2. Observers Defining the Time Arbitrarily
5.2.1. Specific Example of the Modification of the Temperature Perceived by Observers Defining the Time Arbitrarily
5.2.2. Discussion of the Results: The Concepts of Time
6. Conclusions
Conflicts of Interest
References
- De Rham, C. Massive gravity. Living Rev. Relativ. 2014, 17, 7. [Google Scholar] [CrossRef] [PubMed]
- Vainshtein, A.I. To the problem of non-vanishing gravitation mass. Phys. Lett. B 1972, 39, 393–394. [Google Scholar] [CrossRef]
- Babichev, E.; Deffayet, C. An introduction to the Vainshtein mechanism. Class. Quantum Gravity 2013, 30, 184001. [Google Scholar]
- Fierz, M.; Pauli, W. On relativistic wave equations for particles of arbitrary spin in an electromagnetic field. Proc. R. Soc. Lond. Ser. A 1939, 173, 211–323. [Google Scholar] [CrossRef]
- Pauli, W.; Fierz, M. On Relativistic field equations of particles with arbitrary spin in an electromagnetic field. Helv. Phys. Acta 1939, 12, 297–300. [Google Scholar]
- Hinterbichler, K. Theoretical aspects of massive gravity. Phys. Rev. D 2012, 84, 671–710. [Google Scholar] [CrossRef]
- Koyama, K.; Niz, G.; Tasinato, G. Analytic Solutions in Nonlinear Massive Gravity. Phys. Rev. Lett. 2011, 107, 131101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Koyama, K.; Niz, G.; Tasinato, G. Strong interactions and exact solutions in nonlinear massive gravity. Phys. Rev. D 2011, 84, 064033. [Google Scholar] [CrossRef] [Green Version]
- Sbisa, F.; Niz, G.; Koyama, K.; Tasinato, G. Characterizing Vainshtein solutions in massive gravity. Phys. Rev. D 2012, 86, 024033. [Google Scholar]
- Berezhiani, L.; Chkareuli, G.; de Rham, C.; Gabadadze, G.; Tolley, A.J. On Black Holes in Massive Gravity. Phys. Rev. D 2012, 85, 044024. [Google Scholar] [CrossRef]
- Nieuwenhuizen, T.M. Exact Schwarzschild-de Sitter black holes in a family of massive gravity models. Phys. Rev. D 2011, 84, 024038. [Google Scholar] [CrossRef]
- Kodama, H.; Arraut, I. Stability of the Schwarzschild-de Sitter black hole in the dRGT massive gravity theory. Prog. Theor. Exp. Phys. 2014, 2014, 023E02. [Google Scholar] [CrossRef]
- De Rham, C.; Gabadadze, G.; Tolley, A.J. Resummation of massive gravity. Phys. Rev. Lett. 2011, 106, 231101. [Google Scholar] [CrossRef] [PubMed]
- Arkani-Hamed, N.; Georgi, H.; Schwartz, M.D. Effective field theory for massive gravitons and gravity in theory space. Ann. Phys. 2003, 305, 96–118. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Schwartz, M.D. Discrete gravitational dimensions. Phys. Rev. D 2004, 69, 104001. [Google Scholar] [CrossRef]
- Arkani-Hamed, N.; Cohen, A.G.; Georgi, H. (De)Constructing Dimensions. Phys. Rev. Lett. 2001, 86, 4757–4761. [Google Scholar] [CrossRef] [PubMed]
- Arkani-Hamed, N.; Cohen, A.G.; Georgi, H. Electroweak symmetry breaking from dimensional deconstruction. Phys. Lett. B 2001, 513, 232–240. [Google Scholar] [CrossRef]
- Alberte, L.; Chamseddine, A.H.; Mukhanov, V. Massive gravity: Resolving the puzzles. J. High Energy Phys. 2010, 2010, 23. [Google Scholar] [CrossRef]
- Alberte, L.; Chamseddine, A.H.; Mukhanov, V. Massive gravity: Exorcising the ghost. J. High Energy Phys. 2011, 2011, 4. [Google Scholar] [CrossRef]
- Hawking, S.W. Particle creation by black holes. Commun. Math. Phys. 1975, 43, 199–220, Erratum in 1976, 46, 206. [Google Scholar] [CrossRef]
- Gibbons, G.W.; Hawking, S.W. Cosmological event horizons, thermodynamics, and particle creation. Phys. Rev. D 1977, 15, 2738–2751. [Google Scholar] [CrossRef]
- Hartle, J.B.; Hawking, S.W. Path-integral derivation of black-hole radiance. Phys. Rev. D 1976, 13, 2188–2203. [Google Scholar] [CrossRef]
- Arraut, I. Path-integral derivation of black-hole radiance inside the de–Rham-Gabadadze–Tolley formulation of massive gravity. Eur. Phys. J. C 2017, 77, 501. [Google Scholar] [CrossRef]
- Arraut, I. The Astrophysical Scales Set by the Cosmological Constant, Black-Hole Thermodynamics and Non-Linear Massive Gravity. Universe 2017, 3, 45. [Google Scholar] [CrossRef]
- Arraut, I. On the apparent loss of predictability inside the de Rham-Gabadadze-Tolley non-linear formulation of massive gravity: The Hawking radiation effect. Europhys. Lett. 2015, 109, 10002. [Google Scholar] [CrossRef]
- Arraut, I. Komar mass function in the de Rham-Gabadadze-Tolley nonlinear theory of massive gravity. Phys. Rev. D 2014, 90, 124082. [Google Scholar] [CrossRef]
- Unruh, W.G. Notes on black-hole evaporation. Phys. Rev. D 1976, 14, 870. [Google Scholar] [CrossRef]
- Brout, R.; Massar, S.; Parentani, R.; Spindel, P. A primer for black hole quantum physics. Phys. Rep. 1995, 260, 329–454. [Google Scholar] [CrossRef]
- Fulling, S.A.; Matsas, G.E.A. Unruh effect. Scholarpedia 2014, 9, 31789. [Google Scholar] [CrossRef]
- Rubakov, V. Lorentz-violating graviton masses: Getting around ghosts, low strong coupling scale and VDVZ discontinuity. arXiv, 2004; arXiv:hep-th/0407104. [Google Scholar]
- Rubakov, V.A.; Tinyakov, P.G. Infrared-modified gravities and massive gravitons. Phys. Usp. 2008, 51, 759–792. [Google Scholar] [CrossRef]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arraut, I. The Black Hole Radiation in Massive Gravity. Universe 2018, 4, 27. https://doi.org/10.3390/universe4020027
Arraut I. The Black Hole Radiation in Massive Gravity. Universe. 2018; 4(2):27. https://doi.org/10.3390/universe4020027
Chicago/Turabian StyleArraut, Ivan. 2018. "The Black Hole Radiation in Massive Gravity" Universe 4, no. 2: 27. https://doi.org/10.3390/universe4020027



