Polarized Baryon Production in Heavy Ion Collisions: An Analytic Hydrodynamical Study
Abstract
:1. Introduction
2. Basic Equations and Assumptions
3. Some Exact Hydrodynamical Solutions and Polarization
3.1. Hubble Flow
3.2. Rotating and Accelerating Expanding Solution
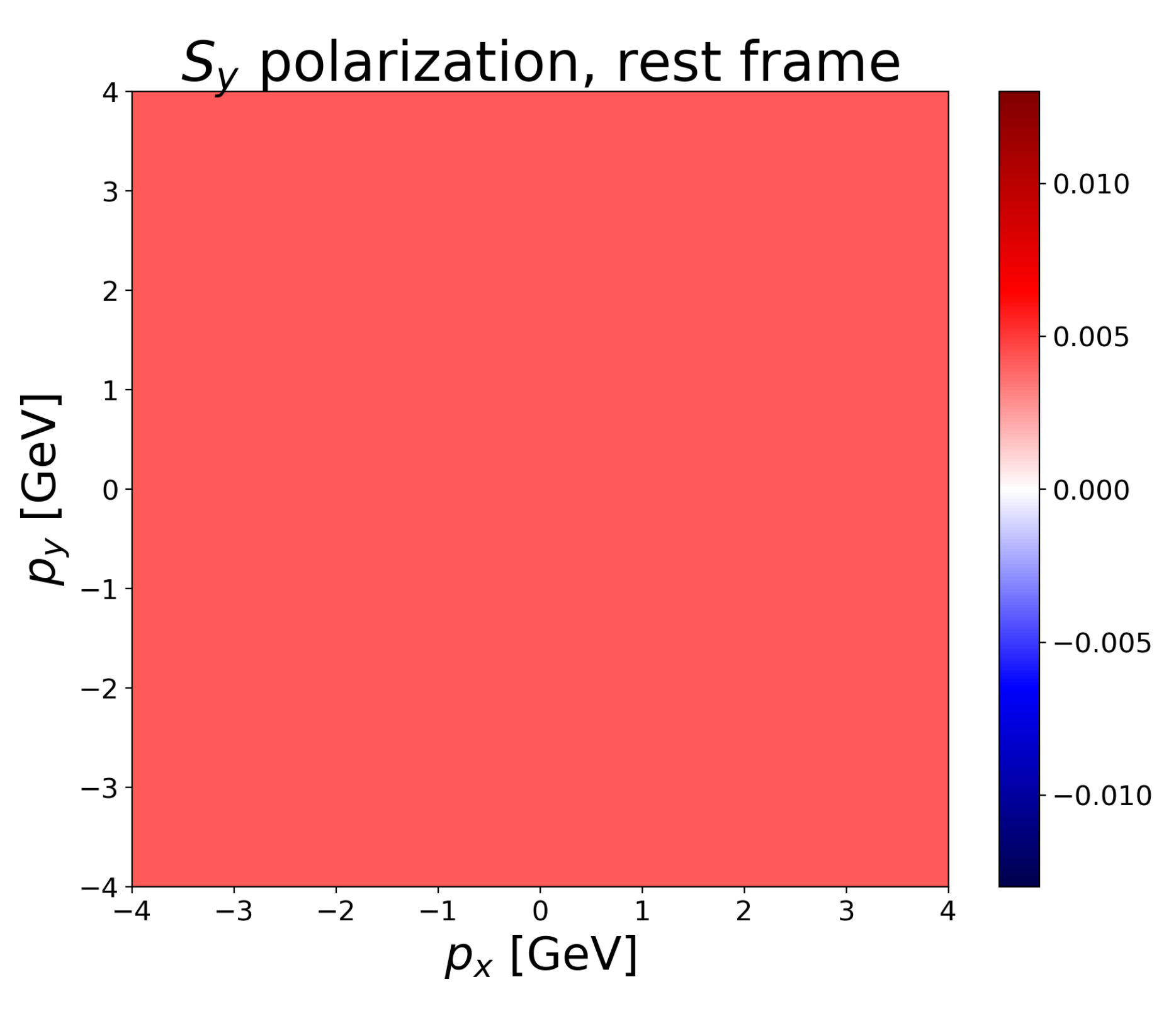
4. Illustration and Discussion
5. Summary and Outlook
Author Contributions
Funding
Conflicts of Interest
Appendix A. Additional Calculations
References
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; et al. STAR Collaboration. Global Λ hyperon polarization in nuclear collisions: Evidence for the most vortical fluid. Nature 2017, 548, 62. [Google Scholar]
- Adam, J.; Adamczyk, L.; Adams, J.R.; Adkins, J.K.; Agakishiev, G.; Aggarwal, M.M.; Ahammed, Z.; Alekseev, I.; Anderson, D.M.; Aoyama, R.; et al. STAR Collaboration. Global polarization of Λ hyperons in Au+Au collisions at = 200 GeV. Phys. Rev. C 2018, 98, 014910. [Google Scholar] [CrossRef]
- Becattini, F.; Chandra, V.; Del Zanna, L.; Grossi, E. Relativistic distribution function for particles with spin at local thermodynamical equilibrium. Ann. Phys. 2013, 338, 32. [Google Scholar] [CrossRef]
- Csernai, L.P.; Becattini, F.; Wang, D.J. Turbulence, Vorticity and Lambda Polarization. J. Phys. Conf. Ser. 2014, 509, 012054. [Google Scholar] [CrossRef]
- Xie, Y.L.; Bleicher, M.; Stöcker, H.; Wang, D.J.; Csernai, L.P. Λ polarization in peripheral collisions at moderate relativistic energies. Phys. Rev. C 2016, 94, 054907. [Google Scholar] [CrossRef]
- Xie, Y.; Wang, D.; Csernai, L.P. Global Λ polarization in high energy collisions. Phys. Rev. C 2017, 95, 031901. [Google Scholar] [CrossRef]
- Karpenko, I.; Becattini, F. Study of Λ polarization in relativistic nuclear collisions at = 7.7 –200 GeV. Eur. Phys. J. C 2017, 77, 213. [Google Scholar] [CrossRef]
- Csörgo, T.; Grassi, F.; Hama, Y.; Kodama, T. Simple solutions of relativistic hydrodynamics for longitudinally and cylindrically expanding systems. Phys. Lett. B 2003, 565, 107–115. [Google Scholar] [CrossRef]
- Csörgo, T.; Csernai, L.P.; Hama, Y.; Kodama, T. Simple solutions of relativistic hydrodynamics for systems with ellipsoidal symmetry. Acta Phys. Hung. A 2004, 21, 73. [Google Scholar] [CrossRef]
- Nagy, M.I. New simple explicit solutions of perfect fluid hydrodynamics and phase-space evolution. Phys. Rev. C 2011, 83, 054901. [Google Scholar] [CrossRef]
- Hatta, Y.; Noronha, J.; Xiao, B.W. Exact analytical solutions of second-order conformal hydrodynamics. Phys. Rev. D 2014, 89, 051702. [Google Scholar] [CrossRef]
- Cooper, F.; Frye, G. Comment on the Single Particle Distribution in the Hydrodynamic and Statistical Thermodynamic Models of Multiparticle Production. Phys. Rev. D 1974, 10, 186. [Google Scholar] [CrossRef]
- Csanád, M.; Nagy, M.I.; Lökös, S. Exact solutions of relativistic perfect fluid hydrodynamics for a QCD equation of state. Eur. Phys. J. A 2012, 48, 173. [Google Scholar] [CrossRef]
- Florkowski, W.; Ryblewski, R. Hydrodynamics with spin—Pseudo-gauge transformations, semi-classical expansion, and Pauli-Lubanski vector. arXiv 2018, arXiv:1811.04409. [Google Scholar]
- Florkowski, W.; Kumar, A.; Ryblewski, R.; Singh, R. Spin polarization evolution in a boost invariant hydrodynamical background. arXiv 2019, arXiv:1901.09655. [Google Scholar] [CrossRef]
- Csanád, M.; Szabó, A. Multipole solution of hydrodynamics and higher order harmonics. Phys. Rev. C 2014, 90, 054911. [Google Scholar] [CrossRef]
- Karpenko, I.; Becattini, F. Lambda polarization in heavy ion collisions: From RHIC BES to LHC energies. Nucl. Phys. A 2019, 982, 519. [Google Scholar] [CrossRef]
| 1 | The vanishing of can also be interpreted as an absence of a conserved particle number density n. All our conclusions would change only by a proportionality factor if we said instead of ; if , we would have had to introduce n. Depending on the EoS (Equation of State) of the matter (one that also contains the conserved particle density n), one could write the function in another form, where the normalization is evident. For example, if one chooses an ultra-relativistic ideal gas, with , , with as EoS, one has . Indeed, in the solutions discussed below, const is satisfied, which means , which is the well-known condition for an adiabatic expansion. |
| 2 | We note that a more general class of solutions is possible [8,9,16] in which the temperature and density fields are supplemented with an arbitrary function of a “scaling variable” S: |
| 3 | Here we changed the notation of Ref. [10]. The rather unfortunate notation used there is now written as . |
| 4 | This has not yet been calculated for this hydrodynamical solution. |
| 5 | The Lorentz matrix performing this boost transformation is the following (in usual 1+3 dimensional block matrix notation): |


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boldizsár, B.; Nagy, M.I.; Csanád, M. Polarized Baryon Production in Heavy Ion Collisions: An Analytic Hydrodynamical Study. Universe 2019, 5, 101. https://doi.org/10.3390/universe5050101
Boldizsár B, Nagy MI, Csanád M. Polarized Baryon Production in Heavy Ion Collisions: An Analytic Hydrodynamical Study. Universe. 2019; 5(5):101. https://doi.org/10.3390/universe5050101
Chicago/Turabian StyleBoldizsár, Bálint, Márton I. Nagy, and Máté Csanád. 2019. "Polarized Baryon Production in Heavy Ion Collisions: An Analytic Hydrodynamical Study" Universe 5, no. 5: 101. https://doi.org/10.3390/universe5050101





