Positron-Hydrogen Scattering, Annihilation, and Positronium Formation
Abstract
:1. Introduction
2. Zeff
3. Positronium Formation
4. Conclusions
Acknowledgments
Conflicts of Interest
Appendix A
References
- Temkin, A. A Note on the Scattering of Electrons from Atomic Hydrogen. Phys. Rev. 1959, 116, 358. [Google Scholar] [CrossRef]
- Feshbach, H. A unified theory of nuclear reactions. II. Ann. Phys. 1962, 19, 287–313. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A. Complex-correlation Kohn T-matrix method of calculating total and elastic cross sections: Electron-hydrogen elastic scattering. Phys. Rev. A 2001, 64, 032709. [Google Scholar] [CrossRef]
- Bhatia, A.K. Electron-He+ elastic scattering. Phys. Rev. A 2002, 66, 064702. [Google Scholar]
- Bhatia, A.K. Electron-hydrogen P-wave elastic scattering. Phys. Rev. A 2004, 69, 032714. [Google Scholar] [CrossRef]
- Bhatia, A.K. Electron-He+ P-wave elastic scattering and photoabsorption in two-electron systems. Phys. Rev. A 2006, 73, 012705. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of electron-hydrogen elastic scattering. Phys. Rev. A 2007, 75, 032713. [Google Scholar] [CrossRef]
- Bhatia, A.K. Applications of the hybrid theory to the scattering of electrons from He+ and Li2+ and resonances in these systems. Phys. Rev. A 2008, 77, 052707. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A.; Drachman, R.J.; Eiserike, H. Generalized Hylleraas Calculation of Positron-Hydrogen Scattering. Phys. Rev. A 1971, 3, 1328. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A.; Eiserike, H. Rigorous precision p-wave positron-hydrogen scattering calculation. Phys. Rev. A 1974, 9, 219. [Google Scholar] [CrossRef]
- Bransden, B.H. Atomic Collision Theory; W.A. Benjamin Inc.: New York, NY, USA, 1970. [Google Scholar]
- Drachman, R.J. Variational Bounds in Positron-Atom Scattering. Phys. Rev. 1968, 173, 190. [Google Scholar] [CrossRef]
- Dalgarno, A.; Lynn, N. An Exact Calculation of Second Order Long Range Forces. Proc. Phys. Soc. A 1957, 70, 223. [Google Scholar] [CrossRef]
- Schwartz, C. Electron Scattering from Hydrogen. Phys. Rev. 1961, 124, 1468. [Google Scholar] [CrossRef]
- Shertzer, J.; Temkin, A. Direct calculation of the scattering amplitude without partial-wave analysis. III. Inclusion of correlation effects. Phys. Rev. A 2006, 74, 052701. [Google Scholar] [CrossRef]
- Temkin, A.; Lamkin, J.C. Application of the Method of Polarized Orbitals to the Scattering of Electrons from Hydrogen. Phys. Rev. 1961, 121, 788. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Temkin, A. Symmetric Euler-Angle Decomposition of the Two-Electron Fixed-Nucleus Problem. Rev. Mod. Phys. 1964, 36, 1050. [Google Scholar] [CrossRef]
- Houston, S.K.; Drachman, R.J. Positron-Atom Scattering by the Kohn and Harris Methods. Phys. Rev. A 1971, 3, 1335. [Google Scholar] [CrossRef]
- Humberston, J.W.; Wallace, J.B.G. The elastic scattering of positrons by atomic hydrogen. J. Phys. B 1972, 5, 1138. [Google Scholar] [CrossRef]
- Gien, T.T. Coupled-state calculations of positron-hydrogen scattering. Phys. Rev. A 1997, 56, 1332. [Google Scholar] [CrossRef]
- Mitroy, J.; Ratnavalu, K. The positron-hydrogen system at low energies. J. Phys. B 1995, 28, 287. [Google Scholar] [CrossRef]
- Mitroy, J. Large Basis Calculation of Positron? Hydrogen Scattering at Low Energies. Aust. J. Phys. 1995, 48, 645–676. [Google Scholar] [CrossRef]
- Mitroy, J. Positronium-Proton Scattering at Low Energies. Aust. J. Phys. 1995, 48, 893–906. [Google Scholar] [CrossRef]
- Kadyrov, A.S.; Bray, I. Recent Progress in the Description of Positron Scattering from Atoms Using the Convergent Close-Coupling Theory. 2016; arXiv:1609.04082. [Google Scholar]
- Higgin, K.; Burke, P.G.; Walters, H.R. Positron scattering by atomic hydrogen at intermediate energies. J. Phys. B 1990, 23, 1345–1357. [Google Scholar] [CrossRef]
- Temkin, A. Polarization and the Triplet Electron-Hydrogen Scattering Length. Phys. Rev. Lett. 1961, 6, 354. [Google Scholar] [CrossRef]
- Drachman, R.J.; (Greenbelt, Maryland, USA). Private communication, 2016.
- Calogero, F. Variable Approach to Potential Scattering; Academic Press: New York, NY, USA, 1971. [Google Scholar]
- Zhou, S.; Li, H.; Kaupppila, W.E.; Kwan, C.K.; Stein, T.S. Measurements of total and positronium formation cross sections for positrons and electrons scattered by hydrogen atoms and molecules. Phys. Rev. A 1997, 55, 361. [Google Scholar] [CrossRef]
- Drachman, R.J. Electron Atomic Collisions. Proc. Int. Conf. Phys. 1971, 277. [Google Scholar]
- Bhatia, A.K. Positron Interactions with Atoms and Ions. J. At. Mol. Condens. Nano Phys. 2014, 1, 45. [Google Scholar]
- Ferrall, R.A. Theory of Positron Annihilation in Solids. Rev. Mod. Phys. 1956, 28, 308. [Google Scholar] [CrossRef]
- DiRienzi, J.; Drachman, R.J. Re-examination of a simplified model for positronium–helium scattering. J. Phys. B 2003, 36, 2409. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Drachman, R.J.; Temkin, A. Annihilation during positron-hydrogen collisions. Phys. Rev. A 1974, 9, 223. [Google Scholar] [CrossRef]
- Green, D.G.; Gribakin, G.F. Positron scattering and annihilation in hydrogen like ions. Phys. Rev. A 2013, 88, 032708. [Google Scholar] [CrossRef]
- Osmon, P.E. Positron Lifetime Spectra in Molecular Gases. Phys. Rev. 1965, 140, A8. [Google Scholar] [CrossRef]
- Fraser, P.A. Positrons and Positronium in Gases. Adv. At. Mol. Phys. 1968, 4, 63–107. [Google Scholar]
- Mohorovicic, S. Möglichkeit neuer Elemente und ihre Bedeutung für die Astrophysik. Astron. Nachr. 1934, 253, 93. [Google Scholar] [CrossRef]
- Charlton, M. Experimental studies of positrons scattering in gases. Rep. Prog. Phys. 1985, 48, 737. [Google Scholar] [CrossRef]
- Stein, T.S.; Kauppila, W.E.; Kwan, C.K.; Parikh, S.P.; Zhou, S. Measurements of positronium formation cross sections for positron-ar and-K scattering. Hyperfine Interact. 1992, 73, 53–63. [Google Scholar]
- Chan, Y.F.; Fraser, P.A. S-wave positron scattering by hydrogen atoms. J. Phys. B 1973, 6, 2504. [Google Scholar] [CrossRef]
- Humberston, J.W. Positronium formation in s-wave positron–hydrogen scattering. Can. J. Phys. 1982, 60, 591–596. [Google Scholar] [CrossRef]
- Khan, A.; Ghosh, A.S. Positronium formation in positron-hydrogen scattering. Phys. Rev. A 1983, 27, 1904. [Google Scholar] [CrossRef]
- Bransden, B.H. Atomic Rearrangement Collisions. Adv. At. Mol. Phys. 1965, 1, 85–148. [Google Scholar]
- Cheshire, I.M. Positronium formation by fast positrons in atomic hydrogen. Proc. Phys. Soc. 1964, 83, 227. [Google Scholar] [CrossRef]
- Kvitsinsky, A.A.; Wu, A.; Hu, C.-Y. Scattering of electrons and positrons on hydrogen using the Faddeev equations. J. Phys. B 1995, 28, 275. [Google Scholar] [CrossRef]
- Bhatia, A.K. Hybrid theory of P-wave electron-hydrogen elastic scattering. Phys. Rev. A 2012, 85, 052708. [Google Scholar] [CrossRef]
- Bhatia, A.K.; Madan, R.N. S-Matrix Method for the Numerical Determination of Bound States. Phys. Rev. A 1973, 7, 523. [Google Scholar] [CrossRef]
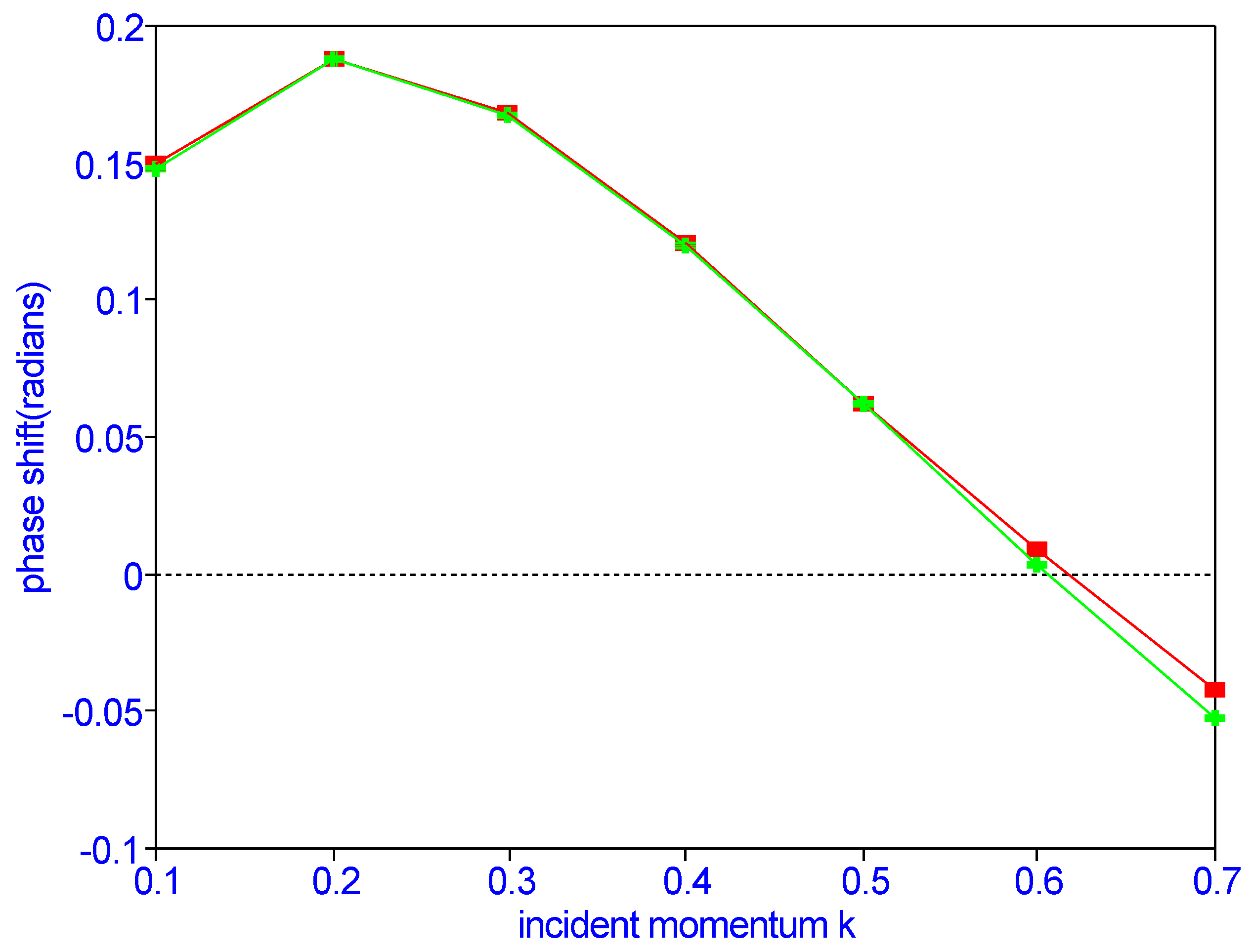
| N | |||
|---|---|---|---|
| 10 | 0.56 | 0.90 | 0.09649 |
| 20 | 0.56 | 0.90 | 0.11619 |
| 35 | 0.60 | 0.91 | 0.11976 |
| 56 | 0.72 | 0.83 | 0.12083 |
| K | N | Present | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 35 | 0.14918 | 0.1483 | 0.151 | 0.149 | 0.148 | 0.1482 | 0.142 | 0.1404 |
| 0.2 | 35 | 0.18803 | 0.1877 | 0.188 | 0.189 | 0.187 | 0.1875 | 0.182 | 0.1767 |
| 0.3 | 35 | 0.16831 | 0.1677 | 0.168 | 0.169 | 0.167 | 0.1671 | 0.159 | 0.1558 |
| 0.4 | 56 | 0.12083 | 0.1201 | 0.120 | 0.123 | 0.119 | 0.1196 | 0.111 | 0.1105 |
| 0.5 | 20 | 0.06278 | 0.0624 | 0.062 | 0.065 | 0.062 | 0.0621 | 0.055 | 0.0536 |
| 0.6 | 20 | 0.00903 | 0.0039 | 0.007 | 0.008 | 0.003 | 0.0033 | −0.002 | −0.004 |
| 0.7 | 20 | −0.04253 | −0.0512 | −0.054 | −0.049 | … | −0.0520 | −0.0588 |
| N | A | ||
|---|---|---|---|
| 10 | 0.56 | 0.90 | −1.86341 |
| 20 | 0.56 | 0.82 | −2.05266 |
| 35 | 0.56 | 0.84 | −2.10074 |
| 56 | 0.52 | 0.84 | −2.10158 |
| k | A | B | C | D |
|---|---|---|---|---|
| 0.1 | 8.092 | 7.363 | 7.5 | 7.5 |
| 0.2 | 5.357 | 5.538 | 5.7 | 5.5 |
| 0.3 | 4.264 | 4.184 | 4.3 | 4.1 |
| 0.4 | 3.370 | 3.327 | 3.3 | 3.5 |
| 0.5 | 2.424 | 2.730 | 2.7 | 3.0 |
| 0.6 | 2.249 | 2.279 | 2.3 | 2.8 |
| 0.7 | 2.069 | 1.950 | … | 2.2 |
| A | B | C | D | E | |
|---|---|---|---|---|---|
| 0.5041 | 0.0010053 | 0.0066228 | 0.009037 | 0.0041 | 0.0038 |
| 0.5476 | 0.0025753 | 0.018783 | ... | … | ... |
| 0.5625 | 0.0026829 | 0.020249 | 0.024795 | 0.0044 | 0.0041 |
| 0.64 | 0.0025604 | 0.022566 | 0.0248 | 0.0049 | 0.0047 |
| 0.6724 | 0.002412 | 0.022350 | ... | … | ... |
| 0.7225 | 0.0021366 | 0.021456 | 0.021164 | 0.0058 | ... |
| 0.75 | 0.0020034 | 0.020835 | 0.019707 | ... | ... |
| 0.81 | 0.0017211 | 0.019256 | ... | ... | ... |
| 0.9025 | 0.0013698 | 0.016760 | ... | ... | ... |
| 1.00 | 0.0010916 | 0.014327 | ... | ... | ... |
© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bhatia, A.K. Positron-Hydrogen Scattering, Annihilation, and Positronium Formation. Atoms 2016, 4, 27. https://doi.org/10.3390/atoms4040027
Bhatia AK. Positron-Hydrogen Scattering, Annihilation, and Positronium Formation. Atoms. 2016; 4(4):27. https://doi.org/10.3390/atoms4040027
Chicago/Turabian StyleBhatia, Anand K. 2016. "Positron-Hydrogen Scattering, Annihilation, and Positronium Formation" Atoms 4, no. 4: 27. https://doi.org/10.3390/atoms4040027





