Proposal of Novel Model for a 2 DOF Exoskeleton for Lower-Limb Rehabilitation
Abstract
:1. Introduction
2. Methods
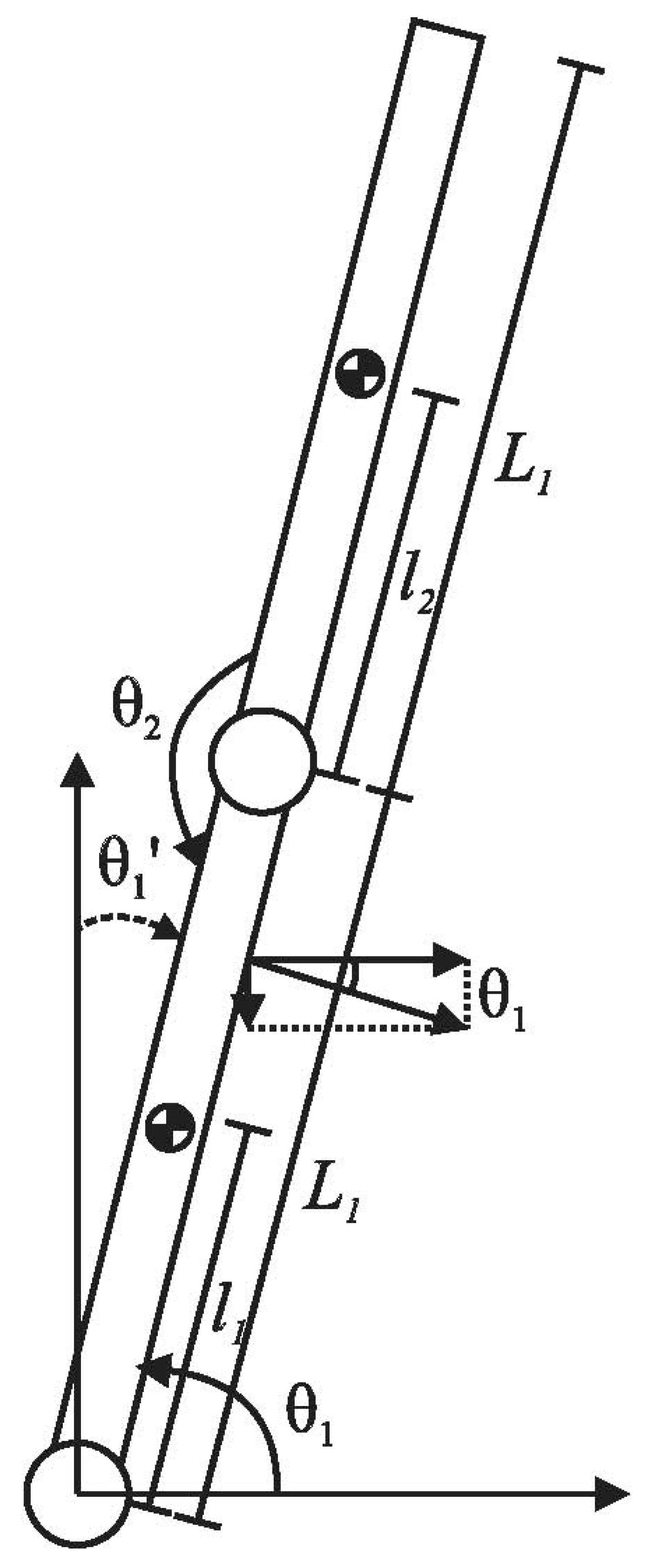
2.1. Model Description
2.2. Linear Approximation of the Model
3. Simulation Results
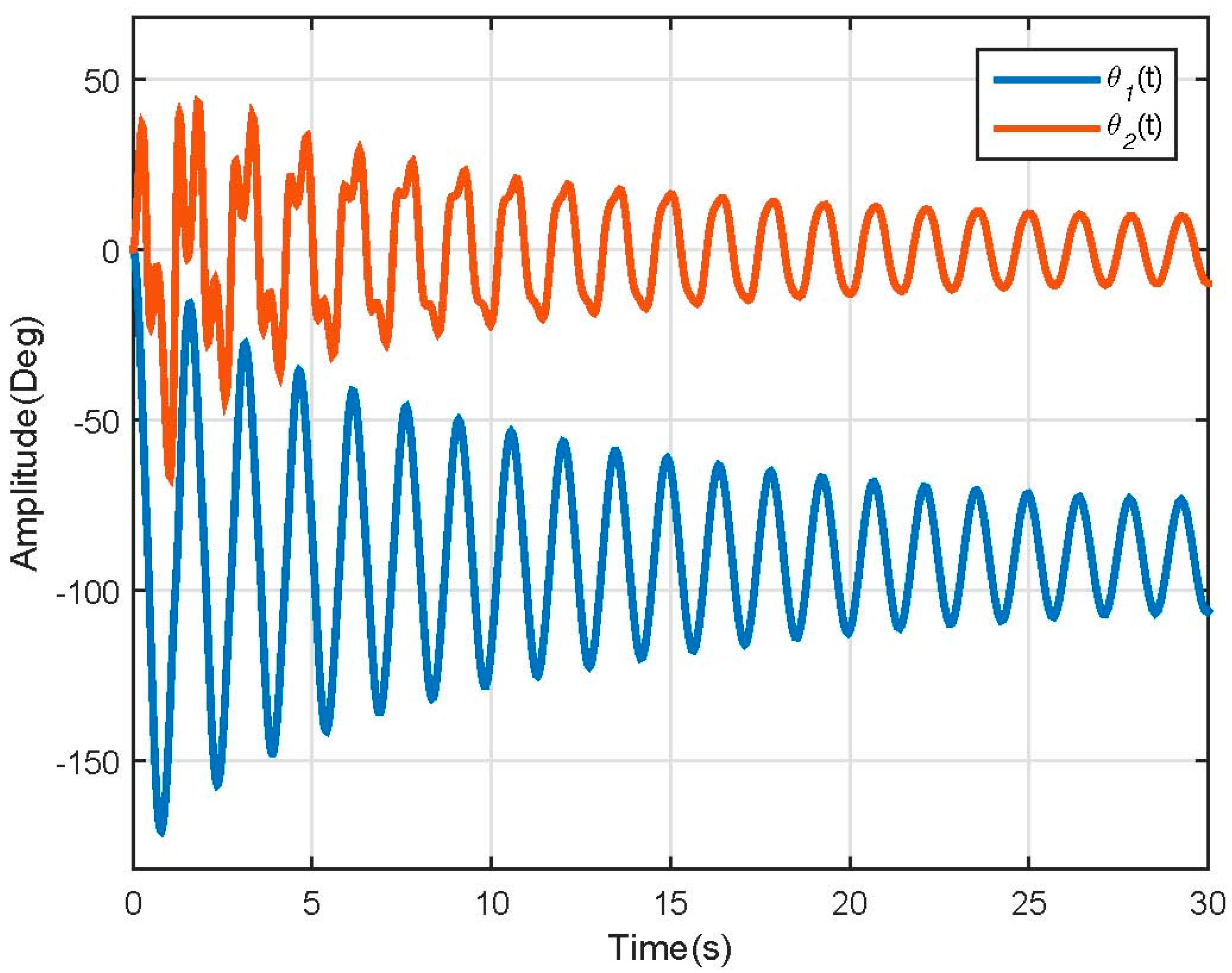
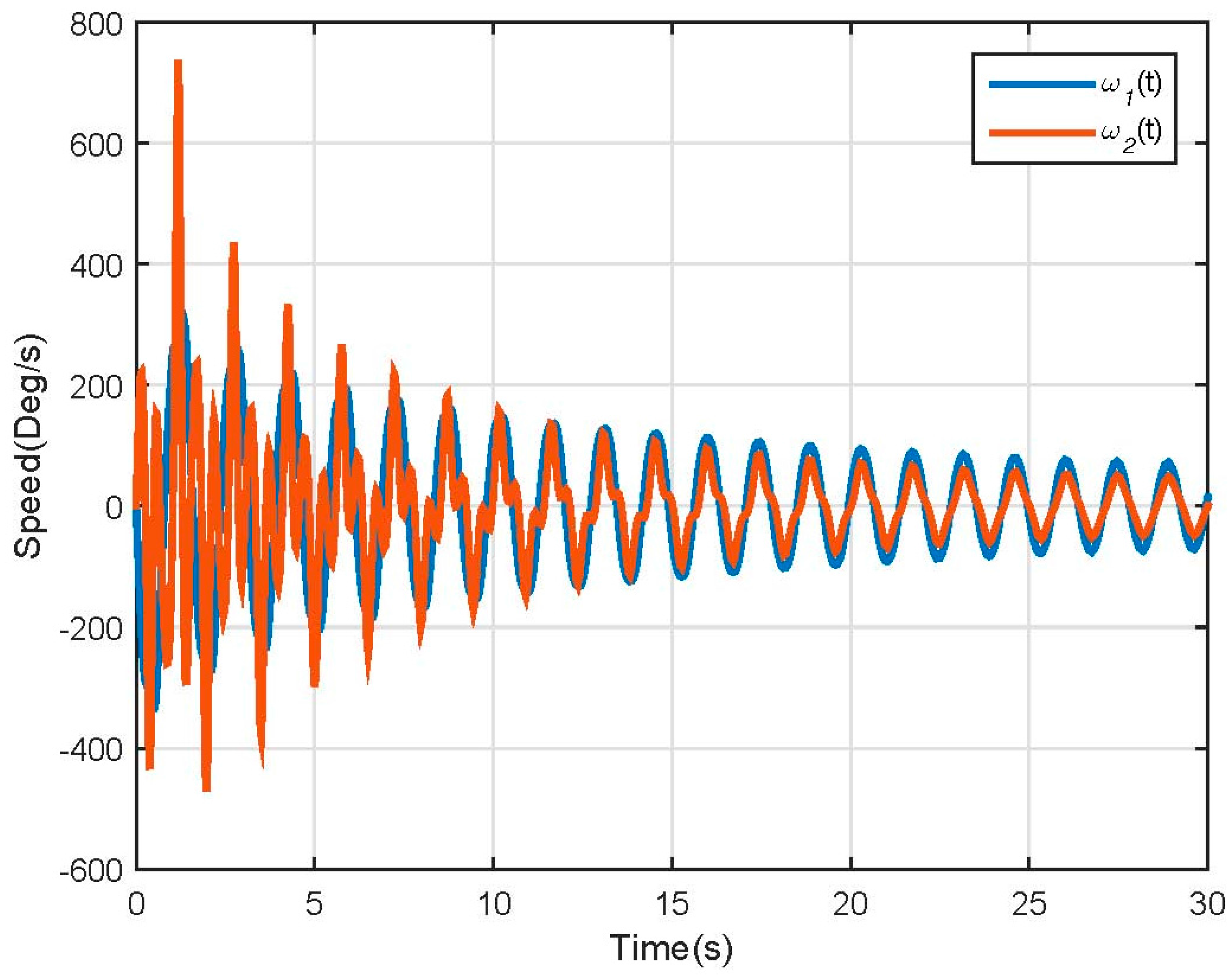
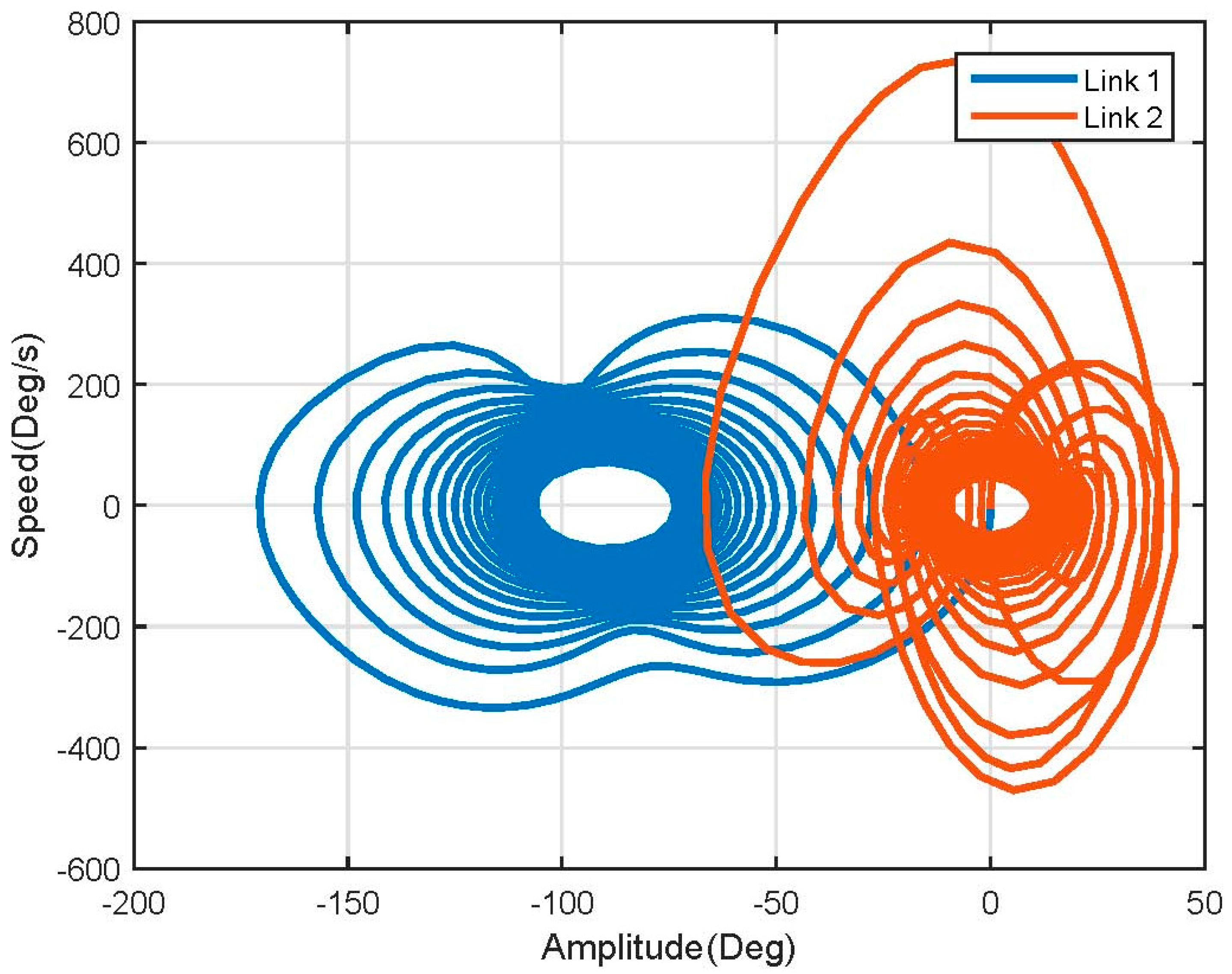
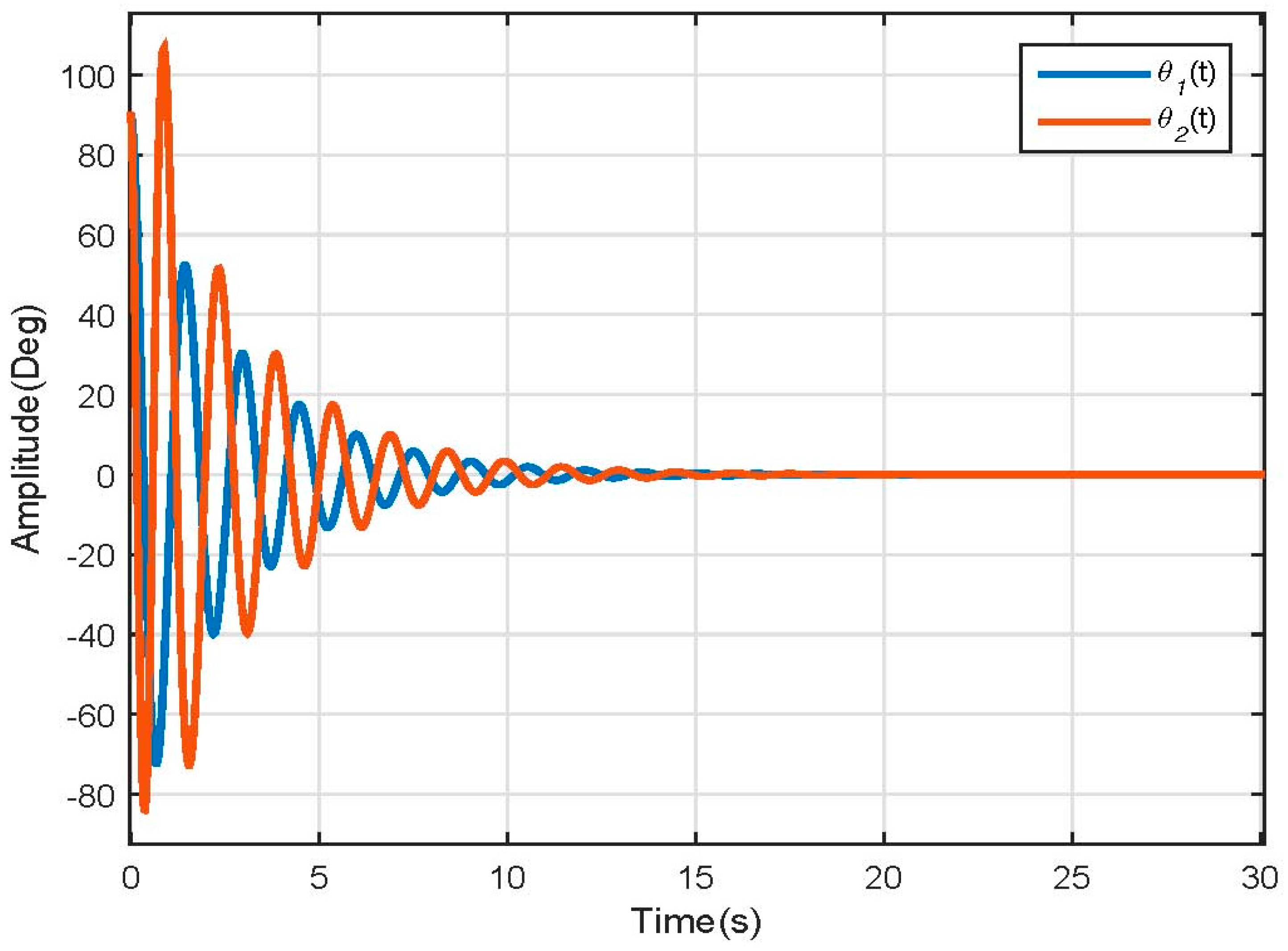
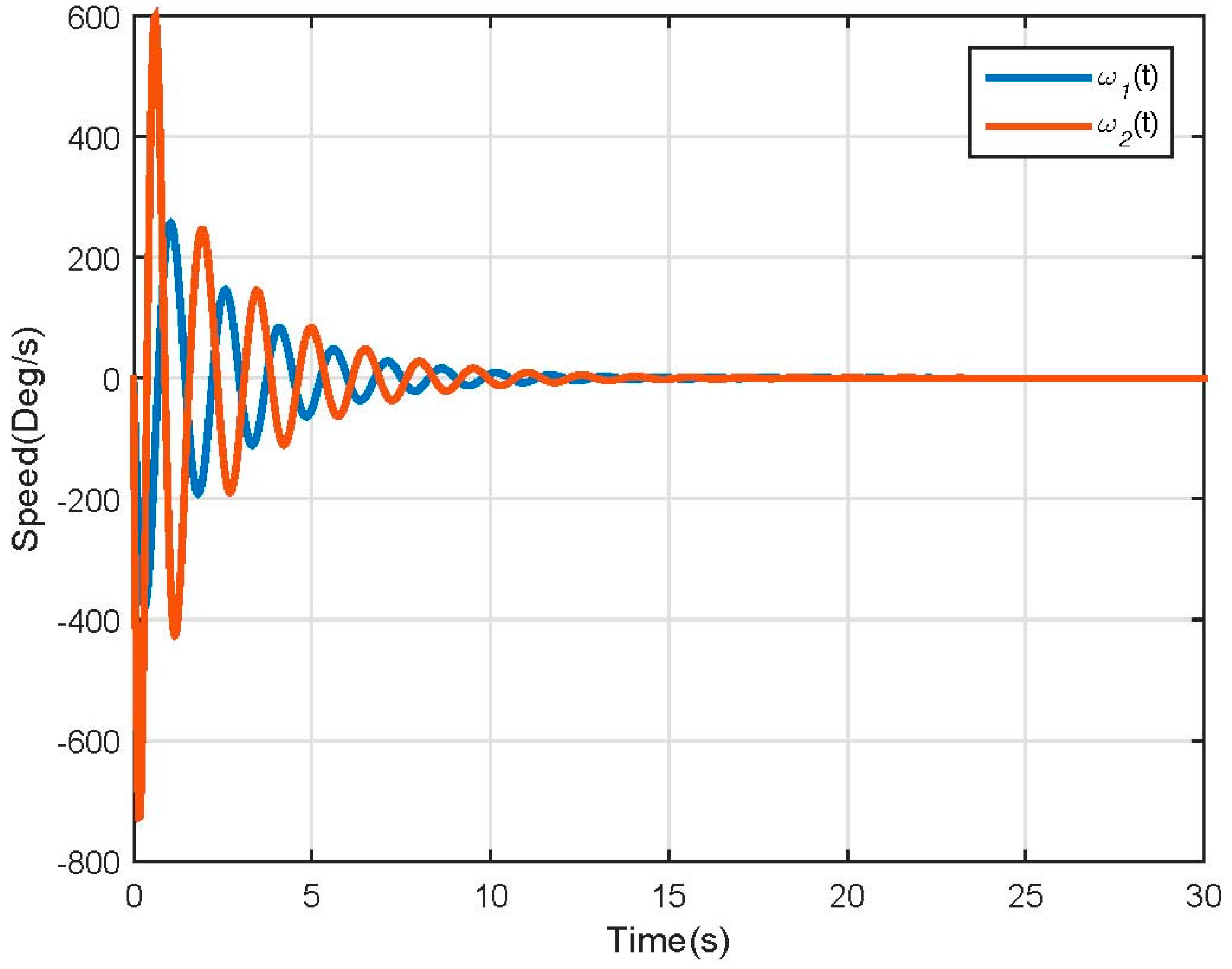
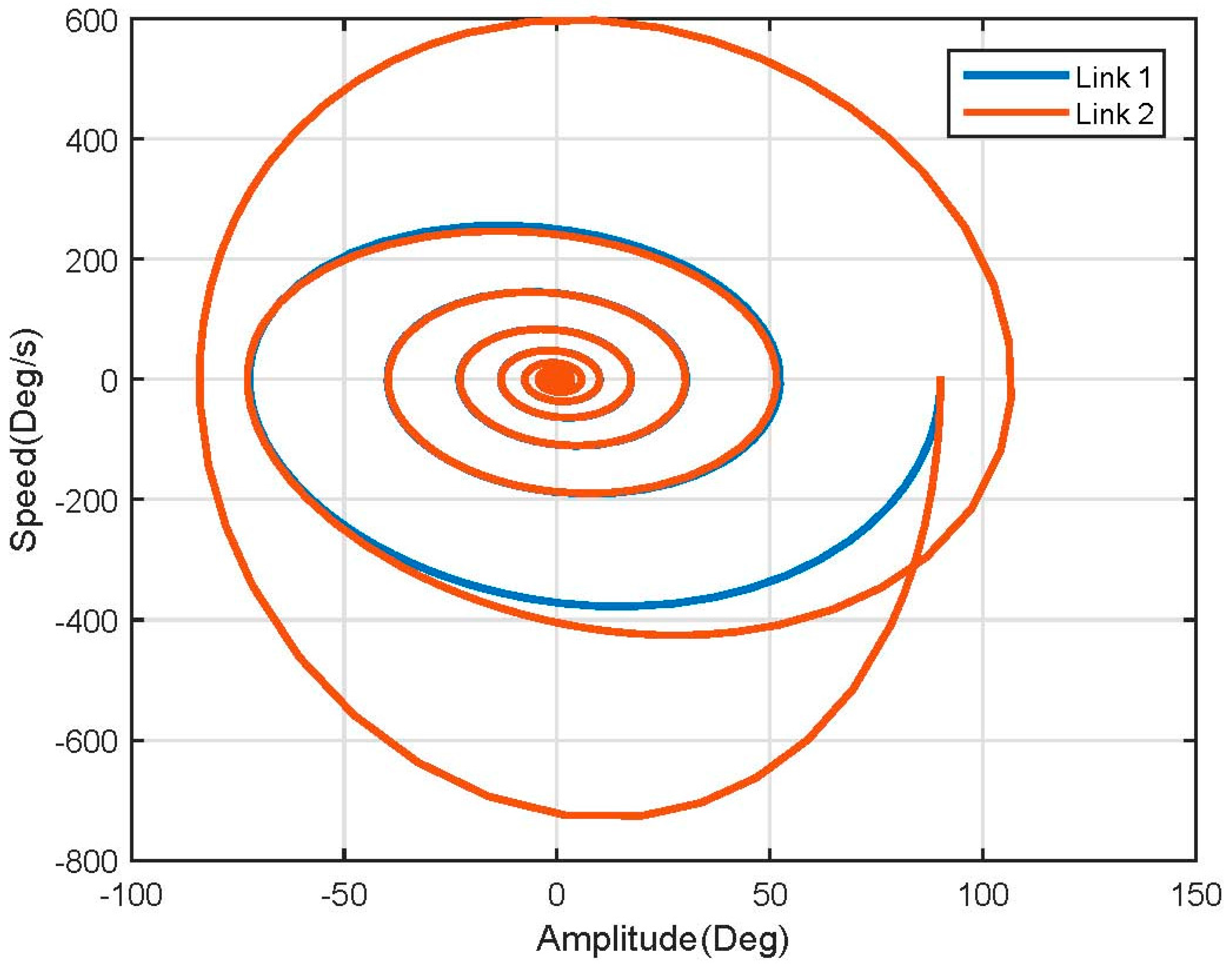
3.1. Dynamic Model Simulation
3.2. Nonlinear Model Simulation

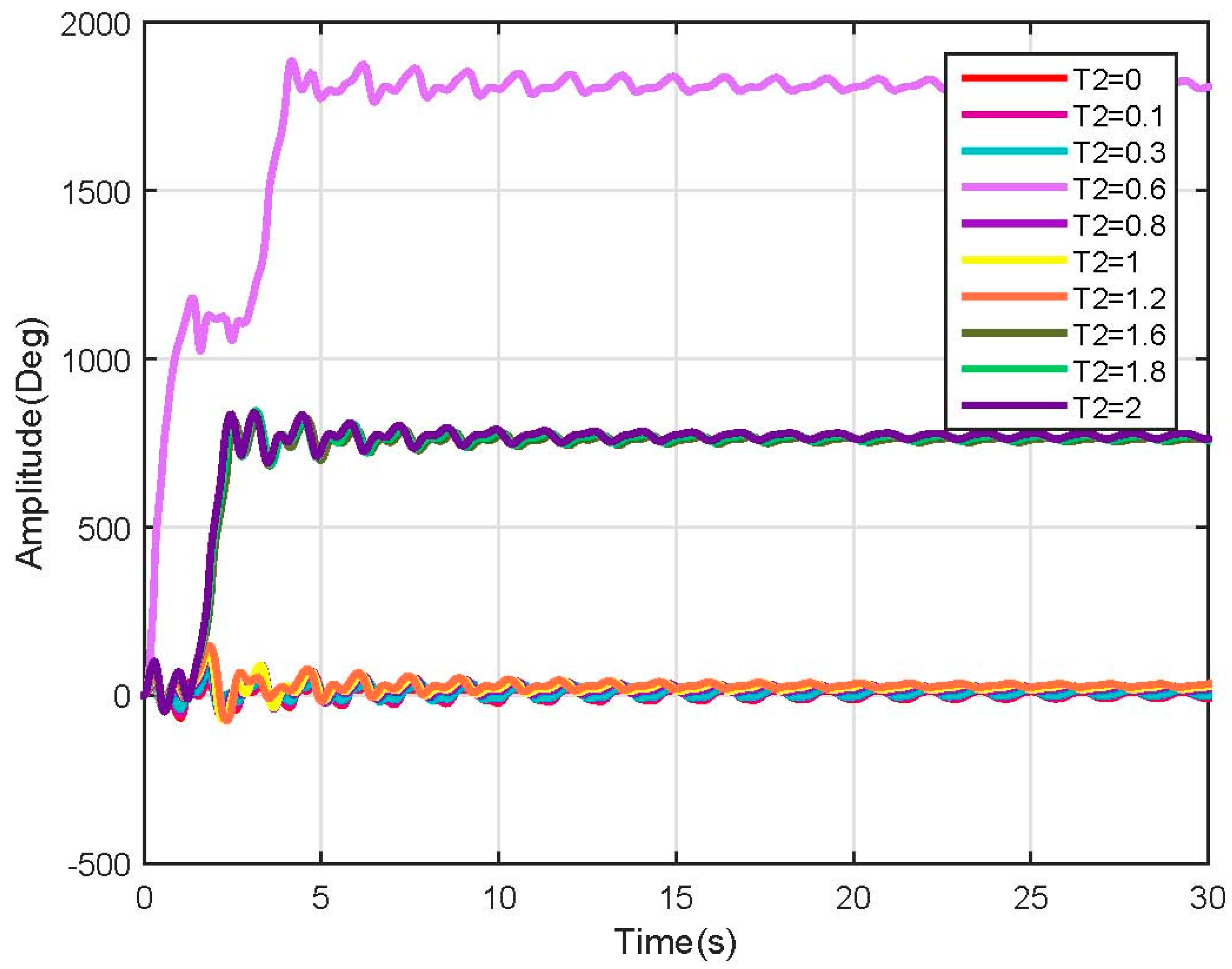


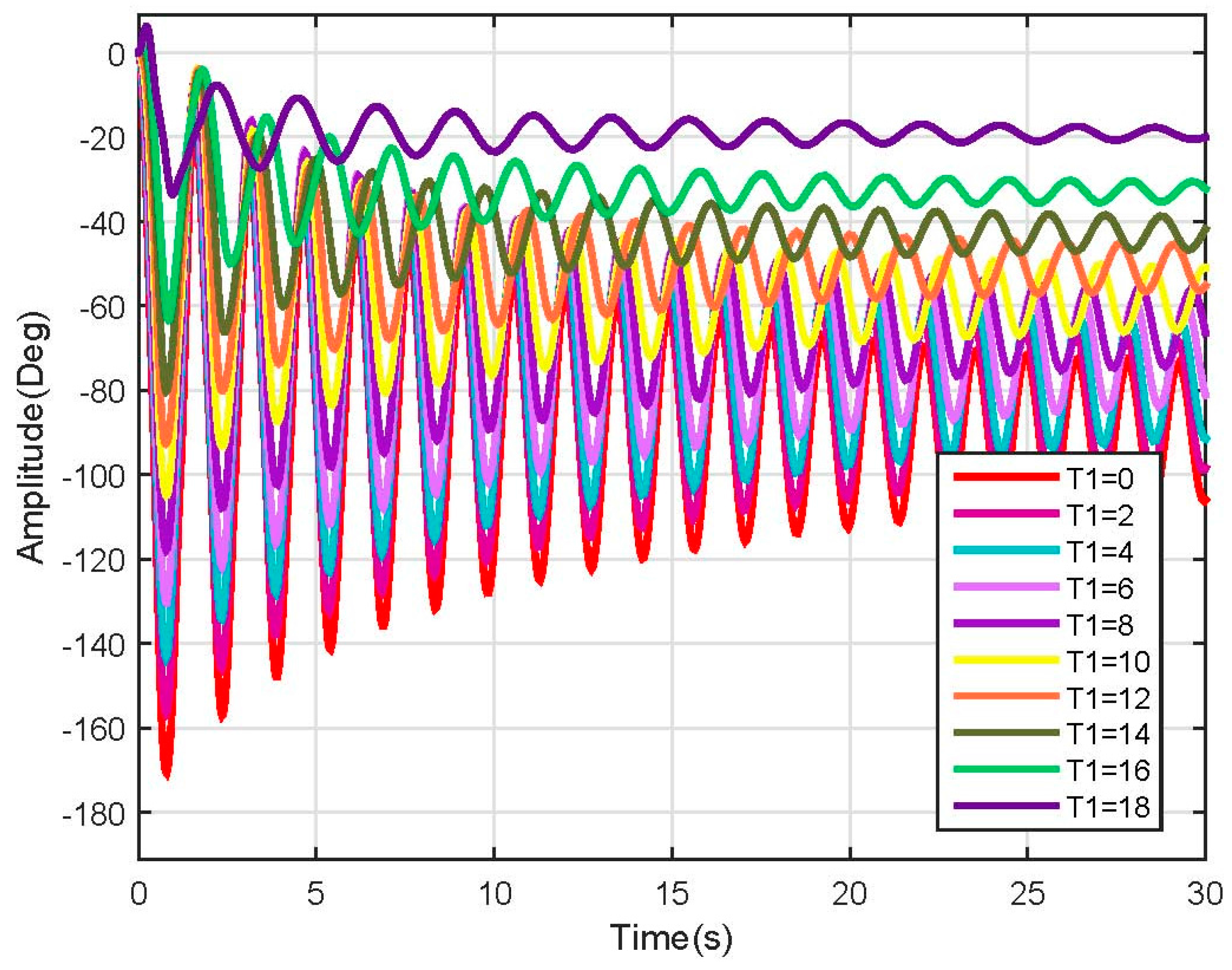
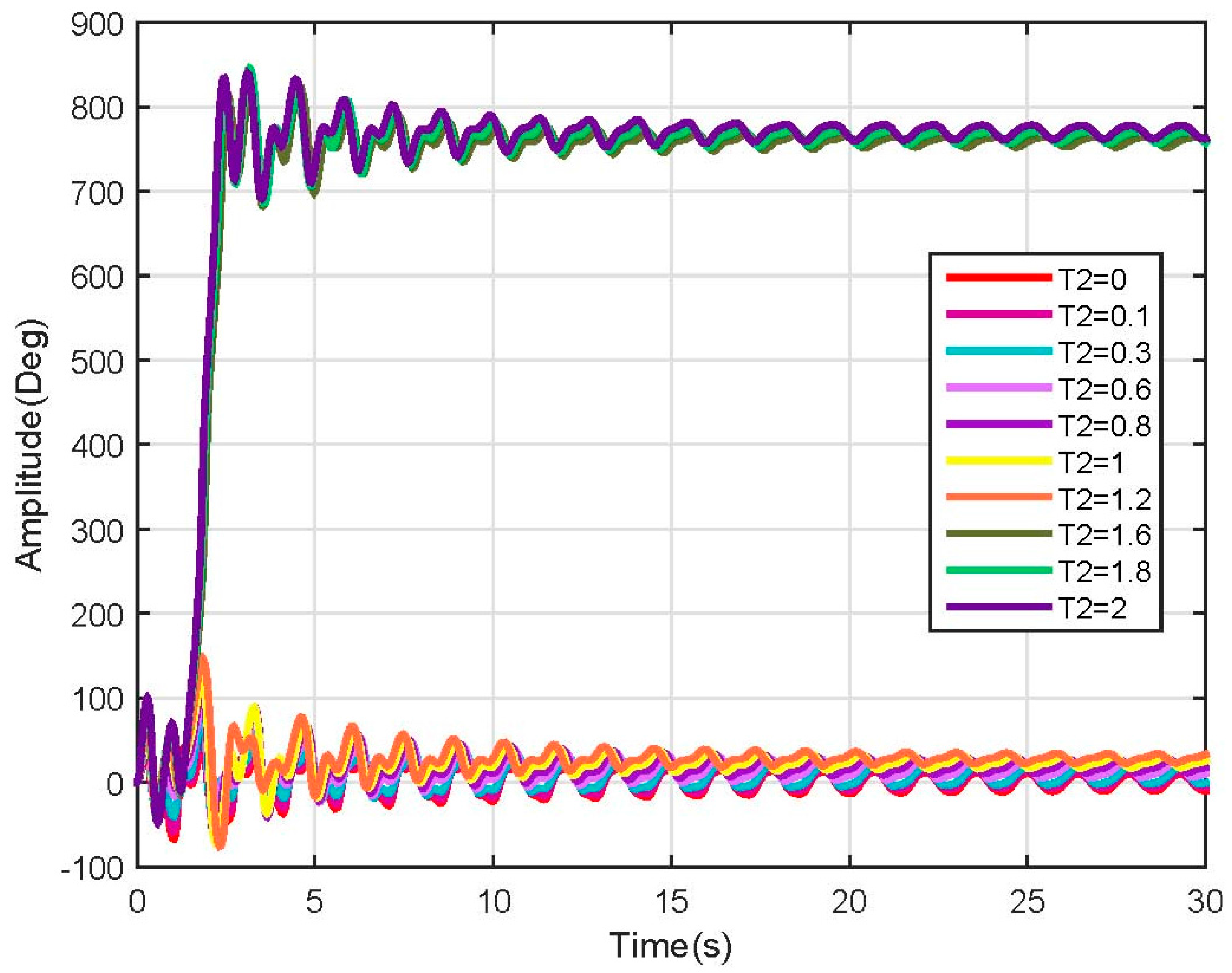
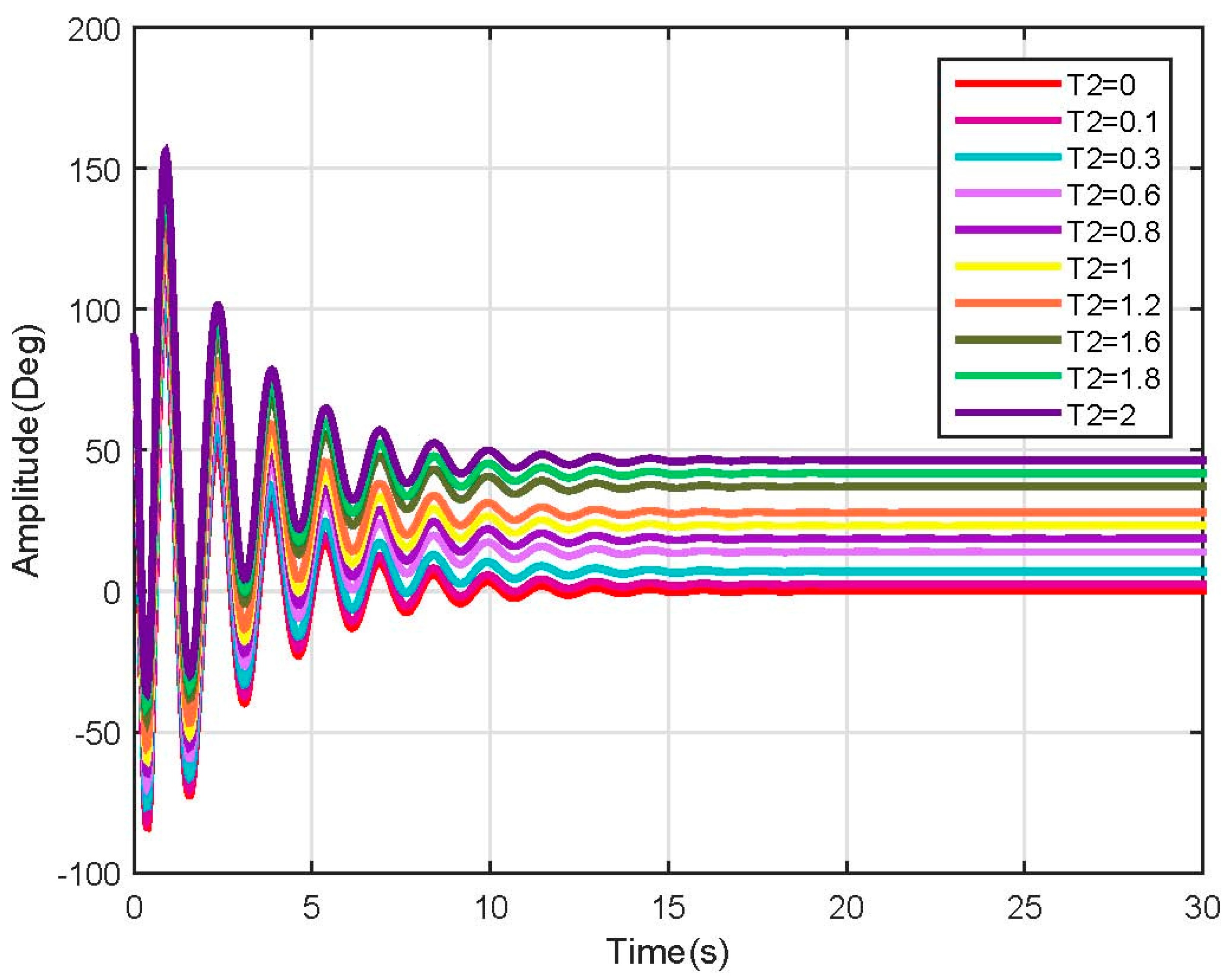
3.3. Linear Model Simulation
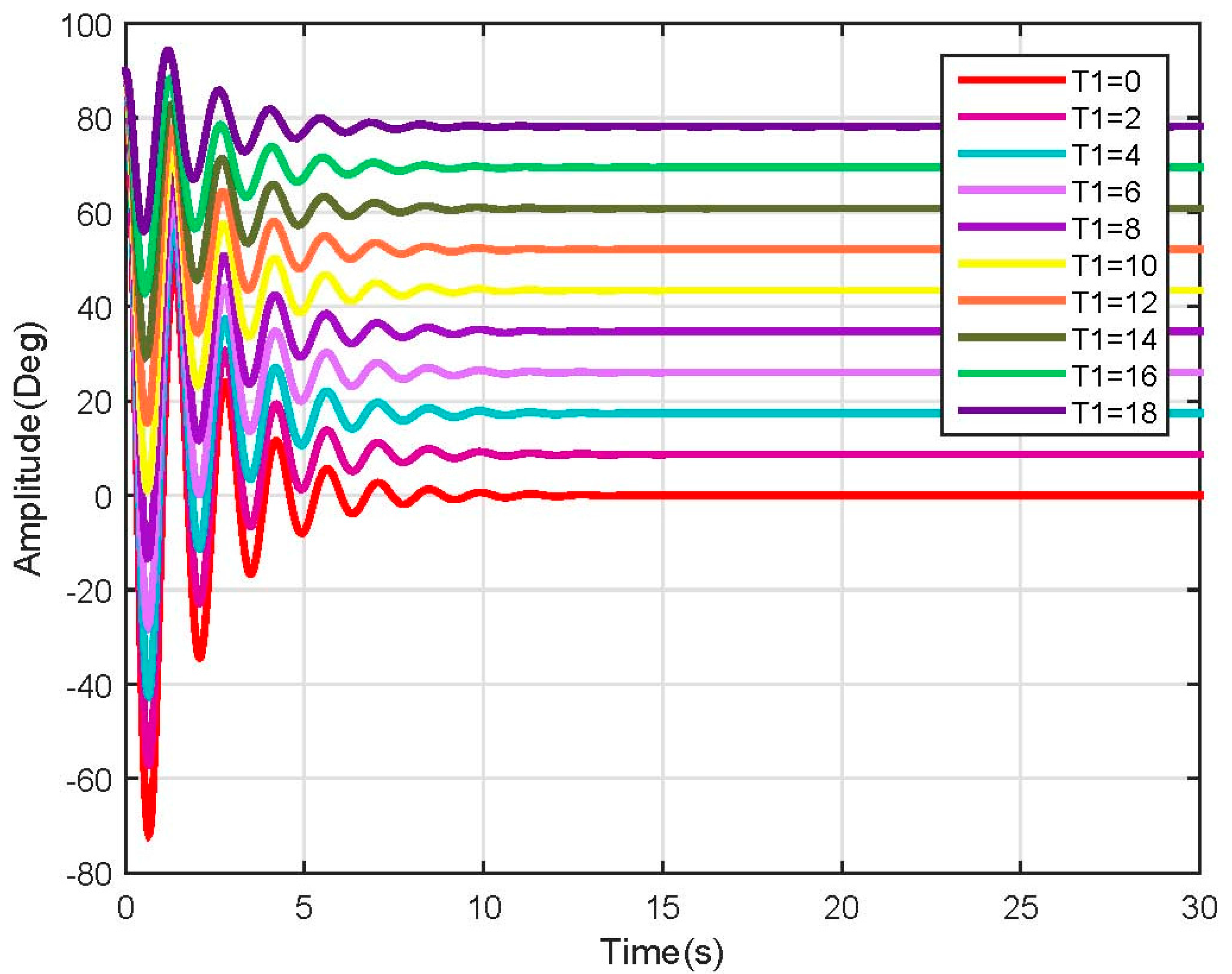
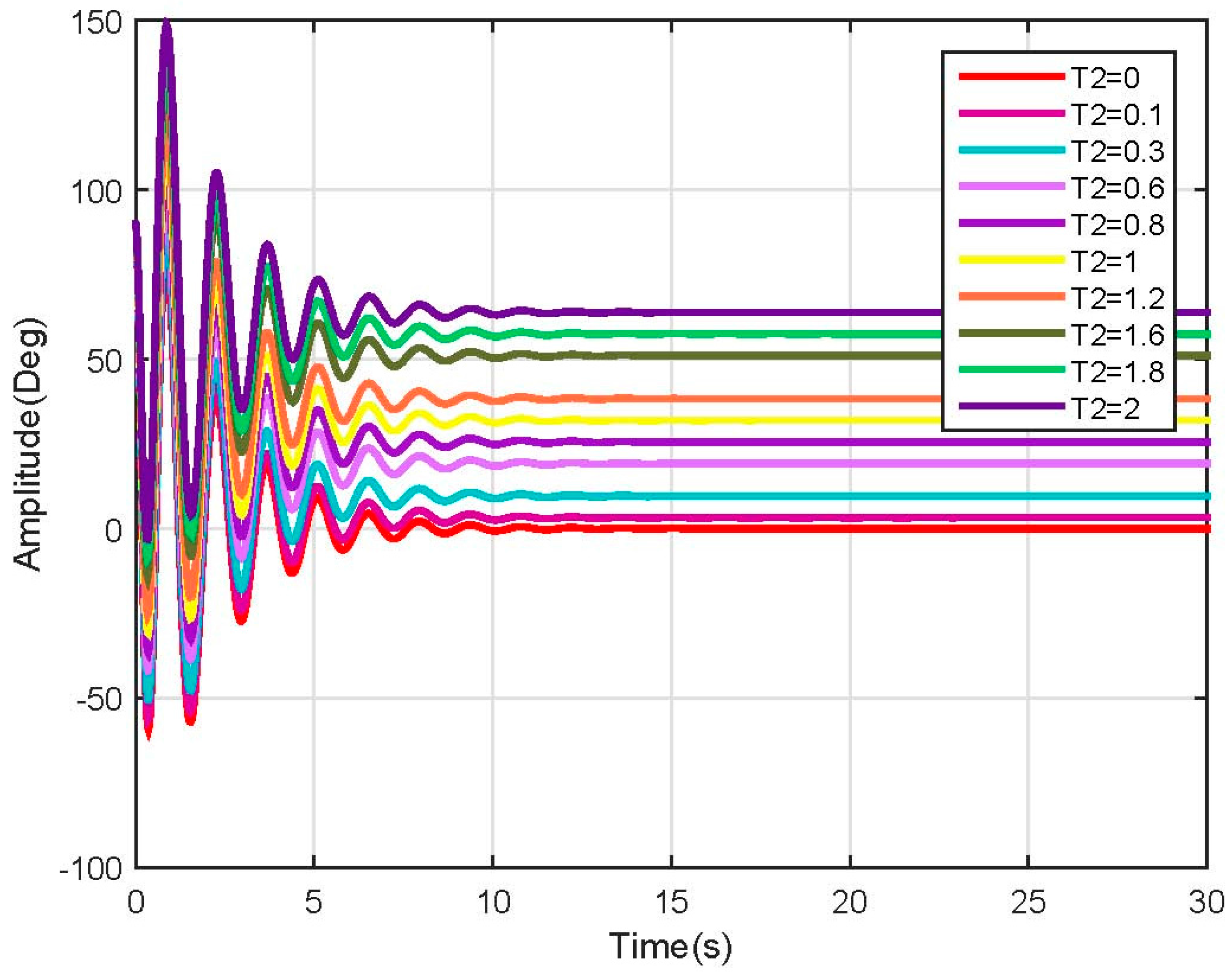
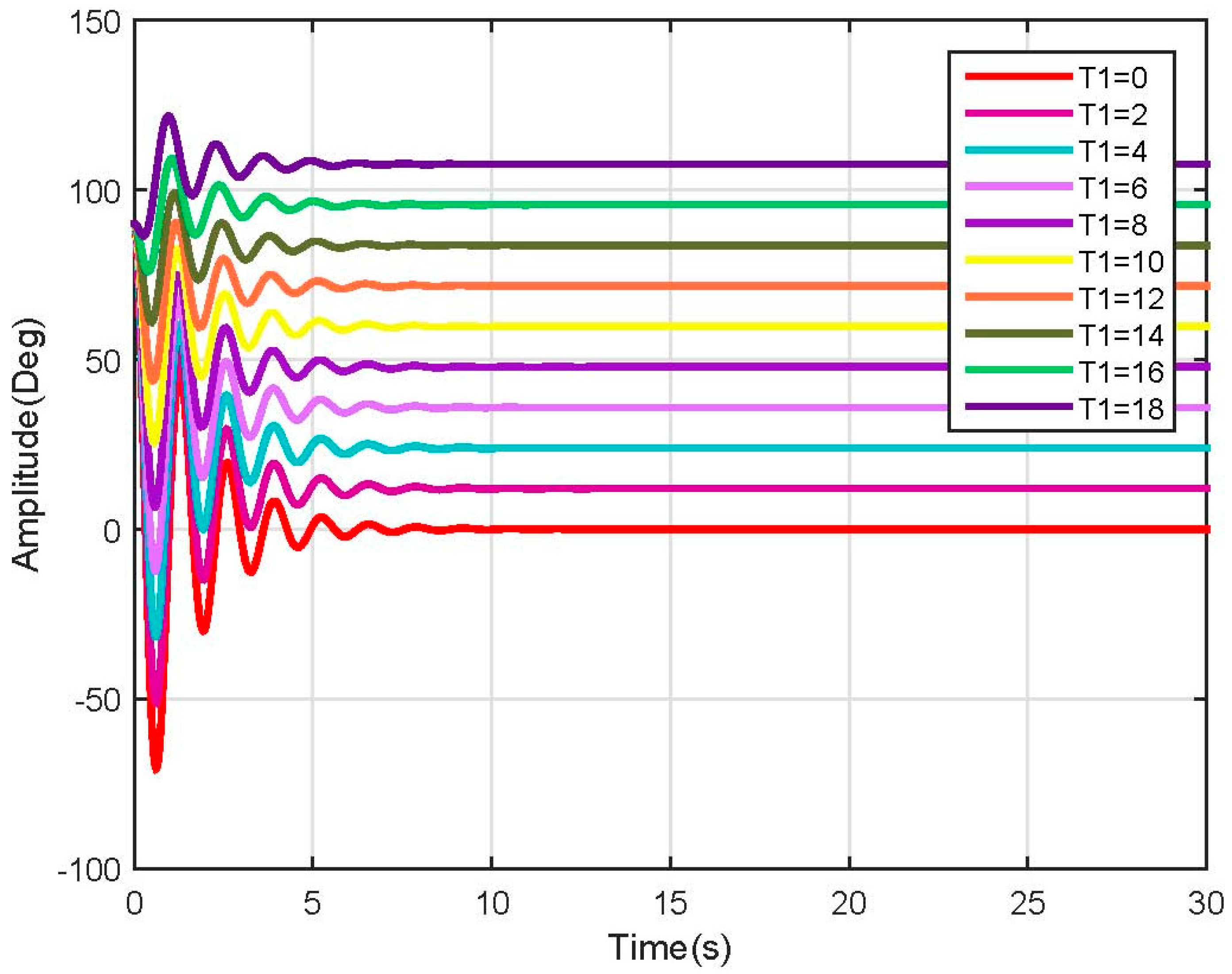
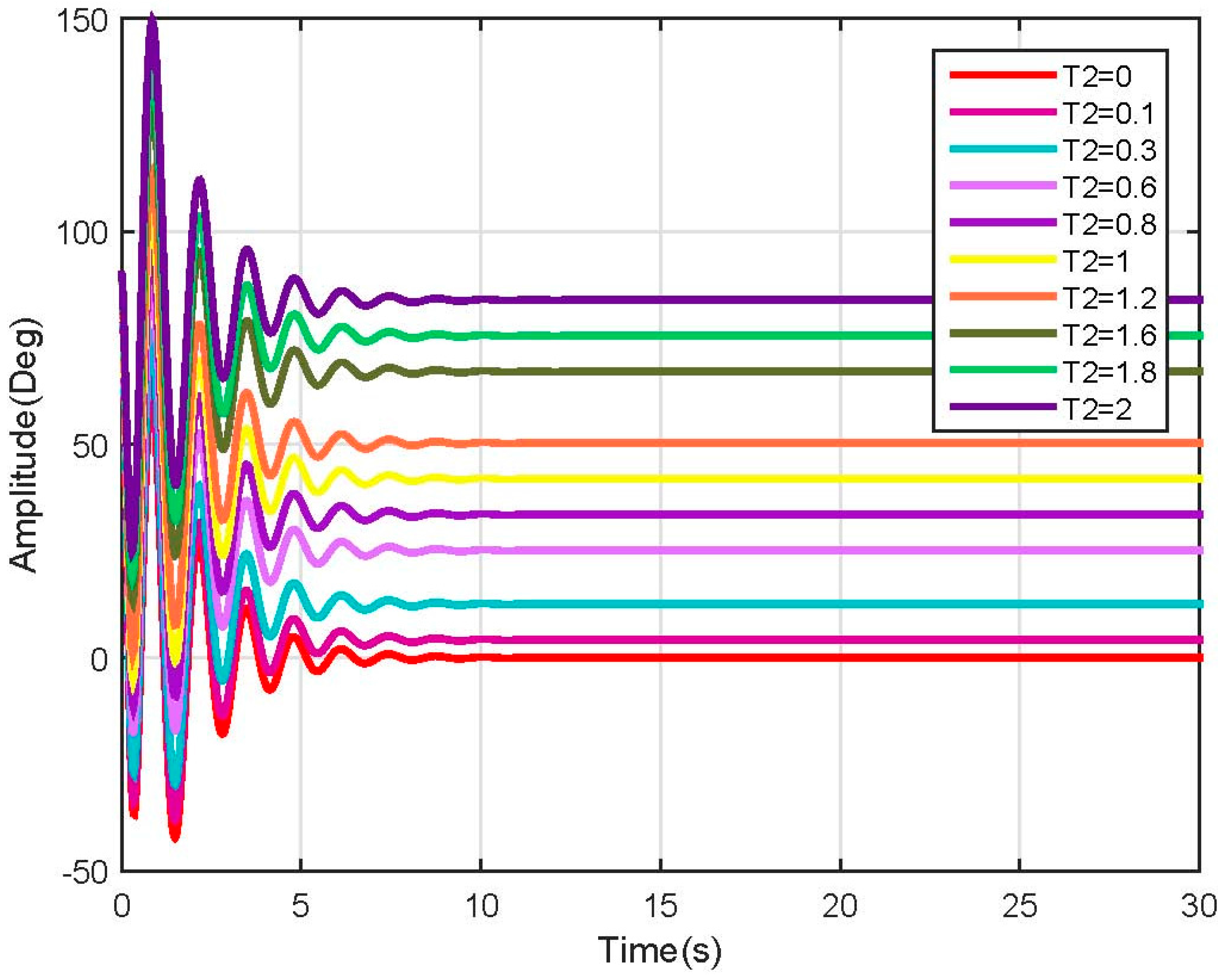
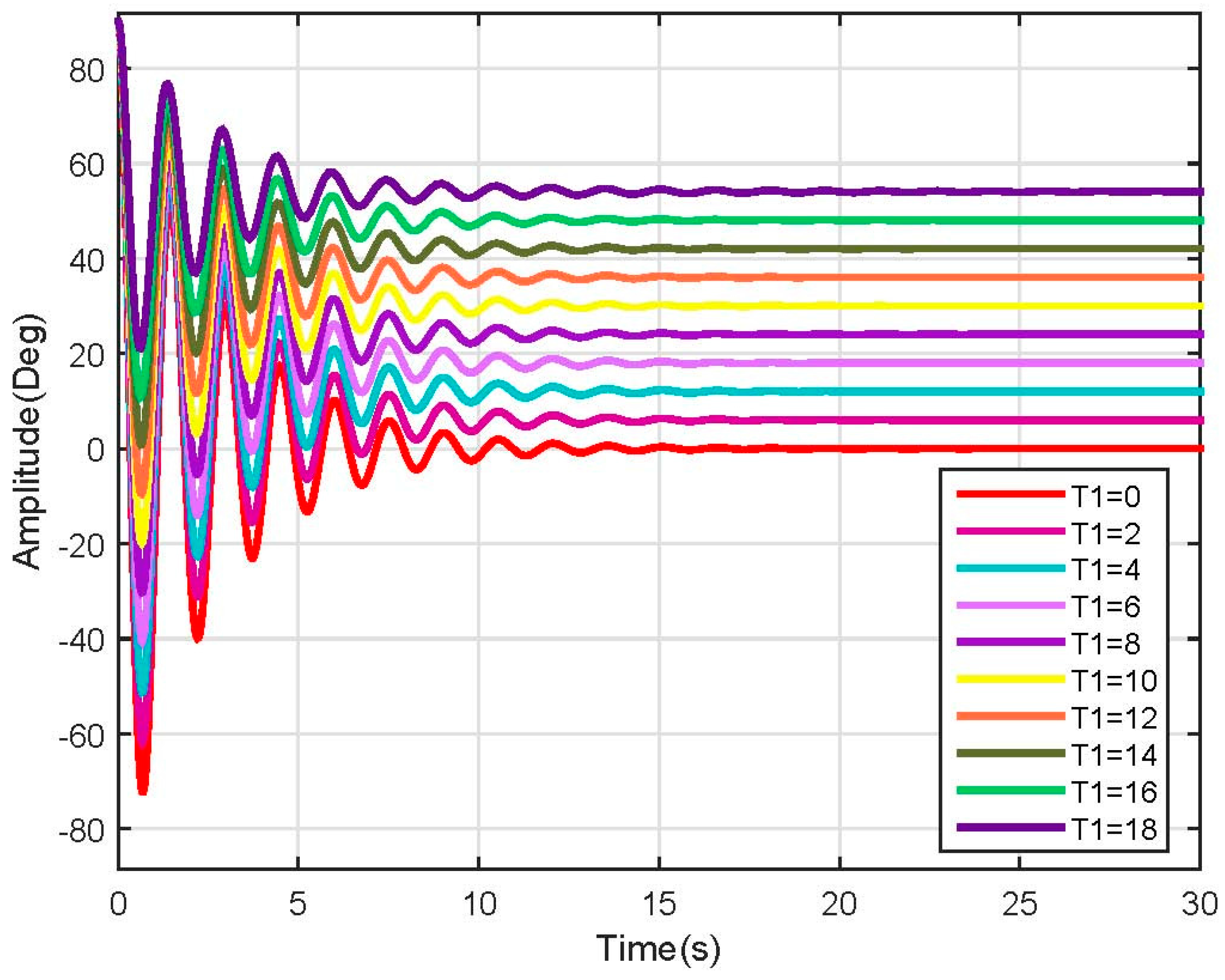
4. Observability and Controllability Analysis
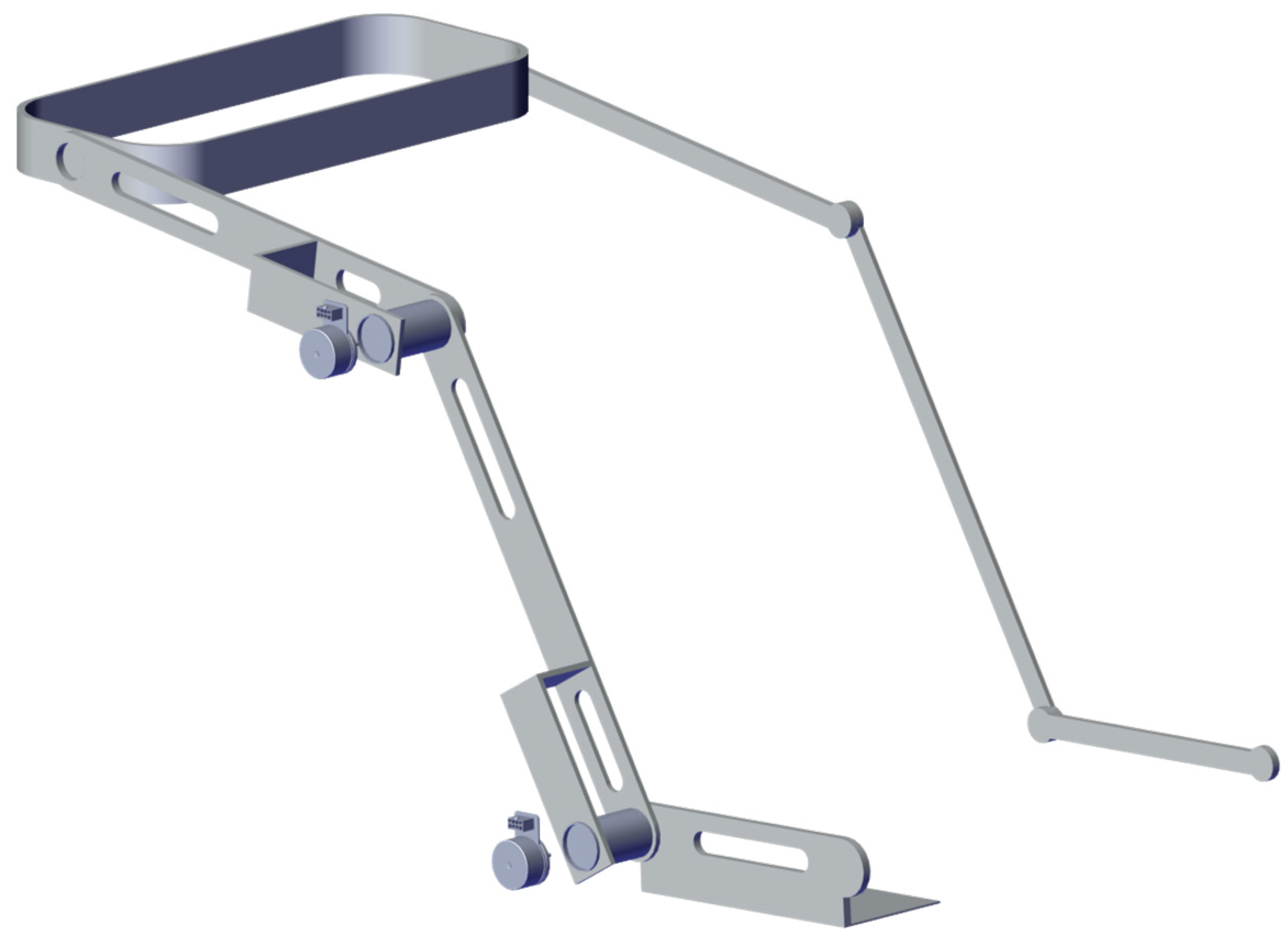
5. Exoskeleton Design Proposal
6. Conclusions
Author Contributions
Conflicts of Interest
References
- Cao, H.; Ling, Z.; Zhu, J.; Wang, Y.; Wang, W. Design Frame of a Leg Exoskeleton for Load-Carrying Augmentation. In Proceedings of the 2009 IEEE International Conference on Robotics and Biomimetics (ROBIO), Guilin, China, 19–23 December 2009. [Google Scholar]
- Jin, X.; Agrawal, S.K. Exploring Laparoscopic Surgery Training with Cable-Driven ARm EXoskeleton (CAREX-M). In Proceedings of the 2015 IEEE International Conference on Rehabilitation Robotics (ICORR), Singapore, 11–14 August 2015. [Google Scholar]
- Misgeld, B.; Schauer, T.; Simanski, O.; Hessinger, M.; Müller, R.; Werthschützky, R.; Pott, P.P. Tool Position Control of an Upper Limb Exoskeleton for Robot-Assisted Surgery. IFAC-PapersOnLine 2015, 48, 195–200. [Google Scholar]
- Banala, S.K.; Agrawal, S.K.; Scholz, J.P. Active Leg Exoskeleton (ALEX) for Gait Rehabilitation of Motor-Impaired Patients. In Proceedings of the 2007 IEEE 10th International Conference on Rehabilitation Robotics (ICORR 2007), Noordwijk, The Netherlands, 13–15 June 2007. [Google Scholar]
- Crema, A.; Mancuso, M.; Frisoli, A.; Salsedo, F.; Raschella, F.; Micera, S. A Hybrid NMES-Exoskeleton for Real Objects Interaction. In Proceedings of the 2015 7th International IEEE/EMBS Conference on Neural Engineering (NER), Montpellier, France, 22–24 April 2015. [Google Scholar]
- Kim, H.; Miller, L.M.; Fedulow, I.; Simkins, M.; Abrams, G.M.; Byl, N.; Rosen, J. Kinematic Data Analysis for Post-Stroke Patients Following Bilateral versus Unilateral Rehabilitation with an Upper Limb Wearable Robotic System. IEEE Trans. Neural Syst. Rehabil. Eng. 2013, 21, 153–164. [Google Scholar] [CrossRef] [PubMed]
- Lee, H.; Kim, J.; Kim, T. A Robot Teaching Framework for a Redundant Dual Arm Manipulator with Teleoperation from Exoskeleton Motion Data. In Proceedings of the 2014 IEEE-RAS International Conference on Humanoid Robots, Madrid, Spain, 18–20 November 2014. [Google Scholar]
- Safavi, S.; Ghafari, A.S.; Meghdari, A. Design of an Optimum Torque Actuator for Augmenting Lower Extremity Exoskeletons in Biomechanical Framework. In Proceedings of the 2011 IEEE International Conference on Robotics and Biomimetics (ROBIO), Karon Beach, Phuket, Thailand, 7–11 December 2011. [Google Scholar]
- Surachai, P. Design and simulation of leg-exoskeleton suit for rehabilitation. Glob. J. Med. Res. 2012, 12, 1–8. [Google Scholar]
- Pan, M.; Zhang, D.; Gao, Z. Novel Design of a Three Degrees of Freedom Hip Exoskeleton Based on Biomimetic Parallel Structure. In Proceedings of the 2011 IEEE International Conference on Computer Science and Automation Engineering (CSAE), Shanghai, China, 10–12 June 2011. [Google Scholar]
- Velandia, C.; Celedón, H.; Tibaduiza, D.A.; Torres-Pinzón, C.; Vitola, J. Design and Control of an Exoskeleton in Rehabilitation Tasks for Lower Limb. In Proceedings of the 2016 XXI Symposium on Signal Processing, Images and Artificial Vision (STSIVA), Bucaramanga, Colombia, 31 August–2 September 2016. [Google Scholar]
- Ferrati, F.; Bortoletto, R.; Pagello, E. Virtual Modelling of a Real Exoskeleton Constrained to a Human Musculoskeletal Model. In Proceedings of the Second International Conference Biomimetic and Biohybrid Systems, Living Machines 2013, London, UK, 29 July–2 August 2013; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Lu, R.; Li, Z.; Su, C.-Y.; Xue, A. Development and Learning Control of a Human limb with a Rehabilitation Exoskeleton. IEEE Trans. Ind. Electron. 2014, 61, 3776–3785. [Google Scholar] [CrossRef]
- Xiuxia, Y.; Yi, Z.; Zhicai, X.; Zhiyong, Y. Total Cource Locomotion Control of Assist Walking Exoskeleton Leg. In Proceedings of the 2011 30th Chinese Control Conference (CCC), Yantai, China, 22–24 July 2011. [Google Scholar]
- Singla, A.; Dhand, S.; Virk, G.S. Mathematical modelling of a hand crank generator for powering lower-limb exoskeletons. Pespect. Sci. 2016, 8, 561–563. [Google Scholar] [CrossRef]
- Cardenas, C.C.V. Modelado, Control Y Monitoreo de un Exoesqueleto Pistir Procesos de Rehabilitacion en Miembro Inferior; Universidad Santo Tomás: Bogotá, Colombia, 2016. [Google Scholar]
- Hanavan, E.P., Jr. A mathematical model of the human body. AMRL TR 1964, 1–149. [Google Scholar]
- Drillis, R.; Contini, C. Body Segment Parameters Artificial Limbs; National Academy of Sciences: Washington, DC, USA, 1964; Volume 8, pp. 44–67. [Google Scholar]
- Winter, D.A. Biomechanics and Motor Control of Human Movement, 4th ed.; John Wiley and Sons, Inc.: Hoboken, NJ, USA, 2009. [Google Scholar]
- Goldstein, H.; Poole, C.; Safko, J. Classical Mechanics, 3rd ed.; Addison Wesley: Indianapolis, IN, USA, 2001. [Google Scholar]
- Young, H.D.; Freedman, R.A. Fisica Universitaria, 12th ed.; Pearson Educación: México City, México, 2009. [Google Scholar]
- Ogata, K. Ingenieria de Control Moderna; Pearson Educación: New York, NY, USA, 2009. [Google Scholar]
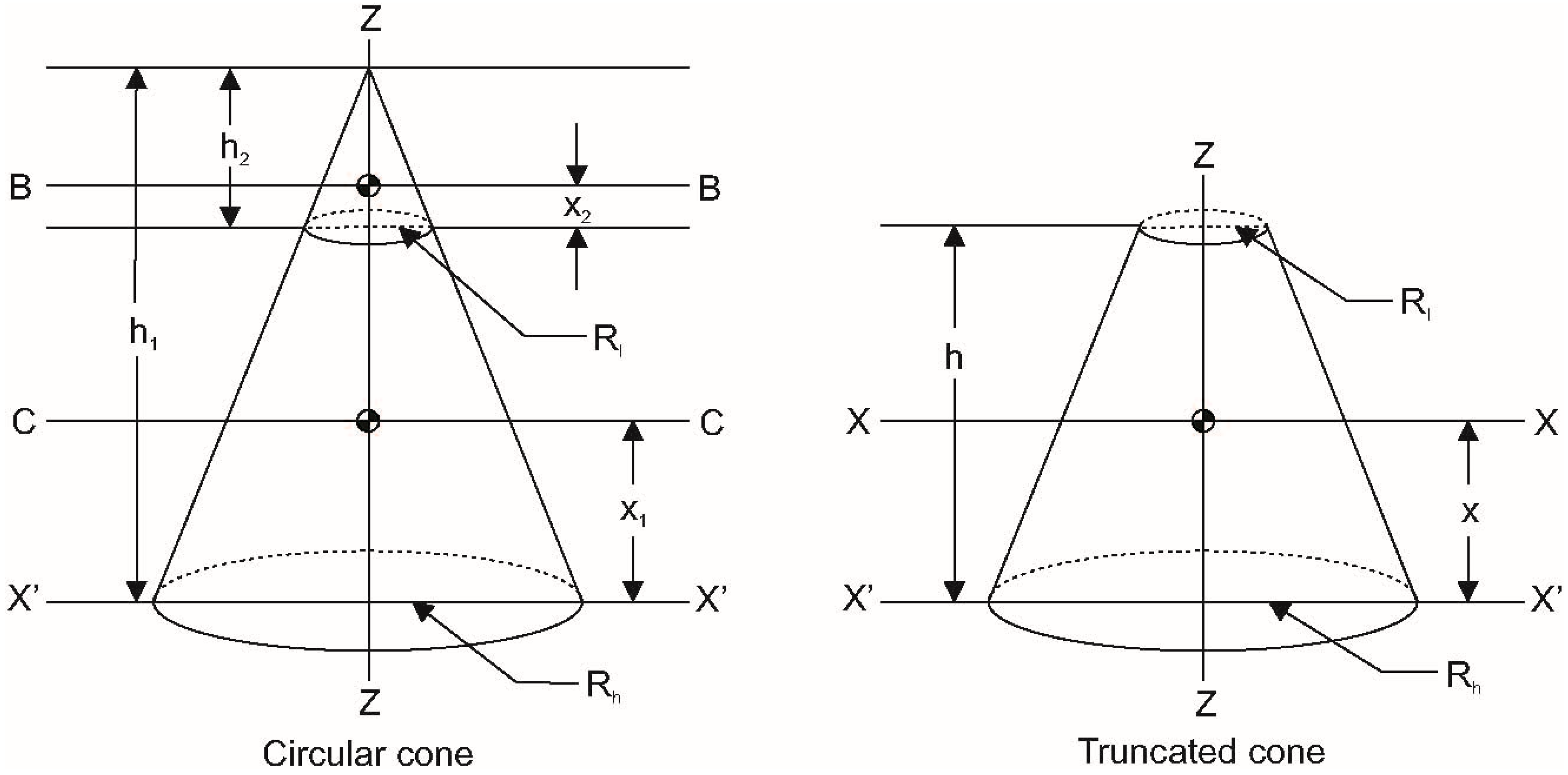





| Limb Section | Parameters |
|---|---|
| Thigh | |
| Leg | |
| Foot |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Velandia, C.C.; Tibaduiza, D.A.; Vejar, M.A. Proposal of Novel Model for a 2 DOF Exoskeleton for Lower-Limb Rehabilitation. Robotics 2017, 6, 20. https://doi.org/10.3390/robotics6030020
Velandia CC, Tibaduiza DA, Vejar MA. Proposal of Novel Model for a 2 DOF Exoskeleton for Lower-Limb Rehabilitation. Robotics. 2017; 6(3):20. https://doi.org/10.3390/robotics6030020
Chicago/Turabian StyleVelandia, Cristian C., Diego A. Tibaduiza, and Maribel Anaya Vejar. 2017. "Proposal of Novel Model for a 2 DOF Exoskeleton for Lower-Limb Rehabilitation" Robotics 6, no. 3: 20. https://doi.org/10.3390/robotics6030020







