Robust Composite High-Order Super-Twisting Sliding Mode Control of Robot Manipulators
Abstract
:1. Introduction
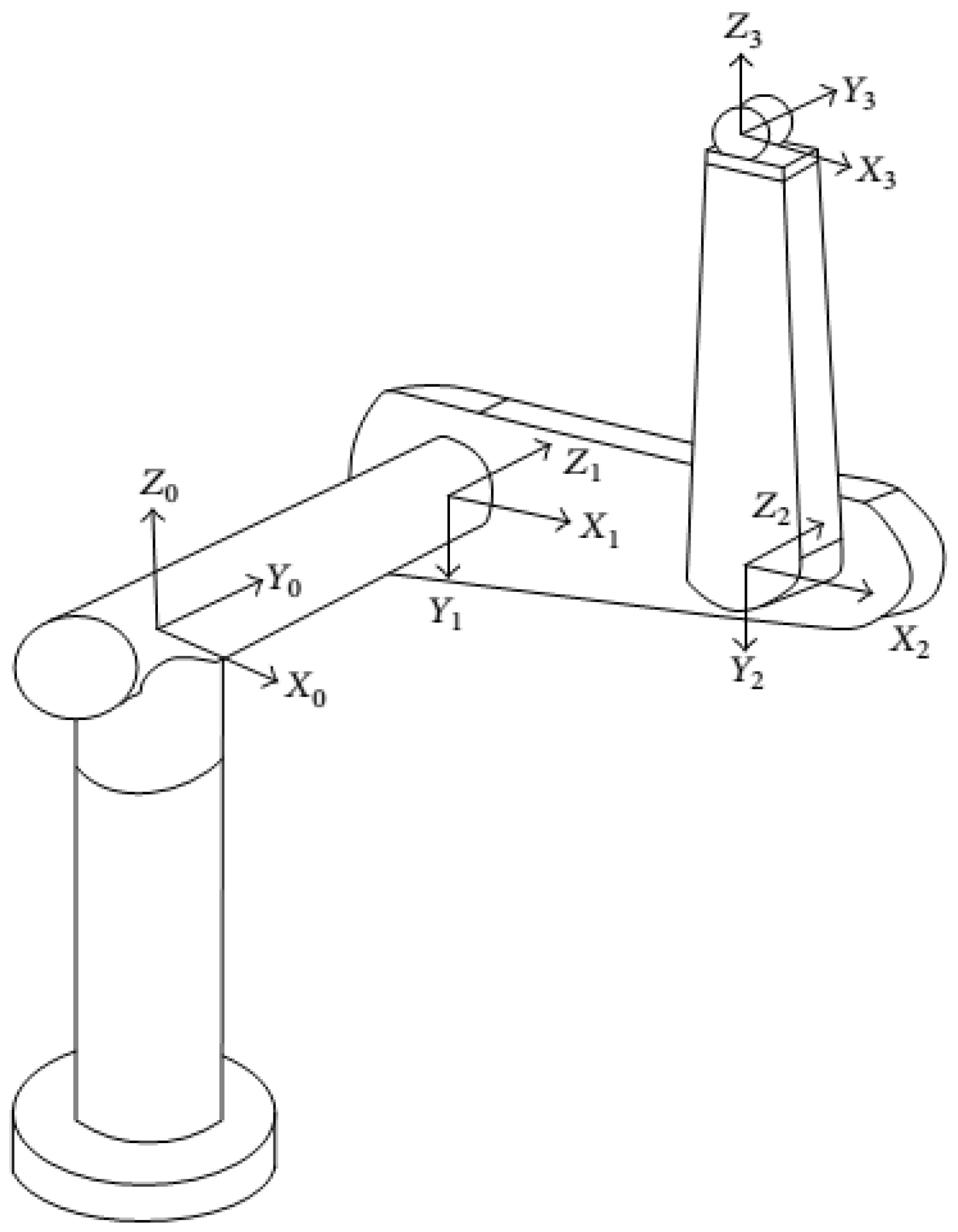
2. Problem Statement and Control Objectives
3. Proposed Method
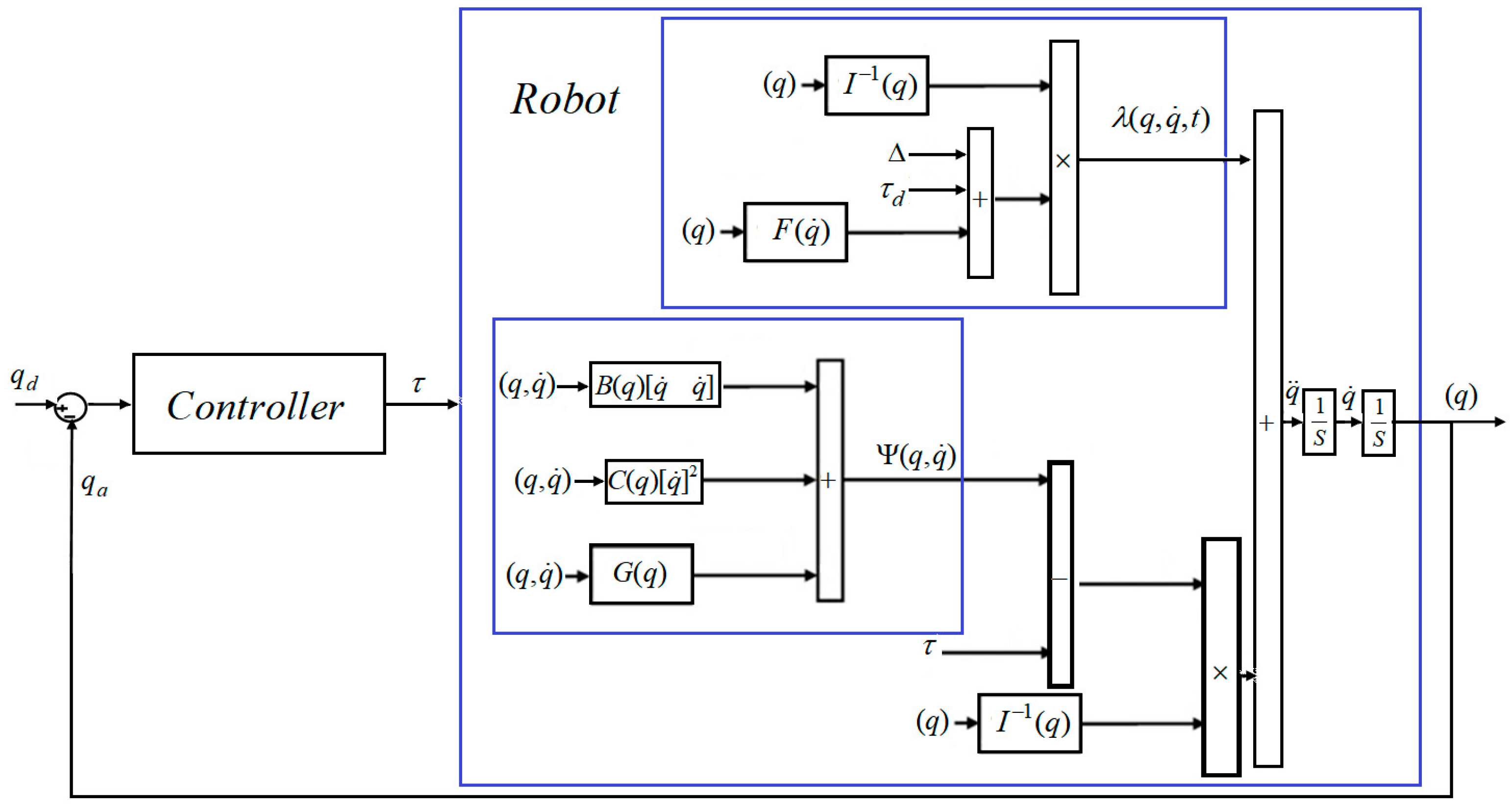
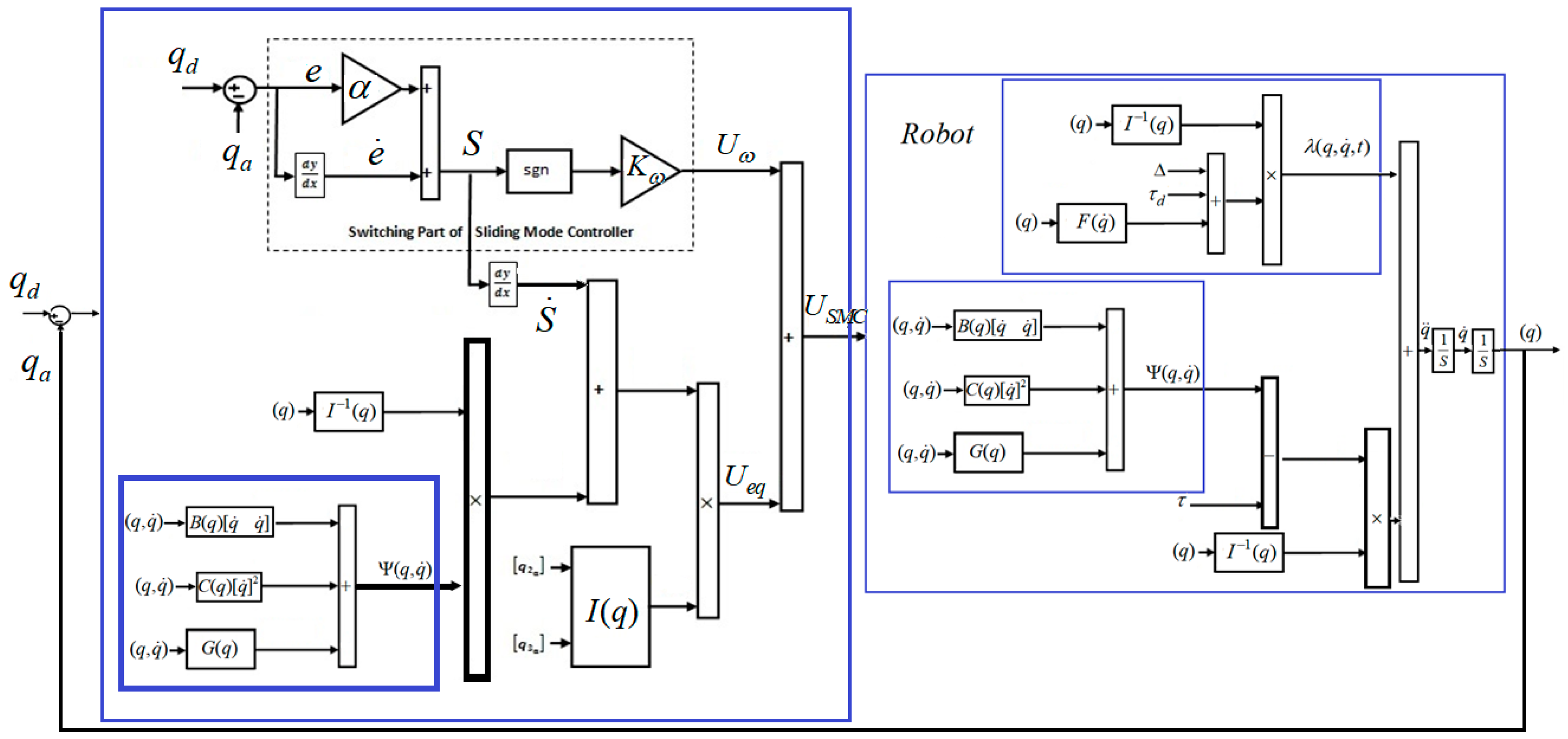
3.1. Traditional Sliding Mode Control Algorithm
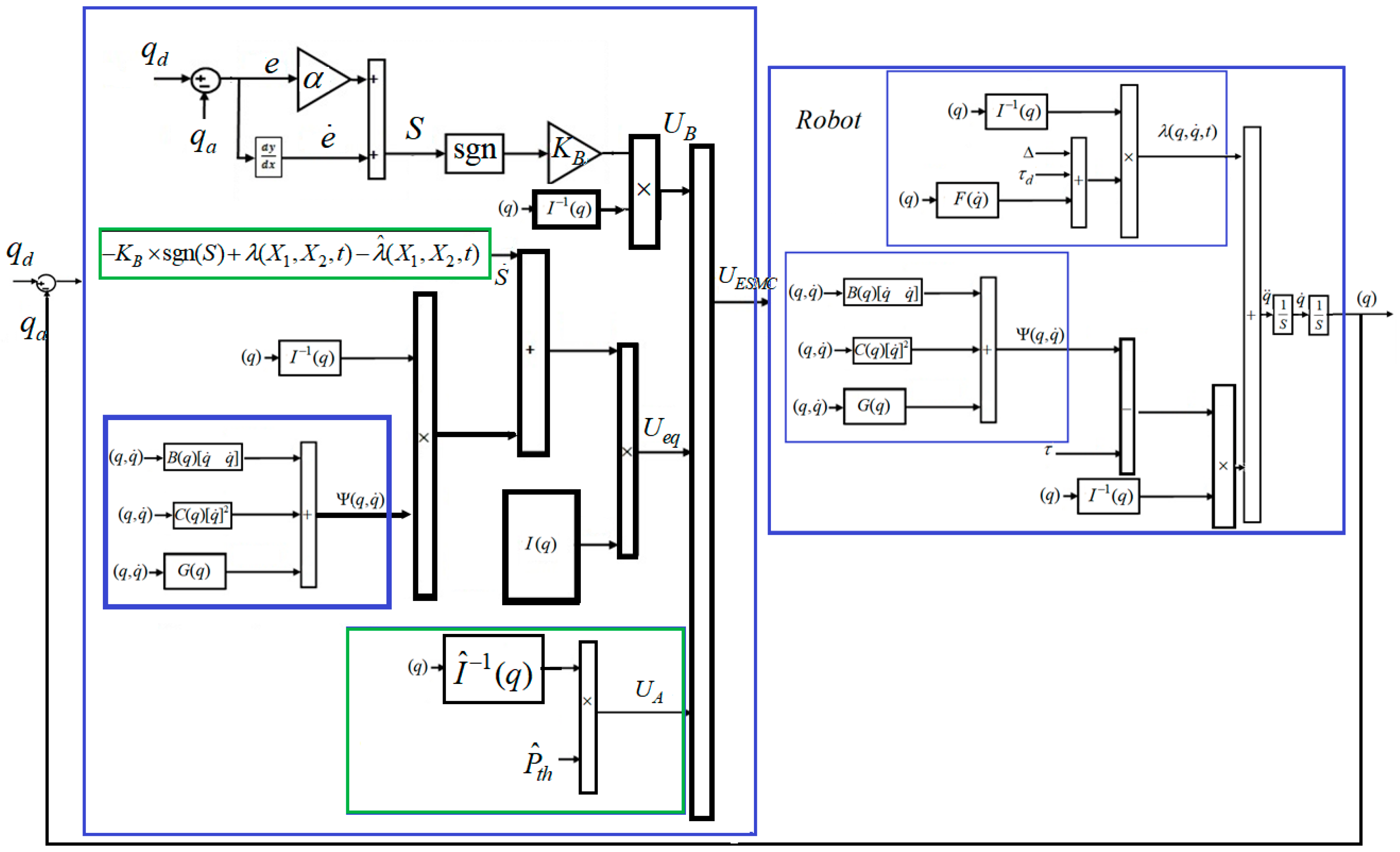
3.2. Estimated State Sliding Mode Control
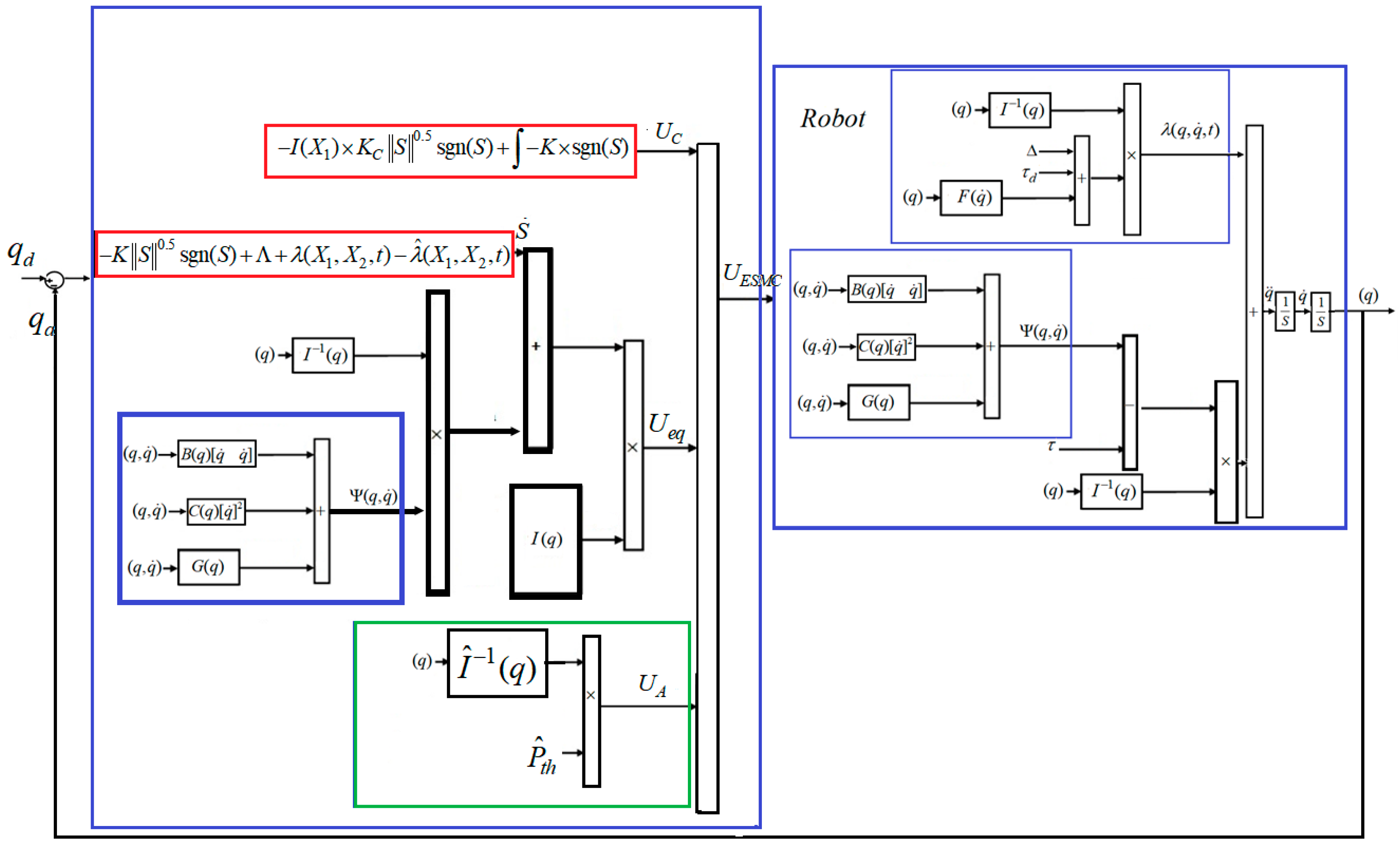
3.3. Proposed Method
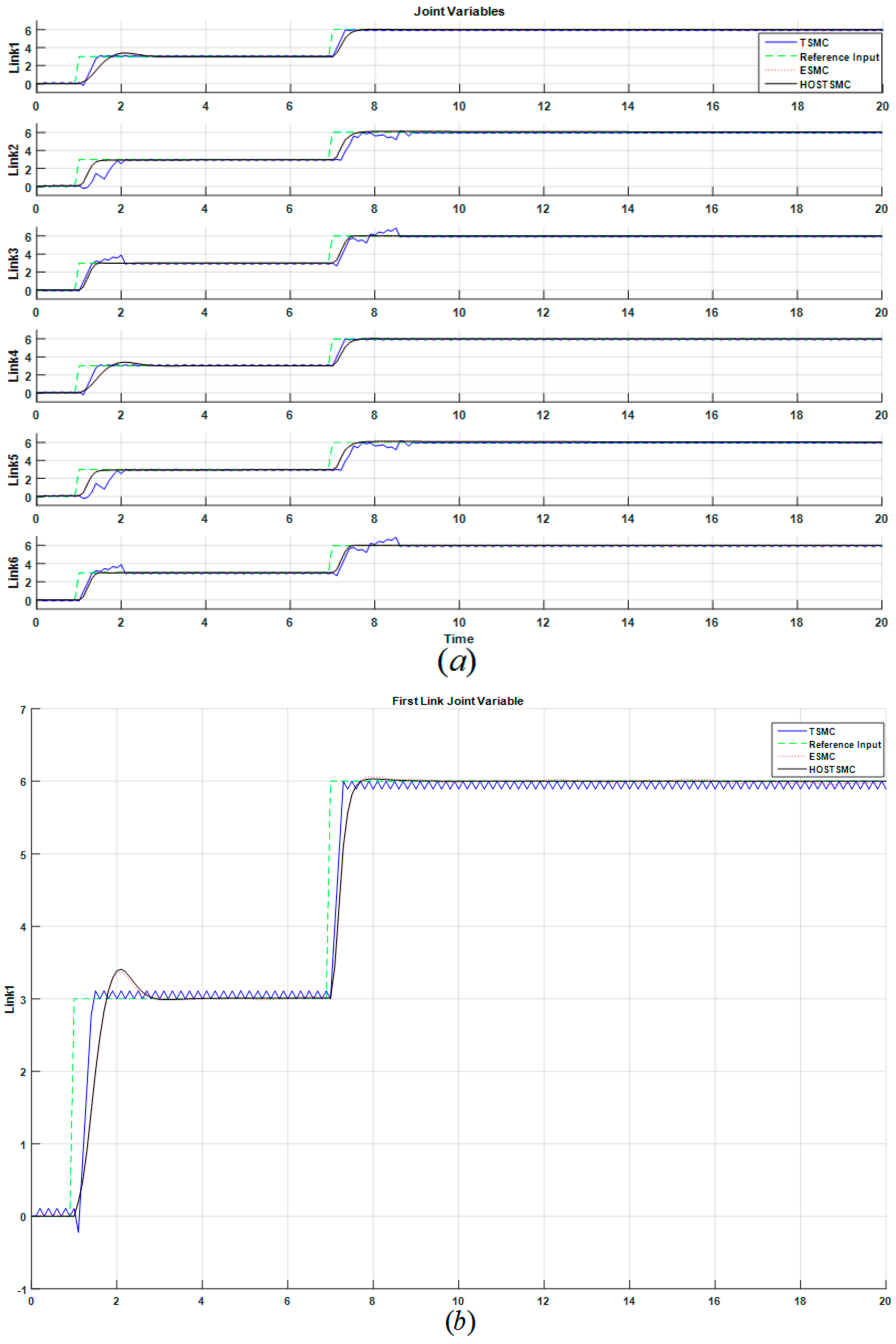
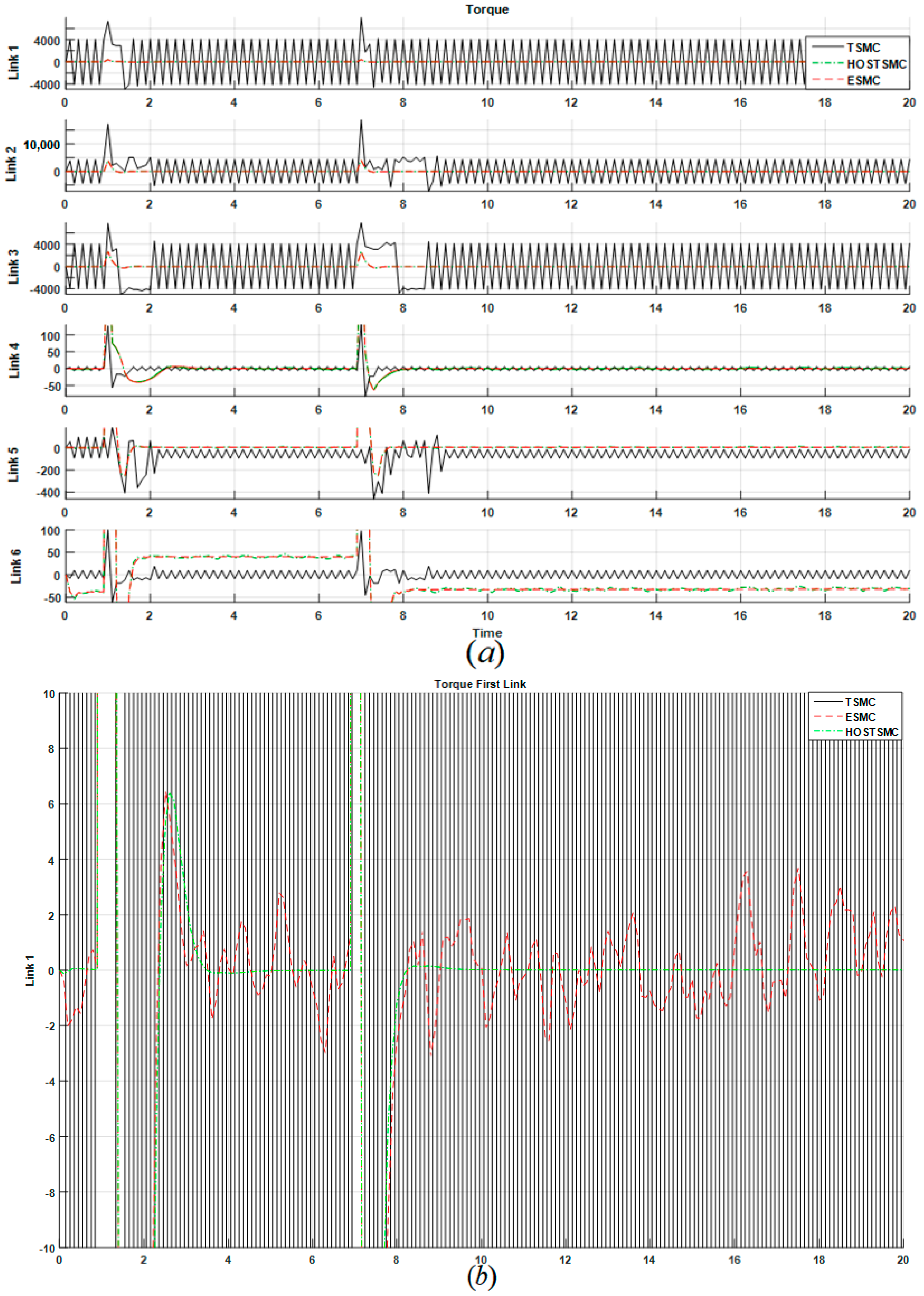
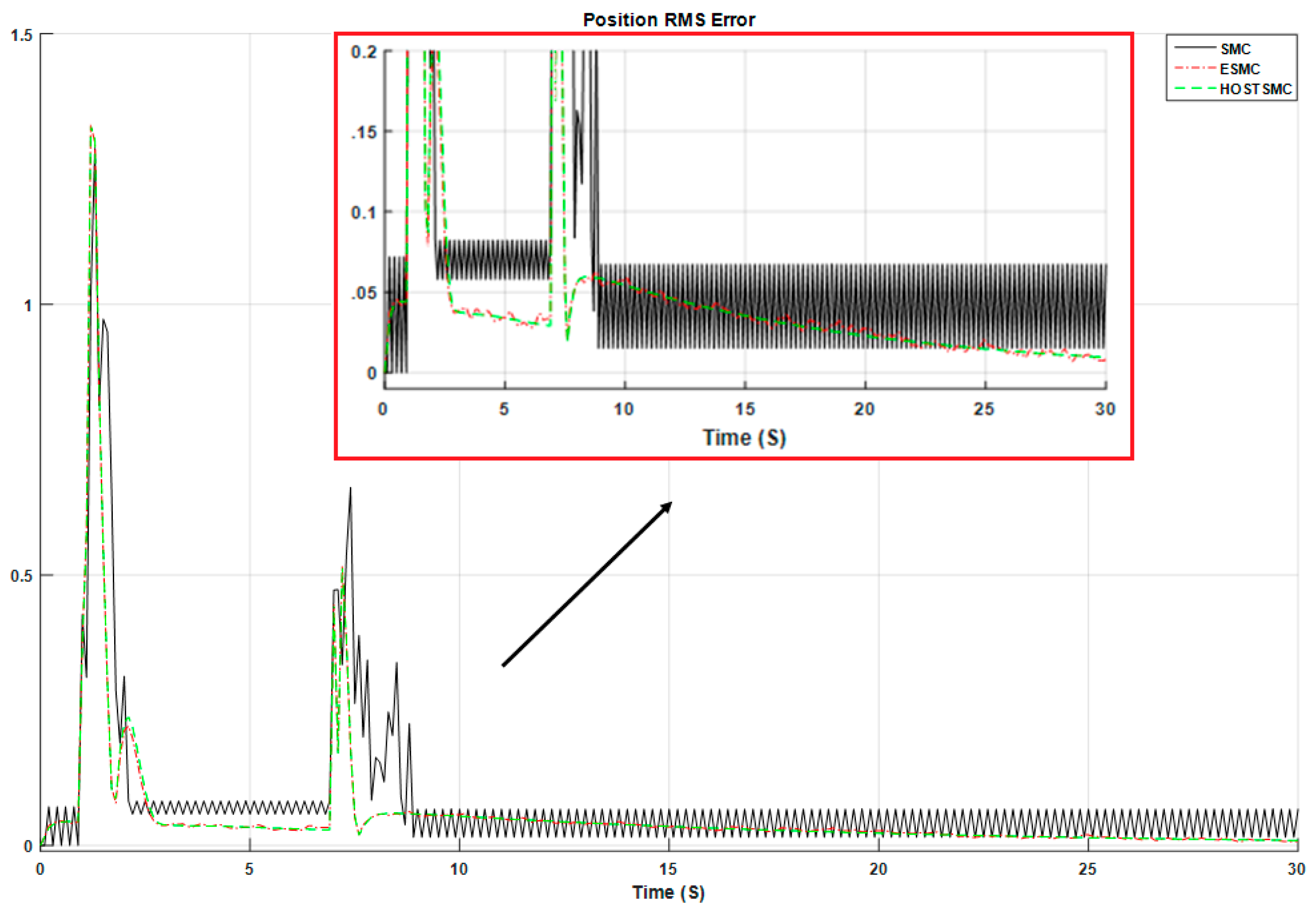
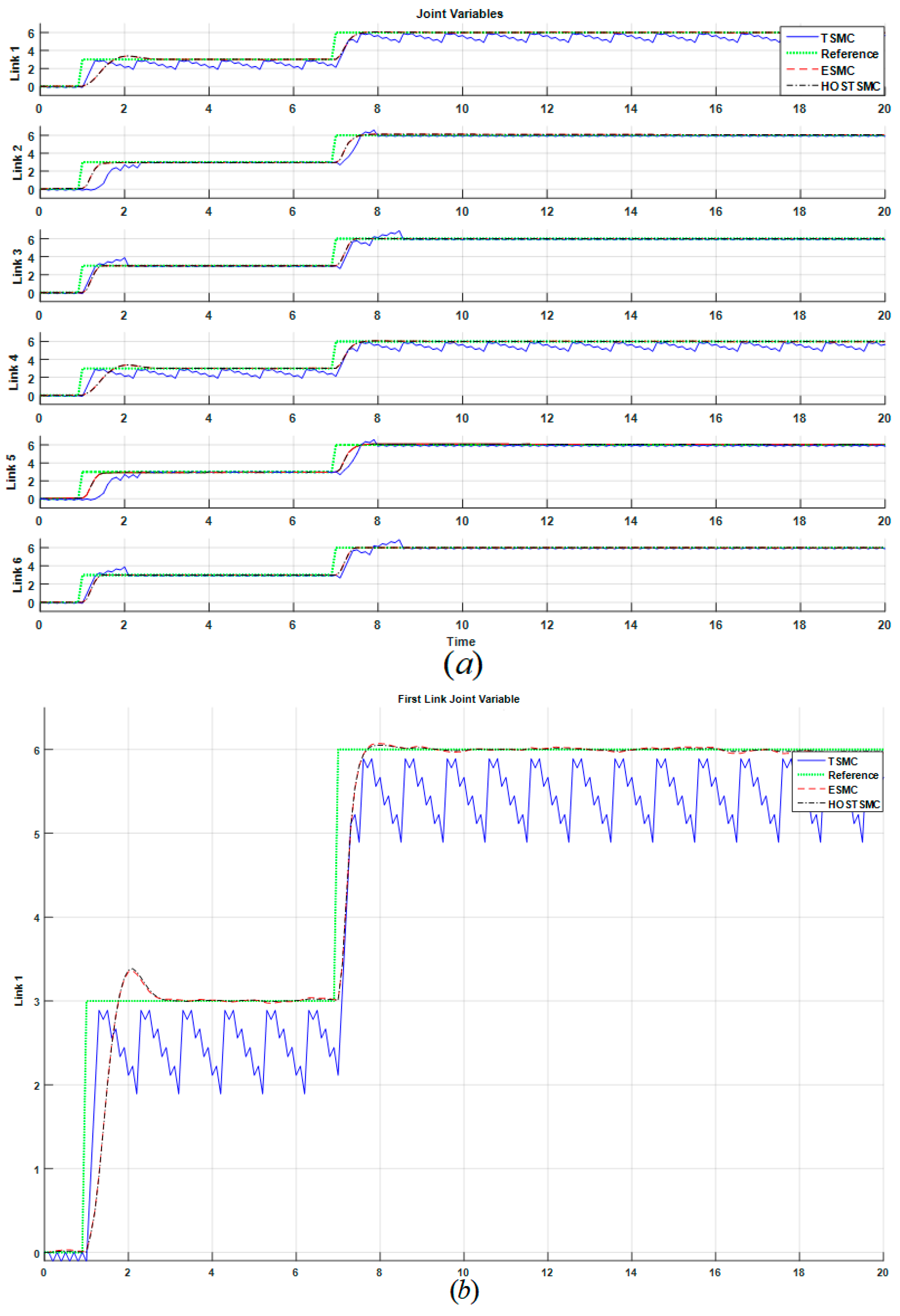
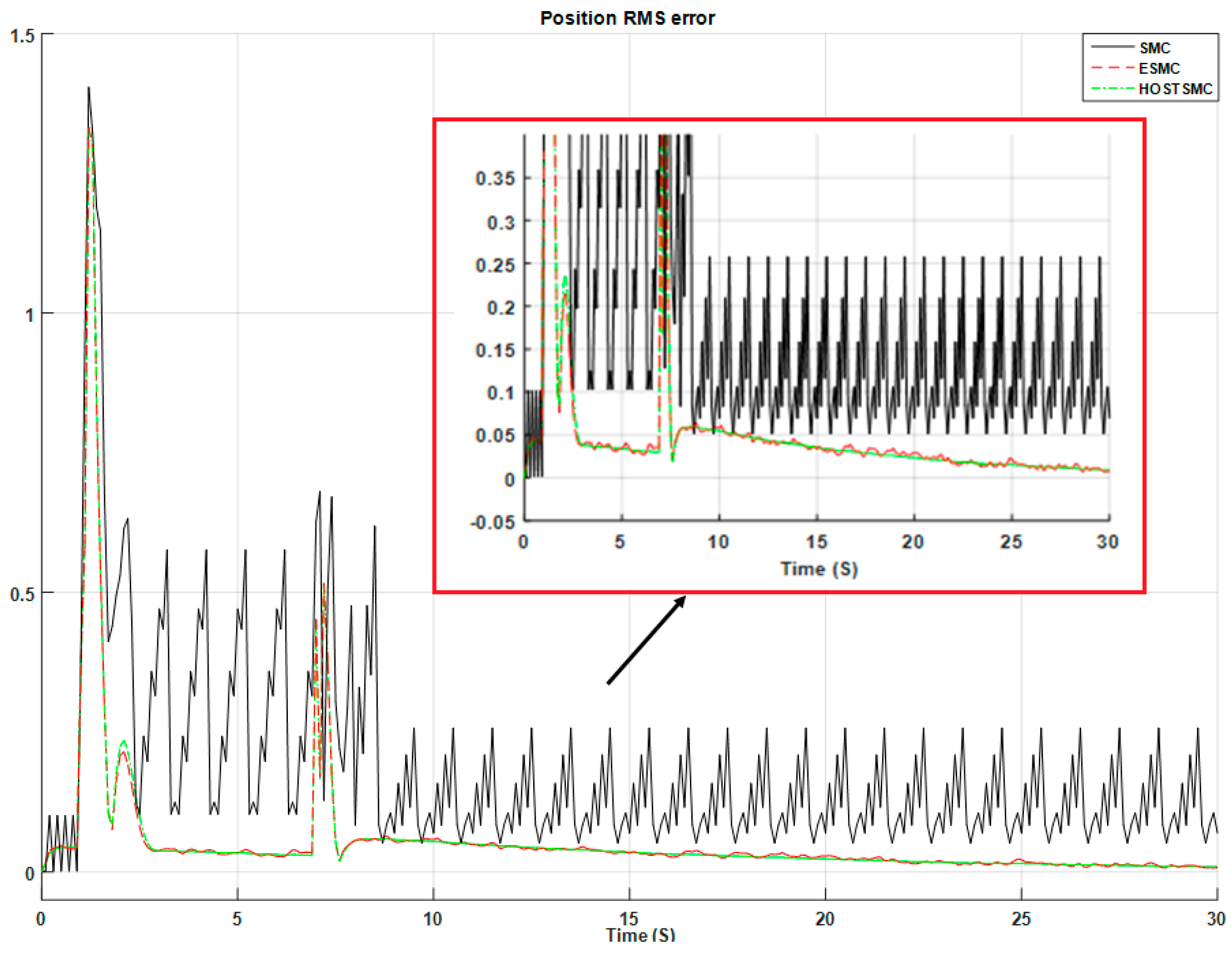
4. Results and Analysis
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Siciliano, B.; Khatib, O. (Eds.) Springer Handbook of Robotics; Springer: Berlin, Germany, 2016; pp. 67–90. [Google Scholar]
- Ngoc Son, N.; Anh, H.P.H.; Thanh Nam, N. Robot manipulator identification based on adaptive multiple-input and multiple-output neural model optimized by advanced differential evolution algorithm. Int. J. Adv. Robot. Syst. 2016, 14. [Google Scholar] [CrossRef]
- Spong, M.W.; Hutchinson, S.; Vidyasagar, M. Seth Hutchinson, and Mathukumalli Vidyasagar. In Robot Modeling and Control; Wiley: New York, NY, USA, 2006; Volume 3. [Google Scholar]
- Alonge, F.; Cirrincione, M.; Pucci, M.; Sferlazza, A. Input–output feedback linearization control with on-line MRAS-based inductor resistance estimation of linear induction motors including the dynamic end effects. IEEE Trans. Ind. Appl. 2016, 52, 254–266. [Google Scholar] [CrossRef]
- Lascu, C.; Jafarzadeh, S.; Fadali, M.S.; Blaabjerg, F. Direct torque control with feedback linearization for induction motor drives. IEEE Trans. Power Electron. 2017, 32, 2072–2080. [Google Scholar] [CrossRef]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electro-Mechanical Systems; CRC Press: Boca Raton, FL, USA, 2009; Volume 34. [Google Scholar]
- Li, H.; Wang, J.; Shi, P. Output-feedback based sliding mode control for fuzzy systems with actuator saturation. IEEE Trans. Fuzzy Syst. 2016, 24, 1282–1293. [Google Scholar] [CrossRef]
- Slotine, J.J.; Sastry, S. Tracking control of non-linear systems using sliding surfaces, with application to robot manipulators. Int. J. Control 1983, 38, 465–492. [Google Scholar] [CrossRef]
- Slotine, J.J.E. Sliding controller design for non-linear systems. Int. J. Control 1984, 40, 421–434. [Google Scholar] [CrossRef]
- Palm, R. Sliding mode fuzzy control. In Proceedings of the IEEE International conference on Fuzzy Systems, San Diego, CA, USA, 8–12 March 1992; pp. 519–526. [Google Scholar]
- Wu, B.; Dong, Y.; Wu, S.; Xu, D.; Zhao, K. An integral variable structure controller with fuzzy tuning design for electro-hydraulic driving Stewart platform. In Proceedings of the 1st International Symposium on Systems and Control in Aerospace and Astronautics, Harbin, China, 19–21 January 2006; pp. 940–945. [Google Scholar]
- Barrero, F.; Gonzalez, A.; Torralba, A.; Galvan, E.; Franquelo, L.G. Speed control of induction motors using a novel fuzzy sliding-mode structure. IEEE Trans. Fuzzy Syst. 2002, 10, 375–383. [Google Scholar] [CrossRef]
- Shahnazi, R.; Shanechi, H.M.; Pariz, N. Position control of induction and DC servomotors: A novel adaptive fuzzy PI sliding mode control. IEEE Trans. Energy Convers. 2008, 23, 138–147. [Google Scholar] [CrossRef]
- Rubio, J.D.J.; Soriano, E.; Juarez, C.F.; Pacheco, J. Sliding mode regulator for the perturbations attenuation in two tank plants. IEEE Access 2017, 5, 20504–20511. [Google Scholar] [CrossRef]
- Aguilar-Ibañez, C. Stabilization of the PVTOL aircraft based on a sliding mode and a saturation function. Int. J. Robust Nonlinear Control 2017, 27, 843–859. [Google Scholar] [CrossRef]
- De Jesús Rubio, J. Sliding mode control of robotic arms with dead-zone. IET Control Theory Appl. 2016, 11, 1214–1221. [Google Scholar] [CrossRef]
- Aguilar-Ibañez, C.; Sira-Ramirez, H.; Acosta, J.Á. Stability of active disturbance rejection control for uncertain systems: A Lyapunov perspective. Int. J. Robust Nonlinear Control 2017, 27, 4541–4553. [Google Scholar] [CrossRef]
- De Jesús Rubio, J. Hybrid controller with observer for the estimation and rejection of disturbances. ISA Trans. 2016, 65, 445–455. [Google Scholar] [CrossRef] [PubMed]
- De Wit, C.C.; Slotine, J.J. Sliding observers for robot manipulators. Automatica 1991, 27, 859–864. [Google Scholar] [CrossRef]
- Spurgeon, S.K. Sliding mode observers: A survey. Int. J. Syst. Sci. 2008, 39, 751–764. [Google Scholar] [CrossRef]
- Palm, R.; Driankov, D. Stability of fuzzy gain-schedulers: Sliding-mode based analysis. In Proceedings of the Sixth IEEE International Conference on Fuzzy Systems, Barcelona, Spain, 5 July 1997; Volume 1. [Google Scholar]
- Xu, J.X.; Pan, Y.J.; Lee, T.H. A gain scheduled sliding mode control scheme using filtering techniques with applications to multilink robotic manipulators. J. Dyn. Syst. Meas. Control 2000, 122, 641–649. [Google Scholar] [CrossRef]
- Piltan, F.; Sulaiman, N.A.S.I.R.I.; AsadiTalooki, I. AsadiTalooki. Evolutionary Design on-line Sliding Fuzzy Gain Scheduling Sliding Mode Algorithm: Applied to Internal Combustion Engine. Int. J. Eng. Sci. Technol. 2011, 3, 7301–7308. [Google Scholar]
- Li, F.; Wu, L.; Shi, P.; Lim, C.C. State estimation and sliding mode control for semi-Markovian jump systems with mismatched uncertainties. Automatica 2015, 51, 385–393. [Google Scholar] [CrossRef]
- Liu, J.; Vazquez, S.; Wu, L.; Marquez, A.; Gao, H.; Franquelo, L.G. Extended state observer-based sliding-mode control for three-phase power converters. IEEE Trans. Ind. Electron. 2017, 64, 22–31. [Google Scholar] [CrossRef]
- Oliveira, J.; Oliveira, P.M.; Boaventura-Cunha, J.; Pinho, T. Chaos-based grey wolf optimizer for higher order sliding mode position control of a robotic manipulator. Nonlinear Dyn. 2017, 90, 1353–1362. [Google Scholar] [CrossRef]
- Han, Y.; Liu, X. Continuous higher-order sliding mode control with time-varying gain for a class of uncertain nonlinear systems. ISA Trans. 2016, 62, 193–201. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Han, F.; Yu, X. Chattering free full-order sliding-mode control. Automatica 2014, 50, 1310–1314. [Google Scholar] [CrossRef]
- Ferrara, A.; Rubagotti, M. A sub-optimal second order sliding mode controller for systems with saturating actuators. IEEE Trans. Autom. Control 2009, 54, 1082–1087. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.J.; Shin, K.S. Backstepping quasi-continuous high-order sliding mode control for a Takagi–Sugeno fuzzy system with an application for a two-link robot control. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2014, 228, 1488–1500. [Google Scholar] [CrossRef]
- Bartolini, G.; Pisano, A.; Punta, E.; Usai, E. A survey of applications of second-order sliding mode control to mechanical systems. Int. J. Control 2003, 76, 875–892. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.J.; Suh, Y.S.; Shin, K.S. Output feedback tracking control of uncertain robot manipulators via higherorder sliding-mode observer and fuzzy compensator. J. Mech. Sci. Technol. 2013, 27, 2487–2496. [Google Scholar] [CrossRef]
- Cruz-Zavala, E.; Moreno, J.A.; Fridman, L. Uniform second-order sliding mode observer for mechanical systems. In Proceedings of the 2010 11th International Workshop on Variable Structure Systems (VSS), Mexico City, Mexico, 26–28 June 2010. [Google Scholar]
- Van, M.; Kang, H.J.; Suh, Y.S. A novel neural second-order sliding mode observer for robust fault diagnosis in robot manipulators. Int. J. Precis. Eng. Manuf. 2013, 14, 397–406. [Google Scholar] [CrossRef]
- Van, M.; Kang, H.J.; Suh, Y.S. A novel fuzzy second-order sliding mode observer-controller for a TS fuzzy system with an application for robot control. Int. J. Precis. Eng. Manuf. 2013, 14, 1703–1711. [Google Scholar] [CrossRef]
- Capisani, L.M.; Ferrara, A.; de Loza, A.F.; Fridman, L.M. Manipulator fault diagnosis via higher order sliding-mode observers. IEEE Trans. Ind. Electron. 2012, 59, 3979–3986. [Google Scholar] [CrossRef]
- Utkin, V.I. Sliding Modes in Control and Optimization; Springer: Berlin, Germany, 1992. [Google Scholar]
- Van, M.; Kang, H.J. Robust fault-tolerant control for uncertain robot manipulators based on adaptive quasi-continuous high-order sliding mode and neural network. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2015, 229, 1425–1446. [Google Scholar] [CrossRef]
- Lu, X. An Investigation of Adaptive Fuzzy Sliding Mode Control for Robotic Manipulators; Carleton University: Ottawa, ON, Canada, 2007. [Google Scholar]
- Fraguela, L.; Fridman, L.; Alexandrov, V.V. Position stabilization of a Stewart platform: High-order sliding mode Observers-based approach. J. Frankl. Inst. 2012, 349, 441–455. [Google Scholar] [CrossRef]
- Van, M.; Ge, S.S.; Ren, H. Finite time fault tolerant control for robot manipulators using time delay estimation and continuous nonsingular fast terminal sliding mode control. IEEE Trans. Cybern. 2017, 47, 1681–1693. [Google Scholar] [CrossRef] [PubMed]
- Shtessel, Y.; Edwards, C.; Fridman, L.; Levant, A. Sliding Mode Control and Observation; Birkhauser: New York, NY, USA, 2014; Volume 10. [Google Scholar]
- Van, M.; Kang, H.J.; Suh, Y.S. Second order sliding mode based output feedback tracking control for uncertain robot manipulators. Int. J. Adv. Robot. Syst. 2013, 10, 16. [Google Scholar] [CrossRef]
- Moreno, J.A.; Osorio, M. A Lyapunov approach to second-order sliding mode controllers and observers. In Proceedings of the 47th IEEE Conference on Decision and Control, Cancun, Mexico, 9–11 December 2008. [Google Scholar]
- Kamal, S.; Bandyopadhyay, B. Higher Order Sliding Mode Control: A Control Lyapunov Function Based Approach. WSEAS Trans. Syst. Control 2014, 9, 38–46. [Google Scholar]
- Piltan, F.; Emamzadeh, S.; Hivand, Z.; Shahriyari, F.; Mirazaei, M. PUMA-560 robot manipulator position sliding mode control methods using MATLAB/SIMULINK and their integration into graduate/undergraduate nonlinear control, robotics and MATLAB courses. Int. J. Robot. Autom. 2012, 3, 106–150. [Google Scholar]

| Conditions | Certain | Uncertain |
|---|---|---|
| SMC | 0.07653 | 0.09834 |
| ESMC | 0.04143 | 0.04915 |
| STSMC | 0.02912 | 0.02926 |
| Conditions | Certain | Uncertain |
|---|---|---|
| SMC | 0.05967 | 0.07340 |
| ESMC | 0.03901 | 0.04415 |
| STSMC | 0.02701 | 0.02734 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tayebi-Haghighi, S.; Piltan, F.; Kim, J.-M. Robust Composite High-Order Super-Twisting Sliding Mode Control of Robot Manipulators. Robotics 2018, 7, 13. https://doi.org/10.3390/robotics7010013
Tayebi-Haghighi S, Piltan F, Kim J-M. Robust Composite High-Order Super-Twisting Sliding Mode Control of Robot Manipulators. Robotics. 2018; 7(1):13. https://doi.org/10.3390/robotics7010013
Chicago/Turabian StyleTayebi-Haghighi, Shahnaz, Farzin Piltan, and Jong-Myon Kim. 2018. "Robust Composite High-Order Super-Twisting Sliding Mode Control of Robot Manipulators" Robotics 7, no. 1: 13. https://doi.org/10.3390/robotics7010013






