The Sensor Network Calculus as Key to the Design of Wireless Sensor Networks with Predictable Performance
Abstract
:1. Introduction
2. Background on Network Calculus
2.1. Modeling of Flows and Performance Characteristics
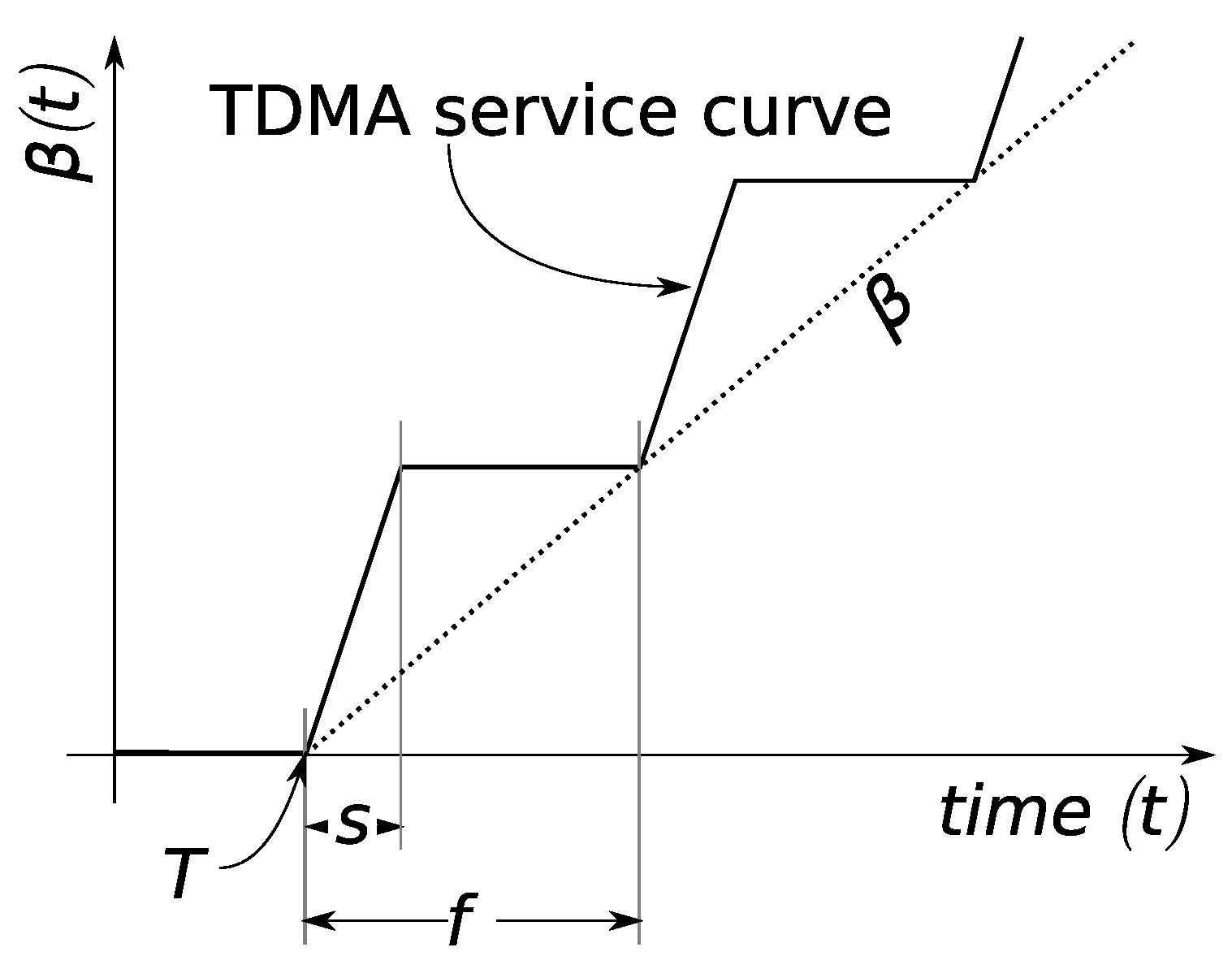
2.2. Network Calculus Performance Analysis
3. The Sensor Network Calculus
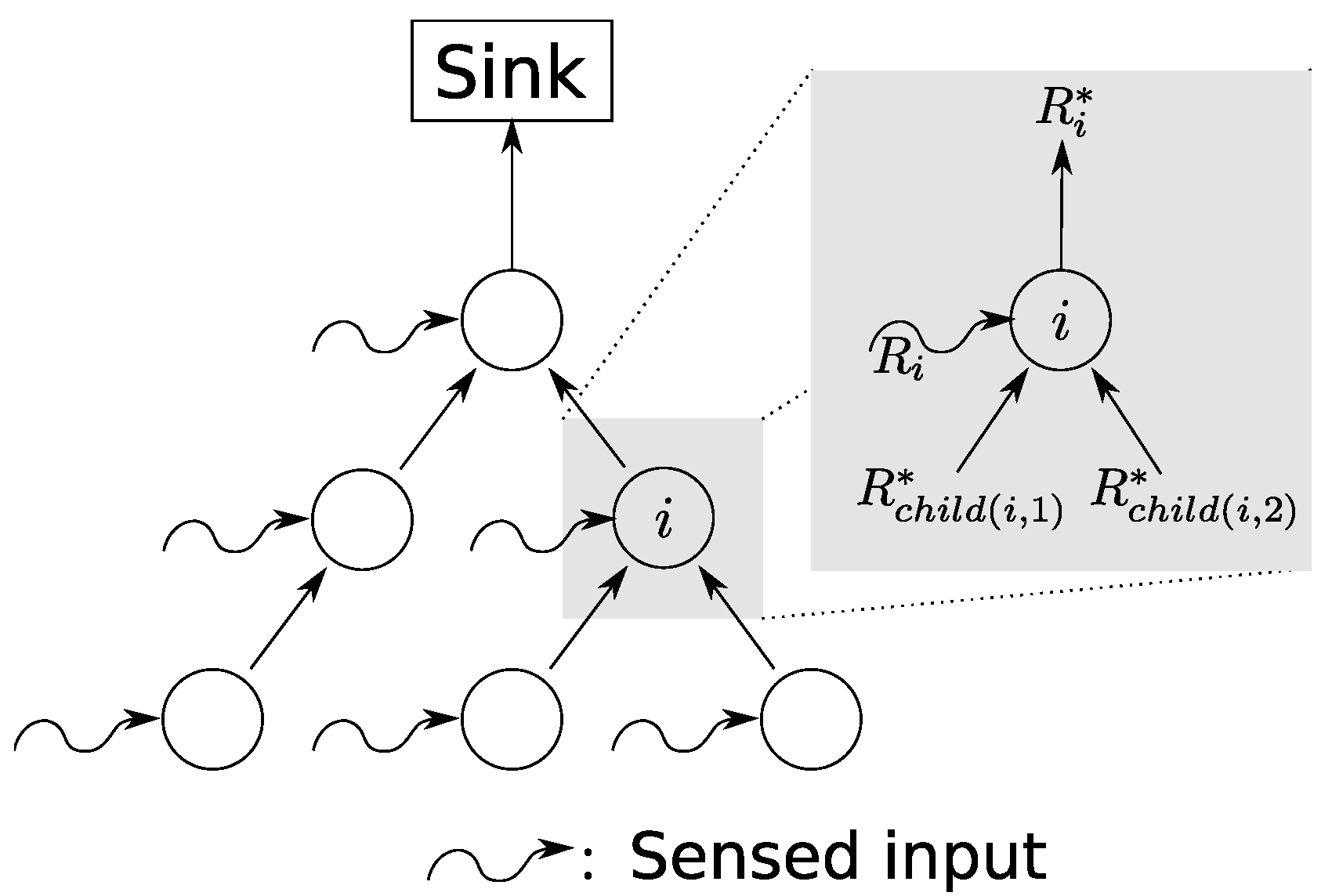
3.1. Sensor Network System Model
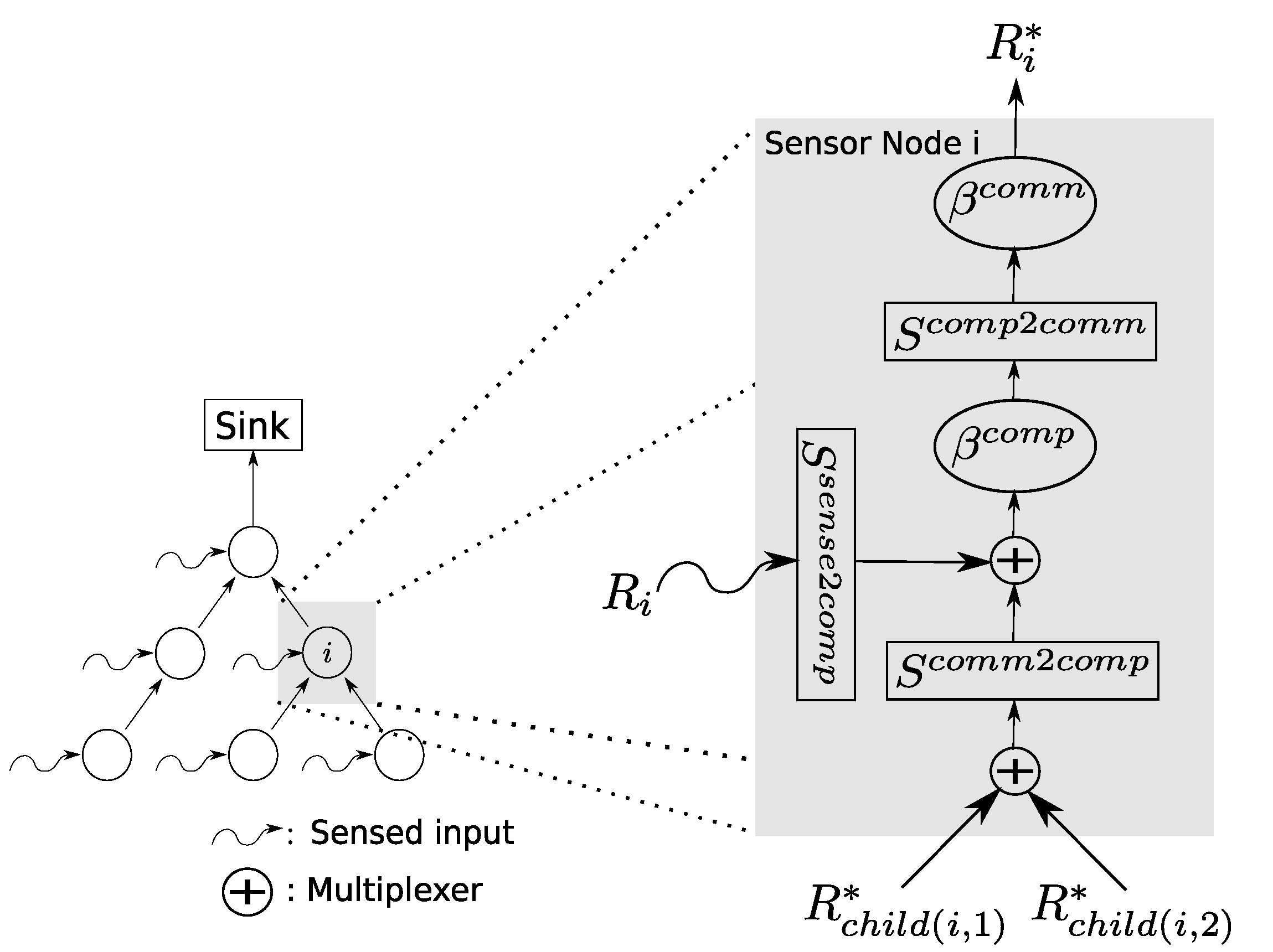
3.2. Incorporation of Network Calculus Components
3.3. Calculation of Network-Internal Traffic Flow
| Algorithm 1: Computation of network-internal traffic. |
|
3.4. Calculation of Performance Bounds
| Algorithm 2: Sink tree PMOO analysis. |
|
4. Advanced SensorNC: In-Network Processing
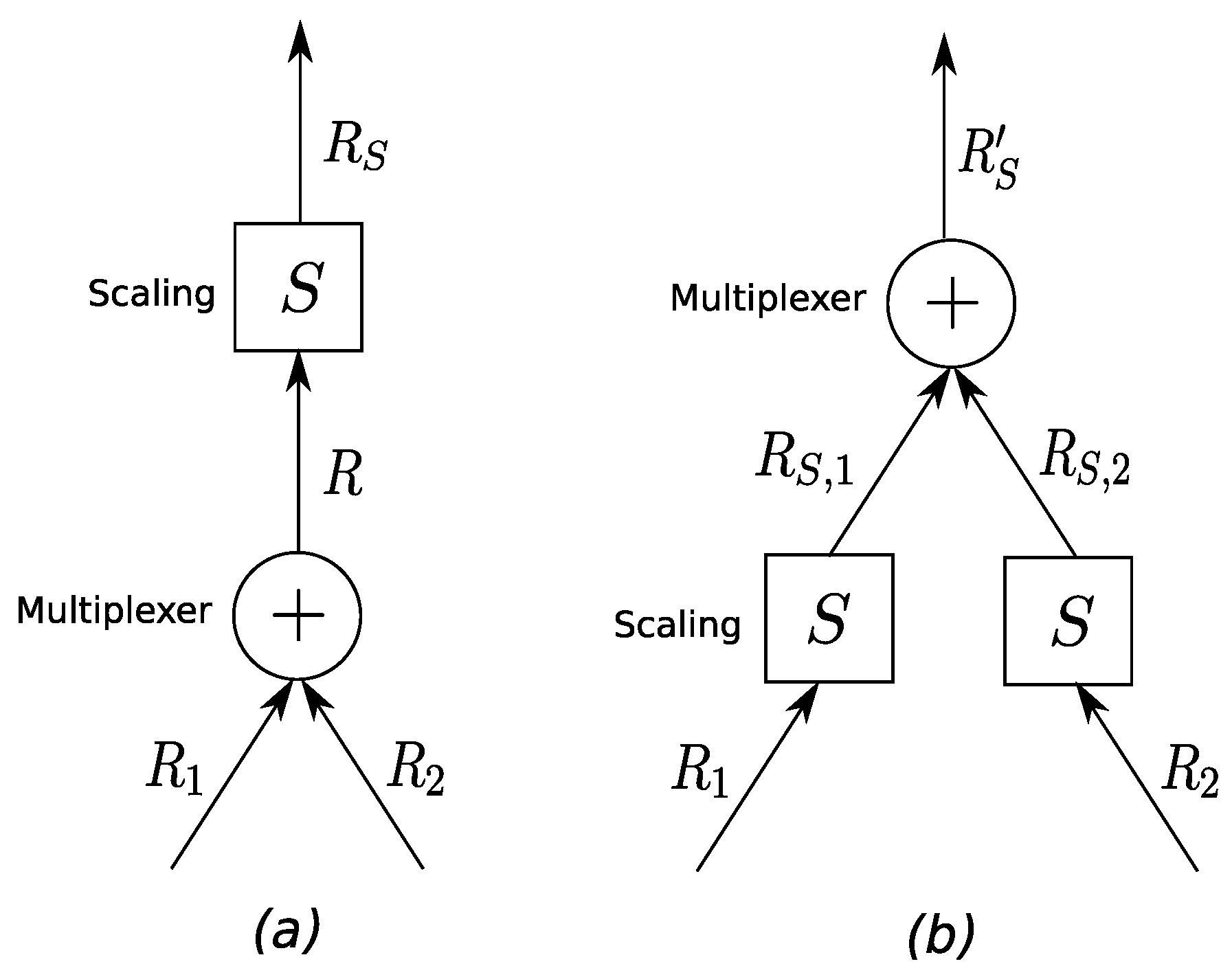
4.1. Background on Data Scaling in Network Calculus
4.2. Data Scaling in Sink Trees
4.3. Effect of Scaling Element Movement on Model Components
4.4. Numerical Experiment
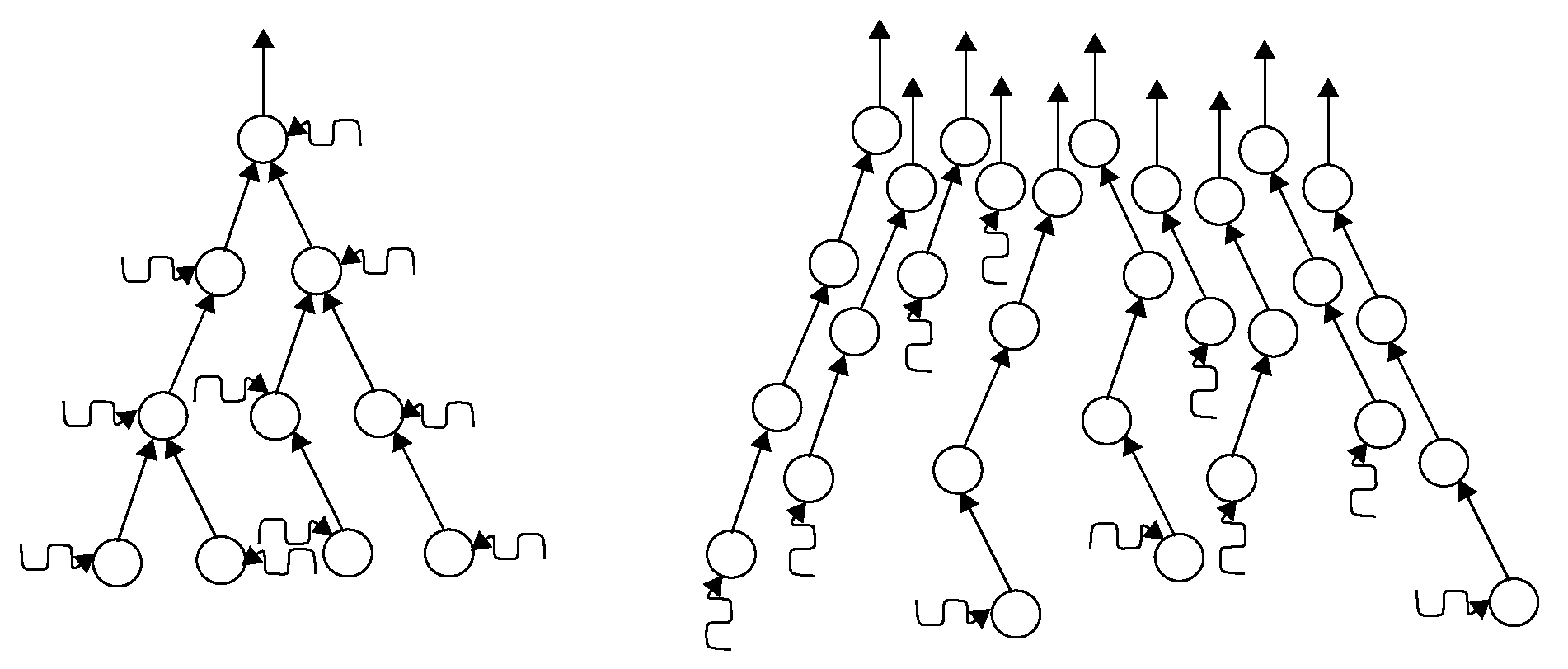
4.4.1. Experimental Design
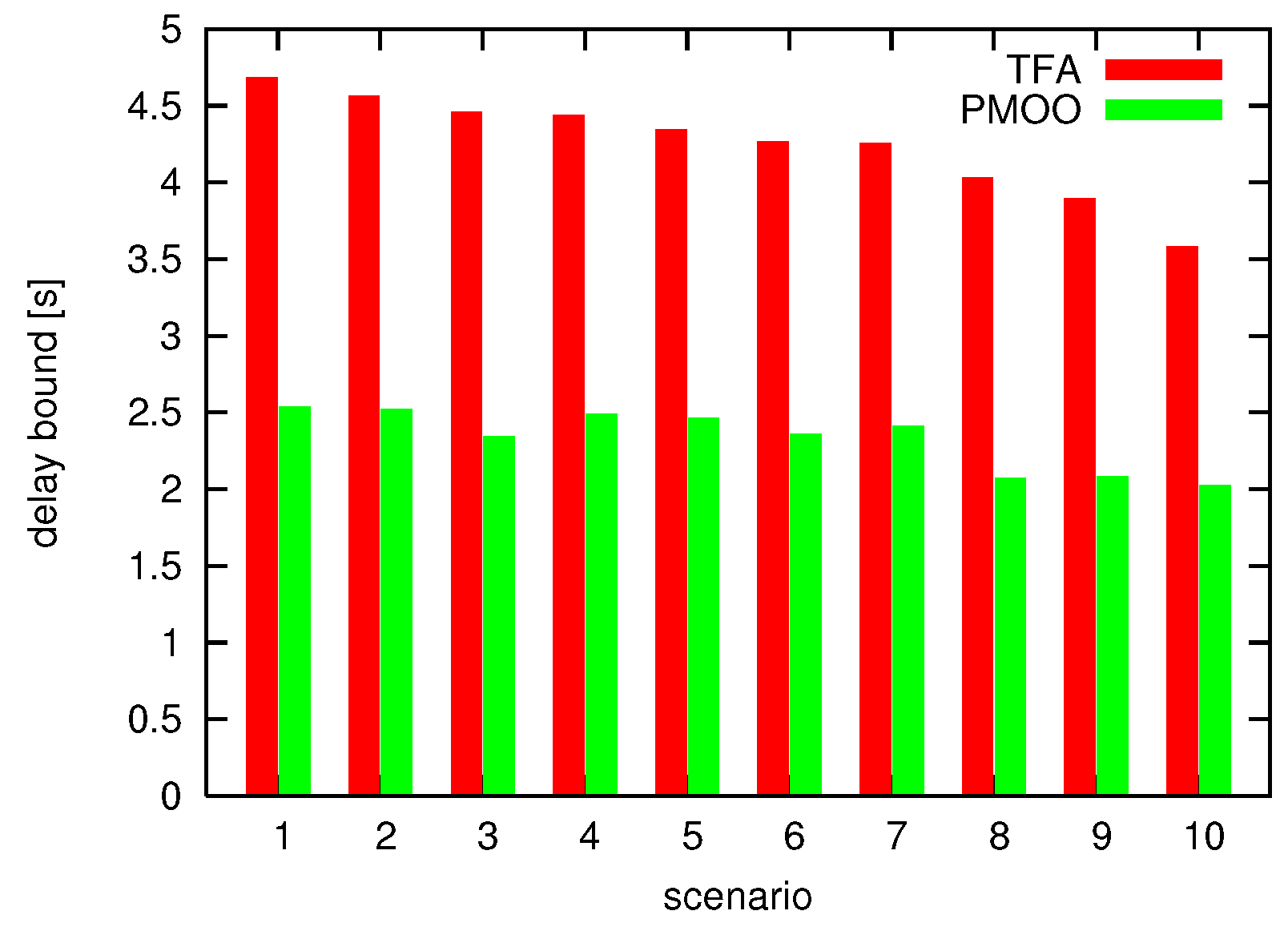
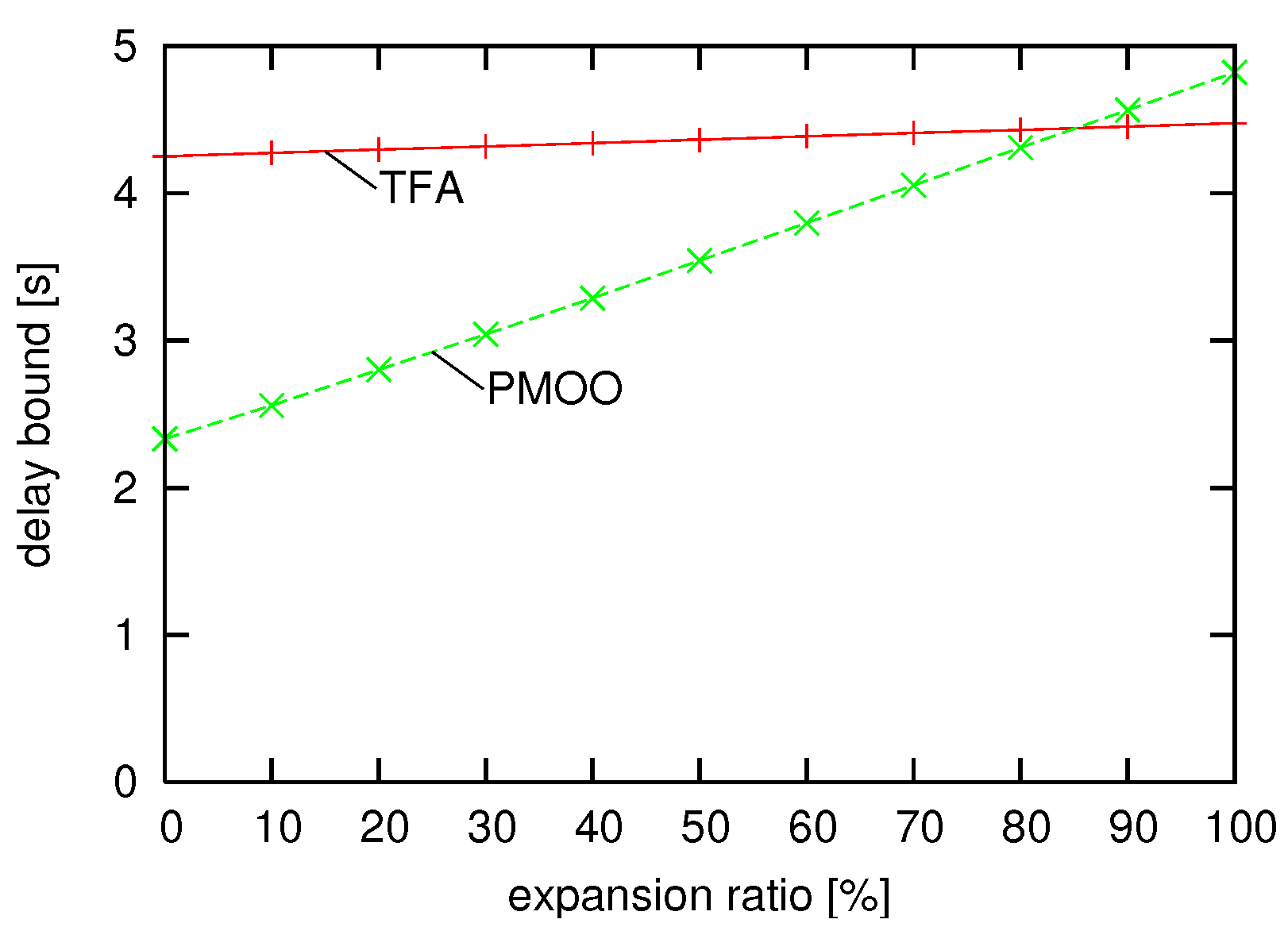
4.4.2. Benefit of End-To-End Analysis
5. Towards Self-Modeling Sensor Networks
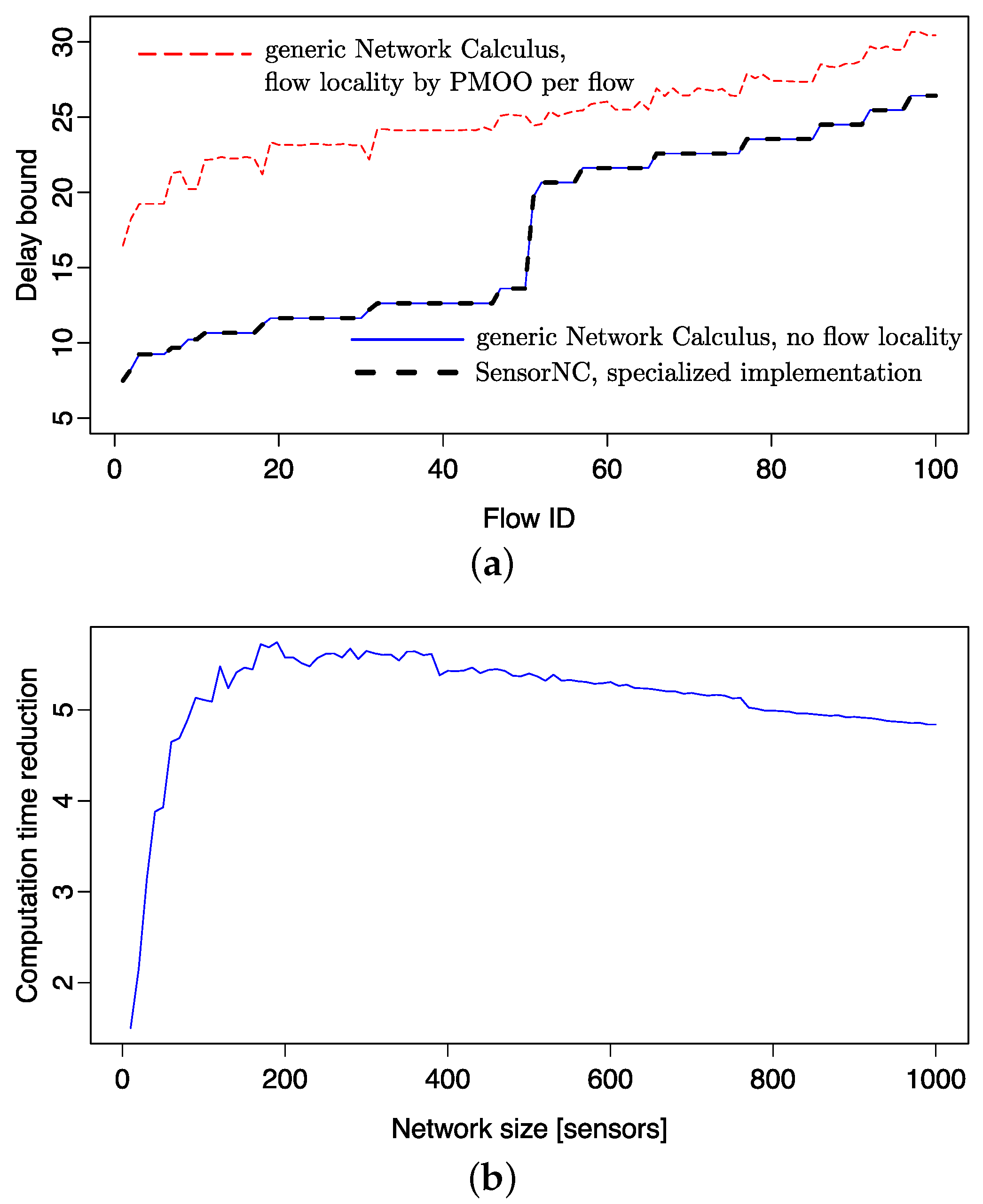
6. Tool Support
7. SensorNC Applications
7.1. Optimal Sink Placement
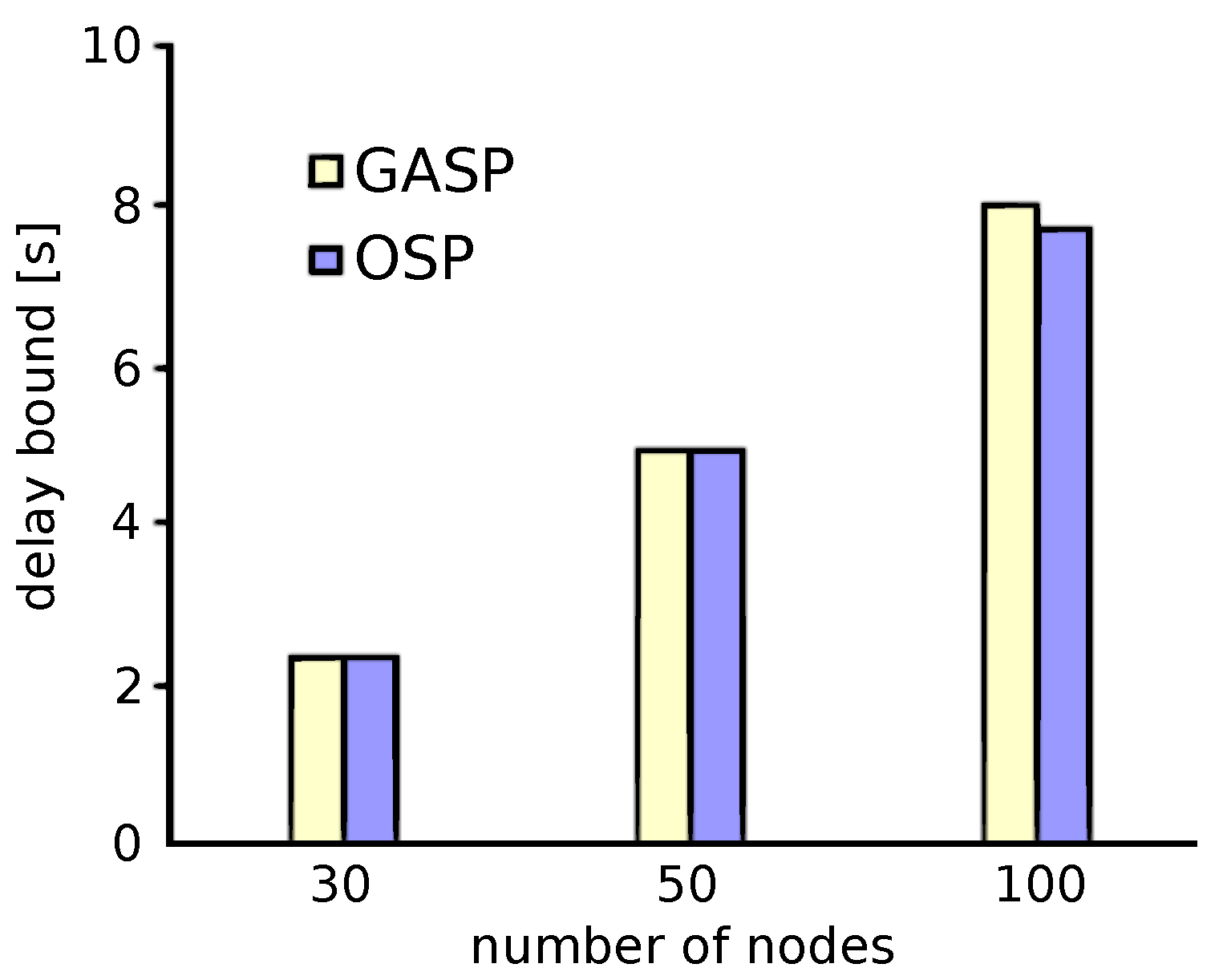
7.1.1. Small-Scale WSNs: Comparison between OSP and GASP
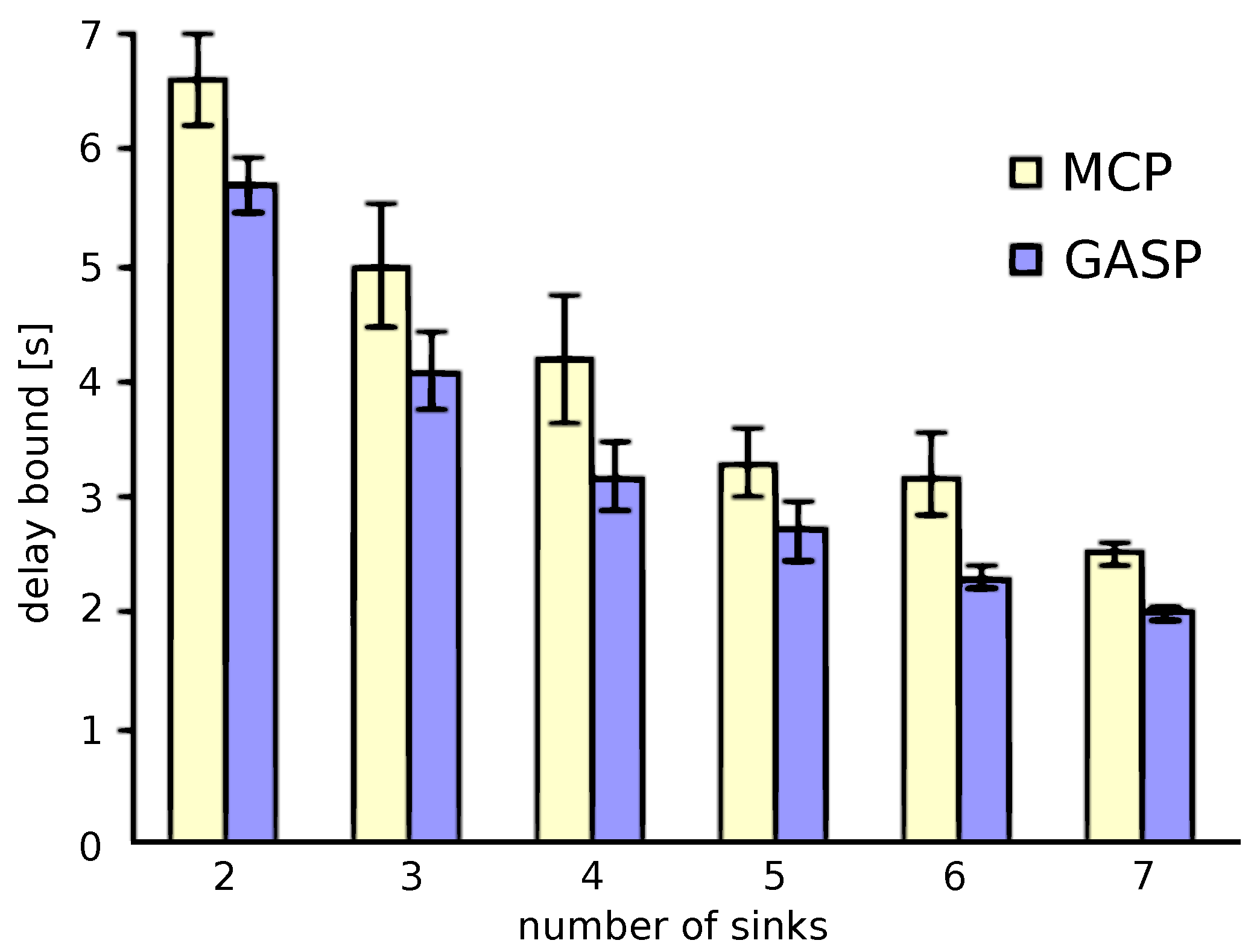
7.1.2. Large-Scale WSNs: Comparison between MCP and GASP
7.2. Node Placement Strategies
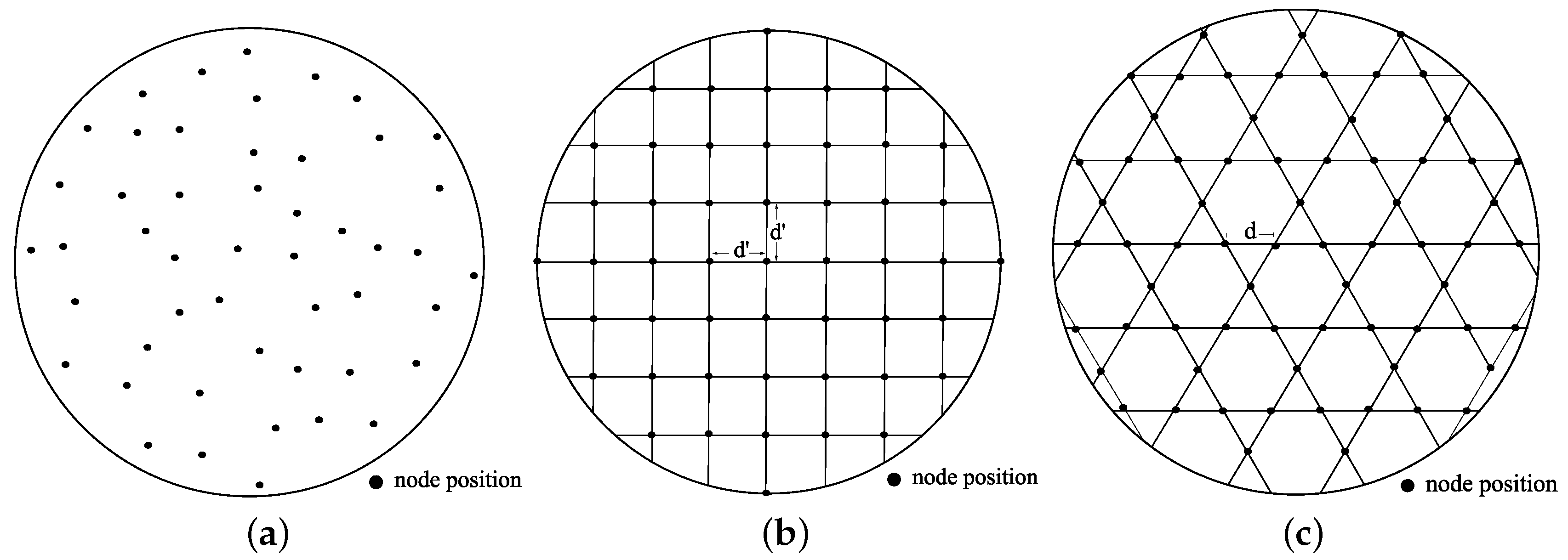
7.2.1. Node Placement Schemes
Uniform Random
Square Grid
Tri-Hexagon Tiling
7.2.2. Results
7.3. TDMA Optimization
7.3.1. General TDMA Design Problem
- Equal slot sizing (ESS): the assignment may be made such that inside a fixed time slot length, each node can transmit enough data to meet all requirements.
- Traffic-proportional slot sizing (TPSS): slots may be assigned such that each node only claims the resources necessary to fulfil its own duties, depending on the input bandwidth and forwarded data streams.
TDMA Design under Equal Slot Sizing
7.3.2. Analytical Solution in the Fluid Setting
Analytical Solution for ESS in General Sink Trees
7.4. Further Applications
8. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Song, H.; Rawat, D.B.; Jeschke, S.; Brecher, C. Cyber-Physical Systems: Foundations, Principles and Applications; Morgan Kaufmann: Burlington, MA, USA, 2016. [Google Scholar]
- Mao, X.; Miao, X.; He, Y.; Li, X.Y.; Liu, Y. CitySee: Urban CO2 monitoring with sensors. In Proceedings of the IEEE Conference on Computer Communications (INFOCOM), Orlando, FL, USA, 25–30 March 2012; pp. 1611–1619. [Google Scholar]
- Liu, Y.; Zhou, G.; Zhao, J.; Dai, G.; Li, X.Y.; Gu, M.; Ma, H.; Mo, L.; He, Y.; Wang, J.; et al. Long-term Large-scale Sensing in the Forest: Recent Advances and Future Directions of GreenOrbs. Front. Comput. Sci. China 2010, 4, 334–338. [Google Scholar] [CrossRef]
- Schmitt, J.B.; Roedig, U. Sensor Network Calculus—A Framework for Worst Case Analysis. In Proceedings of the First IEEE International Conference on Distributed Computing in Sensor Systems (DCOSS’05), Marina del Rey, CA, USA, 30 June–1 July 2005; pp. 141–154. [Google Scholar]
- Chang, C.S. Performance Guarantees in Communication Networks; Springer: London, UK, 2000. [Google Scholar]
- Le Boudec, J.Y.; Thiran, P. Network Calculus: A Theory of Deterministic Queuing Systems for the Internet; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Baccelli, F.; Cohen, G.; Olsder, G.J.; Quadrat, J.P. Synchronization and Linearity: An Algebra for Discrete Event Systems; John Wiley & Sons Ltd.: Hoboken, NJ, USA, 1992. [Google Scholar]
- Gollan, N.; Schmitt, J.B. Energy-Efficient TDMA Design Under Real-Time Constraints in Wireless Sensor Networks. In Proceedings of the 15th International Symposium on Modeling, Analysis, and Simulation of Computer and Telecommunication Systems, 2007 (MASCOTS ’07), Istanbul, Turkey, 24–26 October 2007; pp. 80–87. [Google Scholar]
- Bondorf, S.; Schmitt, J.B. Statistical response time bounds in randomly deployed wireless sensor networks. In Proceedings of the 35th IEEE Local Computer Network Conference (LCN), Denver, CO, USA, 10–14 October 2010; pp. 340–343. [Google Scholar]
- Cattelan, B.; Bondorf, S. Iterative Design Space Exploration for Networks Requiring Performance Guarantees. In Proceedings of the 36th IEEE/AIAA Digital Avionics Systems Conference (DASC 2017), St. Petersburg, FL, USA, 16–21 September 2017. [Google Scholar]
- Koubâa, A.; Alves, M.; Tovar, E. Modeling and Worst-Case Dimensioning of Cluster-Tree Wireless Sensor Networks. In Proceedings of the 27th IEEE International Real-Time Systems Symposium, 2006 (RTSS ’06), Rio de Janeiro, Brazil, 5–8 December 2006; pp. 412–421. [Google Scholar]
- Bouillard, A.; Thierry, É. An Algorithmic Toolbox for Network Calculus. Discret. Event Dyn. Syst. 2008, 18, 3–49. [Google Scholar] [CrossRef]
- Lampka, K.; Bondorf, S.; Schmitt, J.B.; Guan, N.; Yi, W. Generalized Finitary Real-Time Calculus. In Proceedings of the 36th IEEE International Conference on Computer Communications (INFOCOM 2017), Atlanta, GA, USA, 1–4 May 2017. [Google Scholar]
- Schmitt, J.B.; Zdarsky, F.A.; Martinovic, I. Improving Performance Bounds in Feed-Forward Networks by Paying Multiplexing Only Once. In Proceedings of the GI/ITG International Conference on Measurement, Modelling and Evaluation of Computer and Communication Systems (MMB), Dortmund, Germany, 31 March–2 April 2008; pp. 1–15. [Google Scholar]
- Schmitt, J.; Zdarsky, F.A.; Fidler, M. Delay Bounds under Arbitrary Multiplexing: When Network Calculus Leaves You in the Lurch. In Proceedings of the 27th IEEE International Conference on Computer Communications (INFOCOM 2008), Phoenix, AZ, USA, 13–18 April 2008. [Google Scholar]
- Wandeler, E.; Maxiaguine, A.; Thiele, L. Quantitative Characterization of Event Streams in Analysis of Hard Real-Time Applications. In Proceedings of the 10th IEEE Real-Time and Embedded Technology and Applications Symposium (RTAS 2004), Toronto, ON, Canada, 25–28 May 2004; pp. 450–461. [Google Scholar]
- Fidler, M.; Schmitt, J. On the Way to a Distributed Systems Calculus: An End-to-End Network Calculus with Data Scaling. In Proceedings of the Joint International Conference on Measurement and Modeling of Computer Systems, SIGMETRICS/Performance 2006, Saint Malo, France, 26–30 June 2006; pp. 287–298. [Google Scholar]
- Schmitt, J.B.; Zdarsky, F.A.; Thiele, L. A Comprehensive Worst-Case Calculus for Wireless Sensor Networks with In-Network Processing. In Proceedings of the 28th IEEE International Real-Time Systems Symposium (RTSS 2007), Tucson, AZ, USA, 3–6 December 2007; pp. 193–202. [Google Scholar]
- Crossbow Technology Inc. Mote Processor Radio (MPR) Platforms and Mote Interface Boards (MIB), Review B; Crossbow Technology Inc.: San Jose, CA, USA, 2006. [Google Scholar]
- Schmitt, J.B.; Zdarsky, F.A. The DISCO Network Calculator—A Toolbox for Worst Case Analysis. In Proceedings of the 1st International Conference on Performance Evaluation Methodolgies and Tools (ValueTools ’06), Pisa, Italy, 11–13 October 2006. [Google Scholar]
- Bondorf, S.; Schmitt, J.B. The DiscoDNC v2—A Comprehensive Tool for Deterministic Network Calculus. In Proceedings of the 8th International Conference on Performance Evaluation Methodologies and Tools (ValueTools), Bratislava, Slovakia, 9–11 December 2014. [Google Scholar]
- Bondorf, S.; Schmitt, J.B. Boosting sensor network calculus by thoroughly bounding cross-traffic. In Proceedings of the IEEE Conference on Computer Communications (INFOCOM), Hong Kong, China, 26 April–1 May 2015; pp. 235–243. [Google Scholar]
- Hui, J.W.; Culler, D. The Dynamic Behavior of a Data Dissemination Protocol for Network Programming at Scale. In Proceedings of the 2nd International Conference on Embedded Networked Sensor Systems (SenSys ’04), Baltimore, MD, USA, 3–5 November 2004; pp. 81–94. [Google Scholar]
- Schon, P.; Bondorf, S. Towards Unified Tool Support for Real-time Calculus & Deterministic Network Calculus. In Proceedings of the 29th Euromicro Conference on Real-Time Systems (ECRTS 2017), Dubrovnik, Croatia, 28–30 June 2017. [Google Scholar]
- Bondorf, S.; Nikolaus, P.; Schmitt, J.B. Quality and Cost of Deterministic Network Calculus—Design and Evaluation of an Accurate and Fast Analysis. In Proceedings of the ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Systems (SIGMETRICS 2017), Urbana-Champaign, IL, USA, 5–9 June 2017. [Google Scholar]
- Bondorf, S. Better Bounds by Worse Assumptions—Improving Network Calculus Accuracy by Adding Pessimism to the Network Model. In Proceedings of the IEEE International Conference on Communications (ICC 2017), Paris, France, 21–25 May 2017. [Google Scholar]
- Bondorf, S.; Schmitt, J.B. Calculating Accurate End-to-End Delay Bounds—You Better Know Your Cross-Traffic. In Proceedings of the 9th International Conference on Performance Evaluation Methodologies and Tools (ValueTools), Berlin, Germany, 14–16 December 2015; pp. 17–24. [Google Scholar]
- Bondorf, S.; Schmitt, J.B. Improving Cross-Traffic Bounds in Feed-Forward Networks—There is a Job for Everyone. In Proceedings of the GI/ITG International Conference on Measurement, Modelling and Evaluation of Dependable Computer and Communication Systems (MMB & DFT), Münster, Germany, 4–6 April 2016. [Google Scholar]
- Poe, W.Y.; Schmitt, J. Minimizing the Maximum Delay in Wireless Sensor Networks by Intelligent Sink Placement; Technical Report 362/07; University of Kaiserslautern: Kaiserslautern, Germany, 2007. [Google Scholar]
- Poe, W.Y.; Schmitt, J. Placing Multiple Sinks in Time-Sensitive Wireless Sensor Networks Using a Genetic Algorithm. In Proceedings of the 14th GI/ITG Conference on Measurement, Modeling, and Evaluation of Computer and Communication Systems (MMB 2008), Dortmund, Germany, 31 March–2 April 2008. [Google Scholar]
- Poe, W.Y.; Schmitt, J. Node Deployment in Large Wireless Sensor Networks:Coverage, Energy Consumption, and Worst-Case Delay. In Proceedings of the 5th ACM SIGCOMM Asian Internet Engineering Conference (AINTEC), Bangkok, Thailand, 18–20 November 2009. [Google Scholar]
- Jurcik, P.; Koubâa, A.; Severino, R.; Alves, M.; Tovar, E. Dimensioning and Worst-Case Analysis of Cluster-Tree Sensor Networks. ACM Trans. Sens. Netw. 2010, 7, 1–47. [Google Scholar] [CrossRef]
- Schmitt, J.B.; Roedig, U. Worst Case Dimensioning of Wireless Sensor Networks under Uncertain Topologies. In Proceedings of the Workshop on Resource Allocation in Wireless Networks at IEEE WiOpt, Trento, Italy, April 2005. [Google Scholar]
- Schmitt, J.B.; Zdarsky, F.A.; Roedig, U. Sensor Network Calculus with Multiple Sinks. In Proceedings of the Performance Control in Wireless Sensor Networks Workshop at the IFIP Networking, Coimbra, Portugal, 15–19 May 2006; pp. 6–13. [Google Scholar]
- She, H.; Lu, Z.; Jantsch, A.; Zhou, D.; Zheng, L.R. Performance Analysis of Flow-Based Traffic Splitting Strategy on Cluster-Mesh Sensor Networks. Int. J. Distrib. Sens. Netw. 2012. [Google Scholar] [CrossRef] [PubMed]
- Suriyachai, P.; Roedig, U.; Scott, A.C.; Gollan, N.; Schmitt, J.B. Dimensioning of Time-Critical WSNs—Theory, Implementation and Evaluation. JCM 2011, 6, 360–369. [Google Scholar] [CrossRef]
- Cao, Y.; Xue, Y.; Cui, Y. Network-Calculus-Based Analysis of Power Management in Video Sensor Networks. In Proceedings of the Global Communications Conference, 2007 (GLOBECOM ’07), Washington, DC, USA, 26–30 November 2007; pp. 981–985. [Google Scholar]
- Safa, H.; El-Hajj, W.; Zoubian, H. A Robust Topology Control Solution for the Sink Placement Problem in WSNs. J. Netw. Comput. Appl. 2014, 39, 70–82. [Google Scholar] [CrossRef]
- Jurcík, P.; Severino, R.; Koubâa, A.; Alves, M.; Tovar, E. Real-Time Communications Over Cluster-Tree Sensor Networks with Mobile Sink Behaviour. In Proceedings of the 2008 14th IEEE International Conference on Embedded and Real-Time Computing Systems and Applications, Kaohsiung, Taiwan, 25–27 August 2008; pp. 401–412. [Google Scholar]
- Poe, W.Y.; Beck, M.A.; Schmitt, J. Planning the Trajectories of Multiple Mobile Sinks in Large-Scale, Time-Sensitive WSNs. In Proceedings of the 7th IEEE International Conference on Distributed Computing in Sensor Systems (DCOSS 2011), Barcelona, Spain, 27–29 June 2011. [Google Scholar]
- Poe, W.Y.; Beck, M.A.; Schmitt, J.B. Achieving High Lifetime and Low Delay in Very Large Sensor Networks using Mobile Sinks. In Proceedings of the 8th IEEE International Conference on Distributed Computing in Sensor Systems (DCOSS), Hangzhou, China, 16–18 May 2012; pp. 17–24. [Google Scholar]
- Jiang, L.; Yu, L.; Chen, Z. Network calculus based QoS analysis of network coding in Cluster-tree wireless sensor network. In Proceedings of the 2012 Computing, Communications and Applications Conference, Hong Kong, China, 11–13 January 2012; pp. 1–6. [Google Scholar]
- Jin, X.; Guan, N.; Wang, J.; Zeng, P. Analyzing Multimode Wireless Sensor Networks Using the Network Calculus. J. Sens. 2015, 2015, 851608. [Google Scholar] [CrossRef]
- Shang, Z.J.; Cui, S.J.; Wang, Q.S. Network Calculus Based Dimensioning for Industrial Wireless Mesh Networks. Appl. Mech. Mater. 2013, 303–306, 1989–1995. [Google Scholar] [CrossRef]
- Roedig, U.; Gollan, N.; Schmitt, J.B. Validating the Sensor Network Calculus by Simulations. In Proceedings of the Performance Control in Wireless Sensor Networks Workshop (WICON ’07), Austin, TX, USA, 22–24 October 2007. [Google Scholar]
- Ciucu, F.; Schmitt, J. Perspectives on Network Calculus—No Free Lunch, But Still Good Value. In Proceedings of the ACM SIGCOMM 2012 Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications (SIGCOMM ’12), Helsinki, Finland, 13–17 August 2012; ACM: New York, NY, USA, 2012; pp. 311–322. [Google Scholar]
- Schiessl, S.; Naghibi, F.; Al-Zubaidy, H.; Fidler, M.; Gross, J. On the delay performance of interference channels. In Proceedings of the 2016 IFIP Networking Conference, Networking 2016 and Workshops, Vienna, Austria, 17–19 May 2016; pp. 216–224. [Google Scholar]
- Wang, H.; Schmitt, J.; Ciucu, F. Performance Modelling and Analysis of Unreliable Links with Retransmissions using Network Calculus. In Proceedings of the 25th International Teletraffic Congress (ITC 25), Shanghai, China, 10–12 September 2013. [Google Scholar]
- Beck, M.A.; Schmitt, J.B. Window Flow Control in Stochastic Network Calculus—The General Service Case. In Proceedings of the 9th International Conference on Performance Evaluation Methodologies and Tools (Valuetools), Berlin, Germany, 14–16 December 2015; pp. 25–32. [Google Scholar]
- Beck, M.A.; Schmitt, J.B. Generalizing Window Flow Control in Bivariate Network Calculus to Enable Leftover Service in the Loop. Perform. Eval. 2016, 114, 45–55. [Google Scholar] [CrossRef]
- Shekaramiz, A.; Liebeherr, J.; Burchard, A. Network Calculus Analysis of a Feedback System with Random Service. In Proceedings of the 2016 ACM SIGMETRICS International Conference on Measurement and Modeling of Computer Science, Antibes Juan-Les-Pins, France, 14–18 June 2016; pp. 393–394. [Google Scholar]
- Mouradian, A.; Blum, I.A. Formal Verification of Real-Time Wireless Sensor Networks Protocols: Scaling Up. In Proceedings of the 26th Euromicro Conference on Real-Time Systems, Madrid, Spain, 8–11 July 2014; pp. 41–50. [Google Scholar]



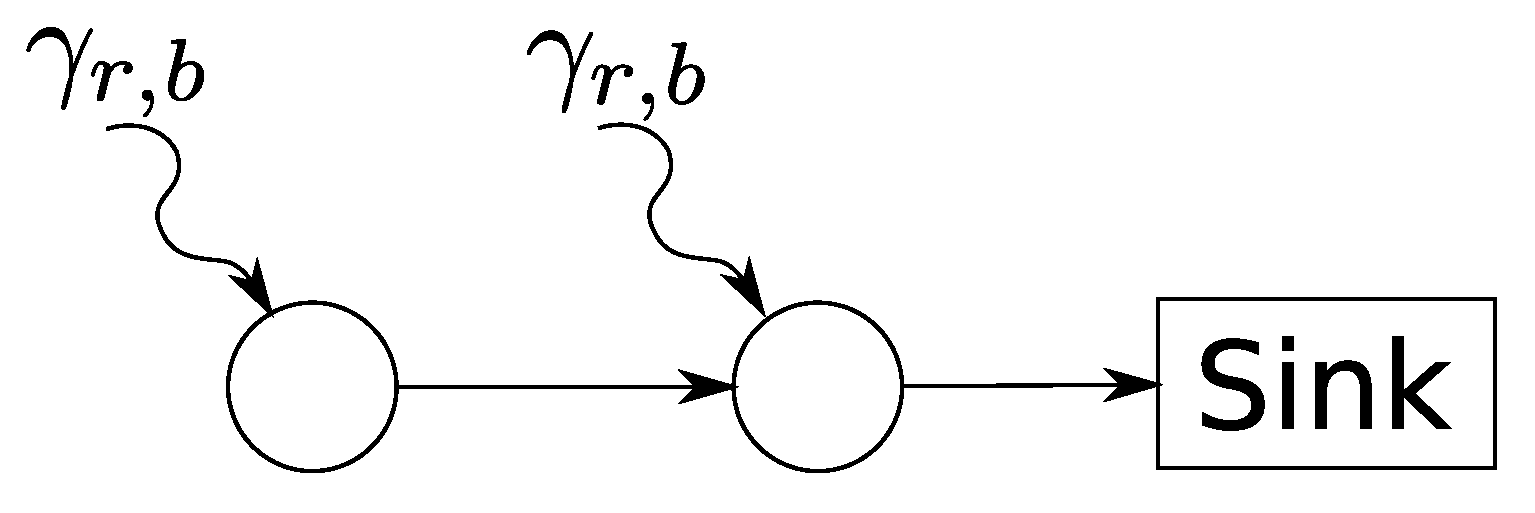


| Quantifier | Definition |
|---|---|
| Non-negative, wide-sense increasing functions passing through the origin | |
| Token-bucket functions with bucket size b and rate r | |
| Rate-latency functions with rate R and latency T | |
| Input function of the flow originating at node i | |
| Aggregate input function for all flows at node i | |
| Aggregate output function for all flows at at node i | |
| , | Arrival curve, arrival curve of flow f |
| Arrival curve of the flow originating at node i | |
| Aggregate arrival curve for all flows at node i | |
| Aggregate output arrival curve for all flows at node i | |
| , | Service curve, service curve of node i |
| , | Left-over service curve, left-over service curve of node i |
| Service curve concatenation with min-plus convolution ⊗ | |
| Output bound computation with (adapted) min-plus deconvolution ⊘ | |
| Left-over service curve computation with non-decreasing subtraction | |
| , | Delay at time t and the time-invariant delay bound at node i |
| , | Backlog at time t and the time-invariant backlog bound at node i |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schmitt, J.; Bondorf, S.; Poe, W.Y. The Sensor Network Calculus as Key to the Design of Wireless Sensor Networks with Predictable Performance. J. Sens. Actuator Netw. 2017, 6, 21. https://doi.org/10.3390/jsan6030021
Schmitt J, Bondorf S, Poe WY. The Sensor Network Calculus as Key to the Design of Wireless Sensor Networks with Predictable Performance. Journal of Sensor and Actuator Networks. 2017; 6(3):21. https://doi.org/10.3390/jsan6030021
Chicago/Turabian StyleSchmitt, Jens, Steffen Bondorf, and Wint Yi Poe. 2017. "The Sensor Network Calculus as Key to the Design of Wireless Sensor Networks with Predictable Performance" Journal of Sensor and Actuator Networks 6, no. 3: 21. https://doi.org/10.3390/jsan6030021




