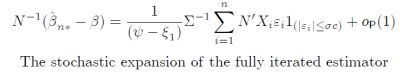Outlier Detection in Regression Using an Iterated One-Step Approximation to the Huber-Skip Estimator

Abstract

In regression we can delete outliers based upon a preliminary estimator and re-estimate the parameters by least squares based upon the retained observations. We study the properties of an iteratively defined sequence of estimators based on this idea. We relate the sequence to the Huber-skip estimator. We provide a stochastic recursion equation for the estimation error in terms of a kernel, the previous estimation error and a uniformly small error term. The main contribution is the analysis of the solution of the stochastic recursion equation as a fixed point, and the results that the normalized estimation errors are tight and are close to a linear function of the kernel, thus providing a stochastic expansion of the estimators, which is the same as for the Huber-skip. This implies that the iterated estimator is a close approximation of the Huber-skip.

1. Introduction and Main Results

Outlier detection in regression is an important topic in econometrics. The idea is to find an estimation method that is robust to the presence of outliers, and the statistical literature abounds in robust methods, since the introduction of M-estimators by Huber [1], see also the monographs Maronna, Martin, and Yohai [2], Huber and Ronchetti [3], and Jurečková, Sen, and Picek [4]. Recent contributions are the impulse indicator saturation method, see Hendry, Johansen, and Santos [5] and Johansen and Nielsen [6], and the Forward Search, see Atkinson, Riani, and Cerioli [7].

The present paper is a contribution to the theory of the robust estimators, where we focus on the Huber [1] skip-estimator that minimizes

$$\sum _{i=1}^n\rho (y_i-{\beta }^{\prime }{X}_i),$$

where the objective function, $\rho ,$ is given by

$$\rho \left(z\right)=\frac{1}{2}min(z^2,c^2)=\frac{1}{2}(z^2{1}_{\left(\right|z|\le c)}+c^2{1}_{\left(\right|z|>c)}).$$

This estimator removes the observations with large residuals, something that, at least in the analysis of economic time series, appears to be a reasonable method.

It is seen that ρ is absolutely continuous with derivative ${\rho }^{\prime }\left(z\right)=z{1}_{\left(\right|z|\le c)},$ but ${\rho }^{\prime }\left(z\right)$ is neither monotone nor absolutely continuous, which makes the calculation of the minimizer somewhat tricky, and the asymptotic analysis rather difficult.

Thus the estimator is often replaced by the Winsorized estimator, which has convex objective function

$${\rho }_1\left(z\right)=\frac{1}{2}{z}^2{1}_{\left(\right|z|\le c)}+c\left(\right|z|-\frac{1}{2}c)1_{\left(\right|z|>c)}$$

with derivative

$${\rho }_1^{\prime }\left(z\right)=z{1}_{\left(\right|z|\le c)}+c\mathrm{sign}\left(z\right)1_{\left(\right|z|>c)},$$

which is both monotone and absolutely continuous and hence a lot easier to analyse, see Huber [1]. Note, however, that the function ${\rho }_1$ replaces the large residuals by $\pm c,$ instead of removing the observation. This is a less common method in time series econometrics.

An alternative simplification is formulated by Bickel [8], who suggested applying a preliminary estimator ${\widehat{\beta }}_{n0}$ and define the one-step estimator, ${\widehat{\beta }}_{n1},$ by linearising the first order condition. He also suggested iterating this by using ${\widehat{\beta }}_{n1}$ as initial estimator for ${\widehat{\beta }}_{n2}$ etc., but no results were given.

In the analysis of the Huber-skip, derived from $\rho ,$ we shall replace β by a preliminary estimator in the indicator function, which leads to eliminating the outlying observations, and run a regression on the retained observations. We shall do so iteratively and study the sequence of recursively defined estimators ${\widehat{\beta }}_{nm}$. We prove under fairly general assumptions on regressors and distribution that for $(m,n)\to \infty ,$ the estimator ${\widehat{\beta }}_{nm}$ has the same asymptotic expansion as the Huber-skip, and in this sense ${\widehat{\beta }}_{nm},$ which is easy to calculate, is a very good approximation to the Huber-skip.

One-step M-estimators have been analysed previously in various situations. Apart from Bickel [8], who considered a situation with fixed regressors and weight functions satisfying certain smoothness and integrability conditions, Ruppert and Carroll [9] considered one-step Huber-skip L-estimators. Welsh and Ronchetti analysed the one-step Huber-skip estimator when the initial estimator is the least squares estimator, as well as one-step M-estimators with general initial estimator but with a function ρ with absolutely continuous derivative [10]. Recently Cavaliere and Georgiev analysed a sequence of Huber-skip estimators for the parameter of an $AR\left(1\right)$ model with infinite variance errors in case the autoregressive coefficient is 1 [11]. Johansen and Nielsen analysed one-step Huber-skip estimators for general $n^{1/2}$ consistent initial estimators and stationary as well as some non-stationary regressors [6].

Iterated one-step M-estimators are related to iteratively reweighted least squares estimators. Indeed the one-step Huber-skip estimator corresponds to a reweighted least squares estimator with weights of zero or unity. Dollinger and Staudte considered a situation with smooth weights, hence ruling out Huber-skips, and gave conditions for convergence [12]. Their argument was cast in terms of influence functions. Our result for iteration of Huber-skip estimators is similar, but the employed tightness argument is different because of the non-smooth weight function.

Notation: The Euclidean norm for vectors x is denoted $\left|x\right|.$ We write $(m,n)\to \infty$ if both m and n tend to infinity. We use the notation $o_{\mathsf{P}}\left(1\right)$ and $O_{\mathsf{P}}\left(1\right)$ implicitly assuming that $n\to \infty ,$ and $\stackrel{P}{\to }$ means convergence in probability and $\stackrel{D}{\to }$ denotes convergence in distribution. For matrices M we choose the spectral norm $\left|\right|M\left|\right|=max{\left\{\mathrm{eigen}\left(M^{\prime }M\right)\right\}}^{1/2}$, so that $\left|\right|x\left|\right|=\left|x\right|$ for vectors $x.$

2. The Model and the Definition of the One-step Huber-skip

We consider the multiple regression model with p regressors X

$$y_i={\beta }^{\prime }{X}_i+{\epsilon }_i,i=1,\cdots ,n,$$

(2.1)

and ${\epsilon }_i$ is assumed independent of $(X_1,\cdots ,X_i,{\epsilon }_1,\cdots ,{\epsilon }_{i-1})$ with known density $\mathsf{f},$ which does not have to be symmetric. These assumptions allow for both deterministic and stochastic regressors. In particular $X_i$ can be the lagged dependent variables as for an autoregressive process, and the process can be stationary or non-stationary.

We consider estimation of both β and${\sigma }^2.$ Thus we start with some preliminary estimator $({\widehat{\beta }}_{n0},{\widehat{\sigma }}_{n0}^2)$ and seek to improve it through an iterative procedure by using it to identify outliers, discard them and then run a regression on the remaining observations. The technical assumptions are listed in Assumption A, see §2.2 below, and allows the regressors to be deterministic or stochastic and stationary or trending.

The preliminary estimator $({\widehat{\beta }}_{n0},{\widehat{\sigma }}_{n0}^2)$ could be a least squares estimator on the full sample, although that is not a good idea from a robustness viewpoint, see Welsh and Ronchetti [10]. Alternatively, the initial estimator, ${\widehat{\beta }}_{n0},$ could be chosen as a robust estimator, as for instance the least trimmed squares estimator of Rousseeuw [13], Rousseeuw and Leroy [14] (p. 180). When the trimming proportion is at most a half, this convergences in distribution at a usual $n^{1/2}$-rate, see Víšek [15,16,17], and as ${\widehat{\sigma }}_{n0}^2$ we would choose the least squares residual variance among the trimmed observations, bias corrected as in (2.7) below.

The outliers are identified by first choosing a ψ giving the proportion of good, central observations and then, because $\mathsf{f}$ is not assumed symmetric, introducing two critical values $\underline{c}$ and $\overline{c}$ so

$${\int }_{\underline{c}}^{\overline{c}}\mathsf{f}\left(v\right)dv=\psi \text{and}{\int }_{\underline{c}}^{\overline{c}}v\mathsf{f}\left(v\right)dv=0.$$

(2.2)

This can also be written as ${\tau }_0=\psi$ and ${\tau }_1=0$, where ${\tau }_k$ are the truncated moments

$${\tau }_k={\int }_{\underline{c}}^{\overline{c}}{v}^k\mathsf{f}\left(v\right)dv\text{for}k\in {\mathbb{N}}_0.$$

(2.3)

If $\mathsf{f}$ is symmetric we find $c=-\underline{c}=\overline{c}$ and ${\tau }_{2k+1}=0,k\in {\mathbb{N}}_0.$ Observations are retained based on $({\widehat{\beta }}_{n0},{\widehat{\sigma }}_{n0}^2)$ if their residuals $y_i-{\widehat{\beta }}_{n0}^{\prime }{X}_i$ are in the interval $[\underline{c}{\widehat{\sigma }}_{n0},\overline{c}{\widehat{\sigma }}_{n0}]$ and otherwise deleted from the sample.

The Huber-skip, ${\widehat{\beta }}_{nH},$ is defined by minimizing

$$\frac{1}{2}\sum _{i=1}^n[{(y_i-X_i^{\prime }\beta )}^2{1}_{(\underline{c}\sigma \le y_i-X_i^{\prime }\beta \le \overline{c}\sigma )}+{\underline{c}}^2{1}_{(y_i-X_i^{\prime }\beta \le \underline{c}\sigma )}+{\overline{c}}^2{1}_{(\overline{c}\sigma \le y_i-X_i^{\prime }\beta )}],$$

for a given $\sigma .$ If the minimum is attained at a point of differentiability of the objective function, then the solution solves the equation

$${\widehat{\beta }}_{nH}={\left(\sum _{i=1}^n{X}_i{X}_i^{\prime }{1}_{(\underline{c}\sigma \le y_i-X_i^{\prime }{\widehat{\beta }}_{nH}\le \overline{c}\sigma )}\right)}^{-1}\sum _{i=1}^n{X}_i{y}_i{1}_{(\underline{c}\sigma \le y_i-X_i^{\prime }{\widehat{\beta }}_{nH}\le \overline{c}\sigma )}=g_n\left({\widehat{\beta }}_{nH}\right).$$

(2.4)

We apply this to propose a sequence of recursively defined estimators $({\widehat{\beta }}_{nm},{\widehat{\sigma }}_{nm}^2)$ by starting with $({\widehat{\beta }}_{n0},{\widehat{\sigma }}_{n0}^2)$ and defining for $m,n=1,2,\cdots$

$$\begin{array}{ccc}\hfill {\mathcal{S}}_{n,m-1}& =& \{i:\underline{c}{\widehat{\sigma }}_{n,m-1}\le y_i-X_i^{\prime }{\widehat{\beta }}_{n,m-1}\le \overline{c}{\widehat{\sigma }}_{n,m-1}\},\hfill \end{array}$$

(2.5)

$$\begin{array}{ccc}\hfill {\widehat{\beta }}_{nm}& =& {\left(\sum _{i\in {\mathcal{S}}_{n,m-1}}{X}_i{X}_i^{\prime }\right)}^{-1}\sum _{i\in {\mathcal{S}}_{n,m-1}}{X}_i{y}_i,\hfill \end{array}$$

(2.6)

$$\begin{array}{ccc}\hfill {\widehat{\sigma }}_{nm}^2& =& \psi {\tau }_2^{-1}{\left(\sum _{i\in {\mathcal{S}}_{n,m-1}}1\right)}^{-1}\sum _{i\in {\mathcal{S}}_{n,m-1}}{(y_i-X_i^{\prime }{\widehat{\beta }}_{n,m})}^2.\hfill \end{array}$$

(2.7)

Thus, the iterated one-step Huber-skip estimators ${\widehat{\beta }}_{nm}$ and ${\widehat{\sigma }}_{nm}^2$ are the least squares estimator of $y_i$ on $X_i$ among the retained observations in ${\mathcal{S}}_{n,m-1}$ based upon ${\widehat{\beta }}_{n,m-1}$ and ${\widehat{\sigma }}_{n,m-1}^2.$ The bias correction factor $\psi {\tau }_2^{-1}$ in ${\widehat{\sigma }}_{nm}^2$ is needed to obtain consistency.

Note that if ${\widehat{\beta }}_{n,m-1}$ and ${\widehat{\sigma }}_{n,m-1}$ are regression- and scale-equivariant, then the updated estimators ${\widehat{\beta }}_{nm}$ and ${\widehat{\sigma }}_{nm}$ are also regression- and scale-equivariant. Indeed, if $y_i$ is replaced by $s{y}_i+X_i^{\prime }d$ for all i for a scalar $s>0$ and a vector $d,$ then ${\widehat{\beta }}_{n,m-1}$ and ${\widehat{\sigma }}_{n,m-1}$ are replaced by $s{\widehat{\beta }}_{n,m-1}+d$ and $s{\widehat{\sigma }}_{n,m-1}$ so that the sets $S_{n,m-1}$ are unaltered, which in turn lead to regression- and scale-equivariance of ${\widehat{\beta }}_{nm}$ and ${\widehat{\sigma }}_{nm}.$

2.1. Asymptotic Results

To obtain asymptotic results we need a normalisation matrix N for the regressors. If $X_i$ is stationary then $N=n^{-1/2}{I}_p.$ If $X_i$ is trending, a different normalisation is needed. For a linear trend component the normalisation is $n^{3/2}$ and for a random walk component it is $n.$ We assume that N has been chosen such that matrices Σ and μ exist for which

$${\widehat{\Sigma }}_n=N^{\prime }{\sum }_{i=1}^n{X}_i{X}_i^{\prime }N\stackrel{\mathsf{D}}{\to }\Sigma \stackrel{a.s.}{>}0,{\widehat{\mu }}_n=n^{-1/2}{N}^{\prime }{\sum }_{i=1}^n{X}_i\stackrel{\mathsf{D}}{\to }\mu .$$

Note that Σ and μ may be stochastic as for instance when $X_i$ is a random walk and $N=n^{-1}$.

The estimation errors are denoted

$${\widehat{u}}_{nm}=\left\{\begin{array}{c}{N}^{-1}({\widehat{\beta }}_{nm}-\beta )\\ n^{1/2}({\widehat{\sigma }}_{nm}-\sigma )\end{array}\right\},$$

(2.8)

and the recursion defined in (2.5), (2.6), and (2.7) can expressed as

$${\widehat{u}}_{nm}=G_n\left({\widehat{u}}_{n,m-1}\right).$$

(2.9)

We introduce coefficient matrices

$${\widehat{\Psi }}_{n1}=\left(\begin{array}{cc}\psi {\widehat{\Sigma }}_n& 0\\ 0& 2{\tau }_2\end{array}\right),{\Psi }_2=\left(\begin{array}{cc}{\xi }_1{\widehat{\Sigma }}_n& {\xi }_2{\widehat{\mu }}_n\\ {\zeta }_2{\widehat{\mu }}_n^{\prime }& {\zeta }_3\end{array}\right),$$

(2.10)

where

$${\xi }_n={\left(\overline{c}\right)}^n\mathsf{f}\left(\overline{c}\right)-{\left(\underline{c}\right)}^n\mathsf{f}\left(\underline{c}\right),n=0,\cdots ,3\text{and}{\zeta }_n={\xi }_n-{\xi }_{n-2}{\tau }_2/\psi ,n=2,3,$$

(2.11)

and ${\tau }_2$ is defined in (2.3), and define

$${\widehat{\Gamma }}_n={\widehat{\Psi }}_{n1}^{-1}{\widehat{\Psi }}_{n2}=\left(\begin{array}{cc}{\psi }^{-1}{\xi }_1{I}_p& {\psi }^{-1}{\xi }_2{\widehat{\Sigma }}_n^{-1}{\widehat{\mu }}_n\\ {\left(2{\tau }_2\right)}^{-1}{\zeta }_2{\widehat{\mu }}_n^{\prime }& {\left(2{\tau }_2\right)}^{-1}{\zeta }_3\end{array}\right).$$

(2.12)

Here $({\widehat{\Gamma }}_n,{\widehat{\Psi }}_{n1},{\widehat{\Psi }}_{n2})\stackrel{D}{\to }(\Gamma ,{\Psi }_1,{\Psi }_2),$ where the limits are defined similarly in terms of Σ and $\mu .$

When $\mathsf{f}$ is symmetric we let $c=-\underline{c}=\overline{c}$ and find ${\zeta }_2={\xi }_2=0,$ so that Γ is diagonal. Moreover from ${\xi }_{2k+1}=2c^{2k+1}\mathsf{f}\left(c\right),$ we find ${\xi }_1/\psi =2c\mathsf{f}\left(c\right)/\psi ,$ and ${\zeta }_3/\left(2{\tau }_2\right)=c^3\mathsf{f}\left(c\right)/{\tau }_2-c\mathsf{f}\left(c\right)/\psi$ and therefore $\Gamma =\mathrm{diag}\{2c\mathsf{f}\left(c\right)/\psi I_p,c\mathsf{f}\left(c\right)(c^2/{\tau }_2-1/\psi )\}$.

Finally, we define a kernel

$$K_n={\widehat{\Psi }}_{n1}^{-1}{\sum }_{i=1}^n\left\{\begin{array}{c}{N}^{\prime }{X}_i{\epsilon }_i\\ n^{-1/2}({\epsilon }_i^2-{\sigma }^2{\tau }_2/\psi )\end{array}\right\}{1}_{\left(\underline{c}\sigma \le {\epsilon }_i\le \sigma \overline{c}\right)}.$$

(2.13)

The analysis of the one-step estimator in Johansen and Nielsen [6] shows that, by linearising $G_n,$ the one-step estimation errors ${\widehat{u}}_{nm}$ satisfy the recursion equation

$${\widehat{u}}_{nm}=G_n\left({\widehat{u}}_{n,m-1}\right)={\widehat{\Gamma }}_n{\widehat{u}}_{n,m-1}+K_n+R_n\left({\widehat{u}}_{n,m-1}\right),$$

(2.14)

for some remainder term $R_n\left({\widehat{u}}_{n,m-1}\right)$. In this notation it is emphasized that the remainder term is a function of the previous estimation error ${\widehat{u}}_{n,m-1},$ see Lemma 5.1 in the Appendix for a precise formulation.

It will be shown in Section 3 that if $max|$eigen$(\Gamma )|<1$ a.s. so that Γ is a contraction, then

$${\widehat{u}}_{nm}-{(I_{1+p}-{\widehat{\Gamma }}_n)}^{-1}{K}_n\stackrel{\mathsf{P}}{\to }0\text{for}(m,n)\to \infty ,$$

that is, for any η and $ϵ>0$ there exist $m_0$ and $n_0$ such that for $m\ge m_0$ and $n\ge n_0$ it holds that

$$\mathsf{P}\left(\right|{\widehat{u}}_{nm}-{(I_{1+p}-{\widehat{\Gamma }}_n)}^{-1}{K}_n|\ge \eta )\le ϵ.$$

We therefore define ${\widehat{u}}_{n*}={(I_{1+p}-{\widehat{\Gamma }}_n)}^{-1}{K}_n$ and note that it satisfies the equation

$${\widehat{u}}_{n*}={\widehat{\Gamma }}_n{\widehat{u}}_{n*}+K_n,$$

(2.15)

and in this sense the estimation error of $(\beta ,\sigma )$ has the same limit distribution as the fixed point of the linear function $u⟼{\widehat{\Gamma }}_{n}u+K_n$.

Moreover it follows from Johansen and Nielsen [19] that, for the case of known $\sigma =1$ and symmetric density, the Huber skip has the stochastic expansion

$${\widehat{\beta }}_{nH}=(I_p,0){(I_{1+p}-{\widehat{\Gamma }}_n)}^{-1}{K}_n+o_{\mathsf{P}}\left(1\right)$$

and hence the same asymptotic distribution as $(I_p,0){\widehat{u}}_{n*}.$

Finally it holds that

$$n^{1/2}({\widehat{\beta }}_{nH}-{\widehat{\beta }}_{nm})\stackrel{\mathsf{P}}{\to }0\text{for}(n,m)\to \infty .$$

Finally the asymptotic distribution of $K_n,$ and therefore ${\widehat{u}}_{n*},$ is discussed in Section 4.

2.2. Assumptions for the Asymptotic Analysis

The assumptions are fairly general, in particular we do not assume that $\mathsf{f}$ is symmetric.

Assumption A Consider model (2.1). Assume

$\left(i\right)$ The density $\mathsf{f}$ has continuous derivative ${\mathsf{f}}^{\prime }$ and satisfies

(a)

${sup}_{v\in \mathbb{R}}\{(1+v^4)\mathsf{f}\left(v\right)+(1+v^2)|{\mathsf{f}}^{\prime }\left(v\right)\left|\right\}<\infty ,$

(b)

it has mean zero, variance one, and finite fourth moment,

(c)

$\overline{c},\underline{c}$ are chosen so ${\tau }_0=\psi$ and ${\tau }_1=0$

$\left(ii\right)$ For a suitable normalization matrix $N\to 0,$ the regressors satisfy, jointly,

(a)

${\widehat{\Sigma }}_n=N^{\prime }{\sum }_{i=1}^n{X}_i{X}_i^{\prime }N\stackrel{\mathsf{D}}{\to }\Sigma \stackrel{a.s.}{>}0,$

(b)

${\widehat{\mu }}_n=n^{-1/2}{N}^{\prime }{\sum }_{i=1}^n{X}_i\stackrel{\mathsf{D}}{\to }\mu ,$

(c)

${max}_{i\le n}\mathsf{E}{\left|n^{1/2}{N}^{\prime }{X}_i\right|}^4=\mathrm{O}\left(1\right).$

$\left(iii\right)$ The initial estimator error satisfies

$$(N^{-1}({\widehat{\beta }}_{n0}-\beta ),n^{1/2}({\widehat{\sigma }}_{n0}-\sigma ))={\mathrm{O}}_{\mathsf{P}}\left(1\right).$$

3. The Fixed Point Result

The fixed point result is primarily a tightness result. Thus, for the moment, only tightness of the kernel $K_n$ is needed, and it is not necessary to establish the limit distribution, which is discussed in Section 4. The first result is a tightness result for the kernel, see (2.13).

Theorem 3.1 Suppose Assumption A $(ib,iic)$ holds. Then $K_n,$ see (2.10) and (2.13), is tight, that is,

$$K_n={\widehat{\Psi }}_{n1}^{-1}{\sum }_{i=1}^n\left\{\begin{array}{c}{N}^{\prime }{X}_i{\epsilon }_i\\ n^{-1/2}({\epsilon }_i^2-{\sigma }^2{\tau }_2/\psi )\end{array}\right\}{1}_{\left(\underline{c}\sigma \le {\epsilon }_i\le \sigma \overline{c}\right)}={\mathrm{O}}_{\mathsf{P}}\left(1\right).$$

The proof follows from Chebyshev’s inequality and the details are given in the appendix.

The next result discusses one step of the iteration (2.14), and it is shown that the remainder term $R_n\left(u\right)$ in (2.14) vanishes in probability uniformly in $\left|u\right|\le U.$

Theorem 3.2 Let m be fixed. Suppose Assumption A holds for the initial estimator ${\widehat{u}}_{n,m-1},$ see (2.8). Then, for all $U>0$, it holds that

$${\widehat{u}}_{nm}={\widehat{\Gamma }}_n{\widehat{u}}_{n,m-1}+K_n+R_n\left({\widehat{u}}_{n,m-1}\right),$$

where the remainder term satisfies

$$\underset{\left|u\right|\le U}{sup}\left|R_n\left(u\right)\right|={\mathrm{o}}_{\mathsf{P}}\left(1\right).$$

The proof involves a chaining argument that was given in Johansen and Nielsen [6], although there the result was written up in a slightly different way as discussed in the appendix.

The iterated estimators start with an initial estimator $({\widehat{\beta }}_{n0},{\widehat{\sigma }}_{n0})$ with tight estimation error, see Assumption A($iii$). This is iterated through the one-step (2.14) and defines the sequence of estimation errors ${\widehat{u}}_{nm}$. We next show that this sequence is tight uniformly in $m.$

Theorem 3.3 Suppose Assumption A holds and that $max\left|\mathrm{eigen}\right(\Gamma \left)\right|<1$ a.s. so that Γ is a contraction. Then the sequence of estimation errors ${\widehat{u}}_{nm}$ is tight uniformly in m

$$\underset{0\le m<\infty }{sup}\left|{\widehat{u}}_{nm}\right|={\mathrm{O}}_{\mathsf{P}}\left(1\right).$$

That is, for all $ϵ>0$ there exist $U>0$ and $n_0>0,$ so that for all $n\ge n_0$ it holds that

$$\mathsf{P}\left(\underset{0\le m<\infty }{sup}\right|{\widehat{u}}_{nm}|>U)<ϵ\text{.}$$

The proof is given in the appendix, but the idea of the proof is to write the solution of the recursive relation (2.14) as

$${\widehat{u}}_{nm}={\widehat{\Gamma }}_n^m{\widehat{u}}_{n0}+\sum _{\ell =1}^m{\widehat{\Gamma }}_n^{\ell -1}\{K_n+R_n\left({\widehat{u}}_{nm}\right)\}.$$

(3.1)

Then, if the initial estimator ${\widehat{u}}_{n0}$ takes values in a large compact set with large probability, it follows from (3.1), by finite induction, that also ${\widehat{u}}_{nm}$ takes values in the same compact set for all $\mathit{m}$, and therefore ${\widehat{u}}_{nm}$ is tight uniformly in $\mathit{m}$.

Finally we give the fixed point result. Theorem 3.4 shows that the estimator has the same limit distribution as the solution of equation (2.15), ${\widehat{u}}_{n*}={(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n,$ which is a fixed point of the linear function $u\mapsto {\widehat{\Gamma }}_{n}u+K_n.$

Theorem 3.4 Suppose Assumption A holds and that $max\left|\mathrm{eigen}\right(\Gamma \left)\right|<1$ a.s. so that Γ is a contraction. Then

$${\widehat{u}}_{nm}-{\widehat{u}}_{n*}={\widehat{u}}_{nm}-{(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n\stackrel{\mathsf{P}}{\to }0for(m,n)\to \infty .$$

That is, for all ϵ and $\eta >0,$ an $n_0>0$ and $m_0>0$ exist so that for all $n\ge n_0$ and $m\ge m_0$ it holds

$$\mathsf{P}\left(\right|{\widehat{u}}_{nm}-{(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n|>\eta )<ϵ.$$

Using ${\sum }_{\ell =1}^m{\widehat{\Gamma }}_n^{\ell -1}={(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}(I_{p+1}-{\widehat{\Gamma }}_n^m)$ we find from (3.1) that

$${\widehat{u}}_{nm}-{(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n={\widehat{\Gamma }}_n^m({\widehat{u}}_{n0}-{(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n)+\sum _{\ell =1}^m{\widehat{\Gamma }}_n^{\ell -1}{R}_n\left({\widehat{u}}_{n,m-\ell }\right).$$

(3.2)

From (3.2) it can be seen that $|{\widehat{u}}_{nm}-{(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n|$ is the sum of two terms vanishing in probability, where the first decreases exponentially. The details are given in the Appendix.

In the special case where σ is known, then ${\widehat{u}}_{nm}$ reduces to ${\widehat{b}}_{nm}=N^{-1}({\widehat{\beta }}_{nm}-\beta )$ and $\Gamma ={\psi }^{-1}{\xi }_1{I}_p,$ and ${\widehat{\beta }}_{nH}$ becomes a fixed point of the mapping $g_n$ defined in (2.4). The estimator ${\widehat{b}}_{n*}={(\psi -{\xi }_1)}^{-1}{\widehat{\Sigma }}_n^{-1}{\sum }_{i=1}^n{N}^{\prime }{X}_i{\epsilon }_i{1}_{(\underline{c}\sigma <{\epsilon }_i\le \overline{c}\sigma )}$ appears as the leading term for other robust estimators, such as the Least Trimmed Squares estimator discussed later on.

A necessary condition for the result is that the autoregressive coefficient matrix Γ is contracting. Therefore Γ is analyzed next.

Theorem 3.5 The autoregressive coefficient matrix Γ in (2.12) has $p-1$ eigenvalues equal to ${\xi }_1/\psi$ and two eigenvalues solving

$${\lambda }^2-(\frac{{\zeta }_3}{2{\tau }_2}+\frac{{\xi }_1}{\psi })\lambda +\frac{1}{2{\tau }_2\psi }({\zeta }_3{\xi }_1-{\zeta }_2{\xi }_2{\mu }^{\prime }{\Sigma }^{-1}\mu )=0,$$

where the coefficients ${\zeta }_n$ and ${\xi }_n$ are given in (2.11).

Further results can be given about the eigenvalues of Γ for symmetric densities, where ${\xi }_2=0,$ and $\Gamma =\mathrm{diag}({\xi }_1{\psi }^{-1}{I}_p,{\zeta }_3/\left(2{\tau }_2\right))$. Note that the quantities $(c,\tau ,{\xi }_n,{\zeta }_n)$ all depend on $\psi ,$ see (2.2), (2.3), and (2.11). If $\mathsf{f}$ is symmetric, we show below, $\left(a\right),$ that ${\xi }_1<\psi$ and a condition, $\left(c\right),$ is given for ${\zeta }_3<2{\tau }_2,$ in which case the eigenvalues of Γ are less than one, and Γ isa contraction. Finally $\left(d\right)$ shows that Γ is a contraction if $\mathsf{f}$ is log-concave.

Theorem 3.6 Suppose $\mathsf{f}$ is symmetric with third moment, ${\mathsf{f}}^{\prime }\left(c\right)\le 0$ for $c>0,$ and ${lim}_{c\to 0}{\mathsf{f}}^{\prime \prime }\left(c\right)<0$. Then

$\left(a\right)$ $0<{\xi }_1/\psi <1$ for $0<\psi <1$ while ${lim}_{\psi \to 0}{\xi }_1/\psi =1$ and ${lim}_{\psi \to 1}{\xi }_1/\psi =0;$

$\left(b\right)$ $0<{\zeta }_3/\left(2{\tau }_2\right)$ for $0<\psi <1$ and ${lim}_{\psi \to 0}{\zeta }_3/\left(2{\tau }_2\right)=1$ and ${lim}_{\psi \to 1}{\zeta }_3/\left(2{\tau }_2\right)=0;$

$\left(c\right)$ if ${\left[c{\{log{\int }_0^c\mathsf{f}\left(x\right)dx\}}^{\prime }\right]}^{\prime }<0$ for $c>0$ then ${\zeta }_3/\left(2{\tau }_2\right)<1$ for $0<\psi <1;$

$\left(d\right)$ ${\{log\mathsf{f}\left(c\right)\}}^{\prime \prime }<0\Rightarrow {\left[c{\{log\mathsf{f}\left(c\right)\}}^{\prime }\right]}^{\prime }<0\Rightarrow {\left[c{\{log{\int }_0^c\mathsf{f}\left(x\right)dx\}}^{\prime }\right]}^{\prime }<0.$

The condition ${\left[c{\{log{\int }_0^c\mathsf{f}\left(x\right)dx\}}^{\prime }\right]}^{\prime }<0$ is satisfied for the Gaussian density that is log-concave and by t-densities that are not log-concave but satisfy ${\left[c{\{log\mathsf{f}\left(c\right)\}}^{\prime }\right]}^{\prime }<0.$ In the robust statistics literature, Rousseeuw uses the condition ${\left[c{\{log\mathsf{f}\left(c\right)\}}^{\prime }\right]}^{\prime }<0$ when discussing change-of-variance curves for M-estimators and assumes log-concave densities [18].

A consequence of Theorem 3.6 is that if $\mathsf{f}$ is symmetric, the roots of the coefficient matrix Γ are bounded away from unity for ${\psi }_0\le \psi \le 1$ for all ${\psi }_0>0.$ The uniform distribution on $[-a,a]$ provides an example where Γ is not contracting since in this situation ${\xi }_1=\psi$ over the entire support. However, the weak unimodality condition ${\mathsf{f}}^{\prime }\left(c\right)\le 0$ in Theorem 3.6 is not necessary, as long as the mode at the origin is large in comparison with other modes.

4. Distribution of the Kernel

It follows from Theorem 3.4 that ${\widehat{u}}_{n*}={(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n$ has the same limit as ${\widehat{u}}_{nm},$ and we therefore find the limit distribution of the kernel $K_n$ in a few situations.

4.1. Stationary Case

Suppose the regressors are a stationary time series. Then the limits Σ and μ in Assumption A$(ia,ib)$ are deterministic and $({\widehat{\Sigma }}_n,{\widehat{\mu }}_n)\stackrel{P}{\to }(\Sigma ,\mu )$. The central limit theorem then shows that

$$K_n\stackrel{\mathsf{D}}{\to }{\mathsf{N}}_{p+1}(0,\Phi ),$$

(4.1)

where

$$\Phi =\left[\begin{array}{cc}{\psi }^{-2}{\sigma }^2{\tau }_2{\Sigma }^{-1}& {\left(2\psi {\tau }_2\right)}^{-1}{\sigma }^3{\tau }_3{\Sigma }^{-1}\mu \\ {\left(2\psi {\tau }_2\right)}^{-1}{\sigma }^3{\tau }_3{\mu }^{\prime }{\Sigma }^{-1}& 4^{-1}{\sigma }^4\{{\tau }_4{\tau }_2^{-2}-{\psi }^{-1}\}\end{array}\right].$$

(4.2)

As a consequence, the fully iterated estimator has limit distribution

$${\widehat{u}}_{n*}={(I_{p+1}-{\widehat{\Gamma }}_n)}^{-1}{K}_n\stackrel{\mathsf{D}}{\to }{(I_{p+1}-\Gamma )}^{-1}{\mathsf{N}}_{p+1}(0,\Phi ).$$

(4.3)

In the special case where the errors are symmetric, we find

$$\begin{array}{ccc}\hfill N^{-1}({\widehat{\beta }}_{n*}-\beta )& =& \frac{1}{(\psi -{\xi }_1)}{\Sigma }^{-1}\sum _{i=1}^n{N}^{\prime }{X}_i{\epsilon }_i{1}_{\left(|{\epsilon }_i|\le \sigma c\right)}+o_{\mathsf{P}}\left(1\right)\stackrel{\mathsf{D}}{\to }{\mathsf{N}}_p\{0,\frac{{\sigma }^2{\tau }_2}{{(\psi -{\xi }_1)}^2}{\Sigma }^{-1}\},\hfill \\ \hfill n^{1/2}({\widehat{\sigma }}_{n*}^2-{\sigma }^2{\tau }_{\psi }/\psi )& =& {\{1-{\zeta }_3{\left(2{\tau }_2\right)}^{-1}\}}^{-1}\sum _{i=1}^n{n}^{-1/2}({\epsilon }_i^2-{\sigma }^2{\tau }_2{\psi }^{-1})1_{\left(|{\epsilon }_i|\le \sigma c\right)}+o_{\mathsf{P}}\left(1\right)\hfill \\ & & \stackrel{\mathsf{D}}{\to }{\mathsf{N}}_p\{0,\frac{{\sigma }^4{\tau }_2^2({\tau }_4-{\psi }^{-1}{\tau }_2^2)}{{(2{\tau }_2-{\zeta }_3)}^2}\},\hfill \end{array}$$

noting that $\psi >{\xi }_1$ and ${\zeta }_3>2{\tau }_2$ are satisfied for symmetric, unimodal distributions by Theorem 3.6$(a,b).$

The limiting distribution of $N^{-1}({\widehat{\beta }}_{n*}-\beta )$ is also seen elsewhere in the robust statistics literature.

First, Víšek [15] (Theorem 1, p. 215) analysed the least trimmed squares estimator of Rousseeuw [13]. The estimator is given by

$${\widehat{\beta }}_n^{LTS}=arg{min}_{\beta \in {\mathbb{R}}^p}{\sum }_{i=1}^{\mathrm{int}\left(n\psi \right)}{r}_{\left(i\right)}^2\left(\beta \right),$$

where $r_{\left(1\right)}^2\left(\beta \right)<\cdots <r_{\left(n\right)}^2\left(\beta \right)$ are the ordered squared residuals $r_i=y_i-X_i^{\prime }\beta$. The estimator has the property that it does not depend on the scale of the problem. Víšek argued that in the symmetric case, the least trimmed squares estimator satisfies

$$N^{-1}({\widehat{\beta }}_n^{LTS}-\beta )=\frac{1}{(\psi -{\xi }_1)}{\Sigma }^{-1}\sum _{i=1}^n{N}^{\prime }{X}_i{\epsilon }_i{1}_{\left(|{\epsilon }_i|\le c\sigma \right)}+{\mathrm{o}}_{\mathsf{P}}\left(1\right),$$

(4.4)

that is, the main term is the same as for ${\widehat{\beta }}_{n*},$ and it follows from Theorem 3.4 that because ${\widehat{\beta }}_n^{LTS}$ and ${\widehat{\beta }}_{n*}$ have the same expansions we have

$$|N^{-1}({\widehat{\beta }}_{nm}-{\widehat{\beta }}_n^{LTS})|\stackrel{\mathsf{P}}{\to }0$$

for $(m,n)\to \infty .$ Thus ${\widehat{\beta }}_{nm}$ can be seen as an approximation to the $LTS$ estimator when there are no outliers.

Second, Jurečková, Sen, and Picek [4] (Theorem 5.5, p. 176) considered a pure location problem with regressor $X_i=1$ and known $\sigma =1$, and found an asymptotic expansion like (4.4) for the Huber-skip, and Johansen and Nielsen [19] showed the similar result for the general regression model. A consequence of this is that the iterated 1-step Huber-skip has the same limit distribution as the Huber-skip, and because ${\widehat{\beta }}_{nm}$ and ${\widehat{\beta }}_{nH}$ have the same expansion, it follows from Theorem 3.4 that

$$n^{1/2}|{\widehat{\beta }}_{nm}-{\widehat{\beta }}_{nH}|\stackrel{\mathsf{P}}{\to }0\text{for}(m,n)\to \infty ,$$

(4.5)

so the iterated estimator is in this sense an approximation to the Huber-skip.

4.2. Deterministic Trends

As a simple example with i.i.d. errors, consider the regression

$$y_i={\beta }_1+{\beta }_{2}i+{\epsilon }_i,$$

where ${\epsilon }_i\in \mathbb{R}$ satisfies Assumption A$\left(i\right).$ Define the normalisation

$$N=\left(\begin{array}{cc}{n}^{-1/2}& 0\\ 0& n^{-3/2}\end{array}\right).$$

Then Assumption A$\left(ii\right)$ is met with $X_i={(1,i)}^{\prime }$ and

$$\Sigma =\left(\begin{array}{cc}1& 1/2\\ 1/2& 1/3\end{array}\right),\mu =\left(\begin{array}{c}1\\ 1/2\end{array}\right),$$

(4.6)

and ${max}_{i\le n}\mathsf{E}{\left|n^{1/2}{N}^{\prime }{X}_i\right|}^4\le 4.$ The kernel has a limit distribution given by (4.1), where the matrix Φ in (4.2) is computed in terms of the Σ and μ derived in (4.6).

If the errors are autoregressive, the derivation is in principle similar, but involves a notationally tedious detrending argument. The argument is similar to that of Johansen and Nielsen [6] (Section 1.5.1), and (4.5) holds.

4.3. Unit Roots

Consider as an example the autoregression $y_i=\beta y_{i-1}+{\epsilon }_i,i=1,\cdots ,n.$ If $\beta =1$ then $X_i=y_{i-1}=y_0+{\sum }_{s=1}^{i-1}{\epsilon }_s$ and we have to choose $N=n^{-1}.$ By the functional Central Limit Theorem

$$n^{-1/2}{\sum }_{i=1}^{\mathrm{int}\left(nu\right)}\left\{\begin{array}{c}{\epsilon }_i\hfill \\ {\epsilon }_i{1}_{\left(\underline{c}\sigma \le {\epsilon }_i\le \sigma \overline{c}\right)}\hfill \\ ({\epsilon }_i^2-{\sigma }^2{\tau }_2/\psi )1_{\left(\underline{c}\sigma \le {\epsilon }_i\le \sigma \overline{c}\right)}\hfill \end{array}\right\}\stackrel{\mathsf{D}}{\to }\left(\begin{array}{c}{W}_{x,u}\\ W_{1,u}\\ W_{2,u}\end{array}\right),$$

where the limit is a Brownian motion with zero mean and variance

$${\Phi }_W=\left[\begin{array}{ccc}{\sigma }^2& {\sigma }^2{\tau }_2& {\sigma }^3{\tau }_3\\ {\sigma }^2{\tau }_2& {\sigma }^2{\tau }_2& {\sigma }^3{\tau }_3\\ {\sigma }^3{\tau }_3& {\sigma }^3{\tau }_3& {\sigma }^4\{{\tau }_4-{\tau }_2^2/\psi \}\end{array}\right].$$

Thus the limit variables Σ and μ in Assumption A$\left(i\right)$ are

$$\Sigma ={\int }_0^1{W}_{x,u}^{2}du,\mu ={\int }_0^1{W}_{x,u}du,$$

while the kernel has limit distribution

$$K_n\stackrel{\mathsf{D}}{\to }{\Psi }_1^{-1}\left(\begin{array}{c}{\int }_0^1{W}_{x,u}d{W}_{1,u}\\ W_{2,1}\end{array}\right),$$

and (4.5) holds. Thus, when the density of ${\epsilon }_i$ is symmetric, ${\widehat{\beta }}_{n*}$ has limit distribution

$$n({\widehat{\beta }}_{n*}-\beta )\stackrel{\mathsf{D}}{\to }\frac{{\int }_0^1{W}_{x,u}d{W}_{1,u}}{(\psi -{\xi }_1){\int }_0^1{W}_{x,u}^{2}du}.$$

When $\psi \to 1$ then ${\xi }_1\to 0$ and ${\tau }_2\to 1$ so $W_{1,u}$ and $W_{x,u}$ become identical and the limit distribution becomes the usual Dickey–Fuller distribution. See also Johansen and Nielsen [6] (Section 1.5.4) for a related and more detailed derivation.

5. Discussion of Possible Extensions

The iteration result in Theorem 3.4 has a variety of extensions. An issue of interest in the literature is whether a slow initial convergence rate can be improved upon through iteration. This would open up for using robust estimators converging for instance at a $n^{1/3}$ rate as initial estimator. Such a result would complement the result of He and Portnoy, who find that the convergence rate cannot be improved in a single step by this procedure that applies least squares to the retained observations [20].

The key is to show that the remainder term of the one-step estimator in Theorem 3.2 remains small in an appropriately larger neighbourhood. The proof of Theorem 3.4 then applies the same way leading to the same fixed point result. The necessary techniques are developed by Johansen and Nielsen [21].

A related algorithm is the Forward Search of Atkinson, Riani, and Cerioli [7,22]. This involves finding an initial set of “good” observations using for instance the least trimmed squares estimator of Rousseeuw [13] and then increase the number of “good” observations using a recursive test procedure. The algorithm involves iteration of one-step Huber-skip estimators, see Johansen and Nielsen [23]. Again the key to its analysis is to improve Theorem 3.2, in this instance to hold uniformly in the cut-off fraction $\psi ,$ see Johansen and Nielsen for details [21].

Another algorithm of interest would be to analyse algorithms such as Autometrics of Hendry and Krolzig [24] and Doornik [25], which involves selection over observations as well as regressors.

In practice it is not a trivial matter to compute the least trimmed squares estimator of Rousseeuw [13]. A number of algorithms have been suggested in the literature, see for instance Hawkins and Olive [26]. Algorithms based on a “concentration” approach start with an initial trial fit that is iterated towards a final fit. It is possible that the abovementioned results will extend to shed some further light on the properties of such resampling algorithms.