The Status of Bridge Principles in Applied Econometrics

Abstract

The paper begins with a figurative representation of the contrast between present-day and formal applied econometrics. An explication of the status of bridge principles in applied econometrics follows. To illustrate the concepts used in the explication, the paper presents a simultaneous-equation model of the equilibrium configurations of a perfectly competitive commodity market. With artificially generated data I carry out two empirical analyses of such a market that contrast the prescriptions of formal econometrics in the tradition of Ragnar Frisch with the commands of present-day econometrics in the tradition of Trygve Haavelmo. At the end I demonstrate that the bridge principles I use in the formal-econometric analysis are valid in the Real World—that is in the world in which my data reside.

1. Introduction

Econometrics is a study of good and bad ways to measure economic relations. This paper is about the use of economic theory in such measurements, and about the need for bridge principles in applied econometrics.1

A long time ago in Fahlbeckska Stiftelsen’s Statsvetenskaplig Tidskrift (1931) [2] (p. 281), Ragnar Frisch insisted (in my words) that economic statistics and parameter estimates tell us nothing about pertinent economic phenomena unless they are produced and analyzed within an economic-theoretic conceptualization. A few years later (cf. Haavelmo (1944) [3] (p. 1)), Trygve Haavelmo professed the same idea: “Theoretical models are necessary tools in our attempts to understand and ‘explain’ events in real life. In fact, even a simple description and classification of real phenomena would probably not be possible or feasible without viewing reality through the framework of some scheme conceived a priori.” I grew up with this idea, and I took it to be valid not just in the paradigms of Frisch and Haavelmo’s econometrics but in all of econometrics. Now I am not so sure. The younger generation of econometricians seems to think differently.

1.1. Three Scenarios for Applied Econometrics

The younger generation of econometricians and the members of Frisch and Haavelmo’s paradigms carry out the theory-data confrontation in different ways. Thus, one may envision three abstract scenarios for the empirical analysis of an economic theory. The scenarios differ in the way the researchers in charge view theory and use it in the measurement of economic relations.

In the first scenario the researcher in charge is an econometrician who, like Frisch, has one leg in mathematical economics and the other leg in mathematical statistics. The theory he confronts with data is an axiomatized theory about a few undefined terms that live and function in an imaginary model world. The researcher acknowledges that there is a definite divide between his model world and the world of observations, and that his data need not provide accurate measurements of the undefined terms of his theory.2 He formulates his theory in a theory universe and uses bridge principles to describe how his theoretical variables are related to his data variables. The theory-data confrontation, then, becomes a triple of two disjoint universes—one for theory and one for data—and a bridge between them. This scenario I take to depict the way formal econometrics in the tradition of Frisch functions.

In the second scenario the researcher in charge is an econometrician who confronts an abstract theory with data. The theory may be axiomatized or formulated in accordance with the semantic view of theories. In Haavelmo’s treatise the theory is taken to comprise a system of ordinary or functional equations that express definitional identities, technical relations, or relations depicting behavior (Haavelmo (1944) [3] (p. 2)). The researcher acknowledges the divide between his model world and the world in which his data resides. To overcome the divide, he identifies his theory variables with true variables in the real world, and he allows the possibility that he might not have accurate observations of all the relevant true variables.3 Thus in the second scenario there is no need for a bridge between theory and data. The researcher formulates his theory, describes his data, and carries out the empirical analysis in a data universe. To me this scenario pictures the way present-day econometrics in the tradition of Haavelmo is carried out.

In the third scenario the researcher uses his knowledge of economic theory and the functioning of economic institutions to formulate his econometric model. The model concerns the behaviour of data variables and may account for both errors of observations and errors in equations. Then, the theory-data confrontation is carried out in a data universe, where the researcher formulates his econometric model and carries out the empirical analysis. It differs from the second scenario in that the model is not derived from the theorems of a pertinent economic theory but springs from the imagination of the researcher in charge. I think this must be a description of the way present-day econometrics is carried out by many young econometricians.

1.2. A Significant Contrast

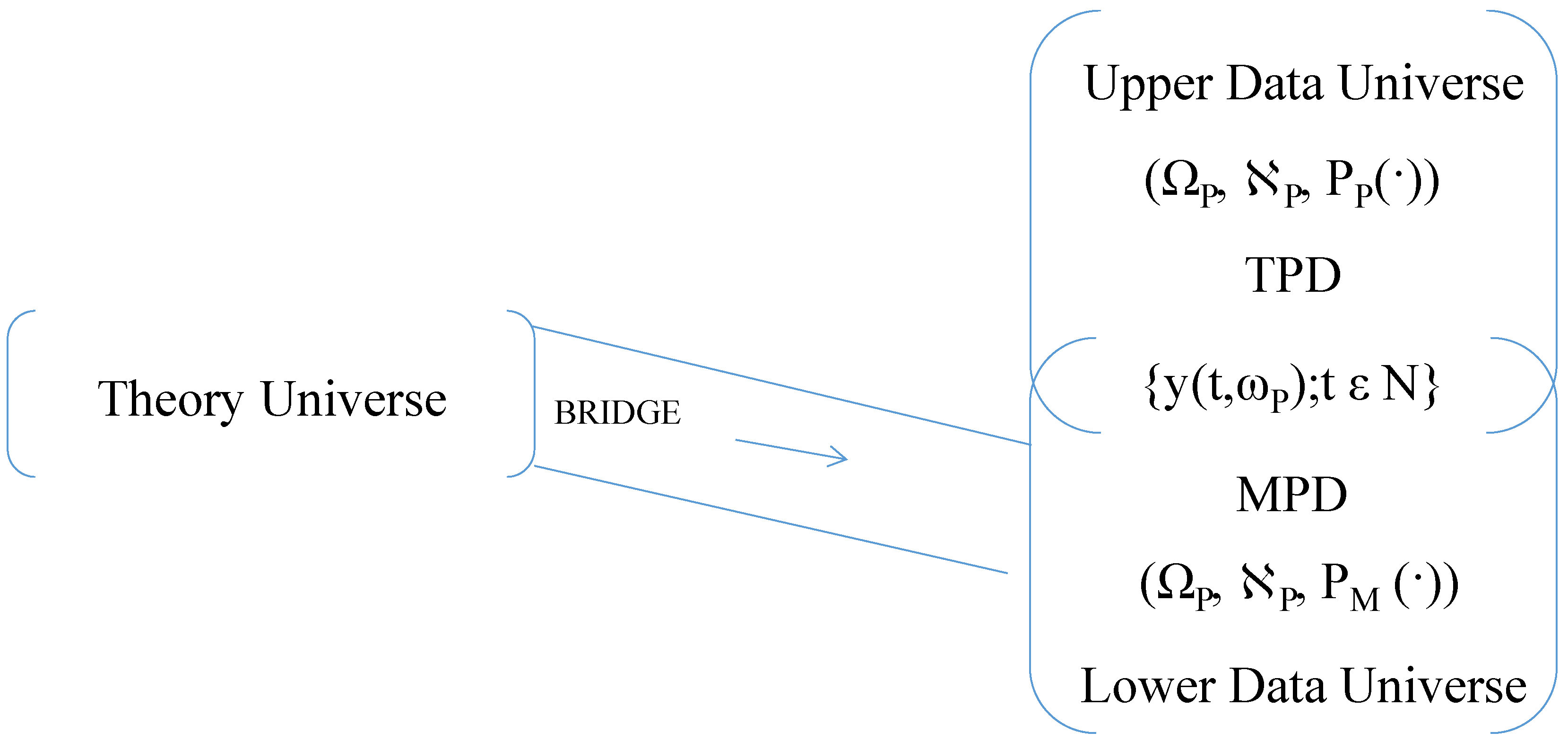
The statistical analyses in the three scenarios differ, and the inferences about social reality that the respective researchers gain from their statistical results also differ. One way to describe the contrast between the empirical analyses in the three scenarios is as follows: The data variables constitute a vector-valued random process, Y = {y(t,ω_P); t ε N}, on a probability space, (Ω_P, ℵ_P, P_P(·)), where N = {0, 1, 2, …}, Ω_P is a subset of a vector space, ℵ_P is a σ-field of subsets of Ω_P, and P_P(·):ℵ_P → [0, 1] is a probability measure. The family of finite-dimensional probability distributions of the members of Y relative to P_P(·) is the true probability distribution of the data variables. I denote it by the acronym TPD in which T is short for true, P for probability, and D for distribution. In the last two scenarios the true values of the estimated parameters are taken to be values of pertinent TPD parameters.

The probability distribution that the researcher in the first scenario derives from the probability distribution of his theory variables and the bridge principles is, also, a family of finite-dimensional probability distributions of the members of Y. I denote it by the acronym MPD in which M is short for marginal, P for probability, and D for distribution. With an MPD I can associate a probability measure, P_M(·):ℵ_P → [0, 1], such that Y has the probability distribution MPD relative to P_M(∙), and such that Y can be thought of as a vector-valued random process on the probability space, (Ω_P, ℵ_P, P_M(·)). In a given theory-data confrontation there may be many MPD distributions. They vary with the models of the theory and the models of the bridge principles. Consequently, parameter estimates in the first scenario are estimates of the parameters of any one of the possible MPD distributions.

1.3. A Figurative Representation of the Contrast

The probability measures, P_P(·) and P_M(∙), are probability measures on one and the same measure space, (Ω_P, ℵ_P). For pedagogical reasons it is useful to think of (Ω_P, ℵ_P, P_P(·)) and (Ω_P, ℵ_P, P_M(·)) as forming part of two different data universes—an upper data universe for (Ω_P, ℵ_P, P_P(·)) and a lower data universe for (Ω_P, ℵ_P, P_M(·)). The picture I have in mind looks roughly like Figure 1. Here, the bridge connects the theory universe with the lower data universe. The two data universes share the pair, (Ω_P, ℵ_P) and the random process, Y. The probability distribution of Y is TPD in the upper data universe and MPD in the lower data universe. I picture in my mind that present-day econometric analyses in accord with the second or third scenario take place in the upper data universe, while formal-econometric analyses in accord with the first scenario happen in the lower data universe.

1.4. The Preferred Scenario

I believe that Frisch and Haavelmo were right in insisting that economic theory is a necessary tool in a researcher’s attempts to understand and explain the economic phenomena that he observes in social reality. An economic theory is a family of models of a finite number of assertions—axioms—concerning a few undefined terms that live and function in a Frischian model world. As such the theory does not describe behavior and events in real life. Instead it delineates characteristic features of objects and relations in social reality that the originator of the theory has observed. The researcher is to determine when and where the given characteristics have empirical relevance.

The researchers in the three scenarios differ in the way they use theory in their empirical analysis. I have misgivings with the third scenario. The researcher’s cavalier use of theory hampers his ability to give a well-founded analysis of his empirical results. Different theories lead to different interpretations of the results, and the researcher ought to reveal on which theory he bases his analysis. Without such information, meaningful discussions of the researcher’s results become difficult.

I have misgivings with the second scenario, too. An economic theory about behavior or events is a family of models of a finite number of axioms. By identifying theoretical variables with true variables in the real world, and by using his assumptions about the true variables and the data variables to describe properties of the TPD, the researcher in effect treats his theory as if it has only one model. The theory, then, becomes a theory about the characteristics, say, of a representative individual or of a typical strike in the public sector of the economy. Such a theory restricts the kind of inference about social reality that a researcher’s empirical results may confer.

I like the first scenario. In it the researcher’s theory is about the characteristics of behavior and not about the characteristics of a representative individual’s behavior. The statistical analysis confers information about how different the individuals may be for whom the theory is empirically relevant. Similarly, the researcher’s theory about characteristics of events; e.g., strikes in the public sector, is about strikes and not about the typical strike. The statistical analysis confers information about how different the groups that conduct the strikes may be and for which the theory is empirically relevant. Such an empirical analysis is novel both in the way theory is used in the statistical analysis and in the way bridge principles are used to form the inference about social reality that the researcher can derive from his statistical results.

The first scenario is the one I prefer. It ought to appeal to applied econometricians once I have convinced them that there is a way to establish the validity of the bridge principles that are used in an empirical analysis. I hope to do that in Section 2 of the paper.

2. The Status of Bridge Principles in Applied Econometrics

The bridge principles play three roles in the empirical analysis in the lower data universe. In one role, the bridge principles translate the theory so that it becomes a statement about relations among variables in the data universe. In the second role, the bridge principles convert the probability distributions of variables in the theory universe into a family of probability distributions of variables in the data universe—the MPD—that plays the role of the data generating process in the empirical analysis. In the third role the bridge principles provide the means by which the researcher can identify the empirically relevant models of his theory that his statistical results determine. The three roles of the bridge principles in the lower data universe depict the way theory is incorporated in the empirical analysis of formal econometrics.

Since the MPD may be very different from the pertinent data generating process, the meaningfulness of the empirical analysis in the lower data universe hinges on the validity of the bridge principles. For that reason it is important to search for a general explication of the status of bridge principles in applied econometrics. I will set out to provide such an explication in this section of the paper.

To explicate the status of bridge principles in applied econometrics, I need to explain what I mean by several new concepts: empirical context, empirical relevance, encompassing, congruence, and a data admissible confidence region.

First, empirical context: In the upper data universe in Figure 1, the empirical context has two components: (1) axioms and loosely formulated assumptions that the pertinent researcher uses to delineate the characteristics of the data generating process; and (2) the prescriptions that underlie the statistical analysis. The second component details, for example, the way the researcher is to search for a data admissible econometric model that parsimoniously encompasses the so-called local data generating process (cf. Bontemps and Mizon (2003) [5] (p. 356,359,366) and Hendry and Krolzig (2003) [6] (p. 380,386–391)).

In the lower data universe in Figure 1, the empirical context has, also, two components: (1) the prescriptions that underlie the statistical analysis and (2) a description of the characteristics of a data admissible mathematical model of the MPD. The prescriptions that underlie the statistical analysis detail the way the researcher is to obtain a consistent estimate of a mathematical model of the MPD. Also, a mathematical model of MPD is data admissible if (1) the estimated mathematical model of MPD satisfies the strictures on which the axioms of the data universe and the prescriptions that underlie the statistical analysis insist; (2) the values that the given model assigns to the parameters of MPD satisfy the strictures on which the theory-axioms, the data-axioms, and the axioms of the bridge insist; and (3) the model lies within a 95% confidence region of the estimated mathematical model of MPD.

Next, empirical relevance: in the upper data universe in Figure 1 the empirical relevance of a theoretical hypothesis is determined the way the validity of a null hypothesis is decided in mathematical statistics. Specifically, the theoretical hypothesis is judged to be empirically relevant in a given empirical context if and only if it cannot be rejected. In contrast, in the lower data universe in Figure 1 a family of models of the theory axioms is empirically relevant if and only if there is a member of the given family which—together with a model of the data axioms and the bridge principles—induces a model of the MPD that belongs to a 95% confidence band of a meaningful statistical estimate of the MPD.

Then, three different concepts of encompassing: exact encompassing, encompassing in the upper data universe, and encompassing in the lower data universe.

Roughly speaking, an econometric model is said to encompass another econometric model if it can account for the results obtained by the latter (cf. Mizon (1984) [7] and Hendry and Richard (1989) [8]). My discussion of encompassing is designed to exhibit the characteristics of the three concepts of encompassing as simply as possible. I consider only cases of parametric encompassing. Also, I adopt the simplest version of the many binding functions that appear in articles on encompassing; e.g., in Gourieroux et al. (1983) [9], Mizon (1984) [7], and Florens et al. (1996) [10]. Finally, since I have had little to say about Bayesian econometrics in the paper, I do not discuss Bayesian ideas of encompassing here. For a comprehensive survey of the development of the encompassing principle in econometrics, the interested reader is referred to Bontemps and Mizon’s (2008) [11] article on “Encompassing: Concepts and Implementation”.

I will discuss the problem of encompassing within the confines of some given formal theory data confrontation as depicted in Figure 1. Hence, I am discussing cases in which there is one measurable space, (Ω_P, ℵ_P), with many different probability measures. I also presume that I am considering the probability distribution of a random vector, y(∙), relative to the given probability measures. The distribution of y(∙) relative to P_P(∙) is the TPD distribution of y(∙). Relative to a particular P_M(∙) the distribution of y(∙) is the MPD distribution corresponding to P_M(∙). I will denote a vector of parameters of the TPD distribution of y(∙) by θ_P and any one of the theoretically possible vectors of parameters of the MPD distribution of y(∙) by θ_M. Also, I will denote an econometric model of MPD by a pair, (M1, θ_M°(∙)) and an econometric model of TPD by a pair, (M2, θ_P°(∙)), where, M1 and M2 , and θ_M°(∙), and θ_P°(∙) are two probability distributions and two estimators of θ_M and θ_P, respectively. Finally, I will let s_n denote a finite sample, y₁, …, y_n, of observations of y(∙).

The fact that there is one true TPD and many “true” MPDs has one particularly important implication: The estimator in an econometric model of the TPD is an estimator of the ”true” value of a pertinent TPD parameter. In contrast, the estimator in an econometric model of the MPD is an estimator of the value of an MPD parameter of any one of the possible mathematical models of the MPD. In different words: In an econometric model of the TPD, (M, θ_P°(∙)), the parameter of M, θ_P, has a true value. In an econometric model of the MPD, (M, θ_M°(∙)), the parameter of M, θ_M, may assume any one of a number of “true” values.

With these remarks in mind I can define the three concepts of encompassing formally as follows:

Definition 1.

Suppose that there are three subsets of R^k, Φ_P, Φ_M, and Φ_S, such that θ_P ε Φ_P, θ_M ε Φ_M, and θ_S ε Φ_S. Suppose, also, that I have obtained n independently and identically distributed observations of y, y₁, …, y_n, and let θ_P°(∙), θ_M°(∙), and θ_S°(∙), respectively, be estimators of θ_P, θ_M, and θ_S in the given sample. Finally, suppose that (M1, θ_S°(∙)) and (M2, θ_P°(∙)) are two different econometric models of the TPD, that (M3, θ_M°(∙)) is an econometric model of the MPD, and that the three estimators are consistent in their respective models. Then,

A.

(M1, θ_S°(∙)) exactly encompasses (M2, θ_P°(∙)) in the upper data universe in Figure 1 if and only if there is a binding function, Γ(∙):Φ_S → Φ_P, such that in M1, the estimates of θ_P and θ_S satisfy the equation : θ_P°(s_n) = Γ(θ_S°(s_n)) a.e..

B.

(M1, θ_S°(∙)) encompasses (M2, θ_P°(∙)) in the upper data universe in Figure 1 if and only if there is a binding function, Γ(∙):Φ_S → Φ_P, such that in M1, Γ(θ_S0) = plim θ_P°(s_n), and in M2, θ_P0 = plim θ_P°(s_n), θ_S0 = plimθ_S°(s_n), and θ_P0 = Γ(θ_S0).

C.

(M3, θ_M°(∙)) encompasses (M2, θ_P°(∙)) in the lower data universe in Figure 1 if and only if there is a value of θ_M ε Φ_M and a binding function, Γ(∙):Φ_M → Φ_P, such that in M3, Γ(θ_M) = plim θ_P°(s_n), and in M2, θ_P0 = plim θ_P°(s_n), θ_M0 = plim θ_M°(s_n), and θ_P0 = Γ(θ_M0).

In reading this definition there are several things to notice. The definition of exact encompassing is in accord with Definition 1 in Bontemps and Mizon (2008) [11] (p. 6). Bontemps and Mizon attribute the definition to Florence et al. (1996) [10]. I have problems with using the definition in the lower data universe for several reasons. Firstly, there need not be a true value of θ_M that I can use to describe the distribution in M1. Secondly, there is no reference to the limiting distributions of the two estimates.

The definition of encompassing in the upper data universe, B, is a rewording of Bontemps and Mizon’s (2003) definition of encompassing (cf. Bontems and Mizon, 2003 [5] (p. 359)). It is interesting in this context that the definition of encompassing in the lower data universe, C, is a natural extension of definition B. To see why, observe that in M3, θ_M = plim θ_M°(s_n). The required θ_M need not satisfy the equation θ_M = θ_M0. However, if θ_M = θ_M0, (M3, θ_M°(∙)) also encompasses (M2, θ_P°(∙)) in the sense of B. In that sense, C is the natural extension of B to the lower data universe in Figure 1.

At last I must say what the meanings of congruence and data admissible confidence sets are in the present context. The concept of congruence plays a pivotal role in the LSE methodology. According to Mizon (1995) [12], in the LSE methodology an econometric model is congruent if it is coherent with a priori theory, coherent with observed sample information, coherent with the measurement system, and encompasses all rival models. For present purposes I will insist on the following modified explication of congruence.

Definition 2.

Suppose that there are two subsets of R^k, Φ_P and Φ_M, such that θ_P ε Φ_P and θ_M ε Φ_M. Suppose, also, that I have n independently and identically distributed observations of y, y₁, …, y_n, and let θ_P°(∙) and θ_M°(∙) be estimators of θ_P and θ_M, respectively. Finally, suppose that (M2, θ_P°(∙)) and (M1, θ_M°(∙)) are different econometric models of the TPD and the MPD with M2 actually being the TPD, and suppose that the estimators, θ_P°(∙) and θ_M°(∙), are consistent in their respective models. Then, (M1, θ_M°(∙)) is a congruent econometric model of TPD if and only if M1 is coherent with the pertinent a priori theory and (M1, θ_M°(∙)) encompasses (M2, θ_P°(∙)) in accord with Definition 1C. The M1 in a congruent econometric model of TPD is termed a congruent model of TPD.

In this definition the a priori theory is a family of models of the axioms of the data universe in a pertinent formal theory-data confrontation. It is, therefore, important to observe that the parameters of M1 in a congruent econometric model of TPD, (M1, θ_M°(∙)), need not satisfy the conditions of a data admissible mathematical model of the MPD.

Definition 3.

Consider a theory-data confrontation in which the sampling scheme that generates the data is adequate. The 95% confidence region around the estimated mathematical model of the MPD is data admissible if it contains both a data admissible mathematical model of the MPD and a congruent model of the TPD.

Theorem 1.

Consider one subset of R^k, Φ_M, and suppose that θ_M1 ε Φ_M, θ_M2 ε Φ_M, and θ_M3 ε Φ_M are, respectively, parameter vectors of three different models of MPD. Suppose, also, that I have n independently and identically distributed observations of y, y₁, …, y_n, and let θ_M°(∙) be an estimator of θ_M1, θ_M2, and θ_M3. Finally, suppose that (M1, θ_M°(∙)), (M2, θ_M°(∙)), and (M3, θ_M°(∙)) are econometric models of the MPD with θ_M1 being the parameter of M1, θ_M2 being the parameter of M2, and θ_M3 being the parameter of M3, and suppose that the estimator, θ_M°(∙), is consistent in the respective models. If M2 and M3 are data admissible, (M2, θ_M°(∙)) and (M3, θ_M°(∙)) encompass each other in accord with Definition 1C. Moreover, if (M1, θ_M°(∙)) is a congruent econometric model of TPD and M1 is a data admissible model of MPD, (M1, θ_M°(∙)) encompasses all the econometric models of the MPD, (M, θ_M°(∙)), with a data admissible mathematical model of MPD, M, and is encompassed by them. However, (M2, θ_M°(∙)) and (M3, θ_M°(∙)) need not be congruent econometric models of TPD.

I will sketch a proof of the theorem and leave the missing details to the reader. First let Φ_P and Φ_M be subsets of R^k, and suppose that the parameter of TPD, θ_P, belongs to Φ_P, and that Φ_M, θ_M1, θ_M2, and θ_M3 are as described in the theorem. Also, let θ_P°(∙) be an estimator of θ_P, let θ_M°(∙) be an estimator of the three θ_Mi, i = 1, 2, 3, and assume that the estimators are consistent in their respective models. Finally, let (MP, θ_P°(∙)) be an econometric model of the TPD. Then observe that if (M1, θ_M°(∙)) is a congruent econometric model of the TPD, there is a binding function, Γ(∙):Φ_M → Φ_P, such that in M1 Γ(θ_M1) = plim θ_P°(s_n), and in MP, θ_P0 = plim θ_P°(s_n), θ_M0 = plim θ_M°(s_n), and θ_P0 = Γ(θ_M0). Next, observe that if M2 and M3 are data admissible, in M2 θ_M2 = plim θ_M°(s_n), and in M3, θ_M3 = plim θ_M°(s_n). Hence with Γ(θ) = θ, (M2, θ_M°(∙)) encompasses (M3, θ_M°(∙)) in the sense of Definition 1C. Finally, observe that if (M1, θ_M°(∙)) is a congruent econometric model of TPD and M1 is data admissible, then (M1, θ_M°(∙)) encompasses both (M2, θ_M°(∙)) and (M3, θ_M°(∙)) in the sense of Definition 1C. However, even though the converse is true, neither (M2, θ_M°(∙)) nor (M3, θ_M°(∙)) need be congruent econometric models of TPD.

The preceding theorem allows me to explicate the status of bridge principles in applied econometrics as follows:

The Status of Bridge Principles in Applied Econometrics.

Consider a theory-data confrontation like the one pictured in Figure 1. The theory is a non-empty family of models of a finite number of assertions concerning a few undefined terms. The bridge comprises a non-empty family of models of a finite number of assertions—the bridge principles—that relate variables in the theory to variables in the data universe. The data universe is as described in a few assertions that delineate the characteristics of the data generating process—the TPD. Assume (1) that there is an empirically relevant model of the theory, and (2) that each data-admissible model of the MPD singles out an empirically relevant model of the theory. Then, the bridge principles are valid in the Real World if and only if all the econometric models of the MPD, (M, θ_M°(∙)), with a data-admissible M are congruent econometric models of the TPD.4

I will exemplify the preceding definitions and the status of bridge principles in an empirical analysis of a simultaneous-equations model the idea of which I learned from reading Aris Spanos’ (1989) [14] and (2012) [15] deliberations about the legacy of Trygve Haavelmo’s (1944) [3] treatise “The Probability Approach in Econometrics”.

3. A Simultaneous-Equation Example

The present simultaneous-equation example considers the equilibrium configurations of a perfectly competitive market for one commodity. I generate artificial data for such a market, describe the way an applied econometrician in present-day econometrics analyses the data, and contrast it with the way an applied econometrician in formal econometrics analyses the same data. The present-day econometrician in this example is taken to be a present-day econometrician in the tradition of Haavelmo.

3.1. Formal Aspects of the Present Theory-Data Confrontation

I begin by formulating the axioms that underlie the formal-econometric analysis of the given market. They are axioms that delineate the characteristics of the theory universe, the two data universes, the Bridge, and the MPD that I need for the two empirical analyses of my data.

3.1.1. Assumptions Concerning the Theory Universe

The theory universe is a triple, (Ω_T, Г_T, (ΩT, ℵ_T, P_T(·))), where Ω_T is a subset of a vector space, Г_T is a finite set of assertions concerning the properties of the vectors in Ω_T, and (ΩT, ℵ_T, P_T(·)) is a probability space, where ℵ_T is a σ field of subsets of the given Ω_T, and P_T(∙)):ℵ_T → [0, 1] is a probability measure.

The assertions in Г_T comprise six axioms, A1–A6.

A1

Ω_T ⊂ R⁵ × R². Thus ω_T ϵ Ω_T only if ω_T = (x, u) for some x ϵ R⁵, u ϵ R², and (x, u) ϵ R⁵ × R².

A2

(x₁, x₂, x₃) € R₊³, x₄ ϵ {1, 2}, x₅ ϵ {1, 2}, u₁ ϵ {−1, 1}, and u₂ ϵ {−1, 1}.

In the intended interpretation of the components of x and u, x₁ and x₂ denote, respectively, the market participants’ intended demand for the commodity and the market participants’ intended supply of the commodity. Also, x₃ denotes the price of the commodity, x₄ and x₅ denote two auxiliary variables, and u₁, and u₂ are two error variables.

In an aggregate sense, the market participants’ intended demand for the commodity is a linear function of its price and the auxiliary variable, x₄. Similarly, the market participants’ intended supply of the commodity is a linear function of its price and the auxiliary variable, x₅. The values of the price variable and the auxiliary variables are such that the demand and supply of the commodity are always equal. Specifically,

A3

x₁ = A + Bx₃ + Cx₄; x₂ = D + Ex₃ + Fx₅; and x₁ = x₂.

The coefficients in the equations in A3 are taken to satisfy the conditions in A4.

A4

A ϵ [8, 10], B ϵ [−2, −1], C = 1, D = 0, E ϵ [1, 2], and F = 1

Relative to P_T(∙), the components of x and u are random variables. A5 and A6 bear witness to that.

A5

Let x(∙):Ω_T → R⁵ and u(∙):Ω_T → R² be defined by the equations, (x(ω_T), u(ω_T)) = ω_T and ω_T ϵ Ω_T. The vector-valued function, (x, u)(∙), is measurable with respect to ℵ_T and has, subject to the conditions on which Г_T insists, a well-defined probability distribution relative to P_T(∙), the RPD, where R is short for researcher, P for probability, and D for distribution.5

A6

Relative to P_T(∙), the components of x have finite means and positive variances, and the covariance matrix of x₄, and x₅ is invertible. Also u₁, and u₂ have means zero, positive variances, and are distributed independently of x₄ and x₅.

In the axioms I insist on strict limits on the values of the constants; e.g., D = 0, C = 1, and B ϵ [−2, −1], to help me display the contrast between present-day econometrics and formal econometrics. I will, also, insist that a model of A1–A4 is a model of the axioms that fixes the values of the constants in A4 but leaves the ranges of values of x and u unrestricted as described in A2. I have specified the range of values of x₄, x₅, u₁, and u₂, but not their probability distribution. The RPD distribution of the four variables has many models. That is an interesting aspect of the example.

The three equations in A3 constitute the theory of the present simultaneous-equation example. I will refer to these equations as the structural equations of the model and to the constants as the structural parameters. Theorem 2 shows how the structural equations can be solved for x₁ and x₃ so that the two variables become linear functions of the two auxiliary variables, x₄ and x₅. I will refer to the resulting system of equations, (1), as the reduced form of the present simultaneous-equation example. The reduced form plays a pivotal role in my deliberations.

Theorem 2.

Suppose that the theory axioms are valid, and let

α = [(A − D)/(E − B)], β = [C/(E − B)], γ = −[F/(E − B)];
a = [(AE − BD)/(E − B)], b = [CE/(E − B)], and c = −[BF/(E − B)].

(1) 

Then, it is the case that x₁ = a + bx₄ + cx₅; and x₃ = α + βx₄ + γx₅.

From the preceding theorem it follows that in each model of A1–A4 the components of x can assume only four values. For example,

if A = 10, B = −2, C = 1, D = 0, E = 1, and F = 1, the four values of x are:

(15/3, 15/3, 9/3, 1, 2); (16/3, 16/3, 10/3, 2, 2);
(13/3, 13/3, 10/3, 1, 1); and (14/3, 14/3, 11/3, 2, 1).

(2)

Similarly, if A = 8, B = −1, C = 1, D = 0, E = 2, and F = 1, the four values of x are:

(20/3, 20/3, 7/3, 1, 2); (22/3, 22/3, 8/3, 2, 2),
(19/3, 19/3, 8/3, 1, 1); and (21/3, 21/3, 9/3, 2, 1).

(3)

Equations (2) and (3) give an indication of the way the RPD distribution of x varies with the models of Г_T.

From Equations (2) and (3) it, also, follows that in each model of axioms A1–A4 the (x, u) vector, can assume sixteen values. For example, in the model of Equation (2)

(16/3, 16/3, 10/3, 2, 2, −1, −1); (16/3, 16/3, 10/3, 2, 2, −1, 1);

(16/3, 16/3, 10/3, 2, 2, 1, −1); and (16/3, 16/3, 10/3, 2, 2, 1, 1)

are four of the 16 possible values of (x, u). In the model of Equation (3)

(21/3, 21/3, 9/3, 2, 1, −1, −1); (21/3, 21/3, 9/3, 2, 1, −1, 1);

(21/3, 21/3, 9/3, 2, 1, 1, −1) and (21/3, 21/3, 9/3, 2, 1, 1, 1)

are four of the 16 possible values of (x, u). Since, (x, u)(ω_T) = ω_T, these vectors are at the same time possible values of ω_T.

According to Theorem 2, the values of the components of (A, B, C, D, E, F) determine the values of the components of (a, b, c, α, β, γ). It is, therefore, interesting that a model of the RPD distribution of x, also, determines the values of the components of (a, b, c, α, β, γ). The two sets of values of a, b, c, α, β, and γ must accord with each other.

Example 1:

Consider the first model of Г_T, where (A, B, C, D, E, F) = (10, −2, 1, 0, 1, 1). According to Theorem 2, the corresponding values of the components of (a, b, c, α, β, γ) are (10/3, 1/3, 2/3, 10/3, 1/3, −1/3). Suppose, now, that the RPD distribution of x₄ and x₅ is as described in the following equations:

P_T({x₄ = 1}) = 0.25; P_T({x₄ = 2}) = 0.75; P_T({x₅ = 1}) = 2/3; P_T({x₅ = 2}) = 1/3.

From these equations and Equations (2) and (3), we see that (cov. x₁,x₄, cov. x₁,x₅) = (0.0625, 0.14815), (cov. x₃,x₄, cov. x₃,x₅) = (0.0625, −0.07407), and (var.x₄, cov. x₄,x₅, var. x₅) = (0.1875, 0, 0.2222). Also, (mean (x₁, x₂, x₄, x₅)) = (4.8056, 3.4722, 1.75, 1.3333). Consequently, with G being the covariance matrix of x₄ and x₅, I can show that

(b, c) = (0.0625, 0.14815)G⁻¹ = (0.3334, 0.6668),

(β, γ) = (0.0625, −0.07407)G⁻¹ = (0.3334, −0.3334),

a = 4.8056 − 0.3334 × 1.75 − 0.6668 × 1.3333 = 3.3331; and

α = 3.4722 − 0.3334 × 1.75 + 0.3334 × 1.3333 = 3.3333.

In this case the two sets of values of a, b, c, α , β, and γ are equal.6

3.1.2. Assumptions Concerning the Two Data Universes

There is a basic data universe in which the data for the present analysis were generated. The basic data universe is a triple, (Ω_P, Г_P, (Ω_P, ℵ_P, P_P(∙)),where Ω_P is a subset of a vector space, Г_P is a finite set of assertions concerning the properties of the vectors in Ω_P, and (Ω_P, ℵ_P, P_P(∙))) is a probability space, where ℵ_P is a σ field of subsets of the given Ω_P, and P_P(∙)):ℵ_P → [0, 1] is a probability measure.

The assertions in Г_P comprise three axioms, D1–D3.

D1

Ω_P⊂ R⁴. Thus, ω_P ϵ Ω_P only if ω_P = y for some y ϵ R⁴.

The four components of the vectors in the data universe, y₁, y₂, y₃, and y₄, are taken to record, respectively, the actual sales and purchases of the given commodity, the price at which the sales were carried out, and the actual values of the two auxiliary variables that we met in the theory universe.

Relative to P_P(∙), the components of y are random variables. D2 and D3 attest to that.

D2

Let y(∙):Ω_P → R⁴ be defined by the equations, y(ω_P) = ω_P and ω_P ϵ Ω_P. The vector-valued function, y(∙), is measurable with respect to ℵ_P and has, subject to the conditions on which Г_P insists, a well-defined probability distribution, the TPD.7

D3

Relative to P_P(∙), y(∙) has finite means and a finite covariance matrix with positive diagonal elements. Finally, the covariance matrix of y₃ and y₄ is invertible.

Here, it is important to observe that, in the intended interpretation of the assumptions about this basic data universe, the TPD is taken to have one “true” model. The researcher does not know the “true” model of TPD.

In a formal theory-data confrontation the axioms of the basic data universe, Г_P, play two roles—one as part of the empirical analysis in the lower data universe of Figure 1 and another as the basic axioms for the empirical analysis in the upper data universe. For the upper data universe these basic axioms delineate an identifiable and low-level-theory-consistent structure of the empirical analysis. The low-level theory—here the Г_P—is taken to “provide a framework within which the high-level theory can be tested” (Bontemps and Mizon (2003) [5] (p. 365)).

In the present case, the researcher in the upper data universe accepts the Г_P axioms of the basic data universe, and observes that they imply that there exists a pair of random variables, ξ₁ and ξ₂, with means 0 and positive variances such that y satisfies two linear equations,

y₁(ω_P) = d + ey₃(ω_P) + fy₄(ω_P) + ξ₁(ω_P); and

(4)

y₂(ω_P) = λ + πy₃(ω_P) + ρy₄(ω_P) + ξ₂(ω_P).

(5)

The researcher, then, adds to the assertions in Г_P the following three assumptions about the TPD distribution of y(∙):

(1)

The observations of y need not be accurate observations of the “true” variables with which the researcher identifies his theory. The “true” values of the constants in Equations (4) and (5) are such that the “true” components of y(∙) satisfy the two equations without error terms.

(2)

There are constants, A, B, C, D, E, and F whose values satisfy the conditions in A4 and the equations in Theorem 2 with the “true” TPD values of d, e, f, λ, π, and ρ in place of a, b, c, α, β, and γ.

(3)

The “true” components of y satisfy the relations:

y₁ = A + By₂ + Cy₃; and y₁ = D + Ey₂ + Fy₄

The assumptions that the researcher in the upper data universe adds to Г_P are assumptions about the characteristics of the TPD. Consequently, they have one “true” model. That is a fact that plays an important role in the empirical analysis of present-day econometrics.

3.1.3. Assumptions Concerning the Bridge and the MPD

The Bridge is a pair, (Ω, Г_T,P), where Ω is a subset of Ω_T × Ω_P, and Г_T,P is a finite set of assertions about the vectors in Ω. It is understood that a researcher’s observations consist of pairs, (ω_T, ω_P), where ω_T ϵ Ω_T, ω_P ϵ Ω_P, and (ω_T, ω_P) ϵ Ω. The components of ω_T are unobservable, while the components of ω_P are observable. For example, in the present example two of the components of ω_T may record the intended demand and intended supply of the commodity in a pertinent market while one of the components of ω_P will record the actual sales and purchases of the commodity in the same market.

The assertions in Г_T,P comprise five axioms, B1–B5.

B1

Ω ⊂ Ω_T × Ω_P. Thus ω € Ω only if ω = (ω_T, ω_P) for some ω_T ϵ Ω_T, ω_P ϵ Ω_P, and (ω_T, ω_P) ϵ Ω_T × Ω; i.e., ω € Ω only if ω = ((x,u), y) for some (x,u) ϵ Ω_T, y ϵ Ω_P, and ((x,u), y) ϵ Ω_T × Ω_P.

B2

Ω_T and Ω_P are disjoint and ℵ_T and ℵ_P are stochastically independent.8

B3

In the probability space, (Ω_T × Ω_P, ℵ, P(∙)), that the probability spaces in the theory universe and the data universe determine, Ω ϵ ℵ, and P(Ω) > 0.

B4

Ω_T⊂ {(x, u) ϵ Ω_T for which there is a y ϵ Ω_P such that ((x, u),y) ϵ Ω}.

B5

For all (ω_T, ω_P) ϵ Ω,

y₁(ω_P) = x₁(ω_T) + u₁(ω_T); y₂(ω_P) = x₃(ω_T) + u₂(ω_T);

y₃(ω_P) = x₄(ω_T); and y₄(ω_P) = x₅(ω_T).

B5 is an interesting axiom that claims several things that it is important to keep in mind. First, if I substitute the reduced form equations in (1) for x₁ and x₃, the first two equations in B5 insist that

y₁(ω_P) = a + bx₄(ω_T)+ cx₅ (ω_T) + u₁(ω_T); and

(6)

y₂(ω_P) = α + βx₄(ω_T)+ γx₅(ω_T) + u₂(ω_T).

(7)

Next, the last two equations in B5 can be read to insist that on a bridge y₃ and y₄ can assume only the values 1 and 2.

A superficial look at axioms B4 and B5 gives the impression that the bridge has only one model. That is not true. So an example is called for. In reading the example, keep in mind that x_i(ω_T) = ω_Ti, i = 1, …, 5, u_j(ω_T) = ω_T5+j, j = 1, 2.

Example 2:

Consider the two models of the A1–A4 axioms, where (1) A = 10, B = −2, C = 1, D = 0, E = 1, and F = 1; and (2) A = 8, B = −1, C = 1, D = 0, E = 2, and F = 1. I will record two vectors in the Ω of each model—see

Table 1. Pairs of vectors in two different Bridges.

	x1	x2	x3	x4	x5	u1	u2	y1	y2	y3	y4
(1)	15/3	15/3	9/3	1	2	−1	−1	4	2	1	2
	15/3	15/3	9/3	1	2	1	−1	6	2	1	2
(2)	20/3	20/3	7/3	1	2	−1	−1	17/3	4/3	1	2
	20/3	20/3	7/3	1	2	1	−1	23/3	4/3	1	2

—and describe the possible values of y₁ and y₂ in the support of the MPD distribution of y(∙) in each model. First, the vectors in the two Ωs:

Then, the possible values of y₁ and y₂ that in the respective models are members of a pair (ω_T, ω_P) ϵ Ω:

$$\begin{array}{l}{\mathrm{y}}_1 \mathsf{ϵ} \{10/3, 11/3, 12/3, 13/3, 16/3, 17/3, 18/3, 19/3\}\\ {\mathrm{y}}_2 \mathsf{ϵ} \{6/3, 7/3, 8/3, 12/3, 13/3, 14/3\}\\ {\mathrm{y}}_1 \mathsf{ϵ} \{16/3, 17/3, 18/3, 19/3, 22/3, 23/3, 24/3, 25/3\}\\ {\mathrm{y}}_2 \mathsf{ϵ} \{4/3, 5/3, 6/3, 10/3, 11/3, 12/3\}\end{array}$$

The preceding example demonstrates that a bridge comprises no more than sixteen different vectors. Also, each model of A1–A4 determines one well defined bridge, and different models of A1–A4 determine different bridges. Finally, the relation between a model of A1–A4 and the bridge which it determines is independent of the RPD.

3.1.4. The MPD Distribution of y(∙)

The probability distribution of the data variables that is derived from the RPD and the bridge principles I have designated by the acronym MPD, where M is short for marginal, P stands for probability, and D is short for distribution. I refer to it as the marginal probability distribution of the data variables.9

Formally, the MPD is the probability distribution of the components of ω_P that is induced by the bridge principles and the probability distribution of the components of ω_T that P_T(·) determines. In the present context, MPD is the probability distribution of y(·) induced by the RPD distribution of (x,u)(·) and the bridge principles.

To describe the MPD distribution of y(∙) I need to introduce two new variables:

For all (ω_T, ω_P) ϵ Ω, v₁(ω_P) = u₁(ω_T), and v₂(ω_P) = u₂(ω_T).

It follows from the bridge principles and from Theorem 2 that v₁(∙) and v₂(∙) are well defined in a given Ω, and satisfy the Equations in (8) and (9) in Theorem 3.

Theorem 3.

Suppose that the theory assumptions and the bridge principles are valid. Then it is the case that, for all ω_P in the support of a given MPD,

y₁(ω_P) = a + by₃(ω_P) + cy₄(ω_P) + v₁(ω_P); and

(8) 

y₂(ω_P) = α + βy₃(ω_P) + γy₄(ω_P) + v₂(ω_P)

(9) 

The two vs obviously vary with Ω. Thus in the first model of the theory universe, v₁(ω_P) = 1 in the subset of Ω_P, in which, y₁(ω_P) ϵ {16/3, 17/3, 18/3, 19/3}; v₁(ω_P) = −1 in the subset of Ω_P, in which, y₁(ω_P) ϵ {10/3, 11/3, 12/3, 13/3}; v₂(ω_P) = 1 in the subset of Ω_P, in which, y₂(ω_P) ϵ {12/3, 13/3, 14/3}; and v₂(ω_P) = −1 in the subset of Ω_P, in which, y₂(ω_P) ϵ {6/3, 7/3, 8/3}.

In the second model of the theory universe, v₁(ω_P) = 1 in the subset of Ω_P, in which, y₁(ω_P) ϵ {22/3, 23/3, 24/3, 25/3}; v₁(ω_P) = −1 in the subset of Ω_P, in which, y₁(ω_P) ϵ {16/3, 17/3, 18/3, 19/3}; v₂(ω_P) = 1 in the subset of Ω_P, in which, y₂(ω_P) ϵ {10/3, 11/3, 12/3}; and v₂(ω_P) = −1 in the subset of Ω_P, in which, y₂(ω_P) ϵ {4/3, 5/3, 6/3}.

For the interpretation of the coming empirical analysis I need two theorems. The validity of the first theorem is an immediate consequence of the definition of the vs and the definition of the MPD that the statement of the theorem gives. The validity of the second theorem follows from the first and from Kolmogorov’s consistency theorem (cf. Stigum (1990) [17] (pp. 346–347)).

Theorem 4.

Suppose that the axioms of the theory universe and the bridge are valid, and let MPD(∙) be an MPD that a model of the theory universe and the bridge determine. Then it is a fact that for any A ⊂ R² and B ⊂ R²,

$$\begin{array}{l}\mathrm{MPD}(\{({\mathrm{y}}_3,{\mathrm{y}}_4,{\mathrm{v}}_1,{\mathrm{v}}_2)({\mathsf{\omega }}_{\mathrm{P}}) ϵ \mathrm{A}\times \mathrm{B}\})=\\ \frac{{\mathrm{P}}_{\mathrm{T}}(\{{\mathsf{\omega }}_{\mathrm{T}} \mathsf{\epsilon } {\mathrm{\Omega }}_{\mathrm{T}}:\left({\mathrm{x}}_4,{\mathrm{x}}_5,{\mathrm{u}}_1,{\mathrm{u}}_2\right)\left({\mathsf{\omega }}_{\mathrm{T}}\right)ϵ\mathrm{A}\times \mathrm{B}\}\cap \{{\mathsf{\omega }}_{\mathrm{T}} \mathsf{\epsilon } {\mathrm{\Omega }}_{\mathrm{T}}\text{ with an }{\mathsf{\omega }}_{\mathrm{P}} \mathsf{\epsilon } {\mathrm{\Omega }}_{\mathrm{P}}\text{ and }({\mathsf{\omega }}_{\mathrm{T}},{\mathsf{\omega }}_{\mathrm{P}}) \mathsf{\epsilon } \mathrm{\Omega }\})}{P_T(\{{\omega }_T\epsilon {\Omega }_{T}withan{\omega }_P\epsilon {\Omega }_{P}and({\omega }_T,{\omega }_P)\epsilon \Omega \})}\end{array}$$

which, since Ω_T ⊂ {ω_T ∈ Ω_T for which there is an ω_P ∈ Ω_P with (ω_T, ω_P) ∈ Ω},

= P_T({(x₄, x₅, u₁, u₂)(ω_T) ϵ A × B}).

From this theorem and the bridge principles it follows that the MPD distribution of (y₃, y₄, v₁,v₂) equals the RPD distribution of (x₄, x₅, u₁, u₂). This fact and Equations (6)–(9) show how the RPD distribution of (x, u) and the bridge principles determine the MPD distribution of y.

Theorem 5.

Suppose that the theory axioms and the axioms of the Bridge are valid. For each model of the theory universe and the Bridge there exists a probability measure P_M(∙):ℵ_P → [0, 1] and two random variables v₁ and v₂ with two important properties. Relative to P_M(∙), (y, v₁, v₂) has the MPD distribution which the model of the theory universe and the Bridge determine. Also, relative to P_M(∙), v₁ and v₂ have the same means and variances as u₁ and u_2, are distributed independently of y₃ an y₄, and satisfy the Equations (10) and (11) for all ω_P ϵ Ω_P; i.e., for all ω_P ϵ Ω_P,

y₁(ω_P) = a + by₃(ω_P) + cy₄(ω_P) + v₁(ω_P); and

(10)

y₂(ω_P) = α + βy₃(ω_P) + γy₄(ω_P) + v₂(ω_P).

(11)

In Equations (10) and (11) the values of (a, b, c, α, β, γ) are the values that the pertinent model of the A1–A4 axioms determines. Also, in the support of the pertinent P_M(∙) the values of the v₁ and v₂ in Equations (10) and (11) coincide with the values of the v₁ and v₂ in Equations (8) and (9). Finally, in the support of the pertinent P_M(∙) y₃ and y₄ can assume only the values 1 and 2.

The last two theorems call for several clarifying remarks. Note first that I derived Equations (8) and (9) from A1–A4 and the bridge principles without involving the RPD distribution of (x, u). The RPD distribution of (x₄, x₅, u₁, u₂) is independent of the models of A1–A4. Hence, for each model of A1–A4 and the bridge principles there are as many MPD distributions of (y₃, y₄, v₁, v₂) as there are RPD distributions of (x₄, x₅, u₁, u₂). Also, for each model of A1–A4 there are as many MPD distributions of (y, v₁, v₂) as there are MPD distributions of (y₃, y₄, v₁, v₂). Finally, even if there is just one RPD distribution of (x₄, x₅, u), there are many MPD distributions of (y, v₁, v₂) since they vary with the models of A1–A4.

4. The Two Empirical Analyses

For the two empirical analyses I am to generate 1249 “observations” of ((x, u), y). The components of (x, u) are unobservable. Hence only the sample of ys will be observed. To generate the sample of ys I proceed as follows. I presume that the components of y in the TPD distribution satisfy the equations,

y₁ = 16/3 + 2/3y₃ + 1/3y₄ + ξ₁; and y₂ = 8/3 + 1/3y₃ − 1/3y₄ + ξ₂

(12)

I presume, also, that y₃, y₄, ξ₁, and ξ₂ are distributed independently of each other, and that their distribution is given by the equations,

P_P({y₃ = 1}) = 0.25; P_P({y₃ = 2}) = 0.75; P_P({y₄ = 1}) = 2/3; P_P({y₄ = 2}) = 1/3; and

P_P({ξ_i = −1}) = P_P({ξ_i = 1}) = 0.5, i = 1,2.

From these equations and the equations in (12) it follows that the joint probability distribution of y₁ and y₂ is as described in

Table 2. The Joint Probability Distribution of y1 and y2.

	y1	16/3	17/3	18/3	19/3	22/3	23/3	24/3	25/3	Py2
y2
4/3		2/576	1/576	6/576	3/576	2/576	1/576	6/576	3/576	1/24
5/3		10/576	5/576	30/576	15/576	10/576	5/576	30/576	15/576	5/24
6/3		12/576	6/576	36/576	18/576	12/576	6/576	36/576	18/576	6/24
10/3		2/576	1/576	6/576	3/576	2/576	1/576	6/576	3/576	1/24
11/3		10/576	5/576	30/576	15/576	10/576	5/576	30/576	15/576	5/24
12/3		12/576	6/576	36/576	18/576	12/576	6/576	36/576	18/576	6/24
Py1		2/24	1/24	6/24	3/24	2/24	1/24	6/24	3/24	1

. But if that is so, then the means and co-variances of the components of y satisfy the equations:

Mean(y₁) = 6.94; Mean(y₂) = 2.806; Mean(y₃) = 7/4; Mean(y₄) = 4/3;

Variance(y₁) = 1.108; Variance(y₂) = 1.046; Variance(y₃) = 0.188; Variance(y₄) = 0.2222;

Covariance(y₁,y₂) = 0; and Covariance(y₃,y₄) = 0.

The corresponding values of ξ₁, and ξ₂ are

Mean(ξ₁) = Mean(ξ₂) = 0: Variance(ξ₁) = Variance(ξ₂) = 1; and Covariance(ξ₁,ξ₂) = 0.

With these probabilities and moments in mind I use the PcGive’s uniform random number generator, ranu(), and PcGive to produce the required data and to carry out the statistical analysis (cf. Dornik (2009) [18] (pp. 158–162) and Dornik and Hendry (2009) [19]). Specifically, I generate 1249 observations of y₁, y₂, y₃, y₄, ξ₁, and ξ₂ with OxMetrics’ random number generator for the uniform distribution, ranu(). The algebra codes in Appendix A detail how the observations were generated. In the printout, y₁ = y6, y₂ = y7, y₃ = y8, y₄ = y9, ξ₁ = u6, and ξ₂ = u7. The results of the statistical analysis are displayed in

Table 3. Means, Standard Deviations, and Correlations of y and u.

Means
	y6	y7	y8	y9	u6	u7
	6.9933	2.7537	1.7406	1.3379	0.053643	−0.047238
Standard Deviations (Using T − 1)
	y6	y7	y8	y9	u6	u7
	1.0569	1.0273	0.43849	0.47317	0.99896	0.99928
Correlation Matrix
	y6	y7	y8	y9	u6	u7
y6	1.0000	−0.0084852	0.28097	0.15833	0.95078	−0.024830
y7	−0.0084852	1.0000	0.15925	−0.17482	−0.027976	0.97712
y8	0.28097	0.15925	1.0000	−0.032943	0.0098421	0.012243
y9	0.15833	−0.17482	−0.032943	1.0000	0.019262	−0.017058
u6	0.95078	−0.027976	0.0098421	0.019262	1.0000	−0.027159
u7	−0.024830	0.97712	0.012243	−0.017058	−0.027159	1.0000

, Figure 2 and Figure 3, and

Table A1. Modelling y6 by OLS-CS with 1249 observations.

Estimates of the constants in Equation (4) and their significance.
	Coefficient	Std.Error	t-Value	t-Prob	Part.R^2
Constant	5.29001	0.1429	37.0	0.0000	0.5237
y8	0.690561	0.06456	10.7	0.0000	0.0841
y9	0.374728	0.05983	6.26	0.0000	0.0305
Measures of the goodness of fit of the estimated equation.
Sigma	0.999521	RSS	1244.80701
R^2	0.107061	F(2,1246) =	74.7 [0.000]**
Adj.R^2	0.105627	log-likelihood	−1770.15
No. of observations	1249	No. of parameters	3
mean(y6)	6.99333	se(y6)	1.0569
Tests of certain probabilistic characteristics of the error term in Equation (13).
Normality test:	Chi^2(2) = 1569.0 [0.0000]**
Hetero test:	F(2,1246) = 0.42845 [0.6516]
Hetero-X test:	F(3,1245) = 0.39513 [0.7565]
RESET23 test:	F(1,1245) = 0.22032 [0.6389]

** indicates that the pertinent null hypothesis is rejected at the one percentage level of significance.

and

Table A2. EQ(2) Modelling y7 by OLS-CS with 1249 observations.

Estimates of the constants in Equation (5) and their significance.
	Coefficient	Std.Error	t-value	t-prob	Part.R^2
Constant	2.62015	0.1430	18.3	0.0000	0.2123
y8	0.359983	0.06458	5.57	0.0000	0.0243
y9	−0.368543	0.05985	−6.16	0.0000	0.0295
Measures of the goodness of fit of the estimated equation.
Sigma	0.999872	RSS	1245.68014
R^2	0.0541462	F(2,1246) =	35.66 [0.000]**
Adj.R^2	0.052628	log-likelihood	−1770.59
No. of observations	1249	no. of parameters	3
mean(y7)	2.75367	se(y7)	1.02727
Tests of certain probabilistic characteristics of the error term in Equation (14).
Normality test:	Chi^2(2) = 1577.5 [0.0000]**
Hetero test:	F(2,1246) = 0.097428 [0.9072]
Hetero-X test:	F(3,1245) = 0.46596 [0.7061]
RESET23 test:	F(1,1245) = 0.80716 [0.3691]

** indicates that the pertinent null hypothesis is rejected at the one percentage level of significance.

in Appendix A. They demonstrate that the probability distribution of (y, ξ) described above is statistically adequate in the sense that it accounts for the chance regularities in the data (cf. Spanos (2012) [15] p. 14).

4.1. An Empirical Analysis in Accord with the Commands of Present-Day Econometrics

In the upper data universe in Figure 1 the researcher begins by estimating the parameters in Equations (4) and (5). His statistical analysis of the data is centered on three basic ideas: (1) In accord with the commands of present-day econometrics he must obtain consistent estimates of the pertinent TPD parameters; (2) An estimate of the parameters in Equations (4) and (5) is theoretically meaningful if it and Theorem 2 determine an acceptable structural model; (3) An economic theory is taken to be empirically relevant if it—in a standard statistical sense—cannot be rejected. In the present case the theory cannot be rejected only if all the vectors in the confidence region around a given estimate of TPD contains just theoretically meaningful parameter vectors.

The results of the researcher’s statistical analysis are recorded in Appendix A. The estimated versions of Equations (4) and (5) are as follows:

y₁ = 5.29001 + 0.690561y₃ + 0.374728y₄ + eu6; and

(13)

y₂ = 2.62015 + 0.359983y₃ − 0.368543y₄ + eu7.

(14)

Except for the normality tests, the diagnostic tests have acceptable results. Also, the sample of ys was obtained with a purely random sampling scheme. This and the fact that the probability distribution of (y, ξ) in (12) is statistically adequate allow the researcher to claim that his parameter estimates are consistent and asymptotically normally distributed.10

The acceptable diagnostic results and the consistency of the researcher’s estimates need not mean that the estimates in (13) and (14) are theoretically meaningful. For an easy check of that, the researcher uses the following inverse of Theorem 2.

Theorem 6.

It follows from the equations in Theorem 2 that

A = a − Bα; B = c/γ; and C = [(E − B)/E]b;

(15)

D = a − Eα; E = b/β, and F = [(B − E)/B]c

(16)

From Equations (15) and (16) and the regression results he obtains the following indirect estimates of the structural parameters;

A = 7.95413; B = − 1.01678, C = 1.05658

(17)

D = 0.26372; E = 1.91832; F = 1.08171

(18)

These estimates demonstrate that the parameters in the estimated equations do not constitute parameters of a theoretically meaningful estimate of the TPD.

Since his estimate of TPD is not theoretically meaningful, the researcher finds it interesting to check if there is a parameter vector in Wald’s confidence band that constitutes a parameter vector of a theoretically meaningful estimate of the TPD.

Wald’s confidence band is as described by the following intervals:

a ϵ (5.00421, 5.57581), b ϵ (0.561441, 0.819681), and c ϵ (0.255068, 0.494388)

(19)

α ϵ (2.33415, 2.90615), β ϵ (0.230823, 0.489143), and γ ϵ (−0.488243,−0.248843)

(20)

In this confidence region the constants in Equations (21) and (22) below constitute, within an admissible margin of error, parameters of a theoretically meaningful estimate of the TPD:

a = 5.00422, b = 0.62545, c = 0.37455

(21)

α = 2.90614, β = 0.36322, γ = −0.36322

(22)

In fact, these two equations and Equations (15) and (16) determine the following values of the structural parameters

A = 8.001, B = −1.03119, and C = 1.00000;

(23)

D = 0.00001, E = 1.72195, and F = 1.00000.

(24)

The results of the statistical analysis in the upper data universe in Figure 1 carry three kinds of information: (1) The estimates do not determine theoretically meaningful values of the structural parameters; (2) With 95% probability there exist parameter vectors that satisfy the researcher’s theoretical hypothesis; and (3) Wald’s confidence region contains parameter vectors that do not satisfy the researcher’s theoretical hypothesis. These three observations leave the researcher in the upper data universe with no other choice than to reject the hypothesis which he formulated in the three assumptions he added to Γ_P. i.e., he must conclude that his theory is not empirically relevant.

4.2. A Formal-Econometric Empirical Analysis

In the lower data universe in Figure 1 the researcher’s empirical deliberations center on three fundamental ideas that describe the prescriptions underlying the statistical analysis, delineate the salient characteristics of a data admissible model of the MPD, and describe what it means for a theory to be empirically relevant. In the present context the prescriptions that underlie the statistical analysis delineate the way the researcher is to obtain a consistent estimate of a mathematical model of the MPD. Also, a mathematical model of the MPD is data admissible if (1) the estimated mathematical model of MPD satisfies the strictures on which the basic-data axioms and the prescriptions that underlie the statistical analysis insist; (2) the values that the given model assigns to the parameters of MPD satisfy the strictures on which the theory axioms and the bridge principles insist; and (3) the model lies within a 95% confidence region of the estimated mathematical model of MPD. Finally, a family of mathematical models of Г_T is empirically relevant if and only if there is at least one member of the family which—with a corresponding model of the axioms of the basic data universe and the Bridge—determines a data-admissible model of the MPD.

The researcher in the lower data universe begins by estimating the parameters in Equations (10) and (11). Since these equations are, formally, like Equations (4) and (5), his estimates are the same as the ones given in Equations (13) and (14). These estimates are not theoretically meaningful. Hence, they cannot be data admissible. Now, the arguments that demonstrate that the parameter values in Equations (21) and (22) are theoretically meaningful suffice to demonstrate that these parameter values are also parameters of a data admissible MPD. Theorem 7 attests to that:

Theorem 7.

Suppose that the theory axioms and the axioms of the Bridge are valid. In the present empirical analysis a theoretically meaningful parameter vector whose components belong in Wald’s confidence intervals is the parameter vector of a data admissible MPD distribution of y.

A simple sketch of a proof runs as follows. Let G be a theoretically meaningful parameter vector whose components belong in Wald’s confidence intervals, let H be the structural parameter vector that it determines, and let Ω(H) be the bridge that H determines. Then, define v₁ and v₂ on Ω(H), formulate the pertinent versions of Equations (8) and (9), and pick an RPD distribution of (x₄, x₅, u₁, u₂). The Equations (8) and (9), Theorem 4, and the given RPD distribution of (x₄, x₅, u₁, u₂) suffice to construct an MPD distribution of (y, v₁, v₂). This MPD distribution is data admissible, and G is its parameter vector.

The preceding theorem makes it possible to establish the next theorem. Theorem 8 is the fundamental theorem of the formal-econometric analysis of my data.

Theorem 8

Suppose that the theory axioms and the axioms of the Bridge are valid. Then a parameter vector whose components belong in Wald’s confidence intervals determines an empirically relevant model of Г_T if and only if it is a theoretically meaningful parameter vector.

It is obvious that the parameter vector of an MPD which an empirically relevant model of Γ_T determines is theoretically meaningful and has components that belong to Wald’s confidence intervals. Hence to establish the theorem it suffices to show that a theoretically meaningful parameter vector whose components belong in Wald’s confidence intervals determines an empirically relevant model of Γ_T. A theoretically meaningful parameter vector determines a model of axioms A1–A4. Also it follows from Theorem 7 that a theoretically meaningful parameter vector whose components belong in Wald’s confidence intervals is the parameter vector of a data admissible MPD. Hence I can conclude the proof by showing that the pertinent data admissible MPD determines a model of an RPD distribution of (x, u). Let the parameter vector in Equations (21) and (22) be the theoretically meaningful vector in question, and let v₁ and v₂ be the random variables that satisfy the equations

y₁(ω_P) − 5.00422 − 0.62545y₃(ω_P) − 0.37455y₄(ω_P) = v₁(ω_P)

(25)

y₂(ω_P) − 2.90614 − 0.36322y₃(ω_P) + 0.36322y₄(ω_P) = v₂(ω_P)

(26)

Then, pick an ω_P° in the support of the MPD distribution of v₁ and v₂, and let

(u₁, u₂) = (v₁, v₂)(ω_P°),

x₁ = 5.00422 + 0.62545y₃(ω_P°) + 0.37455y₄(ω_P°),

x₃ = 2.90614 + 0.36322y₃(ω_P°) − 0.36322y₄(ω_P°),

x₄ = y₃(ω_P°),

and

x₅ = y₄(ω_P°).

The MPD distribution of the right-hand side of these equations determines an RPD distribution of the left-hand side that has all the required properties; i.e., a probability distribution that is a model of the RPD distribution of (x₁, x₃, x₄, x₅, u₁, u₂). That and the equation x₁ = x₂ conclude the proof that the theory universe has an empirically relevant model.

The preceding deliberations show that there is at least one empirically relevant model of Г_T. There may be many more. To find out how many more, the researcher will need two more theorems.

Theorem 9.

Suppose that the theory axioms and the axioms of the Bridge are valid. Then the subsets of Wald's confidence intervals that contain the data admissible parameter vectors are as described below:

a ϵ (5.00421, 5.57581), b ϵ (0.561441, 0.6667), and c ϵ (0.3333, 0.494388)

(27)

α ϵ (2.33415, 2.90615), β ϵ (0.25, 0.489143), and γ ϵ (−0.488243, −0.25)

(28)

I have obtained these intervals in two steps. First I used the equations in A4 and Theorem 2 to determine the acceptable minimum and maximum values of the pertinent parameters; e.g., 2.666 < a < 6.6667 and 0.3333 < b < 0.6667. Then, I compared these maximum and minimum values with the Wald intervals in Equations (19) and (20) and determined the extent of the asked-for intervals in Equations (27) and (28).

Theorem 10.

Suppose that the theory axioms and the axioms of the Bridge are valid. Then the intervals in Equations (27) and (28) imply that the empirically relevant values of the components of (A, B, E) must satisfy the conditions:

7.33831 < A < 11.32278; −1.977552 < B < −0.68265; and 1.14781 < E < 2.667.

(29)

Consequently, in the present empirical context not all the models of the theory axioms are empirically relevant.

The intervals in Equation (29) put added restrictions on the values of B, and E. In doing that, Theorem 10 demonstrates that models of the theory with a B € [−2, −1.977552] and/or an E € [1, 1.14781] cannot be empirically relevant. From this the researcher concludes that the inequalities in Equation (29) demonstrate that all the models of the theory axioms with A € [8, 10], B € (÷1.977552, ÷1], C = 1, D = 0, E € (1.14781, 2], and F = 1 are empirically relevant in the present empirical context. Theorem 11 bears witness to that:

Theorem 11.

Suppose that the theory axioms and the axioms of the Bridge are valid. Then all the models of the theory axioms with A € [8, 10], B € (−1.977552, −1], C = 1, D = 0, E € (1.14781, 2], and F = 1 are empirically relevant in the present empirical context.

4.3. The Contrasts and the Status of B1–B5

In this Section, I will describe the contrasts between the empirical analyses in the two data universes in Figure 1 and conclude the example by establishing the status of the bridge principles, B1–B5, in the present theory-data confrontation.

4.3.1. The Contrasts

The three observations which in a nutshell concretize the results of the empirical analysis in the upper data universe, are also observations that the researcher in the lower data universe made. In the upper data universe the second assertion is to no avail for the empirical relevance of the researcher’s hypotheses because he is unable to assign a probability to his observation of the vector in Equations (21) and (22). In the lower data universe the researcher uses the same vector to show that his theory is empirically relevant. In the upper data universe the third observation leaves the researcher with no other choice than to declare that his theory is not empirically relevant. In the lower data universe the researcher uses a similar observation—Theorem 10—to delineate the subfamily of models of his theory that are empirically relevant.

4.3.2. The Status of B1–B5

The bridge principles play a central role in my deliberations in the lower data universe. It is, therefore, right to question the validity of the axioms of the Bridge. In Stigum (2015) [1], I claimed that there are good reasons to believe in the validity of the bridge principles in the Real World if the 95% confidence region around a meaningful estimate of the pertinent MPD is data admissible. A 95% confidence band is data admissible if it contains a congruent model of the TPD and a data admissible model of the MPD. In this paper, I insist that the bridge principles are valid in the Real World if and only if (1) the MPD in a congruent econometric model of the TPD is data admissible; and (2) all the pairs of econometric models of the MPD, (M1, θ_M°(∙)) with a data-admissible model of the MPD, are congruent.

Next I will show that the Wald intervals in the present example constitute a 95% data-admissible confidence region, and that B1–B5 are valid in the Real World. I begin by showing that the Wald intervals contains a model of MPD that is congruent. In this case there are two econometric models to consider, (M1, θ_M°(∙)) and (M2, θ_P°(∙)), where M1 is any one of the many MPD distributions, θ_M°(∙) is the estimator of (a, b, c, α, β, γ, σ_v1², σ_v2²) in Equations (10) and (11), M2 is the TPD distribution, and θ_P°(∙) is the estimator of (d, e, f, λ, π, ρ, σ_ξ1², σ_ξ2²) in Equations (4) and (5). The estimators are consistent, and in M1 it is a fact that θ_M°(s_n) = θ_P°(s_n) a.e.. Hence, (M1, θ_M°(∙)) exactly encompasses (M2, θ_P°(∙)) no matter which one of the possible MPD distributions one chooses for M1. It is, also, the case that if I choose the components of θ_M1 to have the values ascribed to them in Equations (21) and (22), and if I let θ_P equal θ_P0, where θ_PO = (16/3, 2/3, 1/3, 8/3, 1/3, −1/3, 1, 1), then in M2, plim θ_P°(s_n) = θ_P0 = plim θ_M°(s_n). Hence, with the given choice of M1, M1 is coherent with the pertinent a priori theory, and (M1, θ_M°(∙)) encompasses (M2, θ_P°(∙)) in the sense of Definition 1C. Since the sampling system in the present case is adequate, it follows that with the given choice of θ_M, (M1, θ_M°(∙)) is a congruent econometric model of the TPD.

At last, I must show that the Wald intervals constitute a data-admissible confidence region and that B1–B5 are valid in the real world. I have shown before that the M1 in the congruent model of TPD is data admissible. Hence, the Wald intervals constitute a data-admissible confidence region. It is, also, obvious from my deliberation above that I can substitute for M1 any data admissible model of MPD and obtain a congruent model of TPD. Hence all the data-admissible models of MPD are congruent. But, if that is true, then it is a fact that the bridge principles in the present example are valid in the real world.