Bio-Inspired Flexible Flapping Wings with Elastic Deformation
Abstract
:1. Introduction
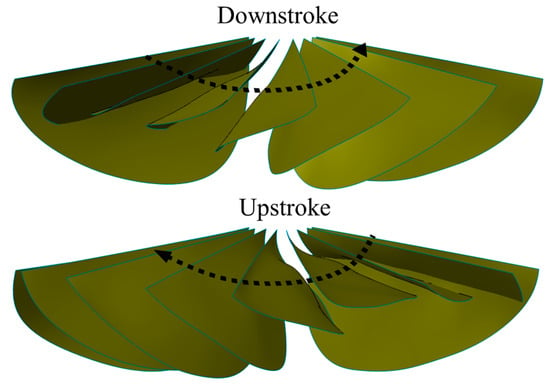
2. Flapping Mechanism and Wing Design
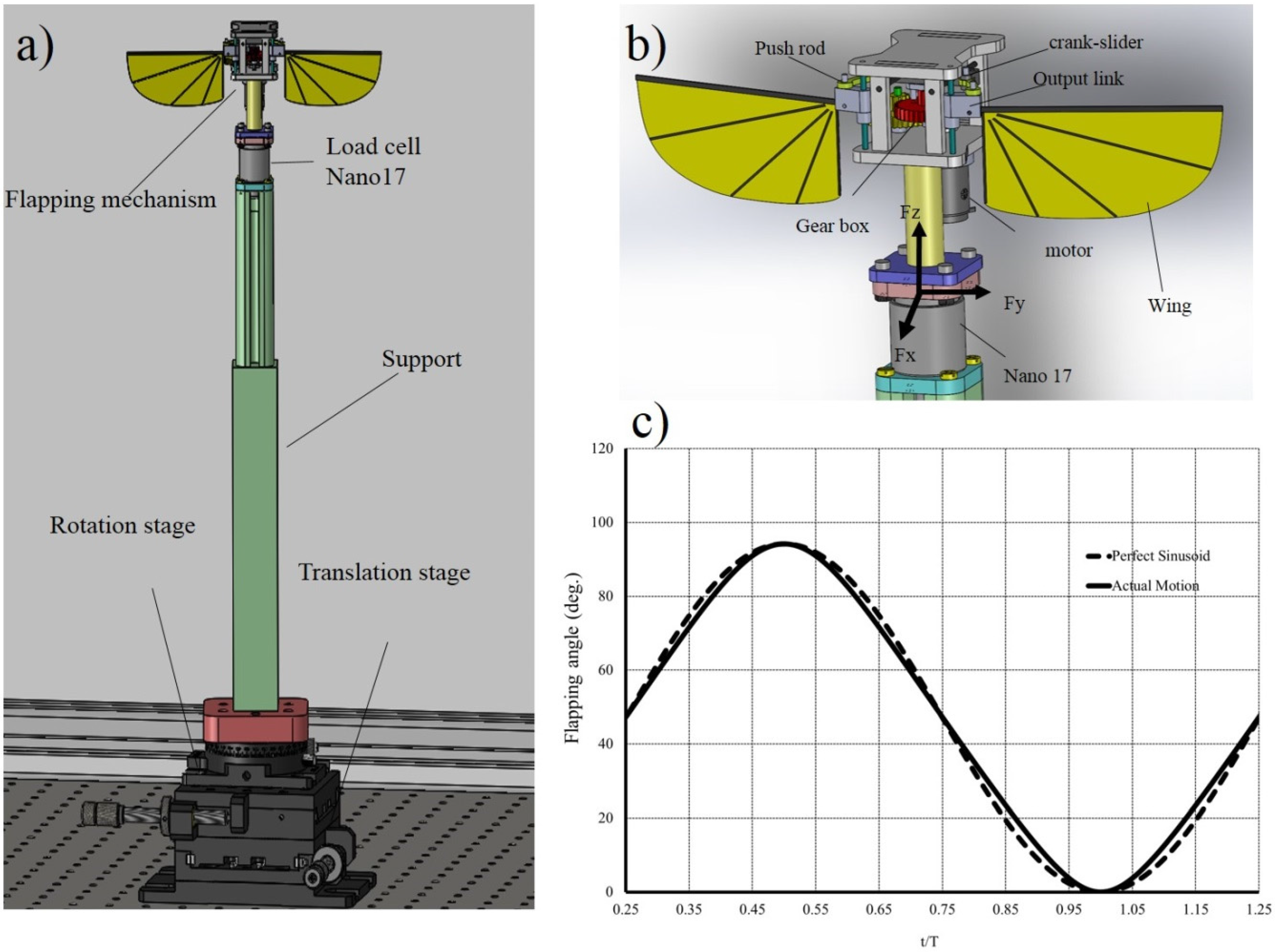
2.1. Flapping Mechanism
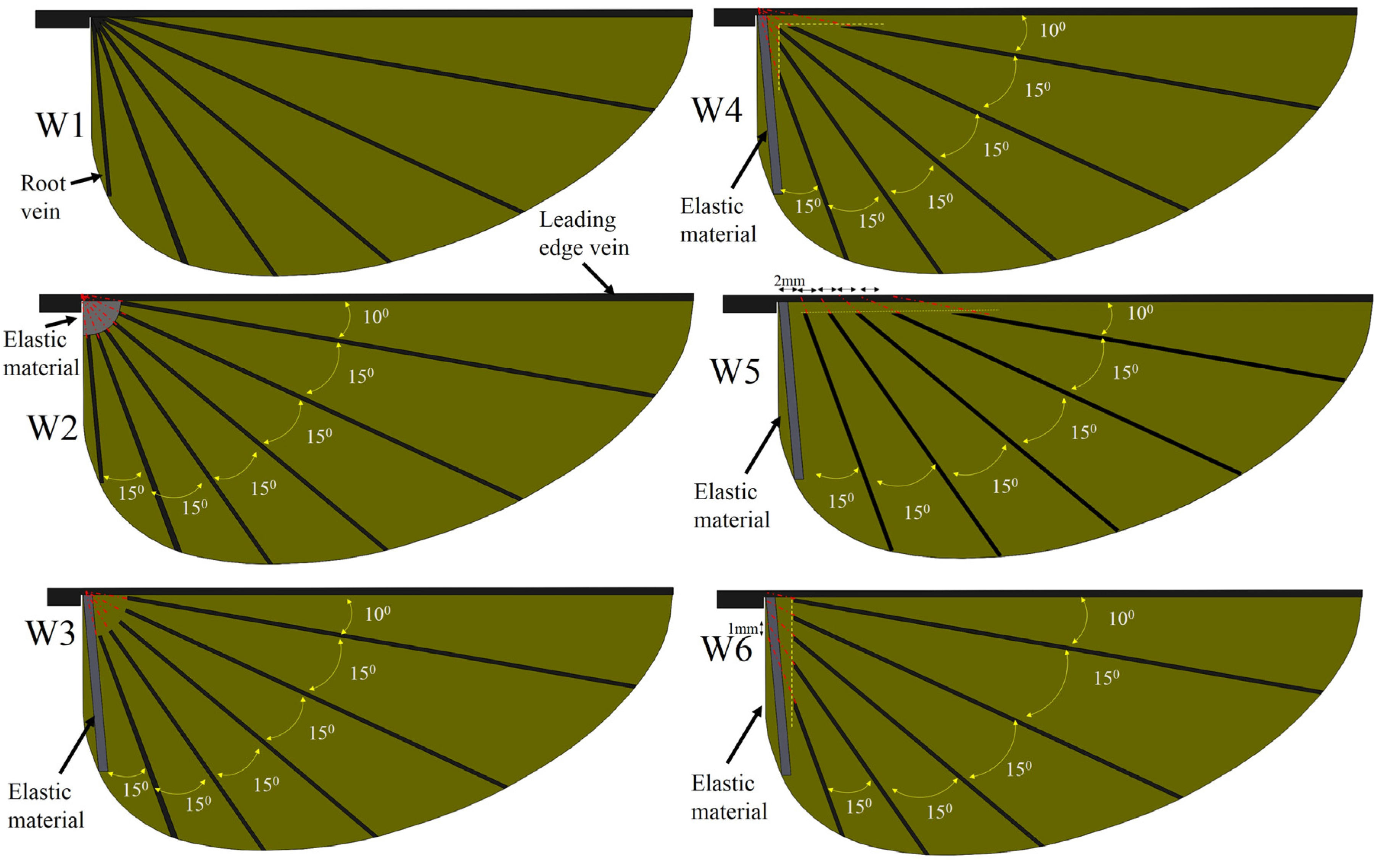
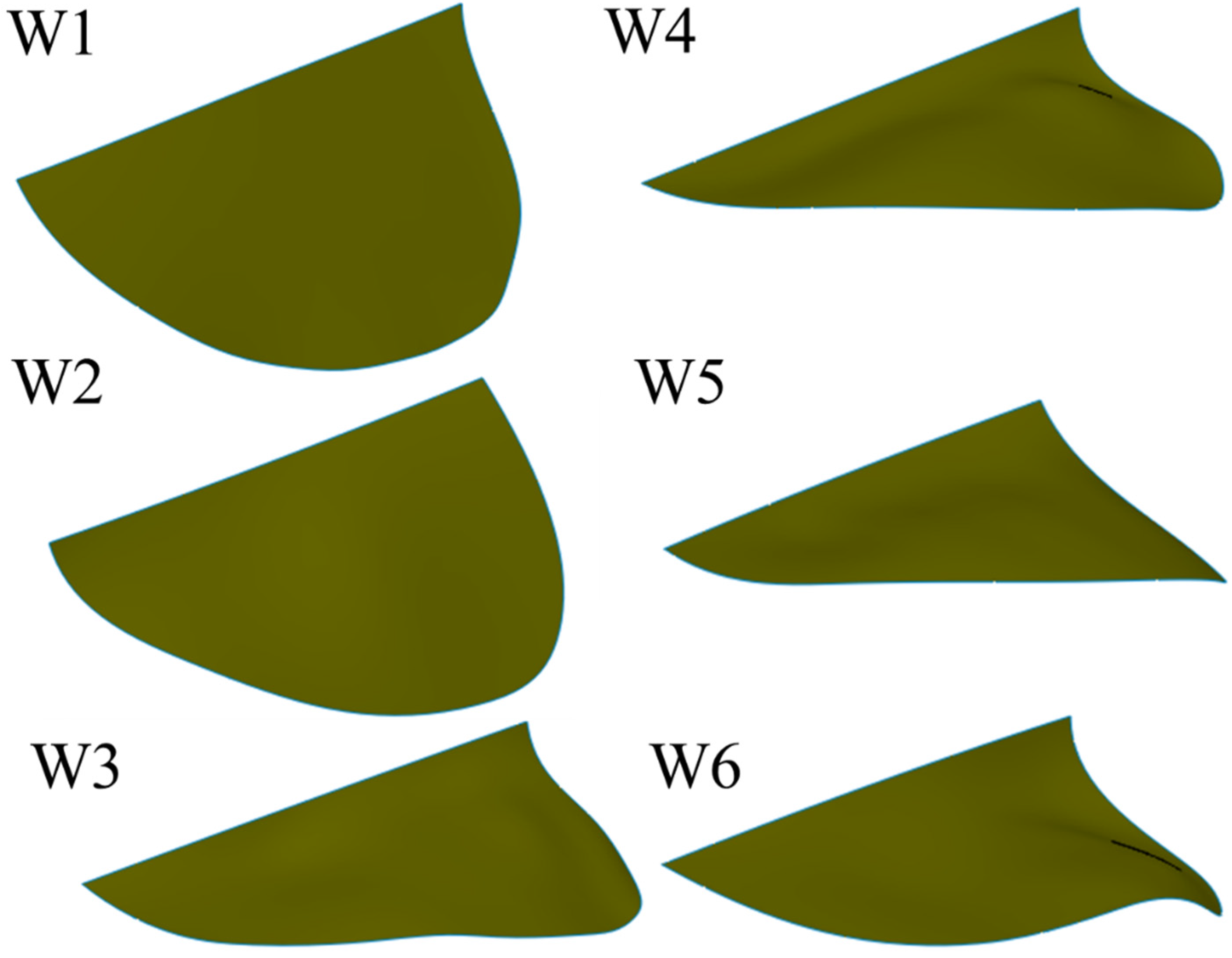
2.2. Flexible Wing Design
2.3. Wing Manufacturing
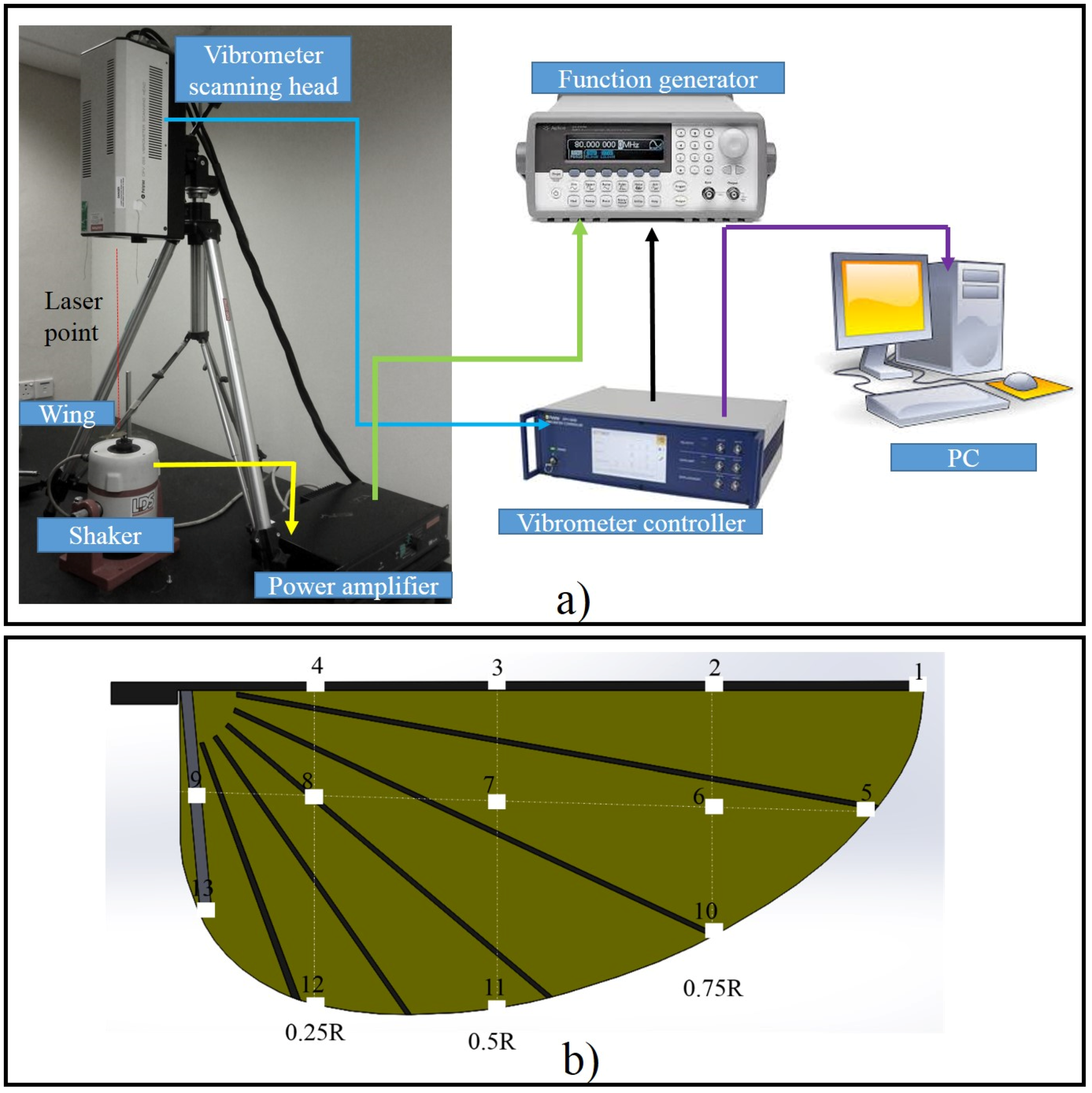
3. Experimental Apparatus and Procedure
3.1. Force Measurement
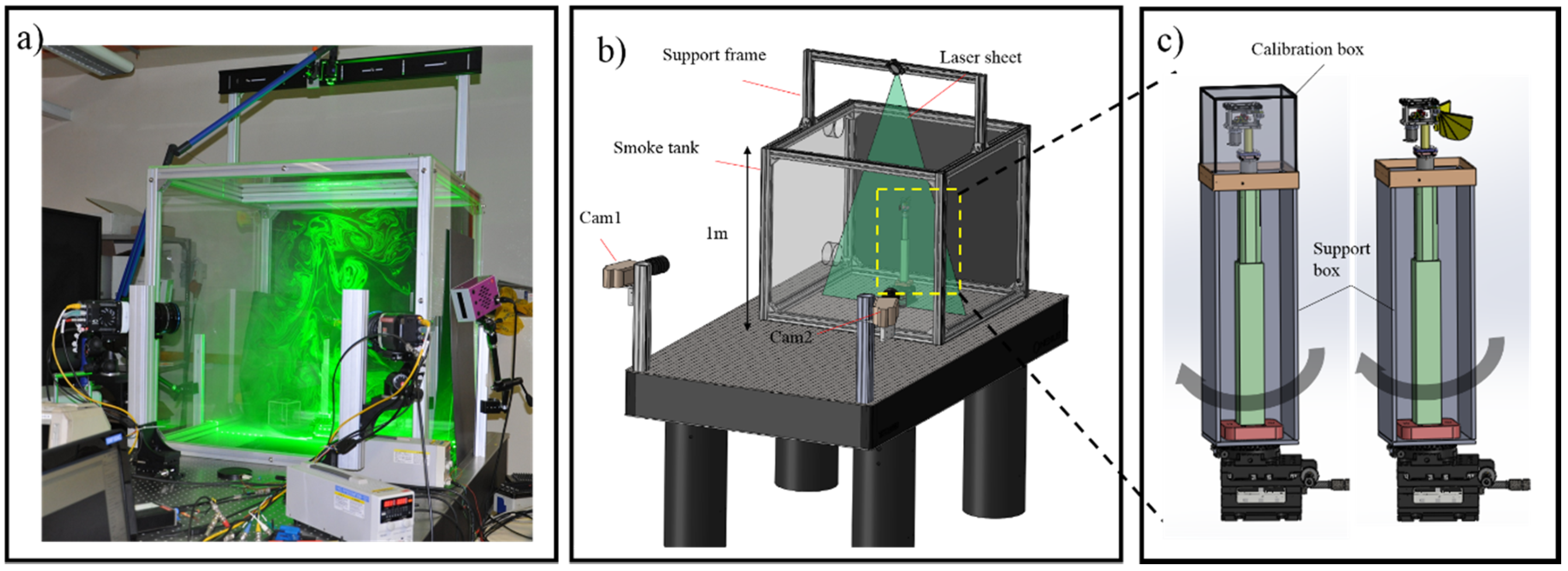
3.2. Particle Image Velocimetry (PIV) and Deformation Measurement
3.3. Natural Frequency Measurement
4. Results and Discussion
4.1. Natural Frequency of Flexible Wings
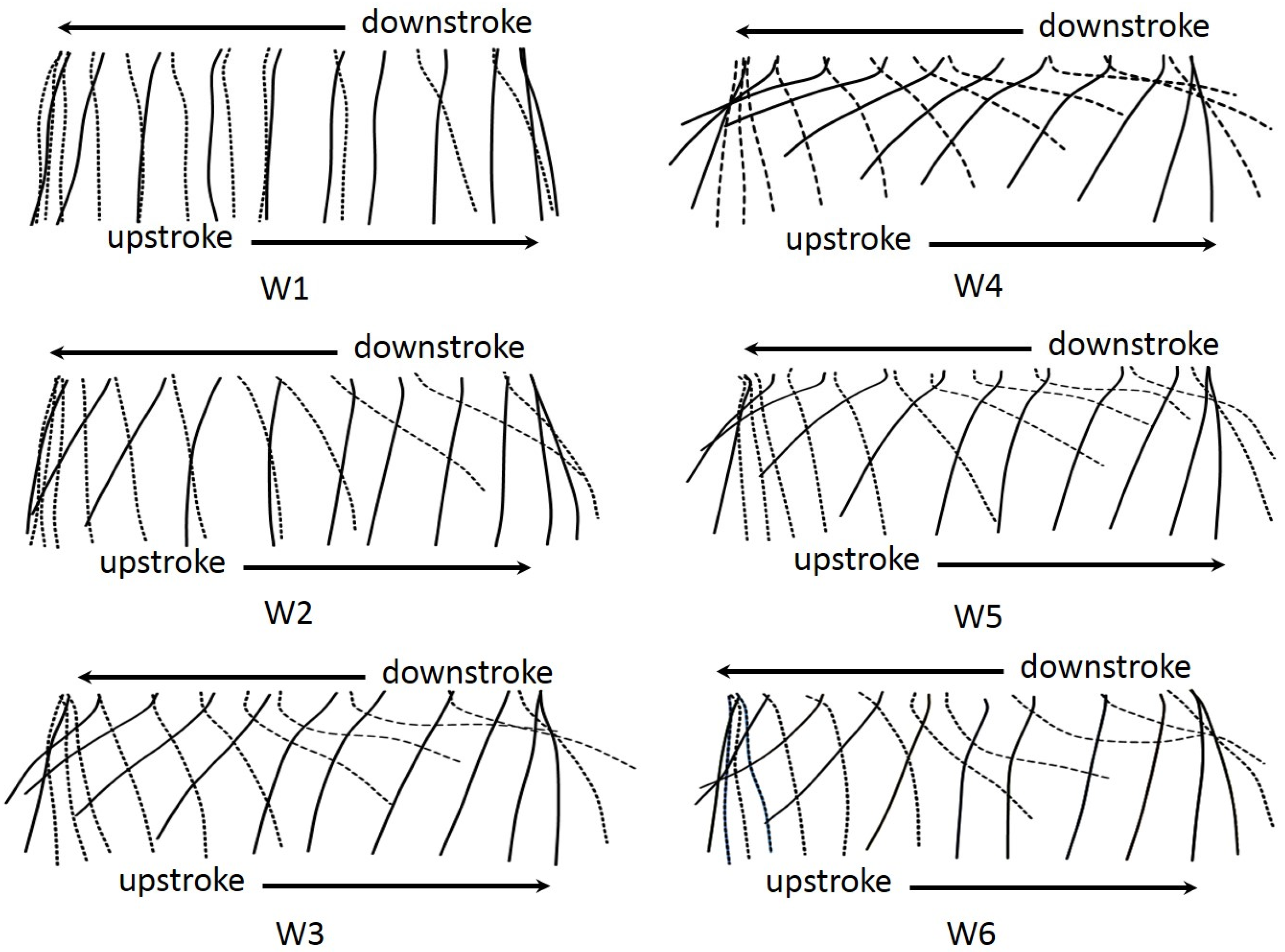
4.2. Wing Deformation
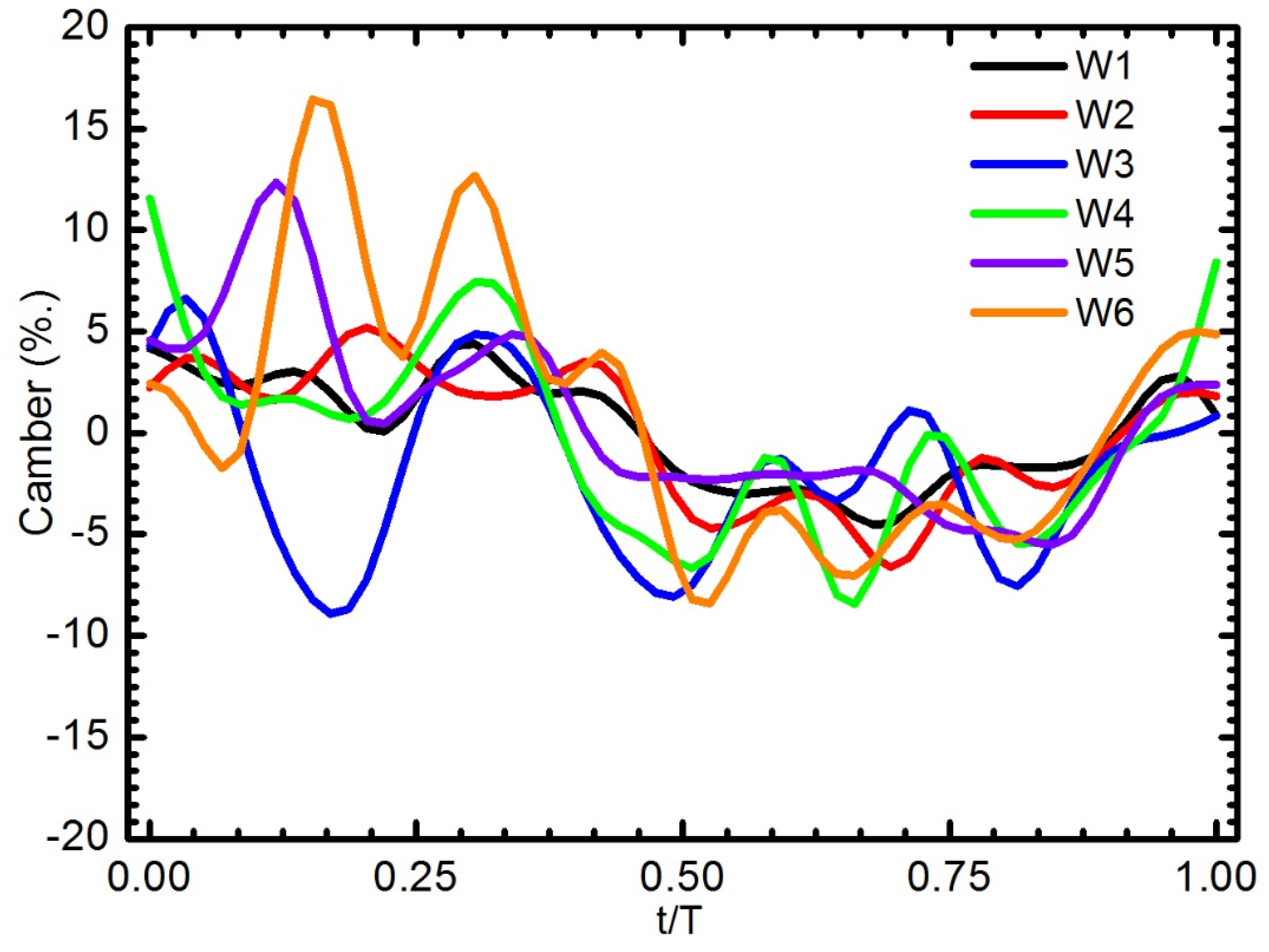
4.2.1. Camber Deformation
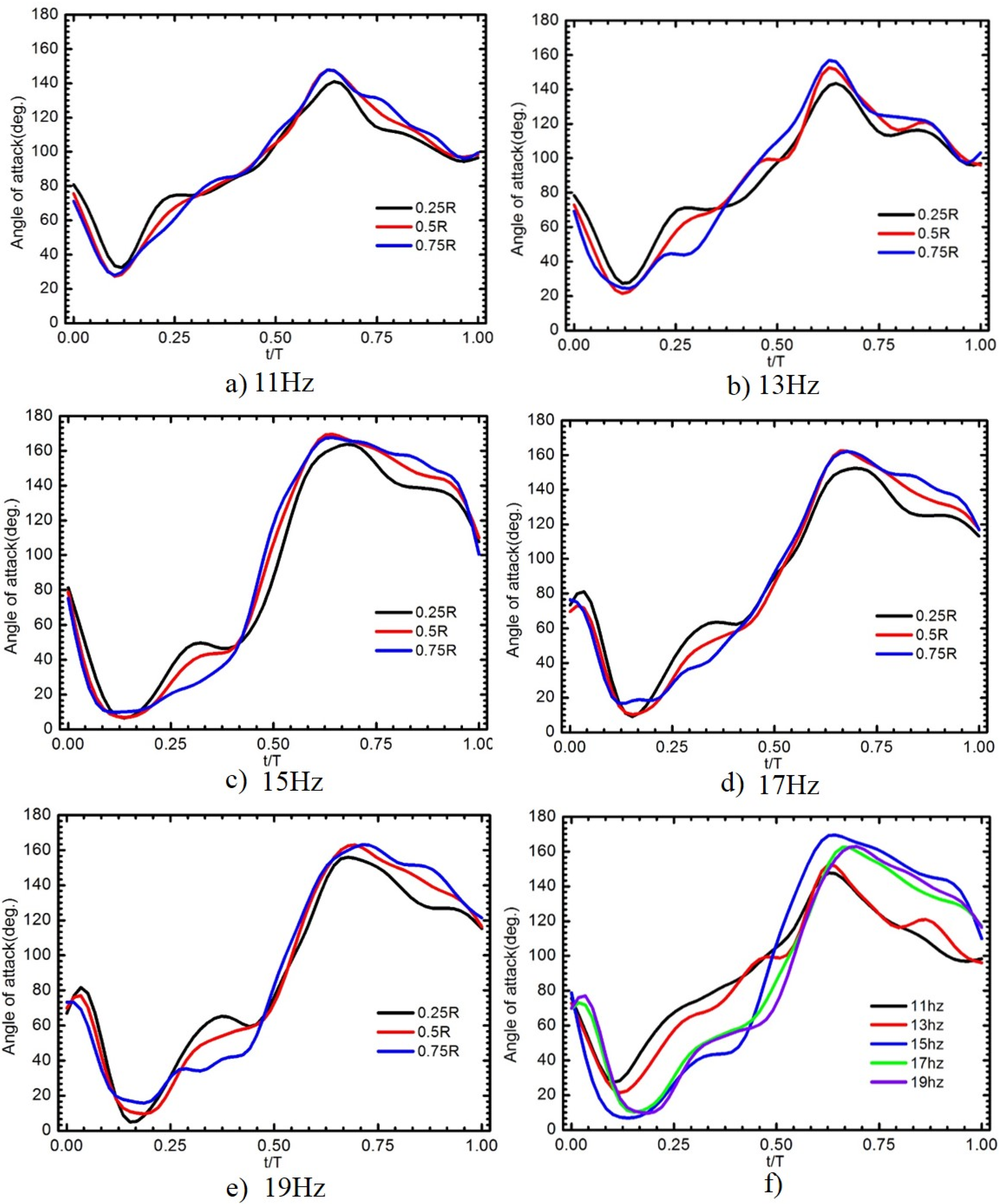
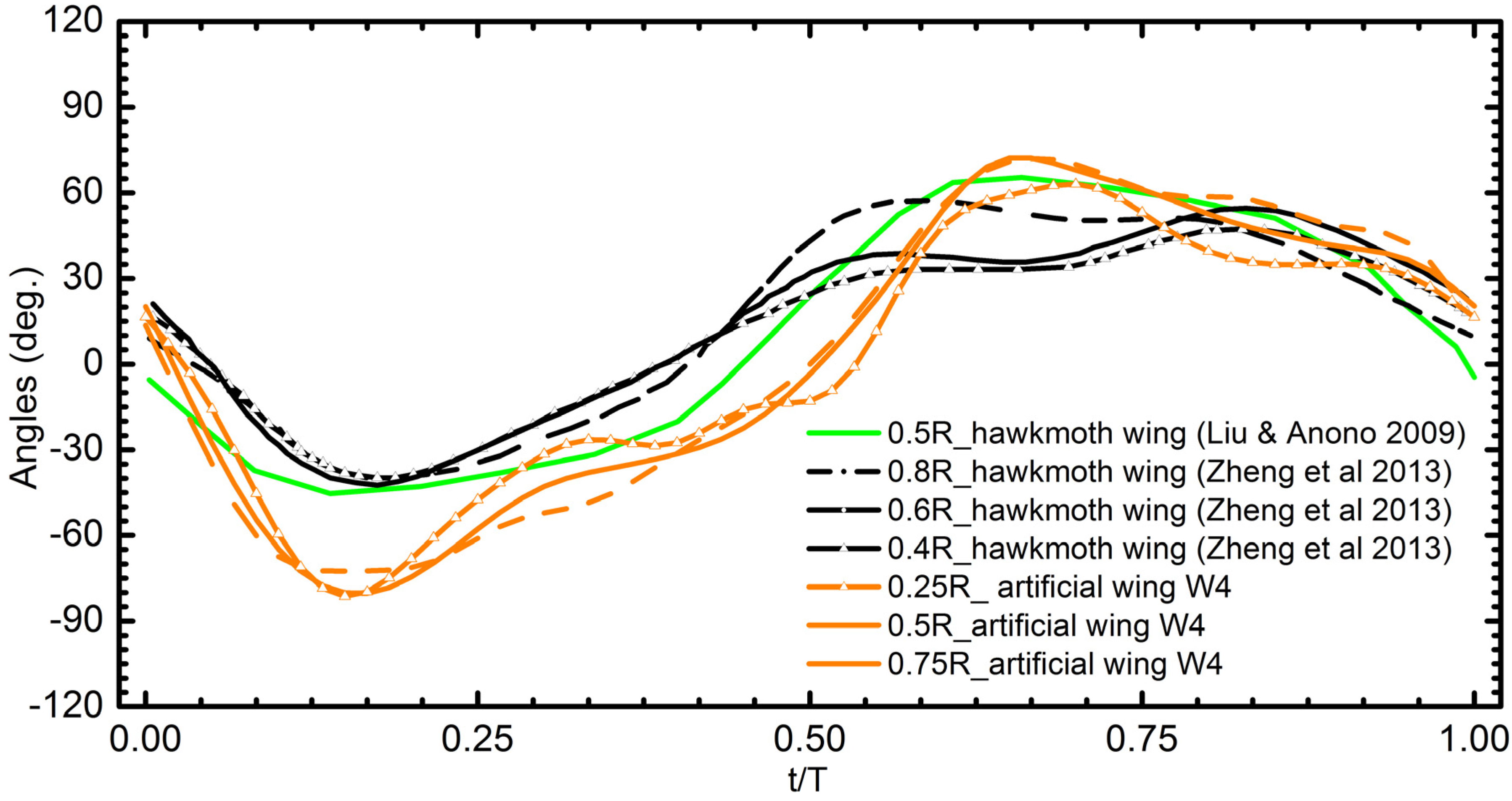
4.2.2. Twisting Deformation
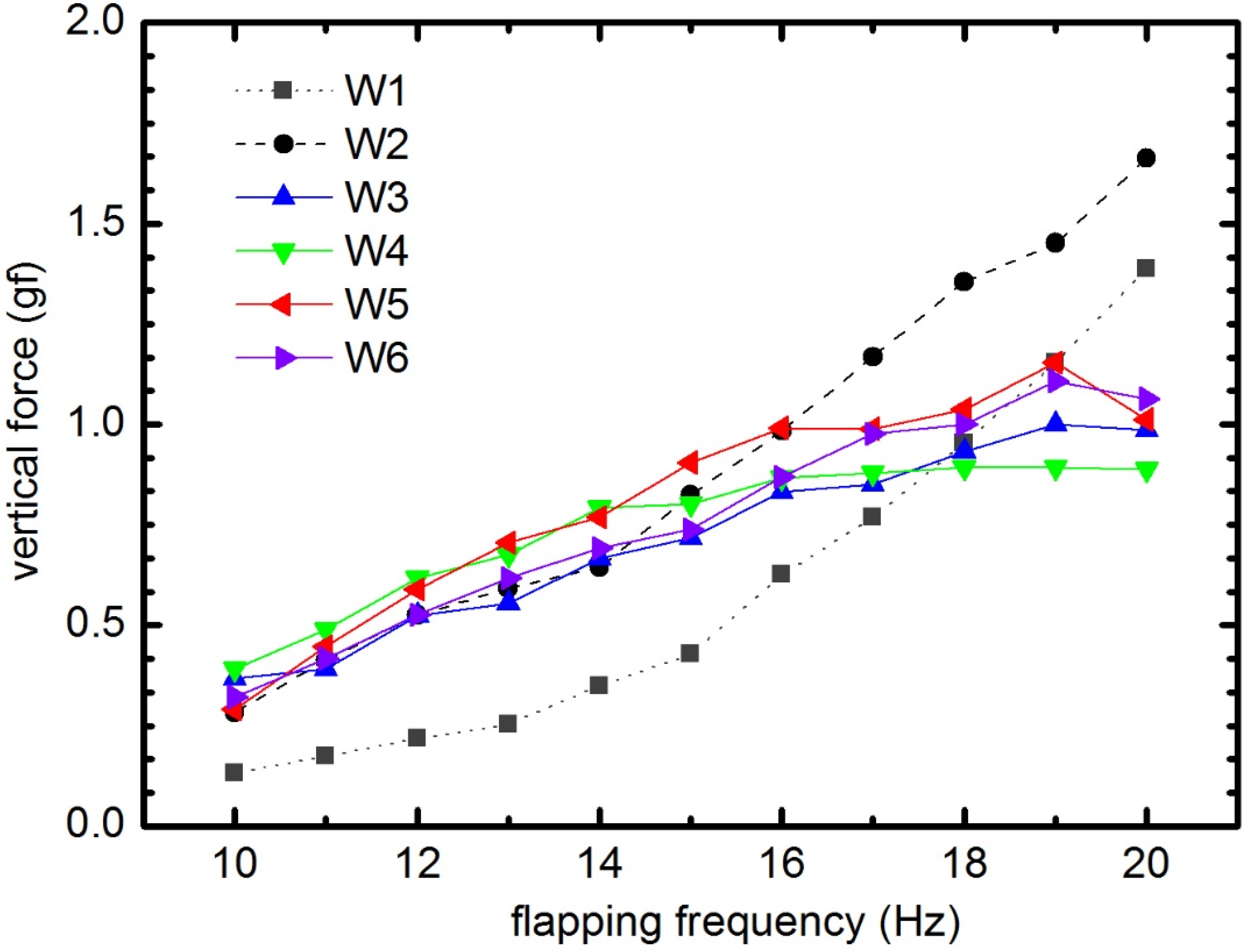
4.3. Force Generation
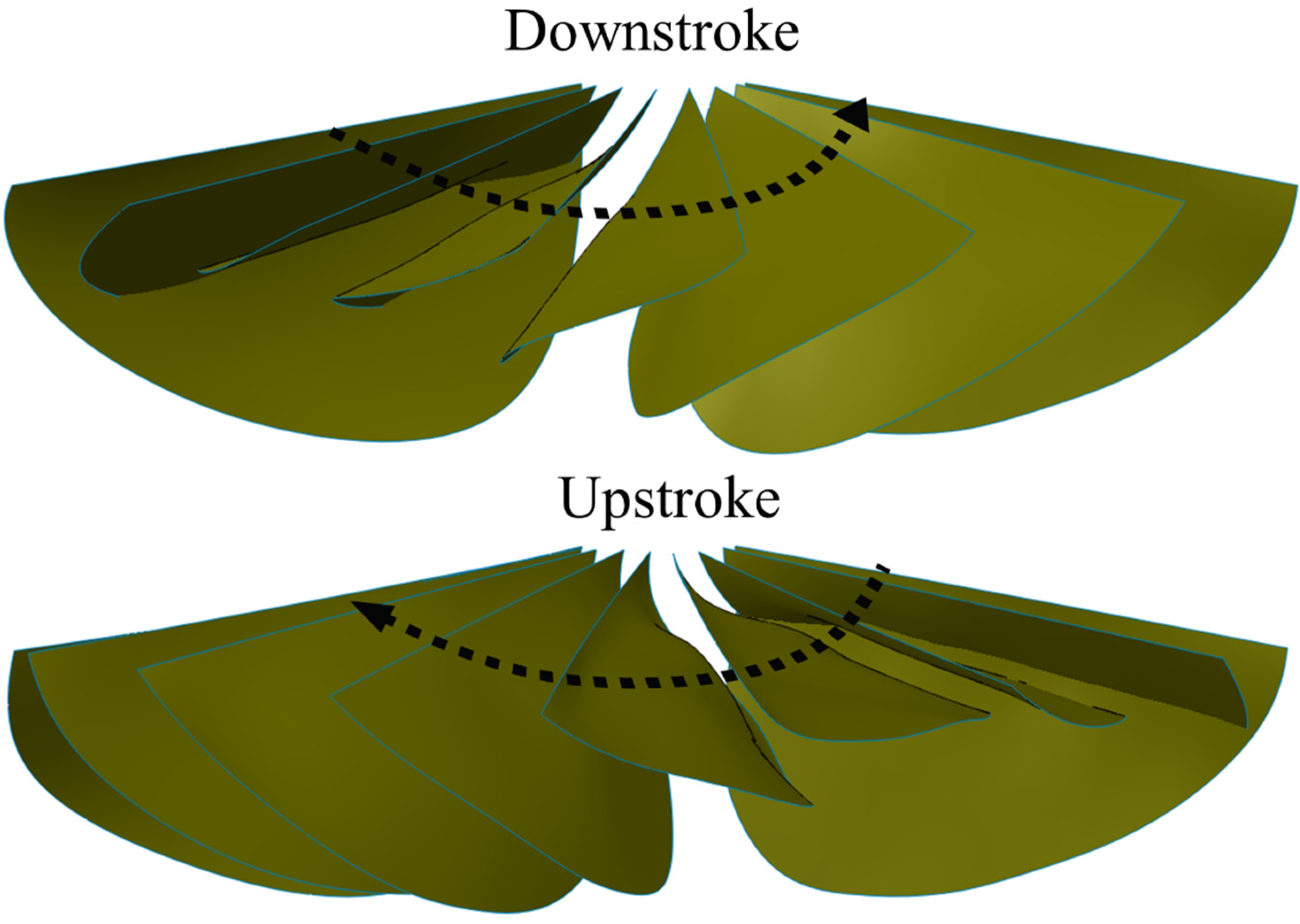
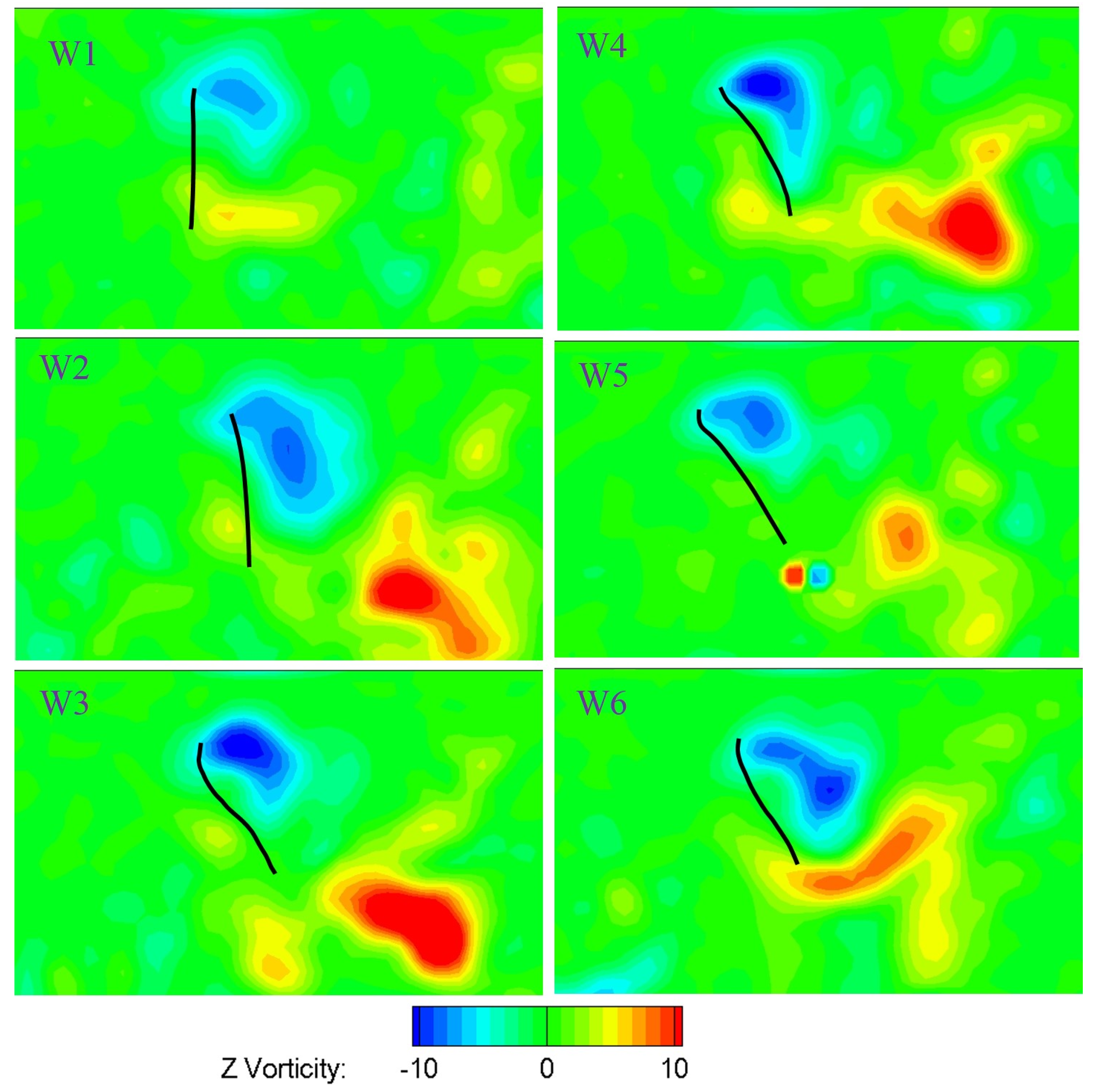
4.4. Flow Structures
5. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Truong, T.V.; Doyoung, B.; Laura, C.L.; Douglas, J.E.; Park, H.C.; Kim, M.J. Flight behavior of the rhinoceros beetle trypoxylus dichotomus during electrical nerve stimulation. Bioinspir. Biomim. 2012, 7. [Google Scholar] [CrossRef]
- Dickinson, M. Insect flight. Curr. Biol. 2006, 16, R309–R314. [Google Scholar] [CrossRef] [PubMed]
- Dudley, R. The Biomechanics of Insect Flight: Form, Function, Evolution; Princeton University Press: Princeton, NJ, USA, 2002. [Google Scholar]
- Dickinson, M.H.; Lehmann, F.-O.; Sane, S.P. Wing rotation and the aerodynamic basis of insect flight. Science 1999, 284, 1954–1960. [Google Scholar] [CrossRef] [PubMed]
- Truong, T.V.; Le, T.Q.; Byun, D.; Park, H.C.; Kim, M. Flexible wing kinematics of a free-flying beetle (rhinoceros beetle Trypoxylus dichotomus). J. Bionic Eng. 2012, 9, 177–184. [Google Scholar] [CrossRef]
- Le, T.Q.; Truong, T.V.; Park, S.H.; Quang Truong, T.; Ko, J.H.; Park, H.C.; Byun, D. Improvement of the aerodynamic performance by wing flexibility and elytra–hind wing interaction of a beetle during forward flight. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Young, J.; Walker, S.M.; Bomphrey, R.J.; Taylor, G.K.; Thomas, A.L.R. Details of insect wing design and deformation enhance aerodynamic function and flight efficiency. Science 2009, 325, 1549–1552. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Huang, Q.; Deng, X.; Sane, S.P. Aerodynamic effects of flexibility in flapping wings. J. R. Soc. Interface 2010, 7, 485–497. [Google Scholar] [CrossRef] [PubMed]
- Hao, W.; Zeng, L.; Yin, C. Measuring the body position, attitude and wing deformation of a free-flight dragonfly by combining a comb fringe pattern with sign points on the wing. Measurement Sci. Technol. 2002, 13, 903. [Google Scholar]
- Zheng, L.; Hedrick, T.L.; Mittal, R. A multi-fidelity modelling approach for evaluation and optimization of wing stroke aerodynamics in flapping flight. J. Fluid Mech. 2013, 721, 118–154. [Google Scholar] [CrossRef]
- Wootton, R.J. The mechanical design of insect wings. Sci. Am. 1990, 263, 114–120. [Google Scholar] [CrossRef]
- Walker, S.M.; Thomas, A.L.; Taylor, G.K. Deformable wing kinematics in the desert locust: How and why do camber, twist and topography vary through the stroke? J. R. Soc. Interface 2009, 6, 735–747. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.M.; Thomas, A.L.R.; Taylor, G.K. Deformable wing kinematics in free-flying hoverflies. J. R. Soc. Interface 2010, 7, 131–142. [Google Scholar] [CrossRef] [PubMed]
- Shkarayev, S.; Silin, D.; Abate, G.; Albertani, R. Aerodynamics of cambered membrane flapping wings. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010; pp. 2010–2058. [Google Scholar]
- Truong, T.V.; Kim, J.; Kim, M.; Park, H.; Yoon, K.; Byun, D. Flow structures around a flapping wing considering ground effect. Exp. Fluids 2013, 54, 1–19. [Google Scholar] [CrossRef]
- Truong, T.V.; Le, T.Q.; Tran, H.T.; Park, H.C.; Yoon, K.J.; Byun, D. Flow visualization of rhinoceros beetle (Trypoxylus dichotomus) in free flight. J. Bionic Eng. 2012, 9, 304–314. [Google Scholar] [CrossRef]
- Truong, T.V.; Doyoung, B.; Kim, M.J.; Yoon, K.J.; Park, H.C. Aerodynamic forces and flow structures of the leading edge vortex on a flapping wing considering ground effect. Bioinspir. Biomim. 2013, 8. [Google Scholar] [CrossRef] [PubMed]
- Truong, T.V.; Le, T.Q.; Park, H.C.; Yoon, K.J.; Kim, M.J.; Byun, D. Non-jumping take off performance in beetle flight (rhinoceros beetle Trypoxylus dichotomus). J. Bionic Eng. 2014, 11, 61–71. [Google Scholar] [CrossRef]
- Le, T.Q.; Truong, T.V.; Tran, H.T.; Park, S.H.; Ko, J.H.; Park, H.C.; Byun, D. How could beetle’s elytra support their own weight during forward flight? J. Bionic Eng. 2014, 11, 529–540. [Google Scholar] [CrossRef]
- Tanaka, H.; Shimoyama, I. Forward flight of swallowtail butterfly with simple flapping motion. Bioinspir. Biomim. 2010, 5. [Google Scholar] [CrossRef] [PubMed]
- Matthew, K.; Karl, K.; Henry, W. Development of the nano hummingbird: A tailless flapping wing micro air vehicle. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2012. [Google Scholar]
- Phan, H.V.; Nguyen, Q.V.; Truong, Q.T.; Truong, T.V.; Park, H.C.; Goo, N.S.; Byun, D.; Kim, M.J. Stable vertical takeoff of an insect-mimicking flapping-wing system without guide implementing inherent pitching stability. J. Bionic Eng. 2012, 9, 391–401. [Google Scholar] [CrossRef]
- Tanaka, H.; Matsumoto, K.; Shimoyama, I. Fabrication of a three-dimensional insect-wing model by micromolding of thermosetting resin with a thin elastmeric mold. J. Micromech. Microeng. 2007, 17, 2485–2490. [Google Scholar] [CrossRef]
- Shang, J.; Combes, S.; Finio, B.; Wood, R. Artificial insect wings of diverse morphology for flapping-wing micro air vehicles. Bioinspir. Biomim. 2009, 4. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.; Stanford, B.; Sällström, E.; Ukeiley, L.; Ifju, P. Structural dynamics and aerodynamics measurements of biologically inspired flexible flapping wings. Bioinspir. Biomim. 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Bhayu, P.R.; Nguyen, Q.-V.; Park, H.C.; Goo, N.S.; Byun, D. Artificial cambered-wing for a beetle-mimicking flapper. J. Bionic Eng. 2010, 7, S130–S136. [Google Scholar] [CrossRef]
- Tanaka, H.; Okada, H.; Shimasue, Y.; Liu, H. Flexible flapping wings with self-organized microwrinkles. Bioinspir. Biomim. 2015, 10. [Google Scholar] [CrossRef] [PubMed]
- Shyy, W.; Kang, C.-K.; Chirarattananon, P.; Ravi, S.; Liu, H. Aerodynamics, sensing and control of insect-scale flapping-wing flight. Proc. R. Soc. A Math. Phys. Eng. Sci. 2016, 472. [Google Scholar] [CrossRef]
- Cheng, B.; Deng, X.; Hedrick, T.L. The mechanics and control of pitching manoeuvres in a freely flying hawkmoth (Manduca sexta). J. Exp. Biol. 2011, 214, 4092–4106. [Google Scholar] [CrossRef] [PubMed]
- Wootton, R.; Herbert, R.; Young, P.; Evans, K. Approaches to the structural modelling of insect wings. Philos. Trans. R. Soc. B Biol. Sci. 2003, 358, 1577–1587. [Google Scholar] [CrossRef] [PubMed]
- Nakata, T.; Liu, H. A fluid–structure interaction model of insect flight with flexible wings. J. Comput. Phys. 2012, 231, 1822–1847. [Google Scholar] [CrossRef]
- Ellington, C.P. The aerodynamics of hovering insect flight. II. Morphological parameters. Philos. Trans. Royal Soc. B 1984, 305, 17–40. [Google Scholar] [CrossRef]
- Wang, Q.; Goosen, J.; Van Keulen, A. Optimal hovering kinematics with respect to various flapping-wing shapes. In Proceedings of the International Micro Air Vehicle Conference and Flight Competition (IMAV), Toulouse, France, 17–20 September 2013. [Google Scholar]
- Ennos, A.R. The importance of torsion in the design of insect wings. J. Exp. Biol. 1988, 140, 137–160. [Google Scholar]
- Combes, S.; Daniel, T. Flexural stiffness in insect wings: Effects of wing venation and stiffness distribution on passive bending. Am. Entomol. 2005, 51, 42–44. [Google Scholar] [CrossRef]
- Hubel, T.Y.; Tropea, C. Experimental Investigation of a Flapping Wing Model. In Animal Locomotion; Taylor, G.K., Triantafyllou, M.S., Tropea, C., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; pp. 383–399. [Google Scholar]
- Kim, D.-K.; Han, J.-H.; Kwon, K.-J. Wind tunnel tests for a flapping wing model with a changeable camber using macro-fiber composite actuators. Smart Mater. Struct. 2009, 18, 024008. [Google Scholar] [CrossRef]
- Campos, D.; Ukeiley, L.; Bernal, L. Flow around flapping flexible flat plate wings. In Proceedings of the 50th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 2012; pp. 9–12. [Google Scholar]
- Tyson, L.H. Software techniques for two- and three-dimensional kinematic measurements of biological and biomimetic systems. Bioinspir. Biomim. 2008, 3. [Google Scholar] [CrossRef]
- Chen, J.-S.; Chen, J.-Y.; Chou, Y.-F. On the natural frequencies and mode shapes of dragonfly wings. J. Sound Vib. 2008, 313, 643–654. [Google Scholar] [CrossRef]
- Walker, S.M.; Thomas, A.L.R.; Taylor, G.K. Photogrammetric reconstruction of high-resolution surface topographies and deformable wing kinematics of tethered locusts and free-flying hoverflies. J. R. Soc. Interface 2009, 6, 351–366. [Google Scholar] [CrossRef] [PubMed]
- Aono, H.; Shyy, W.; Liu, H. Vortex dynamics in near wake of a hovering hawkmoth. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008; p. 583. [Google Scholar]
- Liu, H.; Aono, H. Size effects on insect hovering aerodynamics: An integrated computational study. Bioinspiration Biomim. 2009, 4, 015002. [Google Scholar] [CrossRef] [PubMed]
- Zheng, L.; Hedrick, T.L.; Mittal, R. Time-varying wing-twist improves aerodynamic efficiency of forward flight in butterflies. PLoS ONE 2013, 8, e53060. [Google Scholar] [CrossRef] [PubMed]













| Point | (Hz) | (Hz) | (Hz) |
|---|---|---|---|
| 1 | 25.94 | 52.34 | 81.72 |
| 2 | 25.94 | 52.19 | 81.72 |
| 3 | 25.94 | 52.19 | 80.94 |
| 4 | 25.78 | 51.56 | 80.63 |
| 5 | 26.09 | 52.34 | 81.72 |
| 6 | 26.09 | 52.19 | 81.25 |
| 7 | 26.25 | 52.97 | 81.25 |
| 8 | 26.09 | 52.19 | 81.72 |
| 9 | 26.41 | 52.34 | 81.72 |
| 10 | 26.25 | 52.34 | 81.25 |
| 11 | 26.25 | 51.56 | 80.94 |
| 12 | 26.25 | 52.34 | 81.25 |
| 13 | 25.94 | 52.91 | 80.94 |
| Mean | 26.09 | 51.71 | 81.31 |
| Wing | (Hz) | (Hz) | (Hz) | Mass (g) |
|---|---|---|---|---|
| W1 | 57.03 | 116.25 | 175.16 | 0.138 |
| W2 | 41.41 | 78.59 | 124.22 | 0.148 |
| W3 | 26.09 | 51.71 | 81.31 | 0.132 |
| W4 | 20.16 | 74.53 | 96.56 | 0.134 |
| W5 | 22.03 | 53.91 | 96.88 | 0.149 |
| W6 | 22.19 | 44.84 | 70.94 | 0.136 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Truong, T.V.; Nguyen, Q.-V.; Lee, H.P. Bio-Inspired Flexible Flapping Wings with Elastic Deformation. Aerospace 2017, 4, 37. https://doi.org/10.3390/aerospace4030037
Truong TV, Nguyen Q-V, Lee HP. Bio-Inspired Flexible Flapping Wings with Elastic Deformation. Aerospace. 2017; 4(3):37. https://doi.org/10.3390/aerospace4030037
Chicago/Turabian StyleTruong, Tien Van, Quoc-Viet Nguyen, and Heow Pueh Lee. 2017. "Bio-Inspired Flexible Flapping Wings with Elastic Deformation" Aerospace 4, no. 3: 37. https://doi.org/10.3390/aerospace4030037