Robust Autoland Design by Multi-Model ℋ_∞ Synthesis with a Focus on the Flare Phase

Abstract

Recent advances in the resolution of multi-model and multi-objective control problems via non-smooth optimization are exploited to provide a novel methodology in the challenging context of autoland design. Based on the structured ${\mathcal{H}}_{\infty }$ control framework, this paper focuses on the demanding flare phase under strong wind conditions and parametric uncertainties. More precisely, the objective is to control the vertical speed of the aircraft before touchdown while minimizing the impact of windshear, ground effects, and airspeed variations. The latter is indeed no longer controlled accurately during flare and strongly affected by wind. In addition, parametric uncertainties are to be considered when designing the control laws. To this purpose, extending previous results published by the authors in a conference paper, a specific multi-model strategy taking into account variations of mass and center-of-gravity location is considered. The methodology is illustrated on a realistic aircraft benchmark proposed by the authors, which is fully described in this paper and freely available from the SMAC (Systems Modeling Analysis & Control) toolbox website (http://w3.onera.fr/smac).

1. Introduction

The steady growth of air traffic in recent years has led to drastic safety standards with the goal of limiting the number of accidents. Since approach and landing remain the most critical flight phases (almost 50% of fatal accidents and 75% of non-fatal hull losses between 1997 and 2016 [1]), particular attention has recently focused on improving autoland systems in adverse conditions. With the help of CAT III instrument landing systems (ILS), which are now available in a rapidly growing list of airports, automatic landing control laws have helped to secure these two phases notably in degraded weather conditions (such as fog and crosswinds). However, despite numerous methodological works [2,3,4,5] over the past two decades, the design, tuning, and validation process of final approach and flare control systems remains a challenging and time-consuming task. As is observed in [4], where a complete design framework together with a dedicated software is proposed, the tuning phase requires rather tricky multi-objective optimization. Note, however, that optimizing the parameters of the flare control system (such as initial altitude and vertical velocity profile) becomes much easier when the internal loops are correctly designed and tuned. In our context, a natural choice is to track the vertical velocity. The main difficulty is to obtain fast and accurate responses despite a significant airspeed decrease, possible windshear, and ground effects. Recall indeed that the flare segment generally lasts less than $7$ s and that, to ensure good robust performance properties, the desired vertical speed should be reached at least 1 or $2$ s before touchdown. Unlike the approaches detailed in [4,6,7], either using robust nonlinear dynamic inversion or adaptive control schemes to design the aforementioned inner loops, linear-oriented techniques are often preferred by a majority of contributions. It can be observed indeed that, during approach and landing, airspeed and altitude variations remain rather small so that the aircraft behavior is almost linear. In the field of flight control design, the most popular methods are still based today on eigenstructure assignment [8] or LQR (Linear Quadratic Regulator) control techniques [5]. Both approaches have been successfully used in Airbus and Boeing design offices and have contributed for nearly 30 years to considerable improvements in the flight control design process. In the meantime, ${\mathcal{H}}_{\infty }$ control techniques have been progressively developed and evaluated on various flight control problems—see, for example, [2,3], where the flare phase receives particular attention. Yet, despite promising results even in flight tests [9], this third approach has not become as popular as the other two in the industry. Things are, however, likely to change in the near future with the emergence of new tools based on non-smooth optimization techniques [10,11]. With these approaches, it becomes possible to impose constraints on the structure and the order of the controller. Although convexity is unfortunately lost in that case, the aforementioned algorithms converge to local solutions, which are (in a large majority of standard applications) not so far from the global (non-structured) optimum. Another interesting feature of these new tools is their capacity to handle multiple models and multiple separate channels [12]. This last feature offers new ways to define ${\mathcal{H}}_{\infty }$ design models, which will be used in this paper to solve the flare control problem despite modeling errors and parametric uncertainties, thus extending the results of [13].

The paper is organized as follows. ILS-based automatic landing issues are briefly reviewed in Section 2. The flare control problem is then detailed and solved by a multi-model and multi-channel ${\mathcal{H}}_{\infty }$ design approach in Section 3. Specific attention is devoted in this section to robustness. Implementation issues and nonlinear simulation results are then presented in Section 4. Finally, Section 5 concludes the paper and details a few perspectives. For the sake of completeness, a thorough description of the aircraft model used in the nonlinear simulations is presented in Appendix A. This aircraft model together with a complete description of the design problem is freely available from the SMAC toolbox (dedicated to Systems Modeling, Analysis and Control) website (http://w3.onera.fr/smac).

2. ILS-Based Automatic Landing

As illustrated in Figure 1, automatic landing in the vertical plane can be divided into two main phases: the final approach during which the aircraft must follow a descent path (glide) and the flare segment, which is activated when the landing gear height $H_{LG}$ falls below a threshold value $H_{FLA}$. The latter is most often fixed around $H_{FLA}\approx 50$ ft but might be slightly updated as a function of ground speed. Similarly, in the horizontal plane, the aircraft trajectory must coincide with the runway axis (localizer phase) as long as $H_{LG}\ge H_{DEC}=30$ ft. The alignment phase (or decrab mode) is then activated in order to minimize the lateral efforts on the landing gears at touchdown.

Automatic landing control systems are generally designed on simplified models, using decoupling hypotheses between the longitudinal and the lateral axes. These assumptions, particularly during the landing phase, are usually satisfied without any severe restriction for a large majority of civil and military aircraft.

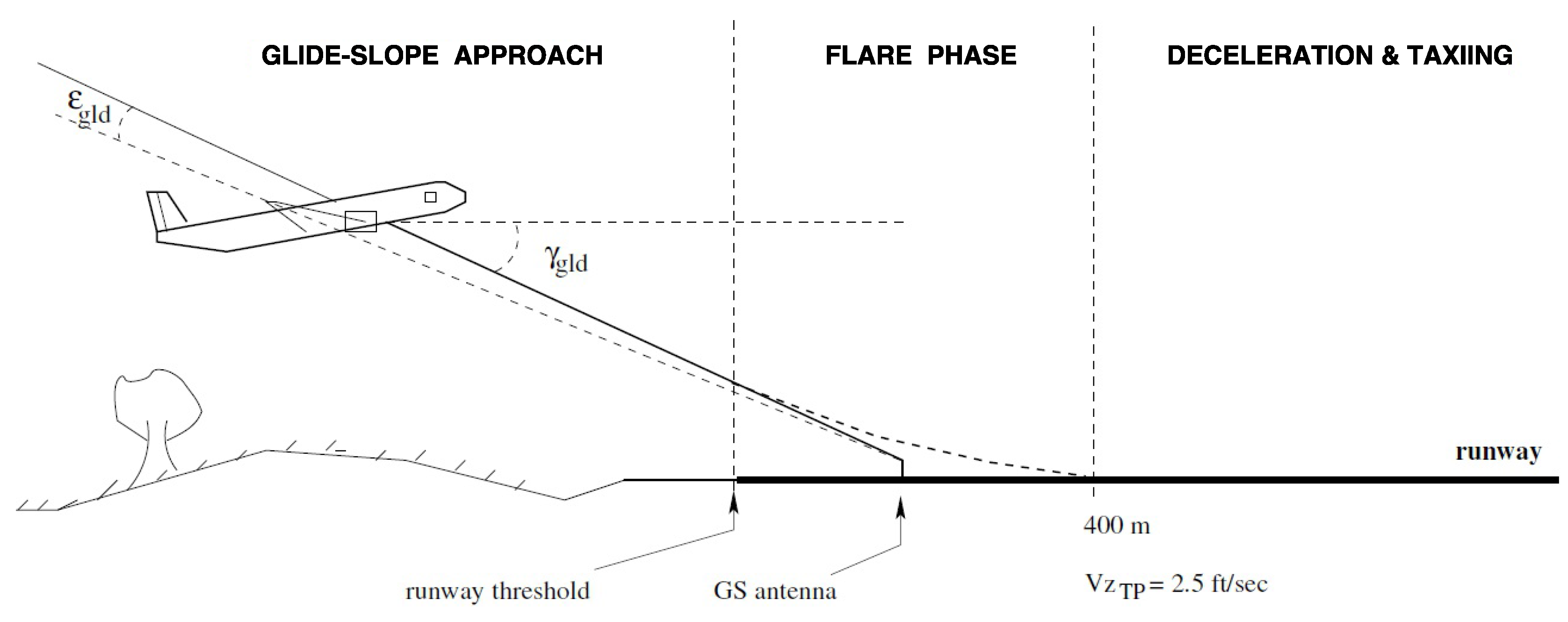
2.1. Final Approach

During the final approach, as already clarified, the trajectory of the aircraft must be kept as close as possible to the ILS beam. This is achieved by simultaneously minimizing the norm of the longitudinal and lateral errors ${\Delta }_z=f\left({ϵ}_{gld}\right)$ and ${\Delta }_y=g\left({ϵ}_{loc}\right)$, where ${ϵ}_{gld}$ is the angular error between the nominal glide path and that of the aircraft (see Figure 1), and ${ϵ}_{loc}$ denotes the lateral angular error in the horizontal plane. In both cases, $f(.)$ and $g(.)$ are elementary altitude-dependent arctangent-based nonlinear functions that convert angular errors into metric deviations.

Moreover, during this phase, the calibrated airspeed $V_c$ is to be kept constant, and the aerodynamic sideslip angle $\beta$ must remain zero. Based on the decoupling assumption and the above constraints, most autoland systems are usually based on two inner control loops. In this paper, the following structures are used for the longitudinal and the lateral axis, respectively:

$$\left[\begin{array}{c}{\delta }_{t{h}_c}\\ {\delta }_{e_c}\end{array}\right]=K_{LON}{\left[\int (v_{c_c}-v_c)\int (v_{z_c}-v_z)v_c{v}_{z}q{n}_z\right]}^{\prime }$$

(1)

$$\left[\begin{array}{c}{\delta }_{a_c}\\ {\delta }_{r_c}\end{array}\right]=K_{LAT}{\left[\int (n_{yc}-n_y)\int ({\varphi }_c-\varphi )n_{y}pr\varphi \right]}^{\prime }$$

(2)

where $v_z$, $n_z$, $n_y$, p, q, r, $\varphi$ denote the vertical speed, the longitudinal and lateral load factors, the roll, the pitch and yaw rates, and the bank angle, respectively. ${\delta }_{th}$, ${\delta }_e$, ${\delta }_a$, ${\delta }_r$ are the control inputs (thrust and elevator/aileron/rudder deflections), while the subscript c stands for a commanded value. The static gains $K_{LON}$ and $K_{LAT}$ are tuned on linearized models by a standard eigenstructure assigment method. The eigenvectors are constrained so as to ensure decoupling between $v_c$ and $v_z$ along the longitudinal axis and between $n_y$ and $\varphi$ along the lateral axis. Note the use of small letters in Equation (1) to denote the longitudinal and the vertical speeds, which correspond here to variations about their nominal or initial values. This notation will further be used in the remaining of the paper.

Thus, the outer control loops are easily tuned. Observing that ${\dot{\Delta }}_z\approx v_z$, a fairly standard proportional controller $k_{p_z}$ can be used to ensure a nominal trajectory in the vertical plane, while the commanded variations $v_{c_c}=\Delta V_{c_c}$ on the calibrated airspeed are simply set to 0:

$$v_{c_c}=0,v_{zc}=k_{p_z}{\Delta }_z$$

(3)

Next, using a bank-to-turn strategy, the lateral deviation ${\Delta }_y$ is controlled via a proportional-derivative action on the bank angle. Finally, the sideslip angle, which is not directly measured, is controlled via the lateral load factor:

$$n_{y_c}=0,{\varphi }_c=k_{p_y}{\Delta }_y+k_{d_y}{\dot{\Delta }}_y$$

(4)

Remark 1.

The derivative term ${\dot{\Delta }}_y$ is not directly accessible to the control law and a pseudo-derivation of ${\Delta }_y$ would introduce a very high noise level since ${ϵ}_{loc}$ is highly affected by noise as well. Then, the following approximation can be used:

$${\dot{\Delta }}_y\approx \chi V_{gr}$$

(5)

where χ and $V_{gr}$ denote the route angle and the ground speed, respectively.

2.2. Flare and Align Phases

The nominal slope during approach is generally fixed to ${\gamma }_{gld}=-3$ deg, and the airspeed is a function of mass and mean wind. For the considered aircraft, whose mass belongs to the interval $[120\mathrm{t},180\mathrm{t}]$, the nominal approach airspeed is around $70{\mathrm{ms}}^{-1}$. The vertical speed $V_z$ then remains above $3.5{\mathrm{ms}}^{-1}$ during this phase but should fall below $1{\mathrm{ms}}^{-1}$ before touchdown. The flare phase, which starts at approximately $50\mathrm{ft}$ above ground and generally lasts less than $7$ s, is then essential for reducing the vertical speed as fast as possible from $3.5$ to less than $1{\mathrm{ms}}^{-1}$. To achieve this goal, the simplest strategy is to update $v_{z_c}$ in the longitudinal outer control loop (Equation (3)). Unfortunately, the inner control loop (Equation (1)) is generally much too slow. Moreover, the airspeed can no longer be controlled accurately during this phase and the throttle must be reduced to idle. A completely new design, to be further detailed in Section 3, is then required.

Initiated $30$ ft above ground, the objective of the align phase is to make sure that the longitudinal axis of the plane coincides with that of the runway at touchdown. This is simply realized by relaxing the constraint on the aerodynamic sideslip angle. Thus, the outer-loop $n_{y_c}=0$ is simply replaced by

$$n_{y_c}=k_{align}\Delta \psi$$

(6)

where $\Delta \psi$ denotes the heading angle error to be reduced to 0. The parameter $k_{align}$ is generally tuned empirically until the decrab objectives are met.

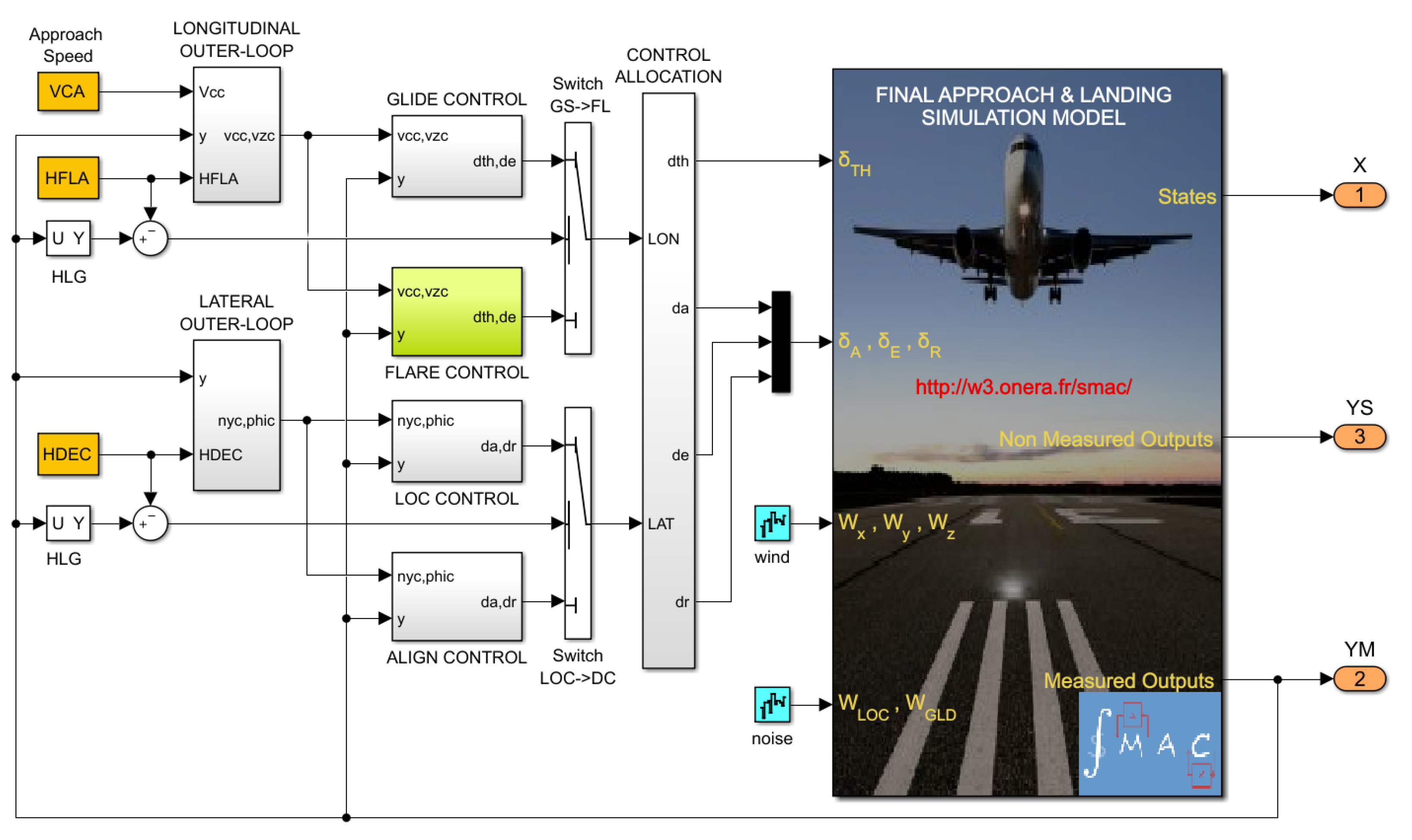
2.3. Overview of the Autoland Architecture

The above four elements consisting of glide, localizer, flare, and alignment control subsystems are now assembled as shown in Figure 2 to define the global autoland system.

These four subsystems are coordinated by two decoupled longitudinal and lateral outer-loops, which, respectively, deliver the desired signals to be followed on each axis ($(v_{cc},v_{zc})$ for the longitudinal axis and $(n_{yc},{\varphi }_c)$ for the lateral axis). Note that these signals are adapted as a function of the landing gear height. Along the longitudinal axis, the desired vertical speed profile $v_{zc}$ is modified when $H_{LG}\le H_{FLA}$ to ensure a soft landing while controlling the impact point. Simultaneously, the control loop gains and architecture are modified by switching from the glide to the flare control system. The same architecture is used along the lateral axis. When $H_{LG}\le H_{DEC}$, the desired lateral acceleration $n_{yc}$ is adapted to minimize the landing gear sideslip angle at touchdown despite crosswind. Simultaneously, the localizer tracking system is deactivated in favor of the alignment control device.

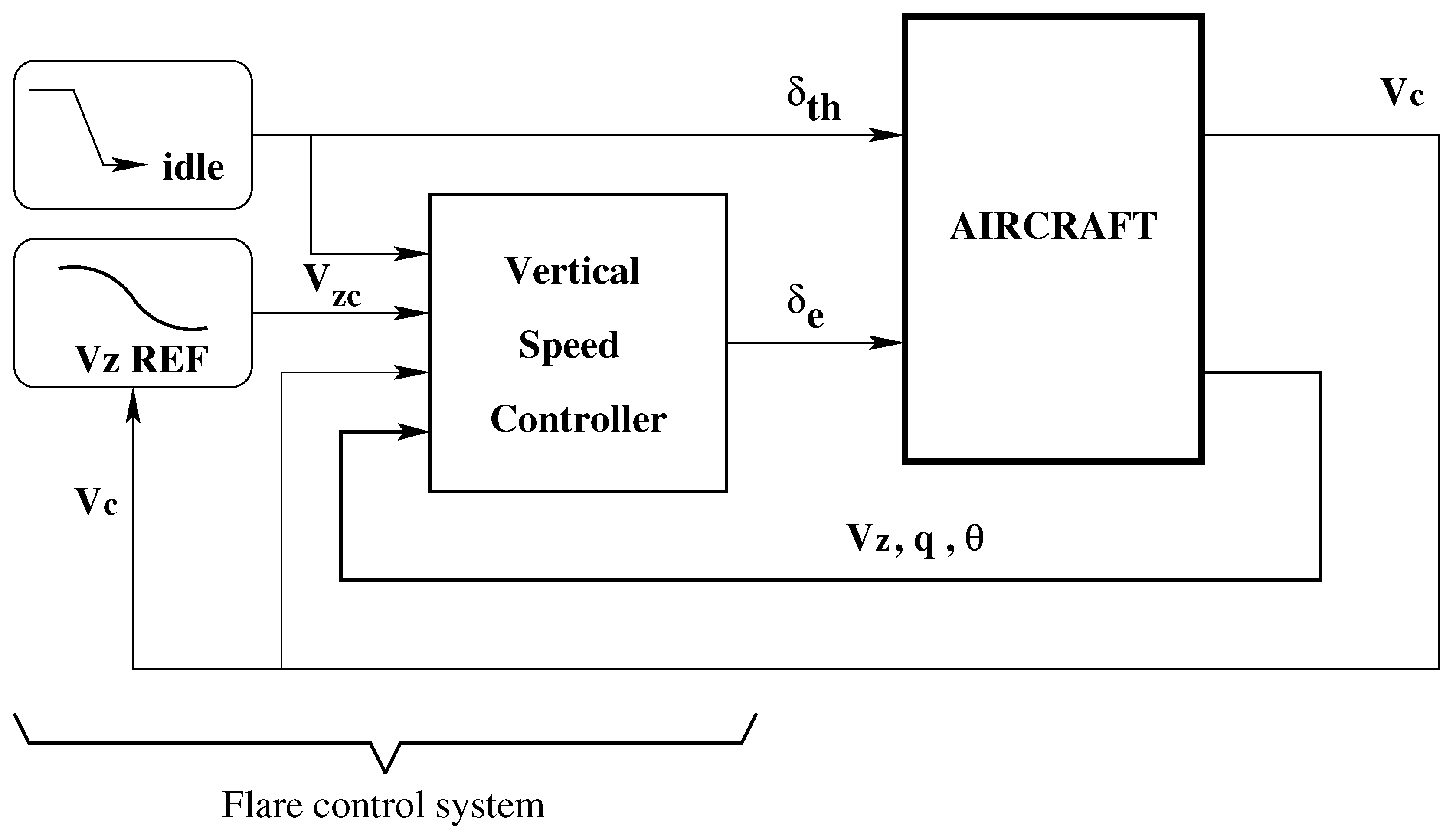
3. Flare Control Design

3.1. Overall Controller Structure

As briefly discussed above, the objective of the flare phase is to provide enhanced vertical speed control capacities so that the aircraft hits the runway about 400 m after threshold with a nominal vertical speed of $2.5$ ft/s. During this short maneuver, rarely exceeding $7$ s, the engines are set to the idle position and the airspeed $V_c$ is no longer accurately controlled (provided, of course that any stall risk is avoided). Along the longitudinal axis, the only remaining active control input is then the elevator deflection. As shown in Figure 3, the general structure of the flare system consists of two nested loops. A reference vertical speed profile is generated by the outer-loop. It depends on both the initialization altitude (generally close to 50 ft) and the ground speed. Despite perturbations and uncertainties, the generated profile should then be tracked accurately thanks to an appropriate tuning of the vertical speed inner-loop controller, whose design is described in the following section.

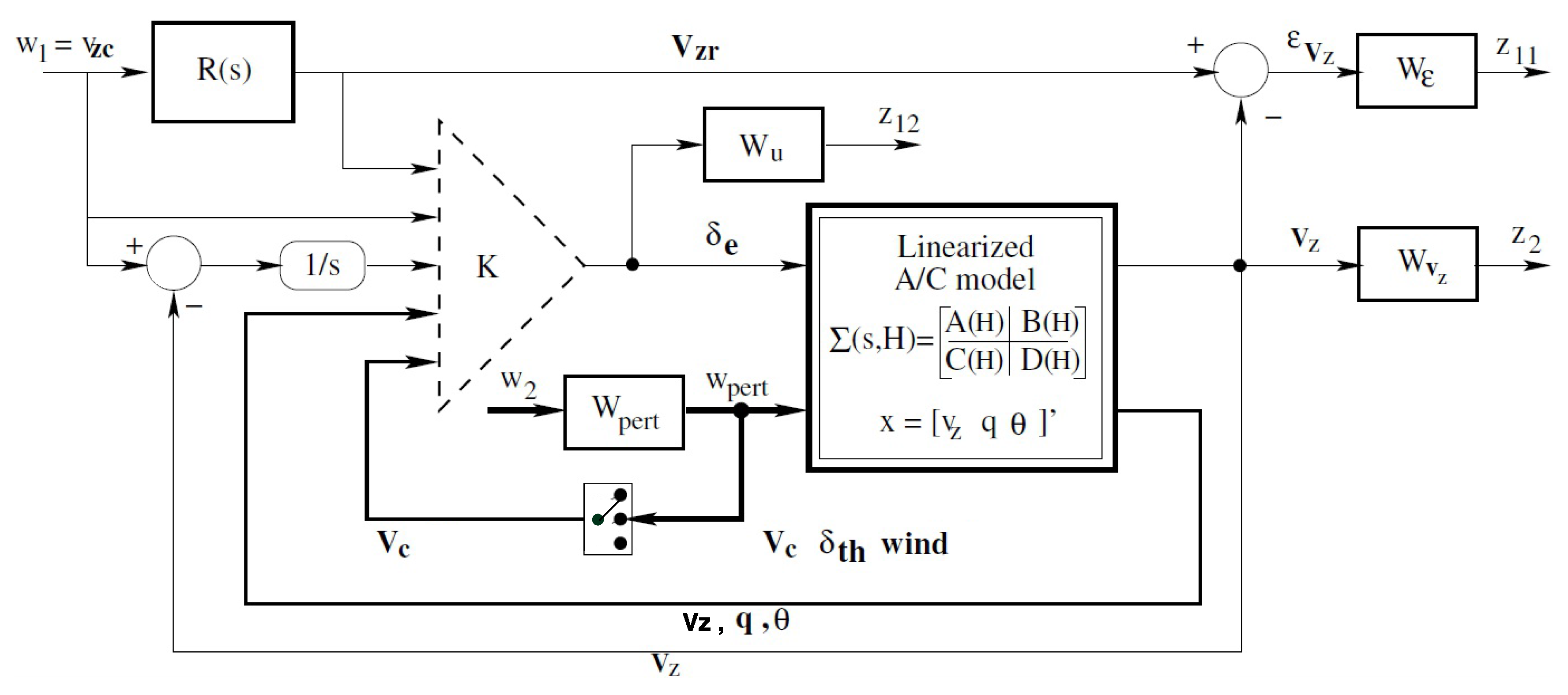
3.2. Vertical Speed Control via Multi-Channel Structured ${\mathcal{H}}_{\infty }$ Optimization

The central objectives and constraints of the flare phase are fundamentally different from those encountered during the final approach. From a control viewpoint, the design problem appears to be simpler since only one variable (the vertical speed) is being tracked and only one control input (the elevator deflection) is being managed. However, the fluctuations of the (no longer controlled) longitudinal airspeed $V_c$ and the engine deceleration generate perturbations, which, in addition to the ground and wind effects, ultimately aggravate the control problem. It appears that modal control techniques (which have been successfully used to tune the glide controller) are no longer the best option to address this specific problem. The latter now falls within the scope of ${\mathcal{H}}_{\infty }$ design methods.

The key issue is then to define an appropriate ${\mathcal{H}}_{\infty }$ design model, which begins with the choice of relevant linear approximations of the aircraft longitudinal dynamics near the ground. Such models are easily obtained with trimming and linearization tools (available with the benchmark package as mentioned in Section A.6) for various points in the flare two-dimensional trajectory (height above runway and kinematic slope). After standard matrix manipulations of the state-space data, the following parameterized set of third-order models is considered:

$$\left[\begin{array}{c}{\dot{v}}_z\\ \dot{q}\\ \dot{\theta }\end{array}\right]=A\left(H\right)\left[\begin{array}{c}{v}_z\\ q\\ \theta \end{array}\right]+B_1\left(H\right)\underset{w_{pert}}{\underbrace{\left[\begin{array}{c}{v}_c\\ {\delta }_{th}\\ w_d\end{array}\right]}}+B_2\left(H\right){\delta }_e$$

(7)

where $\theta$ is the pitch angle, and $H=H_{LG}$ denotes the height of the landing gear above ground (to alleviate notation, especially in Figure 4). Note that, in this model, $v_c$ and ${\delta }_{th}$ are no longer viewed as a state and a control input signal, respectively, but as external perturbations. However, unlike wind inputs $w_d$, these are measured and can then be used for feedback. This is illustrated in the design diagram depicted in Figure 4. Note that the controller to be optimized reduces to a static gain $K\in {\mathbb{R}}^7$. The proposed vertical speed control law structure then reads

$${\delta }_{e_c}=K{\left[v_{z_r}{v}_{z_c}\int (v_{z_c}-v_z)v_{z}q\theta v_c\right]}^{\prime }$$

(8)

where, as shown in the diagram, the signal $v_{z_r}$ coincides with the output of a linear reference model $R\left(s\right)$ to be tracked. The main interest of the proposed structure is to remain close to the one used during the glide segment (see Equation (1)), which will not only simplify the switching strategy but also contribute to an improved safety level.

Let us now focus on the optimization criteria. Beyond the standard closed-loop stability requirements, the objective is to determine the best controller $\widehat{K}$ such that

• the norm of the error ${ϵ}_{v_z}=v_{z_r}-v_z$ is minimized,
• the control activity is such that magnitude and rate saturations are avoided, and
• the perturbations $w_{pert}$ have a negligible effect on the vertical speed variations.

In the ${\mathcal{H}}_{\infty }$ framework [14], the first two objectives are realized through the norm minimization of the following transfer function (using the notation of Figure 4):

$${\mathcal{T}}_{w_1\to {[z_{11},z_{12}]}^{\prime }}\left(s\right)={\mathcal{F}}_l(P_1(s,H),K)$$

(9)

where $P_1(s,H)$ denotes the parameterized (height-dependent) weighted standard interconnection from $w_1$ to ${\left[z_{11}{z}_{12}\right]}^{\prime }$, and ${\mathcal{F}}_l(.,.)$ stands for the lower linear fractional transformation (LFT). The weighting functions $W_{ϵ}\left(s\right)$ and $W_u\left(s\right)$ are chosen following standard rules to be further discussed in Section 3.4. The third objective is then achieved by the ${\mathcal{H}}_{\infty }$ norm minimization of an independent transfer from $w_2$ (with $w_{pert}=W_{pert}\left(s\right)w_2$) to $z_2=W_{v_z}\left(s\right)v_z$:

$${\mathcal{T}}_{w_2\to z_2}\left(s\right)={\mathcal{F}}_l(P_2(s,H),K)$$

(10)

where the three-dimensional filter $W_{pert}\left(s\right)$ is used to shape the input perturbations. However, as this transfer is considered independently of Equation (9), it is not restrictive to consider a static weighting function $W_{pert}\left(s\right)=diag(w_{p_{vc}},w_{p_{\delta th}},w_{p_{wind}})$, where each static gain is used to scale the relative weights of each input perturbation. The three transfers then (Equation (10)) are weighted by a single scalar dynamic filter $W_{v_z}\left(s\right)$. In order to remove any static error (mostly induced by the speed variations) on $v_z$, which could be critical near ground, a high-gain low-pass filter must be used.

Summarizing the above discussion, the controller optimization may now be stated as the following multi-model & multi-channel structured ${\mathcal{H}}_{\infty }$ control design problem:

$$\widehat{K}=\arg \underset{K}{min}\underset{\begin{array}{c}H\le H_{FLA}\\ i=1,2\end{array}}{max}\left\{\parallel {\mathcal{F}}_l(P_i(s,H),K){\parallel }_{\infty }\right\}$$

(11)

3.3. Robustness Against Parametric Uncertainties and Modeling Errors

By simultaneously considering several design models for different values of the height of the landing gear above ground, interesting robustness properties against ground effects modeling errors are enforced in the proposed design process. This is, however, not sufficient in practice, where parametric robustness against mass and center-of-gravity location is also required. To this end, the above multi-objective ${\mathcal{H}}_{\infty }$ design framework is easily generalized to take these additional parametric uncertainties explicitly into account. Thus, the design problem (11) becomes

$$\widehat{K}=\arg \underset{K}{min}\underset{\begin{array}{c}H\le H_{FLA}\\ i=1,2\\ j=1\dots N\end{array}}{max}\left\{\parallel {\mathcal{F}}_l(P_{i,j}(s,H),K){\parallel }_{\infty }\right\}$$

(12)

where the new integer $j\in \{1,\dots ,N\}$ indexes a selection of different models in the (mass × centering) hypercube. A common choice is to consider the vertices of the hypercube. Such a design may then be followed by an analysis phase in order to detect any potential worst-case that could appear inside the hypercube. An iterative design process described in [15] can therefore be considered by incorporating the worst-case scenarios into the initial selection of design models.

3.4. Weight Selection & Resolution Aspects

The above problems (Equations (11) and (12)) are strongly non-convex and cannot be solved with the standard ${\mathcal{H}}_{\infty }$ control optimization tools, which provide unstructured full-order controllers and are unable to optimize separate channels on multiple models. However, using specialized non-smooth optimization techniques, some efficient algorithms have been proposed in [10] and then improved when they were implemented in the H_INFSTRUCT and S_YSTUNE routines of the ${\mathrm{M}}_{{\mathrm{ATLAB}}^{\circledR }}$Robust Control Toolbox [16].

In this application, the H_INFSTRUCT routine was used on an augmented design model with a block-diagonal structure including $16(2\times 4\times 2)$ models associated with

• two values of the landing gear height: $H_{LG}\in \{15\mathrm{m},5\mathrm{m}\},$
• four models (indexed by j) at the vertices of the (mass × centering) hypercube, and
• two separate optimization channels (indexed by i).

Despite potential numerical difficulties, for a given set of weighting functions, a solution is obtained in less than $2\min$ on a standard computer thanks to the efficiency of the specialized non-smooth optimization algorithm implemented in the H_INFSTRUCT routine. Such a limited computational time allows for different trials in the selection of the weighting filters, which are detailed in the next section.

3.4.1. Reference Model on the Vertical Speed

To ensure good time response while remaining compatible with the aircraft dynamics, the reference model is chosen to be

$$R\left(s\right)=\frac{{\omega }^2}{(1+\tau s)(s^2+2\xi \omega s+{\omega }^2)}$$

(13)

where $\tau =0.4$ s, $\omega =1$ rad/s, and $\xi =0.75$.

3.4.2. Performance & Robustness Oriented Weighting Filters

A low-pass filter (enforcing a high performance tracking of slowly varying inputs) is selected for $W_{ϵ}\left(s\right)$ while a high-pass filter (here approximated by a constant) is used for $W_u\left(s\right)$. After a short trial-and-error process, the weights are tuned as follows:

$$W_{ϵ}\left(s\right)=\frac{200}{1+10s},W_u\left(s\right)=20$$

(14)

Note that a constant weighting function is sufficient in our context since the optimized controller is a static gain K. This may not be the case with dynamic controllers, for which roll-off properties generally have to be enforced via high-pass dynamic weighting functions.

Finally, as is already clarified in Section 3.2, static input weighting functions and a high gain low-pass output filter are tuned for the second channel, whose objective is to minimize the effects of perturbations (induced by airspeed, thrust, and wind variations) on the vertical speed:

$$w_{p_{vc}}=w_{p_{\delta th}}=w_{p_{wind}}=1,W_{v_z}\left(s\right)=\frac{100}{1+20s}$$

(15)

3.4.3. Optimization Results

With the above filters, a worst-case ${\mathcal{H}}_{\infty }$ norm is obtained around 1, and the following gains are computed:

$$K=\left[K_1{K}_2\dots K_7\right]=[-0.4-0.07-0.30.815190.3]$$

(16)

In the following, two flare control laws (denoted Law I and Law II) are compared. In the first case (Law I), the airspeed feedback ($V_c$) is not used ($K_7=0$), while in the second case (Law II), the gains are rigorously implemented as they appear in Equations (8) and (16).

4. Nonlinear Implementation & Simulation Results

The structured flare control law resulting from the above optimization process was implemented in a nonlinear closed-loop simulation diagram, as shown in Figure 5. The flare system, highlighted in green, is activated as soon as the height $H_{LG}$ of the landing gear is lower than a prescribed value $H_{FLA}$, which has been classically set here to $50$ ft. To illustrate the benefits of using the longitudinal speed variations during the flare phase, two different controllers are compared with deterministic windsteps first and then with turbulences and ILS noises. Next, specific simulations also illustrate the robustness of the proposed controller by comparing the results of different values of the mass and the center-of-gravity location.

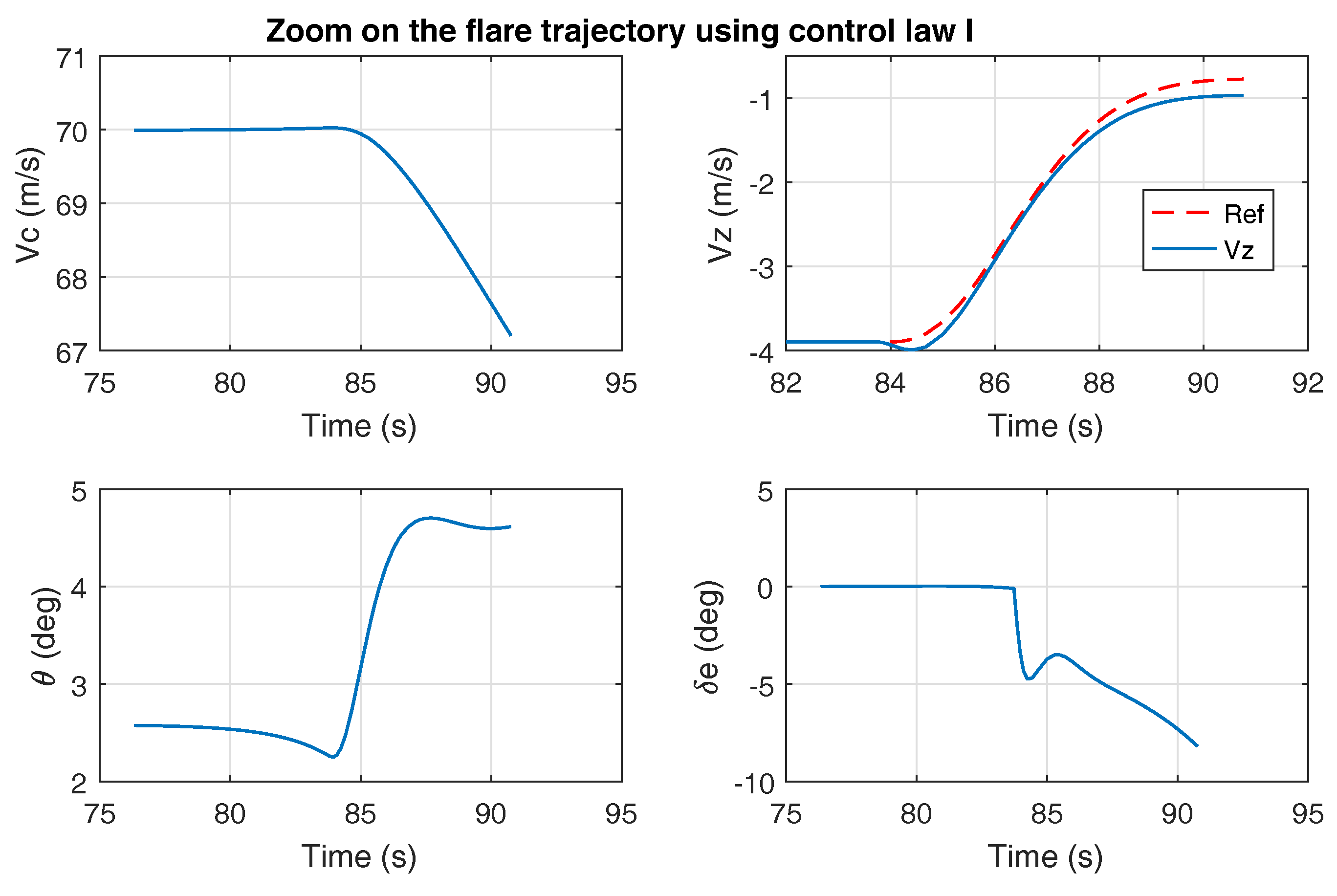
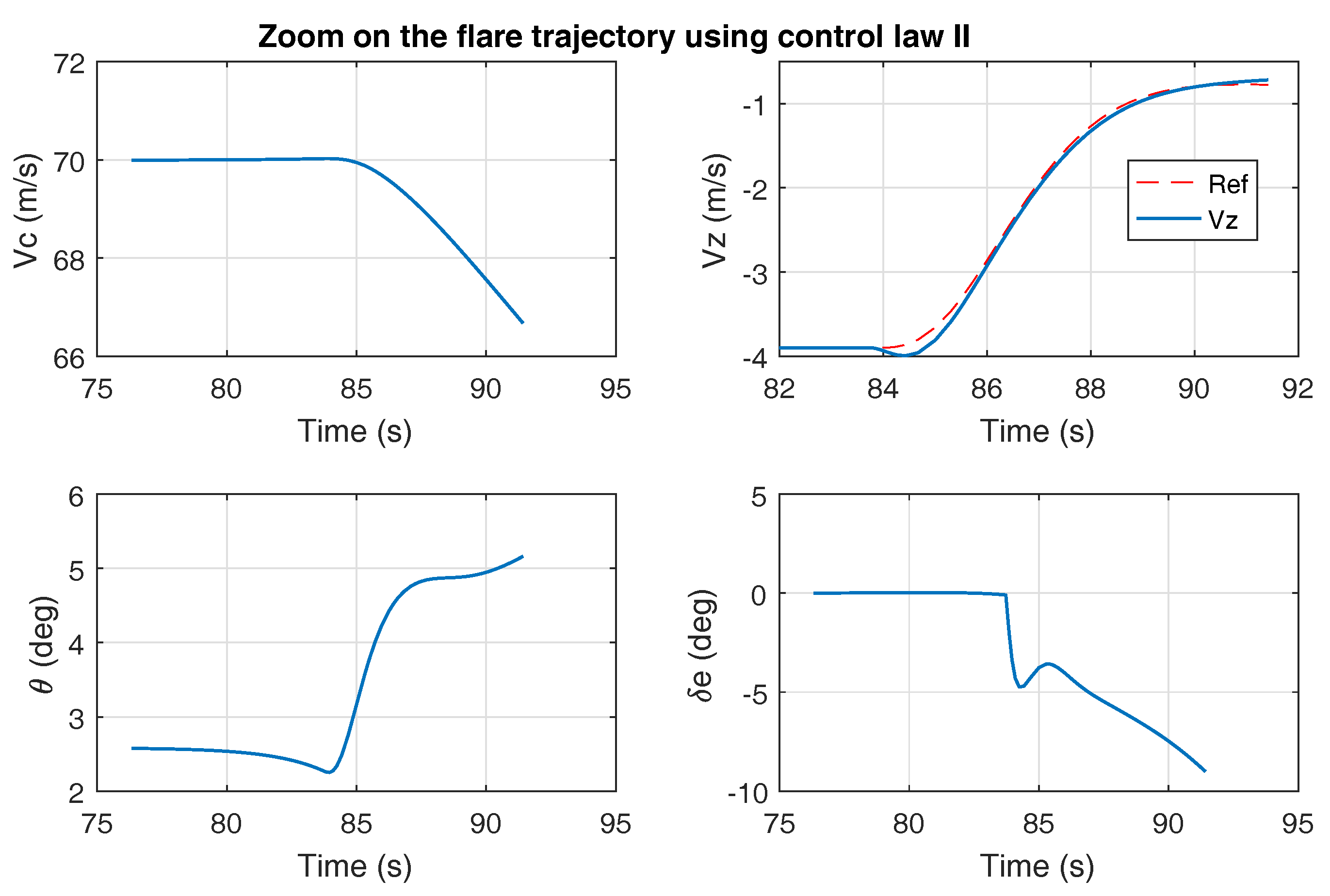
4.1. On the Interest of Using the Airspeed During Flare: Comparison of Laws I & II

In a nominal mass and centering configuration ($mass=150 \mathrm{t}$ and $x_{cg}=21\%$), the last $15$ s of simulation before touchdown (thus focusing on the flare trajectory) are displayed in Figure 6 and Figure 7.

A comparison of the upper-right plots clearly shows that the second controller (using airspeed) outperforms the first one. The second controller is thus used for the remainder of the simulations. In this last case indeed, the vertical speed profile is very close to the reference represented by the dash-dotted red line.

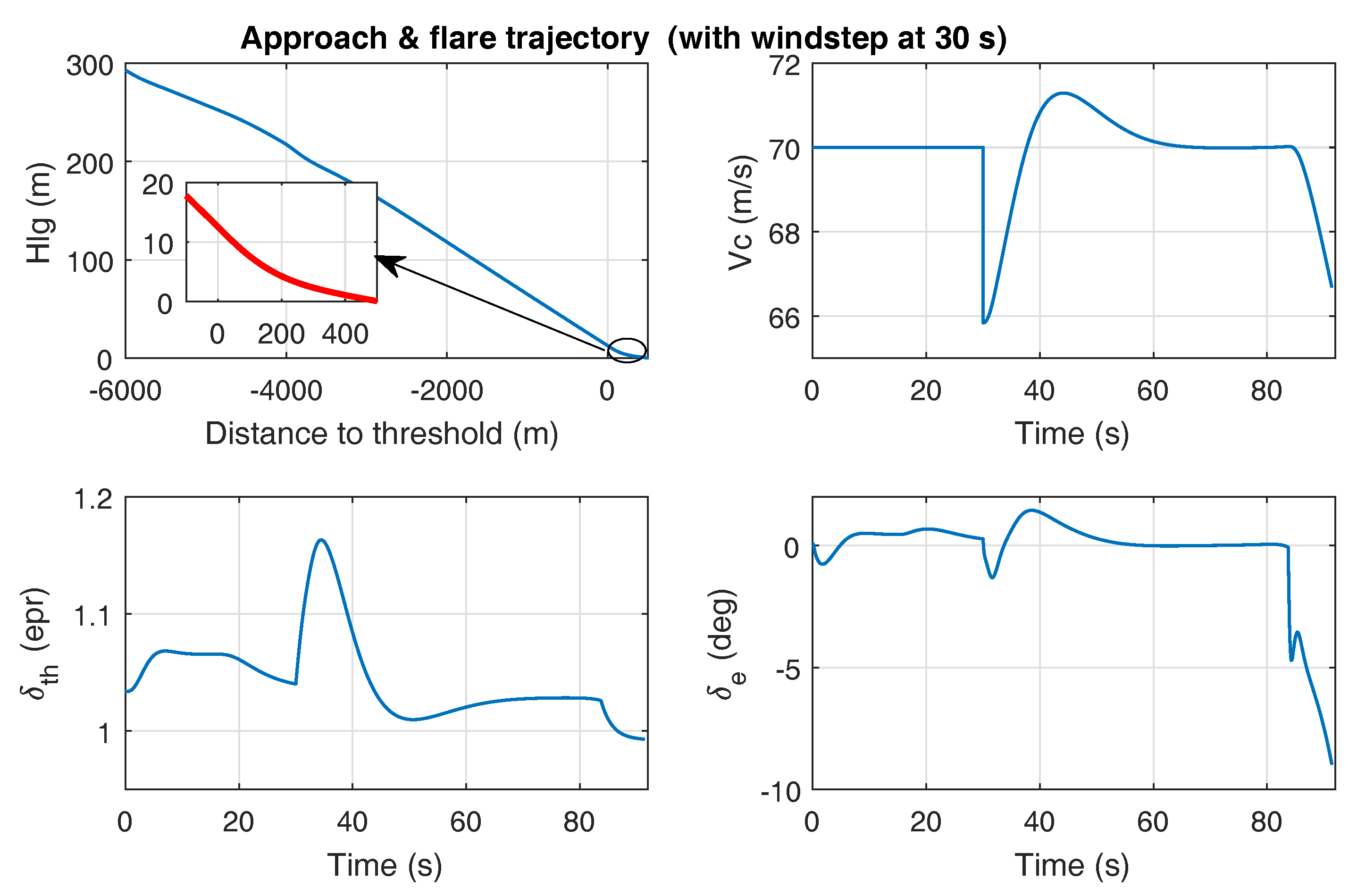
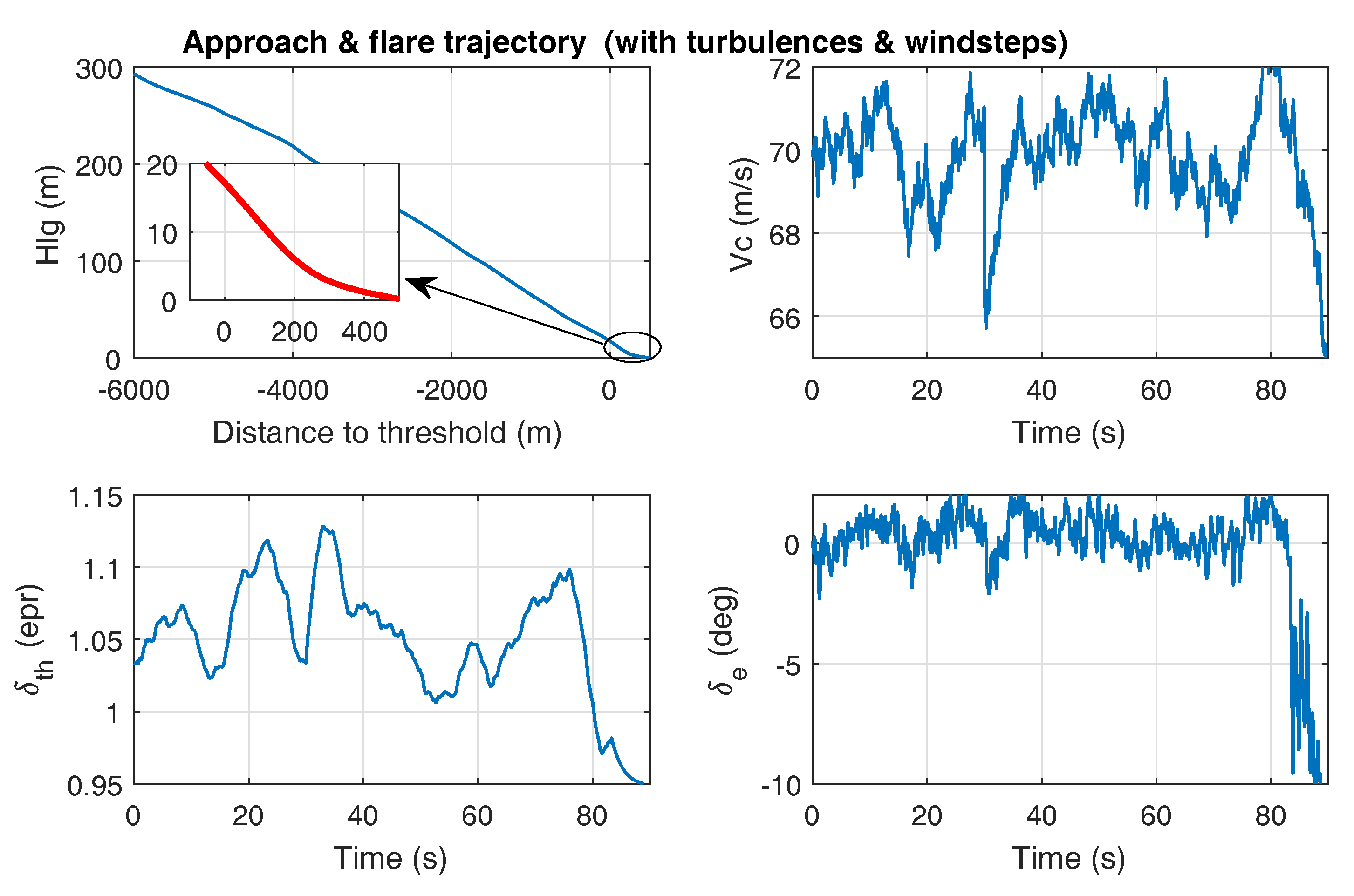
4.2. Wind & Turbulence Effects

Deterministic windsteps and turbulence effects are then analyzed in the following simulations displayed in Figure 8, Figure 9 and Figure 10. In the first two figures, the global trajectory (final approach and flare) is visualized.

In the first case, a windstep is applied at $30$ s (see the upper-right subplot of Figure 8). In the second case (Figure 9), strong turbulence conditions are added. In both situations, the proposed guidance and control system behaves well. The impact point is slightly $400$ m after the hreshold meets the requirements.

Moreover, as is displayed in Figure 10, a zoom on the flare trajectory reveals that the vertical speed remains close to the reference trajectory (upper-right subplot). It is also noted that, during the flare maneuver, the pitch angle is barely decreasing. This property is of high interest to make the autoland system compatible with standard pilots habits.

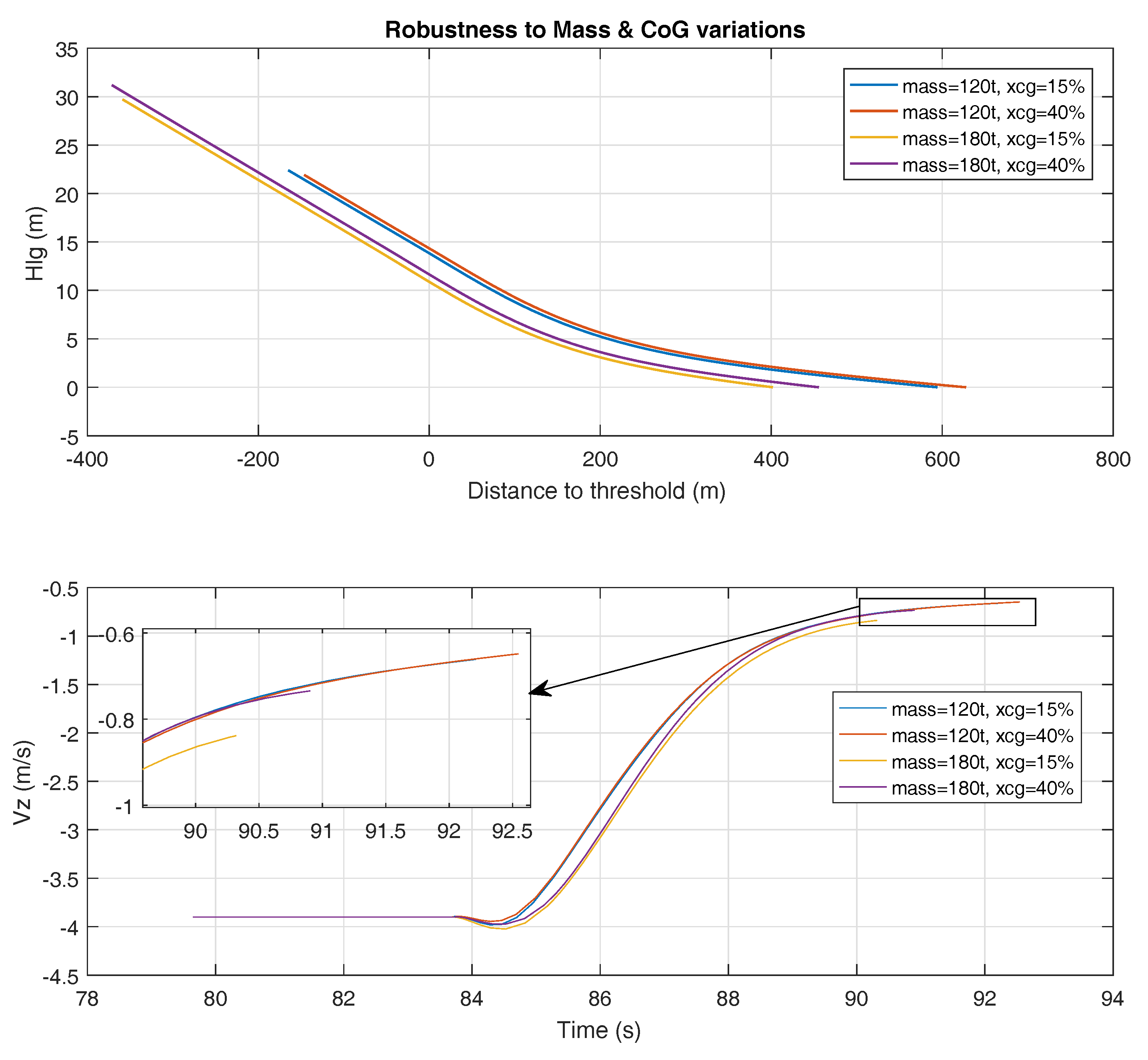
4.3. Illustration of Robustness

To conclude this section, the robustness of the proposed autoland control system is now evaluated through various simulations corresponding to the four extreme configurations of the mass (varying between $120$ t and $180$ t) and the center-of-gravity location ($x_{cg}\in [15\%,40\%]$). The results (showing the two most critical variables in the longitudinal axis, namely, the height of the landing gear and the vertical speed) are presented in Figure 11. A reasonable dispersion of the impact point (lying in the interval $[400\mathrm{m},600\mathrm{m}]$) is observed. It can also be pointed out that the vertical speed is well tracked whatever the flight condition.

5. Conclusions

A new multi-model ${\mathcal{H}}_{\infty }$-based design approach has been proposed and evaluated in this paper to improve and shorten the tuning process of flare control systems. Exploiting new capabilities of ${\mathcal{H}}_{\infty }$ optimization tools, the proposed methodology allows to design a fast and accurate vertical controller despite measured (longitudinal speed variations) and external (wind) perturbations. Thanks to this new controller, the flare outer-loop design becomes much easier and the safety of the whole maneuver is improved. Moreover, thanks to a flexible framework enabled by a multi-model strategy, robustness characteristics against parametric uncertainties and modeling errors are easily taken into account. This is achieved here to enforce robustness against inaccurate modeling of the ground effects and significant variations of the mass and the center-of-gravity location.