1. Introduction
Oil is an important raw material for many industrialized and developing countries, and an important source of export revenues for oil-exporting countries. Because changes in the price of oil can have significant effects on macroeconomic dynamics, it is not surprising that many researchers have applied various econometric techniques that help to model and to forecast changes in the price of oil [
1]. For example, Knetsch [
2] shows that an oil price forecasting technique, derived from the present value model of rational commodity pricing, outperforms forecasts based on futures prices. Reitz
et al. [
3,
4] show how the oil price can be described in the context of a heterogeneous agents model. Kilian [
5] provides a useful survey of recent research on the link between oil prices and macroeconomic dynamics.
Survey data on forecasts of future changes of the price of oil are an alternative to formal econometric techniques when it comes to forecasting the dynamics of the price of oil. An important question, thus, is whether survey data on forecasts of future changes of the price of oil are consistent with the rational-expectations paradigm of economics. Such questionnaires measure market’s expectations directly by surveying a large number of analysts working in the financial industry. Deviations from rationality may arise for several reasons. For example, Pierdzioch
et al. [
6] detected signs of forecaster anti-herding in survey forecasts of the future price of oil. Forecaster anti-herding implies that forecasters try to differentiate their forecasts from the forecasts of others by making “extreme” forecasts. Attempts to differentiate forecasts can easily arise if the forecasters’ reputation and/or income depends not only on the absolute forecast accuracy but also on the relative forecast accuracy. If, for example, many forecasters form an accurate forecast, income of individual forecasters may be low because they share revenues with other forecasters. If so, forecast differentiation can be a rational strategy [
7].
We study the rationality of forecasts of future changes of the price of oil using a general modeling framework that allows forecasters’ loss function to be asymmetric [
8]. Allowing for an asymmetric loss function when testing for rationality of forecasts is important because classic tests of forecast rationality (for example, [
9]) that are carried out by assuming the loss function is symmetric, yield misleading results if forecasters’ loss function is asymmetric [
10]. Asymmetries in forecasters’ loss function can arise because of incentives to differentiate forecasts from the forecasts of others, but asymmetries can arise for other reasons as well. Empirical evidence of an asymmetric loss function has been reported in recent research by Pierdzioch
et al. [
11]. Using survey data on the future price of oil taken from the Survey of Professional Forecasts data compiled by the European Central Bank, they find that the loss forecasters seem to incur when they overestimate the future price of oil is larger than the loss of an underestimation of the same size. They also report that assuming an asymmetric loss function does not necessarily weaken evidence against rationality.
Pierdzioch
et al. [
11] apply the technique advanced by Elliott
et al. [
8] to forecasts of the
level of the future nominal price of oil, which can be problematic because the level of the future price of oil typically undergoes large and significant fluctuations over time. In fact, the dynamics of the nominal price of oil is likely to be difference-stationary, implying that the price of oil may not have a stationary distribution. In this research, we thus use the same dataset used by Pierdzioch
et al. [
11] to test whether their results can be replicated when we transform the data to
rates of change. We find that under an asymmetric loss function forecasters’ rationality can often (but not always) not be rejected. Evidence of forecast rationality is slightly stronger for a so called asymmetric lin-lin loss function than for a so called asymmetric quad-quad loss function. Evidence of forecast rationality is not very strong when we pool forecasts across forecasters.
2. Testing for Forecast Rationality under Asymmetric Loss
Adopting the approach developed by Elliott
et al. [
8], we assume the following loss function,
L:
where
st+ 1 denotes the log change in the price of oil (that is, the annualized rate of change),
ft + 1 denotes the corresponding period-
t forecast,
I denotes the indicator function,
p = 1 for a linear-linear (lin-lin) loss function and
p = 2 for a quadratic-quadratic (quad-quad) loss function, and the asymmetry parameter,
a assumes values in the interval (0.1). In the case of
a = 0.5, the loss function is symmetric.
Given the parameter,
p, that governs the general shape of the loss function, the asymmetry parameter can be consistently estimated using a GMM estimator [
8]. Details are given in [
8], and our description of the estimation approach is brief and informal because we are mainly interested in whether the estimation results reported by [
11] for the level of the price of oil can be replicated for the rate of change. Following [
8] and [
11], we compute GMM estimates of the asymmetry parameter using the following instruments: a constant (Model 1), a constant and the lagged forecast error (Model 2), a constant and the lagged rate of change of the oil price (Model 3), and, a constant, the lagged forecast error, and the lagged rate of change of the oil price (Model 4). With an estimate of the asymmetry parameter in hand, a
J-test can be used to test for forecast rationality. The statistic
Ji(0.5) answers the question of whether forecasters are rational under the maintained assumption of a symmetric loss function. The statistic
Ji(
a) answers the question of whether forecasters are rational, given an estimated asymmetric loss function (lin-lin or quad-quad). Both tests are computed for Model
i= 1–4.
3. Data and Empirical Results
Following [
11], we analyze quarterly oil-price forecasts from the Survey of Professional Forecasts data conducted by the European Central Bank. The data on the actual price of oil are from Thomson Financial Datastream. The sample period is 2002Q4–2010Q4.
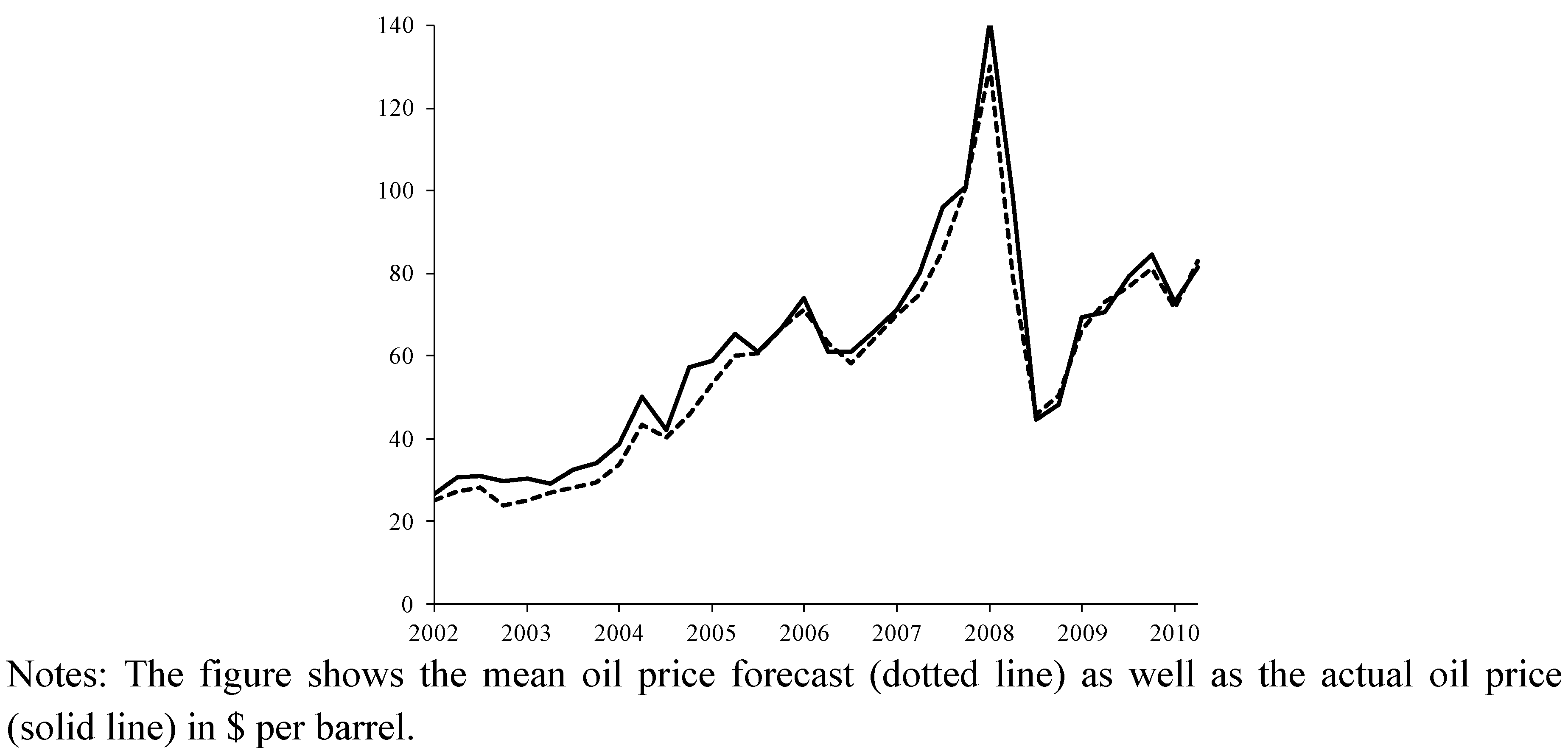
Figure 1 shows the dynamics of the price of oil (solid line) as well as the mean oil price forecast (dotted line). Results of standard tests suggest that the oil price is difference stationary. For example, a standard Augmented-Dickey-Fuller test and a Phillips-Perron test (three lags) yield a test statistic of −3.36 (
p-value = 0.00) and −23.33 (
p-value = 0.00), respectively. The oil price started in 2002 at around 26 dollars per barrel and peaked in 2008 at around 140 dollars per barrel. The price of oil then dropped to 44 dollar per barrel in late 2009. At the end of the sample period, the price of oil hovered around 70 to 80 dollars per barrel. Given the large swings in the price of oil, we study forecast rationality using data for the full sample and for a subsample ending in 2006Q4. We estimate the asymmetry parameter for the full sample and the subsample for a total of 19 forecasters. All 19 forecasters participated in all 35 quarterly survey questionnaires. As compared to the study by Pierdzioch
et al. [
11], the number of forecasts in our sample is slightly smaller (19 as compared to 25) because, for six forecasters, computations did not converge for the short subsample. Pierdzioch
et al. [
11] study pooled data for the subsample period and, thus, estimate the model on the full set of forecasts. In total, we study 665 forecasts.
Figure 1.
The price of oil.
Figure 1.
The price of oil.
Table 1 summarizes the cross-sectional mean values of the estimated asymmetry parameters for the four models. Computations were implemented using the software R (R Development Core Team, [
12]). Replicating results reported by Pierdzioch
et al. [
11], the asymmetry parameter tends to be smaller than 0.5 on average, implying that forecasters experienced a higher loss when their forecast exceeded the future price of oil than when their forecast fell short of the future price of oil by the same magnitude. The asymmetry of forecasters’ loss function is somewhat stronger under a quad-quad than under a lin-lin loss function. The asymmetry of forecasters’ loss function is somewhat stronger in the subsample than in the full sample.
Table 1.
Estimated asymmetry parameter (mean across forecasters).
Table 1.
Estimated asymmetry parameter (mean across forecasters).
| Model specification | a1 | a2 | a3 | a4 |
|---|
| Full sample, lin-lin | 0.31 | 0.30 | 0.30 | 0.29 |
| Full sample, quad-quad | 0.21 | 0.18 | 0.19 | 0.17 |
| Subsample, lin-lin | 0.25 | 0.21 | 0.20 | 0.20 |
| Subsample, quad-quad | 0.16 | 0.12 | 0.11 | 0.11 |
Table 2 summarizes how often the
J-tests indicate rationality irrespective of the loss function, only under an estimated asymmetric loss function, or no rationality at all. Our decision criterion is that we reject rationality of forecasts if one of the
Ji-tests, given a loss function, is significant at the 10% level. While other criteria could be used, our criterion is a conservative one in the sense that it makes it hard not to reject forecast rationality. The null hypothesis is that forecasts are rational. Our criterion is conservative because it allows forecast rationality to be rejected at a relatively large marginal significance level. Results of the
J-test may differ across model specifications. The results of the rationality tests, thus, may depend on the instruments being used to study forecast rationality. It should also be noticed that the
J-test can only computed in case of an asymmetric loss function for Models
i = 2–4. For details, see Elliott
et al. [
8] and Pierdzioch
et al. [
11].
Table 2.
Results of the rationality tests.
Table 2.
Results of the rationality tests.
| Rationality results | Rational under symmetric and asymmetric loss | Rational only under asymmetric loss | Tests indicate violation of rationality under both loss functions |
|---|
| | Forecasts of individual forecasters |
| Full sample, lin-lin | 6 | 12 | 1 |
| Full sample, quad-quad | 4 | 12 | 3 |
| Subsample, lin-lin | 4 | 10 | 5 |
| Subsample, quad-quad | 3 | 11 | 4 |
| | Forecasts pooled across forecasters |
| Full sample, lin-lin | no | no | yes |
| Full sample, quad-quad | no | yes | no |
| Subsample, lin-lin | no | no | yes |
| Subsample, quad-quad | no | no | yes |
The results clearly demonstrate that an asymmetric loss function leads to a rejection of forecast rationality less often than does a symmetric loss function. Moreover, forecast rationality is rejected more often (for approximately 21% to 25% of forecasters) when we estimate the loss function on data for the subsample period. When we pool forecasts across forecasters, we do not find much evidence that an asymmetric loss function helps to reconcile forecasts with the hypothesis of forecast rationality.
Because
Table 1 and
Table 2 highlight some noticeable differences between the full sample and the subsample, we estimate the asymmetry parameter and the
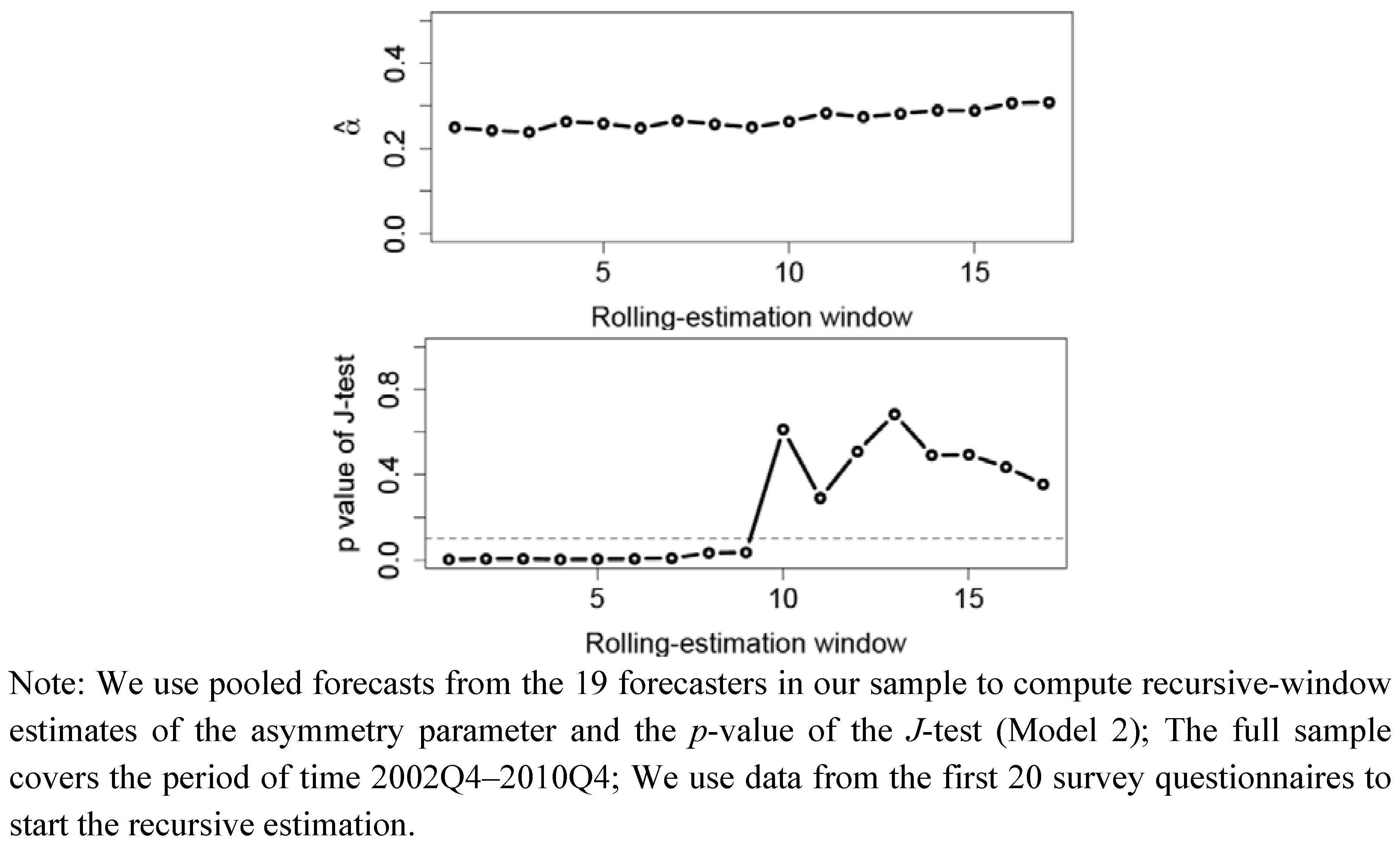
J-test for forecast rationality by means of a recursive-window approach, where we pool data across the 19 forecasters in our sample. Our recursive-window approach, thus, sheds light on the shape of forecasters’ loss function and forecast rationality from an aggregate perspective. We start with data from the first 20 survey questionnaires, and then expand the recursive window successively.
Figure 2 summarizes the results for a lin-lin loss functions. The results for a quad-quad loss function (not reported) are similar. When pooling the survey data across forecasters, the issue of cross-sectional dependence of the data arises. Aretz
et al. [
13] suggest using a bootstrap to take into account cross-sectional dependence. We have not bootstrapped the
p-value reported in
Figure 2 as the change in the
p-value in the second half of the sample is quite strong. Still, it may be interesting in future research to apply the bootstrap studied by Aretz
et al. [
13] to our data.
Figure 2.
Recursive-estimation window.
Figure 2.
Recursive-estimation window.
Two key results emerge. First, the estimated asymmetry parameter tended to increase somewhat during the sample period. (This tendency becomes more apparent when we use a rolling rather than a recursive-window approach.) Second, evidence of forecast rationality, given a lin-lin loss function, is stronger in the second half of the sample period. Forecast rationality cannot be rejected when the
p-value of the
J-test is larger than the 10% (dashed horizontal line). In the first half of the sample period, however, forecast rationality can soundly be rejected. Both results of our rolling-window approach go beyond the results reported in Pierdzioch
et al. [
11]. In their subsample analysis they only study the first half of the sample period (excluding data from 2007Q1 onward). They find that forecast rationality can be rejected in the first half of the sample, and our results corroborate this finding. Our results, however, also show that, at least at the aggregate level, evidence of forecast rationality seems to fluctuate over time, possibly reflecting changes in market conditions. Changing market conditions may lead to time-varying evidence of forecast rationality because, for example, the impact of chartists and fundamentalists on the dynamics of the price of oil varies over time. See Reitz
et al. [
3].