Finite-Time Stabilization of Homogeneous Non-Lipschitz Systems
Abstract
:1. Introduction
2. Preliminary Results
2.1. Finite-Time Stability
- is positive definite on and
- , .
2.2. Finite-Time Stabilizing Feedback
3. Proof of Theorem 2
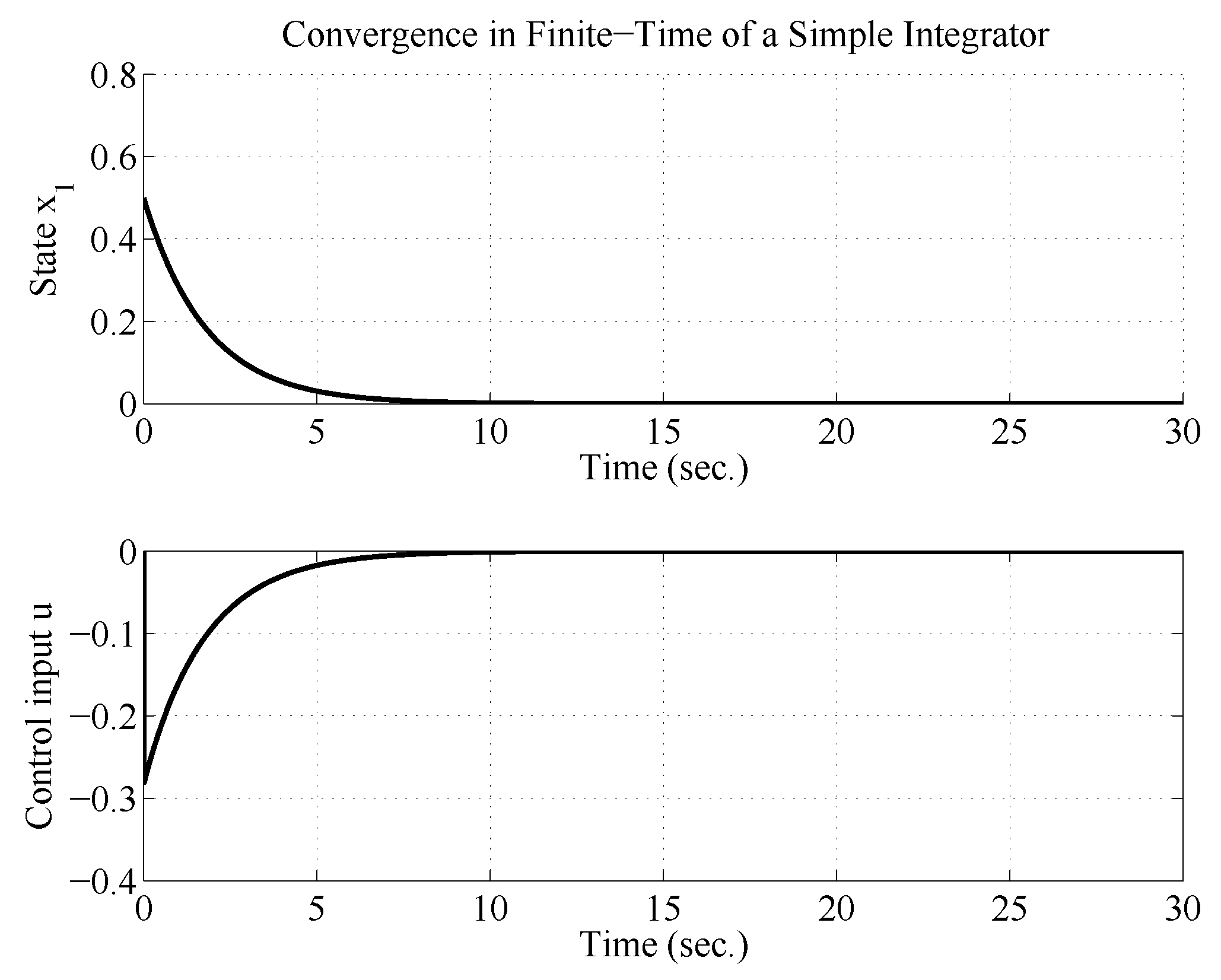
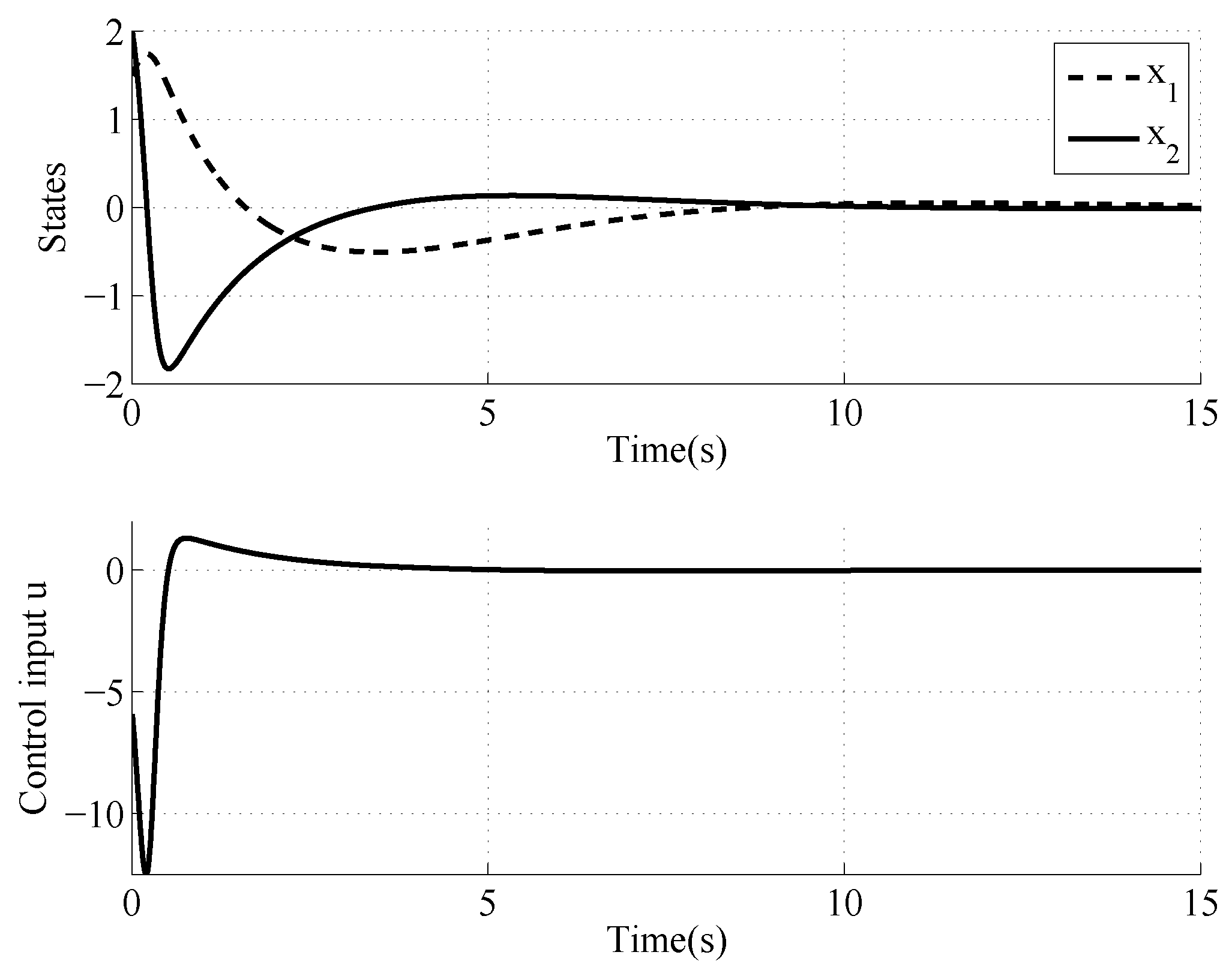
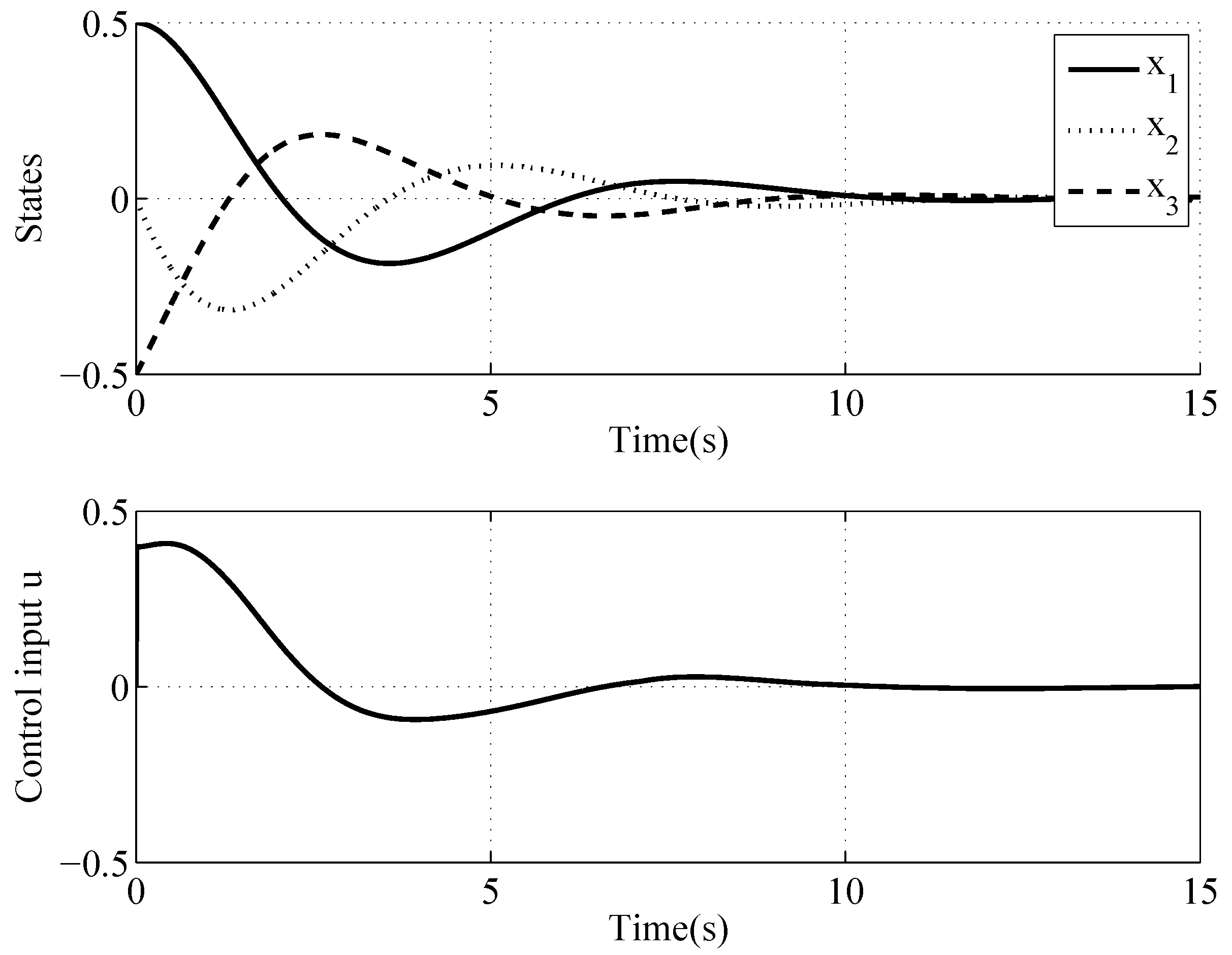
4. Simulations of the Controller
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Byrnes, C.I.; Isidori, A. Asymptotic stabilization of minimum phase nonlinear systems. IEEE Trans. Autom. Control 1991, 36, 1122–1137. [Google Scholar] [CrossRef]
- Isidori, A. Nonlinear Control Systems 2; Springer: New York, NY, USA, 1999. [Google Scholar]
- Palendo, J.; Qian, C. A generalized framework for global output feedback stabilization of genuinely nonlinear systems. In Proceedings of the 44th IEEE Conference on Decision and Control and European Control Conference (CDC-ECC 2005), Seville, Spain, 12–15 December 2005; pp. 2646–2651.
- Coron, J.M.; Praly, L. Adding an integrator for the stabilization problem. Syst. Control Lett. 1991, 17, 89–104. [Google Scholar] [CrossRef]
- Byrnes, C.I.; Isidori, A. New results and examples in nonlinear feedback stabilization. Syst. Control Lett. 1989, 12, 437–442. [Google Scholar] [CrossRef]
- Lin, W.; Qian, C. Adding one power integrator: A tool for global stabilization of higher order lower-triangular system. Syst. Control Lett. 2000, 39, 339–351. [Google Scholar] [CrossRef]
- Praly, L.; Andrea-Novel, B.; Coron, J.M. Lyapunov design of stabilizing controllers for cascaded systems. IEEE Trans. Autom. Control 1991, 36, 1177–1181. [Google Scholar] [CrossRef]
- Bacciotti, A. Local Stabilizability of Nonlinear Control Systems; World Scientific: Singapore, 1992. [Google Scholar]
- Hermes, H. Homogeneous coordinates and continuous asymptotically stabilizing feedback controls. In Differential Equations Stability and Control; Elaydi, S., Ed.; Marcel Dekker: New York, NY, USA, 1991; pp. 249–260. [Google Scholar]
- Kawski, M. Homogeneous stabilizing feedback laws. Control Theory Adv. Technol. 1990, 6, 497–516. [Google Scholar]
- Qian, C.; Lin, W. Non-Lipschitz continuous stabilizers for nonlinear systems with uncontrollable unstable linearization. Syst. Control Lett. 2001, 42, 185–200. [Google Scholar] [CrossRef]
- Ding, S.; Li, S.; Zheng, W. Nonsmooth stabilization of a class of non linear cascaded systems. Automatica 2012, 48, 2597–2606. [Google Scholar] [CrossRef]
- Andreini, A.; Bacciotti, A.; Stefani, G. Global stabilizability of homogeneous vector fields of odd degree. Syst. Control Lett. 1988, 10, 251–256. [Google Scholar] [CrossRef]
- Qian, C. A homogeneous domination approach for global output feedback stabilization of a class of nonlinear systems. In Proceedings of the 2005 American Control Conference, Portland, OR, USA, 8–10 June 2005; Volume 7, pp. 4708–4715.
- Bhat, S.P.; Bernstein, D.S. Continuous finite-time stabilization of the translational and rotational double intergrator. IEEE Trans. Autom. Control 1998, 43, 678–682. [Google Scholar] [CrossRef]
- Hong, Y.; Huang, J.; Xu, Y. On an output feedback finite-time stabilization problem. IEEE Trans. Autom. Control 2001, 46, 305–309. [Google Scholar] [CrossRef]
- Bhat, S.P.; Bernstein, D.S. Lyapunov analysis of finite-time differential equations. In Proceedings of the American Control Conference, Seattle, WA, USA, 21–23 June 1995; Volume 3, pp. 1831–1832.
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of homogeneous systems. In Proceedings of the American Control Conference, Albuquerque, NM, USA, 4–6 June 1997; Volume 4, pp. 2513–2514.
- Bhat, S.P.; Bernstein, D.S. Finite-time stability of continuous autonomous systems. SIAM J. Control Optim. 2000, 38, 751–766. [Google Scholar] [CrossRef]
- Yang, B. Output Feedback Control for Nonlinear Sytems with Unstabilizable and Undetectable Linearization. Ph.D. Thesis, Case Western Reserve University, Cleveland, OH, USA, August 2006. [Google Scholar]
- Qian, C.; Lin, W. Non-Smooth stabilizers for nonlinear systems with uncontrollable unstable linearization. In Proceedings of the 39th IEEE Conference on Decision and Control, Sydney, Australia, 12–15 December 2000; Volume 2, pp. 1655–1660.
- Qian, C.; Lin, W. A continuous feedback approach to global strong stabilization of nonlinear systems. IEEE Trans. Autom. Control 2001, 46, 1061–1079. [Google Scholar] [CrossRef]
- Shen, Y.; Huang, Y. Global finite-time stabilisation for a class of nonlinear systems. Int. J. Syst. Sci. 2012. [Google Scholar] [CrossRef]
- Huang, X.; Lin, W.; Yang, B. Global finite-time stabilization of a class of uncertain nonlinear systems. Automatica 2005, 41, 881–888. [Google Scholar] [CrossRef]
- Hong, Y. Finite-time stabilization and stabilizability of a class of controllable systems. Syst. Control Lett. 2002, 46, 231–236. [Google Scholar] [CrossRef]
- Jammazi, C. Finite-time partial stabilizability of chained systems. Comptes Rendus Math. 2008, 346, 975–980. [Google Scholar] [CrossRef]
- Jammazi, C. On a sufficient condition for finite-time partial stability and stabilization: Applications. IMA J. Math. Control Inf. 2010, 27, 29–56. [Google Scholar] [CrossRef]
- Back, J.; Cheong, S.G.; Shim, H.; Seo, J.H. Nonsmooth feedback stabilizer for strict-feedback nonlinear systems that may not be linearizable at the origin. Syst. Control Lett. 2007, 56, 742–752. [Google Scholar] [CrossRef]
- Nakamura, H.; Yamashita, Y.; Nishitani, H. Homogeneous eigenvalue analysis of homogeneous systems. In Proceedings of the 16th IFAC World Congress, Prague, Czech, 3–8 July 2005.
- Nakamura, H.; Yamashita, Y.; Nishitani, H. Stabilization of homogeneous systems using implicit control Lyapunov functions. In Proceedings of the 7th IFAC Symposium on Nonlinear Control Systems, Pretoria, South Africa, 21–24 August 2007; Volume 7, pp. 561–566.
- Bhat, S.P.; Bernstein, D.S. Geometric homogeneiy with applicatons to finite-time stability. Math. Control Signals Syst. 2005, 17, 101–127. [Google Scholar] [CrossRef]
- Ding, S.; Li, S.; Li, Q. Stability analysis for a second order continuous finite-time control system subject to a disturbance. J. Control Theory Appl. 2009, 7, 271–276. [Google Scholar]
- Duchaine, V.; Gosselin, C.M. Investigation of Human-Robot interaction stability using Lyapunov theory. In Proceedings of the IEEE International Conference in Robotics and Automation, Pasadena, CA, USA, 19–28 May 2008; pp. 2189–2194.
- Campeau-Lecours, A.; Otis, M.J.-D.; Belzile, P.-L.; Gosselin, C. A time-domain vibration observer and controller for physical human-robot interaction. Mechatronics 2016, 36, 45–53. [Google Scholar] [CrossRef]
- Meziane, R.; Li, P.; Otis, M.J.-D.; Ezzaidi, H.; Cardou, P. Safer hybrid workspace using human-robot interaction while sharing production activities. In Proceedings of the IEEE International Symposium on Robotic and Sensors Environments (ROSE), Timisoara, Romania, 16–18 October 2014; pp. 37–42.
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khelil, N.; Otis, M.J.-D. Finite-Time Stabilization of Homogeneous Non-Lipschitz Systems. Mathematics 2016, 4, 58. https://doi.org/10.3390/math4040058
Khelil N, Otis MJ-D. Finite-Time Stabilization of Homogeneous Non-Lipschitz Systems. Mathematics. 2016; 4(4):58. https://doi.org/10.3390/math4040058
Chicago/Turabian StyleKhelil, Nawel, and Martin J.-D. Otis. 2016. "Finite-Time Stabilization of Homogeneous Non-Lipschitz Systems" Mathematics 4, no. 4: 58. https://doi.org/10.3390/math4040058






