An Analysis on the Fractional Asset Flow Differential Equations
Abstract
:1. Introduction
2. Model Formulation
2.1. Fractional Calculus
2.2. Fractional Model
| the market price of an asset at time t, | |
| the fraction of total asset invested in the stock at time t, | |
| the trend-based component of the investor preference at time t, | |
| the value-based component of the investor preference at time t, | |
| the fundamental value, | |
| D | the demand, |
| S | the supply. |
- (A1)
- is increasing and continuously differentiable where , and satisfies that for anyfor some positive constant .
- (A2)
- is continuous and satisfies there being two constants and such that:and for any .
- (A3)
- is continuously differentiable and has the following: there exists two positive constants and such that:and for any .
3. Local Existence and Uniqueness of a Solution
4. Continuation Theorems
5. Stability Analysis
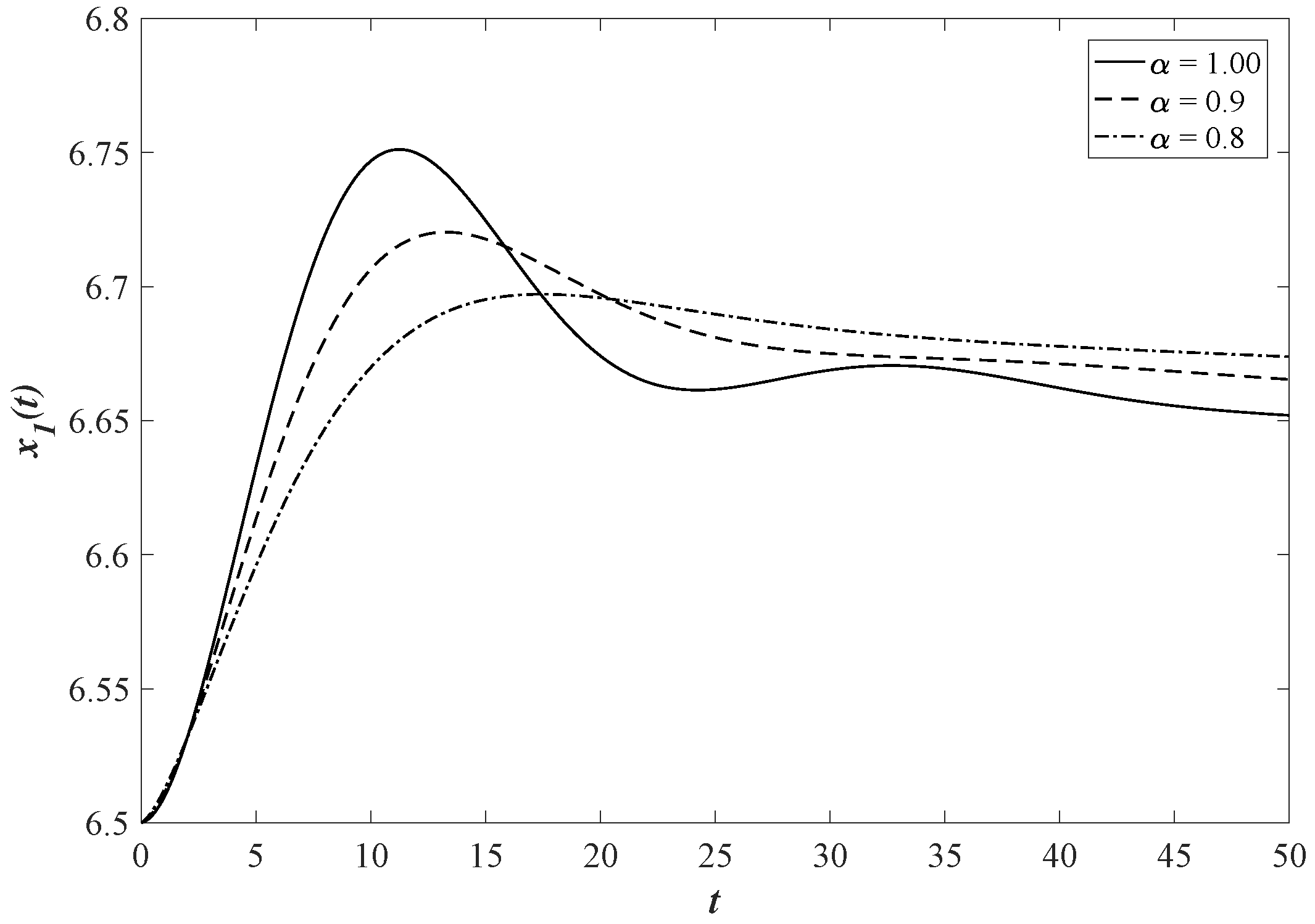
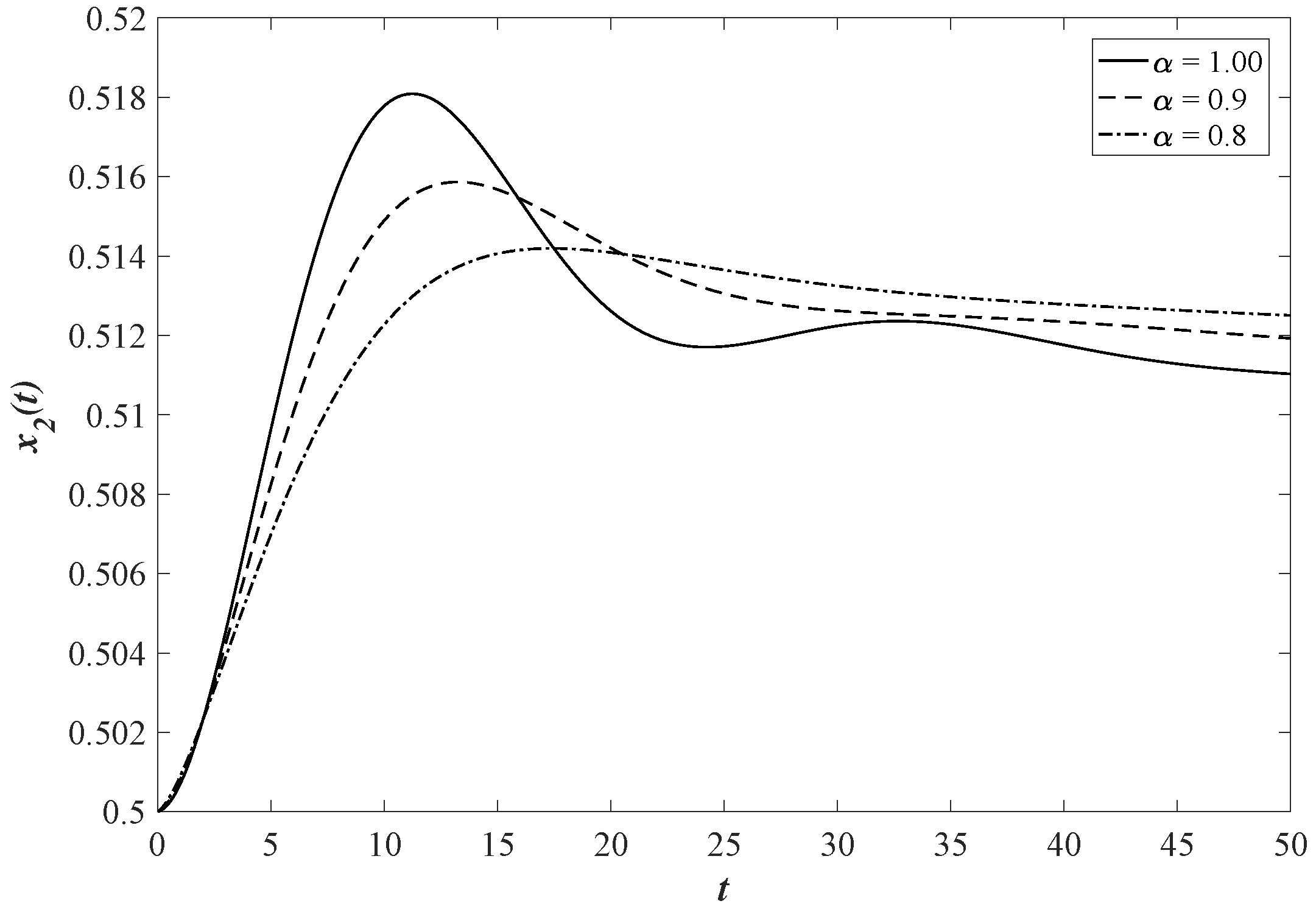
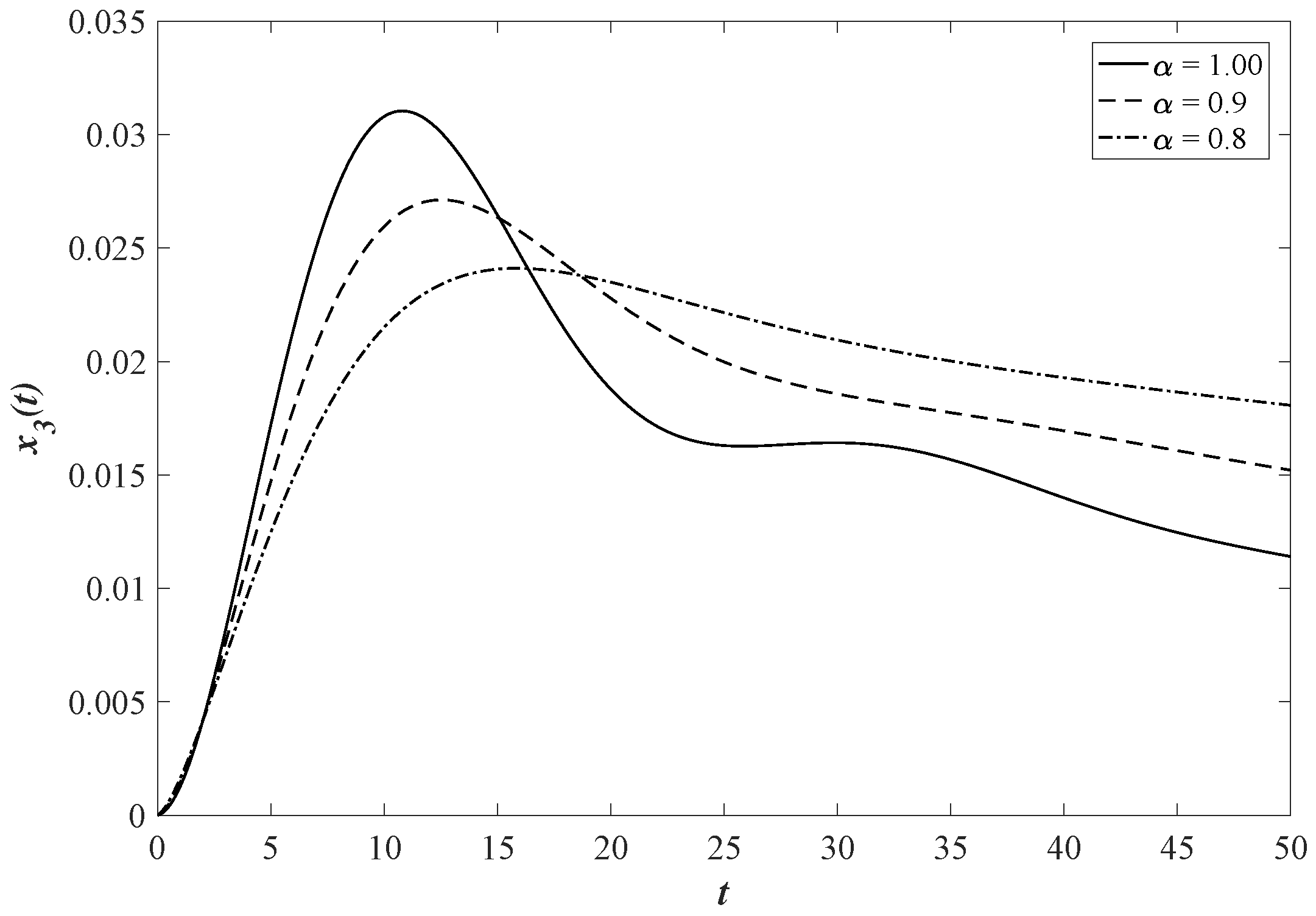
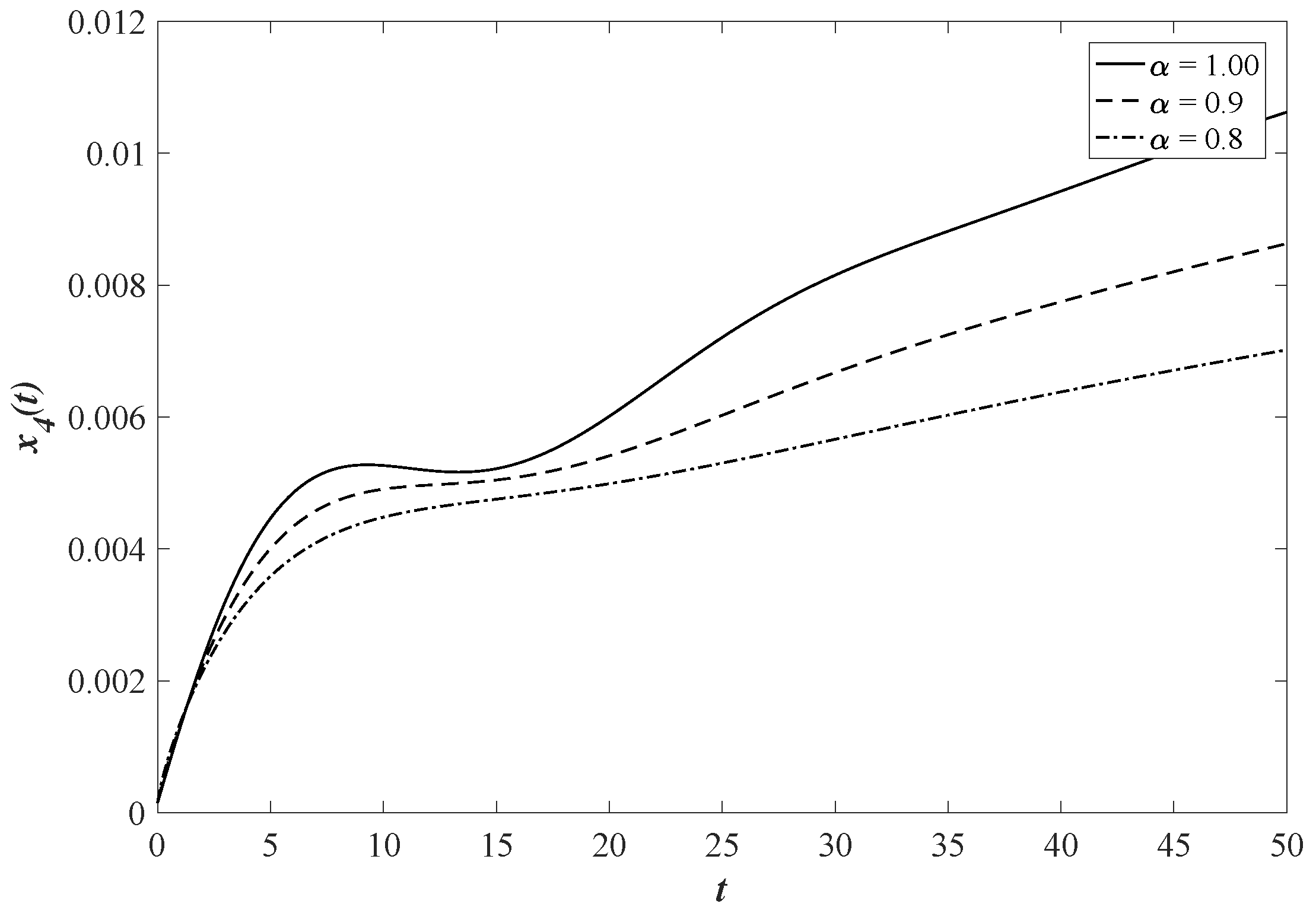
6. Numerical Simulation
7. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ma, J.H.; Chen, Y.S. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system—I. Appl. Math. Mech. 2001, 22, 1240–1251. [Google Scholar]
- Ma, J.H.; Chen, Y.S. Study for the bifurcation topological structure and the global complicated character of a kind of nonlinear finance system—II. Appl. Math. Mech. 2001, 22, 1375–1382. [Google Scholar]
- Cesare, L.D.; Sportelli, M. A dynamic IS-LM model with delayed taxation revenues. Chaos Solitons Fractals 2005, 25, 233–244. [Google Scholar]
- Fanti, L.; Manfredi, P. Chaotic business cycles and fiscal policy: An IS-LM model with distributed tax collection lags. Chaos Solitons Fractals 2007, 32, 736–744. [Google Scholar]
- Frisch, R.; Holme, H. The Characteristic Solutions of a Mixed Difference and Differential Equation Occuring in Economic Dynamics. Econometrica 1935, 3, 225–239. [Google Scholar]
- He, X.Z.; Li, K.; Wei, J.; Zheng, M. Market stability switches in a continuous-time financial market with heterogeneous beliefs. Econ. Model. 2009, 26, 1432–1442. [Google Scholar]
- Chiarella, C.; Dieci, R.; Gardini, L. Asset price dynamics in a financial market with fundamentalists and chartists. Discret. Dyn. Nat. Soc. 2001, 2, 69–99. [Google Scholar]
- He, X.Z.; Zheng, M. Dynamics of moving average rules in a continuous-time financial market model. J. Econ. Behav. Organ. 2010, 76, 615–634. [Google Scholar]
- Chiarella, C.; He, X.Z.; Zheng, M. An analysis of the effect of noise in a heterogeneous agent financial market model. J. Econ. Dyn. Control 2011, 35, 148–162. [Google Scholar]
- Zhou, L.; Li, Y. A generalized dynamic IS-LM model with delayed time in investment processes. Appl. Math. Comput. 2008, 196, 774–781. [Google Scholar]
- Chatterjee, P.; Shukayev, M. A stochastic dynamic model of trade and growth: Convergence and diversification. J. Econ. Dyn. Control 2012, 36, 416–432. [Google Scholar]
- Yang, H.; Li, L.; Wang, D. Research on the stability of open financial system. Entropy 2015, 17, 1734–1754. [Google Scholar]
- Caginalp, G.; Balenovich, D. Asset flow and momentum: Deterministic and stochastic equations. Philos. Trans. R. Soc. 1999, 357, 2119–2133. [Google Scholar]
- Caginalp, G.; Ermentrout, G.B. A kinetic thermodynamics approach to the psychology of dluctuations in financial market. Appl. Math. Lett. 1990, 3, 17–19. [Google Scholar]
- Merdan, H.; Alisen, M. A mathematical model for asset pricing. Appl. Math. Comput. 2011, 218, 1449–1456. [Google Scholar]
- Sullivan, A.; Sheffrin, S.M. Economics: Principles in Action; Prentice Hall: Upper Saddle River, NJ, USA, 2005. [Google Scholar]
- Caginalp, G.; Balenovich, D. Market oscillations induced by the competition between value-based and trend-based investment strategies. Appl. Math. Financ. 1994, 1, 129–164. [Google Scholar]
- Caginalp, G.; Ermentrout, B. Numerical studies of differential equations related to theoretical financial markets. Appl. Math. Lett. 1991, 4, 35–38. [Google Scholar]
- Podlubny, I. Fractional Differential Equations. Mathematics in Science and Engineering; Academic Press: San Diego, CA, USA, 1999; Volume 198. [Google Scholar]
- Area, I.; Batarfi, H.; Losada, J.; Nieto, J.J.; Shammakh, W.; Torres, A. On a fractional order Ebola epidemic model. Adv. Differ. Equ. 2015, 2015, 278. [Google Scholar]
- Sofuoglu, Y.; Ozalp, N. A fractional rrder model on bilingualism. Commun. Fac. Sci. Univ. Ank. Ser. A 2014, 2014, 81–89. [Google Scholar]
- Sofuoglu, Y.; Ozalp, N. Fractional order bilingualism model without conversion from dominant unilingual group to bilingual group. Differ. Equ. Dyn. Syst. 2015, 2015, 1–9. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Hackensack, NJ, USA, 2001. [Google Scholar]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar]
- Dadras, S.; Momeni, H.R. Control of a fractional-order economical system via sliding mode. Phys. A Stat. Mech. Appl. 2010, 389, 2434–2442. [Google Scholar]
- Wang, Z.; Huang, X.; Shi, G. Analysis of nonlinear dynamics and chaos in a fractional order financial system with time delay. Comput. Math. Appl. 2011, 62, 1531–1539. [Google Scholar]
- Chen, W.C. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 2008, 36, 1305–1314. [Google Scholar]
- Li, Q.; Zhou, Y.; Zhao, X.; Ge, X. Fractional order stochastic differential equation with application in european option pricing. Discret. Dyn. Nat. Soc. 2014, 2014, 621895. [Google Scholar]
- Li, C.; Sarwar, S. Existence and contiuation of solution for Caputo type fractional differential equations. Electron. J. Differ. Equ. 2016, 2016, 1–14. [Google Scholar]
- Babakhani, D.; Gejji, V.D. Existence of positive solutions of nonlinear fractional differential equations. J. Math. Anal. Appl. 2003, 278, 434–442. [Google Scholar]
- Diethlm, K.; Ford, N.J. Analysis of fractional differential equations. J. Math. Anal. Appl. 2002, 265, 229–248. [Google Scholar]
- Yu, C.; Gao, G. Existence of fractional differential equations. J. Math. Anal. Appl. 2005, 310, 26–29. [Google Scholar]
- Kou, C.; Zhou, H.; Li, C.P. Existence and continuation theorems of fractional Riemann–Liouville type fractional differential equations. Int. J. Bifurc. Chaos 2012, 22, 1250077. [Google Scholar]
- Deng, W.H.; Li, C.P.; Guo, Q. Analysis of fractional differential equations with multi orders. Fractals 2007, 15, 173–182. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier Science: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Caputo, M. Linear model of dissipation whose Q is almost frequency independent-II. Geophys. J. Int. 1967, 13, 529–539. [Google Scholar]
- Gronwall, T.H. Note on the derivatives with respect to a parameter of the solutions of a system of differential equations. Ann. Math. 1919, 20, 292–296. [Google Scholar]
- Gorenflo, R.; Kilbas, A.A.; Mainardi, F.; Rogosin, S.V. Mittag-Leffer Function, Related Topics and Applications; Springer: New York, NY, USA, 2014. [Google Scholar]
- Tavazoei, M.S.; Haeri, M. Unreliability of frequency-domain approximation in recognising chaos in fractional-order systems. IET Signal Proc. 2007, 1, 171–181. [Google Scholar]
- Petráš, I. Stability of fractional-order systems with rational orders: A survey. Fract. Calc. Appl. Anal. 2009, 12, 269–298. [Google Scholar]
- Ahmed, E.; El-Sayed, A.M.A.; El-Saka, H.A.A. On some Routh–Hurwitz conditions for fractional order differential equations and their applications in Lorenz, Rössler, Chua and Chen systems. Phys. Lett. A 2006, 358, 1–4. [Google Scholar]
- Diethelm, K.; Ford, N.J.; Freed, A.D. Detailed error analysis for a fractional Adams method. Numer. Algorithms 2004, 36, 31–52. [Google Scholar]
- Diethelm, K. An algorithm for the numerical solution of differential equations of fractional order. Electron. Trans. Numer. Anal. 1997, 5, 1–6. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prathumwan, D.; Sawangtong, W.; Sawangtong, P. An Analysis on the Fractional Asset Flow Differential Equations. Mathematics 2017, 5, 33. https://doi.org/10.3390/math5020033
Prathumwan D, Sawangtong W, Sawangtong P. An Analysis on the Fractional Asset Flow Differential Equations. Mathematics. 2017; 5(2):33. https://doi.org/10.3390/math5020033
Chicago/Turabian StylePrathumwan, Din, Wannika Sawangtong, and Panumart Sawangtong. 2017. "An Analysis on the Fractional Asset Flow Differential Equations" Mathematics 5, no. 2: 33. https://doi.org/10.3390/math5020033





