Variable Shape Parameter Strategy in Local Radial Basis Functions Collocation Method for Solving the 2D Nonlinear Coupled Burgers’ Equations
Abstract
:1. Introduction
2. Kernel-Based Trial Functions
2.1. Constant Scaled Kernels
2.2. Variable Shape Parameter
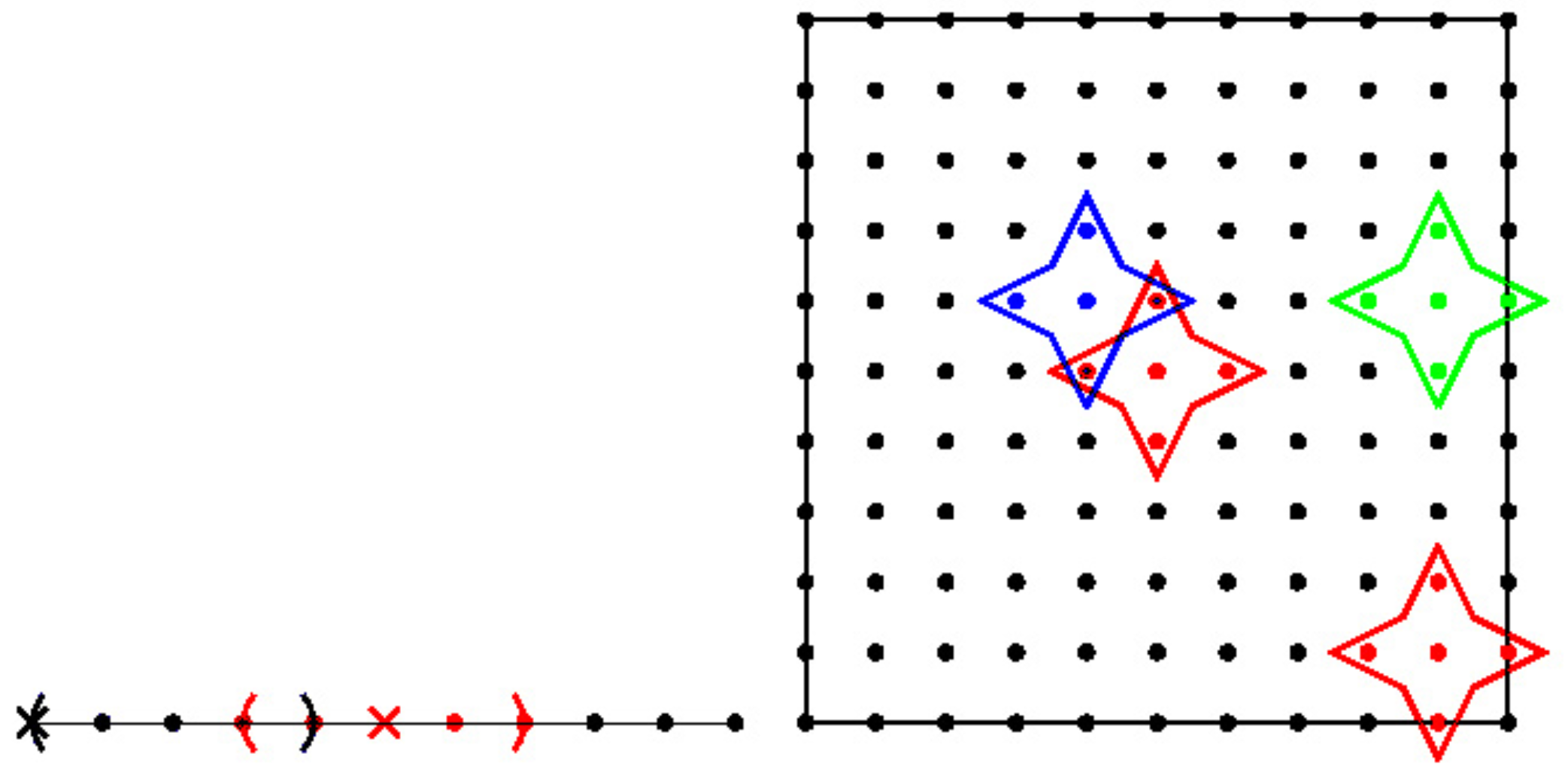
3. Numerical Method
4. Validation of the Method
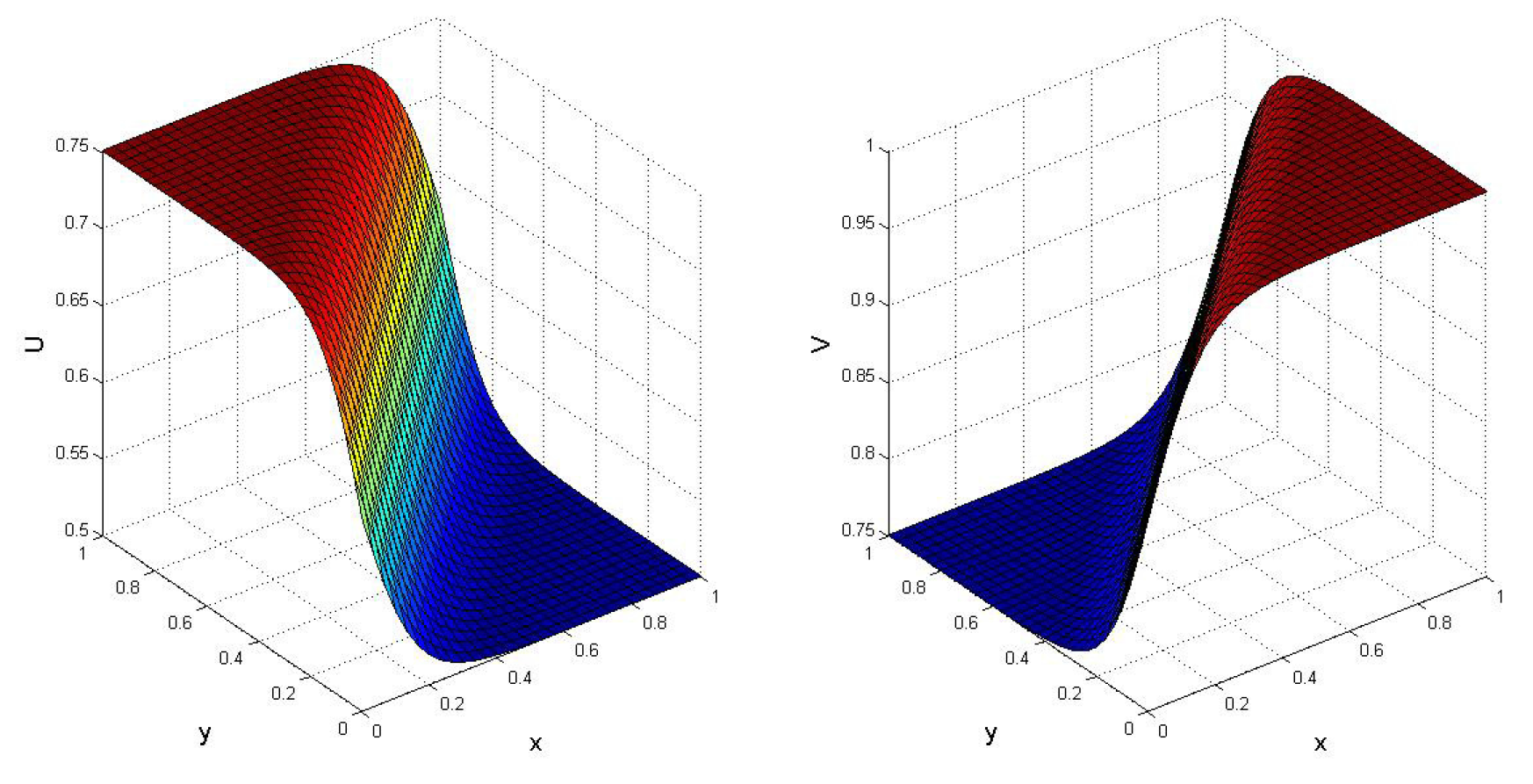
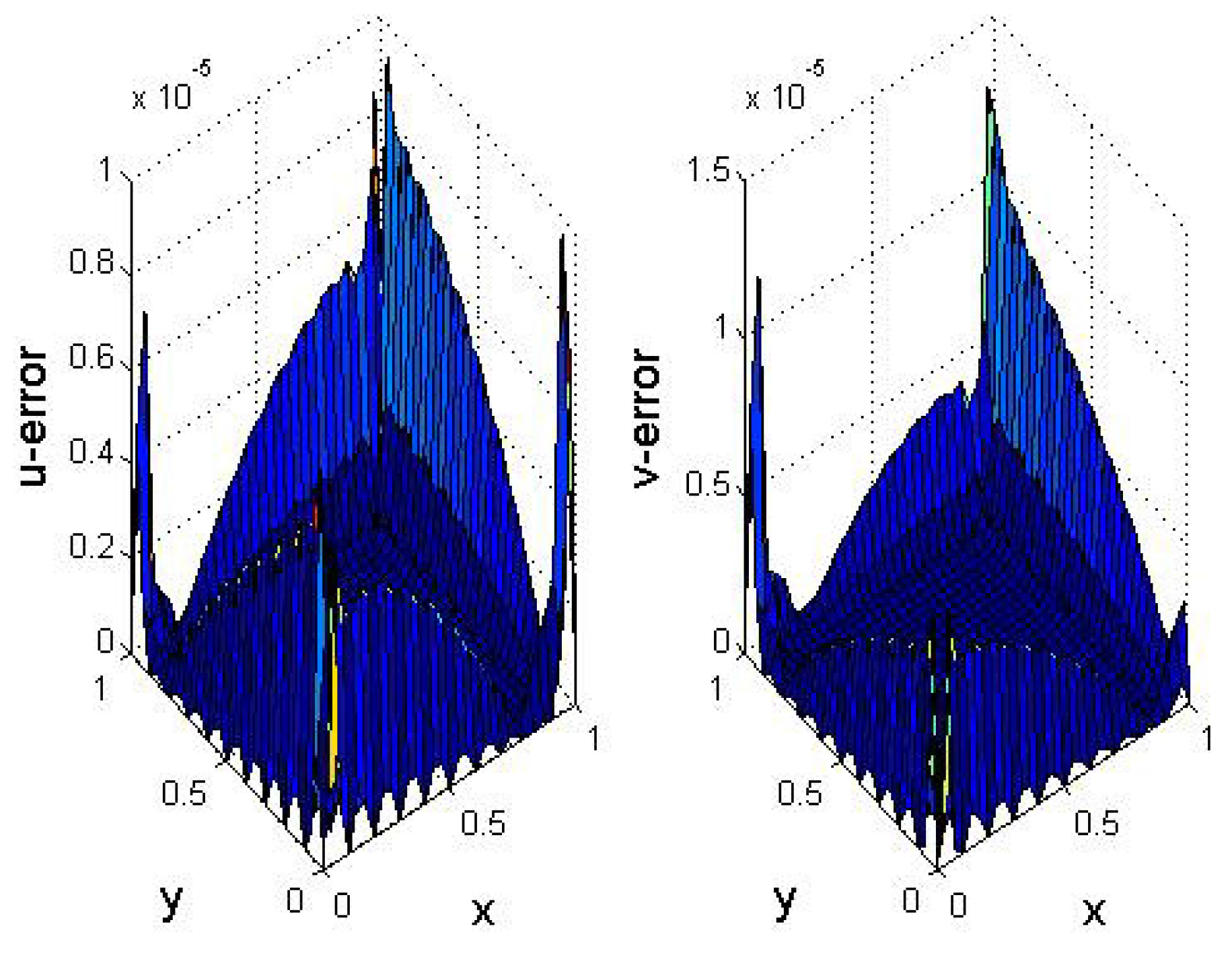
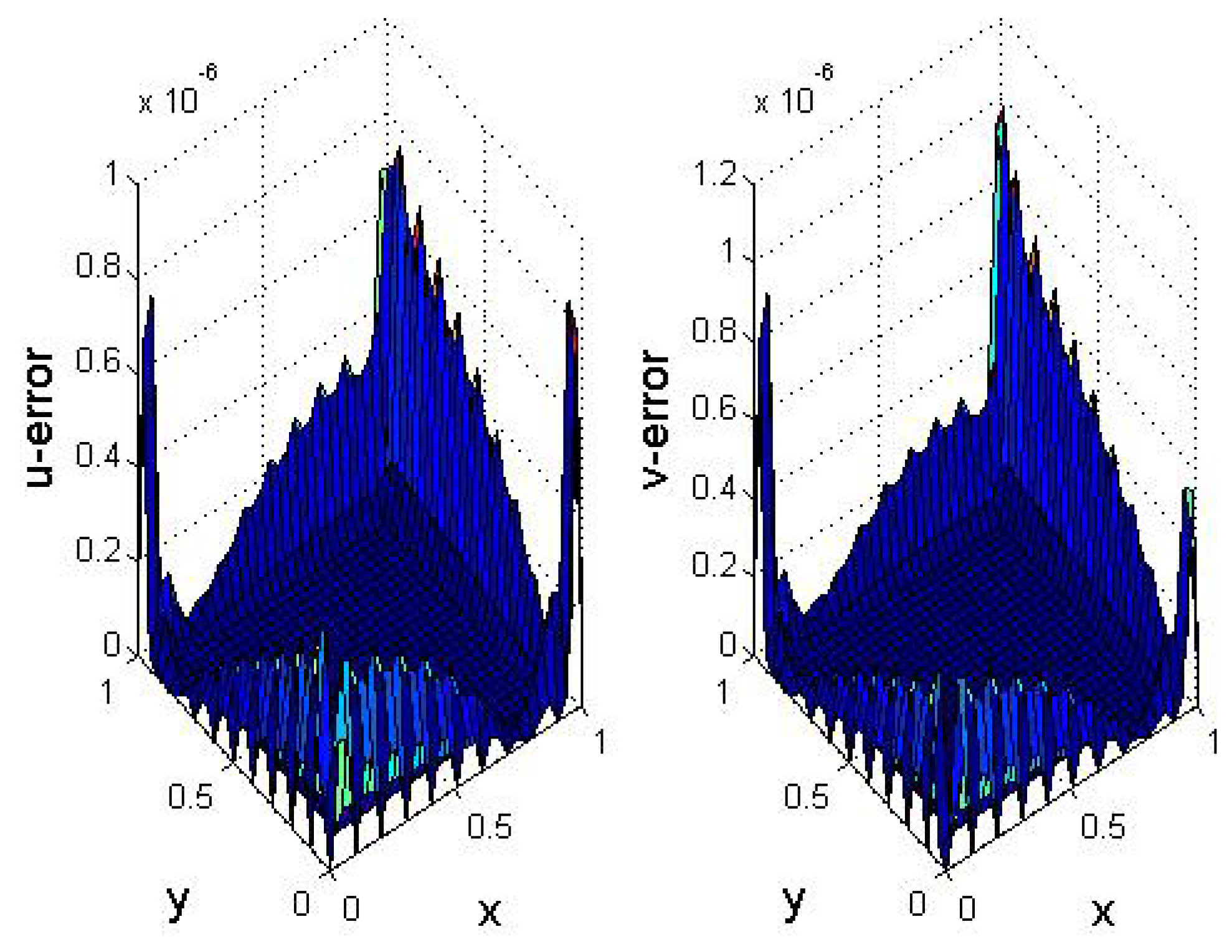
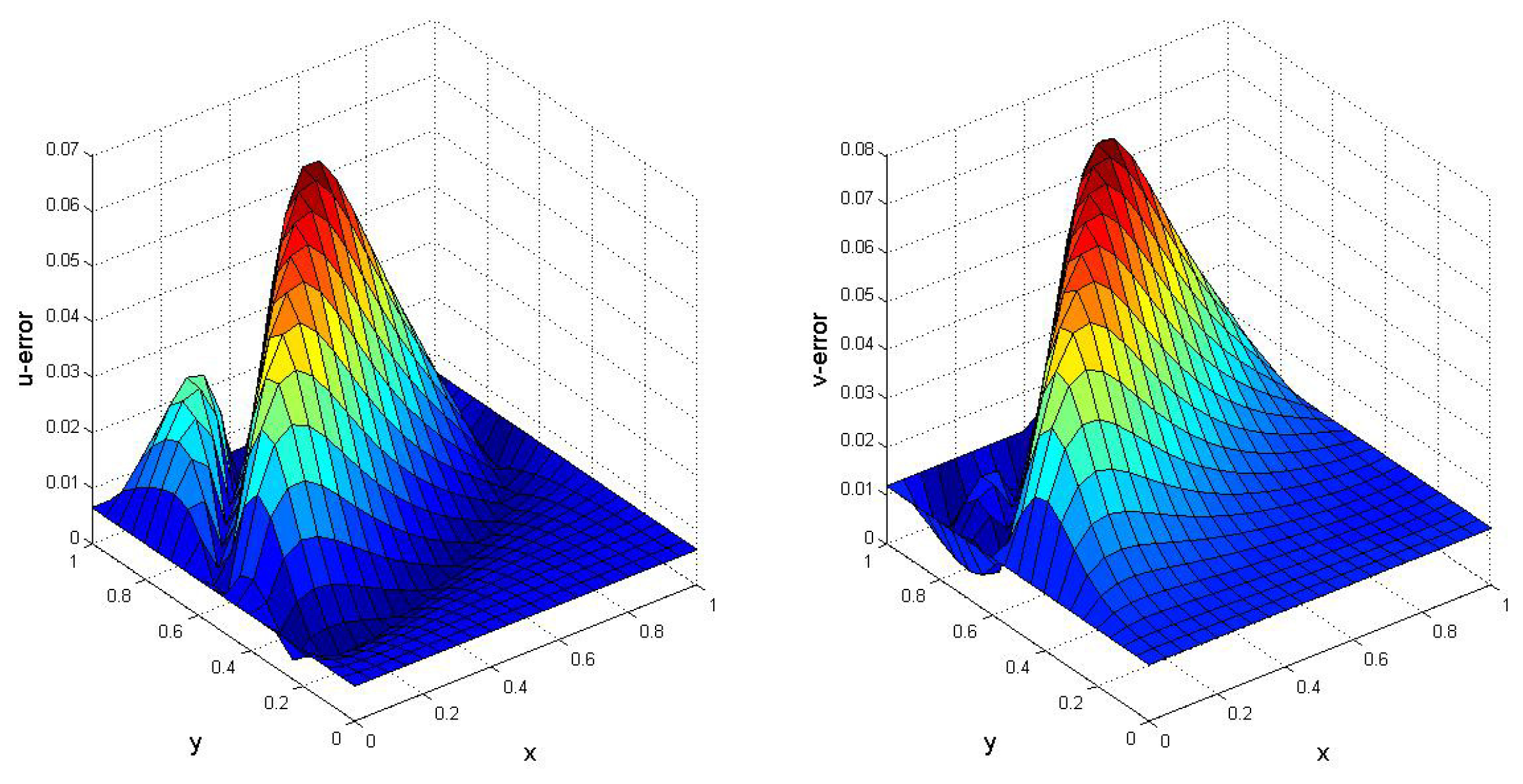
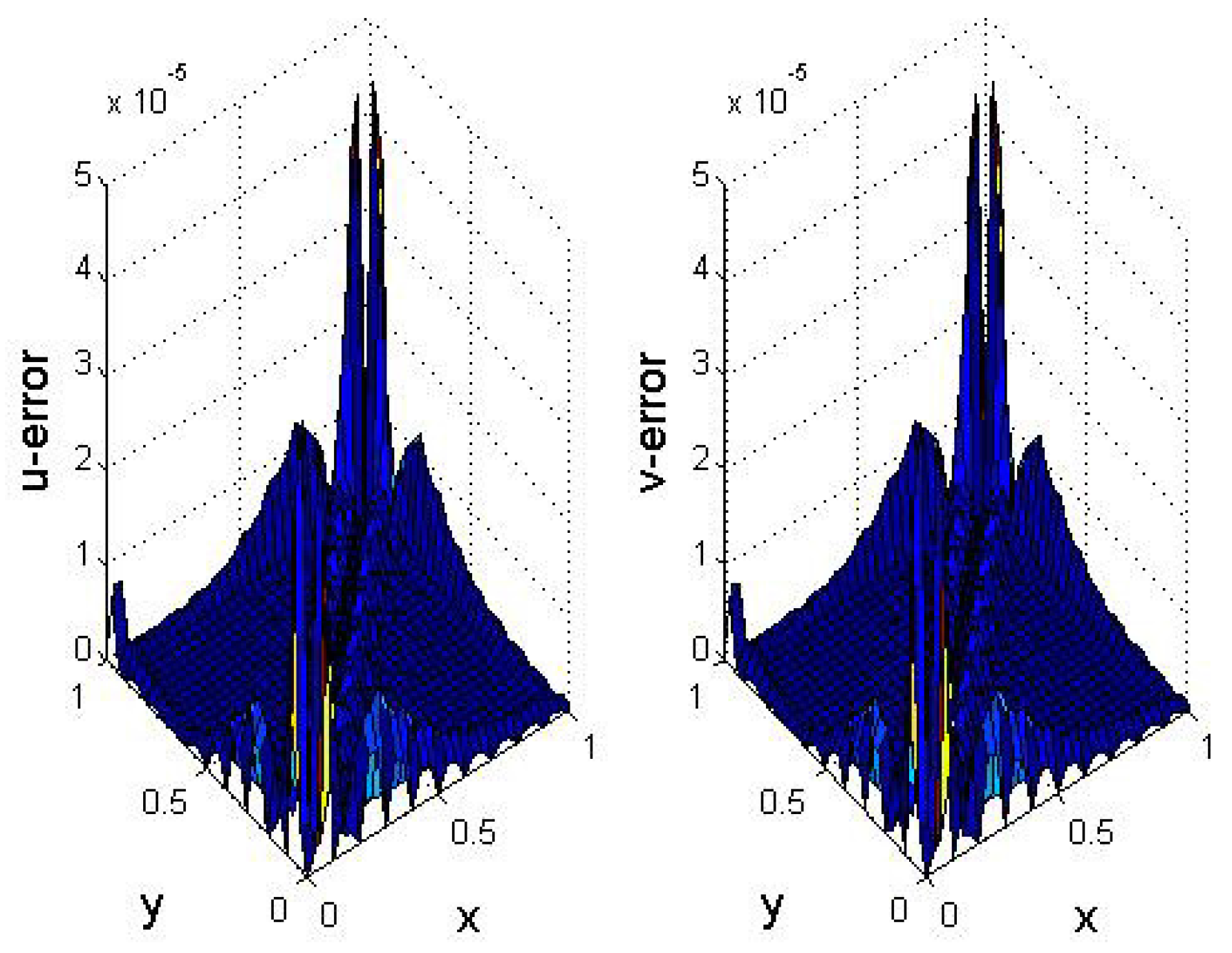
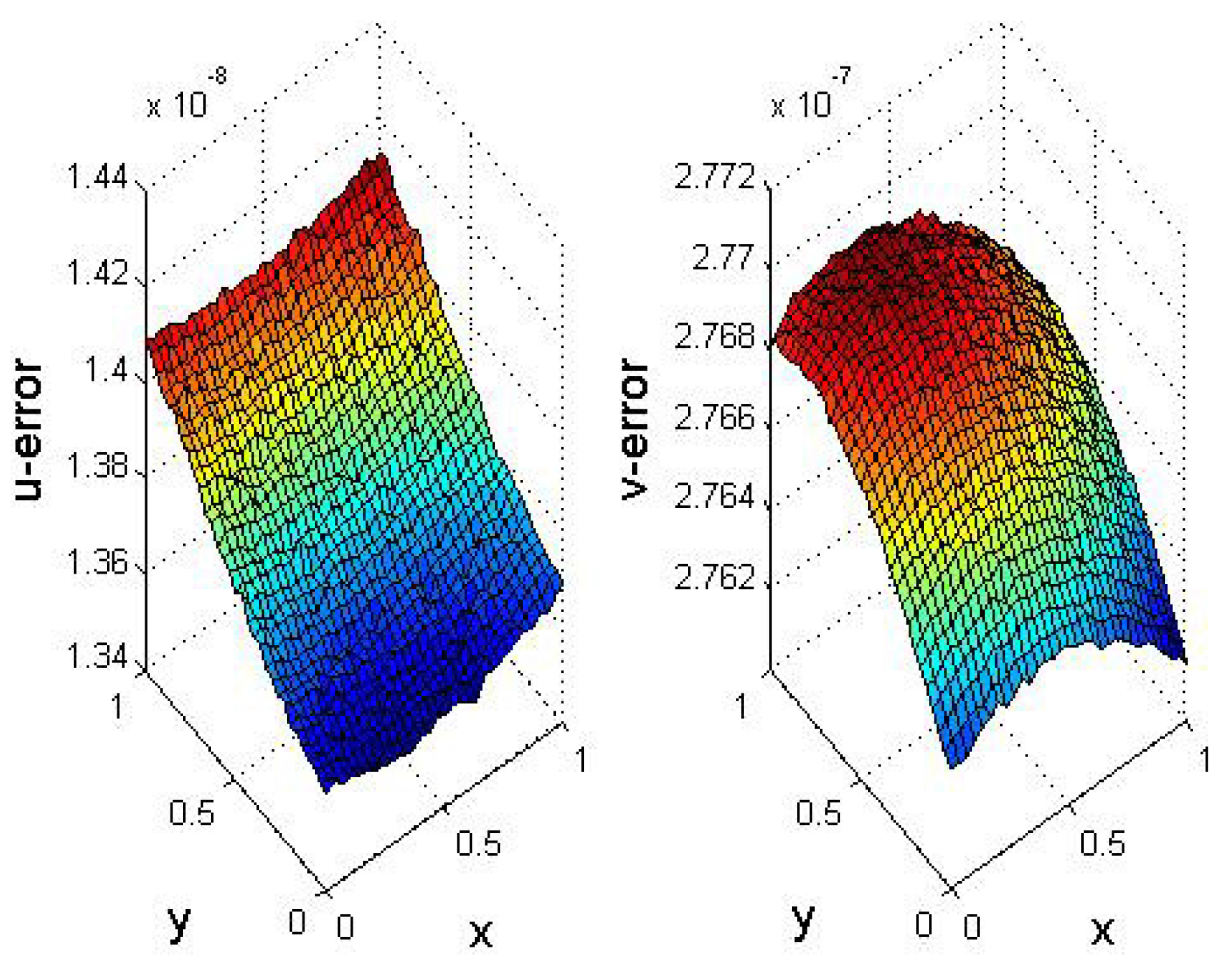
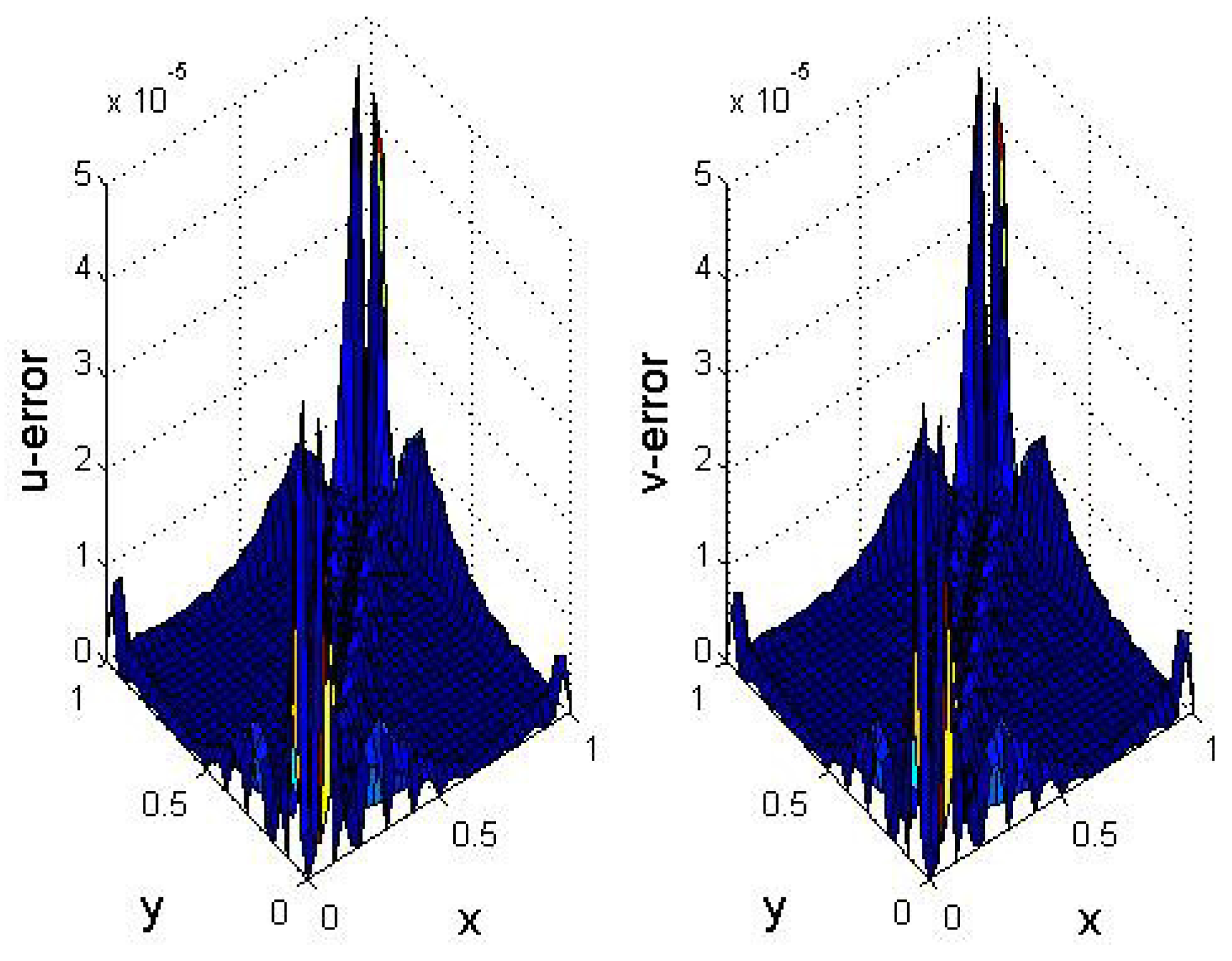
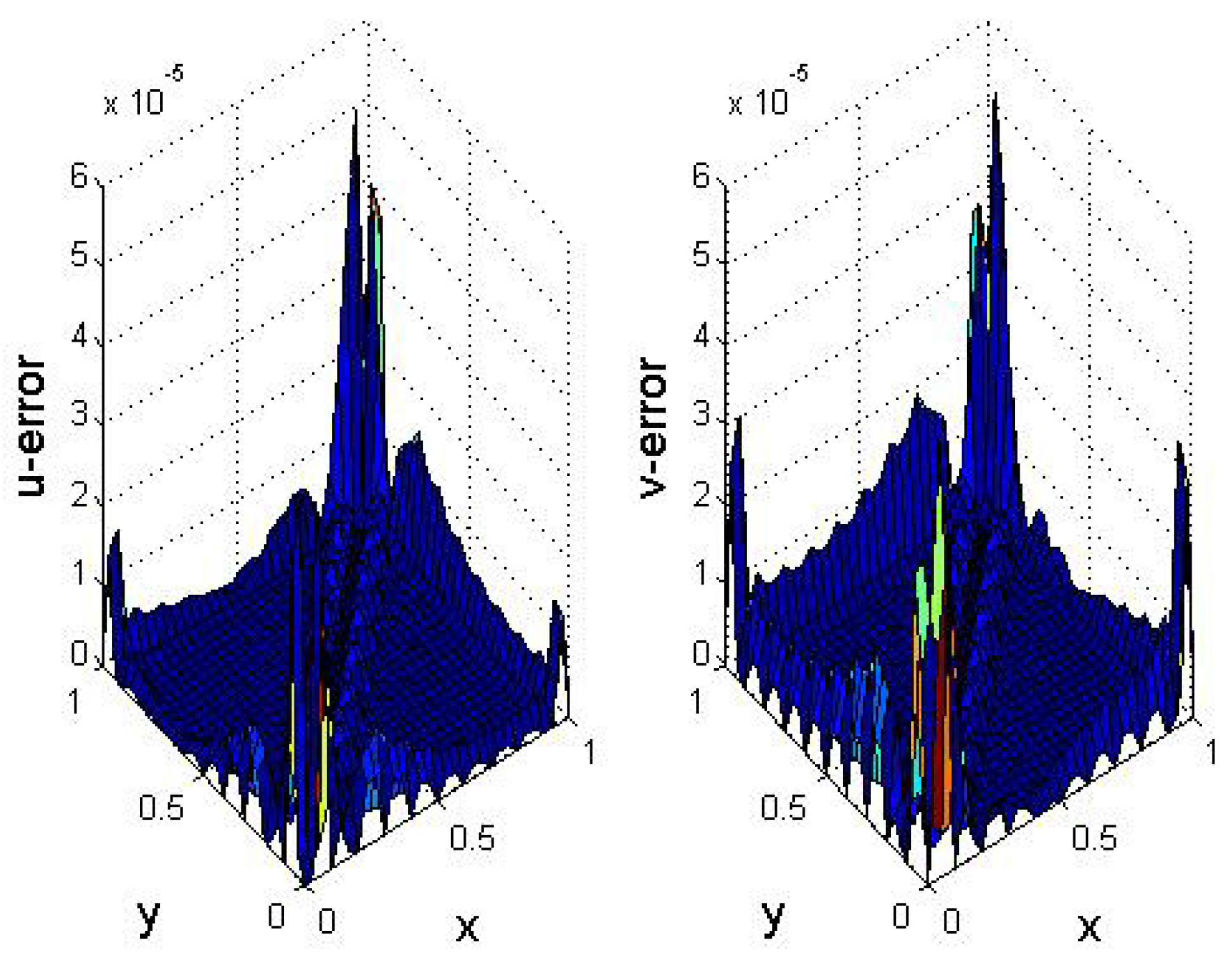
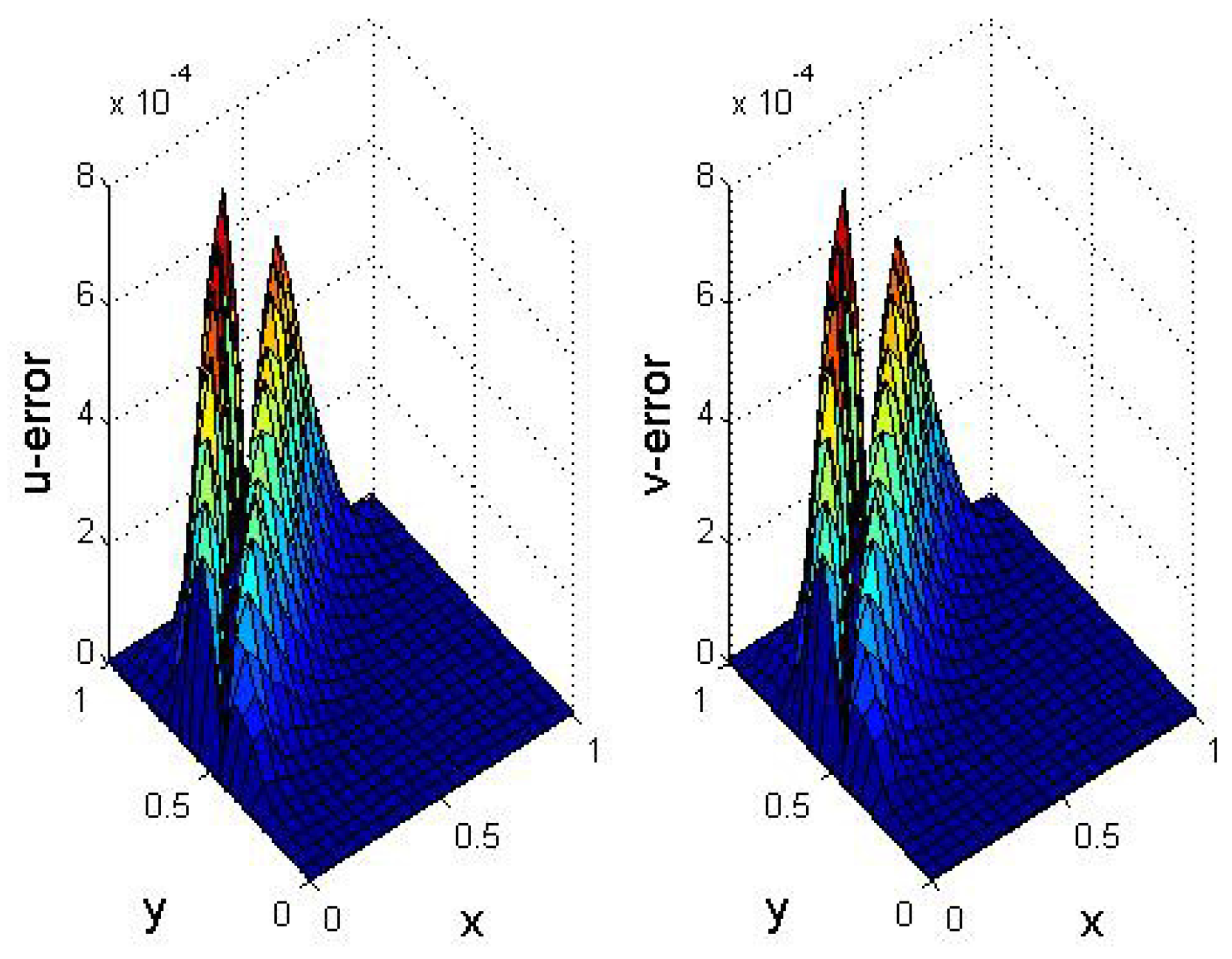
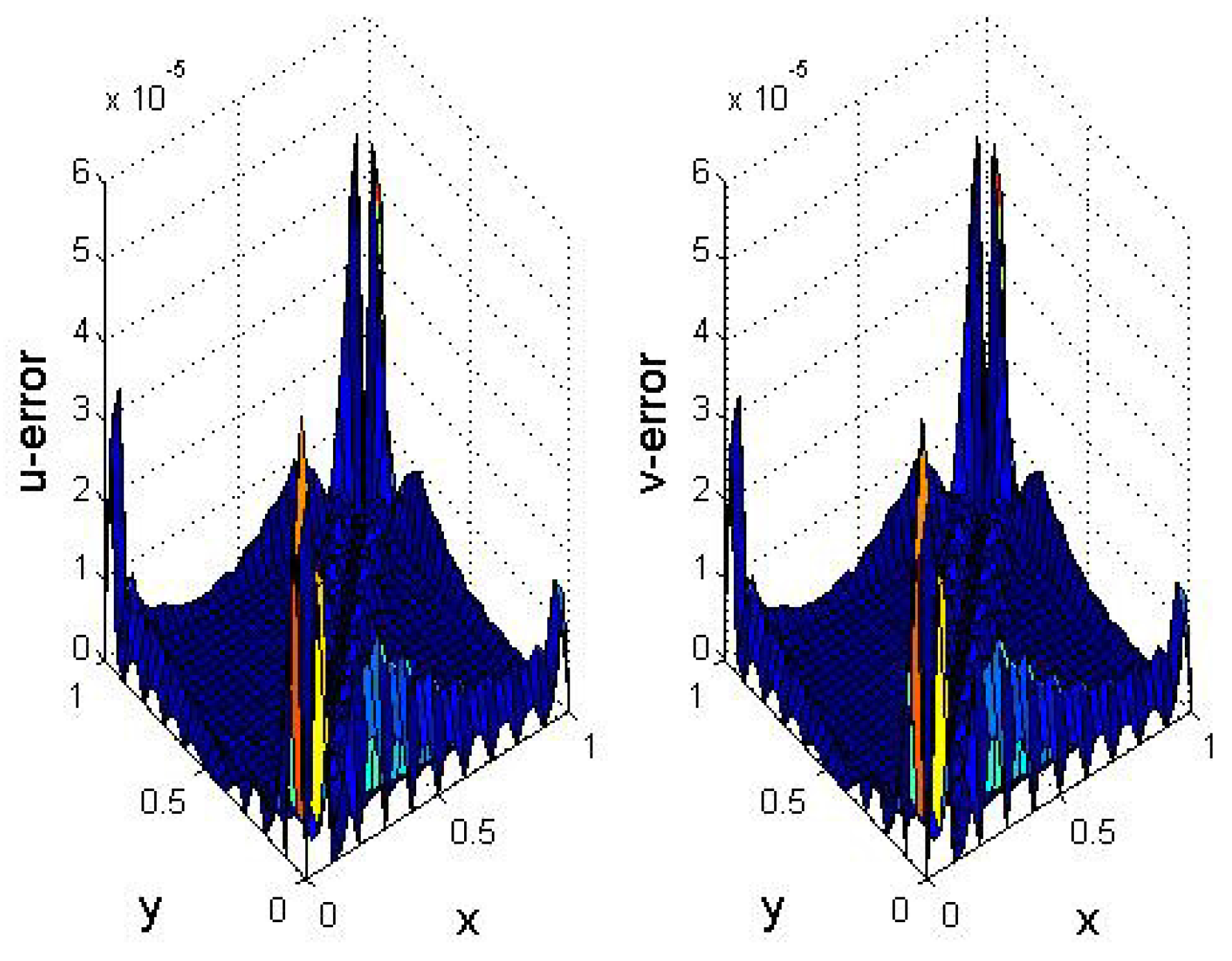
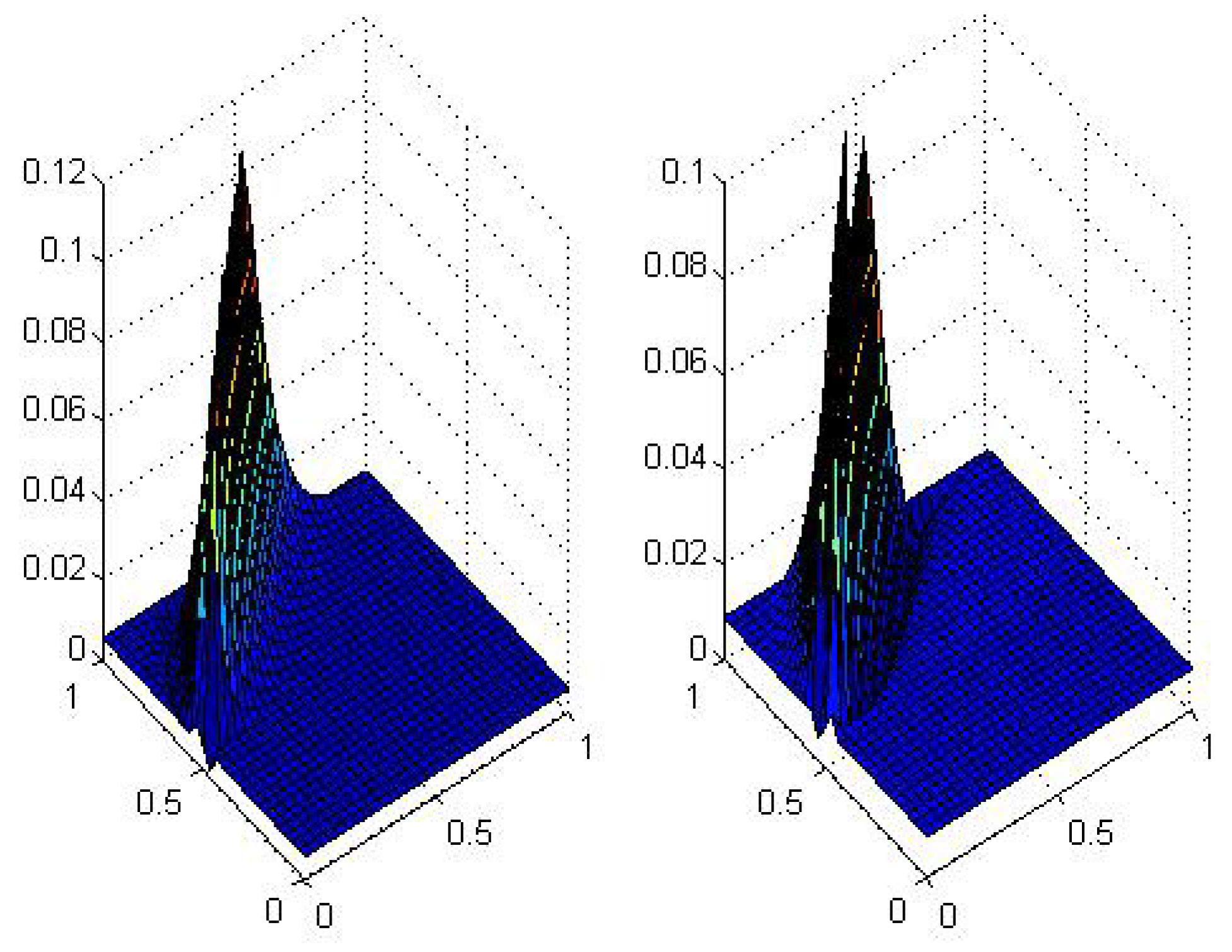
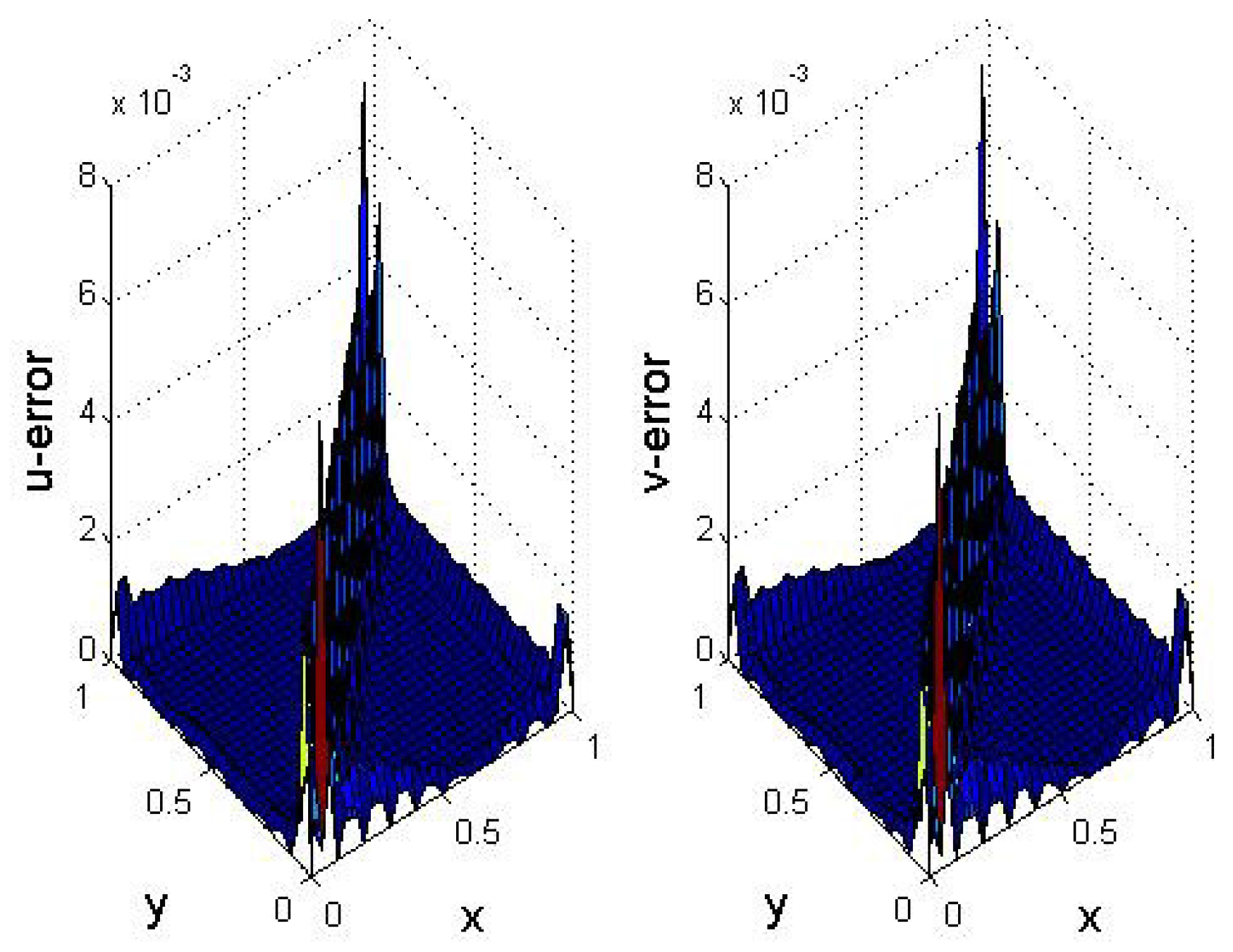
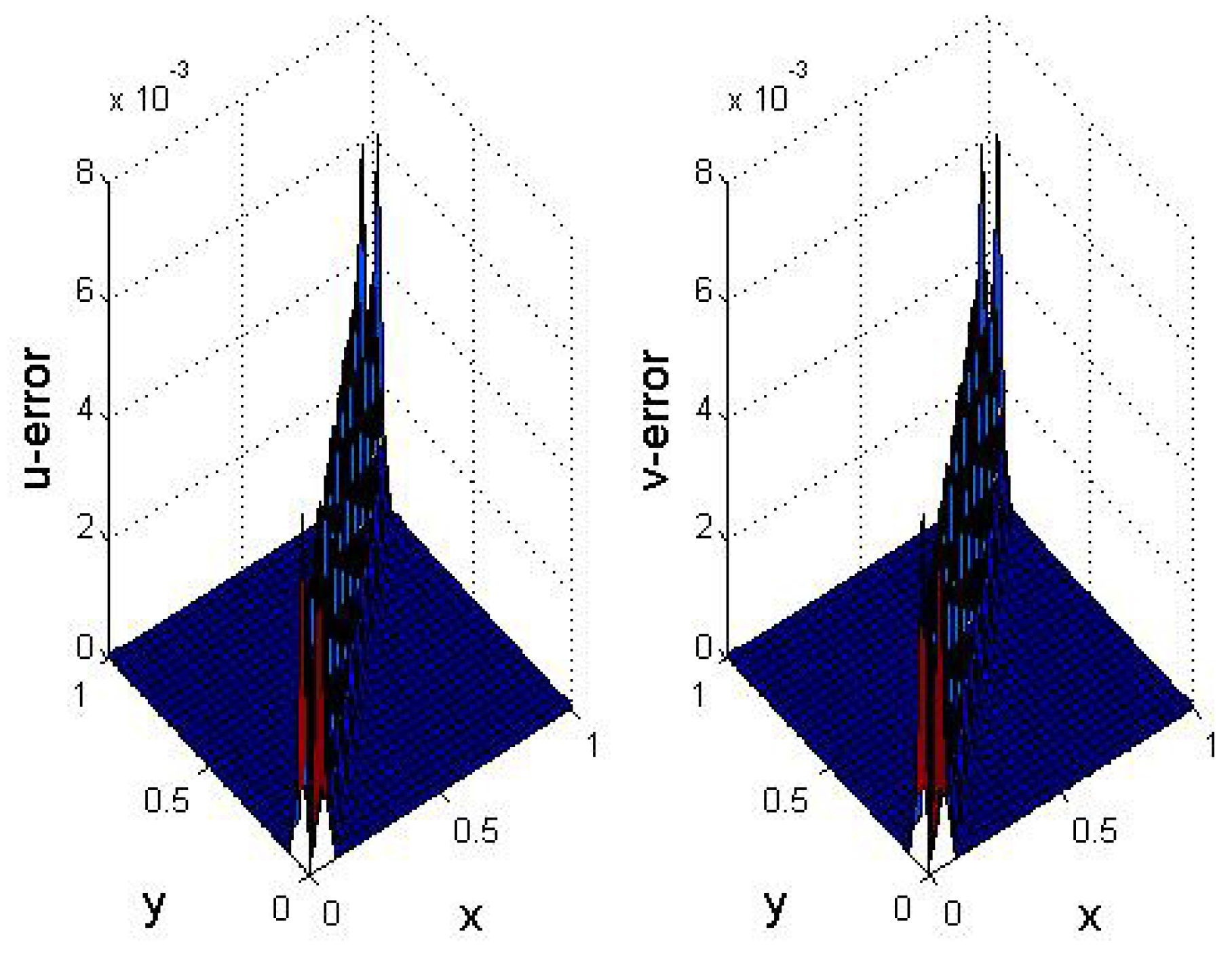
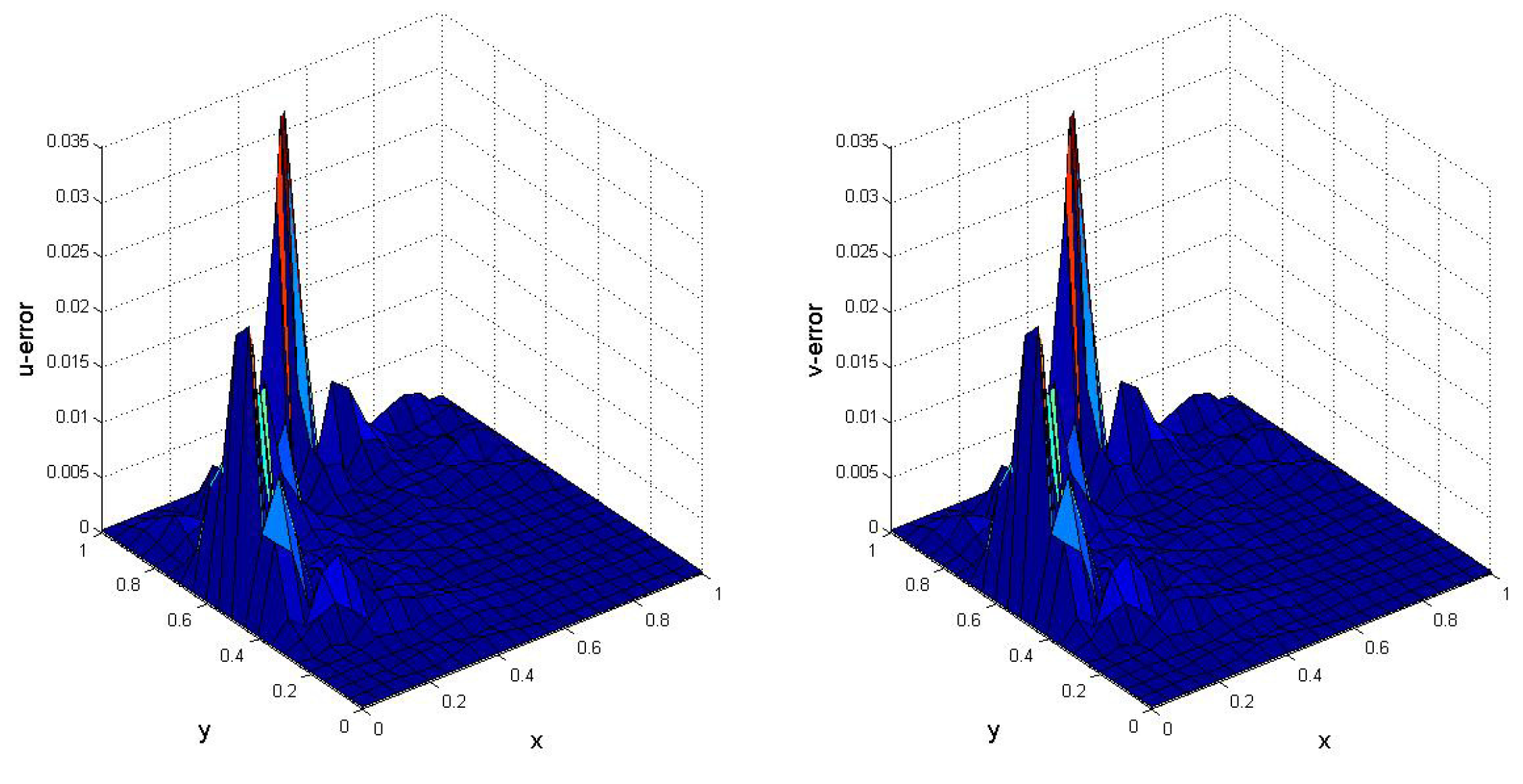
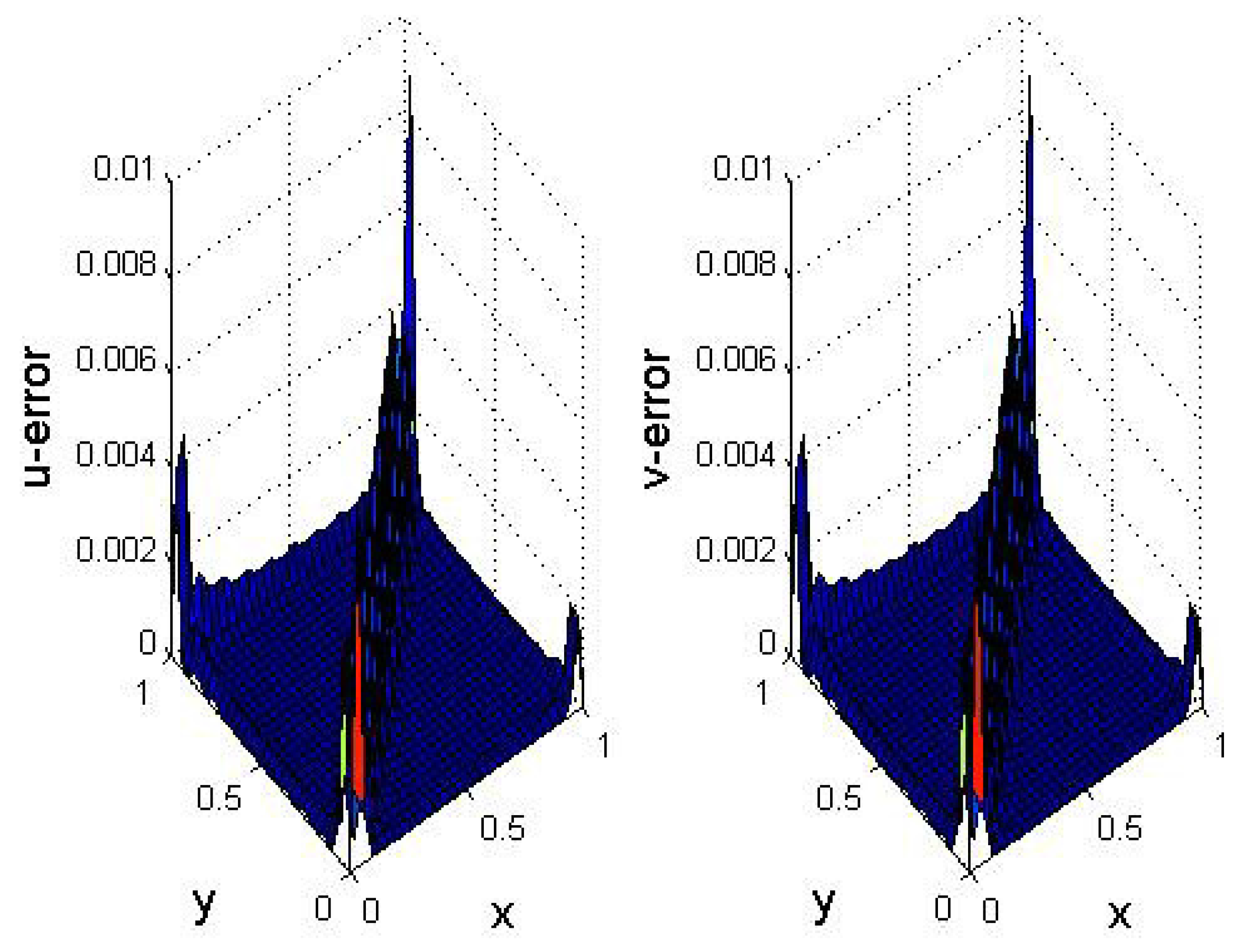
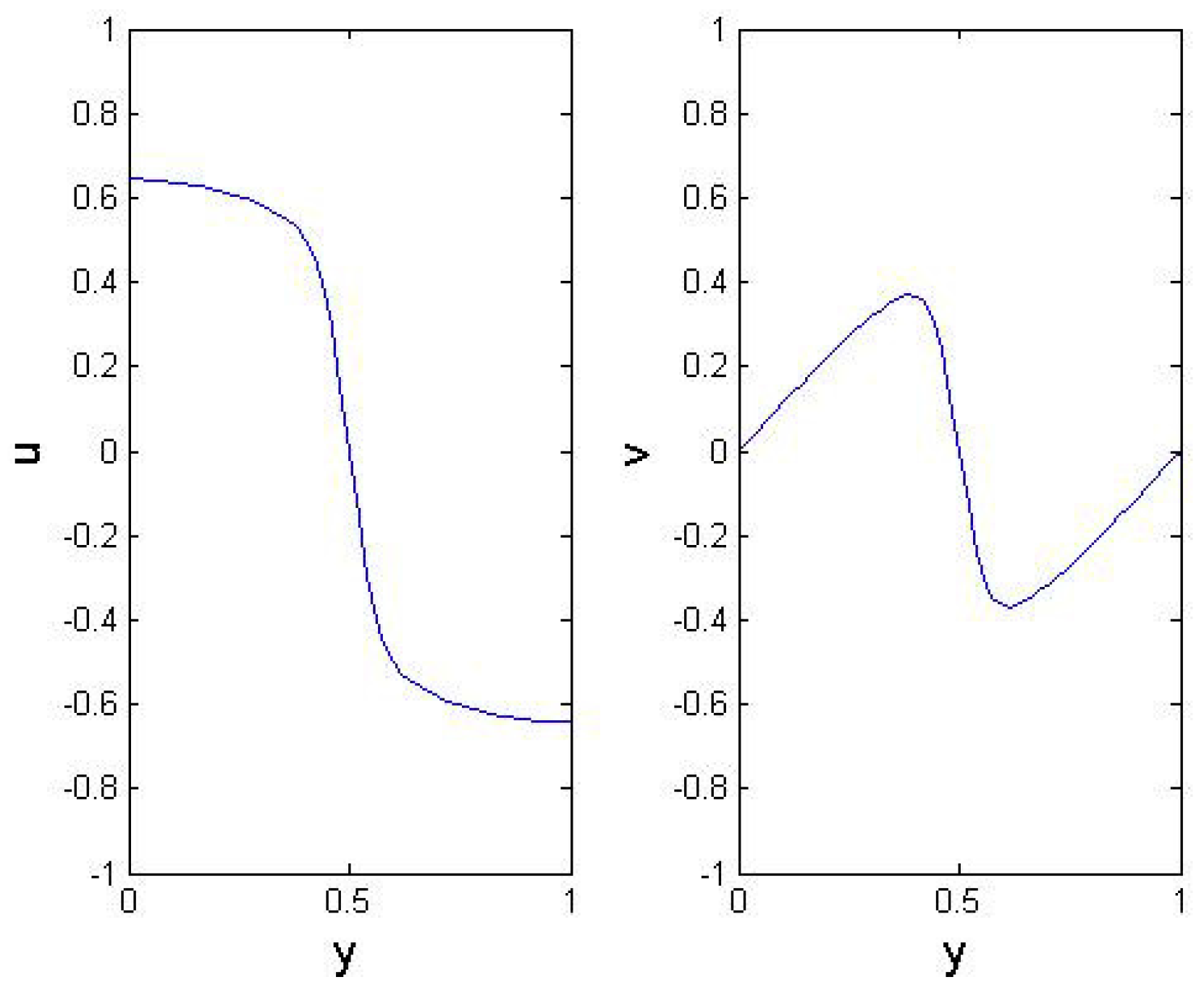
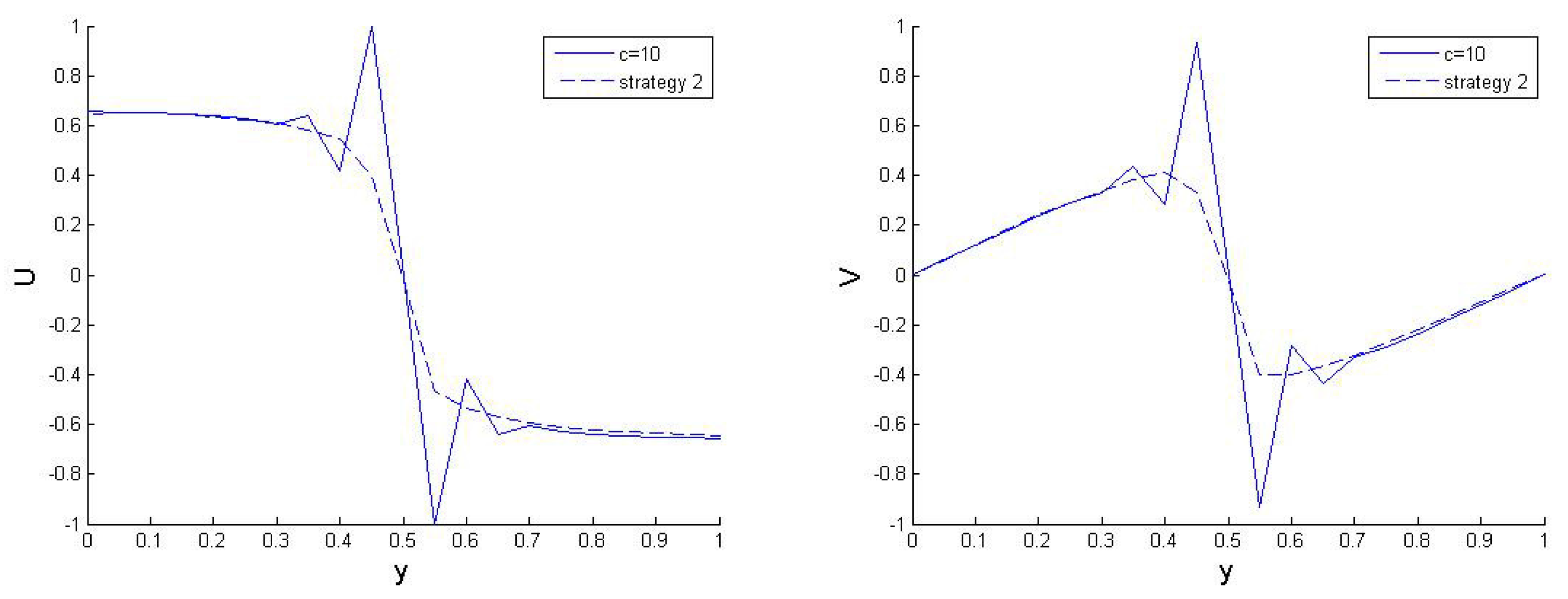
5. Numerical Results
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Belytschko, T.; Krongauz, Y.; Organ, D.; Fleming, M.; Krysl, P. Meshless methods: An overview and recent developments. Comput. Methods Appl. Mech. Eng. 1996, 139, 3–47. [Google Scholar] [CrossRef]
- Franke, C.; Schaback, R. Convergence order estimates of meshless collocation methods using radial basis functions. Adv. Comput. Math. 1998, 8, 381–399. [Google Scholar] [CrossRef]
- Franke, C.; Schaback, R. Solving partial differential equations by collocation using radial basis functions. Appl. Math. Comput. 1998, 93, 73–82. [Google Scholar] [CrossRef]
- Kansa, E.J. Application of Hardy’s multiquadric interpolation to hydrodynamics. In Proceedings of the Society for Computer Simulation (SCS) Multiconference, San Diego, CA, USA, 23–25 January 1986; Volume 4, pp. 111–117. [Google Scholar]
- Schaback, R. A computational tool for comparing all linear PDE solvers. Adv. Comp. Math. 2015, 41, 333–355. [Google Scholar] [CrossRef]
- Schaback, R.; Wendland, H. Kernel techniques: From machine learning to meshless methods. Acta Numer. 2006, 15, 543–639. [Google Scholar] [CrossRef]
- Abbasbandy, S.; Azarnavid, B.; Alhuthali, M.S. A shooting reproducing kernel Hilbert space method for multiple solutions of nonlinear boundary value problems. J. Comput. Appl. Math. 2015, 279, 293–305. [Google Scholar] [CrossRef]
- Azarnavid, B.; Parvaneh, F.; Abbasbandy, S. Picard-Reproducing kernel Hilbert space method for solving generalized singular nonlinear Lane-Emden type equations. Math. Model. Anal. 2015, 20, 754–767. [Google Scholar] [CrossRef]
- Hon, Y.; Schaback, R. Solvability of partial differential equations by meshless kernel methods. Adv. Comput. Math. 2008, 28, 283–299. [Google Scholar] [CrossRef]
- Lee, C.F.; Ling, L.; Schaback, R. On convergent numerical algorithms for unsymmetric collocation. Adv. Comput. Math. 2009, 30, 339–354. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mokhtari, R.; Panahipour, H. A Galerkin-reproducing kernel method: Application to the 2D nonlinear coupled Burgers’ equations. Eng. Anal. Bound. Elem. 2013, 37, 1642–1652. [Google Scholar] [CrossRef]
- Mohammadi, M.; Mokhtari, R.; Schaback, R. A meshless method for solving the 2D Brusselator reaction-diffusion system. Comput. Model. Eng. Sci. 2014, 101, 113–138. [Google Scholar]
- Bozzini, M.; Lenarduzzi, L.; Rossini, M.; Schaback, R. Interpolation with variably scaled kernels. IMA J. Numer. Anal. 2015, 35, 199–219. [Google Scholar] [CrossRef]
- Hardy, R.L. Multiquadric equations of topography and other irregular surfaces. J. Geophys. Res. 1971, 76, 1905–1915. [Google Scholar] [CrossRef]
- Huang, C.S.; Lee, C.F.; Cheng, A.D. Error estimate, optimal shape factor, and high precision computation of multiquadric collocation method. Eng. Anal. Bound. Elem. 2007, 31, 614–623. [Google Scholar] [CrossRef]
- Kansa, E.J.; Aldredge, R.C.; Ling, L. Numerical simulation of two-dimensional combustion using mesh-free methods. Eng. Anal. Bound. Elem. 2009, 33, 940–950. [Google Scholar] [CrossRef]
- Sarra, S.A.; Sturgill, D. A random variable shape parameter strategy for radial basis function approximation methods. Eng. Anal. Bound. Elem. 2009, 33, 1239–1245. [Google Scholar] [CrossRef]
- Golbabai, A.; Rabiei, H. Hybrid shape parameter strategy for the RBF approximation of vibrating systems. Int. J. Comput. Math. 2012, 89, 2410–2427. [Google Scholar] [CrossRef]
- Dehghan, M.; Mohammadi, V. The method of variably scaled radial kernels for solving two-dimensional magnetohydrodynamic (MHD) equations using two discretizations: The Crank-Nicolson scheme and the method of lines (MOL). Comput. Math. Appl. 2015, 70, 2292–2315. [Google Scholar] [CrossRef]
- Dereli, Y.; Schaback, R. The meshless kernel-based method of lines for solving the equal width equation. Appl. Math. Comp. 2013, 219, 5224–5232. [Google Scholar] [CrossRef]
- Mavrič, B.; Šarler, B. Local radial basis function collocation method for linear thermoelasticity in two dimensions. Int. J. Numer. Methods Heart Fluid Flow 2015, 25, 1488–1510. [Google Scholar] [CrossRef]
- Sarra, S. A local radial basis function method for advection-diffusion-reaction equations on complexly shaped domains. Appl. Math. Comp. 2012, 218, 9853–9865. [Google Scholar] [CrossRef]
- Burger, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Ali, A.; Islam, S.U.; Haq, S. A computational meshfree technique for the numerical solution of the two-dimensional coupled Burgers’ equations. Int. J. Comput. Methods Eng. Sci. Mech. 2009, 10, 406–412. [Google Scholar] [CrossRef]
- Nee, J.; Duan, J. Limit set of trajectories of the coupled viscous Burgers’ equations. Appl. Math. Lett. 1998, 11, 57–61. [Google Scholar] [CrossRef]
- Perko, J.; Šarler, B. Weight function shape parameter optimization in meshless methods for non-uniform grids. Comput. Model. Eng. Sci. 2007, 19, 55–68. [Google Scholar]
- Younga, D.; Fana, C.; Hua, S.; Alturi, S. The Eulerian-Lagrangian method of fundamental solutions for two-dimensional unsteady Burgers’ equations. Eng. Anal. Bound. Elem. 2009, 32, 395–412. [Google Scholar] [CrossRef]
- Fletcher, J.D. Generating exact solutions of the two-dimensional Burgers’ equations. Int. J. Numer. Methods Fluids 1983, 3, 213–216. [Google Scholar] [CrossRef]
- Mokhtari, R.; Mohammadi, M. New exact solutions to a class of coupled nonlinear PDEs. Int. J. Nonlinear Sci. Numer. Simul. 2009, 10, 779–796. [Google Scholar] [CrossRef]
- Fletcher, C.A.J. A comparison of finite element and finite difference solution of the one and two dimensional Burgers’ equations. J. Comput. Phys. 1983, 51, 159–188. [Google Scholar] [CrossRef]
- Bahdir, A.R. A fully implicit finite difference scheme for two dimensional Burgers’ equations. Appl. Math. Comput. 2003, 137, 131–137. [Google Scholar]
- Zhang, X.H.; Ouyang, J.; Zhang, L. Element-free characteristic Galerkin method for Burgers’ equation. Eng. Anal. Bound. Elem. 2009, 33, 356–362. [Google Scholar] [CrossRef]
- Zhang, L.; Ouyang, J.; Wang, X.; Zhang, X. Variational multiscale element-free Galerkin method for 2D Burgers’ equation. J. Comput. Phys. 2010, 29, 7147–7161. [Google Scholar] [CrossRef]
- Zhang, W.; Ahang, C.; Xi, G. An explicit Chebyshev pseudospectral multigrid method for incompressible Navier-Stokes equations. Comput. Fluids 2010, 39, 178–188. [Google Scholar] [CrossRef]
- Šarler, B.; Vertnik, R.; Kosec, G. Radial basis function collocation method for the numerical solution of the two-dimensional transient nonlinear coupled Burgers’ equations. Appl. Math. Model. 2012, 36, 1148–1160. [Google Scholar]
- Wendland, H. Scattered data approximation. In Cambridge Mongraph on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Buhmann, M.D. Radial Basis Functions; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Schaback, R. Kernel–Based Meshless Methods. Available online: http://num.math.uni-goettingen.de/schaback/teaching/Appverf-II.pdf (access on 18 July 2007).
- Sanyasiraju, Y.; Satyanarayana, C. On optimization of the RBF shape parameter in a grid-free local scheme for convection dominated problems over non-uniform centers. Appl. Math. Model. 2013, 37, 7245–7272. [Google Scholar] [CrossRef]
- Dehghan, M.; Mohammadi, V. The numerical solution of Fokker–Planck equation with radial basis functions (RBFs) based on the meshless technique of Kansa’s approach and Galerkin method. Eng. Anal. Bound. Elem. 2014, 47, 38–63. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid dynamics I: Surface approximations and partial derivative estimates. Comput. Math. Appl. 1990, 19, 127–145. [Google Scholar] [CrossRef]
- Kansa, E.J. Multiquadrics—A scattered data approximation scheme with applications to computational fluid dynamics II: Solutions to parabolic hyperbolic, and elliptic partial differential equations. Comput. Math. Appl. 1990, 19, 147–161. [Google Scholar] [CrossRef]
- Xiang, S.; Wang, K.M.; Ai, Y.T.; Sha, Y.D.; Shi, H. Trigonometric variable shape parameter and exponent strategy for generalized multiquadric radial basis function approximation. Appl. Math. Model. 2012, 36, 1931–1938. [Google Scholar] [CrossRef]
- Das, P.; Natesan, S. Adaptive mesh generation for singularly perturbed fourth-order ordinary differential equations. J. Comput. Math. 2015, 92, 562–578. [Google Scholar] [CrossRef]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nojavan, H.; Abbasbandy, S.; Allahviranloo, T. Variable Shape Parameter Strategy in Local Radial Basis Functions Collocation Method for Solving the 2D Nonlinear Coupled Burgers’ Equations. Mathematics 2017, 5, 38. https://doi.org/10.3390/math5030038
Nojavan H, Abbasbandy S, Allahviranloo T. Variable Shape Parameter Strategy in Local Radial Basis Functions Collocation Method for Solving the 2D Nonlinear Coupled Burgers’ Equations. Mathematics. 2017; 5(3):38. https://doi.org/10.3390/math5030038
Chicago/Turabian StyleNojavan, Hananeh, Saeid Abbasbandy, and Tofigh Allahviranloo. 2017. "Variable Shape Parameter Strategy in Local Radial Basis Functions Collocation Method for Solving the 2D Nonlinear Coupled Burgers’ Equations" Mathematics 5, no. 3: 38. https://doi.org/10.3390/math5030038







