On Edge Irregular Reflexive Labellings for the Generalized Friendship Graphs
Abstract
:1. Introduction
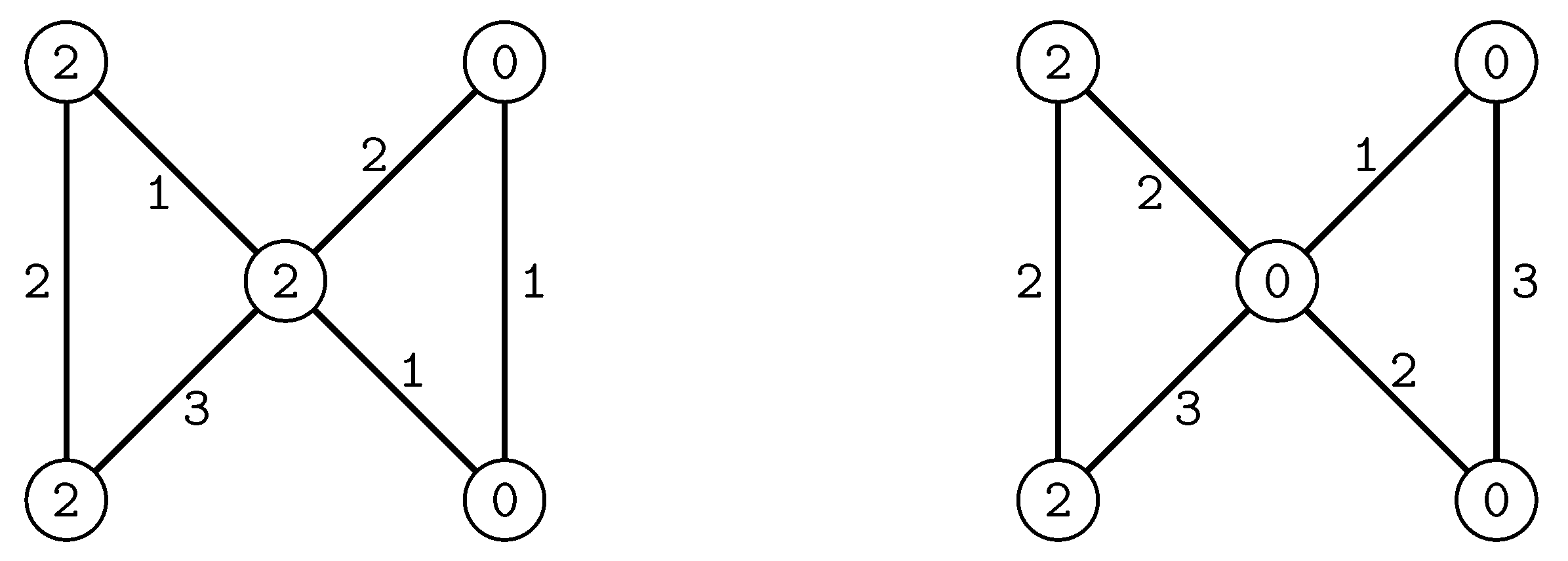
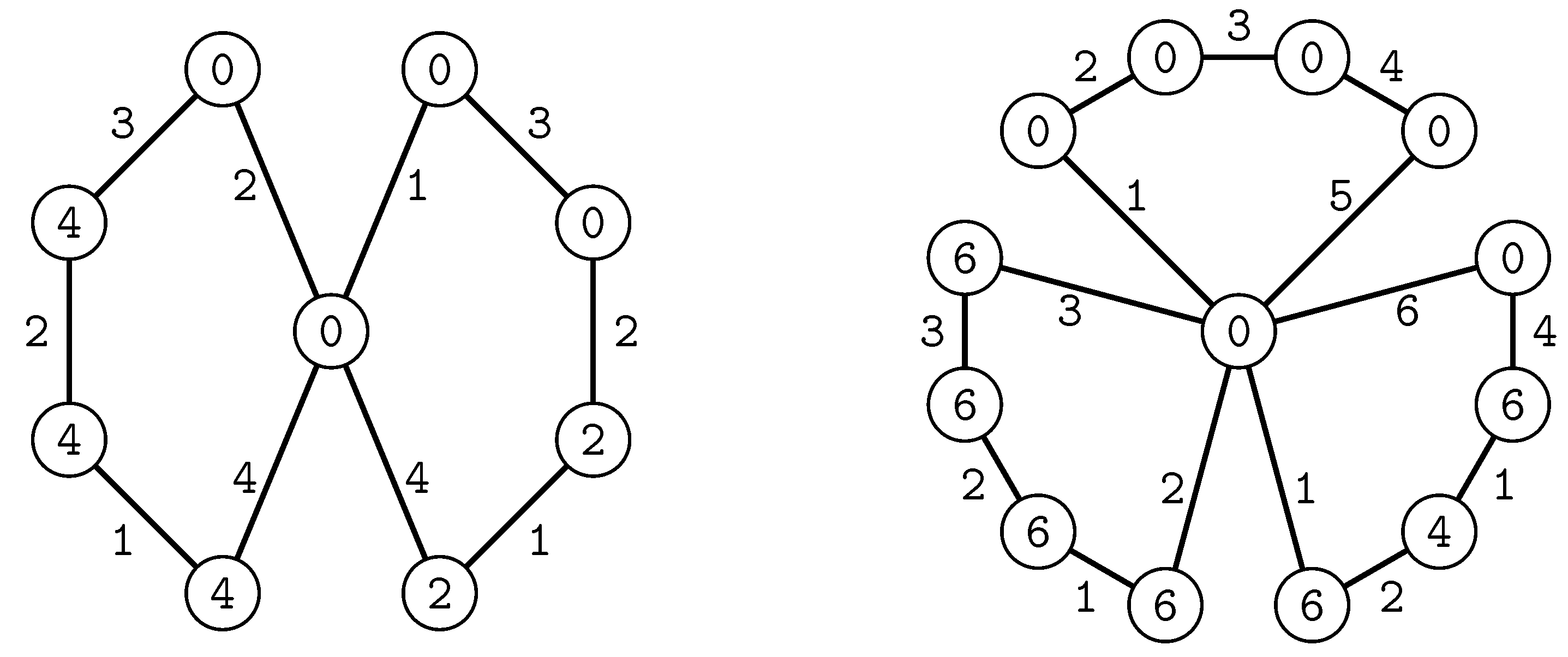
2. Constructing an Edge Irregular Reflexive Labelling for ,
3. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chartrand, G.; Jacobson, M.S.; Lehel, J.; Oellermann, O.R.; Ruiz, S.; Saba, F. Irregular networks. Congr. Numer. 1988, 64, 187–192. [Google Scholar]
- Lehel, J. Facts and quests on degree irregular assignment. In Graph Theory, Combinatorics and Applications; Wiley: New York, NY, USA, 1991; pp. 765–782. [Google Scholar]
- Amar, D.; Togni, O. Irregularity strength of trees. Discret. Math. 1998, 190, 15–38. [Google Scholar] [CrossRef]
- Dimitz, J.H.; Garnick, D.K.; Gyárfás, A. On the irregularity strength of the m × n grid. J. Graph Theory 1992, 16, 355–374. [Google Scholar] [CrossRef]
- Gyárfás, A. The irregularity strength of Km,m is 4 for odd m. Discret. Math. 1998, 71, 273–274. [Google Scholar] [CrossRef]
- Nierhoff, T. A tight bound on the irregularity strength of graphs. SIAM J. Discret. Math. 2000, 13, 313–323. [Google Scholar] [CrossRef]
- Ahmad, A.; Al-Mushayt, O.B.S.; Bača, M. On edge irregularity strength of graphs. Appl. Math. Comput. 2014, 243, 607–610. [Google Scholar] [CrossRef]
- Bača, M.; Jendrol’, S.; Miller, M.; Ryan, J. Total irregular labellings. Discret. Math. 2007, 307, 1378–1388. [Google Scholar] [CrossRef]
- Ahmad, A.; Bača, M.; Siddiqui, M.K. On edge irregular total labelling of categorical product of two cycles. Theory Comput. Syst. 2014, 54, 1–12. [Google Scholar] [CrossRef]
- Brandt, S.; Miškuf, J.; Rautenbach, D. On a conjecture about edge irregular total labellings. J. Graph Theory 2008, 57, 333–343. [Google Scholar] [CrossRef]
- Haque, K.M.M. Irregular total labellings of generalized Petersen graphs. Theory Comput. Syst. 2012, 50, 537–544. [Google Scholar] [CrossRef]
- Ivančo, J.; Jendrol’, S. Total edge irregularity strength of trees. Discuss. Math. Graph Theory 2006, 26, 449–456. [Google Scholar] [CrossRef]
- Jendrol’, S.; Miškuf, J.; Soták, R. Total edge irregularity strength of complete graphs and complete bipartite graphs. Electron. Notes Discret. Math. 2007, 28, 281–285. [Google Scholar] [CrossRef]
- Jendrol’, S.; Miškuf, J.; Soták, R. Total edge irregularity strength of complete graphs and complete bipartite graphs. Discret. Math. 2010, 310, 400–407. [Google Scholar] [CrossRef]
- Nurdin; Salman, A.N.M.; Baskoro, E.T. The total edge-irregular strengths of the corona product of paths with some graphs. J. Combin. Math. Combin. Comput. 2008, 65, 163–175. [Google Scholar]
- Ryan, J.; Munasinghe, B.; Tanna, D. Reflexive irregular labellings. Unpublished work. 2017. [Google Scholar]
- Tanna, D.; Ryan, J.; Semaničová-Feňovčíková, A. Reflexive edge irregular labelling of prisms and wheels. Australas. J. Combin. 2017, 69, 394–401. [Google Scholar]
- Ryjáček, Z.; Schiermeyer, I. The flower conjecture in special classes of graphs. Discuss. Math. Graph Theory 1995, 15, 179–184. [Google Scholar] [CrossRef]
- Bača, M.; Irfan, M.; Ryan, J.; Semaničová-Feňovčíková, A.; Tanna, D. Note on reflexive edge irregular labellings of graphs. Unpublished work. 2017. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bača, M.; Irfan, M.; Ryan, J.; Semaničová-Feňovčíková, A.; Tanna, D. On Edge Irregular Reflexive Labellings for the Generalized Friendship Graphs. Mathematics 2017, 5, 67. https://doi.org/10.3390/math5040067
Bača M, Irfan M, Ryan J, Semaničová-Feňovčíková A, Tanna D. On Edge Irregular Reflexive Labellings for the Generalized Friendship Graphs. Mathematics. 2017; 5(4):67. https://doi.org/10.3390/math5040067
Chicago/Turabian StyleBača, Martin, Muhammad Irfan, Joe Ryan, Andrea Semaničová-Feňovčíková, and Dushyant Tanna. 2017. "On Edge Irregular Reflexive Labellings for the Generalized Friendship Graphs" Mathematics 5, no. 4: 67. https://doi.org/10.3390/math5040067







