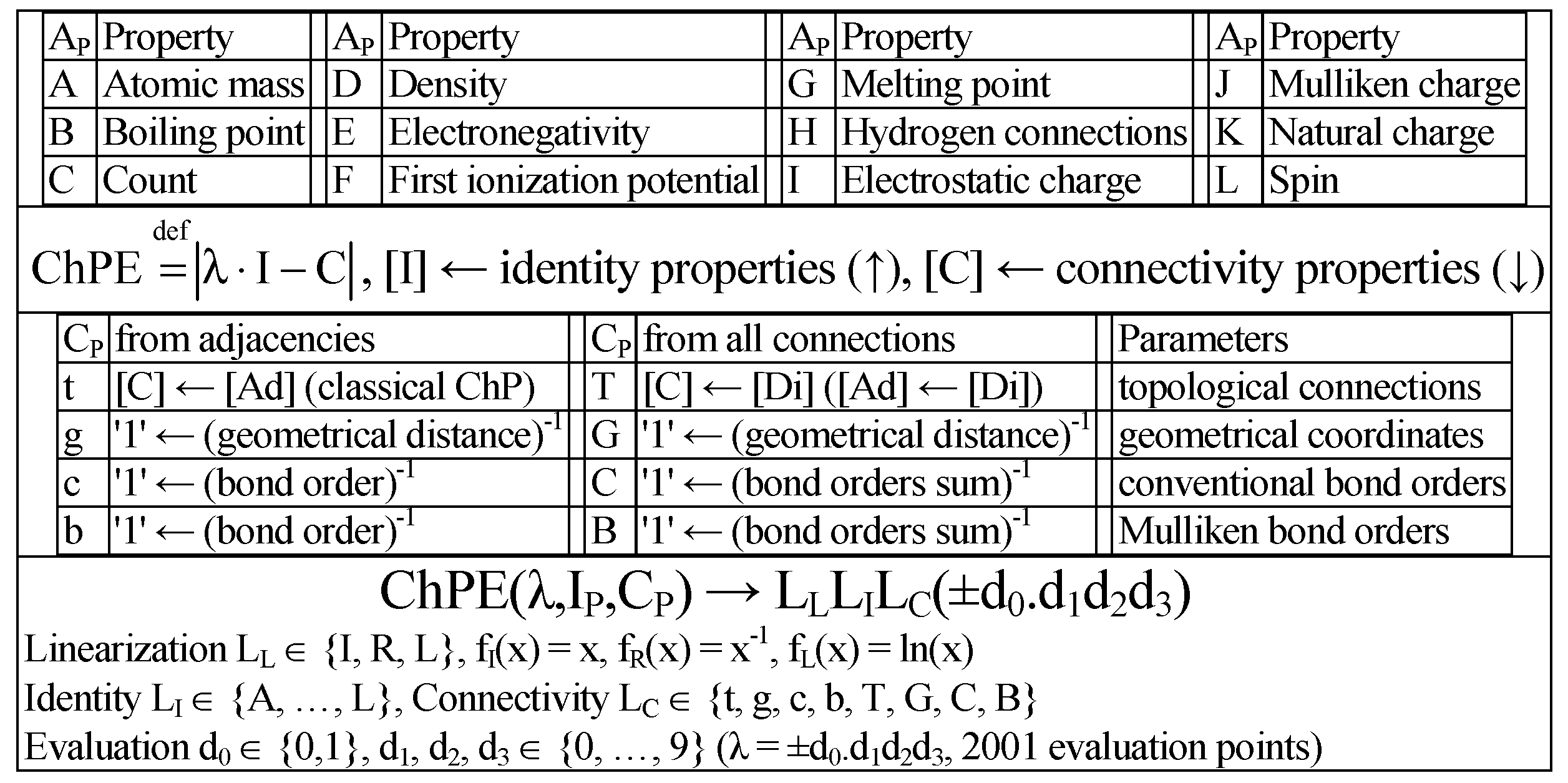
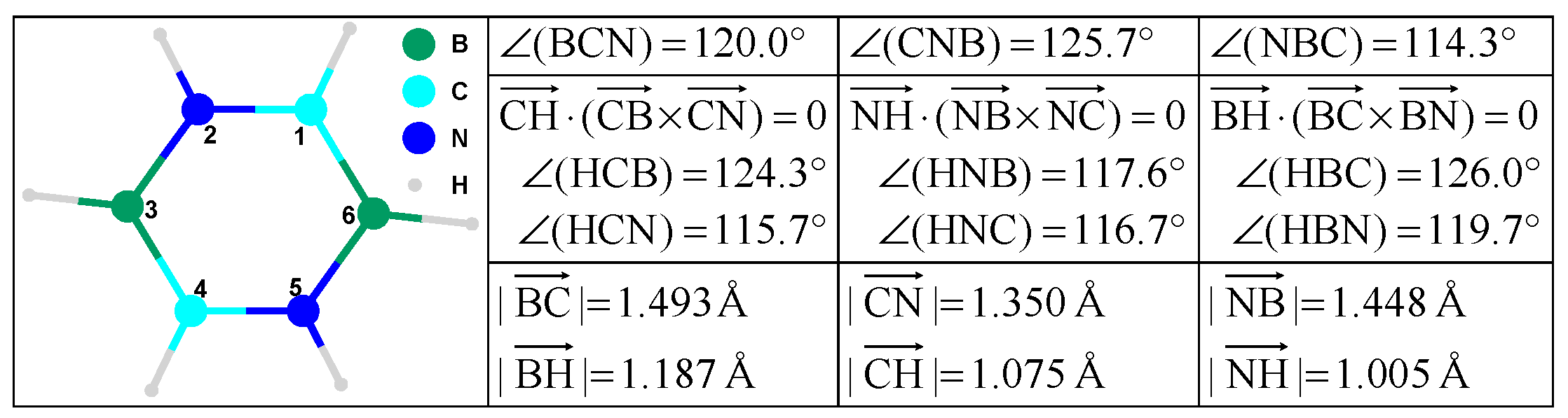2.1. Graphs, Matrices, and the Characteristic Polynomial
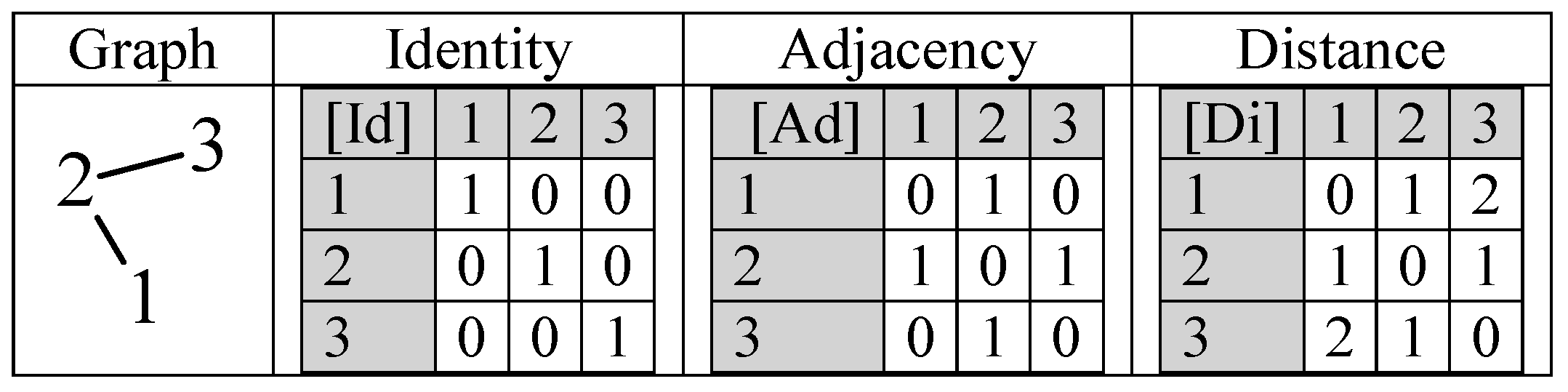
The topology of a graph structure could be expressed as matrices, and, in this regard, three of them are more frequently used: identity, adjacency (vertex–vertex, edge–edge, and vertex–edge), and distance matrices can be built (
Table 2).
The matrices reflect in a 1:1 fashion the graph if the full graph is stored (each vertex pair stored twice, in both ways). The matrices of vertex adjacency ([Ad]) and of edge adjacency are square and the double enumeration of the edges is reflected in symmetry relative to the main diagonal (see
Figure 1).
ChP is the natural construction of a polynomial in which the eigenvalues of the [Ad] are the roots of the ChP. ChP is a polynomial in λ of degree n, where n is the number of atoms. A natural extension is to store in [Id] (instead of unity) non-unity values accounting for the atom types, as well as to store in [Ad] (instead of unity) non-unity values accounting for the bond types.
An extremely important problem in chemistry is to uniquely identify a chemical compound. If the visual identification (looking at the structure) seems simple, for compounds of large size, this alternative is no longer viable. The data related to the structure of the compounds stored into the informational space may provide the answer to this problem. Nevertheless, together with the storing of the structure of the compound another issue is raised—namely, the arbitrary numbering of the atoms (
Figure 2).
For a chemical structure with N atoms stored as a (classical molecular) graph, there exist exactly N! possibilities for numbering the atoms. Unfortunately, storing the graphs as lists of edges and (eventually) vertices does not provide a direct tool to check this arbitrary differentiation due to the numbering. The same situation applies to the adjacency matrices. Therefore, seeking for graph invariants is perfectly justified: an invariant (graph invariant) does not depend on numbering. The adjacency matrix is not a graph invariant and, therefore, it is necessary to go further than the adjacencies.
Important classes of graph invariants are the graph polynomials. To this category belongs the ChP—a graph invariant encoding important properties of the graph. On the other hand, unfortunately, ChP does not represent a bijective image of the graph, as there exist different graphs with the same ChP (i.e., cospectral graphs—the smallest cospectral graphs occurs for 5 vertices [
25]). In order to count the cospectral graphs, one should compare A000088 and A082104 [
26,
27]. The ideal situation is that the invariant should be uniquely assigned to each structure, but this kind of invariant is difficult to find. A procedure to generate a non-degenerate invariant proposed by IUPAC is the international chemical identifier (InChI), which converts the chemical structure to a table of connectivity expressed as a unique and predictable series of characters [
28].
Despite this inconvenience (not representing a bijective image of the graph) due to its link with the partition of the energy [
2], the ChP seems to be one of the best alternatives for quantifying the information from the chemical structure.
Previously, researchers have shown the performance of estimation and/or prediction of the ChP on nonane isomers [
29,
30,
31] as well as in the case of carbon nanostructures [
32,
33]. Furthermore, an online environment has been developed to assist researchers in the calculation of polynomials based on different approaches; this includes the ChP [
34].
2.2. Characteristic Polynomial Extension
When doing calculations on molecular graphs, it is important to consider that, with the increase in the simplification in the graph representation (such as neglecting the type of the atom, bond orders, geometry in the favor of topology), the degeneration of the whole pool of possible calculations increases and there are more molecules with the same representation. This is favorable for the problems seeking similarities but is clearly unfavorable for the problems seeking dissimilarities.
A necessary step to accomplish better coverage of similarity vs dissimilarity dualism is to build and use a family of molecular descriptors, large enough to be able to provide answers for all. In the natural way, such a family should possess a ‘genetic code’—namely, a series of variables from which to (re)produce a (one by one) molecular descriptor, all descriptors being therefore obtained in the same way. It is expected that all individuals of the family are independent of the numbering of the atoms in the molecule (should be molecular invariants).
The construction of such a family needs to consider the following:
Molecules carry both topological and geometrical features (see
Figure 3);
Atom and bond types are essential factors in the expression of the measurable properties;
Atom and/or bond numbering induces an undesired isomorphism;
Geometry and bond types induce other kinds of isomorphism.
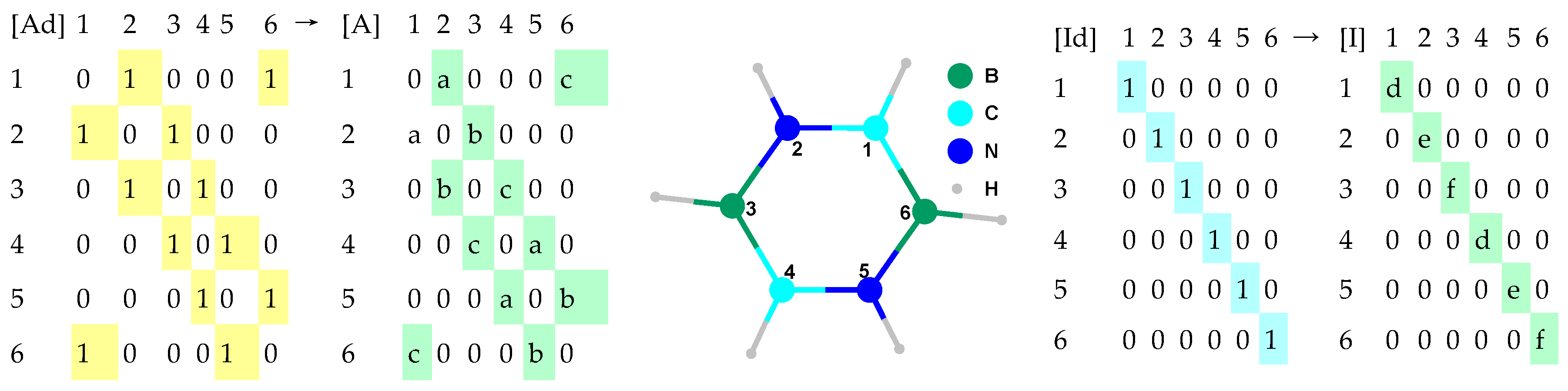
The representation of a molecule could be done using identity and adjacency (
Figure 4).
The distinct identities from
Figure 4 are given using a, b, and c as variables in the case of adjacency and using d, e, and f as variables in the case of identity. This formalism allows the introduction of a natural extension of the ChP from graphs to molecules. There is no determinism in selecting the values of a–f. However,
If a = b = c = d = e = f = 1 then ChPE ← ChP as in classical molecular topology.
If a = b = c = 1.5−1, then [A] accounts for the (inverse of the) bond order.
If a = 1.35−1, b = 1.448−1, and c = 1.493−1 then [A] accounts for the (inverse of the) geometrical distance (in Å).
If d = 12/294, e = 14/294, and f = 10.8/294, then [I] accounts for atomic mass relative to Uuo, the last element from the 7th period of the system of elements.
If d = 2267/ρref, e = 1026/ρref, and f = 2460/ρref, then [I] accounts for the solid state relative density (in m3/kg); ρref can be fixed to 30,000.
If d = 2.55/4.00, e = 3.04/4.00, and f = 2.04/4.00, then [I] accounts for electronegativity relative to Fluorine when the Pauling scale is used.
If d = 1086.2/1312, e = 1402.3/1312, and f = 800.6/1312, then [I] accounts for the first potential of ionization relative to the potential of ionization for Hydrogen.
If d = 3820/3820, e = 63/3820, and f = 2573/3820, then [I] accounts for melting point relative to the diamond allotrope of Carbon (in K).
If d = 1/4, e = 1/4, and f = 1/4, then [I] accounts for the number of hydrogen atoms attached relative to the score of CH4.
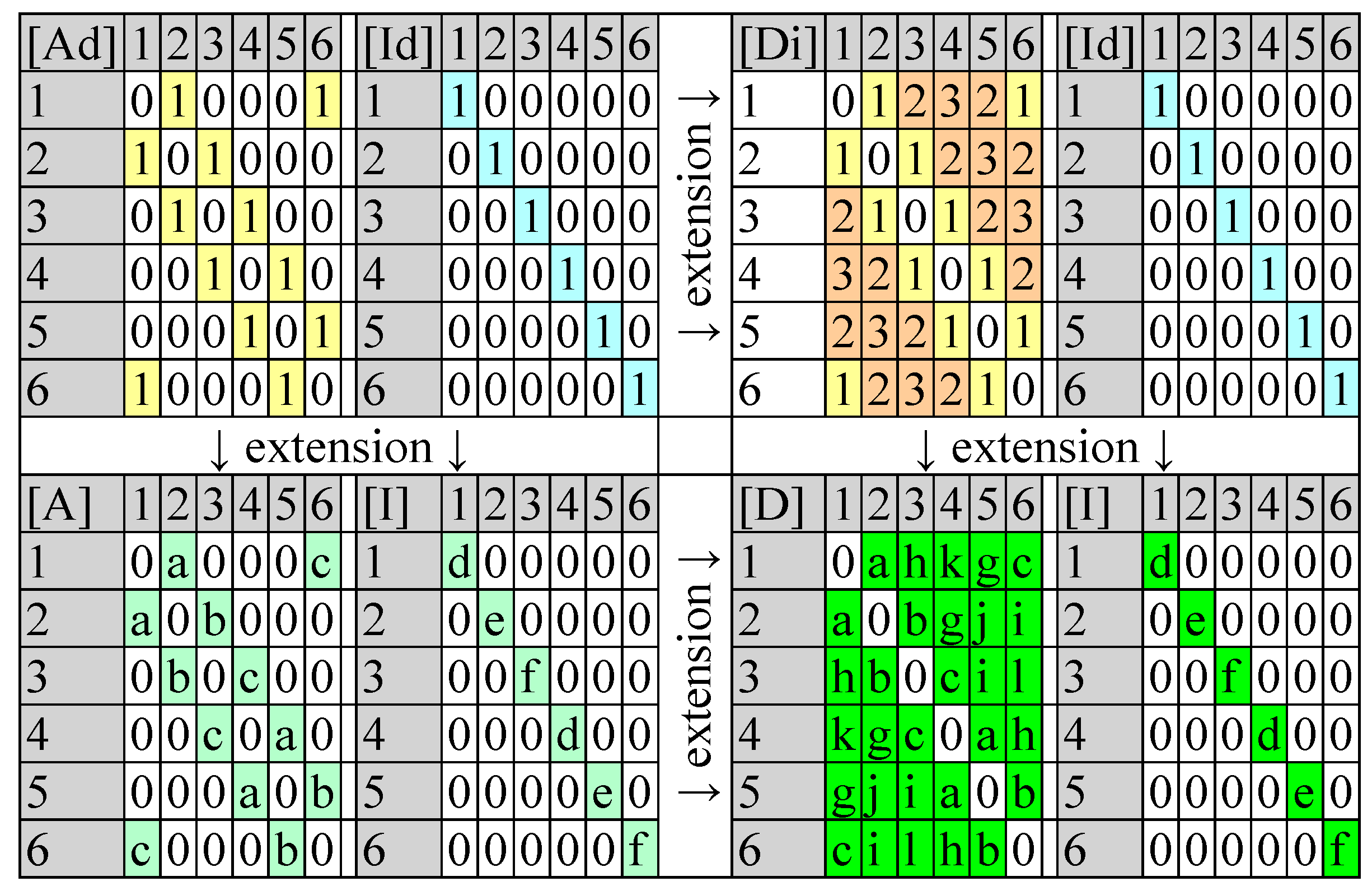
The full extension could include also the distance matrix (
Figure 5).
The extended ChP has the following formula:
where [C] is either [A] or [D], the identities (a, b, and c from [I]) and the connectivity (d, e, f, g, h, i, j, k, and l from [C]).
The single-value entries (0 and 1 ≠ 0 for the classical definition of the ChP) can be upgraded to multi-value (any value), accounting for different atoms and bonds. Obviously, the classical ChP is found when a = b = c = d = e = f = 1 and g = h = i = j = k = l = 0.
Figure 6 shows the ChP extension differently accounting the identities from atomic properties ([I] ← A
P ∈ {A, B, C, D, E, F, G, H, I, J, K, L}) and connectivity properties ([C] ← C
P ∈ {t, g, c, b, T, G, C, B,}).
The extending characteristic polynomial (EChP) is designed for estimation/prediction of molecular properties, so a software implementation was done. EChP(λ, IP, CP) diverges as ChP(λ) does (to ∞) quickly with the increase of λ > 1. Thus, the [−1, 1] range → ‘2001′ grid is useful for evaluation. A linearization (LL) is required and was implemented since biological properties are expressed in log scale. The evaluation is performed at every point (out of 2001), requiring O(n3) operations (where n is the number of atoms).
EChP is a family with 96 (n
I*n
C) polynomial formulas and 288 (*n
L) linearized ones, leading to a total of 576,288 individuals. The FreePascal software was used for implementation since it is very fast and allows a parallelized version to be used with multi-CPUs (chp17chp.pas) [
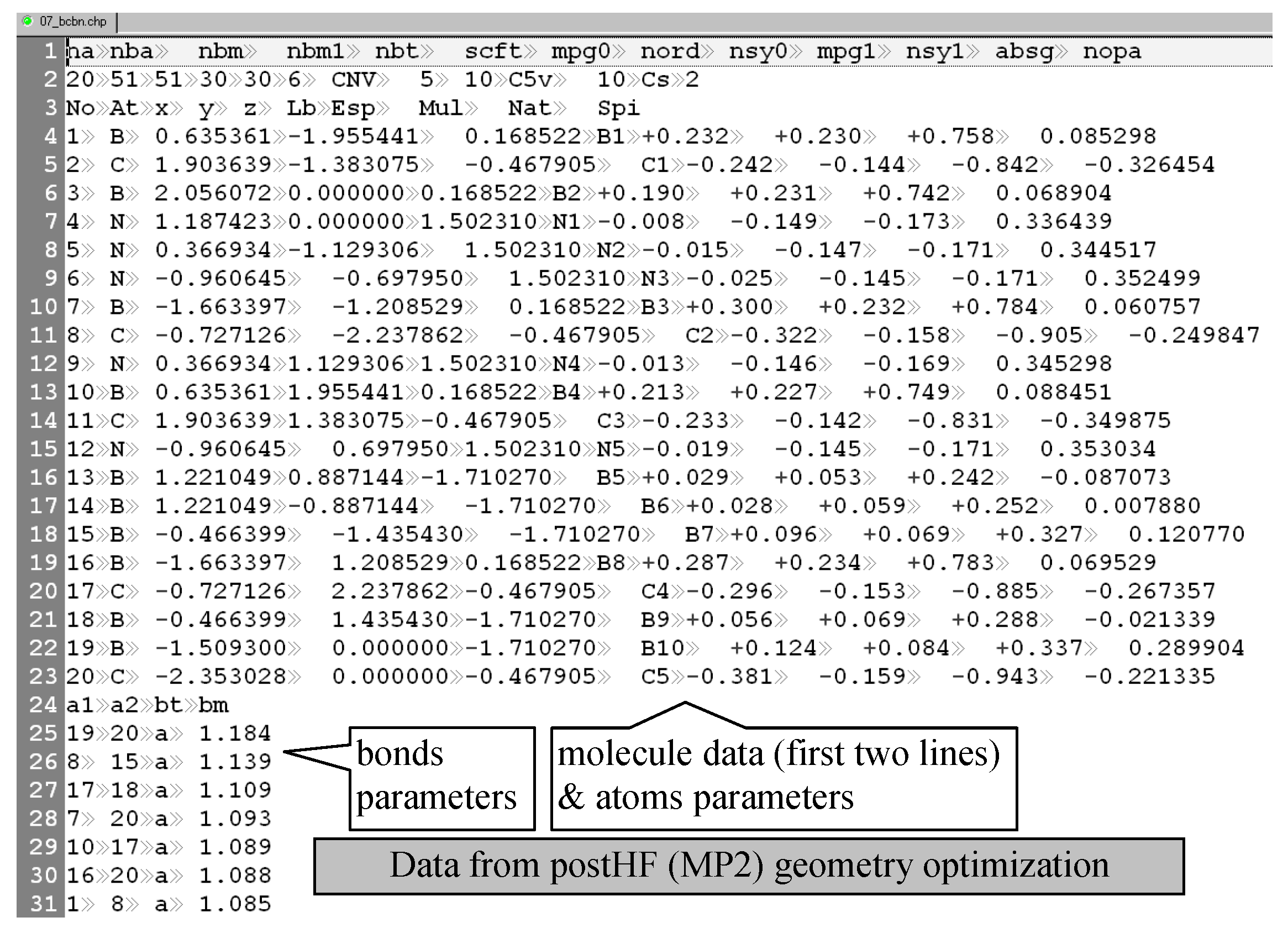
35]. The program requires input files in the ‘chp’ format (such as chfp_17_q.asc, see
Figure 7), and uses a filtering (PHP) program (→chfp_17_t.asc) as well as a molecular property file (such as chfp_17 [prop].txt). The filtering program was designed to look for degenerations and to reduce the pool of descriptors by eliminating the degenerated ones.
The family of EChP descriptors was then used with a series of chemical compounds to obtain associations between the structure and properties as regression equations.
2.3. Numerical Case Study
The case study was conducted on C
20 fullerene congeners with Boron, Carbon, or Nitrogen atoms on each layer (
Figure 8). A sample of 45 distinct compounds was obtained. The generic name of the files was stored as dd_R
1R
2R
3R
4, where dd is the number of the compound in the set and R
1–R
4 are the atoms on layers 1–4 (e.g., 02_bbbn.chp is the second compound in the sample and has boron of the first three layers and nitrogen on the last layer).
The geometries were built at the Hartree-Fock (HF) [
3,
4,
5,
6] 6-31 G [
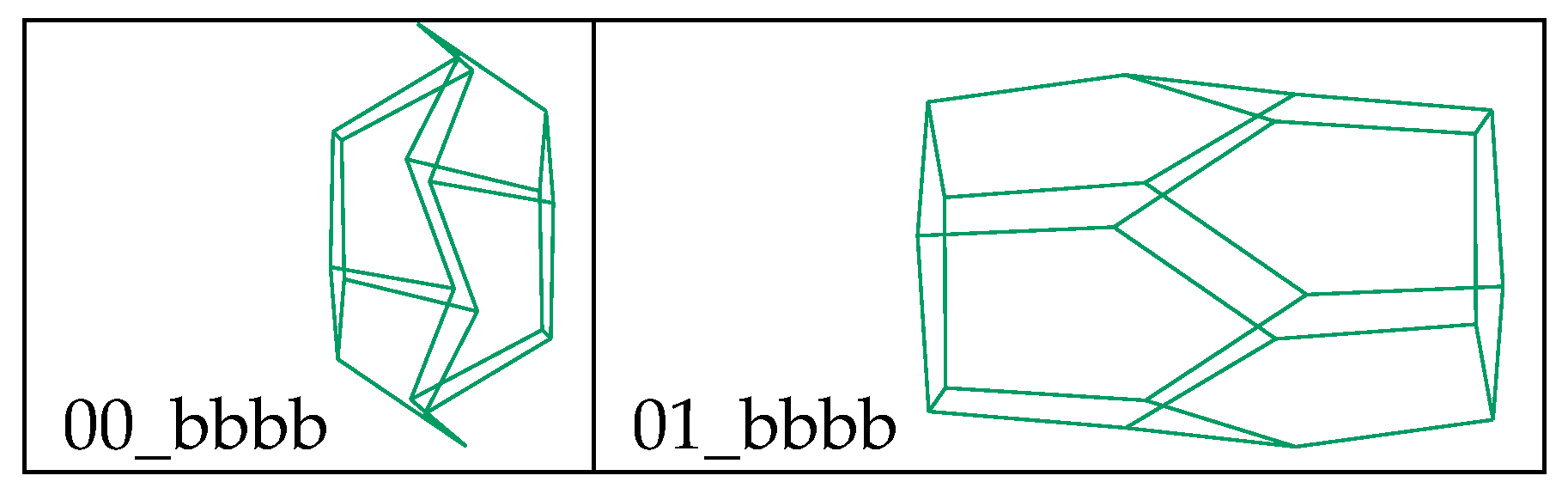
36] level of theory and calculated properties (namely, area and volume) were extracted from these calculations. Two different structures proved stable for bbbb (see
Figure 9) and both were included in the analysis, resulting in a sample of 46 compounds.
The values of the calculated properties are given in
Table 3.
Normal distribution of the data is one assumption that needs to be assessed before any linear regression analysis. Six different tests were used (AD = Anderson-Darling, KS = Kolmogorov-Smirnov, CM = Cramér-von Mises, KV = Kuiper V, WU = Watson U
2, H1 = Shannon’s entropy [
37]) [
38] and the decision was made based on the combined test proposed by Fisher [
39]. The distribution of the investigated properties proved to be not significantly different from the expected normal distribution (see
Table 4, all
p-values > 0.05).
Where for a series of cumulative distribution function values ((f
i)
1≤i≤n):
| Statistic | Formula |
| AD | |
| KS | |
| CM | |
| KV | |
| WU | |
| H1 | |
| FCS | ln(pAD·pKS·pCM·pKV·pWU·pH1) |
The absences of the outliers have also been investigated using Grubb’s test [
40] for the association between volume (vol) and area on the sample of investigated C
20 congeners. The analysis identified three compounds as outliers, their exclusion leading to a performing linear association (
Figure 10).
The values of the EChP descriptors were generated for all molecules in the dataset and were used as input data for searching linear regression models able to explain the investigated properties (area and volume). Three different approaches were used, searching for additive, multiplicative, or full linear dependence (see
Table 5).
The selection of the performing models was done using the adjusted determination coefficient (r
2adj = r
2 − (1 − r
2)*k
D*(
n − k
C)
−1, where
n is the number of compounds in the model). The difference between models with the same properties was tested using the studentized version of the Fisher Z transformation [
41,
42].
The best-performing models identified for the investigated properties are presented in
Table 6 while the characteristics of the models are given in
Table 7.
The relationship between volume and area is translated in the identification of the same EChP descriptors as the explanatory variable (two descriptors for additive models and one descriptor for multiplicative and respective full model, see
Table 6). All models had a capacity of explanation higher than 85%, with the worst performance obtained by multiplicative models and similar performances (without significant difference) obtained by additive and full models (see
Table 8).
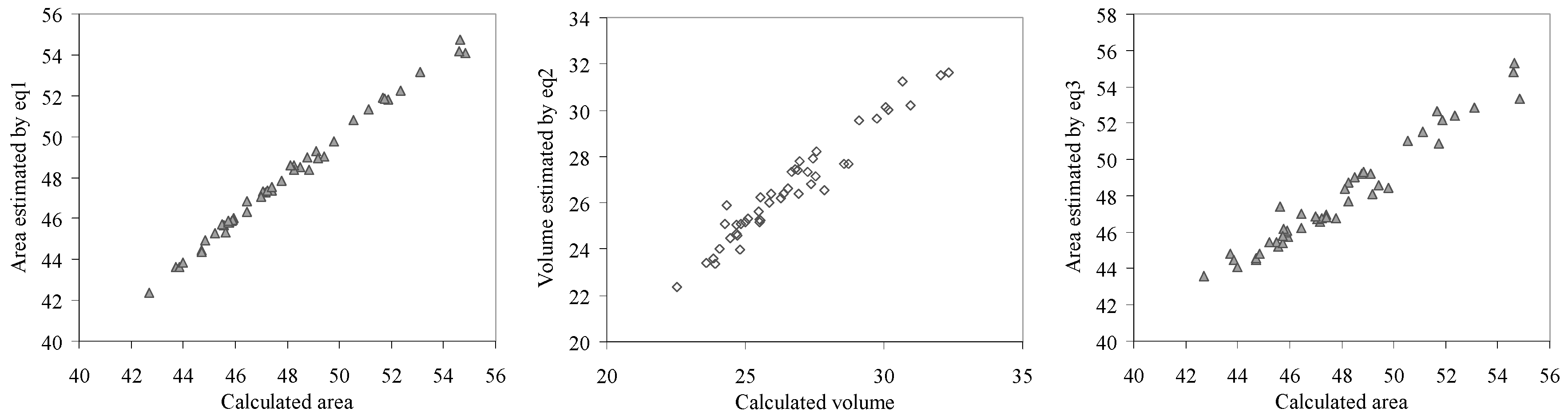
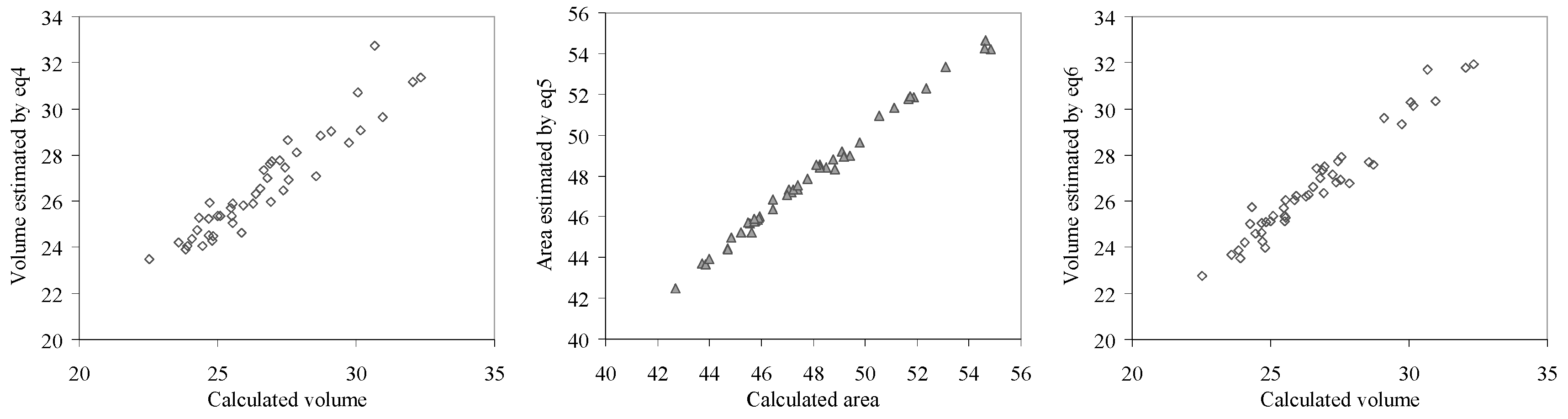
Graphical representations of calculated and estimated area and respective volume by the investigated effects are given in
Figure 11 (eq1– eq3) and
Figure 12 (eq4– eq6).
The model comparison strongly suggests that the best performing models are the additive or the full model for both investigated properties. However, since 03_bbcn is an outlier for the area on the additive model, we can say that choosing the full model will give a correct estimation.
It is important that the performing models identified using the EChP descriptors—the full model—select the same polynomial for both descriptors when both area and volume (”CG” in LCG+0.236, LCG+0.276, and LCG−0.908) are investigated. It should be noted that one descriptor is common for the estimation of the area and of the volume (LCG−0.908) for the C20 fullerene congeners. This fact, in conjunction with the higher correlation between volume and area (r2adj ≈ 0.97), the presence of outliers in one additive model, and the significant higher performance by full models in estimation sustained by goodness-of-fit and the graphical representation of calculated versus estimated, suggests that the best models are those with full effects.