Modeling High Frequency Data with Long Memory and Structural Change: A-HYEGARCH Model
Abstract
:1. Introduction
2. Long Memory GARCH-Type Models
2.1. FIGARCH Model
2.2. HYGARCH Model
3. Structural Change and Relevant Models
3.1. Structural Change in Time Series
3.2. Adaptive-FIGARCH Model
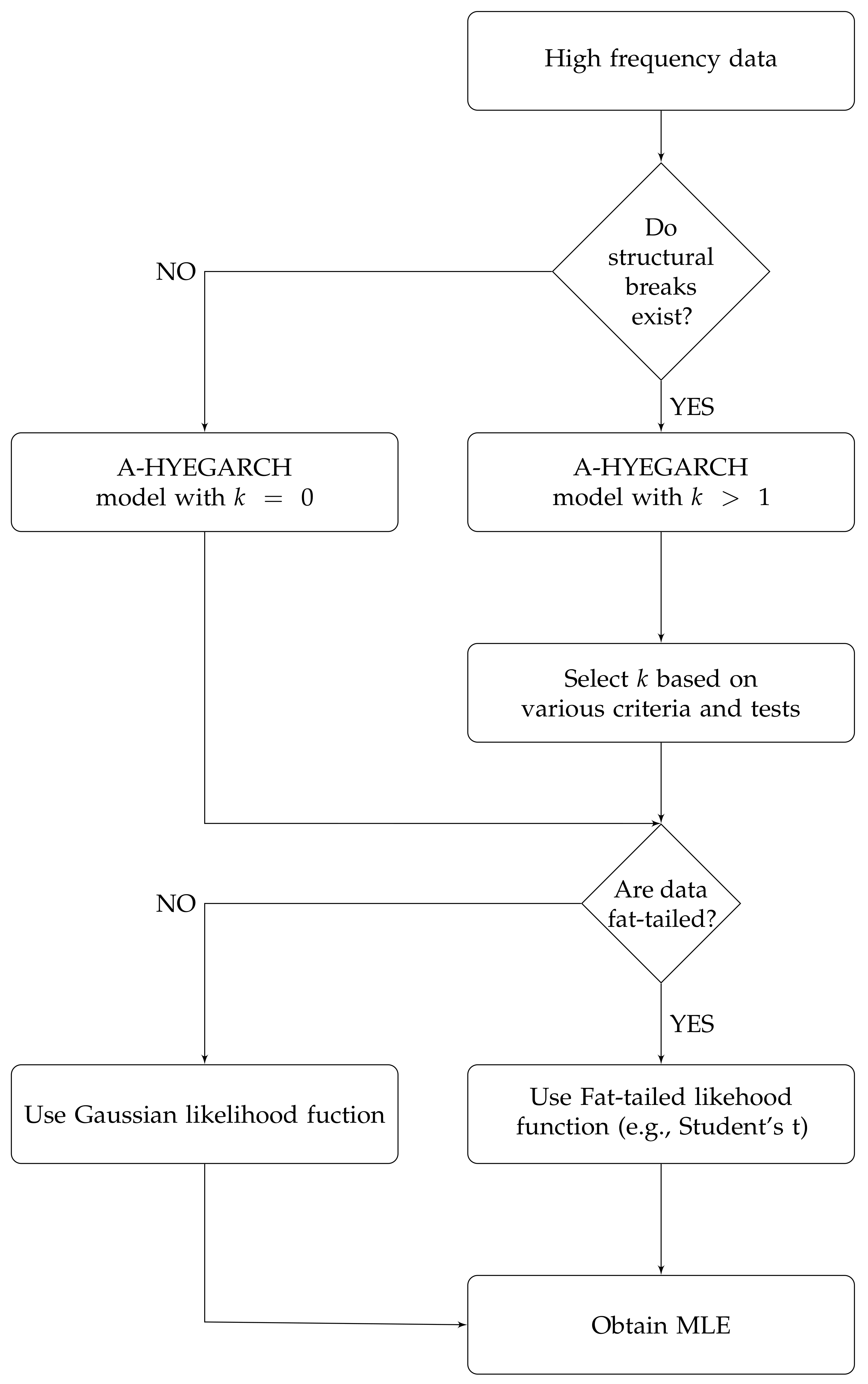
4. The A-HYEGARCH Model
4.1. Step 1: HYEGARCH Model
4.2. Step 2: A-HYEGARCH Model
4.3. Estimation of A-HYEGARCH Models
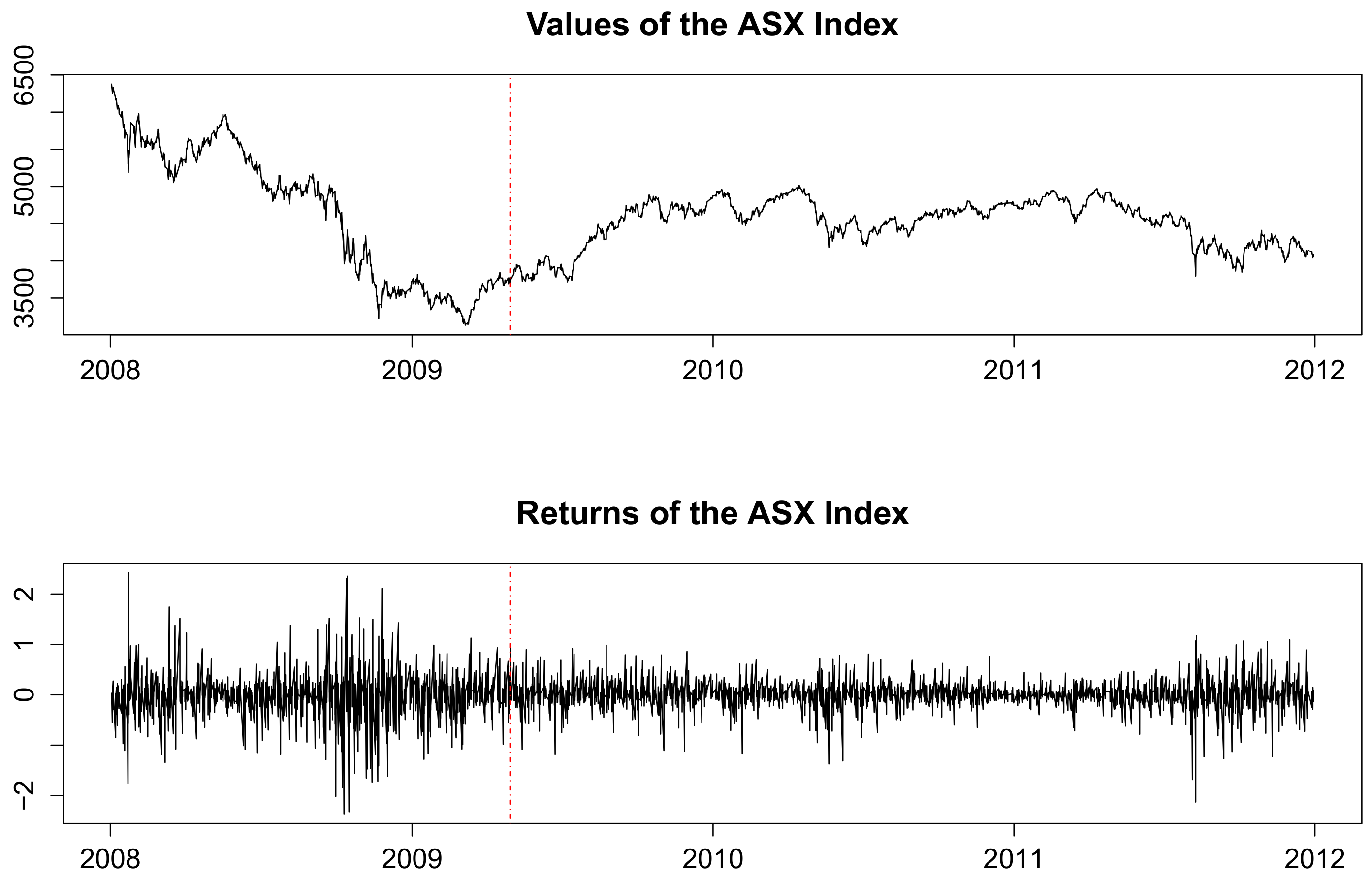
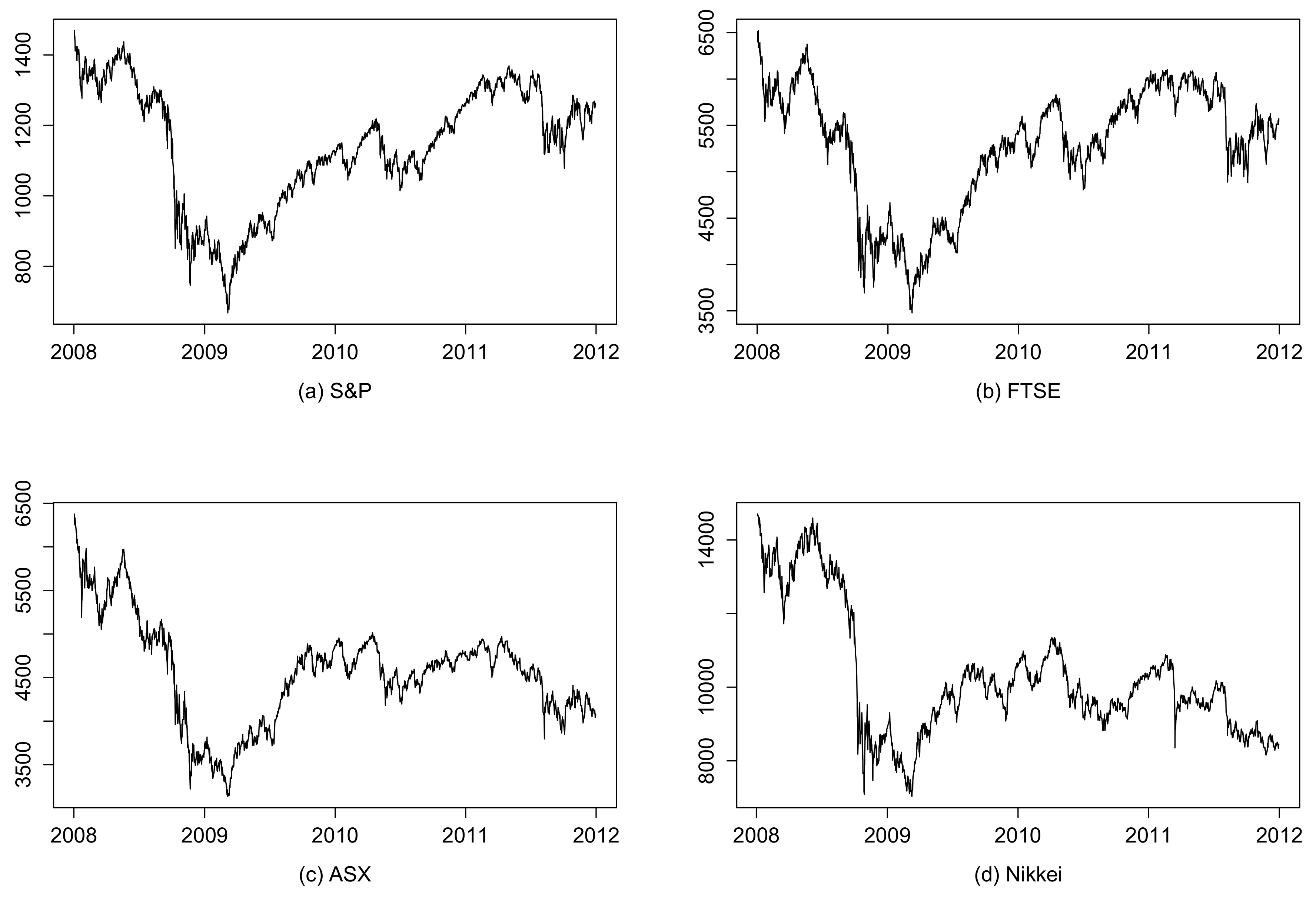
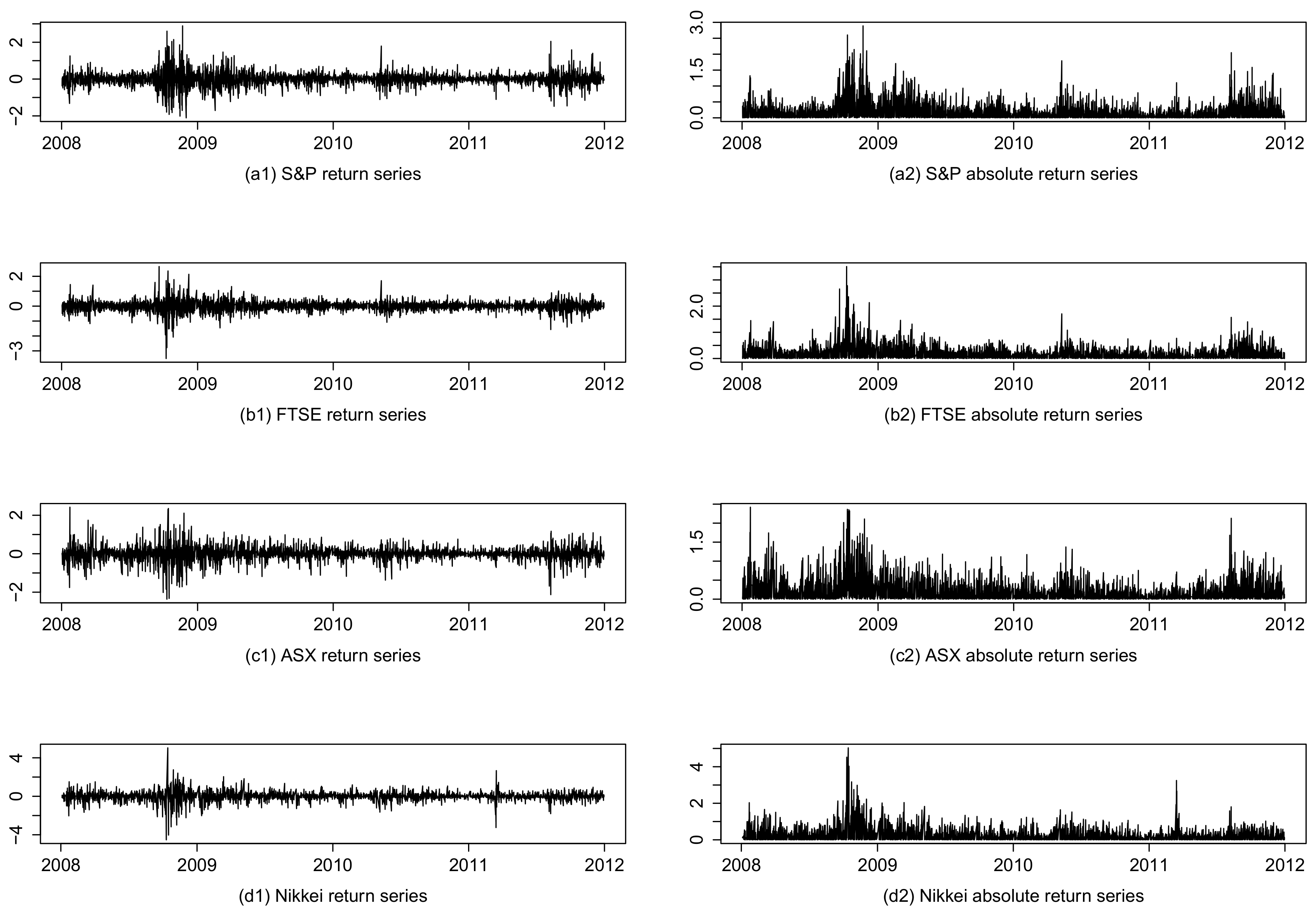
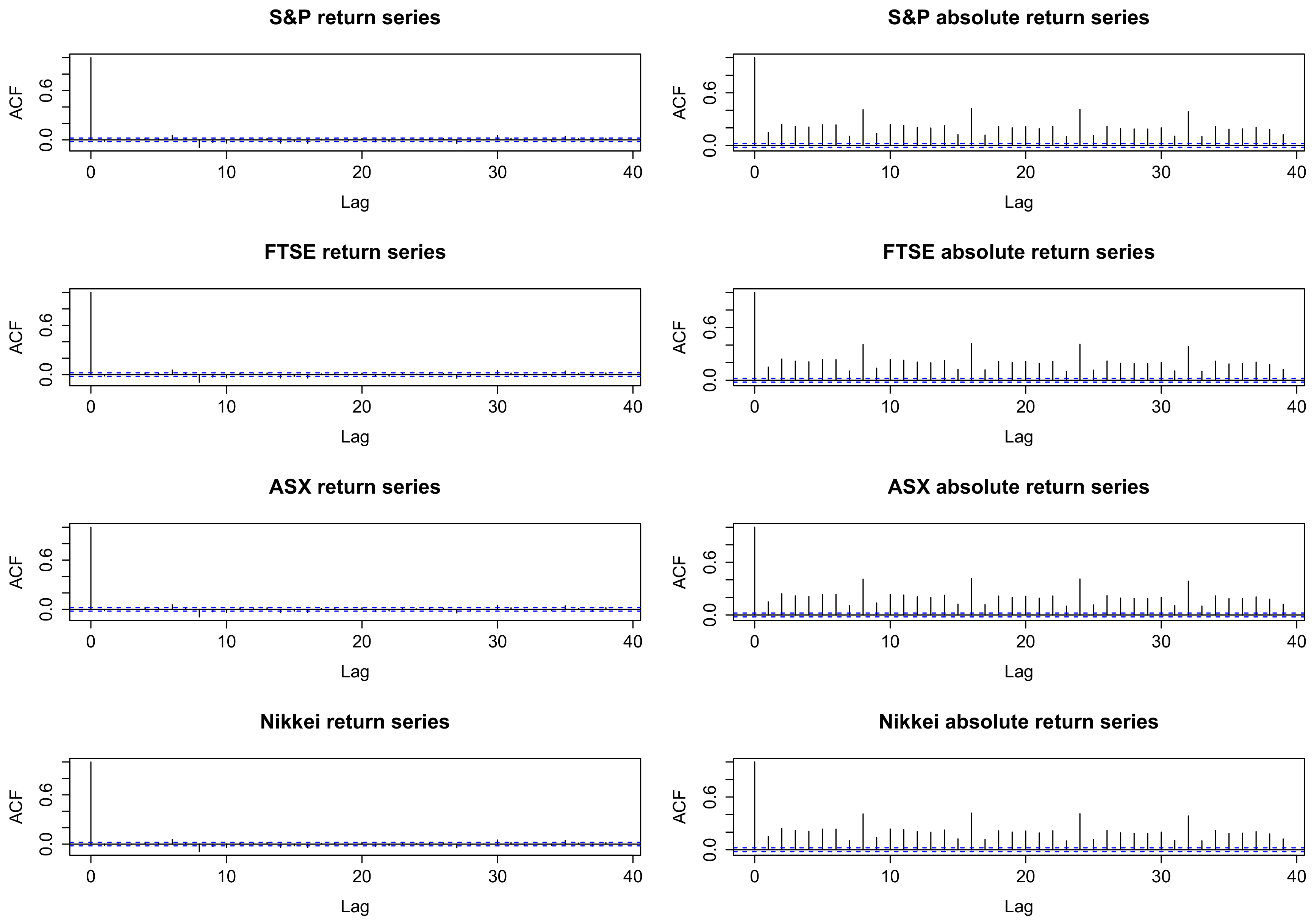
5. Empirical Results
5.1. Procedure of the A-HYEGARCH Model Fitting Empirical Data
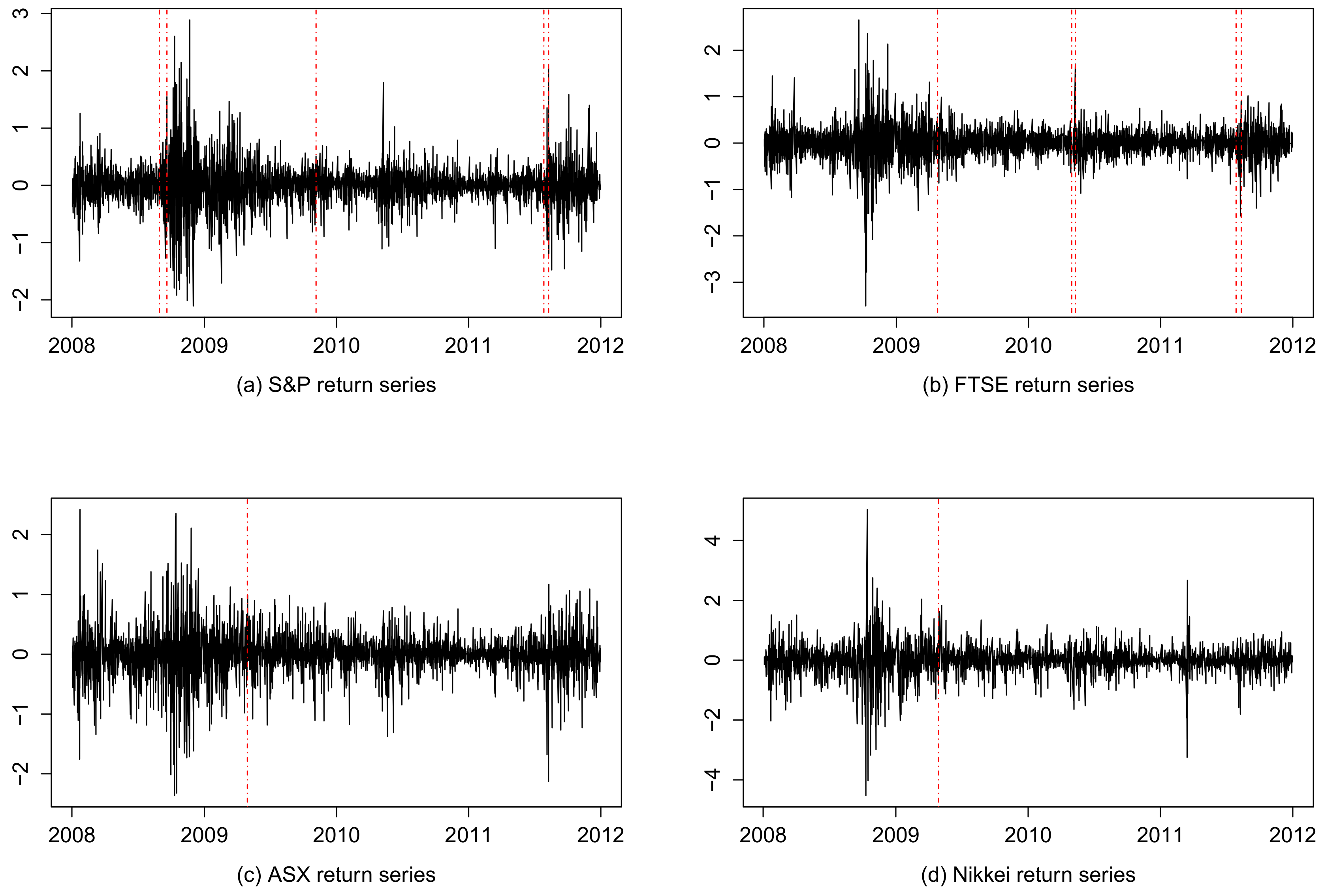
5.2. Structural Change Test
5.3. Model Performance Comparison
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Andersen, Torben G., and Tim Bollerslev. 1997. Intraday periodicity and volatility persistence in financial markets. Journal of Empirical Finance 4: 115–58. [Google Scholar] [CrossRef]
- Andersen, Torben G., and Tim Bollerslev. 1998. Deutsche mark–dollar volatility: intraday activity patterns, macroeconomic announcements, and longer run dependencies. The Journal of Finance 53: 219–65. [Google Scholar] [CrossRef]
- Baillie, Richard T., Tim Bollerslev, and Hans Ole Mikkelsen. 1996. Fractionally integrated generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 74: 3–30. [Google Scholar] [CrossRef]
- Baillie, Richard T., and Claudio Morana. 2009. Modelling long memory and structural breaks in conditional variances: An adaptive figarch approach. Journal of Economic Dynamics and Control 33: 1577–92. [Google Scholar] [CrossRef]
- Balke, Nathan S., and Thomas B. Fomby. 1991. Shifting trends, segmented trends, and infrequent permanent shocks. Journal of Monetary Economics 28: 61–85. [Google Scholar] [CrossRef]
- Batten, Jonathan A., Harald Kinateder, and Niklas Wagner. 2014. Multifractality and value-at-risk forecasting of exchange rates. Physica A: Statistical Mechanics and its Applications 401: 71–81. [Google Scholar] [CrossRef]
- Beine, Michel, and Sébastien Laurent. 2001. Structural change and long memory in volatility: New evidence from daily exchange rates. In Developments in Forecast Combination and Portfolio Choice. Wiley Series in Quantitative Analysis; Hoboken: Wiley, pp. 145–57. [Google Scholar]
- Black, F. 1989. Studies of stock price volatility changes. Paper presented at the 1976 Meeting of the Business and Economic Statistics Section, American Statistical Association, Washington, DC, USA; pp. 177–81. [Google Scholar]
- Bollerslev, Tim. 1986. Generalized autoregressive conditional heteroskedasticity. Journal of Econometrics 31: 307–27. [Google Scholar] [CrossRef]
- Bollerslev, Tim. 1987. A conditionally heteroskedastic time series model for speculative prices and rates of return. The Review of Economics and Statistics 69: 542–47. [Google Scholar] [CrossRef]
- Bollerslev, Tim, and Hans Ole Mikkelsen. 1996. Modeling and pricing long memory in stock market volatility. Journal of Econometrics 73: 151–84. [Google Scholar] [CrossRef]
- Cerra, Valerie, and Sweta Chaman Saxena. 2005. Did output recover from the Asian Crisis? IMF Staff Papers 52: 1–23. [Google Scholar] [CrossRef]
- Choi, Kyongwook, Wei-Choun Yu, and Eric Zivot. 2010. Long memory versus structural breaks in modeling and forecasting realized volatility. Journal of International Money and Finance 29: 857–75. [Google Scholar] [CrossRef]
- Conrad, Christian. 2010. Non-negativity conditions for the hyperbolic garch model. Journal of Econometrics 157: 441–57. [Google Scholar] [CrossRef]
- Conrad, Christian, and Berthold R. Haag. 2006. Inequality constraints in the fractionally integrated garch model. Journal of Financial Econometrics 4: 413–49. [Google Scholar] [CrossRef]
- Corsi, Fulvio. 2009. A simple approximate long-memory model of realized volatility. Journal of Financial Econometrics 7: 174–96. [Google Scholar] [CrossRef]
- Dacorogna, Michael M., Ulrich A. Müller, Robert J. Nagler, Richard B. Olsen, and Olivier V. Pictet. 1993. A geographical model for the daily and weekly seasonal volatility in the foreign exchange market. Journal of International Money and Finance 12: 413–38. [Google Scholar] [CrossRef]
- Davidson, James. 2004. Moment and memory properties of linear conditional heteroscedasticity models, and a new model. Journal of Business & Economic Statistics 22: 16–29. [Google Scholar]
- Diebold, Francis X., and Atsushi Inoue. 2001. Long memory and regime switching. Journal of Econometrics 105: 131–59. [Google Scholar] [CrossRef]
- Ding, Zhuanxin, Clive W.J. Granger, and Robert F. Engle. 1993. A long memory property of stock market returns and a new model. Journal of Empirical Finance 1: 83–106. [Google Scholar] [CrossRef]
- Enders, Walter, and Junsoo Lee. 2004. Testing for a unit root with a nonlinear fourier function. Paper presented at Econometric Society 2004 Far Eastern Meetings, Seoul, Korea, 30 June. Number 457. [Google Scholar]
- Engle, Robert F. 1982. Autoregressive conditional heteroskedasticity with estimates of variance of United Kingdom inflation. Economerica 50: 987–1007. [Google Scholar] [CrossRef]
- Engle, Robert F., and Tim Bollerslev. 1986. Modelling the persistence of conditional variances. Econometric Reviews 5: 1–50. [Google Scholar] [CrossRef]
- Feng, Lingbing, and Yanlin Shi. 2017. Fractionally integrated garch model with tempered stable distribution: A simulation study. Journal of Applied Statistics 44: 2837–57. [Google Scholar] [CrossRef]
- Gallant, A. Ronald. 1984. The fourier flexible form. American Journal of Agricultural Economics 66: 204–8. [Google Scholar] [CrossRef]
- Granger, Clive W.J., and Zhuanxin Ding. 1996a. Modeling volatility persistence of speculative returns. Journal of Econometrics 73: 185–215. [Google Scholar]
- Granger, Clive W.J., and Zhuanxin Ding. 1996b. Varieties of long memory models. Journal of Econometrics 73: 61–77. [Google Scholar] [CrossRef]
- Granger, Clive W.J., and Roselyne Joyeux. 1980. An introduction to long-memory time series models and fractional differencing. Journal of Time Series Analysis 1: 15–29. [Google Scholar] [CrossRef]
- Gray, Stephen F. 1996. Modeling the conditional distribution of interest rates as a regime-switching process. Journal of Financial Economics 42: 27–62. [Google Scholar] [CrossRef]
- Günay, Samet. 2014. Long memory property and structural breaks in volatility: Evidence from Turkey and Brazil. International Journal of Economics and Finance 6. [Google Scholar] [CrossRef]
- Hamilton, James D. 1988. Rational-expectations econometric analysis of changes in regime: An investigation of the term structure of interest rates. Journal of Economic Dynamics and Control 12: 385–423. [Google Scholar] [CrossRef]
- Hamilton, James D., and Raul Susmel. 1994. Autoregressive conditional heteroskedasticity and changes in regime. Journal of Econometrics 64: 307–33. [Google Scholar] [CrossRef]
- Hillebrand, Eric. 2005. Neglecting parameter changes in garch models. Journal of Econometrics 129: 121–38. [Google Scholar] [CrossRef]
- Hosking, Jonathan R.M. 1981. Fractional differencing. Biometrika 68: 165–76. [Google Scholar] [CrossRef]
- Jeanne, Olivier, and Paul Masson. 2000. Currency crises, sunspots and markov-switching regimes. Journal of International Economics 50: 327–50. [Google Scholar] [CrossRef]
- Kristjanpoller, Werner, and Esteban Hernández. 2017. Volatility of main metals forecasted by a hybrid ANN-GARCH model with regressors. Expert Systems with Applications 84: 290–300. [Google Scholar] [CrossRef]
- Lamoureux, Christopher G., and William D. Lastrapes. 1990. Persistence in variance, structural change, and the garch model. Journal of Business & Economic Statistics 8: 225–34. [Google Scholar]
- Lopes, Sílvia R.C., and Taiane S. Prass. 2014. Theoretical results on fractionally integrated exponential generalized autoregressive conditional heteroskedastic processes. Physica A: Statistical Mechanics and Its Applications 401: 278–307. [Google Scholar] [CrossRef]
- Maronna, Ricardo Antonio. 1976. Robust m-estimators of multivariate location and scatter. The Annals of Statistics 4: 51–67. [Google Scholar] [CrossRef]
- Martens, Martin, Michiel De Pooter, and Dick J.C. Van Dijk. 2004. Modeling and Forecasting S&P 500 Volatility: Long Memory, Structural Breaks and Nonlinearity, Working Paper.
- Mood, Alexander M. 1954. On the asymptotic efficiency of certain nonparametric two-sample tests. The Annals of Mathematical Statistics 25: 514–22. [Google Scholar] [CrossRef]
- Morana, Claudio. 2002. Igarch effects: An interpretation. Applied Economics Letters 9: 745–48. [Google Scholar] [CrossRef]
- Morana, Claudio, and Andrea Beltratti. 2004. Structural change and long-range dependence in volatility of exchange rates: Either, neither or both? Journal of Empirical Finance 11: 629–58. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1990. Stationarity and persistence in the garch (1, 1) model. Econometric Theory 6: 318–34. [Google Scholar] [CrossRef]
- Nelson, Daniel B. 1991. Conditional heteroskedasticity in asset returns: A new approach. Econometrica 59: 347–70. [Google Scholar] [CrossRef]
- Nelson, Daniel B., and Charles Q. Cao. 1992. Inequality constraints in the univariate garch model. Journal of Business & Economic Statistics 10: 229–35. [Google Scholar]
- Quoreshi, A.M.M. Shahiduzzaman. 2014. A long-memory integer-valued time series model, INARFIMA, for financial application. Quantitative Finance 14: 2225–35. [Google Scholar] [CrossRef]
- R Core Team. 2017. R: A Language and Environment for Statistical Computing. Vienna: R Foundation for Statistical Computing. [Google Scholar]
- Ross, Gordon J. 2013. Modelling financial volatility in the presence of abrupt changes. Physica A: Statistical Mechanics and its Applications 392: 350–60. [Google Scholar] [CrossRef]
- Shi, Yanlin, and Kin-Yip Ho. 2016. Addressing the Confusion Between Hyperbolic Memory and Regime Switching: The Markov Regime-Switching Hyperbolic Garch Model. Working Paper. Available online: http://dx.doi.org/10.2139/ssrn.2469028 (accessed on 10 February 2018).
- Sims, Christopher A., and Tao Zha. 2006. Were there regime switches in us monetary policy? The American Economic Review 96: 54–81. [Google Scholar] [CrossRef]
- Stock, James H., and Mark W. Watson. 1996. Evidence on structural instability in macroeconomic time series relations. Journal of Business & Economic Statistics 14: 11–30. [Google Scholar]
- Weiss, Andrew A. 1984. Arma models with arch errors. Journal of Time Series Analysis 5: 129–43. [Google Scholar] [CrossRef]
| 1. | Note that FIGARCH (and HYGARCH model introduced in Section 2.2) is proposed using the Gaussian assumption, i.e., . However, existing research suggests that financial time series is rarely Gaussian but leptokurtic. To address this issue, is assumed to follow fat-tailed distributions like Student’s t in the literature. More details and discussions can be found at the end of Section 4.3. |
| 2. | Another potentially powerful approach to incorporate the structural breaks is via higher-order polynomial function. However, Baillie and Morana (2009) suggest that the Spline-FIGARCH model considering such features is outperformed by the A-FIGARCH. Thus, we only adopt the adaptive specification in this paper to model the structural breaks. |
| 3. | See Enders and Lee (2004) and Section 3 of Baillie and Morana (2009) for simulation evidence supporting the adequacy of approximations. |
| 4. | |
| 5. | |
| 6. | |
| 7. | Following Baillie and Morana (2009), we choose for all adaptive models. More parsimonious and comprehensive selections are considered and produce robust results, which are available upon request. |
| 8. | This is consistent with Davidson (2004), who suggests that FIEGARCH may provide more accurate long-memory measure than FIGARCH. Thus, the improvement of HYEGARCH over FIEGARCH may be not as significant as HYGARCH over FIGARCH, in terms of long-memory measure. Nevertheless, the HYEGARCH model has a much more flexible specification and nests FIEGARCH as a special case, providing a more general solution for long-memory modelling. |
| A-HYEGARCH(0,d,0,0) | A-HYEGARCH(1,d,0,0) | A-HYEGARCH(1,d,1,0) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T | d | |||||||||
| d = 0.25 | ||||||||||
| 1000 | 0.25 | 0.1825 | 0.4503 | 0.4116 | 0.0591 | 0.3247 | 0.3193 | 0.1032 | 0.2995 | 0.2812 |
| 3000 | 0.25 | 0.1325 | 0.3547 | 0.3290 | 0.0056 | 0.2219 | 0.2218 | 0.0683 | 0.2521 | 0.2427 |
| 5000 | 0.25 | 0.0814 | 0.2788 | 0.2666 | 0.0078 | 0.1925 | 0.1923 | 0.0564 | 0.2017 | 0.1936 |
| d = 0.35 | ||||||||||
| 1000 | 0.35 | 0.0973 | 0.3484 | 0.3345 | 0.0115 | 0.3189 | 0.3187 | 0.0410 | 0.2661 | 0.2629 |
| 3000 | 0.35 | 0.0850 | 0.3021 | 0.2899 | 0.2152 | 0.2146 | 0.0237 | 0.2063 | 0.2049 | |
| 5000 | 0.35 | 0.0764 | 0.2556 | 0.2439 | 0.0208 | 0.1812 | 0.1800 | 0.0287 | 0.1925 | 0.1903 |
| d = 0.45 | ||||||||||
| 1000 | 0.45 | 0.1317 | 0.3592 | 0.3341 | 0.0145 | 0.3221 | 0.3218 | 0.0264 | 0.2816 | 0.2804 |
| 3000 | 0.45 | 0.2506 | 0.2486 | 0.2174 | 0.2139 | 0.2356 | 0.2333 | |||
| 5000 | 0.45 | 0.0289 | 0.2352 | 0.2334 | 0.2113 | 0.2081 | 0.1770 | 0.1770 | ||
| A-HYEGARCH(0,d,0,k) | A-HYEGARCH(1,d,0,k) | A-HYEGARCH(1,d,1,k) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T | d | |||||||||
| k = 1 | ||||||||||
| 1000 | 0.25 | 0.0962 | 0.3182 | 0.3034 | 0.0860 | 0.2971 | 0.2844 | 0.0624 | 0.2757 | 0.2685 |
| 3000 | 0.25 | 0.1122 | 0.2903 | 0.2678 | 0.0220 | 0.2161 | 0.2150 | 0.0557 | 0.2500 | 0.2437 |
| 5000 | 0.25 | 0.0691 | 0.2424 | 0.2324 | 0.0614 | 0.2376 | 0.2295 | 0.0448 | 0.2007 | 0.1957 |
| 1000 | 0.35 | 0.1398 | 0.3331 | 0.3024 | 0.0868 | 0.3136 | 0.3013 | 0.0746 | 0.2967 | 0.2871 |
| 3000 | 0.35 | 0.0724 | 0.2638 | 0.2536 | 0.0082 | 0.2329 | 0.2327 | 0.0226 | 0.2405 | 0.2394 |
| 5000 | 0.35 | 0.0389 | 0.2295 | 0.2262 | 0.0218 | 0.2236 | 0.2225 | 0.0424 | 0.227 | 0.223 |
| 1000 | 0.45 | 0.0612 | 0.3339 | 0.3283 | 0.2799 | 0.2796 | 0.0106 | 0.3063 | 0.3061 | |
| 3000 | 0.45 | 0.0495 | 0.2404 | 0.2352 | 0.0399 | 0.2140 | 0.2103 | 0.2094 | 0.2076 | |
| 5000 | 0.45 | 0.0404 | 0.2502 | 0.2470 | 0.1985 | 0.1942 | 0.1839 | 0.1831 | ||
| k = 2 | ||||||||||
| 1000 | 0.25 | 0.1285 | 0.3632 | 0.3397 | 0.0556 | 0.3060 | 0.3009 | 0.0845 | 0.3006 | 0.2885 |
| 3000 | 0.25 | 0.0613 | 0.2586 | 0.2512 | 0.0868 | 0.2537 | 0.2384 | 0.0597 | 0.2244 | 0.2163 |
| 5000 | 0.25 | 0.1079 | 0.2764 | 0.2545 | 0.0393 | 0.2119 | 0.2082 | 0.0379 | 0.2055 | 0.2019 |
| 1000 | 0.35 | 0.0682 | 0.3070 | 0.2993 | 0.0689 | 0.3105 | 0.3028 | 0.0839 | 0.3054 | 0.2936 |
| 3000 | 0.35 | 0.0777 | 0.2873 | 0.2765 | 0.0289 | 0.2428 | 0.2411 | 0.0090 | 0.2209 | 0.2207 |
| 5000 | 0.35 | 0.0196 | 0.2138 | 0.2129 | 0.0208 | 0.1834 | 0.1822 | 0.1997 | 0.1978 | |
| 1000 | 0.45 | 0.0558 | 0.2911 | 0.2857 | 0.0253 | 0.2925 | 0.2914 | 0.2911 | 0.2911 | |
| 3000 | 0.45 | 0.2205 | 0.2183 | 0.2358 | 0.2255 | 0.2039 | 0.2015 | |||
| 5000 | 0.45 | 0.0354 | 0.2285 | 0.2257 | 0.1992 | 0.1965 | 0.2055 | 0.2032 | ||
| k = 3 | ||||||||||
| 1000 | 0.25 | 0.0630 | 0.3136 | 0.3072 | 0.0126 | 0.3085 | 0.3082 | 0.0718 | 0.3064 | 0.2979 |
| 3000 | 0.25 | 0.0955 | 0.2777 | 0.2608 | 0.0485 | 0.2204 | 0.2150 | 0.0211 | 0.2152 | 0.2142 |
| 5000 | 0.25 | 0.1113 | 0.2720 | 0.2482 | 0.0261 | 0.1948 | 0.1930 | 0.0450 | 0.2047 | 0.1997 |
| 1000 | 0.35 | 0.0825 | 0.2978 | 0.2861 | 0.0554 | 0.2935 | 0.2882 | 0.0275 | 0.2569 | 0.2554 |
| 3000 | 0.35 | 0.0313 | 0.2394 | 0.2374 | 0.2082 | 0.2081 | 0.0234 | 0.2215 | 0.2203 | |
| 5000 | 0.35 | 0.0480 | 0.2161 | 0.2107 | 0.1881 | 0.1880 | 0.1965 | 0.1955 | ||
| 1000 | 0.45 | 0.0785 | 0.3125 | 0.3025 | 0.0245 | 0.2578 | 0.2567 | 0.2840 | 0.2834 | |
| 3000 | 0.45 | 0.0370 | 0.2412 | 0.2383 | 0.0039 | 0.2263 | 0.2263 | 0.2092 | 0.2071 | |
| 5000 | 0.45 | 0.0156 | 0.2065 | 0.2059 | 0.1948 | 0.1944 | 0.2057 | 0.199 | ||
| k = 4 | ||||||||||
| 1000 | 0.25 | 0.0205 | 0.3268 | 0.3262 | 0.0251 | 0.2939 | 0.2928 | 0.0262 | 0.2441 | 0.2427 |
| 3000 | 0.25 | 0.0478 | 0.2362 | 0.2313 | 0.0344 | 0.2197 | 0.217 | 0.0171 | 0.2069 | 0.2061 |
| 5000 | 0.25 | 0.0870 | 0.2153 | 0.1969 | 0.0403 | 0.2196 | 0.2159 | 0.0186 | 0.1894 | 0.1885 |
| 1000 | 0.35 | 0.0970 | 0.3050 | 0.2891 | 0.0488 | 0.2951 | 0.2910 | 0.2698 | 0.2675 | |
| 3000 | 0.35 | 0.0401 | 0.2181 | 0.2144 | 0.2224 | 0.2214 | 0.0132 | 0.2231 | 0.2227 | |
| 5000 | 0.35 | 0.0371 | 0.2076 | 0.2043 | 0.2129 | 0.2125 | 0.0061 | 0.1773 | 0.1772 | |
| 1000 | 0.45 | 0.0352 | 0.2979 | 0.2958 | 0.0130 | 0.2921 | 0.2918 | 0.2639 | 0.2605 | |
| 3000 | 0.45 | 0.0176 | 0.2436 | 0.2430 | 0.0016 | 0.2392 | 0.2392 | 0.2296 | 0.2246 | |
| 5000 | 0.45 | 0.0054 | 0.1920 | 0.1919 | 0.199 | 0.1979 | 0.1930 | 0.1833 | ||
| A-HYEGARCH(0,0.25,0,k) | A-HYEGARCH (0,0.35,0,k) | A-HYEGARCH (0,0.45,0,k) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T = 1000 | ||||||||||
| k = 0 | 0.3535 | 0.5499 | 0.4213 | 0.3255 | 0.5169 | 0.4015 | 0.2172 | 0.3772 | 0.3084 | |
| 0.1826 | 0.4724 | 0.4357 | 0.1099 | 0.4546 | 0.4411 | 0.0326 | 0.4370 | 0.4358 | ||
| k = 1 | 0.3116 | 0.5484 | 0.4514 | 0.2937 | 0.5203 | 0.4295 | 0.1997 | 0.4290 | 0.3796 | |
| 0.1444 | 0.5077 | 0.4867 | 0.0254 | 0.4945 | 0.4938 | 0.0075 | 0.4642 | 0.4641 | ||
| k = 2 | 0.3482 | 0.5699 | 0.4512 | 0.2783 | 0.5142 | 0.4324 | 0.1767 | 0.4274 | 0.3891 | |
| 0.1272 | 0.4910 | 0.4743 | 0.0881 | 0.4552 | 0.4466 | 0.0354 | 0.4493 | 0.4479 | ||
| k = 3 | 0.2940 | 0.5650 | 0.4825 | 0.2640 | 0.5124 | 0.4392 | 0.1309 | 0.4399 | 0.4199 | |
| 0.1572 | 0.4703 | 0.4433 | 0.0996 | 0.4902 | 0.4800 | 0.0255 | 0.4268 | 0.4260 | ||
| k = 4 | 0.2927 | 0.5563 | 0.4730 | 0.2772 | 0.5299 | 0.4516 | 0.1504 | 0.4320 | 0.4050 | |
| 0.1383 | 0.4612 | 0.4399 | 0.1023 | 0.4566 | 0.4450 | 0.4456 | 0.4454 | |||
| T = 3000 | ||||||||||
| k = 0 | 0.3694 | 0.5307 | 0.3810 | 0.2030 | 0.4321 | 0.3814 | 0.1799 | 0.4394 | 0.4009 | |
| 0.2198 | 0.4301 | 0.3698 | 0.1766 | 0.4253 | 0.3869 | 0.0178 | 0.3840 | 0.3836 | ||
| k = 1 | 0.3335 | 0.5351 | 0.4185 | 0.1805 | 0.4370 | 0.3980 | 0.1477 | 0.4250 | 0.3985 | |
| 0.1902 | 0.4199 | 0.3744 | 0.1690 | 0.4417 | 0.4081 | 0.0037 | 0.4013 | 0.4013 | ||
| k = 2 | 0.2515 | 0.5254 | 0.4613 | 0.1319 | 0.4408 | 0.4206 | 0.1157 | 0.4276 | 0.4117 | |
| 0.1478 | 0.4251 | 0.3986 | 0.1612 | 0.4377 | 0.4069 | 0.4185 | 0.4172 | |||
| k = 3 | 0.2760 | 0.5224 | 0.4436 | 0.1055 | 0.4372 | 0.4243 | 0.0845 | 0.4490 | 0.4410 | |
| 0.1233 | 0.4190 | 0.4004 | 0.1451 | 0.4376 | 0.4129 | 0.3924 | 0.3918 | |||
| k = 4 | 0.3141 | 0.5100 | 0.4018 | 0.1378 | 0.4490 | 0.4274 | 0.0999 | 0.4360 | 0.4244 | |
| 0.1487 | 0.4327 | 0.4063 | 0.1358 | 0.4503 | 0.4293 | 0.0179 | 0.3866 | 0.3861 | ||
| T = 5000 | ||||||||||
| k = 0 | 0.3010 | 0.4992 | 0.3982 | 0.2359 | 0.4001 | 0.3232 | 0.1932 | 0.3482 | 0.2897 | |
| 0.2740 | 0.4985 | 0.4165 | 0.1021 | 0.4339 | 0.4217 | 0.4230 | 0.4230 | |||
| k = 1 | 0.2707 | 0.4635 | 0.3763 | 0.1845 | 0.3874 | 0.3406 | 0.1092 | 0.3451 | 0.3273 | |
| 0.2359 | 0.4849 | 0.4237 | 0.0745 | 0.4098 | 0.4030 | 0.0178 | 0.4064 | 0.4060 | ||
| k = 2 | 0.2172 | 0.4555 | 0.4004 | 0.1461 | 0.3750 | 0.3454 | 0.0844 | 0.3558 | 0.3456 | |
| 0.2220 | 0.4855 | 0.4318 | 0.0647 | 0.4312 | 0.4263 | 0.4102 | 0.4099 | |||
| k = 3 | 0.2339 | 0.4710 | 0.4088 | 0.1652 | 0.3874 | 0.3504 | 0.0688 | 0.3596 | 0.3530 | |
| 0.2306 | 0.5114 | 0.4564 | 0.0599 | 0.4376 | 0.4335 | 0.4170 | 0.4168 | |||
| k = 4 | 0.2465 | 0.4667 | 0.3962 | 0.1597 | 0.3821 | 0.3471 | 0.0994 | 0.3776 | 0.3642 | |
| 0.2320 | 0.4865 | 0.4277 | 0.0601 | 0.4410 | 0.4369 | 0.4188 | 0.4185 | |||
| A-HYEGARCH(1,0.25,0,k) | A-HYEGARCH(1,0.35,0,k) | A-HYEGARCH(1,0.45,0,k) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T = 1000 | ||||||||||
| k = 0 | 0.3168 | 0.5238 | 0.4171 | 0.2450 | 0.4563 | 0.3850 | 0.0675 | 0.3473 | 0.3406 | |
| 0.2382 | 0.4394 | 0.3692 | 0.0874 | 0.4139 | 0.4046 | 0.3553 | 0.3501 | |||
| k = 1 | 0.2845 | 0.5447 | 0.4645 | 0.1855 | 0.4896 | 0.4530 | 0.0476 | 0.4180 | 0.4152 | |
| 0.2009 | 0.5057 | 0.4642 | 0.0362 | 0.4689 | 0.4675 | 0.4389 | 0.4288 | |||
| k = 2 | 0.2719 | 0.5385 | 0.4648 | 0.1546 | 0.4915 | 0.4666 | 0.0483 | 0.3951 | 0.3921 | |
| 0.2041 | 0.5037 | 0.4604 | 0.0416 | 0.4506 | 0.4487 | 0.4332 | 0.4235 | |||
| k = 3 | 0.2487 | 0.5415 | 0.4810 | 0.1625 | 0.5043 | 0.4774 | 0.0827 | 0.4107 | 0.4023 | |
| 0.1826 | 0.4776 | 0.4413 | 0.0631 | 0.4456 | 0.4411 | 0.4163 | 0.4004 | |||
| k = 4 | 0.2196 | 0.5318 | 0.4844 | 0.2160 | 0.4839 | 0.4331 | 0.0188 | 0.3960 | 0.3956 | |
| 0.2362 | 0.4964 | 0.4366 | 0.0482 | 0.4512 | 0.4486 | 0.4145 | 0.4067 | |||
| T = 3000 | ||||||||||
| k = 0 | 0.3894 | 0.5265 | 0.3543 | 0.2344 | 0.4246 | 0.3541 | 0.1550 | 0.3503 | 0.3142 | |
| 0.2727 | 0.4818 | 0.3972 | 0.1100 | 0.3826 | 0.3665 | 0.3665 | 0.3665 | |||
| k = 1 | 0.4085 | 0.5493 | 0.3672 | 0.2415 | 0.4327 | 0.3590 | 0.1097 | 0.3715 | 0.3549 | |
| 0.2794 | 0.4753 | 0.3845 | 0.0988 | 0.3920 | 0.3794 | 0.3823 | 0.3822 | |||
| k = 2 | 0.3552 | 0.5362 | 0.4016 | 0.2183 | 0.4360 | 0.3773 | 0.0937 | 0.3846 | 0.3730 | |
| 0.2663 | 0.4796 | 0.3988 | 0.0857 | 0.4149 | 0.4059 | 0.0134 | 0.4038 | 0.4036 | ||
| k = 3 | 0.3755 | 0.5433 | 0.3926 | 0.2237 | 0.4498 | 0.3902 | 0.0933 | 0.3875 | 0.3761 | |
| 0.2550 | 0.4757 | 0.4016 | 0.1052 | 0.4070 | 0.3932 | 0.0236 | 0.3966 | 0.3959 | ||
| k = 4 | 0.3800 | 0.5500 | 0.3976 | 0.2165 | 0.4548 | 0.4000 | 0.0999 | 0.3954 | 0.3826 | |
| 0.2549 | 0.4801 | 0.4068 | 0.0918 | 0.4058 | 0.3953 | 0.0090 | 0.3918 | 0.3917 | ||
| T = 5000 | ||||||||||
| k = 0 | 0.3584 | 0.4842 | 0.3256 | 0.2809 | 0.4373 | 0.3352 | 0.1708 | 0.3463 | 0.3013 | |
| 0.2371 | 0.4271 | 0.3553 | 0.1292 | 0.3670 | 0.3436 | 0.0204 | 0.3727 | 0.3721 | ||
| k = 1 | 0.3300 | 0.4842 | 0.3543 | 0.2433 | 0.4527 | 0.3818 | 0.1689 | 0.3810 | 0.3415 | |
| 0.2062 | 0.4450 | 0.3944 | 0.1190 | 0.3827 | 0.3637 | 0.3818 | 0.3815 | |||
| k = 2 | 0.3327 | 0.4850 | 0.3529 | 0.2369 | 0.4487 | 0.3811 | 0.1843 | 0.3715 | 0.3225 | |
| 0.2106 | 0.4423 | 0.3889 | 0.1163 | 0.3841 | 0.3661 | 0.3971 | 0.3963 | |||
| k = 3 | 0.3129 | 0.4897 | 0.3766 | 0.2487 | 0.4638 | 0.3915 | 0.1586 | 0.3887 | 0.3549 | |
| 0.2000 | 0.4392 | 0.3910 | 0.1086 | 0.3829 | 0.3672 | 0.4106 | 0.4105 | |||
| k = 4 | 0.3246 | 0.4989 | 0.3789 | 0.2783 | 0.4717 | 0.3808 | 0.1723 | 0.3812 | 0.3400 | |
| 0.2129 | 0.4375 | 0.3822 | 0.1054 | 0.3871 | 0.3725 | 0.0118 | 0.4077 | 0.4076 | ||
| A-HYEGARCH(1,0.25,1,k) | A-HYEGARCH(1,0.35,1,k) | A-HYEGARCH(1,0.45,1,k) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| T = 1000 | ||||||||||
| k = 0 | 0.2015 | 0.3644 | 0.3036 | 0.0876 | 0.3218 | 0.3097 | 0.2947 | 0.2897 | ||
| 0.1061 | 0.3118 | 0.2932 | 0.0471 | 0.3628 | 0.3598 | 0.4070 | 0.4004 | |||
| k = 1 | 0.1394 | 0.4135 | 0.3893 | 0.1061 | 0.4132 | 0.3994 | 0.3585 | 0.3524 | ||
| 0.0851 | 0.4208 | 0.4121 | 0.4226 | 0.4225 | 0.4676 | 0.4522 | ||||
| k = 2 | 0.1279 | 0.4429 | 0.4240 | 0.0502 | 0.3949 | 0.3916 | 0.3767 | 0.3641 | ||
| 0.0687 | 0.4108 | 0.4050 | 0.4111 | 0.4107 | 0.4537 | 0.4385 | ||||
| k = 3 | 0.1580 | 0.4299 | 0.3998 | 0.0641 | 0.3929 | 0.3877 | 0.3682 | 0.3587 | ||
| 0.1002 | 0.3902 | 0.3771 | 0.0076 | 0.4107 | 0.4106 | 0.4491 | 0.4327 | |||
| k = 4 | 0.1309 | 0.4400 | 0.4201 | 0.0354 | 0.3789 | 0.3772 | 0.3710 | 0.3676 | ||
| 0.0771 | 0.3557 | 0.3473 | 0.0134 | 0.3838 | 0.3835 | 0.4393 | 0.4114 | |||
| T = 3000 | ||||||||||
| k = 0 | 0.1453 | 0.2613 | 0.2172 | 0.2247 | 0.2238 | 0.2239 | 0.2013 | |||
| 0.0674 | 0.2950 | 0.2873 | 0.2144 | 0.2127 | 0.2745 | 0.2428 | ||||
| k = 1 | 0.0923 | 0.2956 | 0.2808 | 0.2755 | 0.2707 | 0.3017 | 0.2769 | |||
| 0.0108 | 0.3327 | 0.3325 | 0.2863 | 0.2792 | 0.3375 | 0.3020 | ||||
| k = 2 | 0.0869 | 0.3140 | 0.3018 | 0.2892 | 0.2803 | 0.2815 | 0.2614 | |||
| 0.0250 | 0.3499 | 0.3490 | 0.2811 | 0.2633 | 0.3571 | 0.2954 | ||||
| k = 3 | 0.1231 | 0.3323 | 0.3087 | 0.2718 | 0.2583 | 0.3074 | 0.2823 | |||
| 0.0390 | 0.3481 | 0.3459 | 0.2774 | 0.2674 | 0.3350 | 0.2736 | ||||
| k = 4 | 0.1274 | 0.3230 | 0.2968 | 0.2742 | 0.2684 | 0.3065 | 0.2615 | |||
| 0.0231 | 0.3154 | 0.3145 | 0.2545 | 0.2492 | 0.3077 | 0.2750 | ||||
| T = 5000 | ||||||||||
| k = 0 | 0.0580 | 0.2532 | 0.2465 | 0.0357 | 0.2118 | 0.2087 | 0.3114 | 0.3027 | ||
| 0.0589 | 0.2399 | 0.2326 | 0.2661 | 0.2617 | 0.3214 | 0.2871 | ||||
| k = 1 | 0.2476 | 0.2471 | 0.2606 | 0.2594 | 0.3395 | 0.3254 | ||||
| 0.2390 | 0.2388 | 0.2992 | 0.2800 | 0.3711 | 0.3080 | |||||
| k = 2 | 0.2615 | 0.2612 | 0.0018 | 0.2566 | 0.2566 | 0.3426 | 0.3298 | |||
| 0.0018 | 0.2504 | 0.2504 | 0.2995 | 0.2860 | 0.3661 | 0.3102 | ||||
| k = 3 | 0.2656 | 0.2653 | 0.2388 | 0.2371 | 0.3506 | 0.3380 | ||||
| 0.0110 | 0.2405 | 0.2402 | 0.3089 | 0.3002 | 0.3643 | 0.3048 | ||||
| k = 4 | 0.0177 | 0.2624 | 0.2618 | 0.0208 | 0.2587 | 0.2579 | 0.3505 | 0.3364 | ||
| 0.0135 | 0.2550 | 0.2547 | 0.2915 | 0.2856 | 0.3417 | 0.2921 | ||||
| S&P | FTSE | ASX | Nikkei | |
|---|---|---|---|---|
| Panel A: Descriptive statistics | ||||
| Min | ||||
| Max | 2.8884 | 2.6530 | 2.4190 | 5.0316 |
| Mean | ||||
| S.D. | 0.2558 | 0.2312 | 0.2404 | 0.3101 |
| Skew | 0.2627 | |||
| Kurt. | 18.0721 | 22.7123 | 21.2869 | 39.3868 |
| K.S. | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| J.B. | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 0.0000 | 0.0000 | 0.0000 | 0.0000 | |
| Panel B: Pairwise correlations | ||||
| S&P | 0.0476 | 0.0353 | ||
| FTSE | 0.0463 | |||
| ASX | 0.0066 | |||
| d | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Panel A: S&P | |||||||||
| FIGARCH | 0.0069 | 0.0002 | 0.0482 | 0.9563 | - | 0.9411 | 2.9587 | - | - |
| (0.0013) | 0.0000 | (0.0111) | (0.0028) | (0.0088) | (0.0412) | ||||
| HYGARCH | 0.0071 | 0.0001 | 0.0998 | 0.9541 | 1.0496 | 0.8837 | 2.4009 | - | - |
| (0.0012) | 0.0000 | (0.0195) | (0.0017) | (0.0026) | (0.0160) | (0.0133) | |||
| FIEGARCH | 0.0068 | 0.7963 | - | 0.7405 | 2.5618 | 0.0519 | |||
| (0.0007) | (0.2037) | (0.0122) | (0.0336) | (0.0133) | (0.0150) | (0.0051) | (0.0044) | ||
| HYEGARCH | 0.0069 | 0.7983 | 1.0008 | 0.7294 | 2.5671 | 0.0511 | |||
| (0.0007) | (0.1120) | (0.0121) | (0.0340) | (0.0009) | (0.0131) | (0.0151) | (0.0050) | (0.0044) | |
| Panel B: FTSE | |||||||||
| FIGARCH | 0.0038 | 0.0006 | 0.3015 | 0.8338 | - | 0.5830 | 3.5724 | - | - |
| (0.0014) | (0.0001) | (0.0106) | (0.0040) | (0.0066) | (0.0744) | ||||
| HYGARCH | 0.0038 | 0.0003 | 0.3326 | 0.8287 | 1.0345 | 0.5452 | 3.3689 | - | - |
| (0.0014) | (0.0001) | (0.0117) | (0.0045) | (0.0051) | (0.0072) | (0.0615) | |||
| FIEGARCH | 0.0025 | 2.0009 | 0.5551 | - | 0.9030 | 2.7199 | 0.0840 | ||
| (0.0009) | (0.1899) | (0.0840) | (0.1070) | (0.0126) | (0.0175) | (0.0068) | (0.0082) | ||
| HYEGARCH | 0.0048 | 4.8845 | 0.4221 | 1.0017 | 0.9085 | 3.3806 | 0.0716 | ||
| (0.0009) | (0.1555) | (0.0446) | (0.0523) | (0.0001) | (0.0089) | (0.0419) | (0.0054) | (0.0032) | |
| Panel C: ASX | |||||||||
| FIGARCH | 0.0004 | 0.0957 | 0.9610 | - | 0.8867 | 2.4267 | - | - | |
| (0.0012) | 0.0000 | (0.0103) | (0.0015) | (0.0036) | (0.0148) | ||||
| HYGARCH | 0.0006 | 0.3033 | 0.9435 | 1.1484 | 0.5944 | 2.1465 | - | - | |
| (0.0012) | (0.0001) | (0.0183) | (0.0020) | (0.0060) | (0.0106) | (0.0043) | |||
| FIEGARCH | 0.0016 | 0.9726 | - | 0.9399 | 2.5036 | 0.0947 | |||
| (0.0010) | (0.1440) | (0.0277) | (0.0849) | (0.0161) | (0.0139) | (0.0086) | (0.0112) | ||
| HYEGARCH | 3.1965 | 0.7814 | 1.9430 | 0.9941 | 0.8517 | 2.1654 | 0.0086 | ||
| (0.0015) | (0.2163) | (0.0043) | (0.0593) | (0.0001) | (0.0137) | (0.0042) | (0.0010) | (0.0002) | |
| Panel D: Nikkei | |||||||||
| FIGARCH | 0.0011 | 0.0770 | 0.9462 | - | 0.8637 | 2.2515 | - | - | |
| (0.0013) | (0.0001) | (0.0034) | (0.0004) | (0.0007) | (0.0088) | ||||
| HYGARCH | 0.0009 | 0.1998 | 0.9432 | 1.1550 | 0.6272 | 2.0906 | - | - | |
| (0.0013) | (0.0002) | (0.0056) | (0.0016) | (0.0020) | (0.0019) | (0.0029) | |||
| FIEGARCH | 0.2430 | 0.5857 | 0.1611 | - | 0.7615 | 2.0535 | 0.0028 | ||
| (0.0002) | (0.0810) | (0.0141) | (0.0407) | (0.0045) | (0.0016) | (0.0039) | (0.0001) | ||
| HYEGARCH | 3.4457 | 0.9938 | 0.8002 | 2.1007 | 0.4667 | ||||
| (0.0006) | (0.0934) | (0.0113) | (0.0077) | (0.0001) | (0.0103) | (0.0029) | (0.0278) | (0.0084) | |
| S&P | FTSE | |||||||
|---|---|---|---|---|---|---|---|---|
| A-FIGARCH | A-HYGARCH | A-FIEGARCH | A-HYEGARCH | A-FIGARCH | A-HYGARCH | A-FIEGARCH | A-HYEGARCH | |
| 0.0071 | 0.0071 | 0.0063 | 0.0064 | 0.0036 | 0.0036 | 0.0010 | 0.0040 | |
| (0.0012) | (0.0012) | (0.0004) | (0.0004) | (0.0014) | (0.0014) | (0.0007) | (0.0004) | |
| 0.0019 | 0.0017 | 0.0021 | 0.0026 | 2.0738 | 2.8709 | |||
| 0.0000 | 0.0000 | (0.1658) | (0.2507) | (0.0002) | (0.0001) | (0.3358) | (0.1785) | |
| 0.0441 | 0.0597 | 0.7852 | 0.8150 | 0.4261 | 0.4045 | |||
| (0.0161) | (0.0195) | (0.0088) | (0.0099) | (0.0095) | (0.0096) | (0.0836) | (0.3260) | |
| 0.9514 | 0.9531 | 0.7632 | 0.7648 | 0.3627 | 0.1230 | |||
| (0.0023) | (0.0019) | (0.0289) | (0.0316) | (0.0052) | (0.0050) | (0.0801) | (0.0302) | |
| - | 1.0154 | - | 1.0067 | - | 0.9742 | - | 1.0015 | |
| (0.0023) | (0.0006) | (0.0077) | 0.0000 | |||||
| - | - | -0.1292 | -0.1277 | - | - | |||
| (0.0064) | (0.0056) | (0.0069) | (0.0044) | |||||
| - | - | 0.0353 | 0.0312 | - | - | 0.0688 | 0.0363 | |
| (0.0016) | (0.0015) | (0.0081) | (0.0015) | |||||
| d | 0.9541 | 0.9390 | 0.6313 | 0.5773 | 0.3878 | 0.4219 | 0.8867 | 0.8911 |
| (0.0132) | (0.0156) | (0.0084) | (0.0066) | (0.0074) | (0.0076) | (0.0095) | (0.0053) | |
| 2.5309 | 2.4206 | 2.3700 | 2.4137 | 3.4354 | 3.4410 | 2.7041 | 3.6283 | |
| 0.0000 | (0.0141) | (0.0095) | (0.0106) | (0.0655) | (0.0650) | (0.0170) | (0.0534) | |
| 0.0004 | 0.0019 | 0.0266 | 0.0014 | 0.0024 | ||||
| (0.0001) | 0.0000 | (0.0264) | (0.1067) | (0.0002) | (0.0002) | (0.6054) | (0.1679) | |
| 0.0002 | 0.0004 | 0.2730 | 0.0008 | 0.0014 | 0.0634 | 1.5218 | ||
| (0.0001) | (0.0001) | (0.0219) | (0.0888) | (0.0002) | (0.0002) | (0.3027) | (0.1931) | |
| 0.0003 | 0.0007 | 0.0546 | ||||||
| 0.0000 | (0.0001) | (0.0177) | (0.0735) | (0.0002) | (0.0002) | (0.3092) | (0.1148) | |
| ) | 0.4889 | 0.3969 | ||||||
| 0.0000 | 0.0000 | (0.0170) | (0.0705) | (0.0002) | (0.0002) | (0.3963) | (0.1102) | |
| (0.0001) | 0.0000 | (0.0147) | (0.0621) | (0.0002) | (0.0002) | (0.2118) | (0.0871) | |
| 0.0561 | 0.2460 | 0.0000 | ||||||
| 0.0000 | (0.0001) | (0.0149) | (0.0616) | (0.0002) | (0.0002) | (0.1798) | (0.0878) | |
| 0.0004 | 0.0008 | |||||||
| 0.0000 | (0.0001) | (0.0132) | (0.0549) | (0.0002) | (0.0002) | (0.1530) | (0.0700) | |
| 0.0004 | 0.0004 | 0.0008 | 0.0010 | 0.1948 | 0.2555 | |||
| 0.0000 | 0.0000 | (0.0134) | (0.0584) | (0.0002) | (0.0002) | (0.1440) | (0.0694) | |
| 0.0002 | 0.0004 | 0.0043 | 0.0101 | 0.0003 | 0.0009 | |||
| (0.0001) | 0.0000 | (0.0122) | (0.0518) | (0.0002) | (0.0002) | (0.1365) | (0.0629) | |
| 0.0002 | 0.0002 | 0.0413 | 0.2067 | 0.0001 | 0.0003 | 0.0791 | 0.1247 | |
| (0.0001) | (0.0001) | (0.0125) | (0.0536) | (0.0002) | (0.0002) | (0.1301) | (0.0605) | |
| 0.0002 | 0.0001 | |||||||
| 0.0000 | (0.0001) | (0.0122) | (0.0526) | (0.0002) | (0.0002) | (0.1162) | (0.0566) | |
| 0.0001 | 0.0000 | |||||||
| 0.0000 | 0.0000 | (0.0112) | (0.0495) | (0.0002) | (0.0002) | (0.1096) | (0.0515) | |
| 0.0001 | 0.0255 | 0.1135 | 0.0002 | 0.0000 | 0.0414 | 0.0471 | ||
| 0.0000 | 0.0000 | (0.0111) | (0.0479) | (0.0002) | (0.0002) | (0.1021) | (0.0518) | |
| 0.0001 | 0.0002 | 0.0001 | 0.1722 | 0.1173 | ||||
| (0.0001) | (0.0001) | (0.0112) | (0.0493) | (0.0002) | (0.0002) | (0.1033) | (0.0494) | |
| 0.0001 | 0.0002 | 0.0002 | ||||||
| 0.0000 | (0.0001) | (0.0110) | (0.0490) | (0.0002) | (0.0002) | (0.0934) | (0.0458) | |
| 0.0017 | 0.0021 | 0.0002 | ||||||
| 0.0000 | 0.0000 | (0.0106) | (0.0462) | (0.0001) | (0.0002) | (0.0930) | (0.0468) | |
| ASX | Nikkei | |||||||
|---|---|---|---|---|---|---|---|---|
| A-FIGARCH | A-HYGARCH | A-FIEGARCH | A-HYEGARCH | A-FIGARCH | A-HYGARCH | A-FIEGARCH | A-HYEGARCH | |
| 0.0000 | 0.0000 | |||||||
| (0.0012) | (0.0012) | (0.0008) | (0.0005) | (0.0012) | (0.0012) | (0.0012) | (0.0011) | |
| 0.0050 | 0.0052 | 3.2308 | 1.3881 | 0.0233 | 0.0199 | 4.2225 | 1.1887 | |
| (0.0002) | (0.0002) | (0.0473) | (0.0454) | (0.0004) | (0.0004) | (0.0569) | (0.0332) | |
| 0.2154 | 0.3350 | 0.9747 | 0.9516 | 0.2056 | 0.2529 | 0.9532 | ||
| (0.0164) | (0.0204) | (0.0003) | (0.0007) | (0.0041) | (0.0061) | (0.0005) | (0.0106) | |
| 0.9118 | 0.9181 | 6.1132 | 7.8885 | 0.8590 | 0.8987 | 4.6251 | ||
| (0.0031) | (0.0028) | (0.0782) | (0.1321) | (0.0013) | (0.0023) | (0.0647) | (0.0003) | |
| - | 1.1447 | - | 1.0143 | - | 1.1554 | - | 2.6064 | |
| (0.0089) | (0.0007) | (0.0035) | (0.0020) | |||||
| - | - | - | - | 0.0222 | ||||
| (0.0013) | (0.0007) | (0.0026) | (0.0571) | |||||
| - | - | 0.0049 | 0.0013 | - | - | 0.0136 | 1.2551 | |
| (0.0001) | 0.0000 | (0.0002) | (0.0455) | |||||
| d | 0.7333 | 0.5422 | 0.2122 | 0.3450 | 0.6393 | 0.5391 | 0.2132 | 0.0653 |
| (0.0085) | (0.0116) | (0.0013) | (0.0014) | (0.0019) | (0.0027) | (0.0014) | (0.0001) | |
| 2.2107 | 2.1345 | 2.0409 | 2.0599 | 2.0984 | 2.0683 | 2.0359 | 2.0090 | |
| (0.0065) | (0.0039) | (0.0011) | (0.0016) | (0.0031) | (0.0021) | (0.0010) | (0.0003) | |
| 0.0020 | 0.0047 | 0.0022 | 0.0050 | 0.0189 | 0.0035 | 0.3229 | ||
| 0.0014 | 0.0022 | 0.0729 | 0.0058 | 0.0047 | 0.5264 | |||
| (0.0002) | (0.0003) | (0.0015) | (0.0473) | (0.0006) | (0.0008) | (0.0032) | (0.0420) | |
| 0.0016 | 0.0049 | |||||||
| (0.0002) | (0.0003) | (0.0014) | (0.0459) | (0.0004) | (0.0007) | (0.0031) | (0.0396) | |
| (0.0002) | (0.0000) | (0.0014) | (0.0465) | (0.0005) | (0.0005) | (0.0030) | (0.0374) | |
| 0.0007 | ||||||||
| (0.0002) | (0.0002) | (0.0014) | (0.0447) | (0.0005) | (0.0006) | (0.0030) | (0.0392) | |
| 0.0015 | 0.0820 | 0.0011 | 0.0028 | 0.1064 | ||||
| (0.0002) | (0.0003) | (0.0014) | (0.0450) | (0.0005) | (0.0006) | (0.0030) | (0.0364) | |
| 0.0013 | 0.0100 | |||||||
| (0.0002) | (0.0003) | (0.0013) | (0.0429) | (0.0006) | (0.0006) | (0.0029) | (0.0388) | |
| 0.0009 | 0.0012 | 0.0002 | 0.0487 | 0.0114 | 0.0084 | 0.0067 | 0.2248 | |
| (0.0002) | (0.0002) | (0.0014) | (0.0454) | (0.0007) | (0.0006) | (0.0029) | (0.0379) | |
| 0.0015 | 0.0009 | 0.0030 | 0.0095 | 0.0055 | 0.1998 | |||
| (0.0002) | (0.0002) | (0.0013) | (0.0432) | (0.0004) | (0.0007) | (0.0028) | (0.0414) | |
| 0.0013 | 0.0015 | 0.0035 | 0.1610 | 0.0037 | 0.0021 | 0.0017 | 0.1843 | |
| (0.0002) | (0.0003) | (0.0013) | (0.0437) | (0.0004) | (0.0005) | (0.0029) | (0.0360) | |
| 0.0012 | 0.0029 | |||||||
| (0.0002) | (0.0003) | (0.0013) | (0.0432) | (0.0007) | (0.0005) | (0.0028) | (0.0381) | |
| 0.0002 | 0.0000 | 0.0029 | 0.1985 | |||||
| (0.0002) | (0.0002) | (0.0013) | (0.0419) | (0.0006) | (0.0007) | (0.0028) | (0.0379) | |
| 0.0000 | 0.0002 | |||||||
| (0.0002) | (0.0002) | (0.0013) | (0.0420) | (0.0005) | (0.0007) | (0.0028) | (0.0392) | |
| 0.0005 | ||||||||
| (0.0002) | (0.0003) | (0.0013) | (0.0437) | (0.0005) | (0.0006) | (0.0028) | (0.0364) | |
| 0.0012 | ||||||||
| (0.0002) | (0.0003) | (0.0013) | (0.0434) | (0.0005) | (0.0006) | (0.0028) | (0.0389) | |
| 0.0058 | 0.0000 | 0.0255 | ||||||
| (0.0002) | (0.0002) | (0.0013) | (0.0410) | (0.0004) | (0.0006) | (0.0027) | (0.0371) | |
| Log-Likelihood | AIC | BIC | ||||
|---|---|---|---|---|---|---|
| Panel A: S&P | ||||||
| A-FIGARCH | 2759.8950 | 17.2735 | 0.3884 | 17.0067 | ||
| A-HYGARCH | 2761.6019 | 18.4937 | 0.4231 | 18.2473 | ||
| A-FIEGARCH | 2862.2593 | 25.0606 | 0.8789 | 24.1713 | ||
| A-HYEGARCH | 2862.9020 | 24.5154 | 0.9294 | 23.6702 | ||
| Panel B: FTSE | ||||||
| A-FIGARCH | 2914.8105 | 29.4395 | 1.8242 | 28.9177 | ||
| A-HYGARCH | 2915.0273 | 30.3156 | 1.8479 | 29.7808 | ||
| A-FIEGARCH | 2979.7400 | 24.6949 | 2.1089 | 24.4607 | ||
| A-HYEGARCH | 3008.1578 | 17.9299 | 2.2100 | 17.9626 | ||
| Panel C: ASX | ||||||
| A-FIGARCH | 3110.6813 | 42.3133 | 4.3910 | 36.6143 | ||
| A-HYGARCH | 3117.5465 | 41.5592 | 4.3769 | 35.9641 | ||
| A-FIEGARCH | 3152.0775 | 68.8288 | 4.2316 | 57.0540 | ||
| A-HYEGARCH | 3152.1061 | 71.1686 | 4.2512 | 58.7924 | ||
| Panel D: Nikkei | ||||||
| A-FIGARCH | 2019.0830 | 63.5469 | 6.8523 | 65.5967 | ||
| A-HYGARCH | 2023.5644 | 77.3598 | 6.9062 | 79.2479 | ||
| A-FIEGARCH | 2032.6590 | 46.9280 | 6.6981 | 49.6358 | ||
| A-HYEGARCH | 2153.8684 | 43.5520 | 6.6087 | 43.9113 | ||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shi, Y.; Yang, Y. Modeling High Frequency Data with Long Memory and Structural Change: A-HYEGARCH Model. Risks 2018, 6, 26. https://doi.org/10.3390/risks6020026
Shi Y, Yang Y. Modeling High Frequency Data with Long Memory and Structural Change: A-HYEGARCH Model. Risks. 2018; 6(2):26. https://doi.org/10.3390/risks6020026
Chicago/Turabian StyleShi, Yanlin, and Yang Yang. 2018. "Modeling High Frequency Data with Long Memory and Structural Change: A-HYEGARCH Model" Risks 6, no. 2: 26. https://doi.org/10.3390/risks6020026





