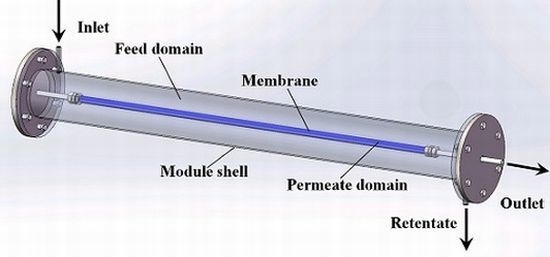
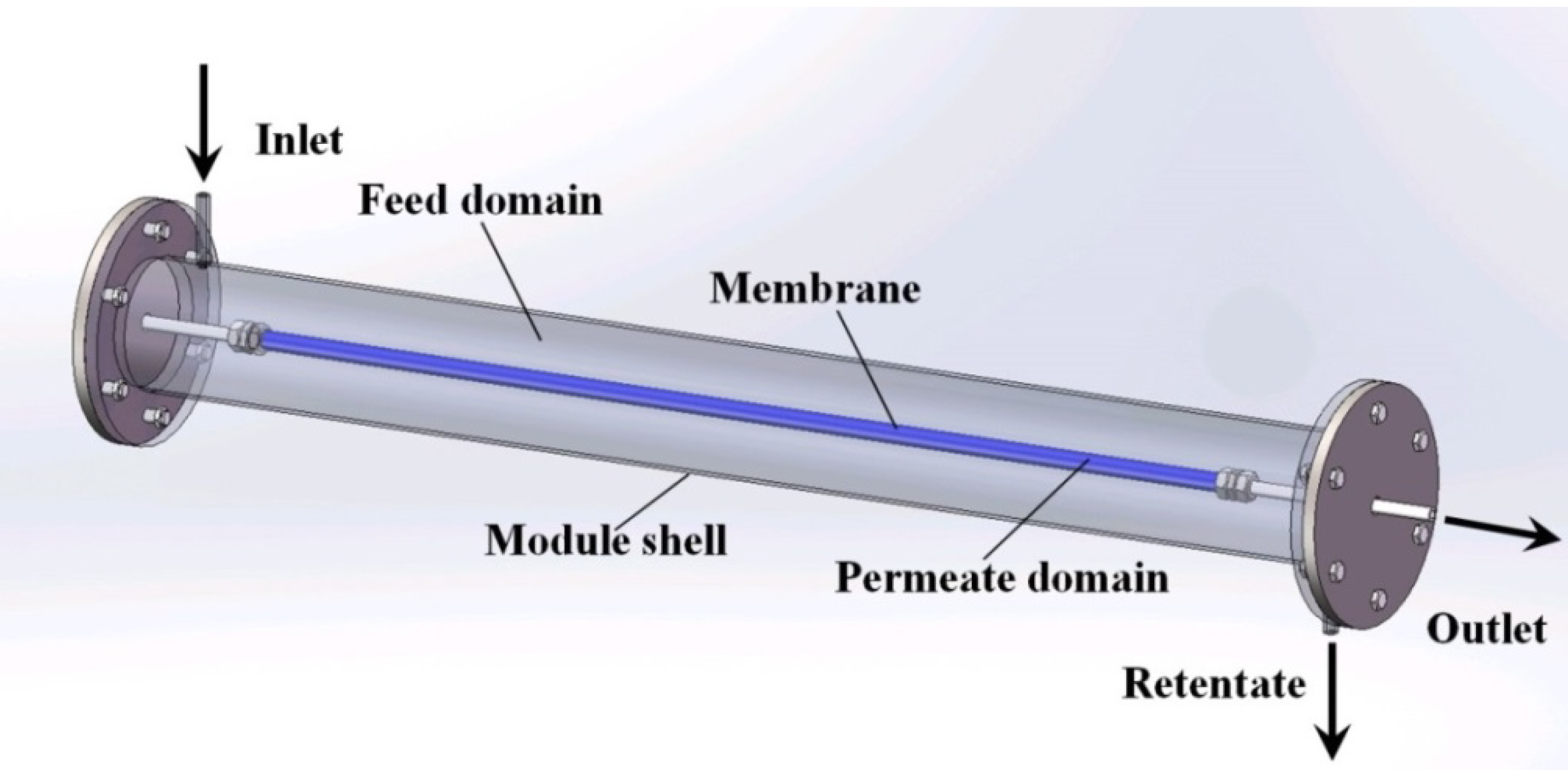
Scale-Up Design Analysis and Modelling of Cobalt Oxide Silica Membrane Module for Hydrogen Processing
Abstract
:1. Introduction
2. The Mathematical Modelling Details
2.1. Mass Transfer in Gas Phase
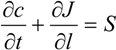
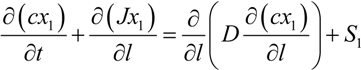
 , and the diffusion term,
, and the diffusion term,  . In liquid or low temperature gas separation in small-scale modules, advection is far more intense than diffusion, so diffusion is always omitted in the component mass balance equation [26,27,28,29,30,31]. This is not the case for industrial gas processes, as the diffusion term cannot be overlooked. In addition, the intrinsic properties of molecular sieve silica membranes show temperature-dependent transport, where high selectivities can be expected at high temperatures [32,33,34]. Consequently, the diffusion coefficient increases [25,35] and diffusion becomes prevalent over advection, in this case.
. In liquid or low temperature gas separation in small-scale modules, advection is far more intense than diffusion, so diffusion is always omitted in the component mass balance equation [26,27,28,29,30,31]. This is not the case for industrial gas processes, as the diffusion term cannot be overlooked. In addition, the intrinsic properties of molecular sieve silica membranes show temperature-dependent transport, where high selectivities can be expected at high temperatures [32,33,34]. Consequently, the diffusion coefficient increases [25,35] and diffusion becomes prevalent over advection, in this case.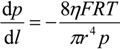
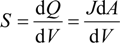
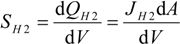
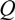 and d
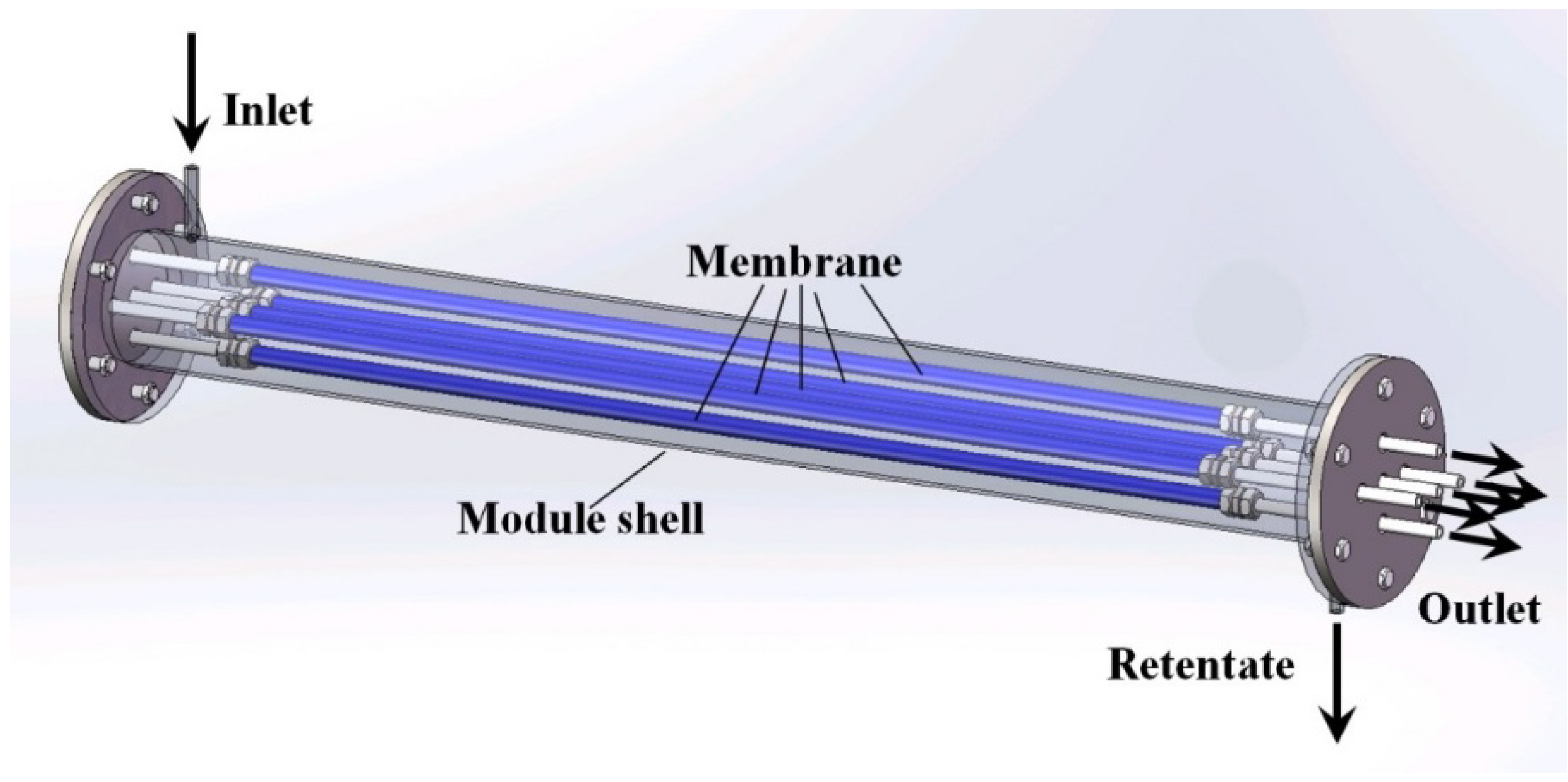
and d  H2 are the total permeate flow rate and the hydrogen permeate flow rate, respectively, JH2 is the hydrogen permeate flux, dA is the permeable area and dV is the computational cell volume. The source terms are zero if the computational cell is not in the permeable region (such as the Swagelok for sealing the membrane and the steel tube). The source terms apply to the permeable region only.
H2 are the total permeate flow rate and the hydrogen permeate flow rate, respectively, JH2 is the hydrogen permeate flux, dA is the permeable area and dV is the computational cell volume. The source terms are zero if the computational cell is not in the permeable region (such as the Swagelok for sealing the membrane and the steel tube). The source terms apply to the permeable region only.2.2. Mass Transfer across Membrane
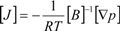
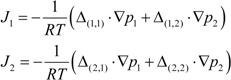
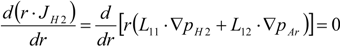
3. Experiment and Model Validation
| Temperature | Feed flow rate (mL min−1) | H2 Feed fraction | Permeate flow rate in experiment (mL min−1) | Permeate flow rate in model (mL min−1) | H2 Permeate fraction in experiment | H2 Permeate fraction in model | Relative error for permeate flow | Relative error for permeate fraction |
|---|---|---|---|---|---|---|---|---|
| 500 °C | 253.9 | 99% | 249.2 | 251.7 | 100% | 99% | 0.01 | 0.01 |
| 49.6 | 82% | 44.2 | 44.7 | 90% | 88% | 0.01 | 0.02 | |
| 35.1 | 76% | 30.7 | 31.3 | 85% | 82% | 0.02 | 0.03 | |
| 13.4 | 18% | 8.9 | 7.9 | 24% | 26% | 0.11 | 0.05 | |
| 400 °C | 142.7 | 98% | 137.7 | 140.8 | 100% | 98% | 0.02 | 0.02 |
| 44.6 | 84% | 39.8 | 40.8 | 91% | 89% | 0.03 | 0.03 | |
| 32.4 | 71% | 27.7 | 25.8 | 79% | 81% | 0.07 | 0.03 | |
| 16.8 | 41% | 12.2 | 10.8 | 51% | 53% | 0.11 | 0.05 |
3.1. Numerical Technique
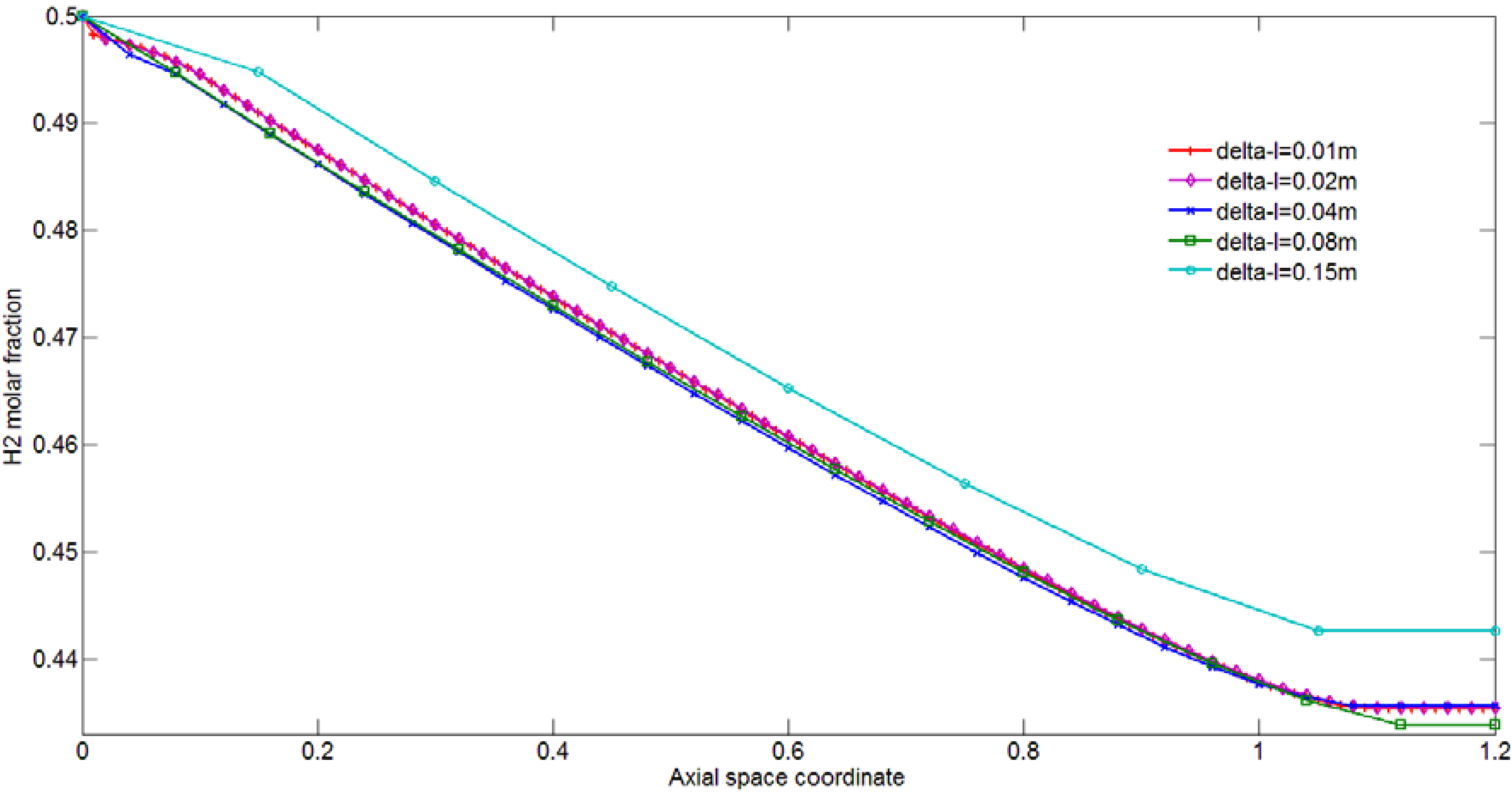
3.2. Process Parameters of Interest
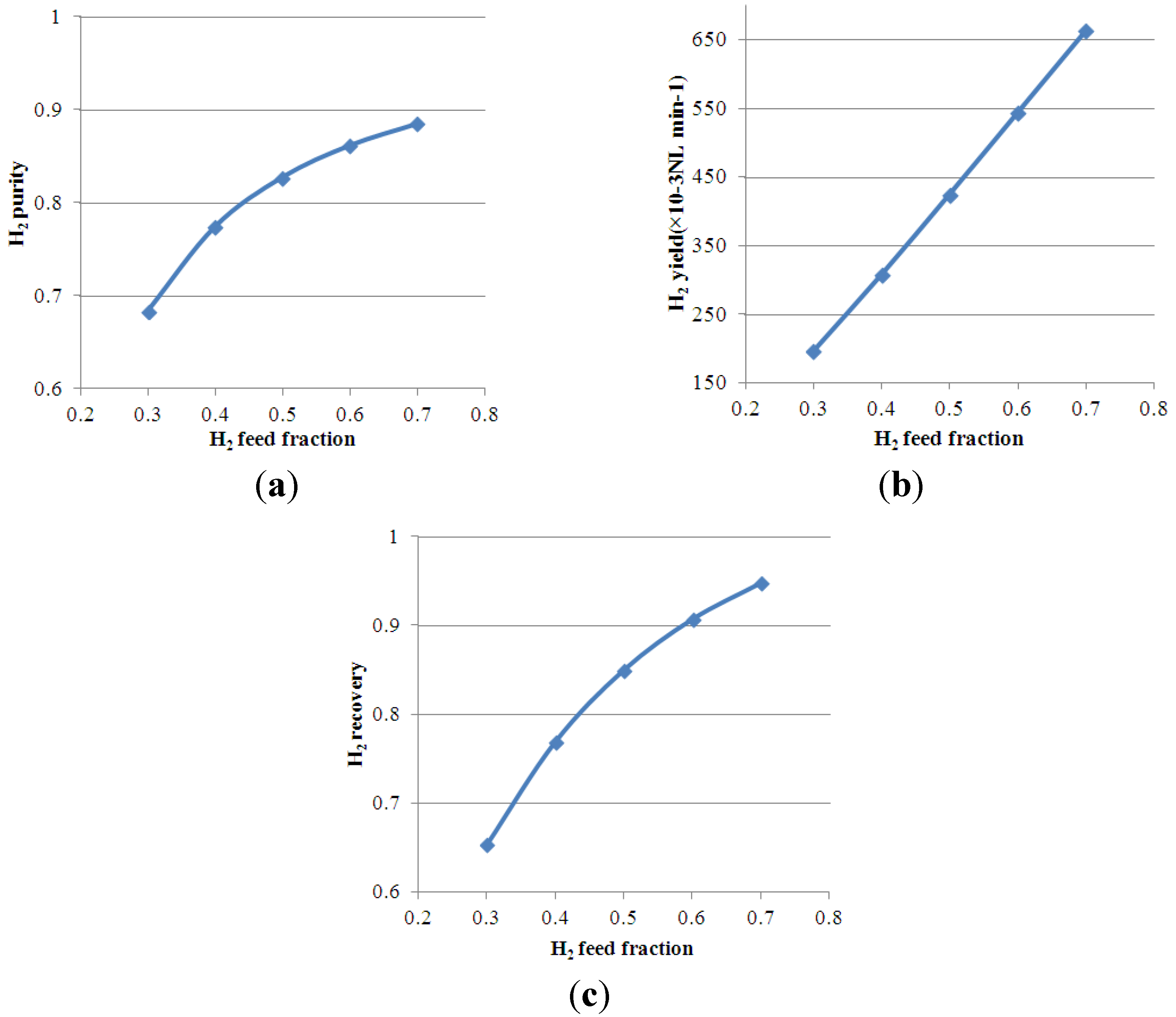
- H2 purity is defined as the H2 permeate molar fraction at the permeate outlet.
- H2 yield is the permeate flow rate at the permeate outlet multiplied by H2 purity.
- H2 recovery is the H2 yield divided by the H2 feed flow rate.
| Operating conditions | Value |
|---|---|
| Temperature | 500 (°C) |
| H2 permeance | 5.80 × 10−8 (mol s−1 m−2 Pa−1) |
| Ar permeance | 5.67 × 10−10 (mol s−1 m−2 Pa−1) |
| Radius of module | 0.05 (m) |
| Membrane radius | 0.007 (m) |
| Retentate pressure | 6 (atm) |
| Permeate pressure | 1 (atm) |
4. Results and Discussion
4.1. Effect of Membrane Length on Process Performance
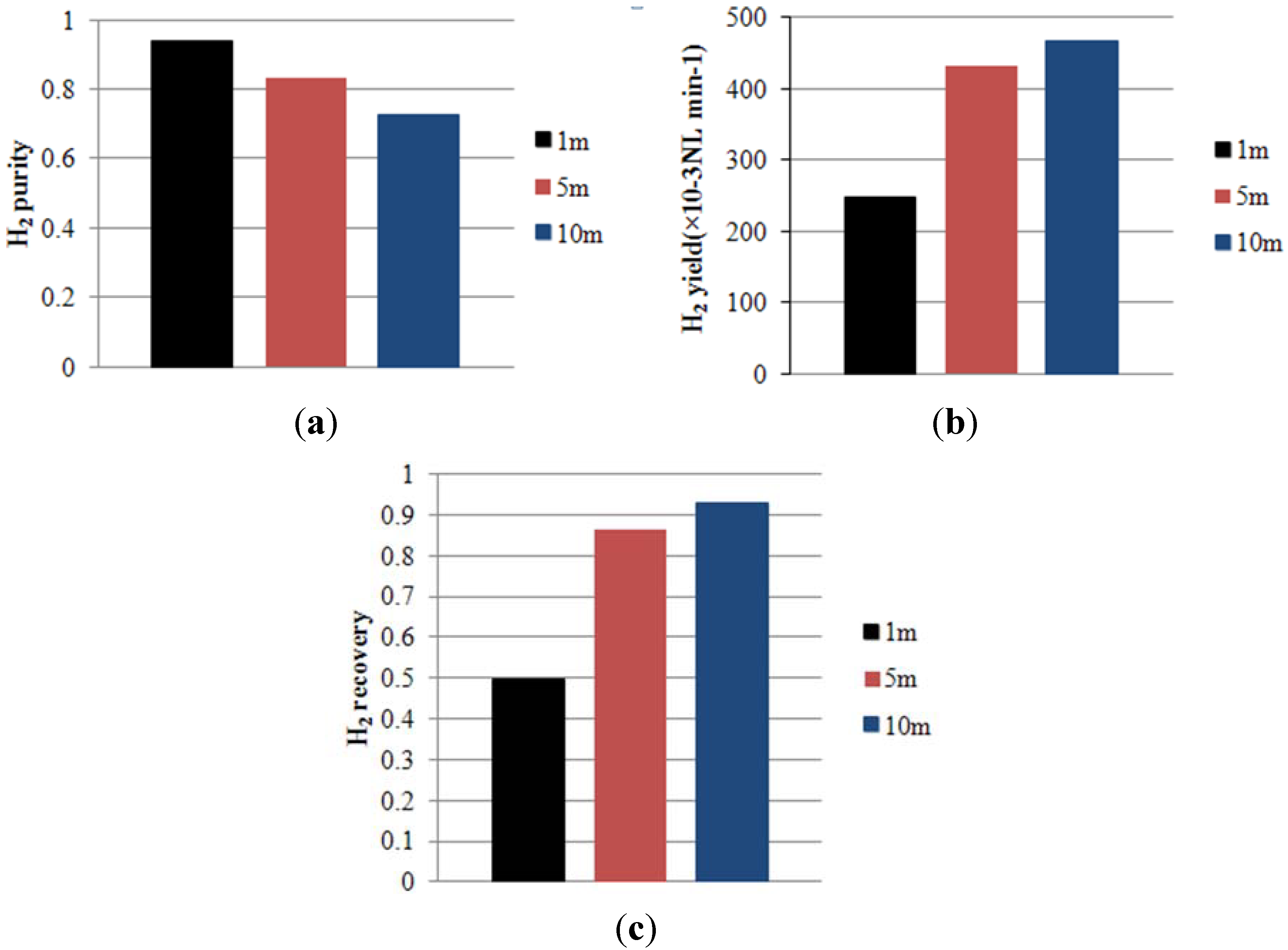
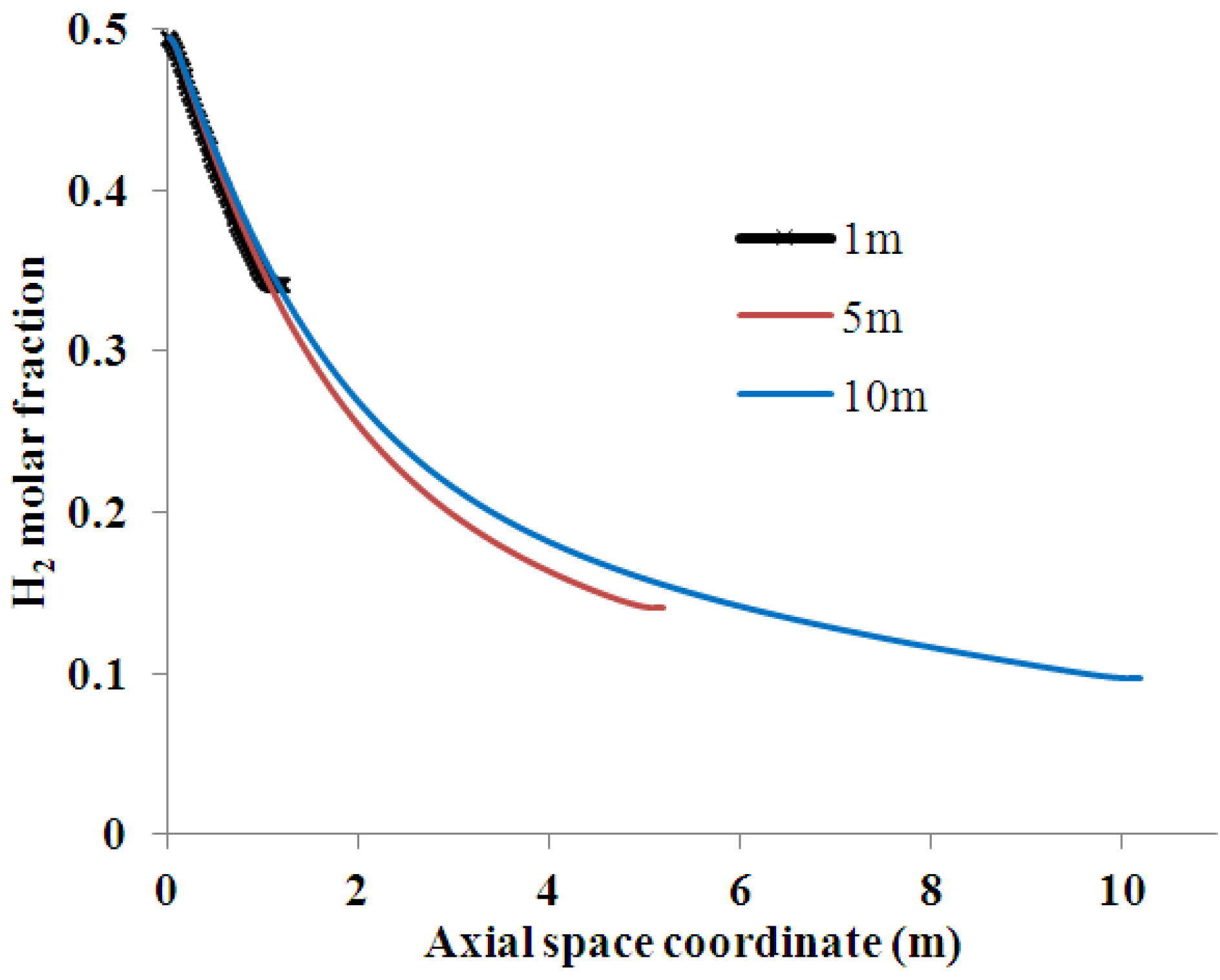
4.2. Effect of Multi-Tube Membranes on Process Performance
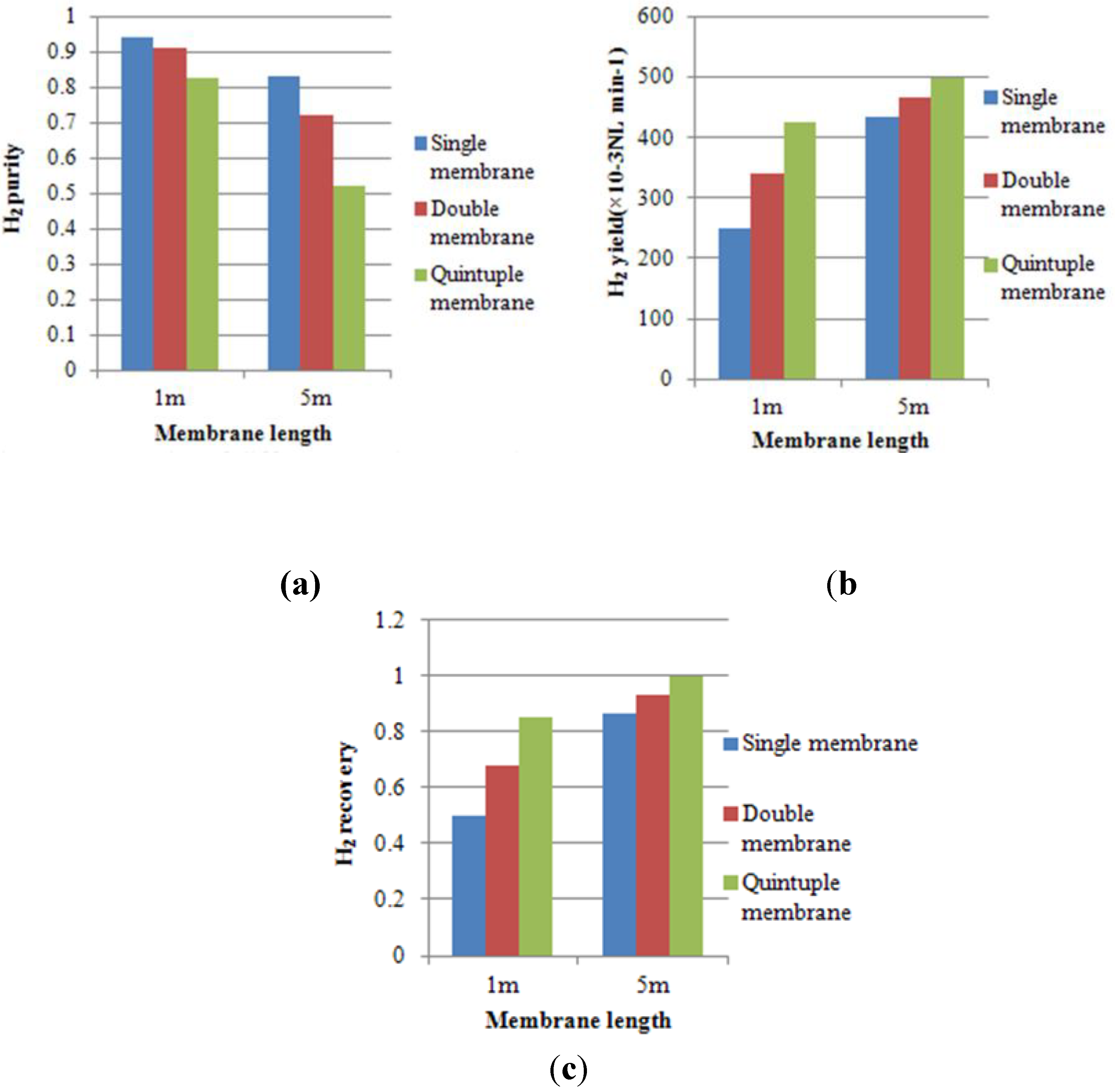

4.3. Effect of Space Velocity on Process Performance

4.4. Effect of H2 Feed Molar Fraction on Process Performance
5. Conclusions
| Nomenclature | |
|---|---|
| c | total molar concentration (mol·m−3) |
| D | Fick diffusivity in gas phase (m2·s−1) |
| Đ | Maxwell-Stefan diffusivity in the membrane (m2·s−1) |
| Đi | Maxwell-Stefan single gas diffusivity in membrane (m2·s−1) |
| Đij | Inter-exchange coefficient between component i and component j (m2·s−1) |
| Đii | self exchange coefficient (m2·s−1) |
| dA | permeable area (m2) |
d 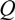 | molar permeate flow rate across membrane (mol·s−1) |
d 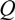 H2 H2 | molar permeate flow rate across membrane of component H2 (mol·s−1) |
| dV | computational volume (m3) |
| F | flow rate (mol·s−1) |
| J | flux (mol s−1·m−2) |
| JH2 | permeate flux across membrane of component H2 (mol s−1·m−2) |
| JAr | permeate flux across membrane of component Ar (mol s−1·m−2) |
| K | Henry’s constant (mol·m−3·Pa−1) |
| l | axial coordinate (m) |
| ∆l | grid size (m) |
| n | the number of grid |
| p | pressure (Pa) |
| q | concentration of adsorbed gas (mol·m−3) |
| R | gas constant (8.314 J·mol−1·K−1) |
| r | radial coordinate |
| S | source term (mol·s−1·m−3) |
| S1 | pressure (Pa) |
| T | temperature (K) |
| t | time |
| x | molar fraction |
| x1 | H2 molar fraction |
| [B] | coefficient matrix in Maxwell-Stefan equation |
| [∆] | inversed matrix of [B] |
| [J] | matrix of flux across membrane |
| [∇p] | matrix of pressure gradient |
| Greek letters | |
|---|---|
| η | viscosity (Pa·s) |
| μ | chemical potential (J·mol−1) |
| μ0 | chemical potential in the chosen standard state (J·mol−1) |
| θ | fractional occupancy of adsorption |
Acknowledgments
Conflict of Interest
References
- Oobatake, M.; Ooi, T. Determination of energy parameters in lennard-jones potentials from second virial coefficients. Progr. Theor. Phys. 1972, 48, 2132–2143. [Google Scholar] [CrossRef]
- Hogarth, W.H.J.; da Costa, J.C.D.; Lu, G.Q. Solid acid membranes for high temperature (>140 Degrees C) proton exchange membrane fuel cells. J. Power Sour. 2005, 142, 223–237. [Google Scholar] [CrossRef]
- Mclellan, B.; Shoko, E.; Dicks, A.L.; da Costa, J.C.D. Hydrogen production and utilisation opportunities for Australia. Int. J. Hydr. Energy 2005, 30, 669–679. [Google Scholar] [CrossRef]
- Park, J.-H.; Kim, J.-N.; Cho, S.-H. Performance analysis of four-bed H2 PSA process using layered beds. AIChE J. 2000, 46, 790–802. [Google Scholar] [CrossRef]
- Yang, S.-I.; Choi, D.-Y.; Jang, S.-C.; Kim, S.-H.; Choi, D.-K. Hydrogen separation by multi-bed pressure swing adsorption of synthesis gas. Adsorption 2008, 14, 583–590. [Google Scholar] [CrossRef]
- Koros, W.J.; Fleming, G.K. Membrane-based gas separation. J. Membr. Sci. 1993, 83, 1–80. [Google Scholar] [CrossRef]
- Li, F.Y.; Xiao, Y.; Ong, Y.K.; Chung, T.S. UV-Rearranged PIM-1 polymeric membranes for advanced hydrogen purification and production. Adv. Energy Mater. 2012, 2, 1456–1466. [Google Scholar] [CrossRef]
- Tomé, L.C.; Mecerreyes, D.; Freire, C.S.R.; Rebelo, L.P.N.; Marrucho, I.M. Pyrrolidinium-based polymeric ionic liquid materials: New perspectives for CO2 separation membranes. J. Membr. Sci. 2013, 428, 260–266. [Google Scholar] [CrossRef]
- Wang, J.; Tsuru, T. Cobalt-doped silica membranes for pervaporation dehydration of ethanol/water solutions. J. Membr. Sci. 2011, 369, 13–19. [Google Scholar] [CrossRef]
- Igi, R.; Yoshioka, T.; Ikuhara, Y.H.; Iwamoto, Y.; Tsuru, T. Characterization of co-doped silica for improved hydrothermal stability and application to hydrogen separation membranes at high temperatures. J. Am. Ceram. Soc. 2008, 91, 2975–2981. [Google Scholar] [CrossRef]
- Smart, S.; Lin, C.X.C.; Ding, L.; Thambimuthu, K.; da Costa, J.C.D. Ceramic membranes for gas processing in coal gasification. Energy Environ. Sci. 2010, 3, 268–278. [Google Scholar] [CrossRef]
- De Vos, R.M.; Verweij, H. Improved performance of silica membranes for gas separation. J. Membr. Sci. 1998, 143, 37–51. [Google Scholar] [CrossRef]
- De Vos, R.M.; Verweij, H. High-selectivity, high-flux silica membranes for gas separation. Science 1998, 279, 1710–1711. [Google Scholar] [CrossRef]
- Da Costa, J.C.D.; Lu, G.Q.; Rudolph, V.; Lin, Y.S. Novel molecular sieve silica (MSS) membranes: Characterisation and permeation of single-step and two-step sol–gel membranes. J. Membr. Sci. 2002, 198, 9–21. [Google Scholar] [CrossRef]
- Miller, C.R.; Wang, D.K.; Smart, S.; da Costa, J.C.D. Reversible redox effect on gas permeation of cobalt doped ethoxy polysiloxane (ES40) membranes. Sci. Rep. 2013, 3, 1–6. [Google Scholar]
- Duke, M.C.; da Costa, J.C.D.; Lu, G.Q.; Petch, M.; Gray, P. Carbonised template molecular sieve silica membranes in fuel processing systems: Permeation, hydrostability and regeneration. J. Membr. Sci. 2004, 241, 325–333. [Google Scholar] [CrossRef]
- Kanezashi, M.; Asaeda, M. Hydrogen permeation characteristics and stability of Ni-doped silica membranes in steam at high temperature. J. Membr. Sci. 2006, 271, 86–93. [Google Scholar] [CrossRef]
- Uhlmann, D.; Liu, S.; Ladewig, B.P.; da Costa, J.C.D. Cobalt-doped silica membranes for gas separation. J. Membr. Sci. 2009, 326, 316–321. [Google Scholar] [CrossRef]
- Yacou, C.; Smart, S.; da Costa, J.C.D. Long term performance cobalt oxide silica membrane module for high temperature H2 separation. Energy Environ. Sci. 2012, 5, 5820–5832. [Google Scholar] [CrossRef]
- Coroneo, M.; Montante, G.; Catalano, J.; Paglianti, A. Modelling the effect of operating conditions on hydrodynamics and mass transfer in a Pd–Ag membrane module for H2 purification. J. Membr. Sci. 2009, 343, 34–41. [Google Scholar] [CrossRef]
- Coroneo, M.; Montante, G.; Paglianti, A. Numerical and experimental fluid-dynamic analysis to improve the mass transfer performances of Pd-Ag membrane modules for hydrogen purification. Ind. Eng. Chem. Res. 2010, 49, 9300–9309. [Google Scholar] [CrossRef]
- Ji, G.; Wang, G.; Hooman, K.; Bhatia, S.; da Costa, J.C.D. Computational fluid dynamics applied to high temperature hydrogen separation membranes. Front. Chem. Sci. Eng. 2012, 6, 3–12. [Google Scholar] [CrossRef]
- Ji, G.; Wang, G.; Hooman, K.; Bhatia, S.; da Costa, J.C.D. Simulation of binary gas separation through multi-tube molecular sieving membranes at high temperatures. Chem. Eng. J. 2013, 218, 394–404. [Google Scholar] [CrossRef]
- Abdel-Jawad, M.M.; Gopalakrishnan, S.; Duke, M.C.; Macrossan, M.N.; Schneider, P.S.; Costa, J.C.D.D. Flowfields on feed and permeate sides of tubular molecular sieving silica (MSS) membranes. J. Membr. Sci. 2007, 299, 229–235. [Google Scholar] [CrossRef]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. A new method for prediction of binary gas phase diffusion coefficients. Ind. Eng. Chem. 1966, 58, 18–27. [Google Scholar]
- Haraya, K.; Obata, K.; Hakuta, T.; Yoshitome, H. Performance of gas separator with high-flux polyimide hollow fiber membrane. Sep. Sci. Technol. 1988, 23, 305–319. [Google Scholar] [CrossRef]
- Feng, X.; Ivory, J.; Rajan, V.S.V. Air separation by integrally asymmetric hollow-fiber membranes. AIChE J. 1999, 45, 2142–2152. [Google Scholar] [CrossRef]
- Murad Chowdhury, M.H.; Feng, X.; Douglas, P.; Croiset, E. A new numerical approach for a detailed multicomponent gas separation membrane model and AspenPlus simulation. Chem. Eng. Technol. 2005, 28, 773–782. [Google Scholar] [CrossRef]
- Pan, C.Y. Gas separation by high-flux, asymmetric hollow-fiber membrane. AIChE J. 1986, 32, 2020–2027. [Google Scholar] [CrossRef]
- Kaldis, S.P.; Kapantaidakis, G.C.; Papadopoulos, T.I.; Sakellaropoulos, G.P. Simulation of binary gas separation in hollow fiber asymmetric membranes by orthogonal collocation. J. Membr. Sci. 1998, 142, 43–59. [Google Scholar] [CrossRef]
- Kaldis, S.P.; Kapantaidakis, G.C.; Sakellaropoulos, G.P. Simulation of multicomponent gas separation in a hollow fiber membrane by orthogonal collocation—Hydrogen recovery from refinery gases. J. Membr. Sci. 2000, 173, 61–71. [Google Scholar] [CrossRef]
- Battersby, S.; Duke, M.C.; Liu, S.; Rudolph, V.; Costa, J.C.D.D. Metal doped silica membrane reactor: Operational effects of reaction and permeation for the water gas shift reaction. J. Membr. Sci. 2008, 316, 46–52. [Google Scholar] [CrossRef]
- Gopalakrishnan, S.; da Costa, J.C.D. Hydrogen gas mixture separation by CVD silica membrane. J. Membr. Sci. 2008, 323, 144–147. [Google Scholar] [CrossRef]
- Battersby, S.; Tasaki, T.; Smart, S.; Ladewig, B.; Liu, S.; Duke, M.C.; Rudolph, V.; da Costa, J.C.D. Performance of cobalt silica membranes in gas mixture separation. J. Membr. Sci. 2009, 329, 91–98. [Google Scholar] [CrossRef]
- Fuller, E.N.; Ensley, K.; Giddings, J.C. Diffusion of halogenated hydrocarbons in helium. The effect of structure on collision cross sections. J. Phys. Chem. 1969, 73, 3679–3685. [Google Scholar] [CrossRef]
- Berman, A.S. Laminar flow in channels with porous walls. J. Appl. Phys. 1953, 24, 1232–1235. [Google Scholar] [CrossRef]
- Coroneo, M.; Montante, G.; Baschetti, M.G.; Paglianti, A. CFD modelling of inorganic membranemodules for gas mixture separation. Chem. Eng. Sci. 2009, 64, 1085–1094. [Google Scholar] [CrossRef]
- Marriott, J.I.; Sørensen, E.; Bogle, I.D.L. Detailed mathematical modelling of membrane modules. Comput. Chem. Eng. 2001, 25, 693–700. [Google Scholar] [CrossRef]
- Kapteijn, F.; Bakker, W.J.W.; Zheng, G.; Moulijn, J.A. Temperature- and occupancy-dependent diffusion of n-butane through a silicalite-1 membrane. Microporous Mater. 1994, 3, 227–234. [Google Scholar] [CrossRef]
- Bettens, B.; Degrève, J.; van der Bruggen, B.; Vandecasteele, C. Transport of binary mixtures in pervaporation through a microporous silica membrane: Shortcomings of Fickian models. Sep. Sci. Technol. 2007, 42, 1–23. [Google Scholar] [CrossRef]
- Krishna, R.; Baur, R. Modelling issues in zeolite based separation processes. Sep. Purif. Technol. 2003, 33, 213–254. [Google Scholar] [CrossRef]
- Wesselingh, J.A.; Krishna, R. Mass Transfer in Multicomponent Mixtures; Delft University Press: Delft, The Netherlands, 2000. [Google Scholar]
- Krishna, R.; Baur, R. Analytic solution of the Maxwell-Stefan equations for multicomponent permeation across a zeolite membrane. Chem. Eng. J. 2004, 97, 37–45. [Google Scholar] [CrossRef]
- Krishna, R.; van Baten, J.M. Insights into diffusion of gases in zeolites gained from molecular dynamics simulations. Microporous Mesoporous Mater. 2008, 109, 91–108. [Google Scholar] [CrossRef]
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Ji, G.; Wang, G.; Hooman, K.; Bhatia, S.K.; Da Costa, J.C.D. Scale-Up Design Analysis and Modelling of Cobalt Oxide Silica Membrane Module for Hydrogen Processing. Processes 2013, 1, 49-66. https://doi.org/10.3390/pr1020049
Ji G, Wang G, Hooman K, Bhatia SK, Da Costa JCD. Scale-Up Design Analysis and Modelling of Cobalt Oxide Silica Membrane Module for Hydrogen Processing. Processes. 2013; 1(2):49-66. https://doi.org/10.3390/pr1020049
Chicago/Turabian StyleJi, Guozhao, Guoxiong Wang, Kamel Hooman, Suresh K. Bhatia, and João C. Diniz Da Costa. 2013. "Scale-Up Design Analysis and Modelling of Cobalt Oxide Silica Membrane Module for Hydrogen Processing" Processes 1, no. 2: 49-66. https://doi.org/10.3390/pr1020049