Parallel Solution of Robust Nonlinear Model Predictive Control Problems in Batch Crystallization
Abstract
:1. Introduction
2. Problem Formulations
2.1. NMPC Formulation
2.2. MHE Formulation
2.3. Robust NMPC Formulation
2.4. Efficient Optimization via the Simultaneous Approach
3. Efficient Parallel Schur Complement Method for Stochastic Programs
4. Performance of Robust NMPC on Batch Crystalization
4.1. Case Study: Multidimensional Unseeded Batch Crystallization Model
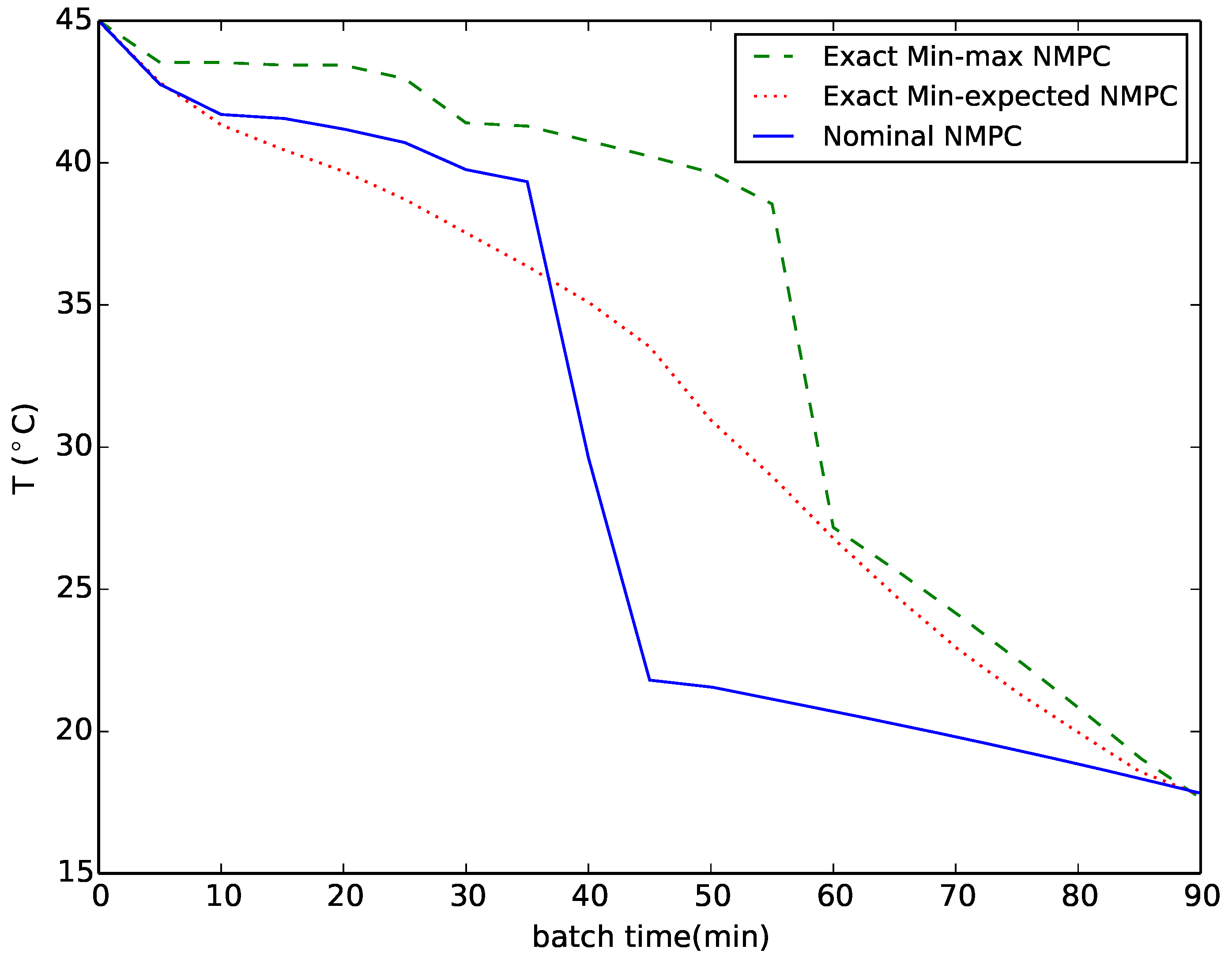
4.2. Numerical Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jiang, Z.P.; Wang, Y. Input-To-State stability for discrete-time nonlinear systems. Automatica 2001, 37, 857–869. [Google Scholar] [CrossRef]
- Magni, L.; Scattolini, R. Robustness and robust design of MPC for nonlinear discrete-time systems. In Assessment and Future Directions of Nonlinear Model Predictive Control; Springer: Berlin Heidelberg, Germmany, 2007; pp. 239–254. [Google Scholar]
- Scokaert, P.; Mayne, D. Min-Max feedback model predictive control for constrained linear systems. IEEE Trans. Autom. Control 1998, 43, 1136–1142. [Google Scholar] [CrossRef]
- Huang, R.; Patwardhan, S.C.; Biegler, L.T. Multi-Scenario-Based robust nonlinear model predictive control with first principle models. Comput. Aided Chem. Eng. 2009, 27, 1293–1298. [Google Scholar]
- Nagy, Z.K.; Braatz, R.D. Robust nonlinear model predictive control of batch processes. AIChE J. 2003, 49, 1776–1786. [Google Scholar] [CrossRef]
- Magni, L.; De Nicolao, G.; Scattolini, R.; Allgöwer, F. Robust model predictive control for nonlinear discrete-time systems. Int. J. Robust Nonlinear Control 2003, 13, 229–246. [Google Scholar] [CrossRef]
- Lucia, S.; Finkler, T.; Engell, S. Multi-Stage nonlinear model predictive control applied to a semi-batch polymerization reactor under uncertainty. J. Process Control 2013, 23, 1306–1319. [Google Scholar] [CrossRef]
- Telen, D.; Houska, B.; Logist, F.; Van Derlinden, E.; Diehl, M.; Van Impe, J. Optimal experiment design under process noise using Riccati differential equations. J. Process Control 2013, 23, 613–629. [Google Scholar] [CrossRef] [Green Version]
- Streif, S.; Kögel, M.; Bäthge, T.; Findeisen, R. Robust Nonlinear Model Predictive Control with Constraint Satisfaction: A relaxation-based Approach. In Proceedings of the 19th IFAC World Congress, Cape Town, South Africa, 24–29 August 2014; pp. 11073–11079.
- Zavala, V.M.; Laird, C.D.; Biegler, L.T. Interior-Point decomposition approaches for parallel solution of large-scale nonlinear parameter estimation problems. Chem. Eng. Sci. 2008, 63, 4834–4845. [Google Scholar] [CrossRef]
- Kang, J.; Cao, Y.; Word, D.P.; Laird, C. An interior-point method for efficient solution of block-structured NLP problems using an implicit Schur-complement decomposition. Comput. Chem. Eng. 2014, 71, 563–573. [Google Scholar] [CrossRef]
- Lubin, M.; Petra, C.; Anitescu, M. The parallel solution of dense saddle-point linear systems arising in stochastic programming. Optim. Methods Softw. 2012, 27, 845–864. [Google Scholar] [CrossRef]
- Cao, Y.; Laird, C.; Zavala, V. Clustering-Based Preconditioning for Stochastic Programs. Comput. Optim. Appl. 2015, 64, 379–406. [Google Scholar] [CrossRef]
- Gay, D.M.; Kernighan, B. AMPL: A Modeling Language for Mathematical Programming, 2nd ed.; Cengage Learning: Boston, MA, USA, 2002; Volume 2. [Google Scholar]
- Watson, J.P.; Woodruff, D.L.; Hart, W.E. PySP: Modeling and solving stochastic programs in Python. Math. Program. Comput. 2012, 4, 109–149. [Google Scholar] [CrossRef]
- Huchette, J.; Lubin, M.; Petra, C. Parallel algebraic modeling for stochastic optimization. In Proceedings of the 1st First Workshop for High Performance Technical Computing in Dynamic Languages, New Orleans, Louisiana, 16–21 November 2014; pp. 29–35.
- Shapiro, A.; Dentcheva, D.; Ruszczynski, A. Lectures on Stochastic Programming: Modeling and Theory; SIAM-Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 2014; Volume 16. [Google Scholar]
- Cuthrell, J.E.; Biegler, L.T. On the optimization of differential-algebraic process systems. AIChE J. 1987, 33, 1257–1270. [Google Scholar] [CrossRef]
- Forsgren, A.; Gill, P.E.; Wright, M.H. Interior methods for nonlinear optimization. SIAM Rev. 2002, 44, 525–597. [Google Scholar] [CrossRef]
- Mesbah, A.; Nagy, Z.; Huesman, A.; Kramer, H.; Van den Hof, P. Real-time control of industrial batch crystallization processes using a population balance modeling framework. IEEE Trans. Control Syst. Technol. 2012, 20, 1188–1201. [Google Scholar] [CrossRef]
- Acevedo, D.; Nagy, Z.K. Systematic classification of unseeded batch crystallization systems for achievable shape and size analysis. J. Cryst. Growth 2014, 394, 97–105. [Google Scholar] [CrossRef]
- Cao, Y.; Acevedo, D.; Nagy, Z.K.; Laird, C.D.; School of Chemical Engineering, Purdue University, West Lafayette, IN, USA. Unpublished work. 2015.
- Gunawan, R.; Ma, D.L.; Fujiwara, M.; Braatz, R.D. Identification of kinetic parameters in multidimensional crystallization processes. Int. J. Modern Phys. B 2002, 16, 367–374. [Google Scholar] [CrossRef]
- Majumder, A.; Nagy, Z.K. Prediction and control of crystal shape distribution in the presence of crystal growth modifiers. Chem. Eng. Sci. 2013, 101, 593–602. [Google Scholar] [CrossRef]
| Control Strategies | Nominal | Average | Standard Deviation | Worst-Case |
|---|---|---|---|---|
| Ideal | 30 | 66 | 499 | |
| Open-loop | 167 | 223 | 1339 | |
| Nominal NMPC | 0.2 | 93 | 159 | 955 |
| Exact Min–max NMPC | 32 | 78 | 113 | 677 |
| Exact Min–expected NMPC | 12 | 99 | 169 | 1076 |
| Type | S | Nominal | Average | Standard Deviation | Worst-Case |
|---|---|---|---|---|---|
| Min–max | 25 | 15 | 99 | 170 | 1062 |
| 50 | 13 | 102 | 178 | 1129 | |
| 75 | 13 | 95 | 156 | 946 | |
| 100 | 25 | 80 | 120 | 767 | |
| Min–expected | 25 | 21 | 89 | 138 | 902 |
| 50 | 11 | 100 | 172 | 1085 | |
| 75 | 12 | 99 | 169 | 1064 | |
| 100 | 12 | 99 | 169 | 1074 |
| # Processors | Full Factorization | Schur Complement Method | ||
|---|---|---|---|---|
| Time(s) | Time(s) | Speedup | ||
| Building Model | 1 | 44.3 | 64.2 | - |
| 2 | - | 34.8 | 1.8 | |
| 5 | - | 14.9 | 4.3 | |
| 10 | - | 8.6 | 7.5 | |
| 20 | - | 6.3 | 10.2 | |
| 25 | - | 4.7 | 13.7 | |
| Solving NLP | 1 | 406 | 426.9 | - |
| 2 | - | 216.3 | 2.0 | |
| 5 | - | 90.8 | 4.7 | |
| 10 | - | 51.0 | 8.4 | |
| 20 | - | 35.8 | 11.9 | |
| 25 | - | 30.0 | 14.2 | |
| Type | S | Nominal | Average | Standard Deviation | Worst-Case |
|---|---|---|---|---|---|
| Min–max | 12 | 18 | 74 | 120 | 744 |
| 25 | 13 | 61 | 96 | 584 | |
| 50 | 11 | 71 | 114 | 655 | |
| Min–expected | 12 | 17 | 81 | 141 | 943 |
| 25 | 12 | 84 | 145 | 949 | |
| 50 | 11 | 84 | 145 | 934 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, Y.; Kang, J.; Nagy, Z.K.; Laird, C.D. Parallel Solution of Robust Nonlinear Model Predictive Control Problems in Batch Crystallization. Processes 2016, 4, 20. https://doi.org/10.3390/pr4030020
Cao Y, Kang J, Nagy ZK, Laird CD. Parallel Solution of Robust Nonlinear Model Predictive Control Problems in Batch Crystallization. Processes. 2016; 4(3):20. https://doi.org/10.3390/pr4030020
Chicago/Turabian StyleCao, Yankai, Jia Kang, Zoltan K. Nagy, and Carl D. Laird. 2016. "Parallel Solution of Robust Nonlinear Model Predictive Control Problems in Batch Crystallization" Processes 4, no. 3: 20. https://doi.org/10.3390/pr4030020