A Modifier-Adaptation Strategy towards Offset-Free Economic MPC
Abstract
:1. Introduction
2. Related Techniques and a Motivating Example
2.1. Plant, Model and Constraints
2.2. Offset-Free Tracking MPC
2.3. Economic MPC
2.4. A Motivating Example
2.4.1. Process and Optimal Economic Performance
2.4.2. Model and Controllers
- EMPC0 is the standard economic MPC and uses no disturbance model, i.e., and .
- EMPC1 uses a state disturbance model, i.e., and .
- EMPC2 uses a nonlinear disturbance model [29], in which the disturbances act as a correction to the kinetic constants, i.e., is obtained by integration of the following ODE system:and .
2.4.3. Implementation Details
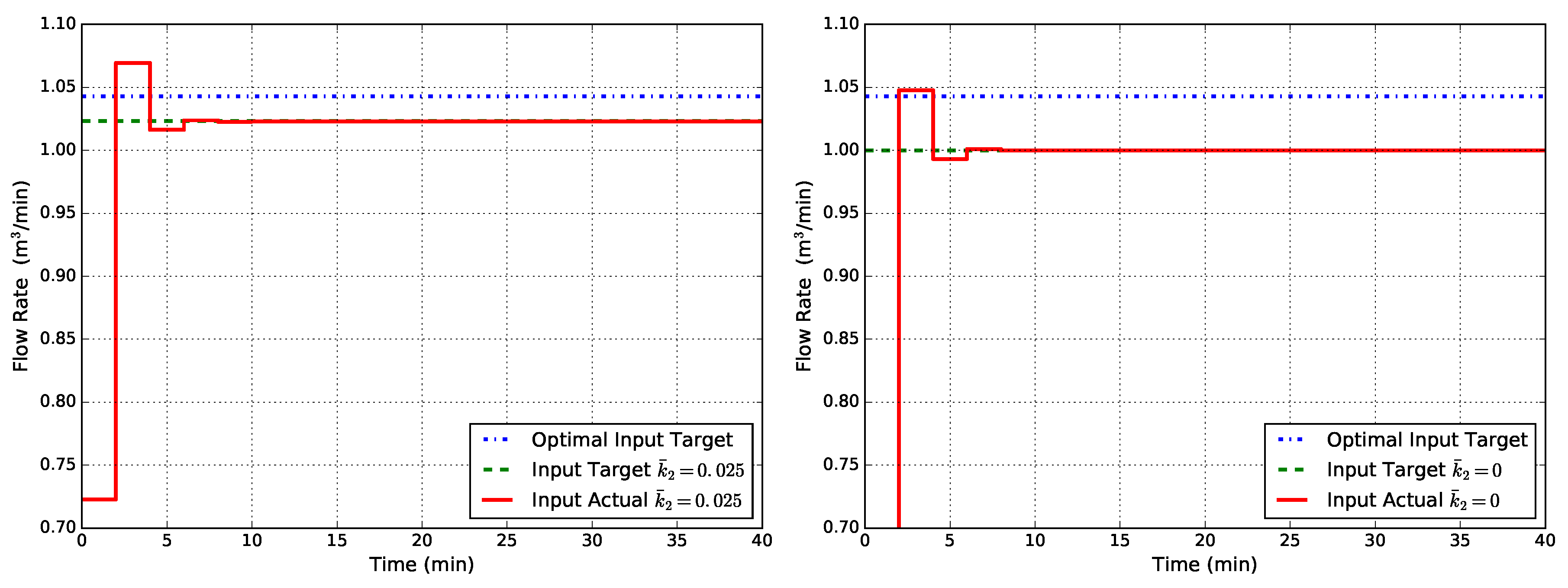
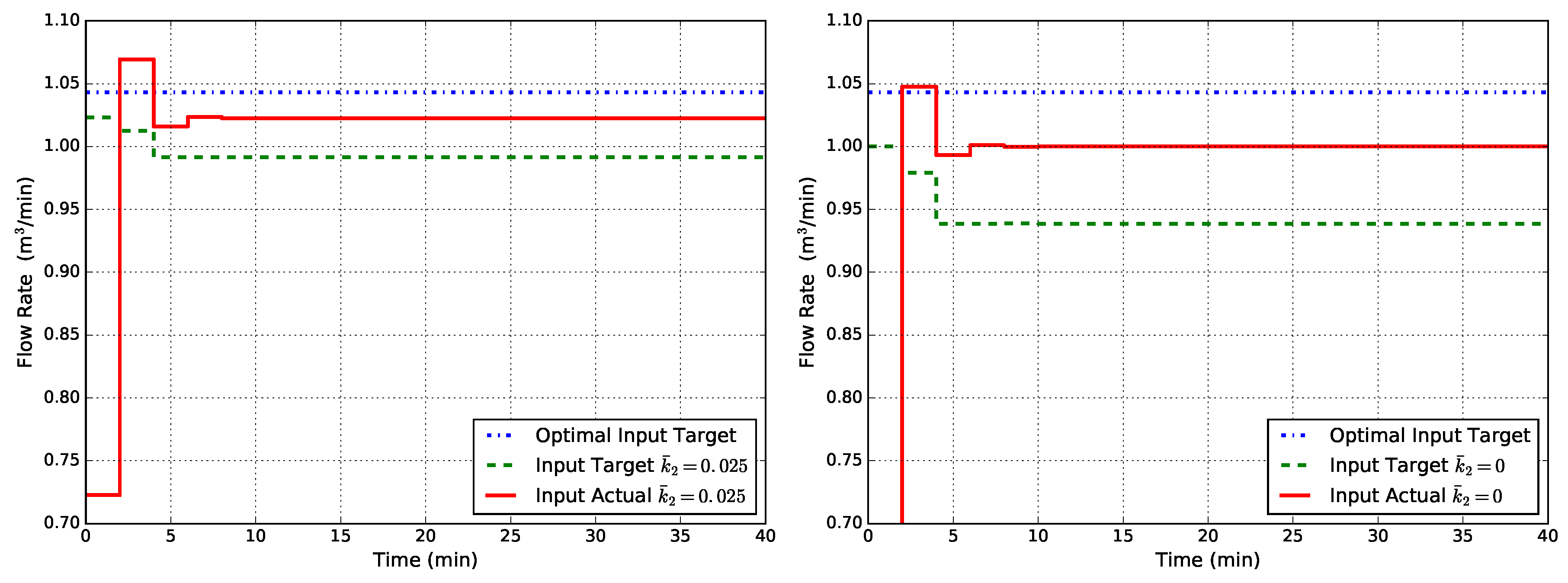
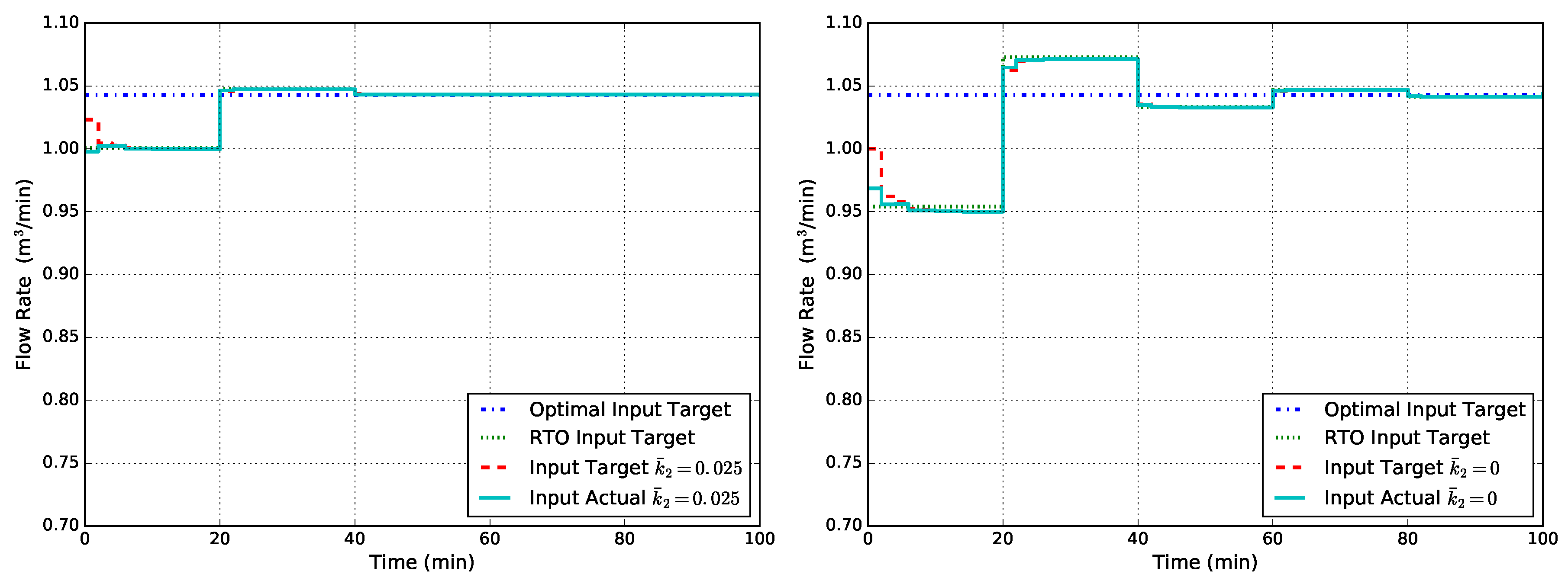
2.4.4. Results
3. Proposed Method
3.1. RTO with Modifier-Adaptation
3.2. Proposed Technique
3.3. Summary
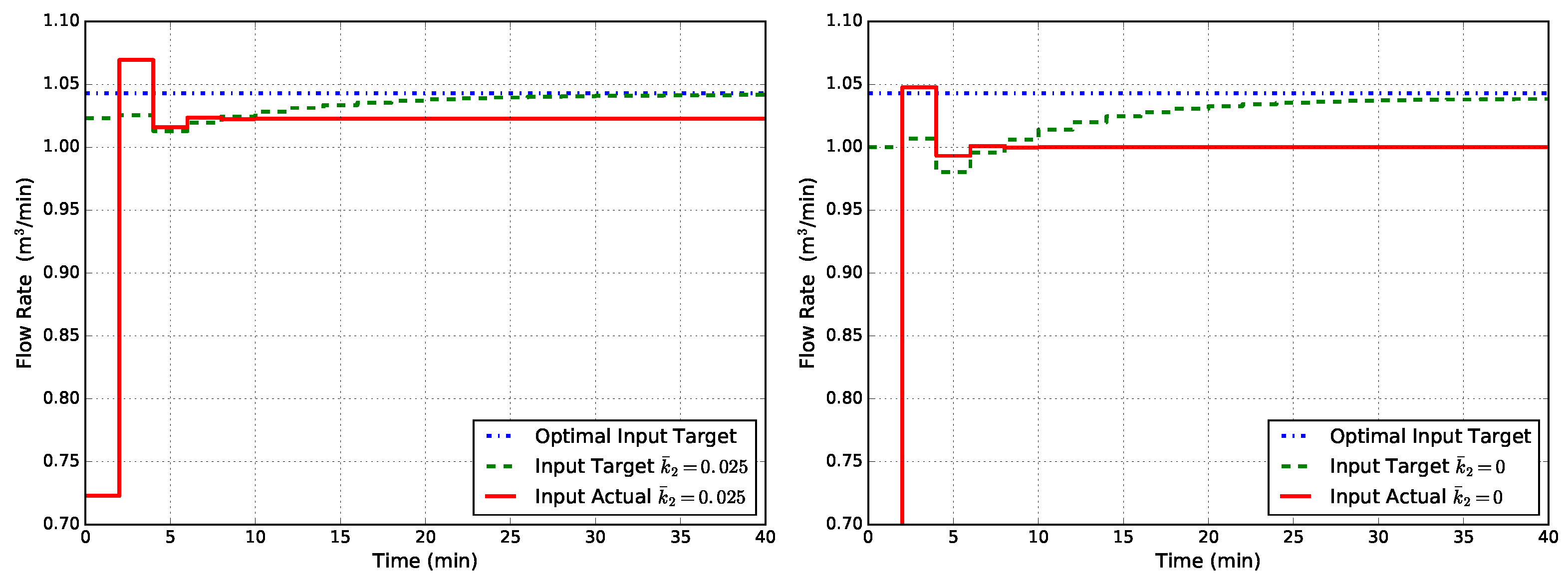
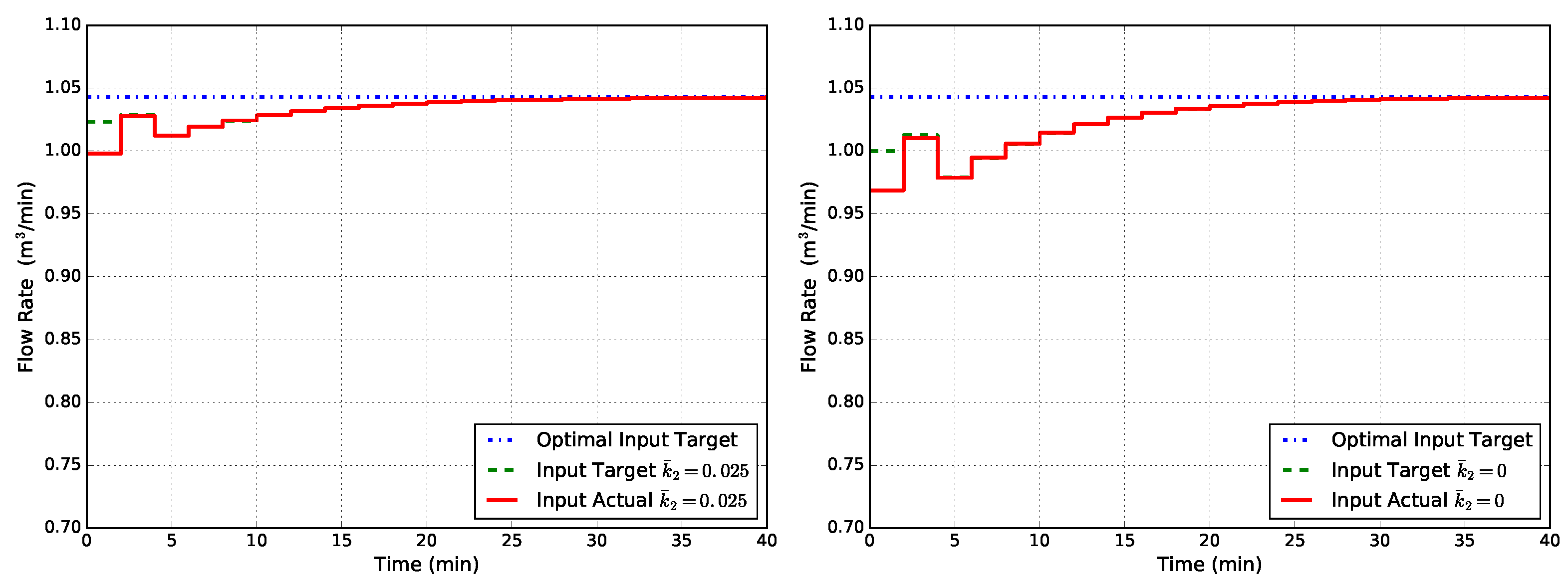
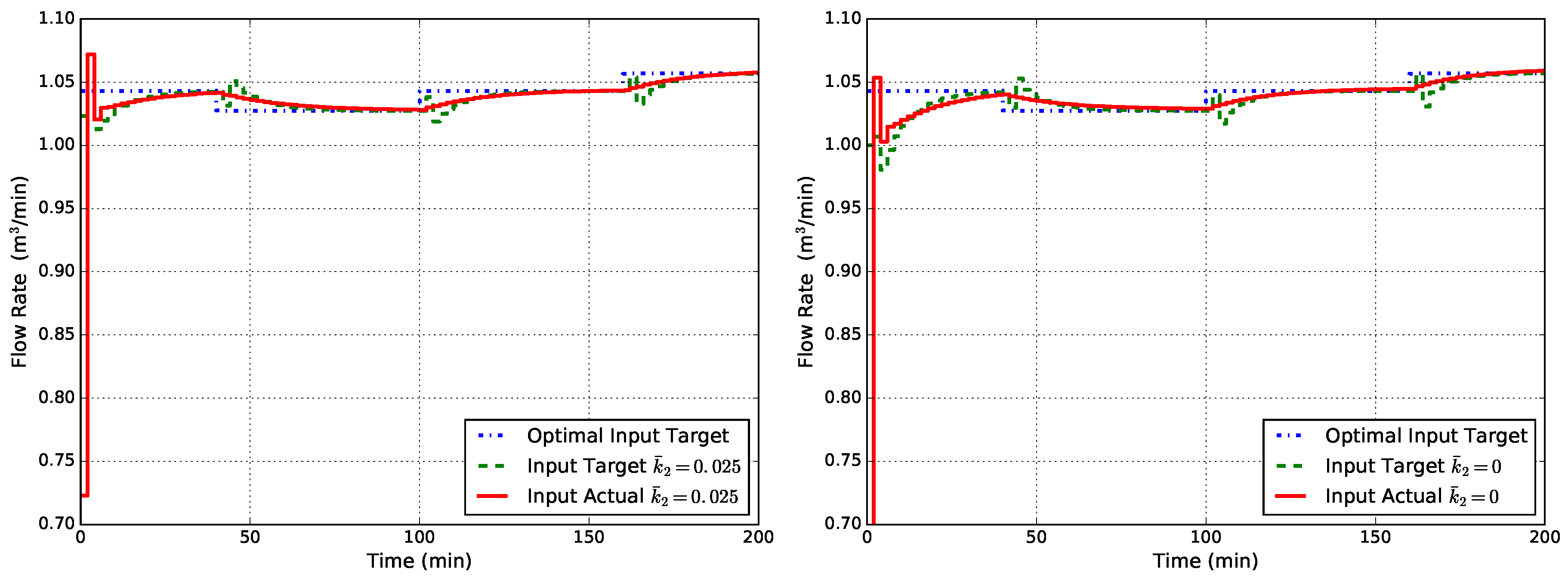
4. Results and Discussion
Further Comments
- EMPC2 (non-linear disturbance model). However, this is sort of an unfair choice. The disturbance has been positioned exactly where the uncertainties are, and this is cannot be considered as a general technique.
- MPC1-MT (economic modified target with tracking stage cost). This is the best general achievement at the moment and allows one to obtain offset-free economic performance for arbitrary plant-model mismatch.
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Engell, S. Feedback control for optimal process operation. J. Process Control 2007, 17, 203–219. [Google Scholar] [CrossRef]
- Guay, M.; Zhang, T. Adaptive extremum seeking control of nonlinear dynamic systems with parametric uncertainties. Automatica 2003, 39, 1283–1293. [Google Scholar] [CrossRef]
- Guay, M.; Peters, N. Real-time dynamic optimization of nonlinear systems: A flatness-based approach. Comput. Chem. Eng. 2006, 30, 709–721. [Google Scholar] [CrossRef]
- Muske, K.R.; Badgwell, T.A. Disturbance modeling for offset-free linear model predictive control. J. Process Control 2002, 12, 617–632. [Google Scholar] [CrossRef]
- Pannocchia, G.; Rawlings, J.B. Disturbance models for offset-free model-predictive control. AIChE J. 2003, 49, 426–437. [Google Scholar] [CrossRef]
- Pannocchia, G. Offset-free tracking MPC: A tutorial review and comparison of different formulations. In Proceedings of the 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 527–532.
- Marlin, T.E.; Hrymak, A.N. Real-time operations optimization of continuous processes. AIChE Sympos. Ser. 1997, 93, 156–164. [Google Scholar]
- Chen, C.Y.; Joseph, B. On-line optimization using a two-phase approach: An application study. Ind. Eng. Chem. Res. 1987, 26, 1924–1930. [Google Scholar] [CrossRef]
- Garcia, C.E.; Morari, M. Optimal operation of integrated processing systems: Part II: Closed-loop on-line optimizing control. AIChE J. 1984, 30, 226–234. [Google Scholar] [CrossRef]
- Skogestad, S. Self-optimizing control: The missing link between steady-state optimization and control. Comput. Chem. Eng. 2000, 24, 569–575. [Google Scholar] [CrossRef]
- François, G.; Srinivasan, B.; Bonvin, D. Use of measurements for enforcing the necessary conditions of optimality in the presence of constraints and uncertainty. J. Process Control 2005, 15, 701–712. [Google Scholar] [CrossRef]
- Forbes, J.F.; Marlin, T.E. Model accuracy for economic optimizing controllers: The bias update case. Ind. Eng. Chem. Res. 1994, 33, 1919–1929. [Google Scholar] [CrossRef]
- Chachuat, B.; Marchetti, A.G.; Bonvin, D. Process optimization via constraints adaptation. J. Process Control 2008, 18, 244–257. [Google Scholar] [CrossRef]
- Chachuat, B.; Srinivasan, B.; Bonvin, D. Adaptation strategies for real-time optimization. Comput. Chem. Eng. 2009, 33, 1557–1567. [Google Scholar] [CrossRef]
- Marchetti, A.G.; Chachuat, B.; Bonvin, D. Modifier-adaptation methodology for real-time optimization. Ind. Eng. Chem. Res. 2009, 48, 6022–6033. [Google Scholar] [CrossRef]
- Alvarez, L.A.; Odloak, D. Robust integration of real time optimization with linear model predictive control. Comput. Chem. Eng. 2010, 34, 1937–1944. [Google Scholar] [CrossRef]
- Alvarez, L.A.; Odloak, D. Optimization and control of a continuous polymerization reactor. Braz. J. Chem. Eng. 2012, 29, 807–820. [Google Scholar] [CrossRef] [Green Version]
- Marchetti, A.G.; Luppi, P.; Basualdo, M. Real-time optimization via modifier adaptation integrated with model predictive control. IFAC Proc. Vol. 2011, 44, 9856–9861. [Google Scholar] [CrossRef]
- Marchetti, A.G.; Ferramosca, A.; González, A.H. Steady-state target optimization designs for integrating real-time optimization and model predictive control. J. Process Control 2014, 24, 129–145. [Google Scholar] [CrossRef]
- Kadam, J.V.; Schlegel, M.; Marquardt, W.; Tousain, R.L.; van Hessem, D.H.; van Den Berg, J.H.; Bosgra, O.H. A two-level strategy of integrated dynamic optimization and control of industrial processes—A case study. Comput. Aided Chem. Eng. 2002, 10, 511–516. [Google Scholar]
- Kadam, J.; Marquardt, W.; Schlegel, M.; Backx, T.; Bosgra, O.; Brouwer, P.; Dünnebier, G.; Van Hessem, D.; Tiagounov, A.; De Wolf, S. Towards integrated dynamic real-time optimization and control of industrial processes. In Proceedings of the Foundations of Computer-Aided Process Operations (FOCAPO2003), Coral Springs, FL, USA, 12–15 January 2003; pp. 593–596.
- Kadam, J.V.; Marquardt, W. Integration of economical optimization and control for intentionally transient process operation. In Assessment and Future Directions of Nonlinear Model Predictive Control; Springer: Berlin/Heidelberg, Germany, 2007; pp. 419–434. [Google Scholar]
- Biegler, L.T. Technology advances for dynamic real-time optimization. Comput. Aided Chem. Eng. 2009, 27, 1–6. [Google Scholar]
- Gopalakrishnan, A.; Biegler, L.T. Economic nonlinear model predictive control for periodic optimal operation of gas pipeline networks. Comput. Chem. Eng. 2013, 52, 90–99. [Google Scholar] [CrossRef]
- Maeder, U.; Borrelli, F.; Morari, M. Linear offset-free model predictive control. Automatica 2009, 45, 2214–2222. [Google Scholar] [CrossRef]
- Morari, M.; Maeder, U. Nonlinear offset-free model predictive control. Automatica 2012, 48, 2059–2067. [Google Scholar] [CrossRef]
- Rawlings, J.B.; Mayne, D.Q. Model Predictive Control: Theory and Design; Nob Hill Pub.: San Francisco, CA, USA, 2009. [Google Scholar]
- Pannocchia, G.; Gabiccini, M.; Artoni, A. Offset-free MPC explained: Novelties, subtleties, and applications. IFAC-PapersOnLine 2015, 48, 342–351. [Google Scholar] [CrossRef]
- Würth, L.; Hannemann, R.; Marquardt, W. A two-layer architecture for economically optimal process control and operation. J. Process Control 2011, 21, 311–321. [Google Scholar] [CrossRef]
- Zhu, X.; Hong, W.; Wang, S. Implementation of advanced control for a heat-integrated distillation column system. In Proceedings of the 30th Annual Conference of IEEE Industrial Electronics Society (IECON), Busan, Korea, 2–6 November 2004; Volume 3, pp. 2006–2011.
- Rawlings, J.B.; Angeli, D.; Bates, C.N. Fundamentals of economic model predictive control. In Proceedings of the 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3851–3861.
- Angeli, D.; Amrit, R.; Rawlings, J.B. Receding horizon cost optimization for overly constrained nonlinear plants. In Proceedings of the 48th IEEE Conference on Decision and Control (CDC), Shanghai, China, 15–18 December 2009; pp. 7972–7977.
- Heidarinejad, M.; Liu, J.; Christofides, P.D. Economic model predictive control of nonlinear process systems using Lyapunov techniques. AIChE J. 2012, 58, 855–870. [Google Scholar] [CrossRef]
- Ellis, M.; Christofides, P.D. On finite-time and infinite-time cost improvement of economic model predictive control for nonlinear systems. Automatica 2014, 50, 2561–2569. [Google Scholar] [CrossRef]
- Angeli, D.; Amrit, R.; Rawlings, J.B. On average performance and stability of economic model predictive control. IEEE Trans. Autom. Control 2012, 57, 1615–1626. [Google Scholar] [CrossRef]
- Faulwasser, T.; Bonvin, D. On the design of economic NMPC based on an exact turnpike property. IFAC-PapersOnLine 2015, 48, 525–530. [Google Scholar] [CrossRef]
- Faulwasser, T.; Bonvin, D. On the design of economic NMPC based on approximate turnpike properties. In Proceedings of the 54th IEEE Conference on Decision and Control (CDC), Osaka, Japan, 15–18 December 2015; pp. 4964–4970.
- Faulwasser, T.; Korda, M.; Jones, C.N.; Bonvin, D. Turnpike and dissipativity properties in dynamic real-time optimization and economic MPC. In Proceedings of the 53rd IEEE Conference on Decision and Control, Los Angeles, CA, USA, 15–17 December 2014; pp. 2734–2739.
- Faulwasser, T.; Korda, M.; Jones, C.N.; Bonvin, D. On Turnpike and Dissipativity Properties of Continuous-Time Optimal Control Problems. arXiv preprint arXiv:1509.07315, 2015; arXiv:1509.07315. [Google Scholar]
- Ellis, M.; Durand, H.; Christofides, P.D. A tutorial review of economic model predictive control methods. J. Process Control 2014, 24, 1156–1178. [Google Scholar] [CrossRef]
- Ellis, M.; Liu, J.; Christofides, P.D. Economic Model Predictive Control: Theory, Formulations and Chemical Process Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Marchetti, A.G.; Chachuat, B.; Bonvin, D. A dual modifier-adaptation approach for real-time optimization. J. Process Control 2010, 20, 1027–1037. [Google Scholar] [CrossRef]
- Brdys, M.A.; Tatjewski, P. Iterative Algorithms for Multilayer Optimizing Control; World Scientific: London, UK, 2005. [Google Scholar]
- Bunin, G.A.; François, G.; Srinivasan, B.; Bonvin, D. Input filter design for feasibility in constraint-adaptation schemes. IFAC Proc. Vol. 2011, 44, 5585–5590. [Google Scholar] [CrossRef]
- Navia, D.; Briceño, L.; Gutiérrez, G.; De Prada, C. Modifier-adaptation methodology for real-time optimization reformulated as a nested optimization problem. Ind. Eng. Chem. Res. 2015, 54, 12054–12071. [Google Scholar] [CrossRef]
- Bunin, G.A.; François, G.; Bonvin, D. Exploiting local quasiconvexity for gradient estimation in modifier-adaptation schemes. In Proceedings of the 2012 American Control Conference (ACC), Montreal, QC, Canada, 27–29 June 2012; pp. 2806–2811.
- Serralunga, F.J.; Mussati, M.C.; Aguirre, P.A. Model adaptation for real-time optimization in energy systems. Ind. Eng. Chem. Res. 2013, 52, 16795–16810. [Google Scholar] [CrossRef]
- Gao, W.; Wenzel, S.; Engell, S. Modifier adaptation with quadratic approximation in iterative optimizing control. In Proceedings of the IEEE 2015 European Control Conference (ECC), Linz, Austria, 15–17 July 2015; pp. 2527–2532.
- Brdys, M.A.; Tatjewski, P. An algorithm for steady-state optimising dual control of uncertain plants. In Proceedings of the IFAC Workshop on New Trends in Design of Control Systems, Smolenice, Slovak, 7–10 September 1994; pp. 249–254.
- Costello, S.; François, G.; Bonvin, D. A directional modifier-adaptation algorithm for real-time optimization. J. Process Control 2016, 39, 64–76. [Google Scholar] [CrossRef]


| Description | Symbol | Value | Unit |
|---|---|---|---|
| Kinetic Constant 1 | |||
| Kinetic Constant 2 | |||
| Reactor volume | V | ||
| A feed concentration | |||
| B feed concentration | |||
| A price | |||
| B price |
© 2016 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaccari, M.; Pannocchia, G. A Modifier-Adaptation Strategy towards Offset-Free Economic MPC. Processes 2017, 5, 2. https://doi.org/10.3390/pr5010002
Vaccari M, Pannocchia G. A Modifier-Adaptation Strategy towards Offset-Free Economic MPC. Processes. 2017; 5(1):2. https://doi.org/10.3390/pr5010002
Chicago/Turabian StyleVaccari, Marco, and Gabriele Pannocchia. 2017. "A Modifier-Adaptation Strategy towards Offset-Free Economic MPC" Processes 5, no. 1: 2. https://doi.org/10.3390/pr5010002






