Stochasticity in the Parasite-Driven Trait Evolution of Competing Species Masks the Distinctive Consequences of Distance Metrics
Abstract
:1. Introduction
2. The Mathematical Model
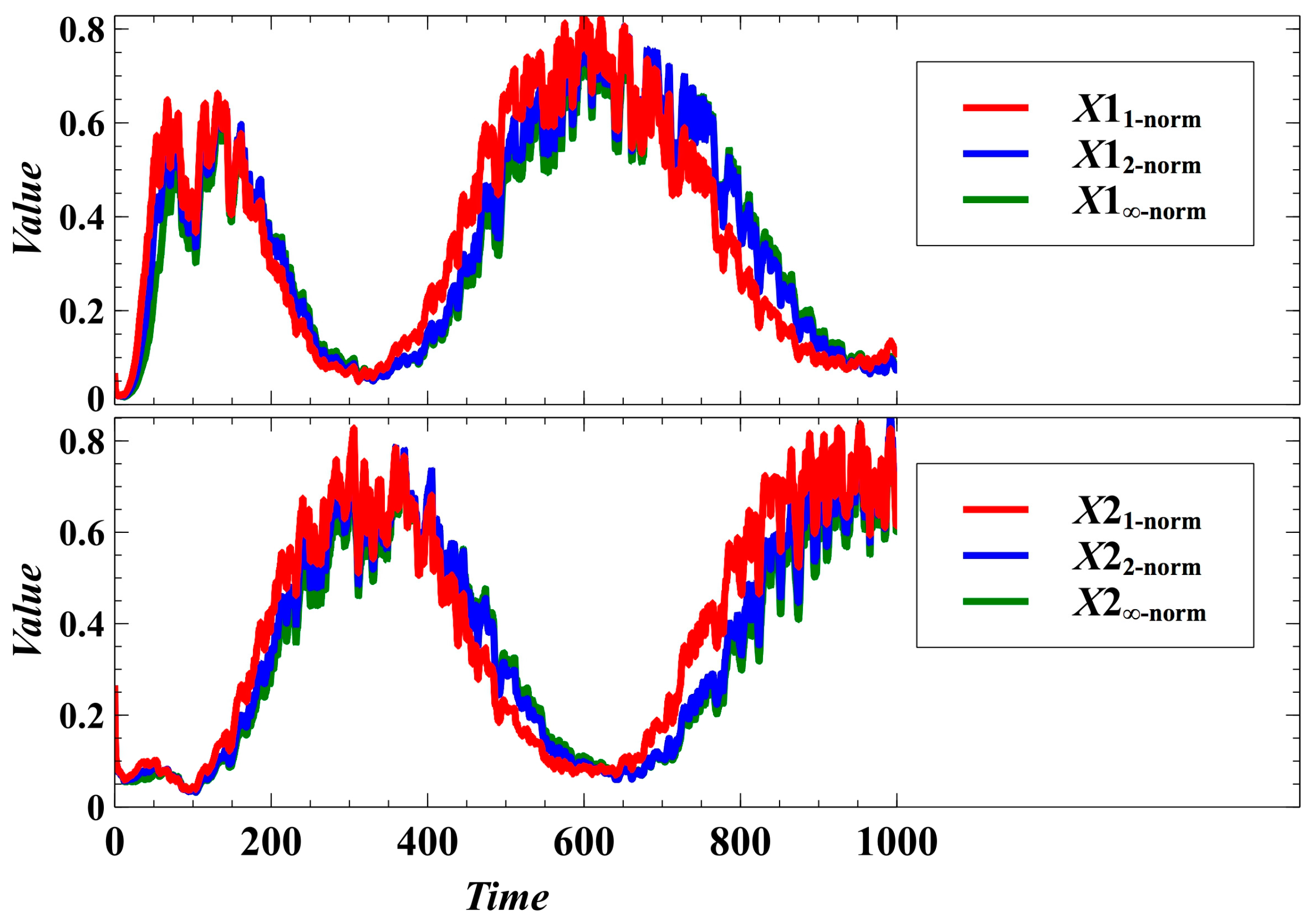
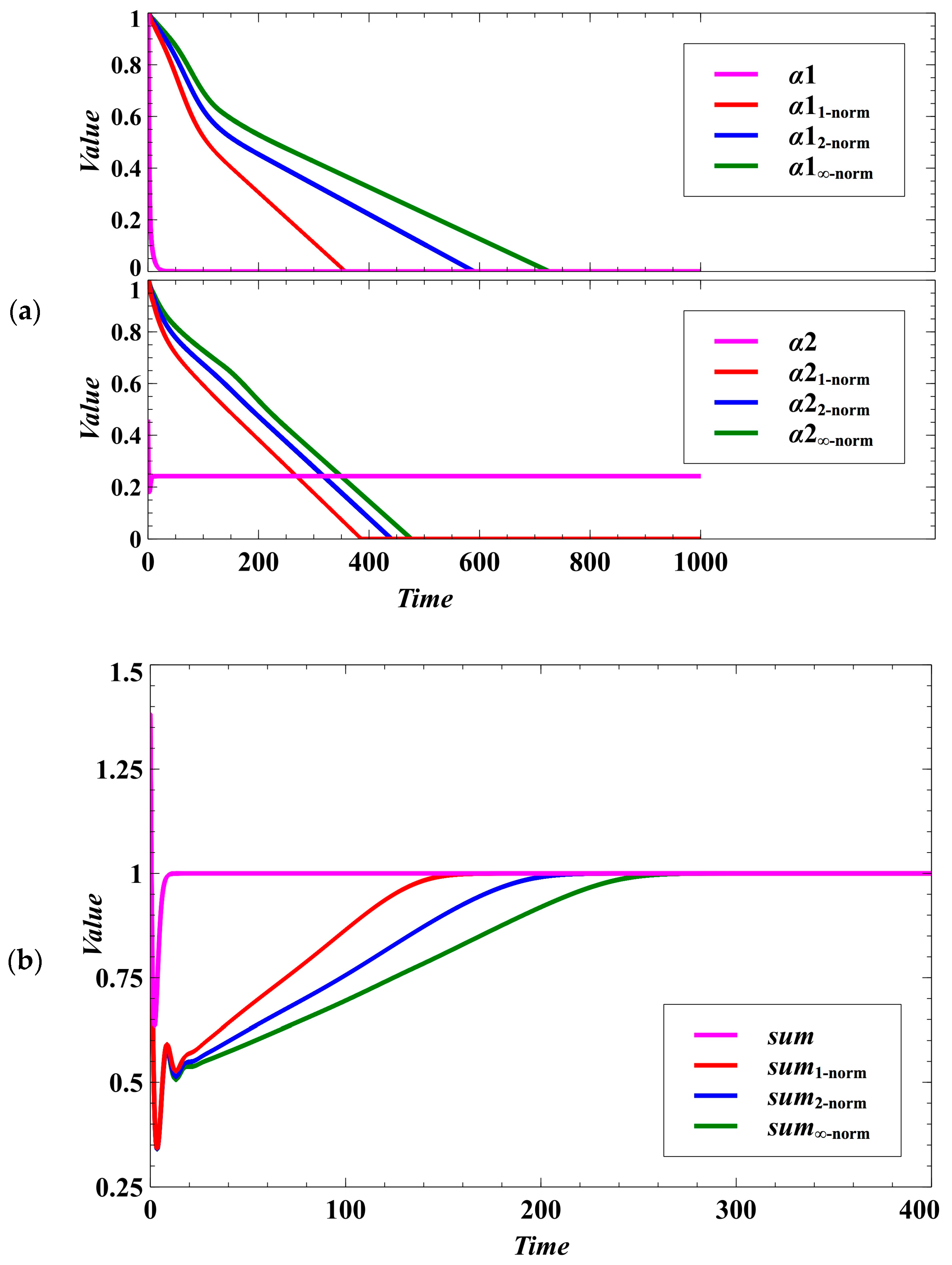
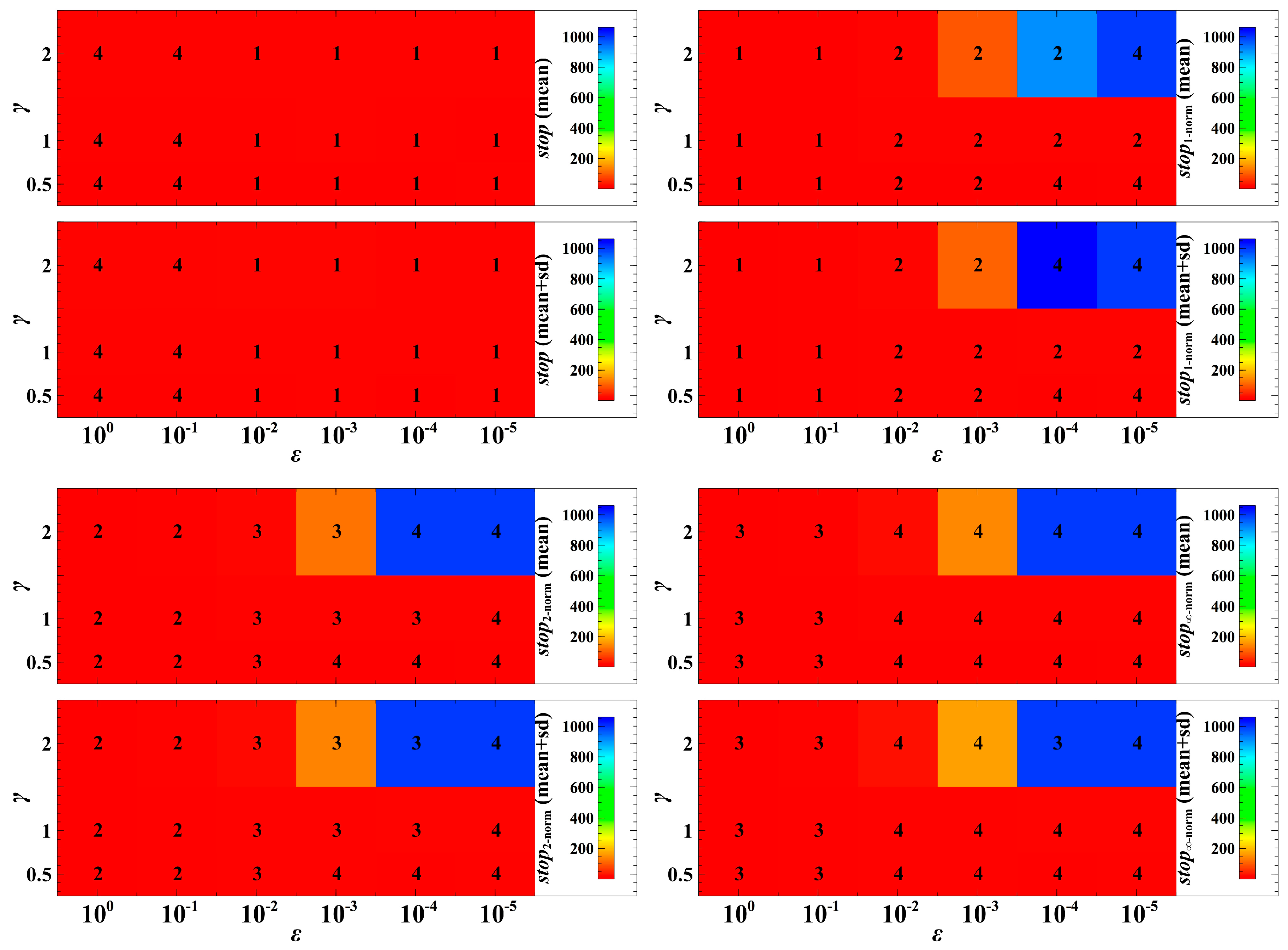
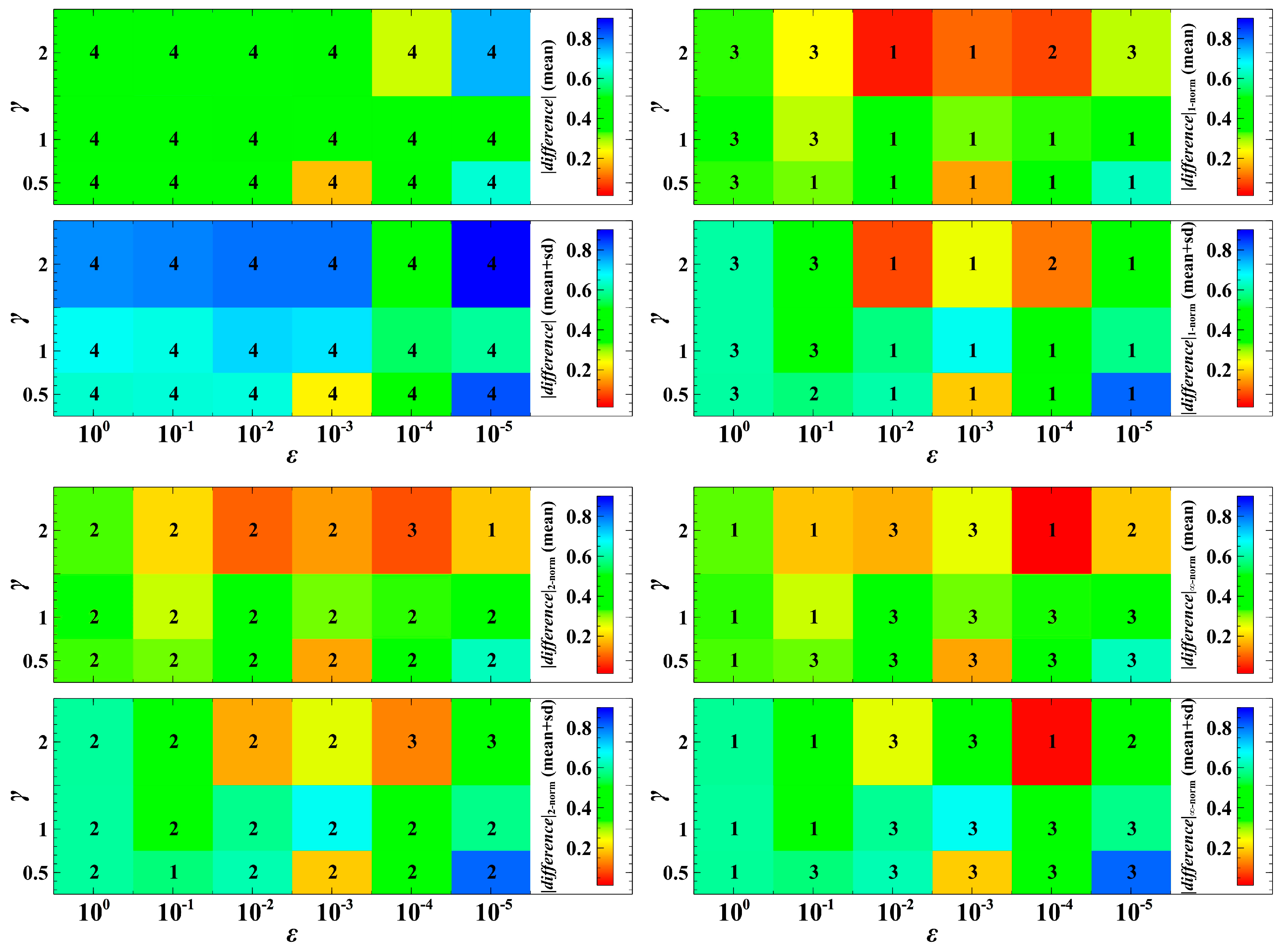
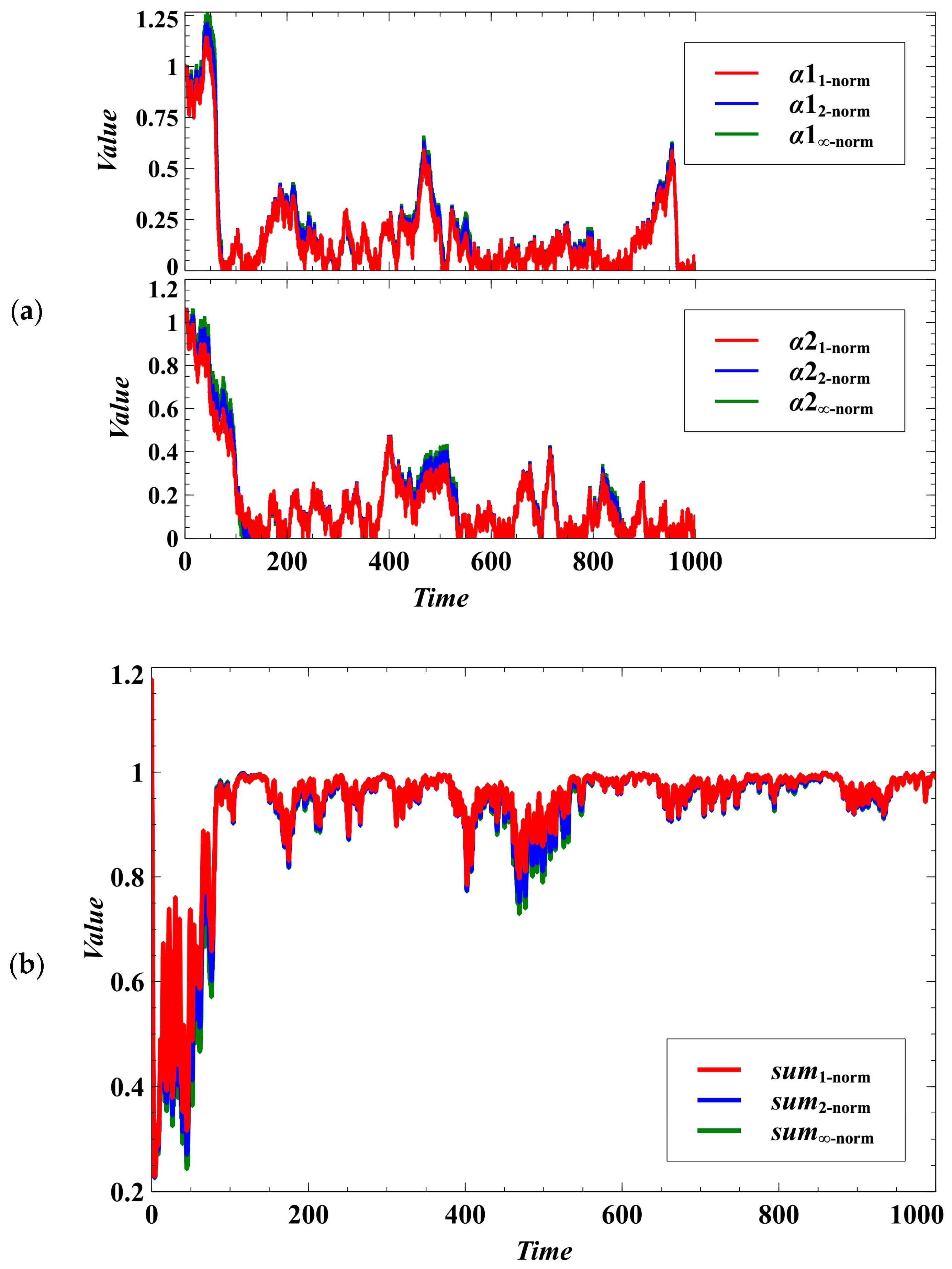
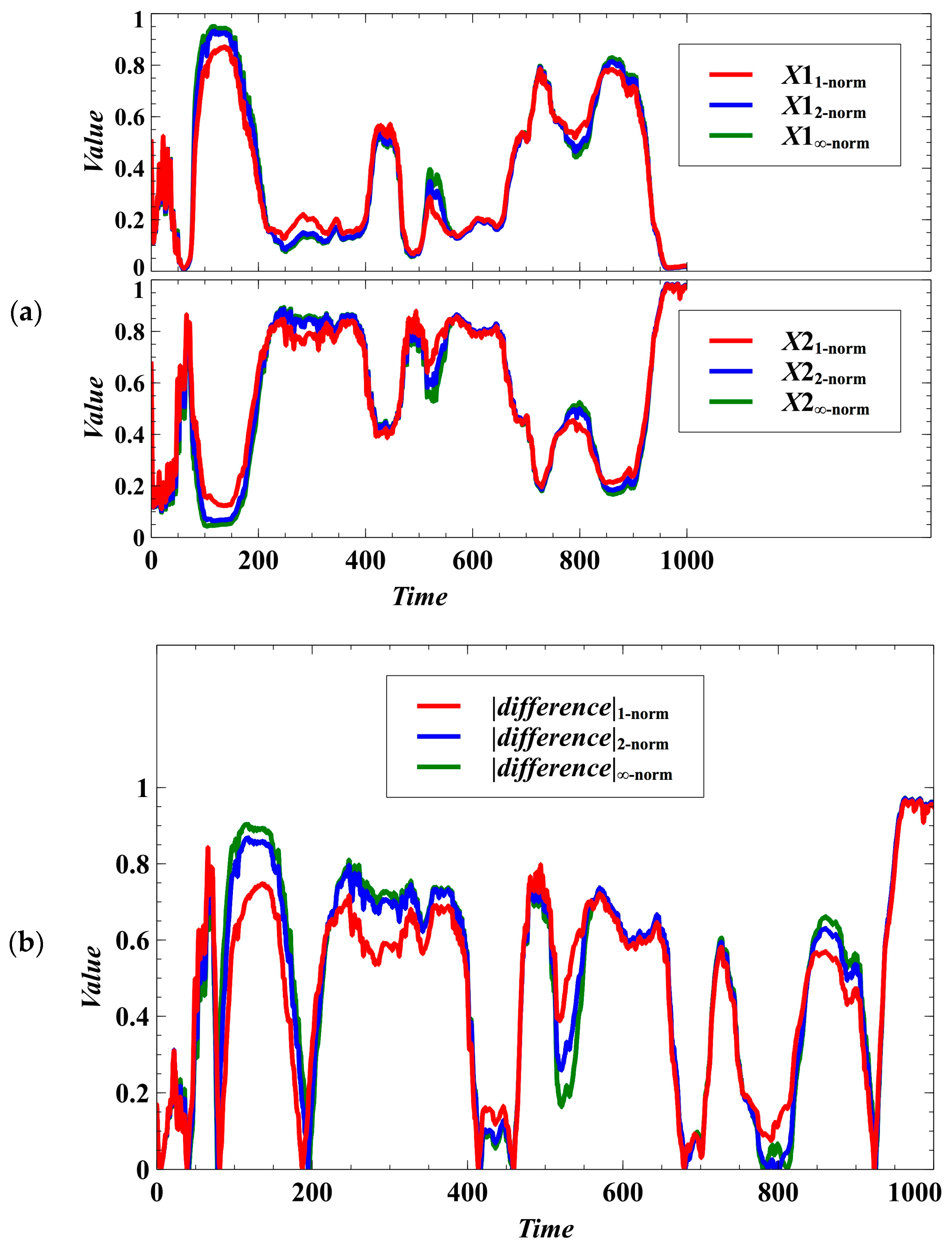
3. Simulation Results and Discussion
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A. Methods
Appendix B.
References
- Dougherty, E.R.; Carlson, C.J.; Bueno, V.M.; Burgio, K.R.; Cizauskas, C.A.; Clements, C.F.; Seidel, D.P.; Harris, N.C. Paradigms for parasite conservation. Conserv. Biol. 2015, 30, 724–733. [Google Scholar] [CrossRef] [PubMed]
- Hatcher, M.J.; Dick, J.T.A.; Dunn, A.M. Diverse effect of parasites in ecosystems: Linking interdependent processes. Front. Ecol. Environ. 2012, 10, 186–194. [Google Scholar] [CrossRef]
- Hudson, P.J.; Dobson, A.P.; Lafferty, K.D. Is a healthy ecosystem one that is rich in parasites? Trends Ecol. Evol. 2006, 21, 381–385. [Google Scholar] [CrossRef] [PubMed]
- Horwitz, P.; Wilcox, B.A. Parasites, ecosystems and sustainability: An ecological and complex systems perspective. Int. J. Parasitol. 2005, 35, 725–732. [Google Scholar] [CrossRef] [PubMed]
- Cortez, M.J.V.; Rabajante, J.F.; Tubay, J.M.; Babierra, A.L. From epigenetic landscape to phenotypic fitness landscape: Evolutionary effect of pathogens on host traits. Infect. Genet. Evol. 2017, 51, 245–254. [Google Scholar] [CrossRef] [PubMed]
- Rabajante, J.F.; Tubay, J.M.; Ito, H.; Uehara, T.; Kakishima, S.; Morita, S.; Yoshimura, J.; Ebert, D. Host-parasite red queen dynamics with phase-locked rare genotypes. Sci. Adv. 2016, 2, e1501548. [Google Scholar] [CrossRef] [PubMed]
- Rabajante, J.F.; Tubay, J.M.; Uehara, T.; Morita, M.; Ebert, D.; Yoshimura, J. Red queen dynamics in multi-host and multi-parasite interaction system. Sci. Rep. 2015, 5, 10004. [Google Scholar] [CrossRef] [PubMed]
- Perc, M.; Gomez-Gardeñes, J.; Szolnoki, A.; Floria, L.M.; Moreno, Y. Evolutionary dynamics of group interactions on structured populations: A review. J. R. Soc. Interface 2013, 10, 20120997. [Google Scholar] [CrossRef] [PubMed]
- Perc, M.; Szolnoki, A. Coevolutionary games–A mini review. Biosystems 2010, 99, 109–125. [Google Scholar] [CrossRef] [PubMed]
- Maslov, A.; Sneppen, K. Population cycles and species diversity in dynamic Kill-the-Winner model of microbial ecosystems. Sci. Rep. 2017, 7, 39642. [Google Scholar] [CrossRef] [PubMed]
- Barraclough, T.G. How do species interactions affect evolutionary dynamics across whole communities? Annu. Rev. Ecol. Evol. Syst. 2015, 46, 25–48. [Google Scholar] [CrossRef]
- Raharinirina, N.A.; Brandt, G.; Merico, A. A trait-based model for describing the adaptive dynamics of coral-algae symbiosis. Front. Ecol. Evol. 2017, 5, 31. [Google Scholar] [CrossRef]
- Klauschies, T.; Vasseur, D.A.; Gaedke, U. Trait adaptation promotes species coexistence in diverse predator and prey communiteis. Ecol. Evol. 2016, 6, 4141–4159. [Google Scholar] [CrossRef] [PubMed]
- Rabajante, J.F.; Babierra, A.L. Branching and oscillations in the epigenetic landscape of cell-fate determination. Prog. Biophys. Mol. Biol. 2015, 117, 240–249. [Google Scholar] [CrossRef] [PubMed]
- Mougi, A.; Kondoh, M. Adaptation in a hybrid world with multiple interaction types: A new mechanism for species coexistence. Ecol. Res. 2014, 29, 113–119. [Google Scholar] [CrossRef]
- Mougi, A. Coevolution in a one predator-two prey system. PLoS ONE 2010, 5, e13887. [Google Scholar] [CrossRef] [PubMed]
- Abrams, P.A.; Matsuda, H.; Harada, Y. Evolutionarily unstable fitness maxima and stable fitness minima of continuous traits. Evol. Ecol. 1993, 7, 465–487. [Google Scholar] [CrossRef]
- Mougi, A. Stability of an adaptive hybrid community. Sci. Rep. 2016, 6, 28181. [Google Scholar] [CrossRef] [PubMed]
- Papkou, A.; Gokhale, C.S.; Traulsen, A.; Schulenburg, H. Host-parasite coevolution: Why changing population size matters. Zoology 2016, 119, 330–338. [Google Scholar] [CrossRef] [PubMed]
- Penczykowski, R.M.; Forde, S.E.; Duffy, M.A. Rapid evolution as a possible constraint on emerging infectious diseases. Freshw. Biol. 2011, 56, 689–704. [Google Scholar] [CrossRef]
- Yoshioka, H. A simple game-theoretic model for upstream fish migration. Theory Biosci. 2017, 136, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Jost, J.; Pepper, J. Individual optimization efforts and population dynamics: A mathematical model for the evolution of resource allocation strategies, with applications to reproductive and mating systems. Theory Biosci. 2008, 127, 31–43. [Google Scholar] [CrossRef] [PubMed]
- Stone, E.A.; Sidow, A. Constructing a meaningful evolutionary average at the phylogenetic center of mass. BMC Bioinform. 2007, 8, 222–235. [Google Scholar] [CrossRef] [PubMed]
- Parker, G.A.; Smith, J.M. Optimality theory in evolutionary biology. Nature 1990, 348, 27–33. [Google Scholar] [CrossRef]
- Smith, J.M. Optimization theory in evolution. Annu. Rev. Ecol. Syst. 1978, 9, 31–36. [Google Scholar] [CrossRef]
- Hengenius, J.B.; Gribskov, A.E.; Rundell, A.E.; Umulis, D.M. Making models match measurements: Model optimization for morphogen patterning networks. Semin. Cell Dev. Biol. 2014, 35, 109–123. [Google Scholar] [CrossRef] [PubMed]
- Han, L.; Ma, Z.; Hethcote, H.W. Four predator prey models with infectious diseases. Math. Comput. Model. 2001, 34, 849–858. [Google Scholar] [CrossRef]
- Erwin, D.H. The topology of evolutionary novelty and innovation in macroevolution. Philos. Trans. R. Soc. B 2017, 372, 20160422. [Google Scholar] [CrossRef] [PubMed]
- Mitteroecker, P.; Huttegger, S.M. The concept of morphospaces in evolutionary and developmental biology: Mathematics and metaphors. Biol. Theory 2009, 4, 54–67. [Google Scholar] [CrossRef]
- Myerson, R.B. Utilitarianism, egalitarianism, and the timing effect in social choice problems. Econometrica 1981, 49, 883–897. [Google Scholar] [CrossRef]
- Dadlani, A.; Kumar, M.S.; Maddi, M.G.; Kim, K. Mean-field dynamics of inter-switching memes competing over multiplex social networks. IEEE Commun. Lett. 2017, 21, 967–970. [Google Scholar] [CrossRef]
- Sahneh, F.D.; Scoglio, C. Competitive epidemic spreading over arbitrary multilayer networks. Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 2014, 89, 062817. [Google Scholar] [CrossRef] [PubMed]
- Danchin, E.; Charmantier, A.; Champagne, F.A.; Mesoudi, A.; Pujol, B.; Blanchet, S. Beyond DNA: Integrating inclusive inheritance into an extended theory of evolution. Nat. Rev. Genet. 2011, 12, 475–486. [Google Scholar] [CrossRef] [PubMed]
- Das, K. A mathematical study of a predator-prey dynamics with disease in predator. ISRN Appl. Math. 2011, 2011, 1–16. [Google Scholar] [CrossRef]
- Han, J.; Kamber, M.; Pei, J. Data Mining: Concepts and Techniques; Morgan Kaufmann Publishers: Burlington, MA, USA, 2012. [Google Scholar]
- Hudson, P.; Greenman, J. Competition mediated by parasites: Biological and theoretical progress. Trends Ecol. Evol. 1998, 13, 387–390. [Google Scholar] [CrossRef]
- Bowers, R.G.; Turner, J. Community structure and the interplay between interspecific infection and competition. J. Theor. Biol. 1997, 187, 95–109. [Google Scholar] [CrossRef] [PubMed]
- Yan, G. Parasite-mediated competition: A model of directly transmitted macroparasites. Am. Nat. 1996, 148, 1089–1112. [Google Scholar] [CrossRef]
- Price, P.W.; Westoby, M.; Rice, B. Parasite-mediated competition: Some predictions and tests. Am. Nat. 1988, 131, 544–555. [Google Scholar] [CrossRef]
- Schmid-Hempel, P. Evolutionary Parasitology: The Integrated Study of Infections, Immunology, Ecology, and Genetics; Oxford University Press: Hong Kong, China, 2011. [Google Scholar]
- Poulin, R. Evolutionary Ecology of Parasites, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2006. [Google Scholar]
- Ridley, M. Evolution, 3rd ed.; Blackwell Publishing: Hoboken, NJ, USA, 2004. [Google Scholar]
- Hendry, A.P.; Kinnison, M.T. (Eds.) Microevolution: Rate, Pattern, Process; Kluwer Academic Publisher: Dordrecht, The Netherlands, 2001. [Google Scholar]
- Oksanen, L. Evolution of exploitation ecosystems I. Predation, foraging ecology and population dynamics in herbivores. Evol. Ecol. 1992, 6, 15–33. [Google Scholar] [CrossRef]
- Weitz, J.S.; Eksin, C.; Paarporn, K.; Brown, S.P.; Ratcliff, W.C. An oscillating tragedy of the commons in replicator dynamics with game-environment feedback. Proc. Natl. Acad. Sci. USA 2016, 113, e7518–e7525. [Google Scholar] [CrossRef] [PubMed]
- Platt, T.G.; Bever, J.D. Kin competition and the evolution of cooperation. Trends Ecol. Evol. 2009, 24, 370–377. [Google Scholar] [CrossRef] [PubMed]
- Jover, L.F.; Cortez, M.H.; Weitz, J.S. Mechanism of multi-strain coexistence in host-phase systems with nested infection networks. J. Theor. Biol. 2013, 332, 65–77. [Google Scholar] [CrossRef] [PubMed]
- Lafferty, K.D.; Allesina, S.; Arim, M.; Briggs, C.J.; De Leo, G.; Dobson, A.P.; Dunne, J.A.; Johnson, P.T.; Kuris, A.M.; Marcogliese, D.J.; et al. Parasites in food webs: The ultimate missing links. Ecol. Lett. 2008, 11, 533–546. [Google Scholar] [CrossRef] [PubMed]
- Hochberg, M.E.; Holt, R.D. The coexistence of competing parasites. I. The role of cross-species infection. Am. Nat. 1990, 136, 517–541. [Google Scholar] [CrossRef]
- Anderson, R.M.; May, R.M. Regulation and stability of host-parasite population intersections: I. Regulatory processes. J. Anim. Ecol. 1978, 47, 219–247. [Google Scholar] [CrossRef]
- Brunner, F.; Eizaguirre, C. Can environmental change affect host/parasite-mediated speciation? Zoology 2016, 119, 384–394. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, T. Probability in biology: Overview of a comprehensive theory of probability in living systems. Prog. Biophys. Mol. Biol. 2013, 113, 67–79. [Google Scholar] [CrossRef] [PubMed]

© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Buhat, C.A.H.; Talabis, D.A.S.J.; Cueno, A.L.; Gavina, M.K.A.; Babierra, A.L.; Cuaresma, G.A.; Rabajante, J.F. Stochasticity in the Parasite-Driven Trait Evolution of Competing Species Masks the Distinctive Consequences of Distance Metrics. Processes 2017, 5, 74. https://doi.org/10.3390/pr5040074
Buhat CAH, Talabis DASJ, Cueno AL, Gavina MKA, Babierra AL, Cuaresma GA, Rabajante JF. Stochasticity in the Parasite-Driven Trait Evolution of Competing Species Masks the Distinctive Consequences of Distance Metrics. Processes. 2017; 5(4):74. https://doi.org/10.3390/pr5040074
Chicago/Turabian StyleBuhat, Christian Alvin H., Dylan Antonio S. J. Talabis, Anthony L. Cueno, Maica Krizna A. Gavina, Ariel L. Babierra, Genaro A. Cuaresma, and Jomar F. Rabajante. 2017. "Stochasticity in the Parasite-Driven Trait Evolution of Competing Species Masks the Distinctive Consequences of Distance Metrics" Processes 5, no. 4: 74. https://doi.org/10.3390/pr5040074




