A New Approximation Method with High Order Accuracy
Abstract
:1. Introduction
2. RBF Interpolation
3. Univariate B-Spline Quasi-Interpolants
4. New Quasi-Interpolation Method
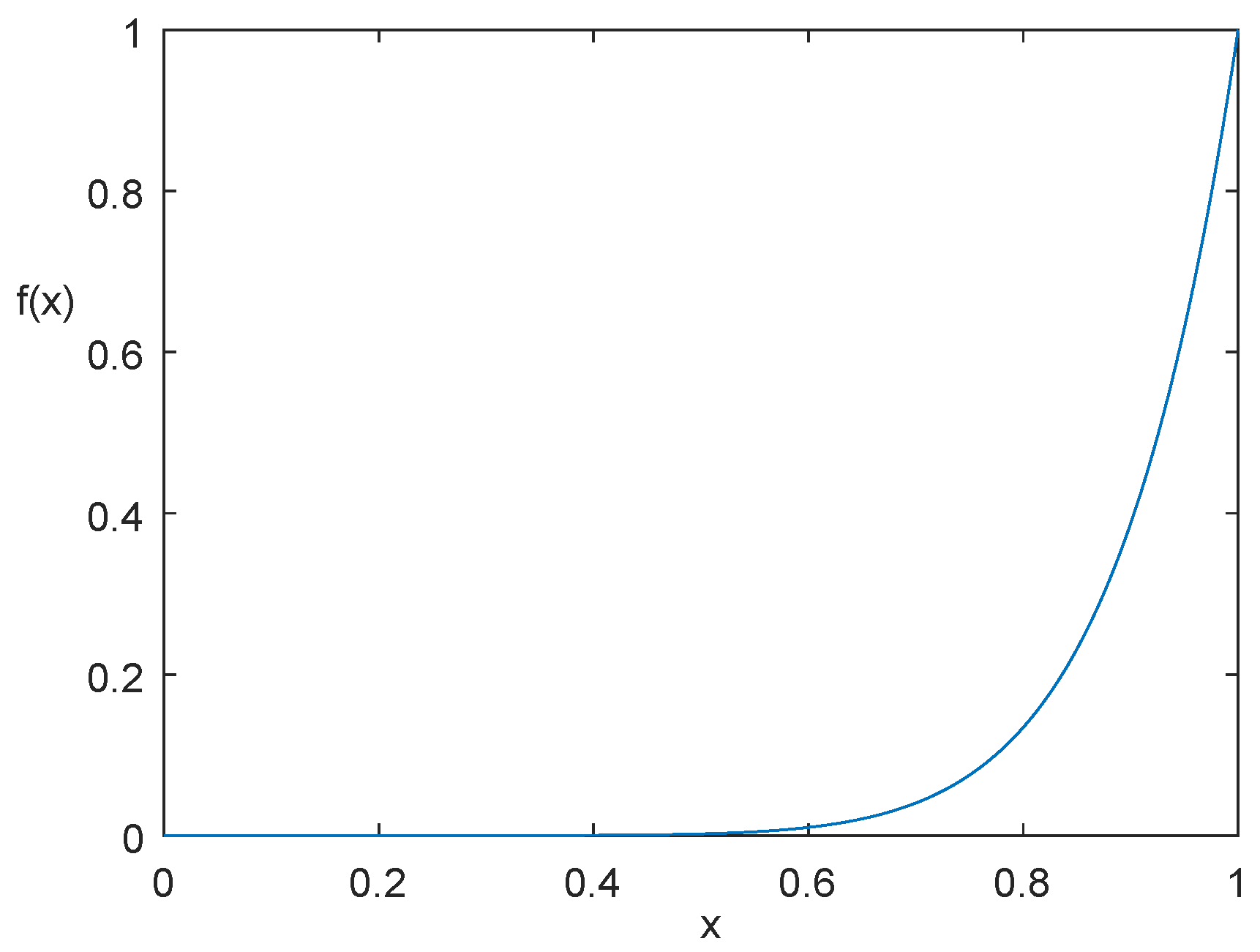
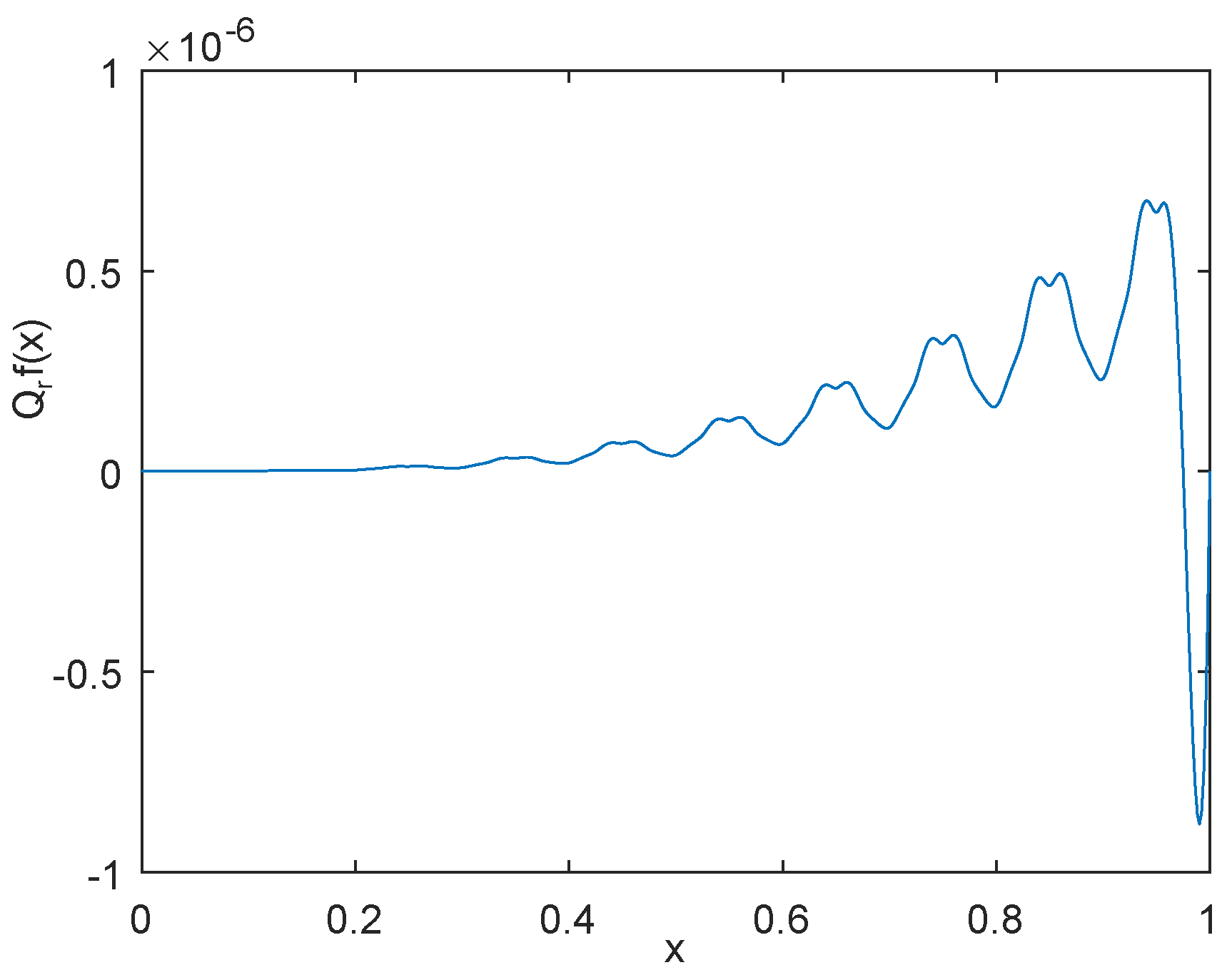
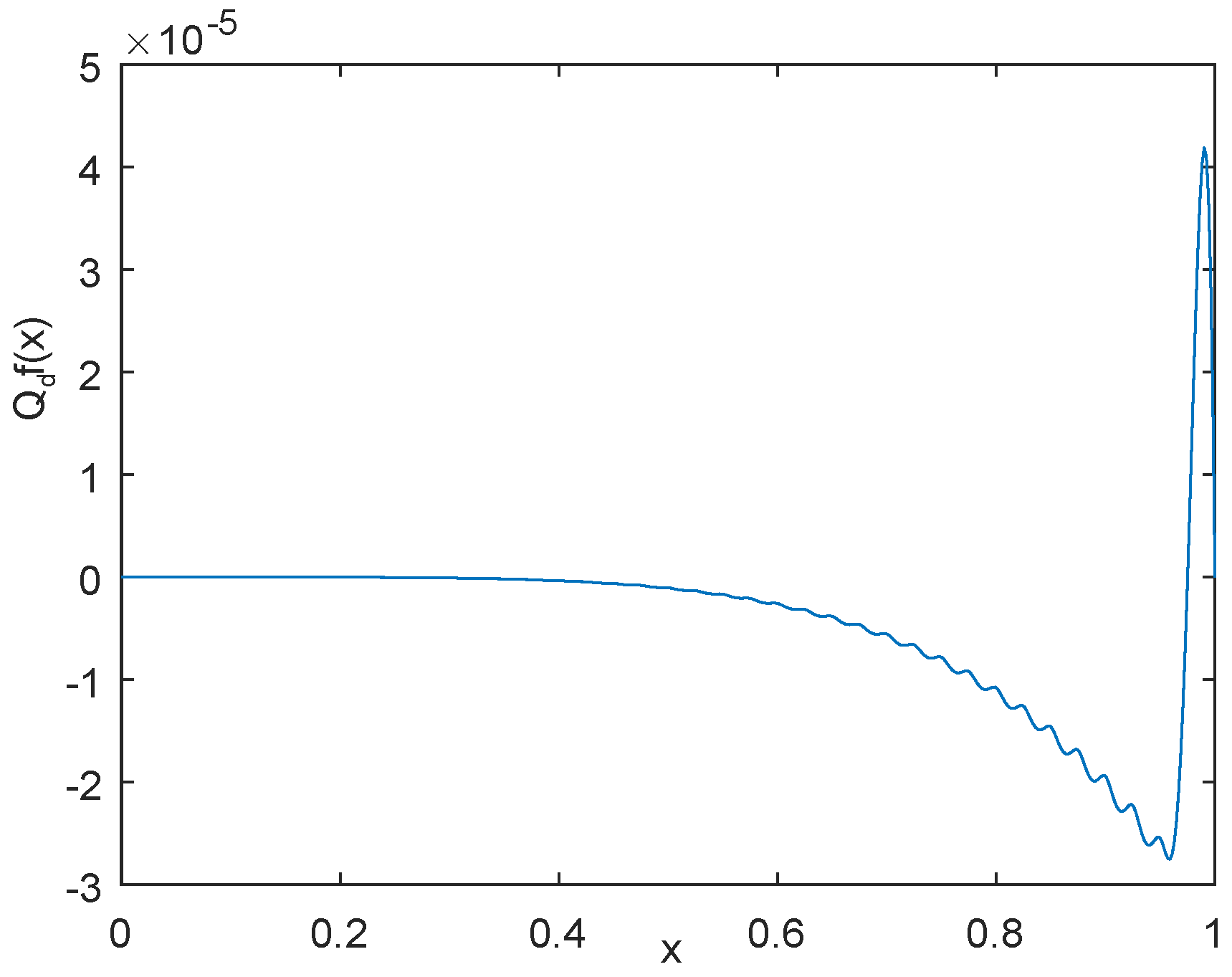
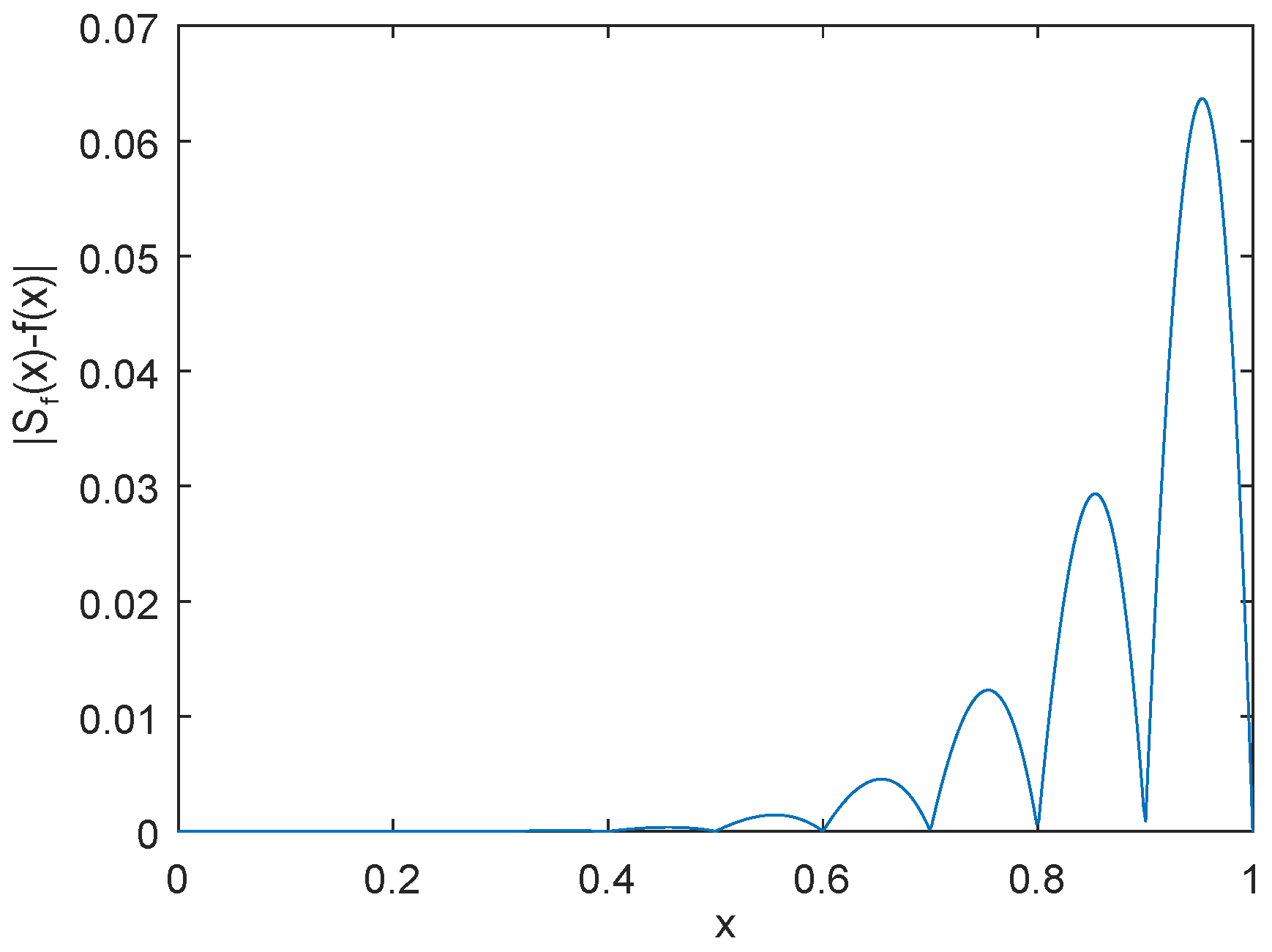
5. Numerical Example
6. Conclusions
Acknowledgments
Conflicts of Interest
References
- Buhmann, M.D. Radial Basis Functions. Theory and Implementations; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Micchelli, C.A. Interpolation of scattered data: Distance matrices and conditionally positive definite functions. Constr. Approx. 1986, 2, 11–22. [Google Scholar] [CrossRef]
- Powell, M.J.D. The theory of radial basis function approximation in 1990. In Advances in Numerical Analysis; Light, W., Ed.; Oxford Scinece Publications: Oxford, UK, 1992; Volume II. [Google Scholar]
- Schaback, R. Error estimates and condition number for radial basis function interpolation. Adv. Comput. Math. 1995, 3, 251–264. [Google Scholar] [CrossRef]
- Wendland, H. Scattered data approximation. In Cambridge Monographs on Applied and Computational Mathematics; Cambridge University Press: Cambridge, UK, 2005; Volume 17. [Google Scholar]
- Wu, Z.M. Compactly supported positive definite radial functions. Adv. Comput. Math. 1995, 4, 283–292. [Google Scholar] [CrossRef]
- Fasshauer, G.E. Meshfree Approximation Methods with Matlab; World Scientific Publishing: Singapore, 2007. [Google Scholar]
- Jiang, Z.W.; Wang, R.H.; Zhu, C.G.; Xu, M. High Accuracy Multiquadric Quasi-interpolation. Appl. Math. Model. 2011, 35, 2185–2195. [Google Scholar] [CrossRef]
- Jiang, Z.W.; Wang, R.H. Numerical solution of one-dimensional SineCGordon equa- tion using high accuracy multiquadric quasi-interpolation. Appl. Math. Comput. 2012, 218, 7711–7716. [Google Scholar]
- Ali, H.A.; Gardner, R.T.; Gardner, G.A. A collocation method for Burgers’ equation using cubic B-splines. Comput. Methods Appl. Mech. Eng. 1992, 100, 325–337. [Google Scholar] [CrossRef]
- Dağ, İ.; Irk, D.; Saka, B. A numerical solution of the Burgers’ equation using cubic B-splines. Appl. Math. Comput. 2005, 163, 199–211. [Google Scholar] [CrossRef]
- Dağ, İ.; Saka, B.; Boz, A. B-spline Galerkin methods for numerical solutions of the Burgers’ equation. Appl. Math. Comput. 2005, 166, 506–522. [Google Scholar] [CrossRef]
- Ramadan, M.A.; El-Danaf, T.S.; Alaal, F. A numerical solution of the Burgers’ equation using septic B-splines. Chaos Solitons Fract. 2005, 26, 795–804. [Google Scholar] [CrossRef]
- Saka, B.; Dağ, İ. Quartic B-spline collocation methods to the numerical solutions of the Burgers’ equation. Chaos Solitons Fract. 2007, 32, 1125–1137. [Google Scholar] [CrossRef]
- Saka, B.; Dağ, İ. A numerical study of the Burgers’ equation. J. Frankl. Inst. 2008, 345, 328–348. [Google Scholar] [CrossRef]
- Zaki, S.I. A quintic B-spline finite elements scheme for the KdVB equation. Comput. Methods Appl. Eng. 2000, 188, 121–134. [Google Scholar] [CrossRef]
- Zhu, C.G.; Wang, R.H. Numerical solution of Burgers’ equation by cubic B-spline quasi-interpolation. Appl. Math. Comput. 2009, 208, 260–272. [Google Scholar] [CrossRef]
- Sablonnière, P. Univariate spline quasi-interpolants and applications to numerical analysis. Rend. Sem. Mat. Univ. Pol. Torino 2005, 63, 211–222. [Google Scholar]
- Krige, D.G. A Statistical Approach to Some Mine Valuation and Allied Problems on the Witwatersrand. Master’s Thesis, University of Witwatersrand, Johannesburg, South Africa, 1951. [Google Scholar]
- Madych, W.R. Miscellaneous error bounds for multiquadric and related interpolators. Comput. Math. Appl. 1992, 24, 121–138. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- De Boor, C. A Practical Guide to Splines; Revised edition; Springer: New York, NY, USA, 2001. [Google Scholar]
- Sablonnière, P. Quasi-interpolants splines sobre particiones uniforms. In Proceedings of the 1st Meeting in Approximation Theory of the University of Jaén, Ubeda, Spain, 29 June–2 July 2000; Prépublication IRMAR 00-38. Rennes, France, June 2000. [Google Scholar]
- Cavoretto, R.; De Marchi, S.; De Rossi, A.; Perracchione, E.; Santin, G. Partition of unity interpolation using stable kernel-based techniques. Appl. Numer. Math. 2016. [Google Scholar] [CrossRef]
- Cavoretto, R.; De Rossi, A.; Perracchione, E. Efficient computation of partition of unity interpolants through a block-based searching technique. Comput. Math. Appl. 2016, 71, 2568–2584. [Google Scholar] [CrossRef]
- Caira, R.; Dell’Accio, F. Shepard-Bernoulli operators. Math Comput. 2007, 76, 299–321. [Google Scholar] [CrossRef]
- Caira, R.; Dell’Accio, F.; Di Tommaso, F. On the bivariate Shepard-Lidstone operators. J. Comput. Appl. Math. 2012, 236, 1691–1707. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Di Tommaso, F. Scattered data interpolation by Shepard’s like methods: Classical results and recent advances, Dolomites Research Notes on Approximation. Dolomites Res. Notes Approx. 2016, 9, 32–44. [Google Scholar]
- Costabile, F.A.; Dell’Accio, F.; Di Tommaso, F. Enhancing the approximation order of local Shepard operators by Hermite polynomials. Comput. Appl. Math. 2012, 64, 3641–3655. [Google Scholar] [CrossRef]
- Costabile, F.A.; Dell’Accio, F.; Di Tommaso, F. Complementary Lidstone interpolation on scattered data sets. Numer. Algorithms 2013, 64, 157–180. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Di Tommaso, F. Complete Hermite-Birkhoff interpolation on scattered data by combined Shepard operators. J. Comput. Appl. Math. 2016, 300, 192–206. [Google Scholar] [CrossRef]
- Dell’Accio, F.; Di Tommaso, F.; Hormann, K. On the approximation order of triangular Shepard interpolation. IMA J. Numer. Anal. 2016, 36, 359–379. [Google Scholar] [CrossRef]
- De Marchi, S.; Dell’Accio, F.; Mazza, M. On the constrained mock-Chebyshev least-square. J. Comput. Appl. Math. 2015, 280, 94–109. [Google Scholar] [CrossRef]
© 2017 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Z. A New Approximation Method with High Order Accuracy. Math. Comput. Appl. 2017, 22, 11. https://doi.org/10.3390/mca22010011
Jiang Z. A New Approximation Method with High Order Accuracy. Mathematical and Computational Applications. 2017; 22(1):11. https://doi.org/10.3390/mca22010011
Chicago/Turabian StyleJiang, Ziwu. 2017. "A New Approximation Method with High Order Accuracy" Mathematical and Computational Applications 22, no. 1: 11. https://doi.org/10.3390/mca22010011





