Photonic Quantum Noise Reduction with Low-Pump Parametric Amplifiers for Photonic Integrated Circuits

Abstract

An approximation-free and fully quantum optic formalism for parametric processes is presented. Phase-dependent gain coefficients and related phase-pulling effects are identified for quantum Rayleigh emission and the electro-optic conversion of photons providing parametric amplification in small-scale integration of photonic devices. These mechanisms can be manipulated to deliver, simultaneously, sub-Poissonian distributions of photons as well as phase-dependent amplification in the same optical quadrature of a signal field.

1. Introduction

Small-scale integration of photonic devices holds the prospect of overcoming speed limits associated with back-and-forth conversions between the electrical and optical domains for signal processing and transmission. Integrated photonic platforms [1,2,3] will contain their own low-power optical sources, which will be used for on-chip signal processing. However, the low levels of power rule out any significant nonlinear effects for χ⁽²⁾ and χ⁽³⁾, the second- and third-order susceptibilities. For instance, a recently reported phase-sensitive amplifier [4] operating on χ⁽³⁾ in semiconductor materials can only deliver output signal powers of less than −31 dBm for input pump powers of −1 dBm.

Yet, two recently identified parametric processes [5] have the potential to operate as integral parts of a photonic integrated circuit (PIC) with a high degree of photonic conversion (>90%), as they require low pump powers (<10 mW) and very short interaction lengths. Parametric amplification and phase shifts can be performed with first-order susceptibility quantum Rayleigh emissions [6] in the form of optically linear parametric (OLP) effects and the corresponding electro-optic susceptibility-based conversion of photons [7] in the form of electro-optic parametric (EOP) processes, both of which require low optical pump powers and short interactions lengths of a few microns for OLP interactions and a few centimeters for EOP. These interactions can be highly efficient and require only a pair of a pump and a signal optical waves, and functional devices can be fabricated with well-established technologies [8].

As parametric processes of photonic conversions constitute a major mechanism for generating nonclassical states of light [9,10,11], any new insights into such interactions should be of particular interest in the design and operation of functional devices. Quantum optic noise reduction and phase-sensitive amplification will benefit an optical transmission system throughout the entire link and, in particular, at the receiver and detection stages of operation [12]. Quantum noise stems from fluctuations in the distribution of number of photons and/or the distribution of associated phases of the optical fields [12], and include: the vacuum fluctuations of any electromagnetic field of radiation, the spontaneous emission of photons by an excited electric dipole polarization, the Poisson distribution as a function of time of the number of photons in a coherent beam of light, fluctuations in the state of polarization, and so on.

Experimentally, given the very low efficiency of parametric conversion of photons carried out by χ⁽²⁾ and χ⁽³⁾-based materials, the undepleted pump approximation becomes a critical aspect of the interaction, along with the phase-matching condition. Theoretically, photonic noise reduction through variance squeezing—below the standard quantum limit (SQL) [9] of an optical coherent state [9,10]—is implemented by simultaneous amplification of a field quadrature of phase φ (defined by adding two output fields or phasor modes) and attenuation of the corresponding conjugate quadrature φ + π/2. This leads to the definition of a virtual photon annihilation operator [10,11] which is the superposition of various levels of a photon annihilation operator a and a photon creation operator a*. This type of quadrature noise-squeezing requires a two-photon output per interaction [10] and it is linked to the Bogoliubov transformation for boson particles. For example, the output annihilation operator of the signal mode a_s is given as a superposition of the input operators weighted by c-number functions; that is, a_s(z) = c₁(z) a_s(0) + ${i e}^{{i\phi }_{pr}}$ c₂(z) a*_i(0), where the subscripts denote signal (s) and idler (i) waves, and φ_pr identifies the pump phase(s) of the interaction term. This expression is based on the approximation of the undepleted pump, which is treated classically by ignoring its operators, resulting in a gain coefficient g_o which is not allowed to vary at all, leading to many significant properties being discarded as a result of the linearization of the rate equations.

While the cross-coupling between a*_i and a_s arises from the parametric conversion of photons, the self-coupling term has no physical origin being a mathematical artefact as a result of the conventional solution containing, simultaneously, an amplifying (+g_o = χ⁽²⁾·√P_p) and an attenuating (−g_o), exponential factors defined by the product of a susceptibility and the pump power P_p. Commonly used functions are c₁(z) = cosh (g_oz) and c₂(z) = sinh (g_oz) for a phase-matching condition [13]. However, no explanation has ever been provided as to how the same parametric process can, physically, amplify and attenuate simultaneously the signal wave. Indeed, a formal integration of Equation (22) of [13] yields a_s(z) − a_s(0) = ${i e}^{{i\phi }_{pr}}$ g_o ∫ a*_i(z)dz, indicating that c₁ = 1 for any condition and remains unchanged throughout the propagation. Whether the input signal operator is amplified or attenuated at a particular point z in the dielectric medium will depend on the local value of the relative phase between the pump(s) and the signal and idler waves. This is not the case with the Bogoliubov-type solution which has a phase-independent gain coefficient g_o.

Furthermore, if the classical pump amplitude—in the driving term of the formal integral noted above—is replaced by its quantum optic representation (i.e., c_p·a_p), then the driving force a_p·a*_i on the right-hand side of that equality would oscillate at an angular frequency −(ω_p − ω_i) = −ω_s, indicating that only a_s is changed without any appearance of a creation operator a_s*, as suggested by the Bogoliubov transformation. Additional physical deficiencies of the Bogoliubov solution are outlined in Appendix A below.

Consequently, an approximation-free and fully quantum optic formalism for parametric processes is needed and developed in Section 2 below, based on the concepts outlined in [5]. The parametric amplification consists of stimulated emission of photons, which adopt the same characteristics as the stimulating beam. The direction of photon coupling (e.g., for four photon-mixing interactions between the central frequency pump(s) and the sideband frequency signal/idler waves) depends on the phase difference between the two pairs of waves. This process is also accompanied by spontaneously emitted photons [14,15,16], which have arbitrary phases and states of polarization. The spontaneous emission provides the seed photons to be amplified in the absence, at the input, of another stimulating optical wave.

The critical role of the parametrically engendered phases has been demonstrated experimentally [15,16,17]. A physically meaningful phase-sensitive (PS) gain coefficient was identified in [14], (Equations (24)–(29)) along with its spectral bandwidth.

The remainder of this article involves no approximations and presents, in Section 2, a fully quantum optic derivation of the parametric equations of motion describing the evolution of the complex c-number functions of the photon annihilation and creation operators, based on the concepts outlined in [18,19]. Section 3 presents a generalized phase-dependent (PD) gain coefficient for parametric interactions, and a physically meaningful explanation for the generation from spontaneous emission of an idler wave phase-conjugated to the signal, and quadrature waves for maximal amplification and attenuation. Applications are outlined in Section 4, followed by a discussion, in Section 5, of new features emerging from a fully quantum optic approach to parametric amplification.

2. Quantum Optic Parametric Equations of Motion

Quantum optically, in the Heisenberg picture, the evolution of a physical process is described by relevant varying operators, while the initial-state wave functions are kept unchanged. A varying operator itself is the product of a basic operator and a c-number complex function, whose values are determined by the Heisenberg equations of motion [18,19]. The initial conditions are determined by the expectation values of the basic operator. The c-number functions for coherent states of light are the eigenvalues α (alpha) numbers, and combinations of these can be measured experimentally [20].

The phase dependence of the parametric gain coefficient and the related phase-pulling effect—presented in Appendix B for the classical fields—can also be derived quantum optically by means of the Heisenberg equations of motion for the annihilation and creation operators of all the optical fields—including the pumps—involved in the interactions.

Quantum mechanically (e.g., [18,19]), the Hamiltonian of interaction Ĥ_int, which describes the exchange of photons by stimulated emission involving an electric dipole polarization operator $\widehat{d}$ at point z and time t, and an additional optical field, takes the form:

$${\widehat{H}}_{int}=\hslash {\omega }_j\chi \mathrm{\Gamma }(\widehat{d}{â}_j^{†}+{\widehat{d}}^{†}{â}_j)$$

(1)

where the reduced Planck’s constant and the relevant susceptibility are, respectively, denoted by ħ and χ. The constant of proportionality Γ relates the Hamiltonian expressed in terms of the electric field operators to the Hamiltonian Ĥ_int associated with photon annihilation and creation operators, ${â}_j$ and ${â}_j^{†}$, of the ω_j field (j = 1, 2, 3, 4). These are defined by (see Appendix B for spatial field distributions):

$${â}_j(z,t)={â}_j(t)f_j(x,y,z)e^{-i({\omega }_{j}t-{\beta }_{j}z)}$$

(2a)

$${â}_j^{†}(z,t)={â}_j^{†}(t)f_j(x,y,z)e^{i({\omega }_{j}t-{\beta }_{j}z)}$$

(2b)

The Heisenberg equation of motion for ${\widehat{a}}_1$ leads to

$$\frac{\partial }{\partial t}{\widehat{a}}_1=-\frac{i}{\hslash }[{\widehat{a}}_1,{\widehat{H}}_{\mathrm{int}}]=-i{\omega }_1\chi \mathrm{\Gamma }\widehat{d}$$

(3)

after keeping only terms of the same frequency. For a χ⁽³⁾-based interaction, ω₂ + ω₃ = ω₁ + ω₄ and

$$\widehat{d}={\widehat{a}}_2{\widehat{a}}_3{\widehat{a}}_4^{†}$$

(4)

Thus, the photon annihilation operator $\widehat{a}$ acts on a coherent state |α> to generate a complex α (alpha) number (i.e., $\widehat{a}$|α> = α|α>), which has an amplitude and a phase of α = A e^−iφ, as shown in Equations (5)–(9) of [20]. No phase operator is involved in this quantum derivation. Equation (3) is in fact the equivalent of Equation (7.12) of [18], and the α complex numbers correspond to the “c-number functions” of Equations (3.14) and (3.15) of the trial solutions of [21]. The composite wave function of coherent states [22] is:

|Ψ> = |α₁> |α₂> |α₃> |α₄>

(5)

Combining Equations (2)–(4) leads to this equation of motion:

$$\frac{\partial }{\partial t}{\widehat{a}}_1=-i{\omega }_1\chi {\mathrm{\Gamma }}^{(3)}{\widehat{a}}_2{\widehat{a}}_3{\widehat{a}}_4^{†}$$

(6)

which is similar in structure to Equation (14) of [19]. Next, both sides of Equation (6) are multiplied from the right by |Ψ> and from the left by <Ψ| to produce the corresponding eigenvalues of the annihilation operators, so that:

$$\frac{\partial }{\partial t}{\alpha }_1=-i{\omega }_1\kappa {\mathrm{\Gamma }}^{(3)}{\alpha }_2{\alpha }_3\alpha {*}_4$$

(7)

After defining α = A e^−iφ, R₁ = (A₂A₃A₄)/A₁; θ = φ₂ + φ₃ − φ₄ − φ₁ + ∫ (∆β + ∆β^NL)dz, and κ = 2n γ⁽³⁾/k_o1;4 (the overlap integral γ⁽³⁾, defined in Equation (B7) below), and substituting into Equation (7), we obtain the rate equations for the amplitude and the phase of the eigenvalue α₁:

$$\frac{\partial }{\partial t}{A}_1=-{\omega }_1\kappa {\mathrm{\Gamma }}^{(3)}{R}_1{A}_1\sin \theta$$

(8)

$$\frac{\partial }{\partial t}{\varphi }_1={\omega }_1\kappa {\mathrm{\Gamma }}^{(3)}{R}_1\cos \theta$$

(9)

These equations for the complex functions of the operators’ c-number functions mirror Equations (B1)–(B6) derived below from the Poynting theorem of the flow of energy and can also be solved by means of elliptic functions [23,24]. The parametric interactions of χ⁽²⁾-based materials satisfy identical equations of motions.

The mixing of four photons within a single optical beam of one frequency can lead to inter-quadrature coupling of photons, with one photon returning into the same quadrature state (p), and another photon crossing into the second quadrature state (q) as a consequence of the relative phase being −π/2, that is, φ_p + φ_p − φ_p − φ_q = −π/2. This is a much weaker version of the OLP exchange of power ([6], Equation (5)).

3. Phase-Dependent Gain Coefficients and Phase-Pulling Effects

An input–output transfer function for the expectation values of the signal or idler powers P_1;4 can be found by recalling the relation between the flux of photons N = |α|² and the optical power of a beam [22] (i.e., P = ħ·ω·N). This will unify the classical (Appendix B) and quantum optic rate Equations (8) and (9) above.

A formal integration of Equation (B1) will define a gain factor G_1;4(z, θ) and an output power P_1;4(z), which are:

$$G_{1;4}(z,\theta )=exp{\displaystyle {\int }_0^z{g}_{1;4}(s,\theta )ds}$$

(10)

P_1;4(z) = G_1;4(z, θ) P_1;4(0)

(11)

The phase-dependence of the parametric conversion of photons is determined by the gain coefficient g of Equation (B2) through the relative phase θ of Equations (B4) and (B5). Photons of signal and idler waves will be absorbed by the pump for 0 < θ < π, and will be amplified for −π < θ < 0. The minimum level of input optical power corresponds to the spontaneous emission [14].

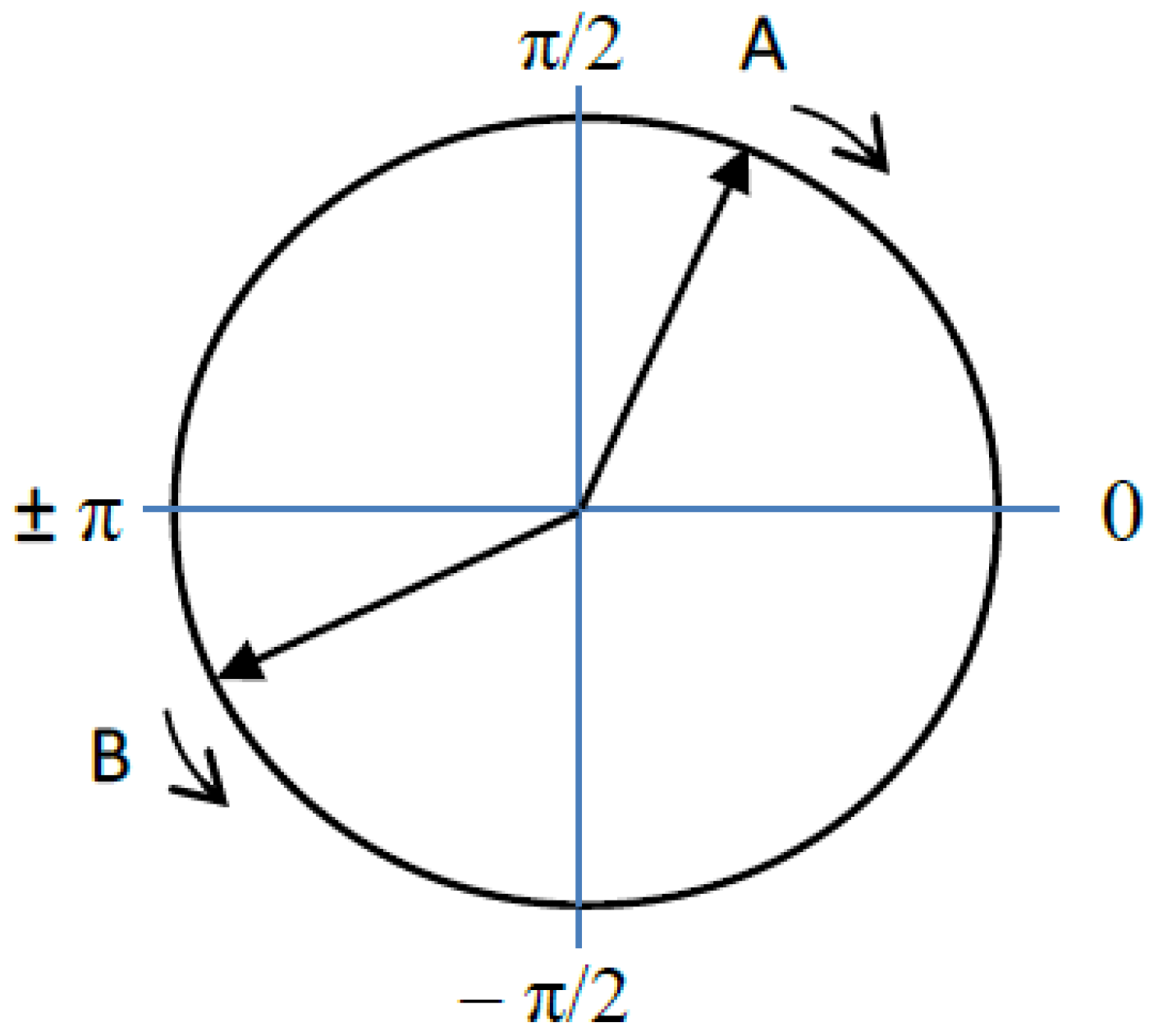
The power ratio r_1;4(z) of Equation (B3) also plays the role of a saturation factor, reducing the gain coefficient for higher input levels of P_1;4. A higher power ratio r_1;4(z) leads to a higher gain coefficient g, but also speeds θ towards −π/2. This is a parametric phase-pulling effect which, for P_pump >> P_signal/idler, can overcome a phase-mismatch Δβ + Δβ^NL ≠ 0, as explained in the next paragraph.

The parametric phase-pulling (PPP) effect undergone by the signal wave emerges from the rate of change of φ₄, which dominates the shift in the relative phase θ in Equations (B4)–(B6) for P₂ = P₃ > P₁ >> P₄. This is illustrated in Figure 1. From Equation (B4), for −π/2 < θ < π/2, the relative phase will rotate clockwise on the phasor circle (in the negative direction) towards −π/2; for π/2 < θ < 3π/2, it will rotate in the positive direction as –cos θ > 0. This field phasor rotation suggests the possibility of reducing phase fluctuations as the relative phase, if dominated by the ratio r_1;4 , is shifting towards the same optimal phase of −π/2, regardless of the initial phase values. In the process, the gain coefficient g₁ increases in value and becomes locked-in at the optimal value of θ for a phase-matched interaction.

For a vanishing total phase mismatch, with P₂ = P₃ > P₁ >> P₄ and spontaneous emission initiating one sideband wave P₄, its phase φ₄ change will dominate the shift of the relative phase to bring about θ = −π/2 = φ₂(0) + φ₃(0) − φ₁(0) − φ₄ at the output. By adjusting the initial pump phases φ₂(0) + φ₃(0), a conjugate phase φ₄ = −φ₁(0) can be obtained.

From Equations (B1)–(B6) we find that by setting φ₂(0) + φ₃(0) = 0, the propagating quadrature waves of φ_1;4 = ±π/4 and φ_1;4 = π ± π/4 are, respectively, amplified (+) and attenuated (−), being separated by π rad. Their nonlinearly induced phases are obtained from Equation (B6). Other input phases are pulled towards these values by the PPP effect of the last term of Equation (B6). The parametric phase-pulling effect will shift the arbitrary phases of photons towards a common value, thereby reducing the level of phase-noise, as demonstrated experimentally in [25].

4. Simultaneous Amplification of a Signal and Sub-Poissonian Distributions of Photons

In the previous two sections, we have identified the parametric phase-dependent gain coefficient and the related parametric phase-pulling effect as fundamental mechanisms underpinning two-photon output per interaction for χ⁽²⁾ and χ⁽³⁾ parametric processes for any level of optical powers and conditions. In this section, we consider the possibility of generating sub-Poissonian distributions of photons with the assistance of optically linear parametric (OLP) [6] and electro-optic parametric (EOP) [7] interactions, which involve only one-photon output per interaction—with one-photon input—although the EOP conversion requires one microwave photon. The rate equations for these processes are presented in Appendix C for a phase-dependent gain coefficient and the related phase-pulling effect (cf., Appendix B), and they are derived in a similar manner to Section 2 above by setting the appropriate electric dipole operators.

Let us consider a strong optical pump of angular frequency ω_o in the form of a coherent state of light, which is characterized by an eigenvalue α possessing a large average number of photons ‹N› = N_o, and a narrow phase-dispersion ([26], Section 8a) centered on its average value φ_o. Although the optical pump is commonly considered to remain undepleted, its temporal waveform N(t) displays photon number fluctuations which should fall within the Poisson distribution, with a quantum noise standard deviation of √N_o. A simple method for reducing the fluctuations of a strong pump would have its beam split into two equal parts and each part launched into one branch of an optical time-delay (τ) interferometric filter, so that, at the output, the number of photons will be proportional to N_out = 0.5 [N(t) + N(t + τ) + 2√N(t)·√N(t + τ)·cos (ω_oτ)]. The cosine term can be eliminated by adjusting the time delay so that cos (ω_oτ) = 0, leading to a Fourier transform of the superposition of two replicas of the photon number waveform. Their spectral power S(f)·cos² (πfτ) is shaped by a filter profile, which will attenuate high electrical frequencies of the photocurrent or photon-number sinusoidal waves associated which sharp rises and falls in the photon number fluctuations.

4.1. OLP Optical Couplers

An optical directional coupler (ODC), composed of two parallel and identical optical waveguides, can operate as a phase-sensitive (PS) amplifier when the signal power launched into one waveguide is much smaller than the pump power propagating in the other waveguide. This operation would be described by Equations (C2) and (C3) of Appendix C, indicating that the phase-sensitive gain coefficient g_s = g_a of a signal is inversely proportional to the square root of the signal’s power √P_s, thereby reducing the level of fluctuations in the output number of photons by enhancing the gain for the smaller number of photons. As a result, a sub-Poissonian distribution of photons is generated through the saturation-like amplification, which is the consequence of the stimulating field being different from the pumping field.

The possibility of generating a sub-Poissonian distribution of photons through signal-dependent differential gain can be assessed by imposing the condition that the input range [0.7N_o; 1.4N_o] of number of signal photons N_s(0)—covering most of a Poissonian distribution of average N_o—is reduced to the interval of the standard deviation (i.e., [N_o(L) − √N_o(L); N_o(L) + √N_o(L)]) at the output after an interaction length L.

An estimate of the reduced range can be assessed by inserting Equations (C2) and (C3) into the equivalent of Equations (10) and (11) above, with the powers converted into numbers of photons, to obtain the equality N_s,j(L) = N_s,j(0) Gs,j(L) (with input j = 1 for 0.7N_o and j = 2 for 1.4N_o) and, after setting N_p >> N_s,j, we obtain for the ratio µ_j = N_s,j/N_o the following expression:

ln µ_j(L) = ln µ_j(0) + ∫ [g_s,j(z) − g_o(z)]dz

(12a)

ln µ_j(L) = ln µ_j(0) + ∫ g’_o(z) (N_s,j − N_o(z))dz

(12b)

where g’_o(z) = dg_s/dN_s evaluated at N_s = N_o(z) so that g’_o = 2γ·√N_p·(−0.5)·N_o(z)^−3/2 from Equations (C2) and (C3) for maximal gain, and having used the linear relation g_s,j(z) ≈ g_o(z) + g’_o(z) (N_s,j − N_o(z)), that is, a truncated power series expansion of g_s(N_s). The design parameters include the coupling coefficient between the waveguides [6], the pump number of photons N_p, and the length of interaction L. An attempt to reduce ln µ_j to a target value close to zero may require more than one amplifying stage.

As an additional application, the gain coefficient can rotate the state of polarization of an optical beam through differential amplification of the x-polarized and y-polarized components if the optical powers are not equal, with the pump being polarized at an angle of π/4 rad relative to the axes.

For low levels of signal powers, the phase-pulling effect of Equations (C4)–(C6) and Figure 1 brings all signal phases towards the optimal value for maximum amplification, thereby reducing phase fluctuations. Thus, photons with a broad range of phases have their phases brought together by the phase-pulling effect, resulting in a coherent beam of photons. As an application, a binary phase-encoded signal {−π/2, π/2} can be converted into an amplitude binary {“1”, “0”} with a phase-sensitive ODC amplifier.

Another saturation-like mechanism which further increases the gain for weaker signals is the phase dependence of the gain coefficient identified in Appendix C. The phase-pulling effect tends to equalize the levels of powers between the pump power P_p and the signal power P_s, particularly so for an input phase difference of φ_p − φ_s = mπ (where m = 0, ± 1, ± 2,… an integer). For P_p >> P_s, the relative phase shift towards a maximal gain is dominated by the signal’s PPP-induced phase of Equation (C6), which is inversely proportional to √P_s. In this way, a weaker signal will reach the maximum gain condition faster than a stronger signal.

The phase-sensitive ODC device can support only degenerate frequency amplification (i.e., (ω_pump = ω_signal)) but one ODC will amplify any wavelength of a wavelength division multiplexed signal, provided that a suitable pump frequency comb is available. Amplification of nondegenerate frequencies can be delivered by EOP waveguides as outlined in the next section.

4.2. EOP Converters

The parametric amplification of a signal whose frequency is different from that of an available pump can be implemented with an appropriately designed electro-optic modulator. The EOP interaction [7] provides external control of the PS amplification through the phase of the microwave modulating signal.

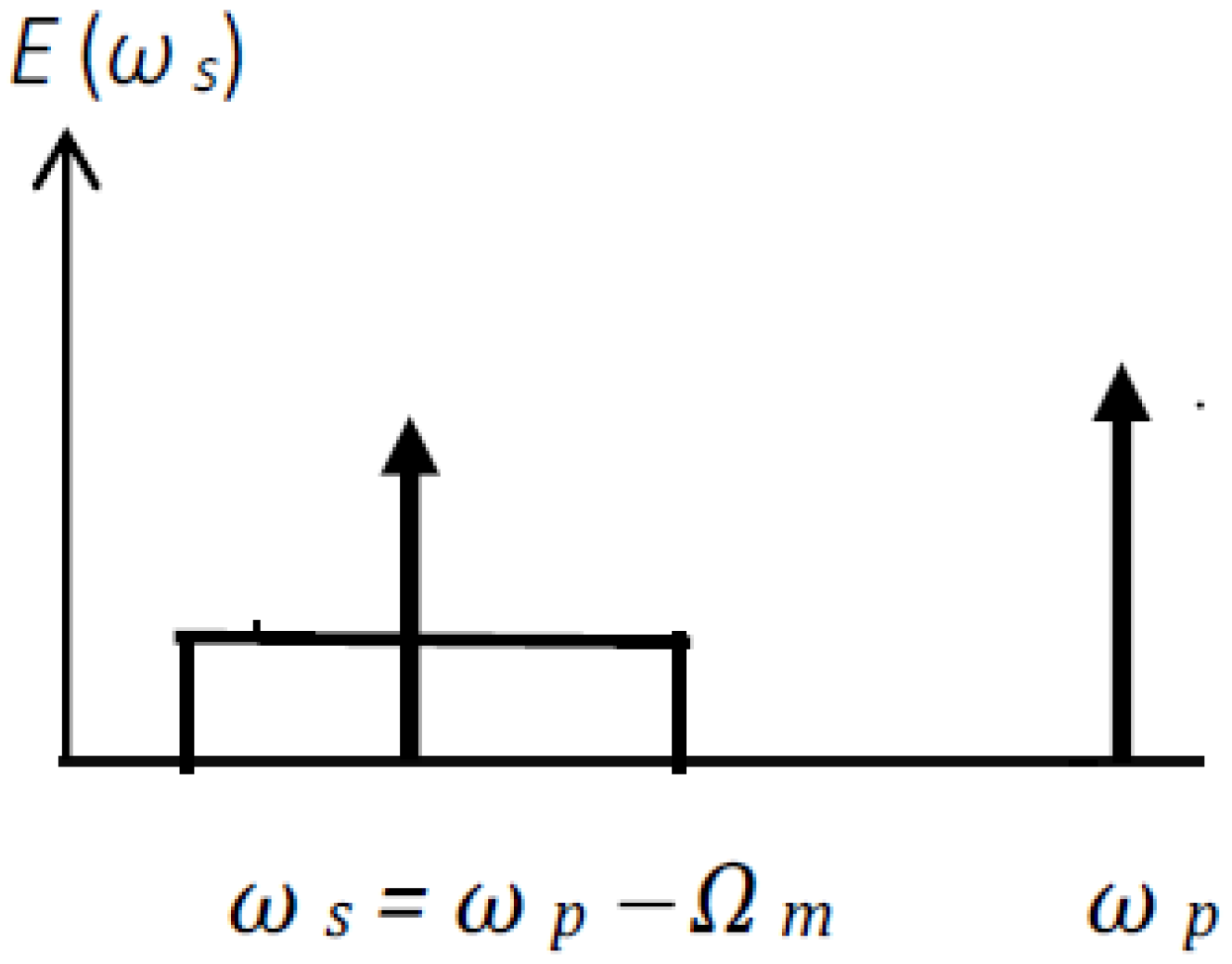
An electro-optic phase-sensitive amplifier (EO-PSA) will consist of an electro-optic waveguide with electrodes designed for traveling microwave modulating signals. By adjusting the phases of the microwave field and of the optical pump wave, a frequency downshifted input signal can be amplified or attenuated [7] as illustrated in Figure 2. An optical pump with a narrow spectral bandwidth can amplify and filter out a similarly narrow signal bandwidth through the EOP process of frequency translation [7,27]. The frequency downshifting ω_p − Ω_m = ω_s would be easy to implement because it generates microwave photons, requiring only a limited level of input microwave power. Broadband amplification with EOP devices is possible by operating multiple optical pump waves.

The PS gain coefficient, which decreases as the signal’s power grows—see Equations (C2) and (C3) of Appendix C—will reduce amplitude fluctuations, while the PPP effect will narrow the range of phase variations carried by the signal (see Figure 1).

5. Discussion—Physical Aspects of PS Gain Coefficients

The conventional method of experimental noise reduction through the interference between a signal and its phase-conjugate replica (e.g., [20,28,29] relies on parametric conversions of photons in χ⁽²⁾ and χ⁽³⁾-based materials. These techniques, however, constitutes only a particular case of a broader picture of parametric processes.

The approximated mathematical solution of Equations (A1) and (A2) below is inconsistent with the rigorous and physically meaningful solution published in 1962 in [23]—and expanded in 2013 in [24]—and which was largely overlooked because of its complexities involving elliptic functions. Nevertheless, its physical features can be extracted from the interlinked rate equations of motion for the powers and phases of the optical waves involved in the parametric processes as presented in [5,6,7,14]. As a result, one identifies, classically, a phase-dependent gain coefficient and a related phase-pulling effect. The rigorous solution rules out simultaneous amplification and attenuation of the signal and idler waves as indicated in Equations (A1) and (A2) of Appendix A.

Equally, an approximation-free and fully quantum optic analysis of parametric processes—see Section 2 above—reveals that the conversion of photons involves a parametric gain coefficient which depends on the relative phase between the pump waves and signal/idler waves and is inversely proportional to the square root of its power, as well as identifying a parametric phase-pulling effect, for any levels of optical powers.

The parametric interactions also incorporate a phase-pulling effect capable of countering a phase-mismatch condition and tending to equalize the levels of power among the waves taking part in the mixing of photons. Amplitude noise reduction is achievable for any levels of signal power as the gain coefficient displays a saturation-like property. The same characteristic is also exhibited by the related PPP effect.

The similarities between OLP and EOP processes, on the one hand, and the three- or four-photon mixing interactions, on the other hand, are evident, as all these processes belong to the same group of physical phenomena whereby the optical fields drive the atomic electrons into oscillation with no absorption of energy between resonant energy states.

The mathematical technique of linearizing—on the basis of assumptions and approximations [30]—the parametric nonlinear coupled wave equations brings about loss of physical properties and the appearance of physical inconsistencies as pointed out in the Introduction and Appendix A. The differential equations derived under the condition of undepleted pump approximation do not include the variation of the conversion-related phase, or the possibility of power coupling reversal, which is a major feature of parametric processes.

Possible operations of carrying out phase-sensitive amplification at low levels of optical power and over short interaction lengths may benefit from the versatility offered by parametric processes involving only two optical waves. Functional operations can be implemented at low levels of pump power and over short distances of a few wavelengths for OLP interactions and centimeters for EOP interactions.

Equally, a combination of OLP and EOP devices will also involve only two interacting optical waves with the EOP effect providing direct interfacing between the electrical and optical domains through the electro-optic effect of a suitable crystal interleaved with silica waveguides.

6. Conclusions

A physical analysis of parametric processes reveals a common feature of phase-dependent gain coefficients accompanied by a phase-pulling effect. Phase-sensitive amplification can be achieved at low levels of optical power and over short interaction lengths by means of optically linear and electro-optic parametric conversions of photons. With only two optical waves needed for signal processing, (e.g., amplification, noise reduction, filtering, etc.), the EOP–based devices will have the advantage of direct external control for different signal and pump frequencies.

These physical mechanisms can generate sub-Poissonian distributions of photons through a saturation-like effect, using only integrated photonic circuits.