1. Introduction
The subject of fluid structure interaction (FSI) is very complex and involves the coupled interaction of fluid flows with solid bodies, rigid and elastic. In this paper we analyze a simple version of such a problem by investigating the forces upon flexible fibers attached to a basal body and held in different configurations. This three dimensional investigation was conducted at low Reynolds numbers (between 0 and 9000) and is an extension of our previous two-dimensional study [
1].
While our study remains at a more fundamental level, applications for this problem are plentiful. The modeling of unmanned air vehicles (UAV), for instance, is a very important and well studied FSI problem corresponding to aerodynamic flows. One key objective in these problems is the optimal design of the aircraft (rigid-body) through minimization of the forces acting on it. Additionally, FSI has several medical applications; numerical studies have been done to analyze airflow in human vocal folds. Specifically, the modeling of the interaction between air and vocal chords when talking is important planning vocal surgeries, and in voice rehab. Understanding the dynamics of elastic structures and their interaction with fluids can greatly advance the medical industry [
2,
3].
The terminal configuration, including velocity and orientation, of a rigid body in a fluid flow is a well studied problem for over a century and continues to be explored (see for instance, [
4,
5,
6,
7,
8,
9,
10]). The classical problem of the terminal orientation of a body itself is a difficult problem which is compounded by the addition of flexibility [
11,
12,
13,
14,
15,
16]. The current paper is a part of our ongoing contribution to the broader subject of terminal configurations in fluid-solid interaction and aims to extend the results of our previous work [
1]. Experimental and numerical studies have revealed that deformable bodies in a flow reconfigure their orientations in order to reduce drag. An important metric for the bending behavior is the drag exponent or “Vogel exponent” [
17,
18] which indicates the rate at which drag force on the body varies with the velocity, given by the expression
where
according to previous studies. The current paper considers flexible fibers, attached to a basal body, submerged in a flow with speeds 0–50 cm/s. The effect of fiber length and orientation, upon the bending behavior are examined.
The paper is structured as follows. In
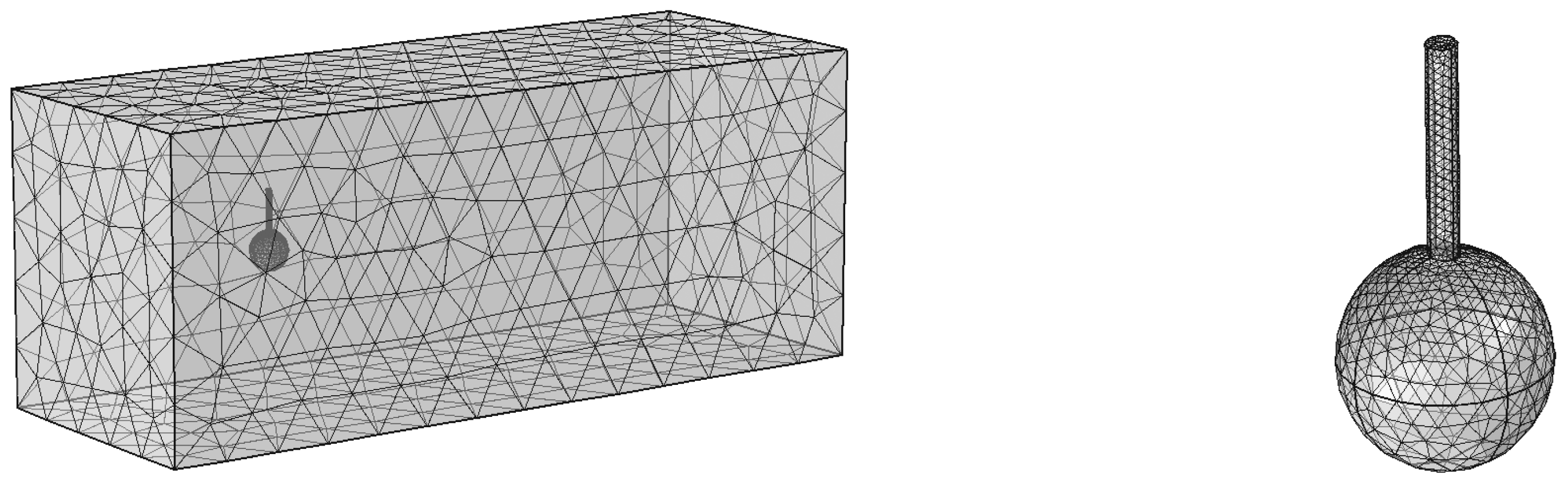
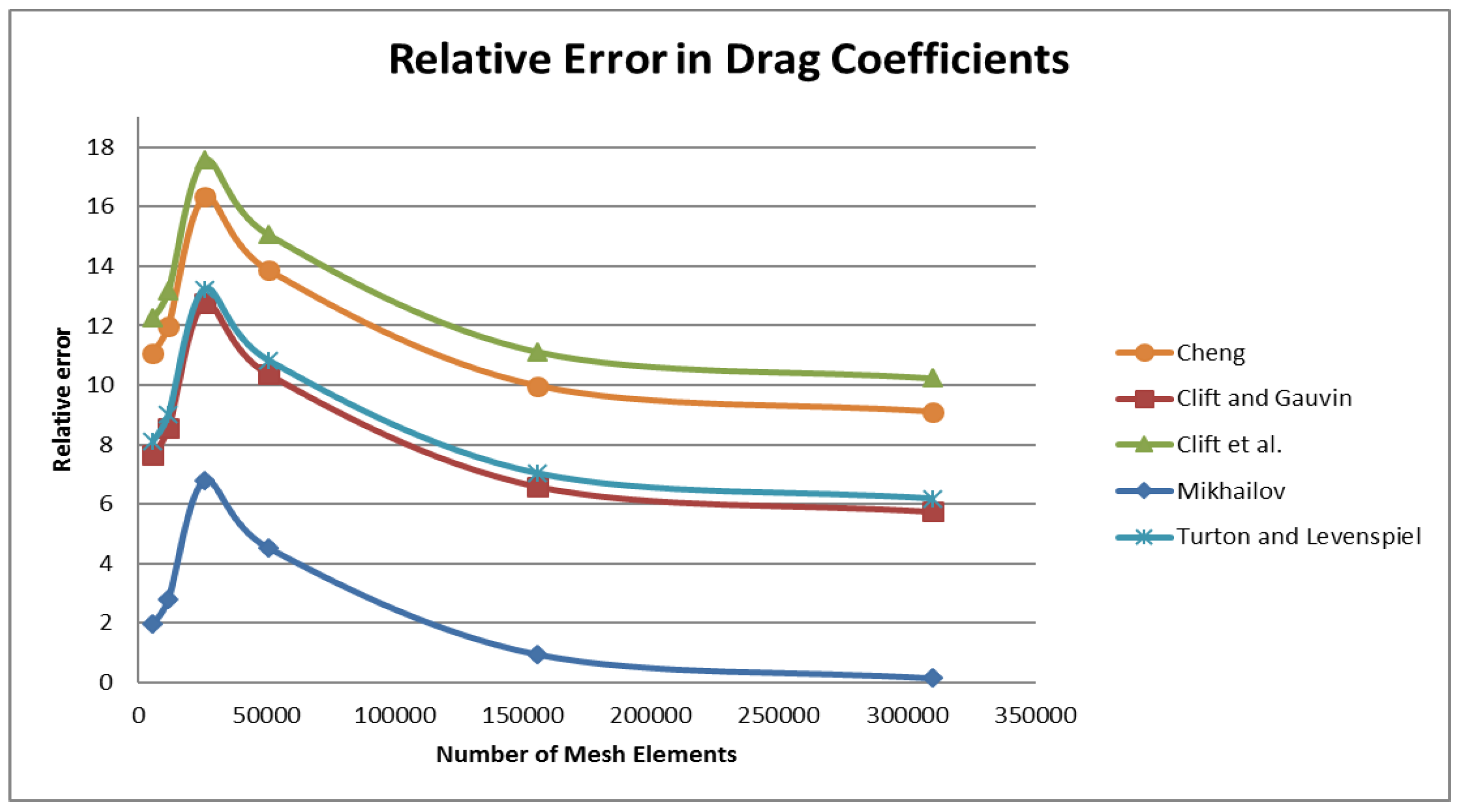
Section 2 we describe the numerical setup we use for our analysis. As part of this setup, we first perform a benchmark of the methods we use to make sure they can reproduce classical results (
Section 2.2.1). We choose a simplified three dimensional problem—the flow around a ball-and use the drag coefficient to gauge our numerical calculations. We then perform a convergence study to determine the optimal mesh density that will be used in the main study (
Section 2.2.2). In
Section 3 we describe the results of our analysis of the ball and fiber system and offer conclusions and plans for future work in
Section 4.
3. Results
In this section, we describe the numerical solutions generated with COMSOL. Additionally, we discuss similar results to the two-dimensional simulations performed in [
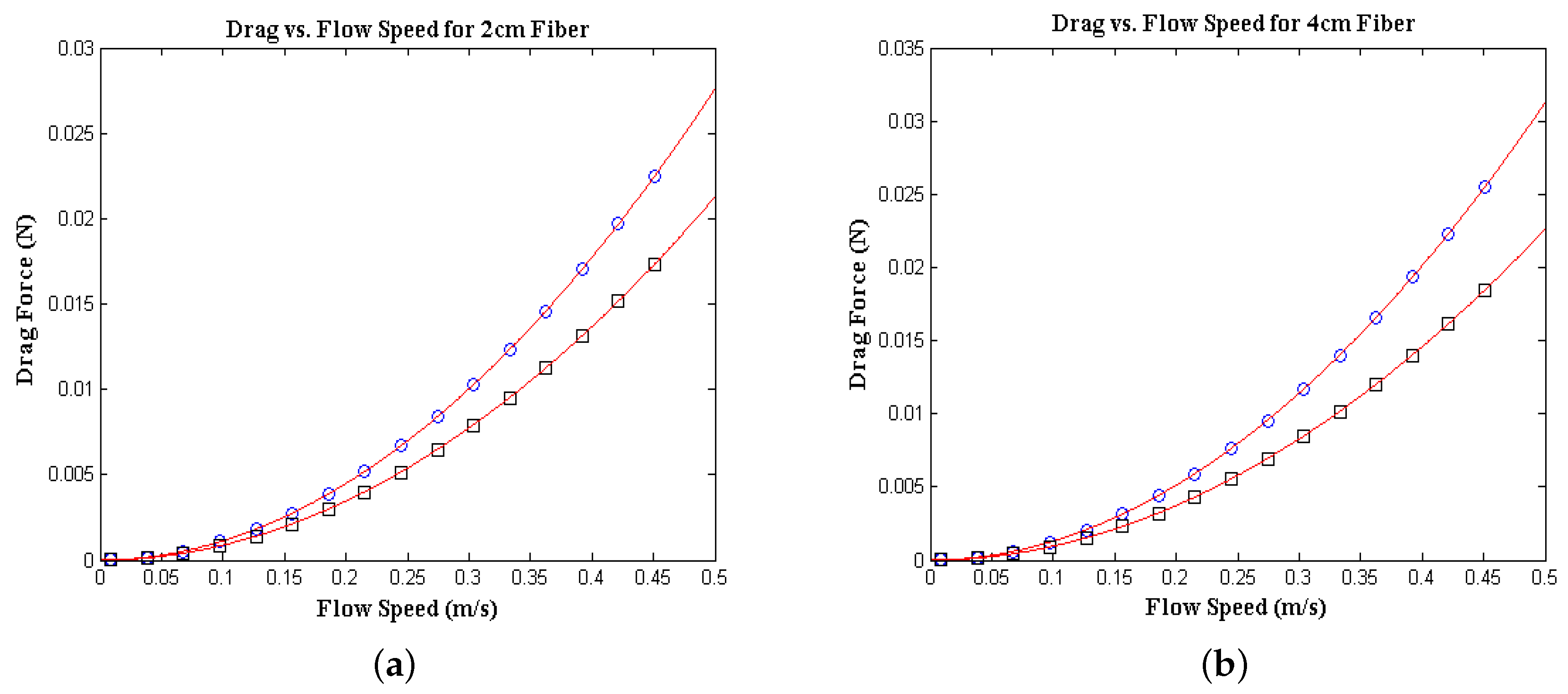
1] such as deformation angles, drag and Vogel exponents. The change in the drag force on the ball and fiber system with the flow speed is depicted in
Figure 3.
The graphs show the change in the drag force for fibers of lengths 2 and 4 cm respectively. We notice that an increase in fiber length leads to a significant increase in drag force. The red lines in the figure represent exponential least squares fits, i.e.,
The drag coefficients and Vogel exponents [
17],
α, for the parameter range examined in this study are summarized in
Table 4. We can see from this table that the Vogel exponents are much closer to the standard inertial drag model with
. The flexible body appears to be much stiffer, and bends less due to the properties of the solid such as the bulk modulus.
We also examined the average bending behavior of the fibers by computing the deflection angle of the line connecting the points of suspension and free ends of the fiber. Spherical coordinates are used as the reference frame. The Cauchy number (
Ca), defines the ratio of inertial to elastic forces in the system and is given by
where
ρ is the density of the fluid,
U is the characteristic velocity and
K is the bulk modulus of the fiber which is taken to be 4 GPa (based on our previous experiments with Nylon fibers). Gosselin et al. [
13] note that the drag on a flexible rectangular plate can be seen to depend on an appropriate scaling of
, defined by
(where
is the drag coefficient) such that for
the flexible plate transitions to a reconfigured state. As in our previous studies, we use a simple rescaling of the Cauchy number,
to bring it to the same scale as in previous work. The initial coordinates
were calculated using the coordinates of the center of the sphere. That is, for the 90 degree case, we have
,
, and
. For the 45 degree case a geometrical argument was used to deduce
,
, and
. The coordinates of the tip of the fiber, denoted
were measured using an averaging probe around the boundary representing the tip of the fiber. Our coordinate system is denoted by
, where
φ is the measure of the angle from the vertical and
θ is the measure of the angle in the
plane. Typically, the bending in the
direction,
φ, is that being compared to the 2-dimensional results. Here
and
, where
.
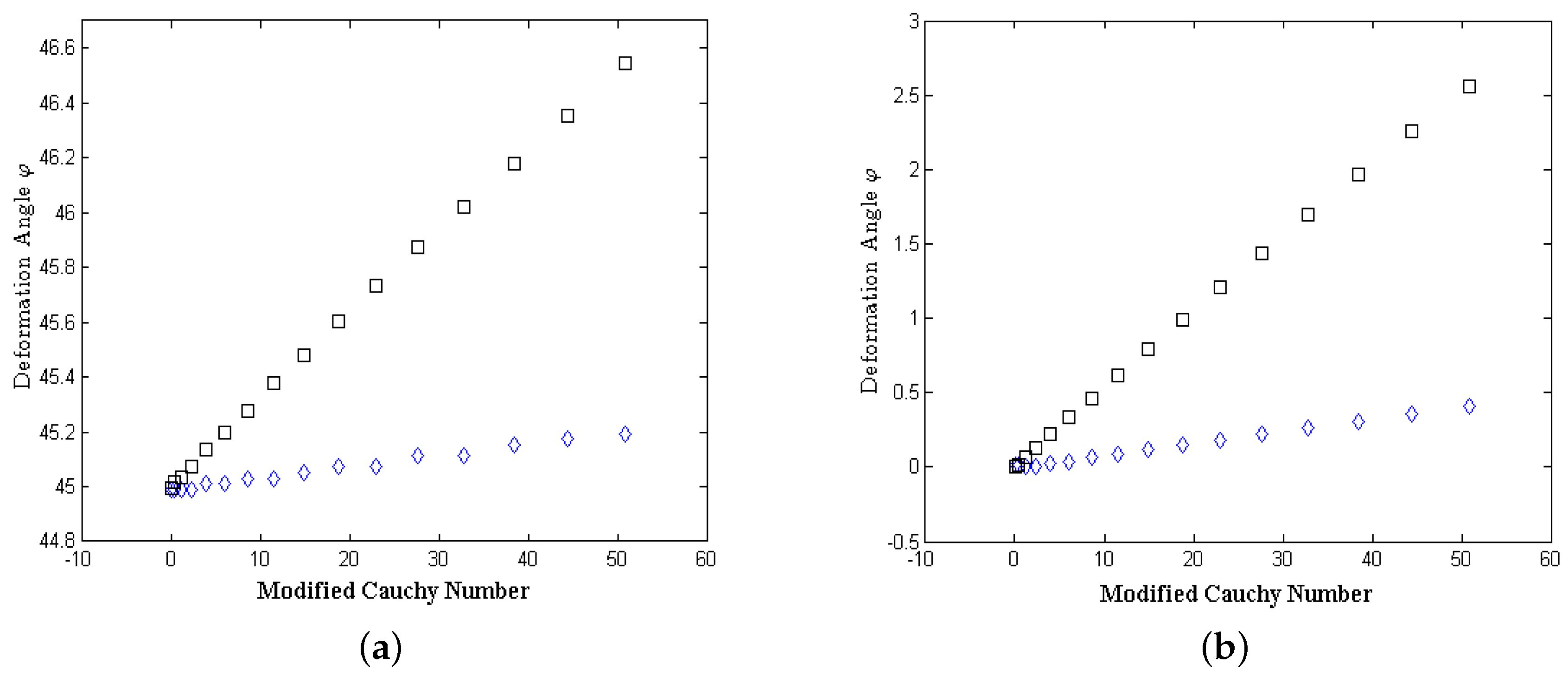
We can see from
Figure 4 that an increase in fiber length corresponds to an increase in bending. Furthermore, for higher
, the difference between the deformation angles among varying fiber lengths increases. For
of approximately 50, the difference between the 4 cm and 2 cm fibers in initial configuration of 45 degrees is around
. Additionally, the difference in the 90 degree case seems more significant. The difference among fiber lengths seem to vary about
in this case. If we compare among the two images we see that, qualitatively, the different configuration angles produce similar deformation. Although, the difference is subtle, it appears that the 90 degree configuration changes with modified Cauchy number at a faster rate. The fiber represented here is merely a prototype to model different scenarios, in which bending may be more prominent. For example, the hair that lines the skin is much thinner than the fiber used, and thus has different structural properties. We expect that these type of fibers should bend more. For the two-dimensional study, we used a fiber of different length and resulted in significant bending [
1].
One main goal in computations is to reduce the dimensionality of the problem to make the modeling easier. It is important to check the validity of this reduction, however. In this section we compare the simulations in two and three dimensions. The results of the two-dimensional simulations were reported in our previous paper [
1]. In the two-dimensional experiments, we see the Vogel exponents to be significantly smaller than those of the three dimensional problem, for the same geometric setup and parameter values. In 2-D we see Vogel exponents ranging from
to
, however, in 3-D we see that the Vogel exponents follow closer to the exponents of a rigid body. Specifically, we have found that the exponents range from
to
.
The deformation in the plane was measured (φ) in both two and three dimensions. We found no significant percentage increase in bending between the slowest flow speed of m/s and fastest flow speed of m/s. We measured the initial configurations of and for both the 2 cm and 4 cm fibers. For the 2 cm fiber the percentage increase in bending is rather small. Specifically, for we see an increase of about in 2-D versus an increase of approximately for 3-D. The initial configuration shows an percentage increase of approximately for the 2-D fiber versus an increase of approximately for the 3-D fiber.
The 4 cm fiber bends much more, but shows no significant difference between two and three dimensions. For the initial configuration of
we have an percentage increase of about
for 2-D fiber and
for 3-D fiber. For the initial configuration of
we see an increase of approximately
for the 2-D fiber and
for the 3-D fiber. More accurate calculations and relative percentage differences are seen in
Table 5 and
Table 6.