1. Introduction
The transition of the boundary layer from laminar to turbulent flow has attracted research interest for more than a century as it plays an important role in both fundamental studies of fluid mechanics and in engineering applications [
1]. In this transition process, relatively small environmental disturbances introduced into the flow may amplify, interact with other nonlinear modes and lead to laminar flow breakdown. During the initial receptivity stage, the small amplitude disturbances are transformed into internal unstable Tollmien–Schlichting (TS) waves within the boundary layer [
2]. If the TS waves amplify to sufficient amplitude [
3], strong non-linear effects become significant and generate a series of two-dimensional (2D) harmonic waves resonantly [
4]. As an enhancement of non-linear interaction, the harmonic waves are unstable to infinitesimal three-dimensional (3D) broadband disturbances that are always present both naturally and in experiments [
5]. Based on their interacting mechanism, the normal transition can be subdivided into two kinds: fundamental transition first observed in [
6] or subharmonic transition first discovered in [
7].
In fundamental resonance, the TS wave interacts with the 3D disturbance wave of a given spanwise periodicity, resulting in an overall 3D structure with a “peak and valley distribution” in the spanwise direction for the streamwise disturbance velocity [
6]. Λ-vortices in an aligned pattern appearing with tips at the peak positions when the 3D disturbance amplitudes have attained a magnitude of comparable order as the 2D TS wave.
Λ-vortices also occur in the subharmonic resonance, but are formed in a different way. The 3D structures are initiated by a 2D fundamental TS wave with frequency
and its spanwise subharmonic wave with frequency
[
8]. The subharmonic wave rapidly amplifies to reach a magnitude of the order of the TS wave and leads to distortion in the spanwise direction [
9]. Then, groups of weak Λ-vortices are formed in a staggered pattern.
In [
9], the authors showed experimentally that, in the late stage of transition flow, the local behavior of the disturbances in the vicinity of
-structures is very similar with regard to both fundamental and subharmonic resonances. The main common features of the transition process include: (a) the formation of
-structures; (b) the appearance of spikes (large negative streamwise disturbance velocity in the time series) near the tips of
-structures; and (c) the formation of ring-like vortices departing away from the
-vortex and moving upward in the external part of the boundary layer. Although the physical observations of transition have been widely recorded in the literature [
6,
9,
10], little consensus has been reached on a common mechanism behind the transition. In the experiments of [
11], an Adverse-Pressure-Gradient (APG) boundary layer transition is induced by a TS wave plus initially weak broadband disturbances. The observed
-vortices, intensive
-shape high shear (HS) layers,
-vortices, ring-like vortices and associated spikes seen in time-traces and other phenomena are distributed randomly in time and space and have somewhat distorted shapes. However, it is reported that their general properties are qualitatively similar across sub-harmonic, harmonic and broadband disturbances.
Since the local behaviors of the vortex are quite similar in the late stage of transition, there is a strong interest in a theory to explain the common features of vortex evolution. In [
10], the authors found that the first sign of randomness in the transition process was observed at a position corresponding to the tip of the Λ-vortex. In an experimental study of [
12], a 3D Soliton-like Coherent Structures (SCS), essentially a wave packet accompanied with a high shear layer, is proposed to be the building block of the vortical coherent structures, which leads to turbulent burst [
11]. Similarly, the Direct Numerical Simulation (DNS) results of [
13] indicated that turbulence is not generated by vortex breakdown, but rather by positive and negative spikes and consequent high shear layers. A follow-on study by [
14] further proposed that the shear layer instability is the “mother of turbulence”. Both studies proposed theories suggesting a universal mechanism for turbulence generation and sustainment in [
12,
14]. Though different theories exist, the transition processes are essentially based on the existence of coherent flow structures and the formation of high wavenumber components, which is the precursor of turbulence. Therefore, the present study directly applies a local wavenumber detector, wavelet analysis to investigate the relationship between the typical vortical structure and the high wavenumber components, which is captured by a high order combined compact difference scheme in numerical simulations [
15,
16]. It can be shown that the local high wavenumber components in the streamwise direction mainly cluster inside the high shear layer region. The authors observe such behavior across fundamental, subharmonic resonance and transition induced by the broadband disturbance. The last case is the most general scenario, and hence, it is the focus of the present study.
Numerical simulation provides a helpful tool to investigate how spatial disturbance signals evolve temporally. Such studies have provided significant results to the study of boundary layer transition [
10,
17,
18,
19,
20], but only a few of them present a spatial spectrum of the disturbance as in this study. The present study uses recently-developed high order combined compact difference schemes with non-uniform grids for numerical simulations of the Navier–Stokes (NS) equations for flat plate boundary layer transitions [
15,
16,
21]. While these schemes are “DNS-like”, they however are highly optimized for boundary layer transitions, i.e., having (a) low-numerical dispersion/dissipation to preserve wave speed and amplitude, (b) non-uniform gridding in the wall-normal direction to capture the high velocity gradients near the wall and (c) reported good comparisons with the experiments of [
22] for Zero-Pressure-Gradient (ZPG) and [
23] for APG for
(Reynolds number based on displacement thickness
) up to 1200. In the present study, simulation results of the experiments from [
11] on the APG boundary layer transition with
up to 1130 are analyzed in detail. Furthermore the Continuous Wavelet Transform (CWT) is used as the signal identifier to demonstrate the local high wavenumber spectrum in the boundary layer transition. This technique has been used to investigate turbulence by many researchers, e.g., in [
24], the authors used wavelet analysis to demonstrate the Richardson cascade in turbulent flow.
The organization of this paper is as follows:
Section 2 gives a brief description of the Combined Compact Difference (CCD)-based numerical model used to simulate the experiment of [
11] on APG boundary layer transition.
Section 3 makes a qualitative comparison between the simulation results and the experiment. It demonstrates the common features of the vortex in the boundary layer across fundamental and subharmonic transition also existing in broadband disturbance.
Section 4 discusses the application of CWT to analyze transition signals demonstrating that CWT is a good identifier of high wavenumber components in transition flow.
Section 5 tracks the evolution of a typical Λ-vortex showing that the high wavenumber components are imbedded in the associated spike region, and high shear layers developed in transition boundary layer flow.
Section 6 provides the conclusion.
2. Numerical Model
In the numerical model of the boundary layer flow used here, all variables in the Navier–Stokes equation are expressed in non-dimensional form and related to their dimensional counterparts, denoted by bars or uppercase, as follows:
where
,
and
denote the coordinates of streamwise, wall-normal and spanwise direction, respectively, and
,
,
are the corresponding velocity components in each direction,
is the characteristic length,
is the freestream velocity,
is the kinematic viscosity and
is a reference Reynolds number.
,
,
and
are used to denote the corresponding dimensional spatial and temporal coordinates. The NS equations are solved using a vorticity-velocity formulation with corresponding vorticity components in non-dimensional form given as:
In addition, the total flow field
is decomposed into a steady 2D base flow
and an unsteady 3D disturbance flow
, which is expressed as:
with:
2.1. Computational Domain
The computational domain was setup to closely match the experimental environment of [
11]. The physical system is that of an APG boundary layer flow (with Hartree parameter
= −0.115) over a flat plate, which is disturbed by a blowing and suction strip at a certain upstream location. A comparison sketch of the distance from leading edge, disturbance source location and main region of interest along the streamwise direction are sketched in
Figure 1. The rectangular computational domain is shown schematically in
Figure 2. The computational domain is 500 mm × 25.3 mm × 48 mm in the streamwise (
), wall-normal (
) and spanwise (
) directions, respectively, and started at 250 mm from the leading edge. The blowing and suction strip was located over 287 mm to 308 mm to simulate the disturbance sources used by [
11]. The amplitude of the disturbances were calibrated to that at location
X = 450 mm using available experimental results. The main region of interest was over
X of 450 mm to 530 mm where experimental data are reported, even though the experimental section continued to 1490 mm. The present computational domain, though smaller, covers this region of interest and extends to
X = 580 mm, after which a buffer domain was used until
X = 753 mm.
The length of the domain in the wall-normal direction in the simulation covers about 12-times boundary layer displacement thickness , with typical turbulent structures extending upwards to 5. Thus, there is no suppression of turbulence development. The measured disturbance signals in the experiment repeats every 48 mm in the spanwise direction; hence, the spanwise domain size used here is one disturbance wavelength, of 48 mm.
2.2. Simulation of Base Flow
The steady base flow solution
was first obtained from numerical integration of the NS equations to a steady state:
At the inflow boundary, the solution of the Falkner–Skan equation was used to specify the base flow variables. No-slip and no-penetration conditions were used at the wall. The wall vorticity was calculated from the velocity field considering the continuity condition. The vorticity vanished at the freestream boundary where
was prescribed as:
where the form of
is given later in
Section 3.
At the outflow boundary, all equations were solved dropping the second
-derivative terms, and
is calculated from:
A more detailed description of these boundary conditions in a Blasius boundary layer flow is found in [
15].
2.3. Simulation of Base Flow
The NS equations consist of three vortex transport equations:
where:
and three velocity Poisson Equations [
19,
25]:
All disturbance flow variables vanished at the inflow boundary. Potential flow held at the freestream boundary so that the vorticity components vanished. Equations (18) and (20) were solved for
and
at the freestream boundary. For
, the local wall-normal gradient was prescribed to impose an exponential decay [
26]:
where
and
and
are the streamwise and spanwise wavenumbers, respectively.
At the wall boundary, no-slip conditions were used. The vorticity components were calculated from their relationship with velocity [
19,
26,
27]. A buffer domain method was used at the outflow boundary to allow disturbances to travel out of the computational domain without upstream reflection. Periodicity conditions were employed at the spanwise boundaries at
= 0 and
=
. Centerline symmetry is not assumed here, unlike, e.g., other reported work [
19,
26,
27], so that the asymmetric disturbance waves could develop freely.
2.4. Numerical Method
Since the unsteady disturbance flow was assumed to be spanwise periodic, the disturbance flow variables
and the terms
were expanded using Fourier modes:
where
and
is the lowest spanwise Fourier mode, which is related to the spanwise wavelength
by:
Substituting Equation (22) into Equations (12) to (20) gave a set of
governing equations for each
-plane integration domain. The nonlinear terms
,
and
of the vorticity transport equations were evaluated pseudo-spectrally using fast Fourier transform for conversion from Fourier space to physical space and back with the 3/2 rule used for de-aliasing [
28].
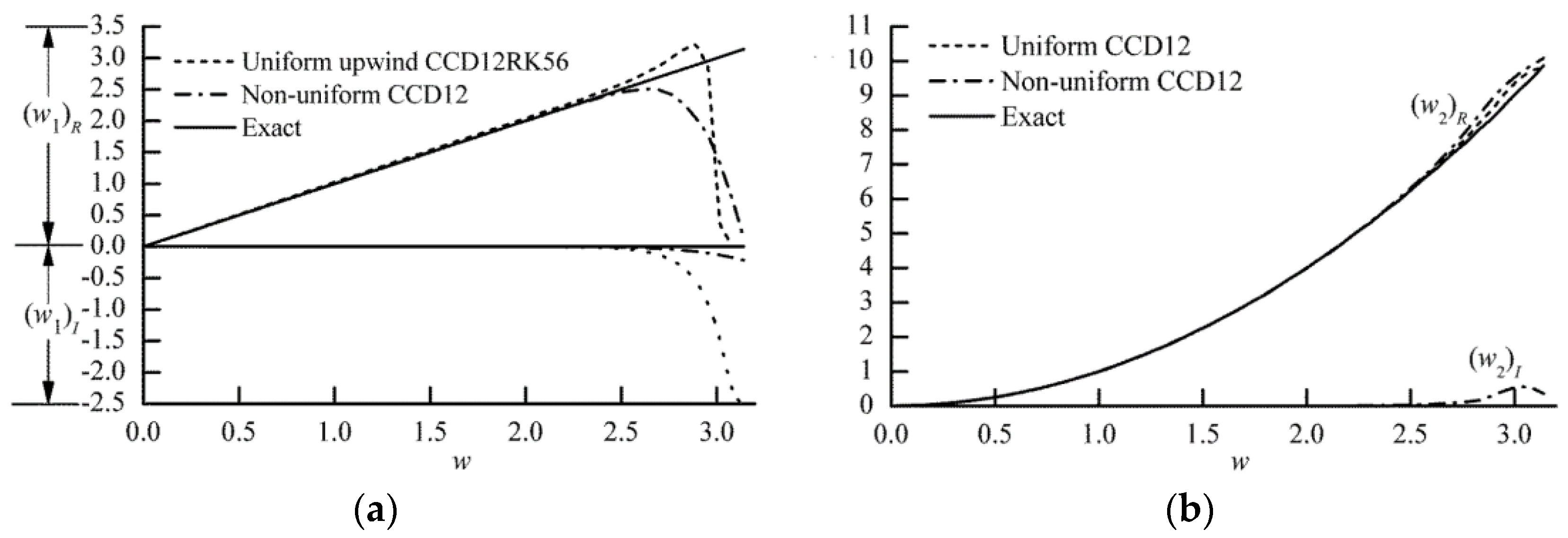
Combined Compact Difference (CCD) schemes up to 12th-order accuracy were used in the streamwise and wall-normal directions as reported in [
15,
16]. The spectral resolution of these schemes can be demonstrated by the modified wavenumber analysis following [
29], wherein the scaled wavenumber
where
is the physical wavenumber and
is the grid spacing. The modified scaled wavenumber
i.e., the one represented by the finite difference scheme, is typically complex. The closer
is to
, the more accurate is the scheme. The modified wavenumber analysis for each scheme used in the simulation is presented in
Figure 3. The upwind CCD scheme co-optimized with fourth order 5 to 6 alternating stage Runge–Kutta (RK) scheme (denoted as uniform upwind CCD12RK56 in
Figure 3a) was used for the
term in Equations (12) to (14) and (18) to (20) in order to preserve low-dispersion (related to the real part of
) and low-dissipation errors for wave propagation (related to the imaginary part of
). This scheme also suppressed numerical oscillations introduced from the buffer domain, because of the very negative
near
= 3. The
terms in Equations (12) to (14) and (18) to (20) are discretized with a centered difference scheme (denoted as uniform CCD12 in
Figure 3b) [
15]. In the wall-normal
direction, the CCD schemes were directly constructed on a non-uniform grid without the use of coordinate transform. The spectral resolution for the non-uniform CCD12 scheme used for
is given in
Figure 3a, and that for
is given in
Figure 3b. A second-order 5 to 6 alternating stage Strong Stability Preserving (SSP) RK scheme was used for the term
to allow a larger time step. All of the schemes presented in
Figure 3 have a high spectral resolution up to
= 2.5, and detailed analyses of these schemes are given in [
15,
16]. A multigrid method is used to solve the velocity Poisson Equation (19). A stable stretching grid [
16] was used in the
direction to obtain fine resolution in the near-wall region.
In the present simulations, 1000 uniform grid points with
= 0.5 mm were used in the streamwise direction, which represented a resolution of about 61 grid points per TS wavelength. Since 12th-order CCD schemes was used in this direction, a scaled wavenumber as high as 2.5 could be accurately simulated, implying that harmonic waves with the wavenumber roughly 25-times the TS wave could be accurately captured [
15]. Considering that the TS scaled wavenumber in the present simulation is 0.103 (TS wavenumber ×
= 205.9 rad/m × 0.5 × 10
−3 m), the highest wavenumber that can be accurately resolved is thus about 5000 rad/m (205.9 rad/m × 2.5/0.103). In the wall-normal direction, 120 grid points were used. A stable stretching grid was used in the near-wall region with grid sizes ranging from 0.01 to 0.62 mm. This had been demonstrated to successfully resolve the large velocity gradient of the high shear layer in the boundary layer transition flow [
16]. Sixteen Fourier modes were used in the spanwise direction. The total number of grid points used in this study was 3.84 × 10
6.
was selected to be as small as 6.56 × 10
−6 s so that the maximum CFL number in the streamwise direction (
)
0.12, which satisfied the scheme optimization condition given in [
15]. This
also satisfied the stability criterion in the wall-normal direction as detailed in [
16]. As all variables were non-dimensionalized in Equation (1), the needed kinematic viscosity
used was 1.526 × 10
−5 m
2/s, as in the experiments by [
11]. The reference velocity was selected to be
= 30.52 m/s. The reference length
was set as 0.05 m, so that the reference Reynolds number
is 105. The local Reynolds number based on displacement thickness
ranged from 820 to 1130 over the computational domain.
It is noted that the number of grid points in the present simulation (1000 streamwise × 120 wall normal × 32 spanwise) would usually be insufficient to resolve the full-scale vortex motion even in this low-Reynolds number turbulent boundary layer when using lower resolution schemes. As a comparison, a similar study on fundamental resonance using Direct Numerical Simulation (DNS) in [
19] on the ZPG transition flow up to the stage where the
-vortex was formed used fourth order finite difference schemes on a grid of 3000 (streamwise) × 65 (wall-normal) × 32 (spanwise). The highest wavenumber disturbances dominated in the streamwise direction necessitating finer grid point in this direction. In [
30] where a second order finite difference scheme in each direction was used, typically 4096 × 400 × 128 grids were needed to simulate a fully-developed turbulent boundary layer. Here, the use of 12th order CCD schemes allowed the grid points in the streamwise direction to be significantly reduced. In particular for the experiment of [
11], which the present results are being compared to, the highest disturbance frequency recorded is around 1100 Hz (
Figure 19 in [
11]). Since the TS wave frequency is 109.1 Hz, this means about 10 harmonics of TS wave exist. As the TS wave number is 205.9 rad/m, hence the wavenumber of the 10th harmonic is 2059 rad/m. Considering that the amplitude of broadband disturbance is comparable with the harmonics of TS wave, the disturbance should thus be resolved by the present numerical scheme with resolution up to 5000 rad/m. The flow parameters, grid resolution and size of the computational domain are summarized in
Table 1.
The preceding analysis shows that the present resolution can capture the major vortical motion during the transition. Further as the present study is on an APG boundary layer and also focuses on mid-stage including ring-like vortices formed after
-vortices, the velocity gradients in the wall-normal direction are larger than in [
19], necessitating the stretching grid with higher resolution in the near-wall region. The comparison with experiments from [
11] as given below demonstrates that grid used was sufficient to resolve the dynamics of the most energetic vortices, enabling the numerical simulation to realistically model the vortex evolution in the transition flow experiment.
2.5. Continuous Wavelet Transform
The CWT used to investigate the evolution of coherent structures is described next. The CWT is defined as:
where
is the mother wavelet and
is the scale of the transform and can be determined by:
is the centered frequency of the wavelet;
is the wavenumber spectrum of the signal; and
is the grid space or sampling period.
The most commonly-used wavelet is the complex-valued Morlet wavelet because it gives information on the phase and has good resolution for the high wavenumber components [
31]. The complex-valued Morlet wavelet used here is given by:
where
is the non-dimensional frequency, taken to be six, as in [
32].
2.6. Excitation of Disturbance Waves
The disturbance waves in experiment of [
11] were produced by blowing and suction of air through a slit with point-like sources on the flat-plate surface perpendicular to the flow direction and located at distance
= 300 mm from the leading edge. The disturbance signals consisted of two main components: the signal corresponding to the fundamental 2D TS wave and broadband 3D pseudorandom small-amplitude signals (“noise” of the TS wave). The broadband signals have approximately the same amplitudes in the frequency spectrum, but different phases for the spectral modes. The broadband signals repeat in the spanwise direction with a period of 48 mm.
In the present simulation, the disturbances are introduced from the wall-normal velocity component
in the spanwise spectral space. The TS wave is generated by:
where
is the disturbance frequency and is 109.1 Hz,
is the random signal, discussed later, and
is used to adjust the amplitude to make the r.m.s. streamwise velocity
(maximum in
) equal to around 4% of the freestream velocity at
= 450 mm. It is noted that this is a relatively large amplitude so that the broadband disturbance wave can develop nonlinearly even at the initial stage and trigger vortex formation in a shorter distance downstream. This is so that a smaller computational domain can be used. However this amplitude should not be too large as to distort the base flow. This selection of the initial amplitude follows that used in the experiment (see
Section 2.8 for a validation) where similar arguments are used to justify the initial amplitude.
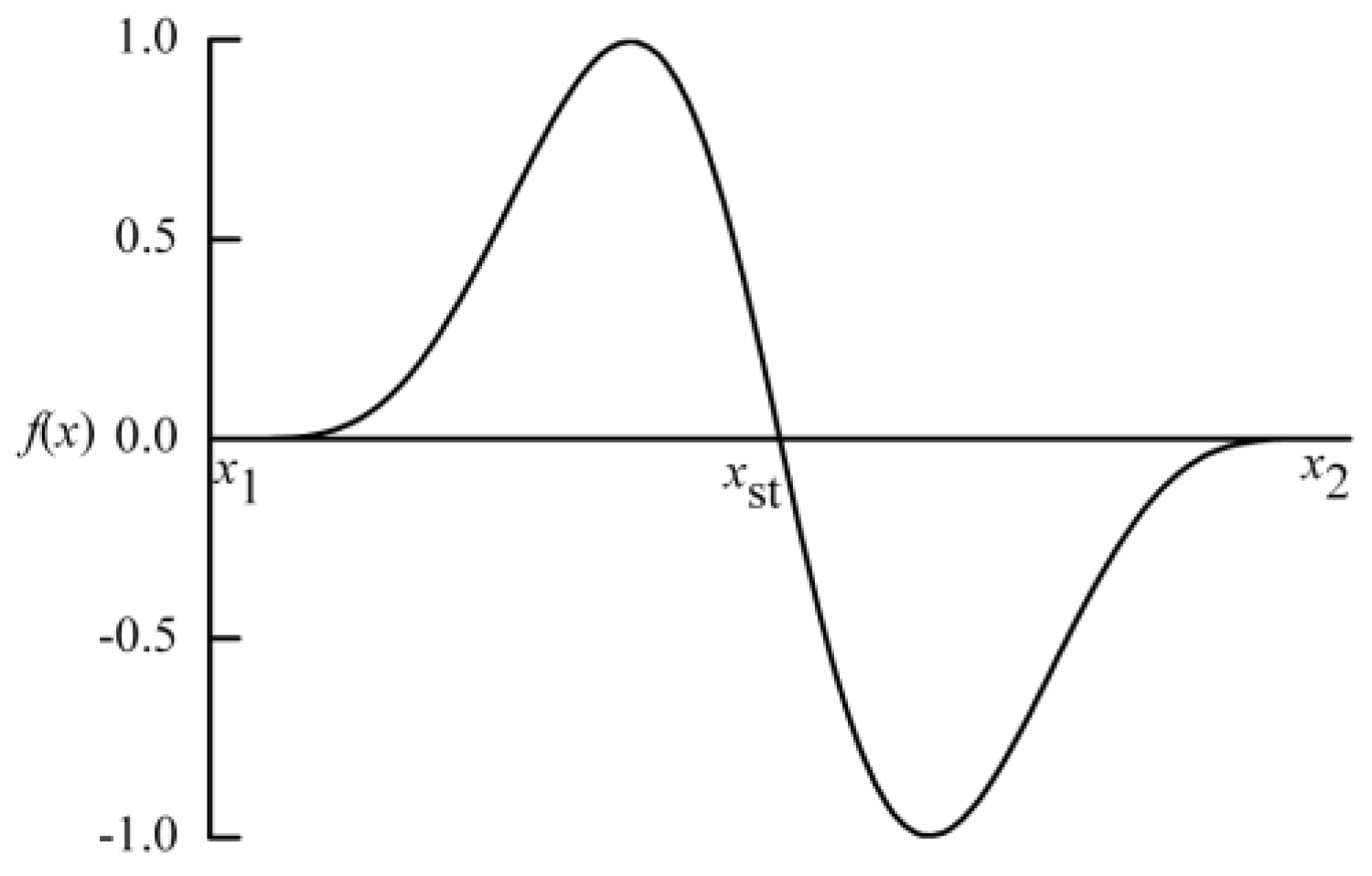
The spatial dependence was introduced via the disturbance distribution function developed in the present study. It is selected to satisfy the following three conditions:
Disturbances start and end with zero amplitude: .
No discontinuity for the first derivative at the beginning and the end of the strip, i.e.,
The form is conservative, so that .
Conditions (1) and (2) make the transition from disturbance source to the wall smooth, while Condition (3) enforces the law of mass conservation to the imposed disturbances. One possible choice that is used here is:
The shape is shown in
Figure 4.
The randomized disturbance
in Equation (27) is first generated in the Fourier space with the frequency band up to six-times the TS wave. The inverse Fourier transform is used to recover the signal in the time space as shown in
Figure 5. This broad band signal has randomized phases, but the same normalized amplitude, as shown in
Figure 6 for its spectrum. This signal amplitude is about 2% of
of the fundamental TS wave (refer to
Figure 6 in [
11]). Besides
in Equation (27), an additional 14 different signals were imposed on the real and imaginary parts of the Fourier modes
, where
= ±1, ±2, ±3,..., ±7. Thus, by construction, all of these spanwise Fourier modes have the same spectrum shown in
Figure 6.
2.7. Code Validation
Since randomized disturbances are used in the present simulation of the experiment of [
11], a direct quantitative comparison between the results is not possible. However, the subharmonic resonance experiment of [
23] is very similar to the present case with the only difference being the source of disturbance. The comparison was reported earlier in [
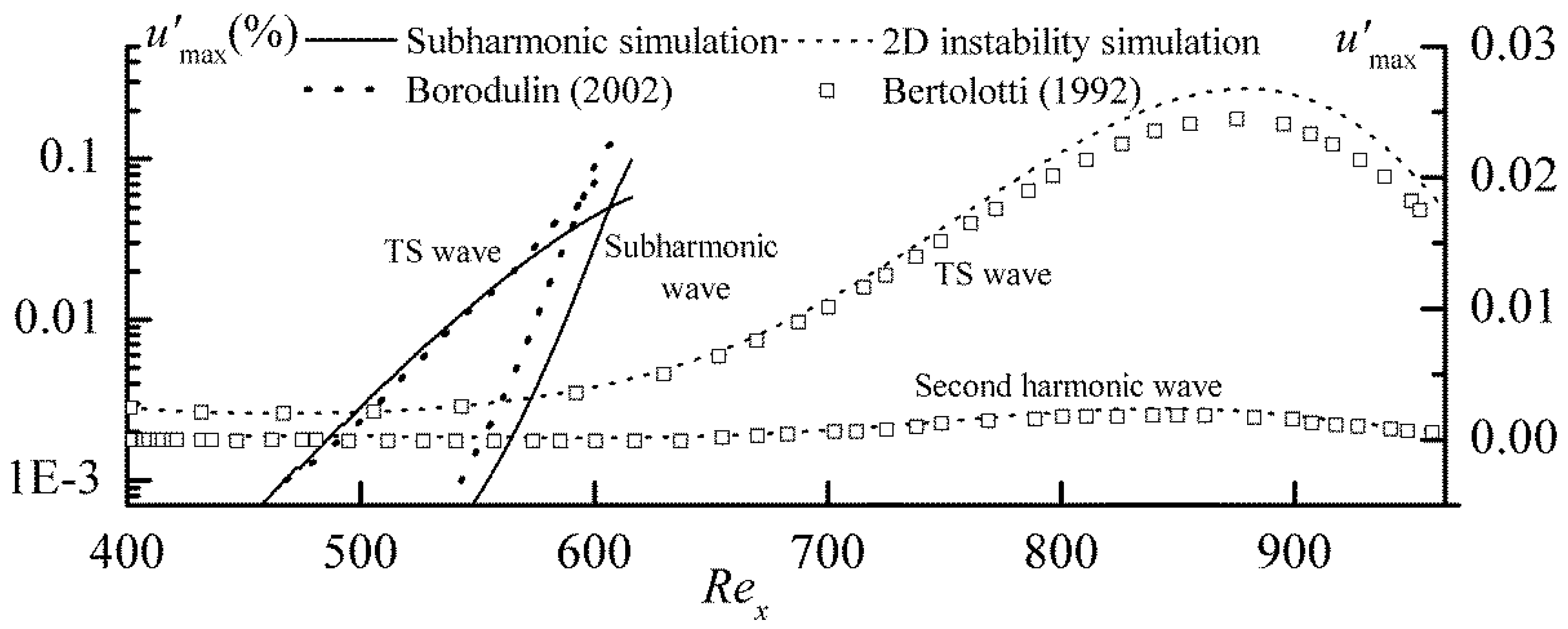
15] where the TS wave interacted non-linearly with the subharmonic wave, and the amplitude of the latter amplified dramatically along the downstream direction, as shown in
Figure 7, where the streamwise disturbance amplitudes of different components are plotted against Reynolds number
(the length scale
refers to the distance from the leading edge). Although the simulated amplification of the subharmonic wave is slightly weaker than in the experiment, the agreement was generally good.
In addition, the CCD12RK56 scheme on the uniform grid is validated by simulating 2D amplification of the TS wave in [
33]. As shown in
Figure 7, the initial amplitude of TS wave is small, but as it amplifies, its second harmonic wave is triggered. The results compare well with [
33]. More details are found in [
15].
2.8. Comparison of Settings between Simulation and Experiment
Before further investigation of the coherent structures via the simulation, the simulation results are first compared with the experiment to calibrate for the initial conditions and base flow. The non-dimensional freestream velocity in Equation (10) is prescribed as:
where
is the Hartree parameter fixed as −0.115 and
is selected as 8.295 to match the freestream velocity gradient in the experiments of [
11]. Detailed comparisons of the base flow are not presented here, but are found in [
21], including comparisons of the streamwise distribution of freestream velocity, base flow velocity and the boundary layer displacement thickness.
In [
11], the disturbance flow is first measured at the initial section
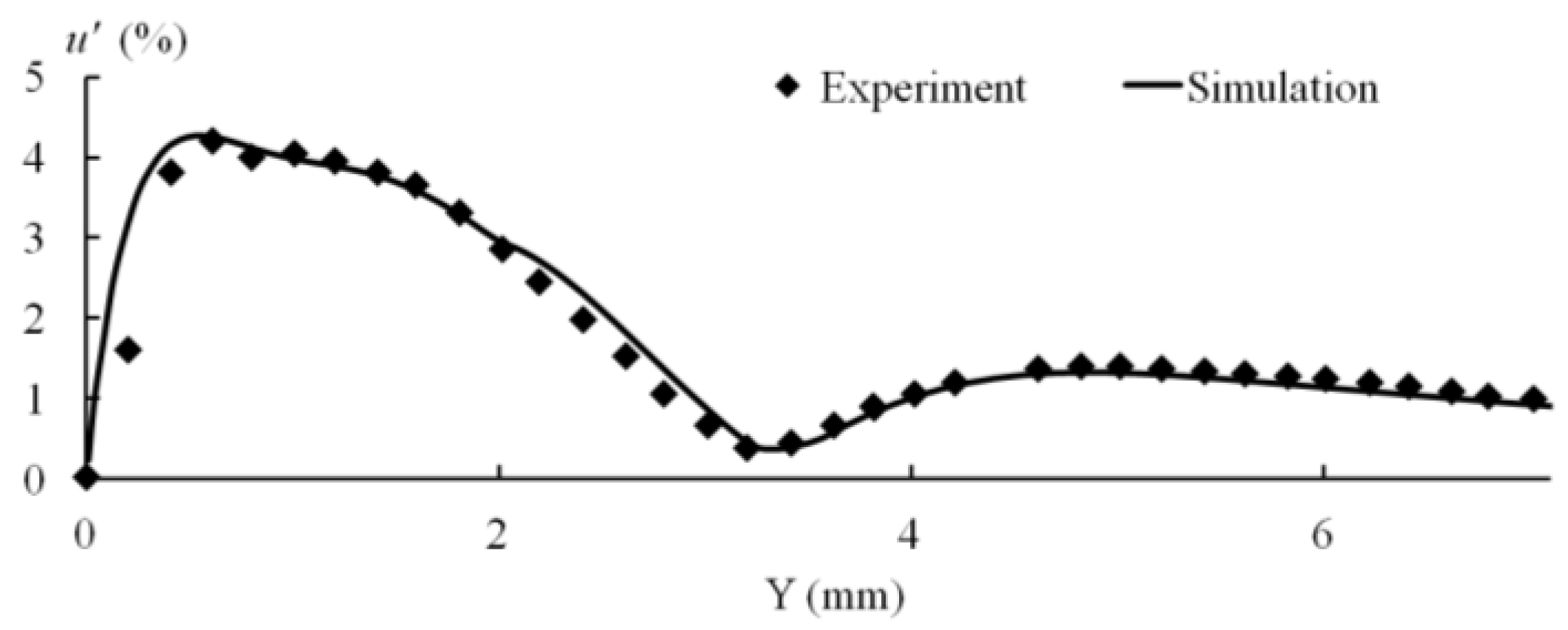
X = 450 mm. The initial amplitudes of the TS wave and broadband disturbances are adjusted to match the experimental condition at this location. The wall-normal profile of the TS wave amplitude at
X = 450 mm is shown in
Figure 8 along with the simulation showing that a good match was achieved.
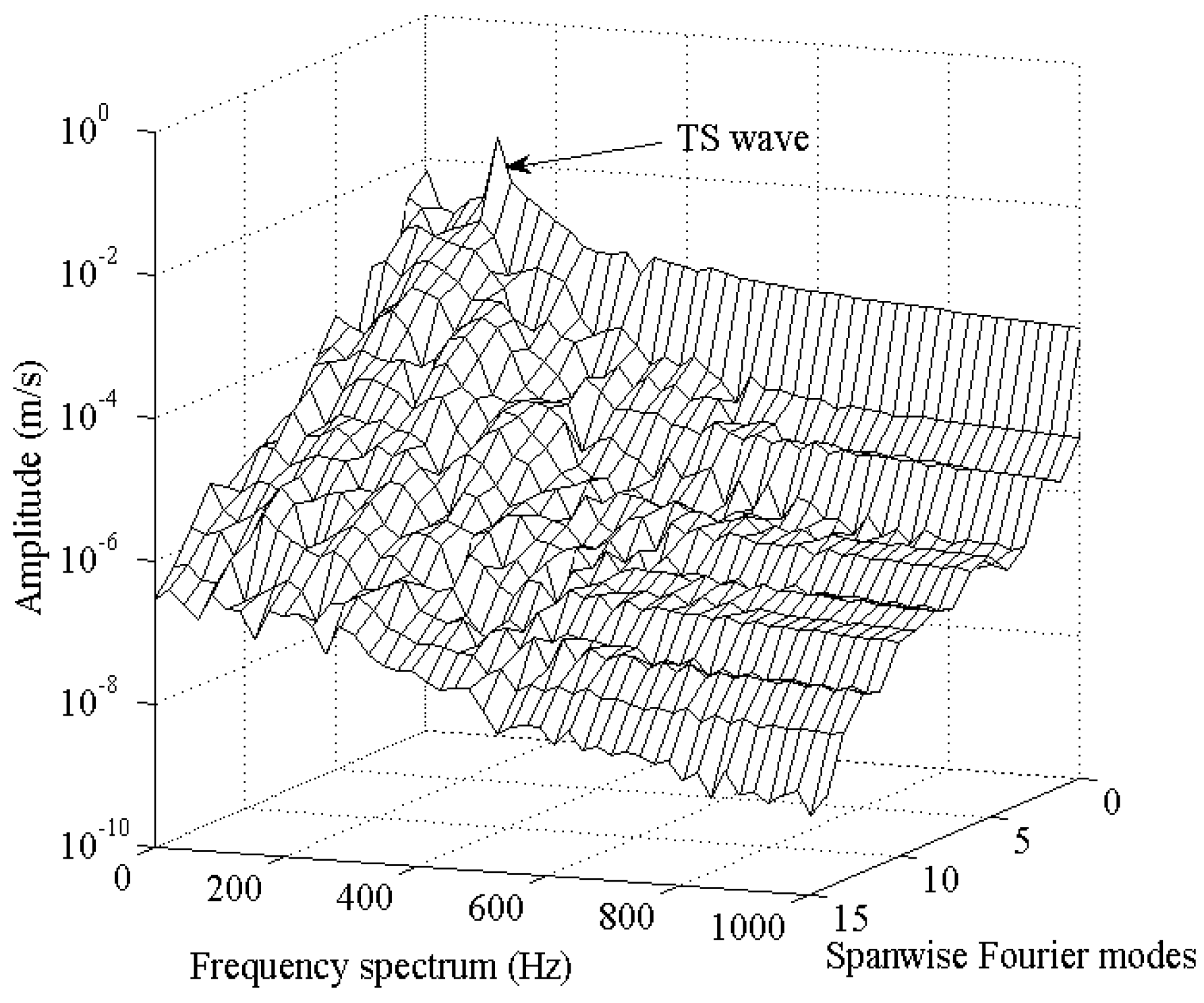
The wave amplitude spectrum plotted against frequency and spanwise Fourier modes is shown in
Figure 9. The TS wave amplitude is dominant at a frequency of 109 Hz and spanwise Fourier Mode 0. The disturbance wave amplitudes decay with both the frequency and Fourier mode.
4. Characteristic Signal Pattern of Coherent Structures
The signal pattern from a transition flow experiment is usually analyzed using the time series of streamwise disturbance velocity [
8,
12], as it is experimentally easier to record the velocity at a certain location with a point probe than to record the entire velocity field. However, this is not a constraint in simulations. To further investigate the disturbance signal evolution, it is more insightful to analyze the spatial-temporal development of the disturbance signal, which can demonstrate how the high wavenumber components develop as the vortex evolves.
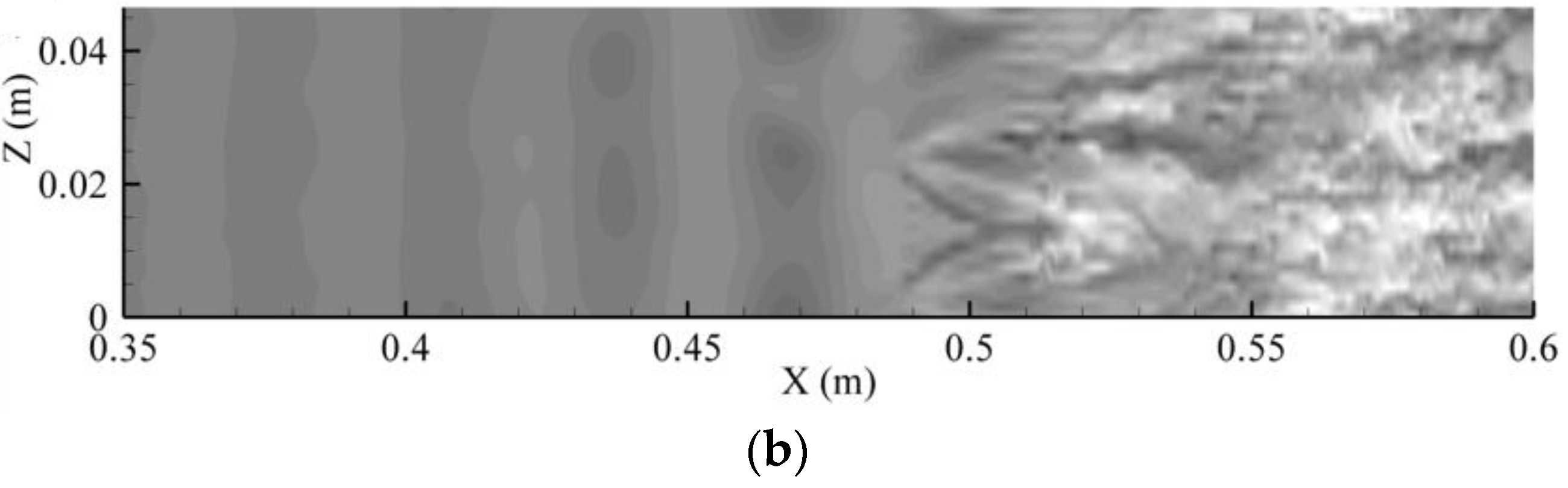
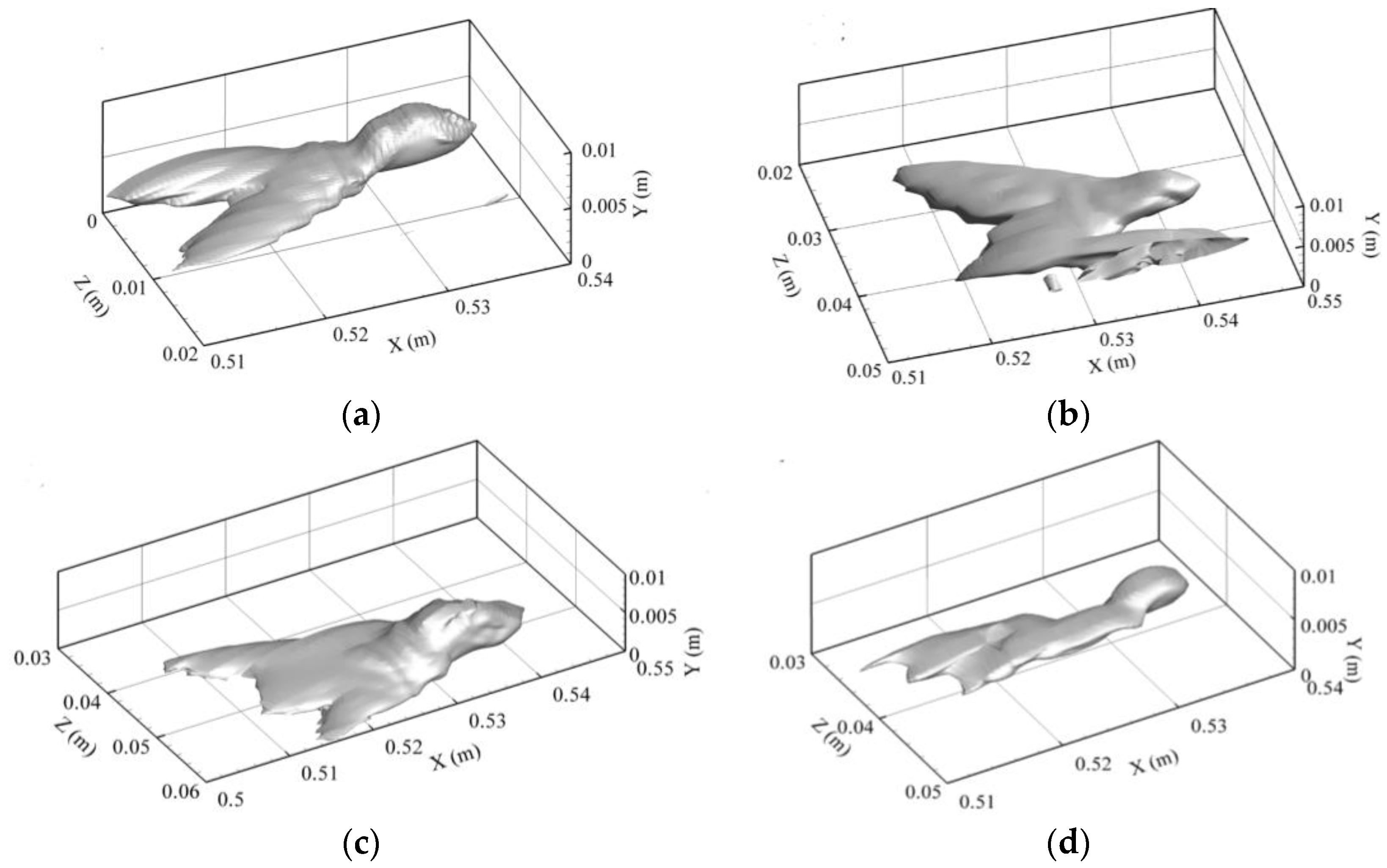
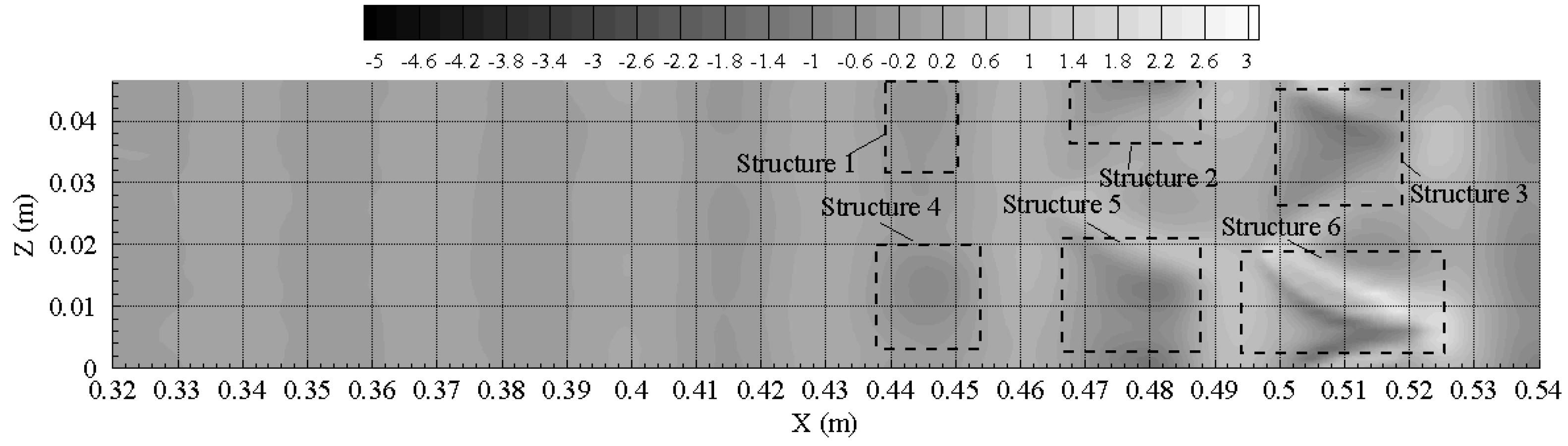
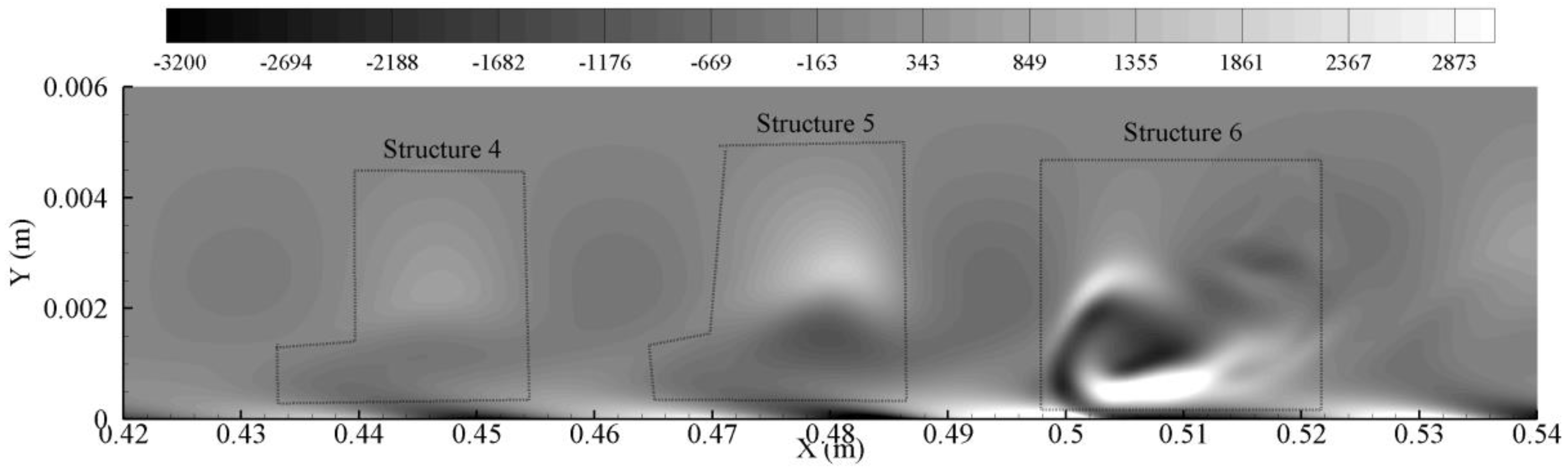
Flow structures with different shapes are shown in
Figure 14 via the
contour at
Y = 1.18 mm and at
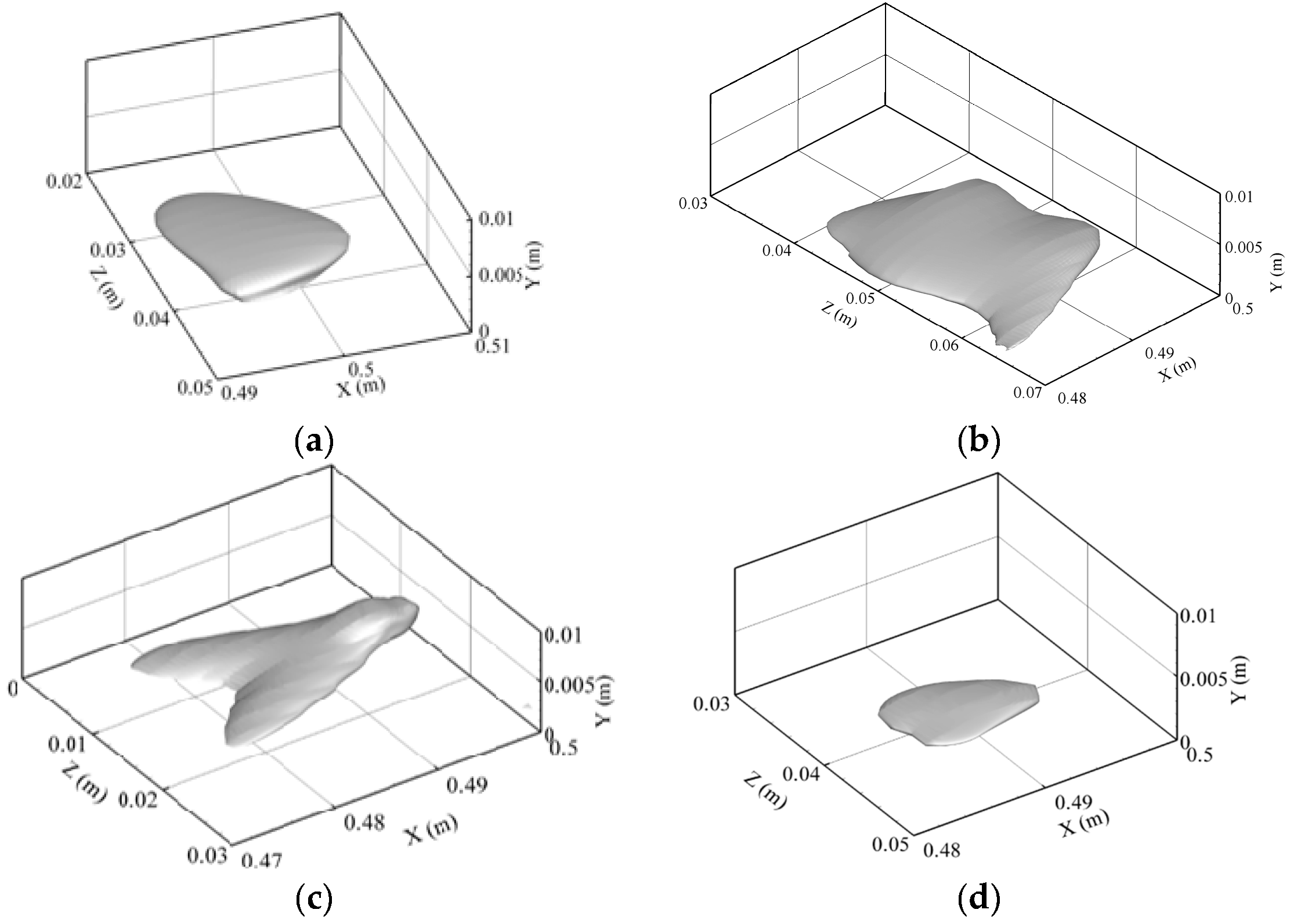
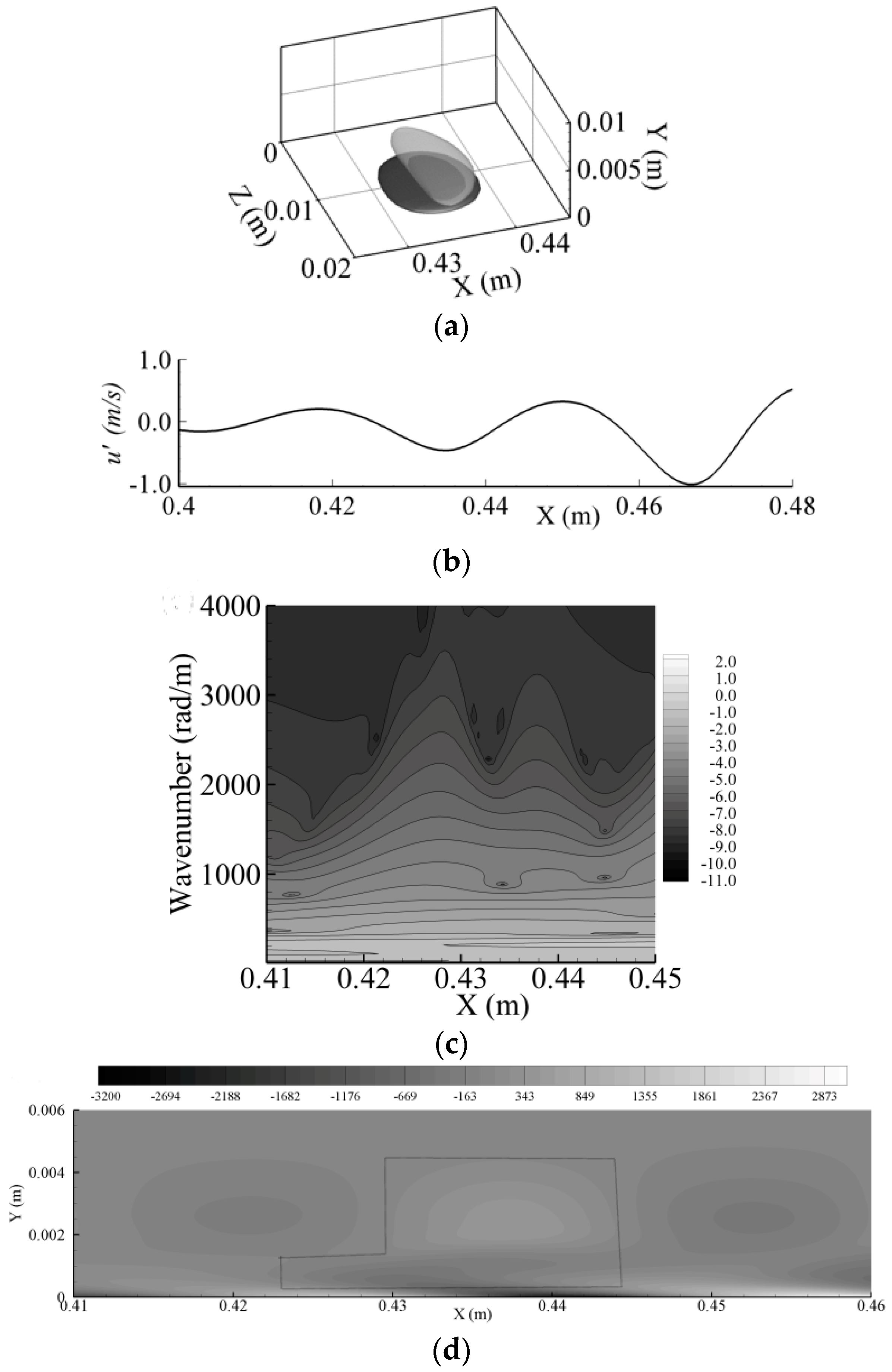
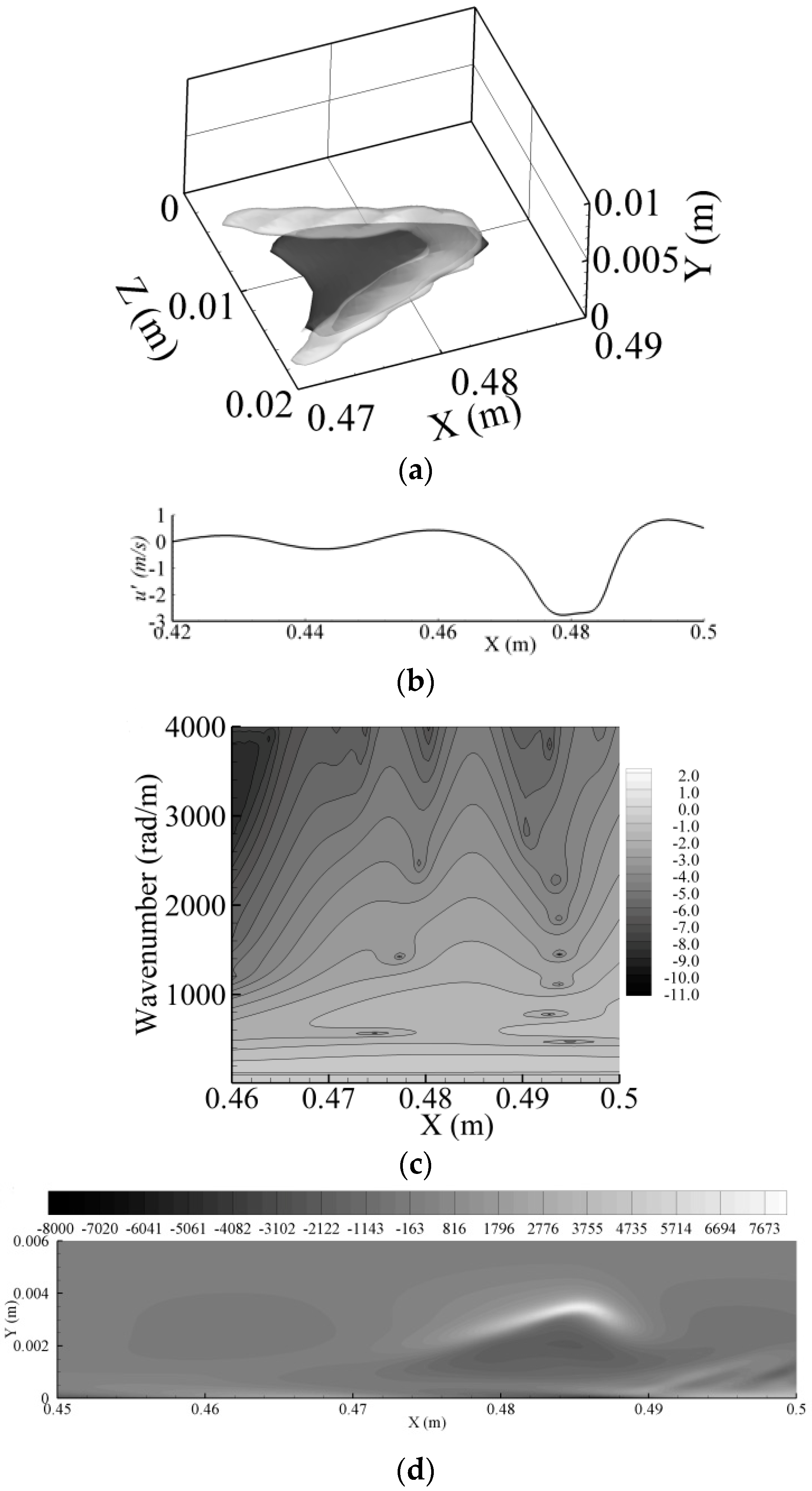
T = 0.056 s. This particular time is chosen for discussion as the coherent structures exhibit a whole range of evolution behavior with random spatial locations and asymmetric shapes. Structures 1 and 4 are in their primary stage with rhombus-like shapes, where Structures 2, 3, 5 and 6 are in the developed stage with quasi-Λ-shapes.
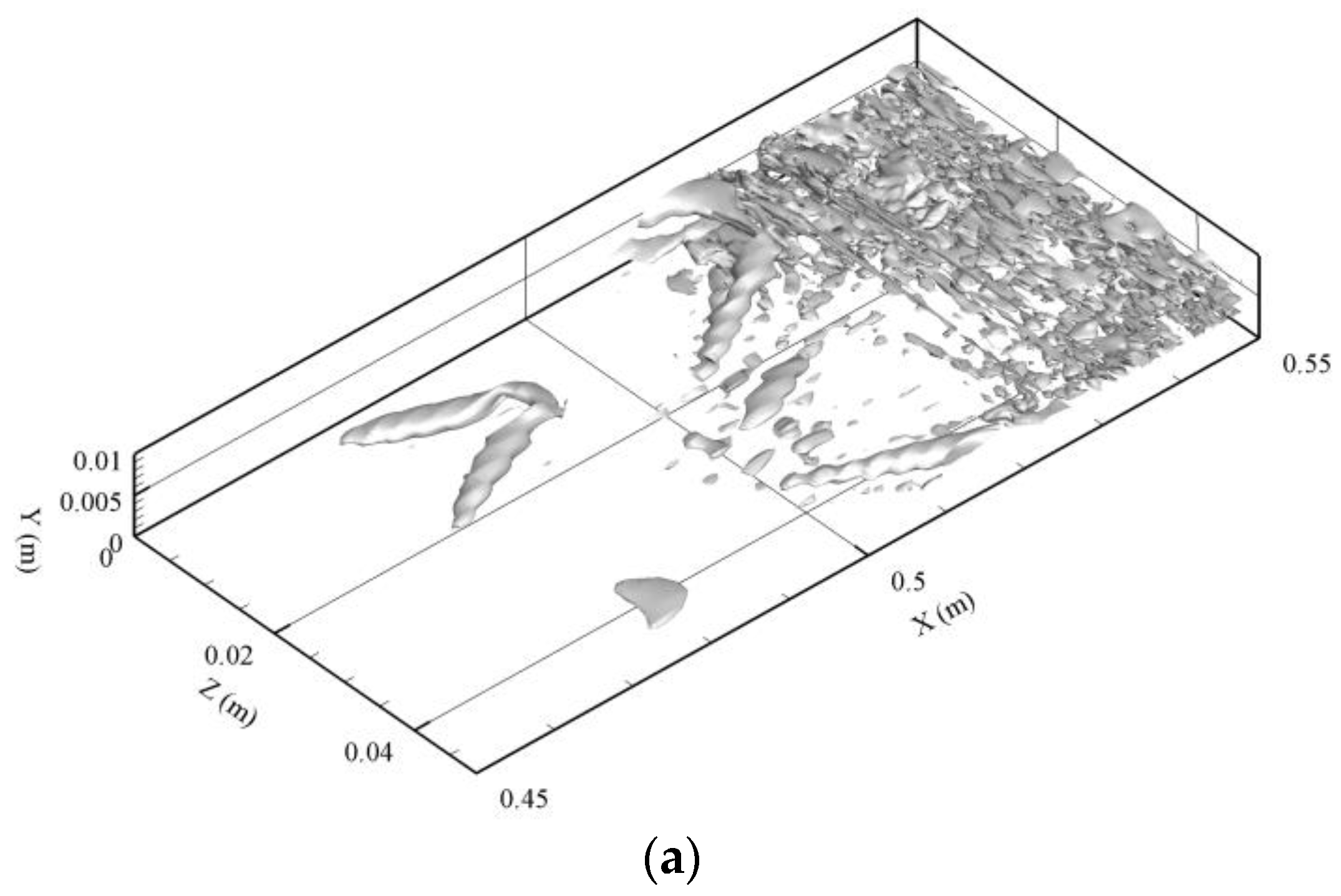
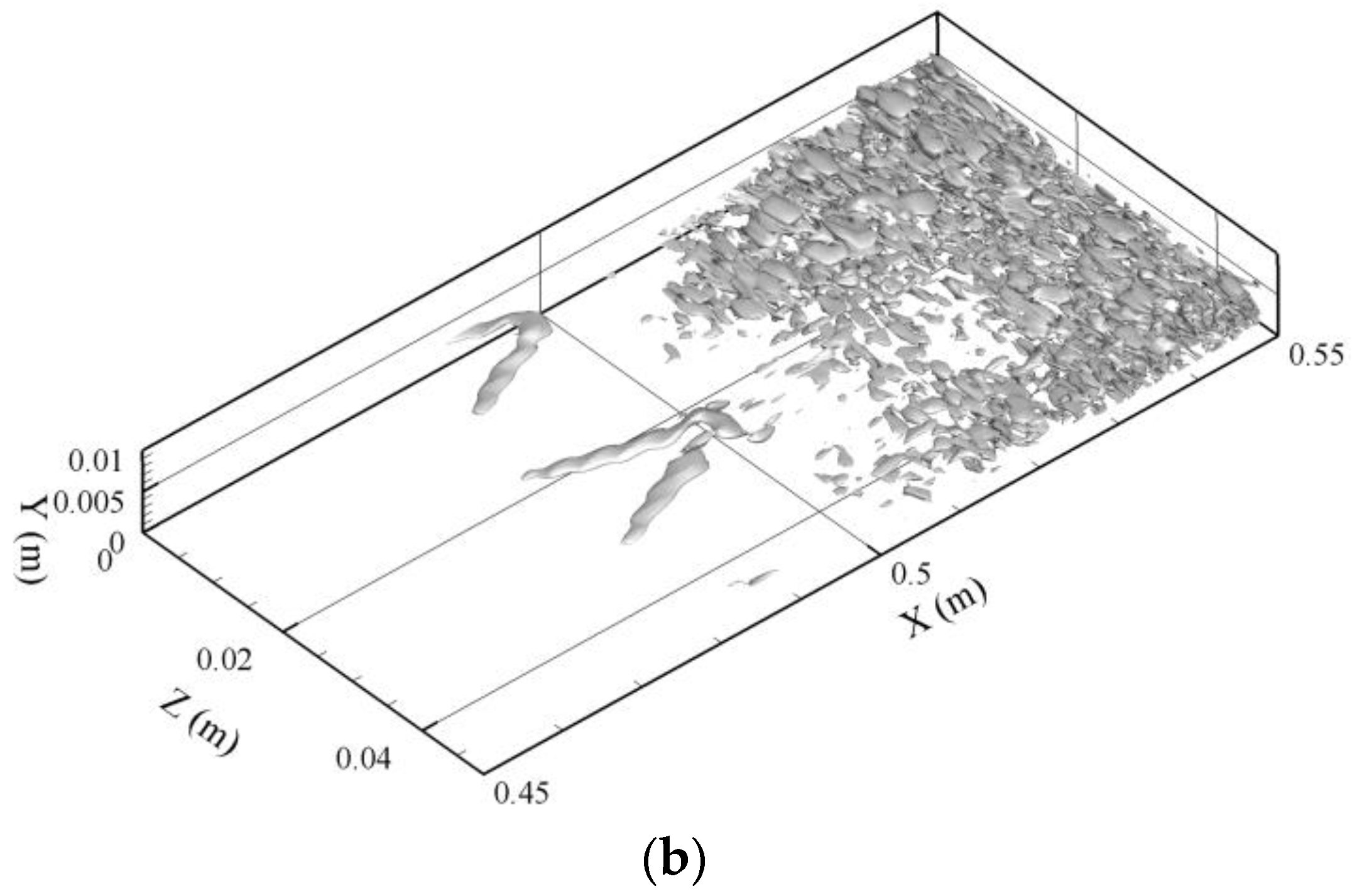
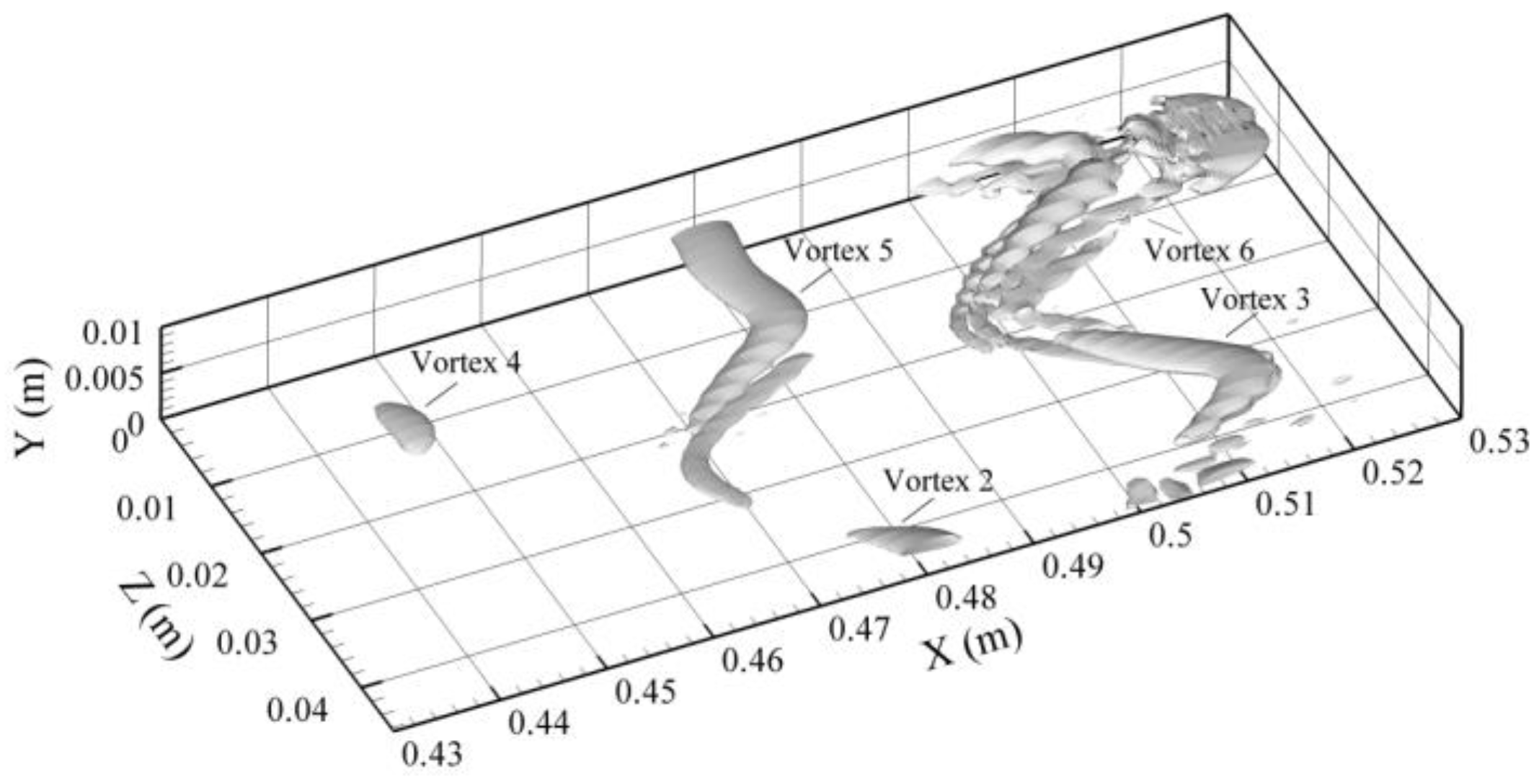
Figure 15 presents the evolution of vortex visualized by the Q-criterion at
T = 0.056 s. Structure 1 in
Figure 14 has not developed a vortex, while Structure 4 forms a very weak primary Λ-vortex, which is a precursor of the well-known
-vortex. Meanwhile, Structures 2 and 5 have developed to the stage of a quasi-
-vortex. Structure 3 has formed a
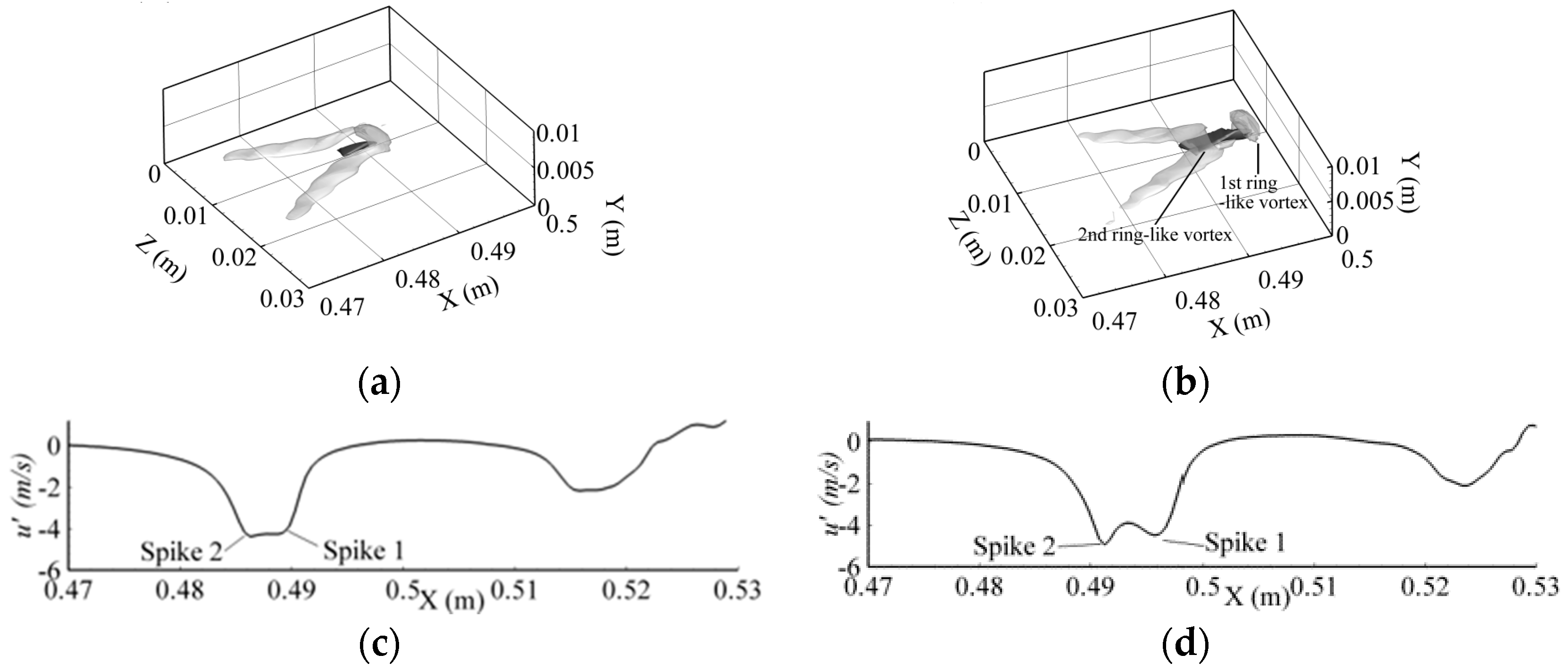
-vortex with two asymmetric legs. Structure 6 has developed to a later stage when the first ring-like vortex has started to separate.
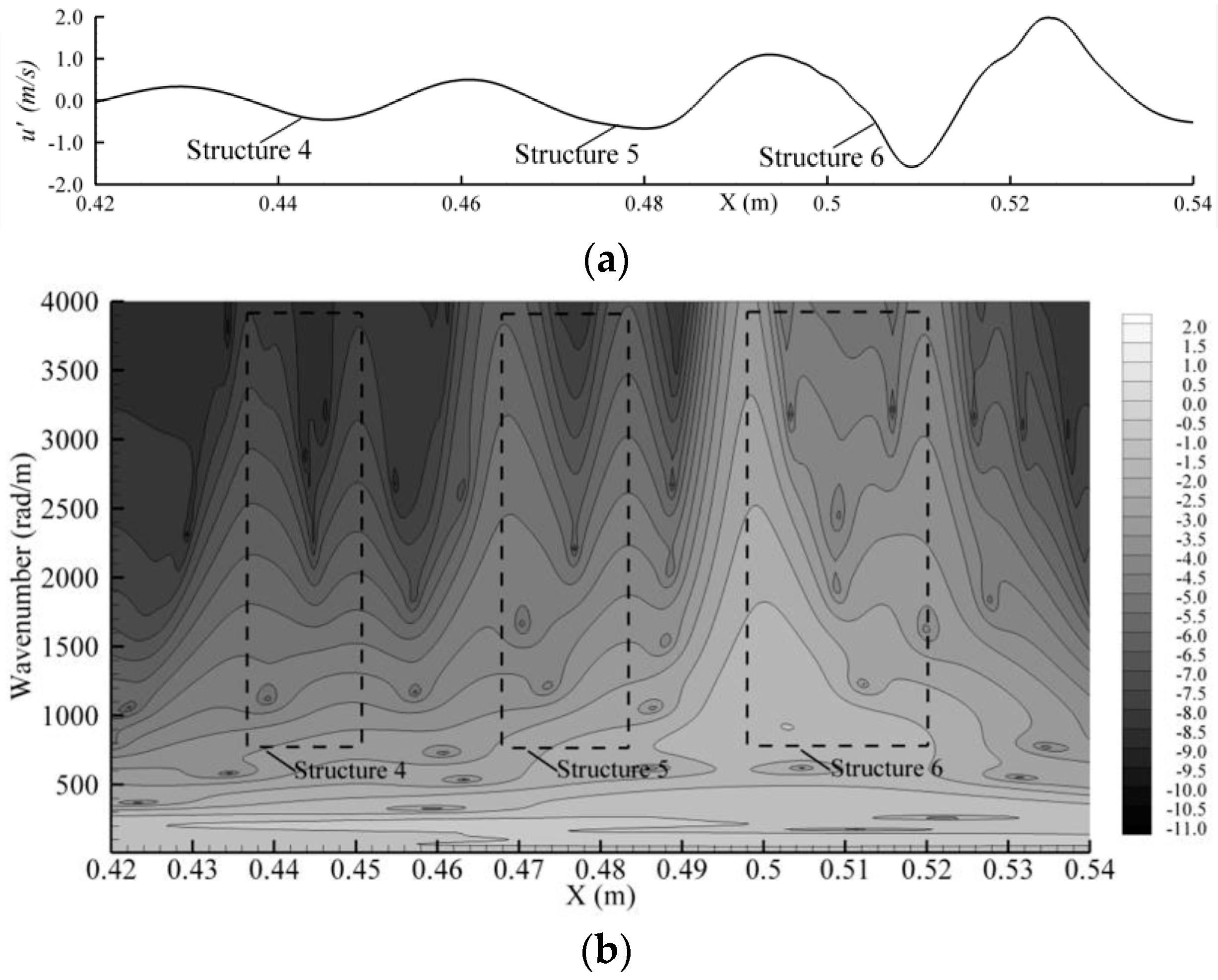
CWT is next performed on in the downstream direction. The highest wavenumber that CWT can resolve depends on the spectral resolution of the numerical scheme used. The present CCD scheme resolves the effective scaled wavenumber is up to 2.5, i.e., up to 5000 rad/m, as discussed earlier.
Figure 16a plots the streamwise disturbance velocity
at
T = 0.056 s,
Y = 1.18 mm,
Z = 13.5 mm, which goes through the spanwise centers of Structures 4, 5 and 6 in
Figure 14.
Figure 16b plots the corresponding wavelet contour in absolute amplitude (m/s) on the log
10 scale so that the small-scale wave amplitudes are also seen. The energy at wavenumbers smaller than 500 rad/m mainly corresponds to the fundamental TS wave, subharmonic wave and the secondary harmonic wave with the wave energy continuously increasing along the downstream direction. The figure also shows energy peak structures at wavenumbers larger than 1000 rad/m, indicating a discontinuous energy distribution in this region. The peak structures are also amplifying with downstream distance. After
X = 0.5 m, the energy at the high wavenumber is almost the same as in the low wavenumber.
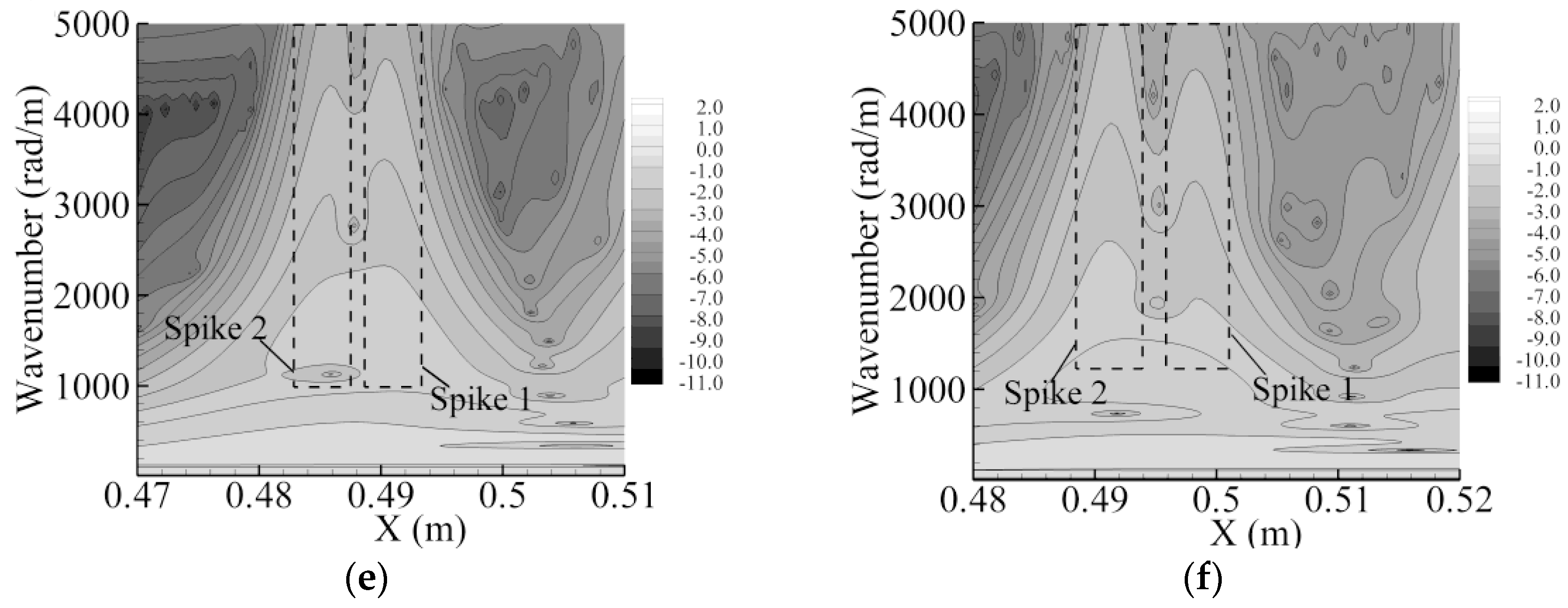
The twin-peak region (demarcated by dashed lines in
Figure 16) for Structure 4 extends from
X = 0.436 m to 0.454 m, for Structure 5 from
X = 0.468 m to 0.486 m and for Structure 6 from
X = 0.498 m to 0.522 m. A comparison with
Figure 14 and
Figure 15 shows that these twin-peak regions coincided with the spatial region of the coherent structures. The two peaks of Structures 4 and 5 in
Figure 16 are physically located very close so that the two peaks occurred within the one complete structure seen in
Figure 15. For Structure 6, the two peaks are somewhat separated in
Figure 16, and Vortex 6 in
Figure 15 is just at the stage when the first ring-like vortex separates from
-vortex. The two peaks with larger amplitude are spatially associated with these two vortices. Thus, the high wavenumber components in the wavelet spectrum are as expected spatially coincident with the coherent structures with a clustering of energetic high wavenumber components at the streamwise edge locations of the coherent structures.
The above discussion shows that as the coherent structures develop further downstream, the energy at high wavenumber becomes more prominent. Moreover, it indicates that prior to the formation of
-vortex, the high wavenumber structure has already arisen upstream and is composed of two wave packets corresponding to the twin-peak CWT signals of the coherent structures in
Figure 16. As the primary coherent structure evolves to the
-vortex, the two wave packets are still spatially connected though amplified. At a further stage when the front wave packet becomes strong enough, it separates from the rear wave packet. In physical space, this corresponds to the separation of the first ring-like vortex from the
-vortex. Here, we also note that the CWT results reflect the presence of subharmonic waves, specifically via a slightly high amplitude (lighter) band at a wavenumber around 100 rad/m over
X= 0.46 to 0.54 m, while the harmonics of the TS wave are always present (the TS wave here has a wavenumber of 205.9 rad/m). Thus, both subharmonic and harmonic waves are generated.
Figure 17 plots the contour of the shear
at
Z = 0.0135 m, i.e., the spanwise location is just around the centers of Structures 4, 5 and 6 shown in
Figure 14. It can be seen that the high shear structures, especially for Structures 4 and 5 (the dark regions at round
Y = 1 mm), coincide with the wavelet structure patterns in the streamwise direction shown in
Figure 16. Therefore, the high wavenumber components are imbedded in the high shear layer structures near the wall. Details about the high shear structures are discussed in the next section. It is also noted that the high shear
is the dominant component of spanwise disturbance vorticity
during the transition stage discussed in this paper; the subsequent discussion focuses on
and
.
6. Conclusions
A high order accuracy numerical model is used to simulate the experiments of [
11] on an APG boundary layer transition induced by broadband disturbances. The numerical simulation results demonstrate that there may be common features in the boundary layer transition induced by small amplitude disturbances and particularly in the development of coherent structures. A wavelet analysis further shows that the local spectral components of the Λ-vortex and its associated high shear layer contain two wave packets during most of its life.
Due to the use of initial broadband disturbances in the simulations here, the coherent structures that arise in the transition process are distributed randomly both spatially and temporally. The coherent structures have different shapes, and most of them are asymmetric. However, they are qualitatively similar to those observed in the typical fundamental and subharmonic resonances. They all have a tip at their head and one or two legs at the rear.
Although the coherent structures exhibit different shapes and spatial distributions in the simulation of broadband disturbances, their spectrum are quite similar. They always contain a twin-peak structure, which forms prior to the maturity of the Λ-vortex. As the Λ-vortex evolves to the Ω-vortex and at a later stage when the first ring-like vortex forms, the two peaks of the high wavenumber components separate. The front one is related to the first spike or the first ring-like vortex and the rear one to the second spike or the other ring-like vortex. Thus, the results reveal the source location of high wavenumber disturbance in boundary layer transition flow: they are originally imbedded in the spike region and wall-region high shear layer and evolve with them.