1. Introduction
Traditional drug delivery methods involve the intravenous injection of drugs, which travel through the circulatory system until they are distributed throughout the body. When treating localized diseases, however, this approach is undesirable because a much larger dosage is required for an indicated amount to reach a small area, while the rest of the drug is wasted. Moreover, the toxicity and negative effects of the medication affect the whole body instead of being localized to the target region. These disadvantages are specifically relevant to drastic drug therapy and recent interest and development in cancer treatments such as chemotherapy and IL-2 (interleukin-2).
In response to these issues, renewed efforts in the research and development of this technology have yielded several new methods of drug delivery, namely, magnetic drug targeting, which involves the binding of drugs to magnetic particles that allow the drug to be guided to the area of interest using an external magnetic field. There have been numerous promising trials [
1,
2] and models of the behavior of ferrofluids intended for applications in retinal detachment restoration [
3,
4,
5], magnetic separation for fluid filtering [
6,
7], drug therapy for in-stent restenosis [
8], and localized cancer treatment [
9,
10,
11,
12,
13,
14] validating the plausibility of this method.
In this study, a mathematical model is proposed that describes the behavior of such particles. Previous research has shown that it is insufficient to only consider the force balance between cross-stream magnetic attraction and drag given a uniform flow across the cross-section of the pipe in light of the significance of diffusion and no-slip near the vessel walls [
15,
16,
17]. As such, studies have evolved from accounting only for magnetic and drag forces [
9] to tracking particle trajectories when subjected to an external magnet under power-law flow [
10]. Recent models have even considered diffusion and sources of stochasticity with Brownian motion and interactions with red blood cells [
11,
12].
This study aims to integrate all of the previously mentioned aspects into a single model that considers independent particle trajectories by incorporating the diffusive motion of magnetic particles in response to collisions with red blood cells into a stochastic ordinary differential equation model that accounts for Brownian motion, Stokes drag force, magnetic force, and pulsating power-law flow. As an improvement on the accuracy and applicability of previous models, this study explores various viscosity models and rheology to account for the realistic properties of blood.
To take advantage of magnetic drug targeting, past research has investigated the optimal environment for its usage. It was found not to be conducive to the treatment of internal structures [
11] and less effective for drug delivery in large vessels since the particles must overcome a larger distance and stronger flow [
12]. Thus, this model focuses on targeting superficial tumors, up to 20 mm deep, accessible through arterioles and venules with low velocities and diameters, according to the extrema investigated, to increase the probability of capture. The advantage of using superparamagnetic particles is that they are characterized by randomly oriented dipoles, until a magnetic field is introduced. When compared to ferromagnetic particles, superparamagnetic particles return to random dipole orientations after the magnetic field is removed from the system. This property makes superparamagnetic particles suitable for biological use because they will not cluster after the drug is delivered and the magnet is consequently removed. The lack of agglomeration is an imperative advantage of paramagnetic particles used in human vasculature as it avoids occluding vessels and blood flow. This model is also flexible and adaptable to different particle, vessel, magnet, and flow conditions and this study describes the effect of variations in parameters such as red blood cell collisions, magnetic moment, and initial injection position on the capture rate. Specifically, the computations show a steep variation in the capture rate due to changes in the magnetic moment within a certain range and demonstrate the importance of the consideration of red blood cells not only as contributors to viscosity, but also as sources of diffusion.
2. Governing Equations
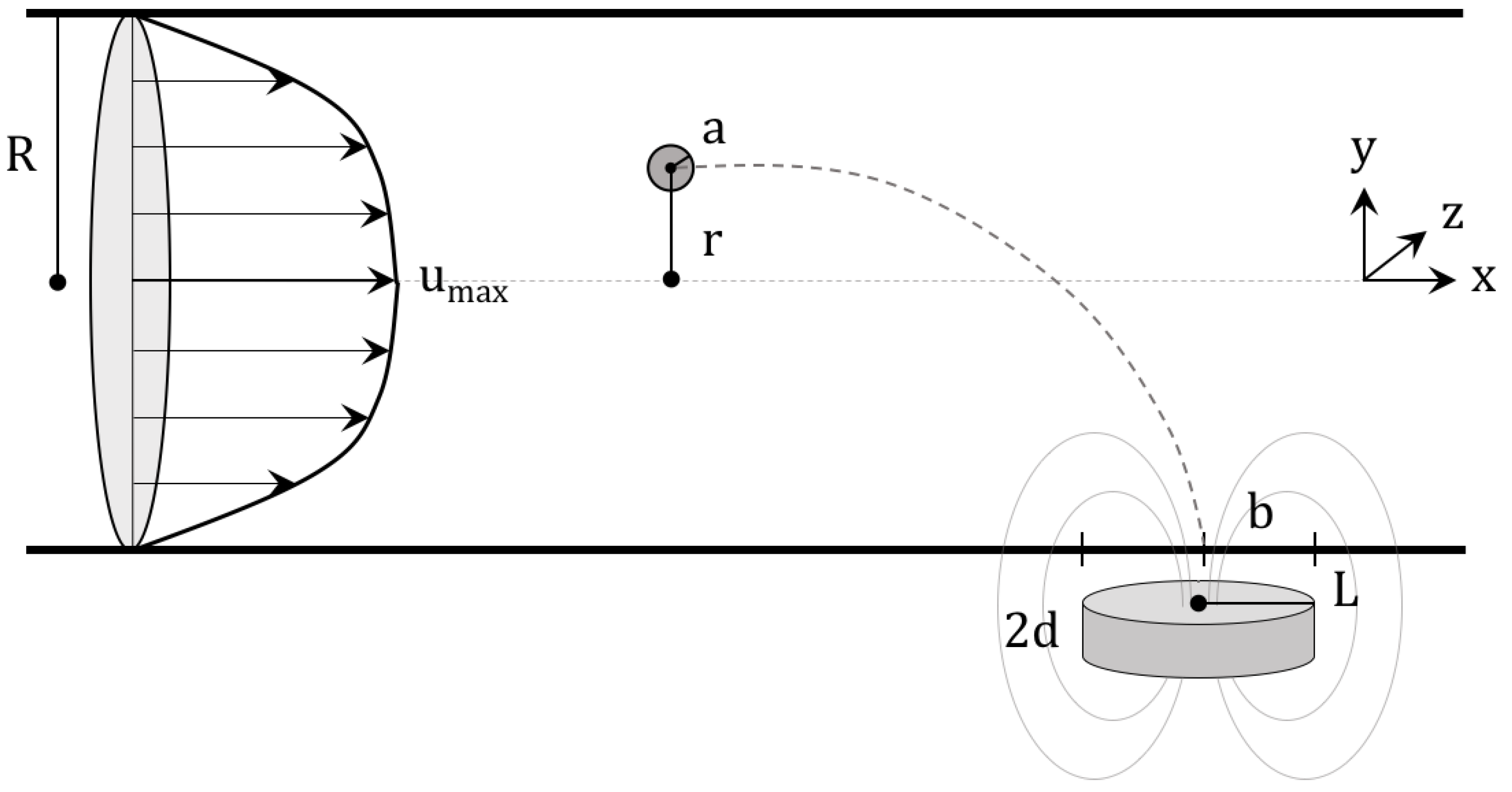
In this study, blood flow is modeled as a pipe flow, with zero velocity in the radial and angular directions. This can be described as shown in
Figure 1, where a magnetic particle of radius
a is released a distance
r from the center of a vessel of radius
R to be drawn by a magnet to a tumor of radius
b.
The velocity of the fluid in the axial direction is a power-law profile described by the equation
where
is the maximum velocity of the blood in the pipe, which occurs at the center (
) of the pipe,
is the oscillatory velocity component,
is the oscillatory frequency,
n is the flow behavior index, and
t is time. Equation (
1) offers a general conceptualization of blood flow that accounts for the pulsation from the pumping of the heart. This oscillation is highly relevant in vessels closer to the heart, but the effect of the pulsatile flow decreases in smaller vessels, where viscous forces dominate. The importance of pulsation can be evaluated using the Womersley parameter,
, which scales the inertial force of oscillation and viscous force [
18]. Since magnetic drug targeting focuses on small topical vasculature, however, the oscillatory component is relatively small so that
is negligible in vessels where magnetic drug targeting is effective. That is, in vessels of the size addressed in this paper, the value of
is on the order of
according to
, where
R is the relevant distance metric,
m for the radius of the vessel considered in this study;
is the angular frequency of the pulsatile flow, approximately 1 Hz for the average person;
is the density of the fluid, on the order of
kg/m
for whole blood; and
is the dynamic viscosity of the fluid, for which
kg/ms is used as an order of magnitude approximation since it is relatively accurate throughout most of the vessel (and does not significantly affect the Womersley parameter since
is rooted). Thus, since
is small, much less than 1, the pulsatile frequency is sufficiently low that the flow is practically in phase and the velocity profile develops within each period so that
can be neglected for the vessels considered. Similarly, it should be noted that settling is not included in the model, as the sedimentation velocity is on the order of
m/s according to
, where
is the difference in the densities of the particle and fluid, which is on the order of
kg/m
;
g is gravitational acceleration;
a is the radius of the particle,
m in this paper; and
is the dynamic viscosity of the fluid, which, as before, is on the order of
kg/ms. As such, the effects of settling are negligible for the purposes of this paper. With these factors accounted for, the model is appropriately simplified and questions regarding the motion of particles in these vessels can be addressed.
As the particle travels through this fluid, a drag force is generated, leading to the following force balance:
where
is the velocity of the particle relative to that of the blood and
D is the drag coefficient. Due to the low Reynolds number and the small size of the nanoparticles relative to the vessel, the forces on the particle are local. That is, when the differential equation for the balance between drag and external forces is solved for the velocity, the time constant is extremely small, indicating that the terminal velocity is reached nearly instantaneously. As such, it can be reasonably assumed that the particle travels at the terminal velocity,
, that satisfies Equation (
2) and that the drag on individual particles can be expressed as Stokes drag
in which
is the dynamic viscosity of the blood.
For the attraction of the particle to the tumor location, this study considers a point dipole as an intermediate for the construction of the field for a cylindrical permanent magnet. The magnetic field, denoted by , is related to the inductance, , according to . Here, is the permeability and can be expressed as in terms of , the magnetic susceptibility, which is assumed to be constant.
To begin, we represent a point dipole magnet with some magnetic moment
m. The scalar magnetic field potential can be obtained from
where
is the magnetic moment vector and
is the vector pointing from the point dipole to the center of the nanoparticle. This potential field yields the following equation for the induced magnetic field
The point dipole is then placed some distance d from the blood vessel to represent the size of the magnet.
The cylindrical magnet, which is more practical both because it is more realistically conceivable and because it produces a stronger field, can be imagined as many dipoles integrated over the volume of the magnet. For a cylindrical magnet with a height of
and a radius of
L, then, the strength of the magnetic field is given by
where
is a scalar that corresponds to the strength of the magnet and
h is the vertical distance measured from the surface of the magnet [
19]. This paper uses two separate equations to obtain the magnetic force acting on the particle. The first is given by
with
signifying the particle’s magnetization and
V the volume of the particle [
10]. The Clausius–Mossotti formula for a spherical particle is then used to produce a uniform magnetization throughout the particle
from which the following force equation follows:
The second magnetic force model is derived from the equation:
A Langevin function can then be used to relate
to
, so that
where
is the Boltzmann constant,
T is the temperature measured in Kelvin, and
is the magnetic saturation of the particle, given by
where
is the density of the magnetic particles and
is the mass saturation magnetization [
5].
The representation proposed here also utilizes multiple viscosity models: power-law, Cherry [
12], Carreau [
20], and constant viscosity. The Cherry model is based on a fit to empirical blood viscosity data, but the analytical expressions of the other models can be represented meaningfully. The power-law model is given by
where
is the flow consistency index. Next, the Carreau viscosity model is defined as
where
is the viscosity at infinite shear rate,
is the viscosity at zero shear rate, and
is the relaxation factor. In both,
is the local shear rate, which can be expressed as
from the definition of the shear rate as the gradient of the velocity profile. When all of this information impacting the potential motion of a particle through the vessel is combined, including the fact that the particles are sufficiently small that diffusion becomes important, it yields a Stochastic Differential Equation (SDE) that can be developed to realistically model the trajectories of the particles. The SDE has the form
where
is the drift of the particle,
is a standard Wiener process random variable, and
. The drift is the sum of the velocity of the blood flow,
, as defined in Equation (
1), and the terminal slip velocity and is therefore given by
As for the other term in the equation,
is the diffusion matrix of the SDE, which is defined as the root of the variance
J. The variance accounts for both Brownian motion, which is modeled as
and the diffusion due to collisions with red blood cells, which is modeled as
where
is the radius of red blood cells and
is the local shear rate. This equation is well established for calculating the flux due to a sheared suspension of an inhomogenous distribution of particles [
12,
21]. The diffusion is thus defined as
where
is the 3-by-3 identity matrix.
3. Results and Discussion
To be explicit, in the following numerical analysis, experimentally-derived values are taken for some of the constants in the following analysis to not only display general trends within the model, but also to provide numerical simulation of realistic proportions. The advantage of this is to both verify the consistency of the simulations with measured values from previous experiments as well as to produce estimates for quantities that are, practically, extremely difficult to measure. Some universal constants that are used include
m for the tumor radius, the release location as
m upstream from the tumor from the center of the vessel (except when a distribution of starting positions is applied),
m as the radius of the vessel consistent with venules and arterioles, as desired, and particle radius of
m consistent with commercially available products and previously conducted theoretical studies [
10,
22].
3.1. Viscosity Models
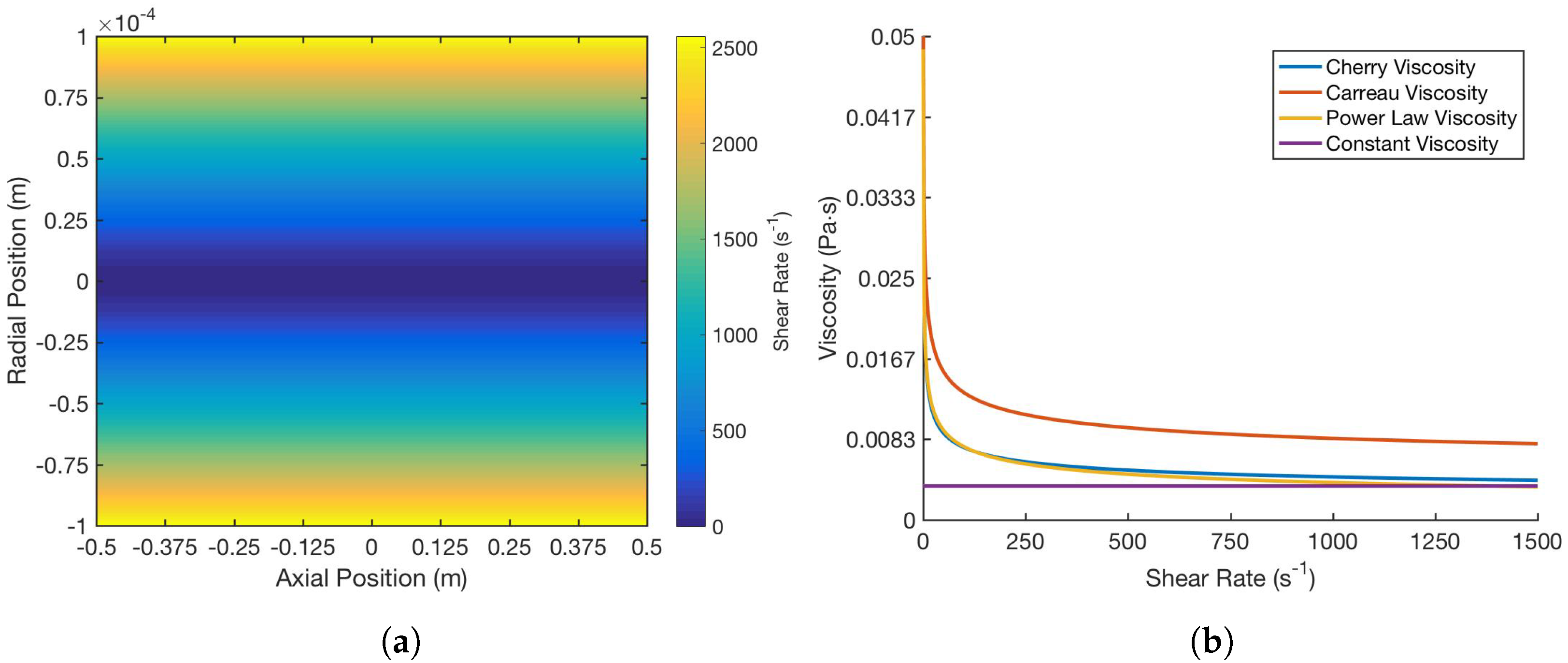
The behavior and properties of blood are unique relative to each patient. In order to account for the variability of blood viscosity, several models are incorporated to examine the effect of altering viscosity on the effectiveness of the drug delivery: power-law, Cherry, Carreau, and constant viscosity models. It is immediately clear from
Figure 2a that the model preserves the intuitive behavior of blood as a shear-thinning fluid and of its flow in the vessel, with logically decreasing viscosity as the shear rate increases, or as the radial distance from the center of the blood vessel increases. Moreover, as shown in
Figure 2b, the models are all internally consistent in terms of the trend and end behavior of the relationship between shear rate and viscosity.
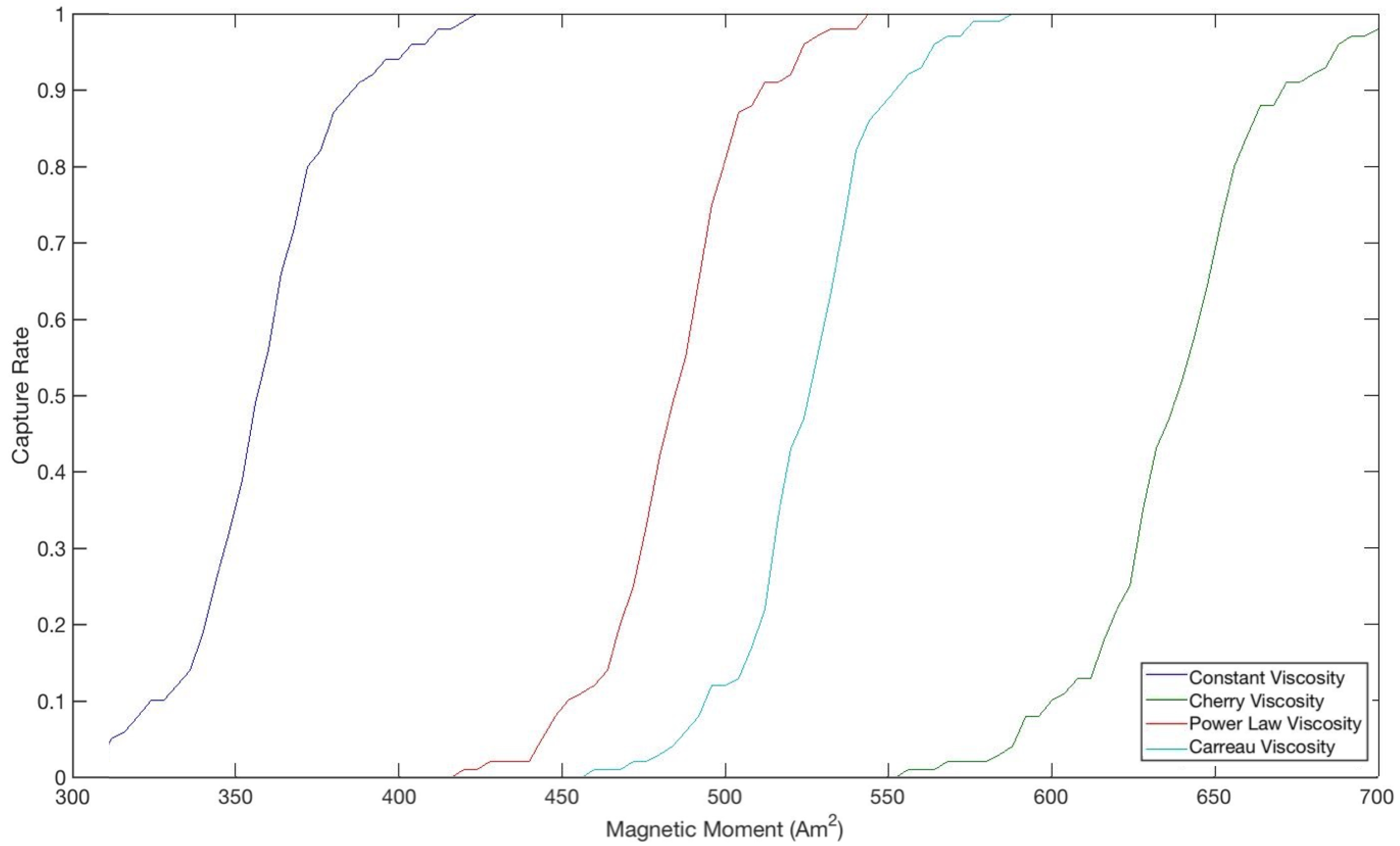
As can also be seen, both the shear rate and viscosities, and specifically the value the viscosity approaches as the shear rate increases, are consistent with average statistics and measurements that have been made in human vessels of this size. From the juxtaposition of
Figure 2 and
Figure 3, it can be deduced that lower viscosities lead to higher capture rates, as they do not supply as much resistance to the path of the particles toward the tumor and thus do not require as large a magnetic force when compared to higher viscosities. The shape of the curves in
Figure 3 is also very suggestive in terms of the variation of the capture rate due to changes in magnetic moment within a certain range. Although this range differs for each viscosity model, the overall trend is consistent, showing a steep variation in the capture rate due to small changes in the magnetic moment within a certain range. That is, for example, decreasing the magnetic moment by about 60 Am
lowers the capture rate from 90% to 10% irrespective of the viscosity model despite the offset among them. This implies that, especially with limitations on the strength of the magnet, there exists a tradeoff and, presumably, an optimal magnetic moment that would produce the highest capture rate without incurring unwanted costs. However, the implication is bidirectional in that not only does this seem to suggest that very small changes in the magnetic moment around the
capture rate mark will improve the performance of the drug therapy greatly, but also that it may be difficult to get into the
range in the first place and small inaccuracies or deviations in the magnetic moment may drastically diminish the capture rate.
It is useful to observe that since the behavior of the viscosity models is nearly identical for the purposes of this paper, and share the core characteristics (shape, asymptotic behavior, etc.), generality is not lost when using the Cherry model with
throughout the rest of the paper, as it is the most computationally simple. Additionally, it should be noted that it has been shown that blood viscosity can be reduced with magnetic fields [
24], and one limitation of this model in representing the behavior of blood during magnetic drug targeting is that it does not consider this effect. This is an interesting point for future study, as the decrease in viscosity will lead to less interference in the trajectory of the particle and, potentially, an increase in capture rate. Nevertheless, the effect described is expressed in the magnitude of the viscosity, while the relative properties and flow behavior of the blood should be conserved and still be consistent with the model presented in this paper.
3.2. Magnetic Field
Magnetic drug targeting relies on an external magnetic field to guide particles to the target location. Logically, this magnetic field has a significant effect on capture rate. Two magnetic models were considered in this study: point dipole model and cylindrical magnet model, with the behavior of the point dipole used mainly to inform on that of the cylindrical magnet, as a composition of dipoles. For
, 1 T was used as an order-of-magnitude estimate for the magnetic strength, with
as presented in Equation (
6). With a dipole magnet, the smallest possible magnetic moment to yield a 100% capture rate for a particle with a radius of
m is found to be about 730 Am
. When the particle radius is
m, the minimal magnetic moment for a 100% capture rate is about 365 Am
. By extrapolating from this data, the particle radius and the magnetic moment are found to be inversely proportional to one another when keeping a constant capture rate.
When comparing the point dipole magnet and the cylindrical magnet, the cylindrical model obviously maintains its strength over a larger distance than any one of its component dipoles and can thus attract particles farther away from the tumor. To ensure a capture rate, with a cylindrical magnet and red blood cell collisions, the magnetic moment necessary is 766 Am, or the thickness of the magnet can be increased to about m at the original magnetic moment of 730 Am. The benefit of modeling the cylindrical magnet as the sum of many dipoles over a volume rather than as an abstraction with one strong dipole is that it maintains the integrity of the field over the entire tumor. Furthermore, the slow degradation of the field of the cylindrical magnet as compared to the dipole causes the slip velocity to be strong further form the tumor so that the capture rate is improved.
3.3. Release Point
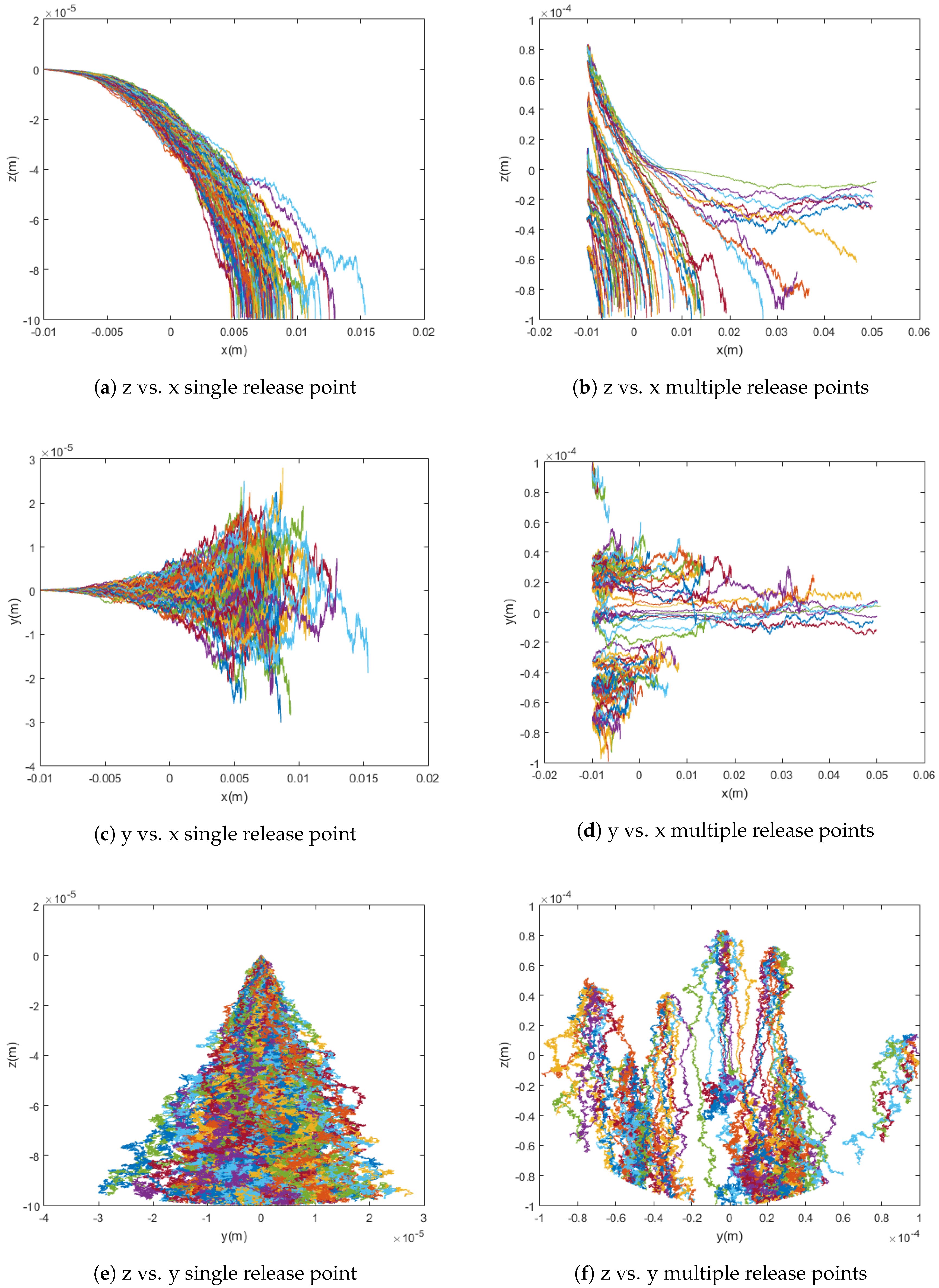
A major concern with the magnetic attraction of particles injected into a vessel is the ability to capture the particles successfully regardless of their position on a cross-section of the vessel as the drug dissipates and mixes with the blood. In a basic situation, the particle is released at location (−0.01 m, 0 m, 0 m), which is located at the center of the vessel, one centimeter away from the origin. When the injection site is moved further on the x-axis from the tumor site and at the top of the vessel with respect to the center, expressed by the coordinates (−0.06 m, 0 m, 9 × m), the capture rate is zero. This decline in capture is due to diffusion since the particles are at the furthest possible location from the target and have a greater probability of collision with the top of the vessel wall, causing its motion to stop due to the no-slip model implemented in this study. In this situation, there is also more distance to overcome, and the center of the vessel, where the blood flow is strongest, must be crossed. Alternately, when the z-value is zero, the particles are located at the center of the vessel, allowing for more flexibility regarding injection farther on the x-axis from the tumor site. In fact, when released at the center of the vessel, particles as far as m from the center of the tumor are successfully captured. The closer particles are injected to the tumor, the larger the probability of capture, but to a certain degree. When released too close to the target, there is not enough time for the magnet to attract the particle for capture, and the particle is whisked away before it reaches the tumor.
In practice, when the drug is injected into the bloodstream, it spreads out over the cross-section of the vessel, at various
z and
y values. To model this more realistically, random initial release points were incorporated into the trajectory simulations to determine their effect on capture rate. The particles are released at random uniformly distributed points within a spherical region whose radius is equal to that of the blood vessel. This and its effect on the capture rate can be seen in
Figure 4 below.
In a simulation using the point dipole model with Am, changing the release point from a single release point to randomly distributed release points changed the capture rate from 91% to 81%. In this case, the cloud release method centered at the middle of the vessel yields a slightly lower capture rate than the single release point method due to the optimal initial placement of all simulated particles in the latter method when compared to the random distribution of the former.
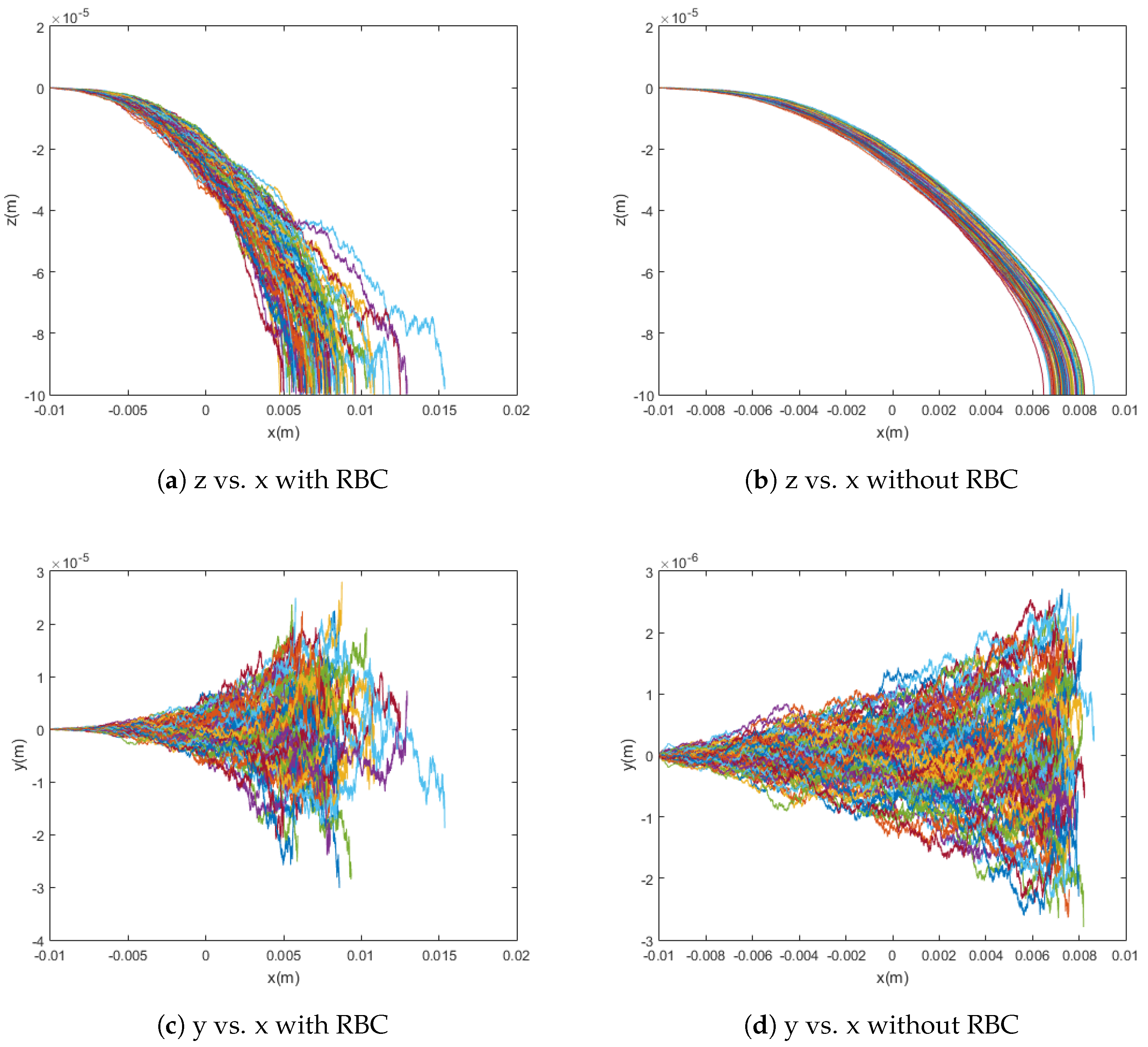
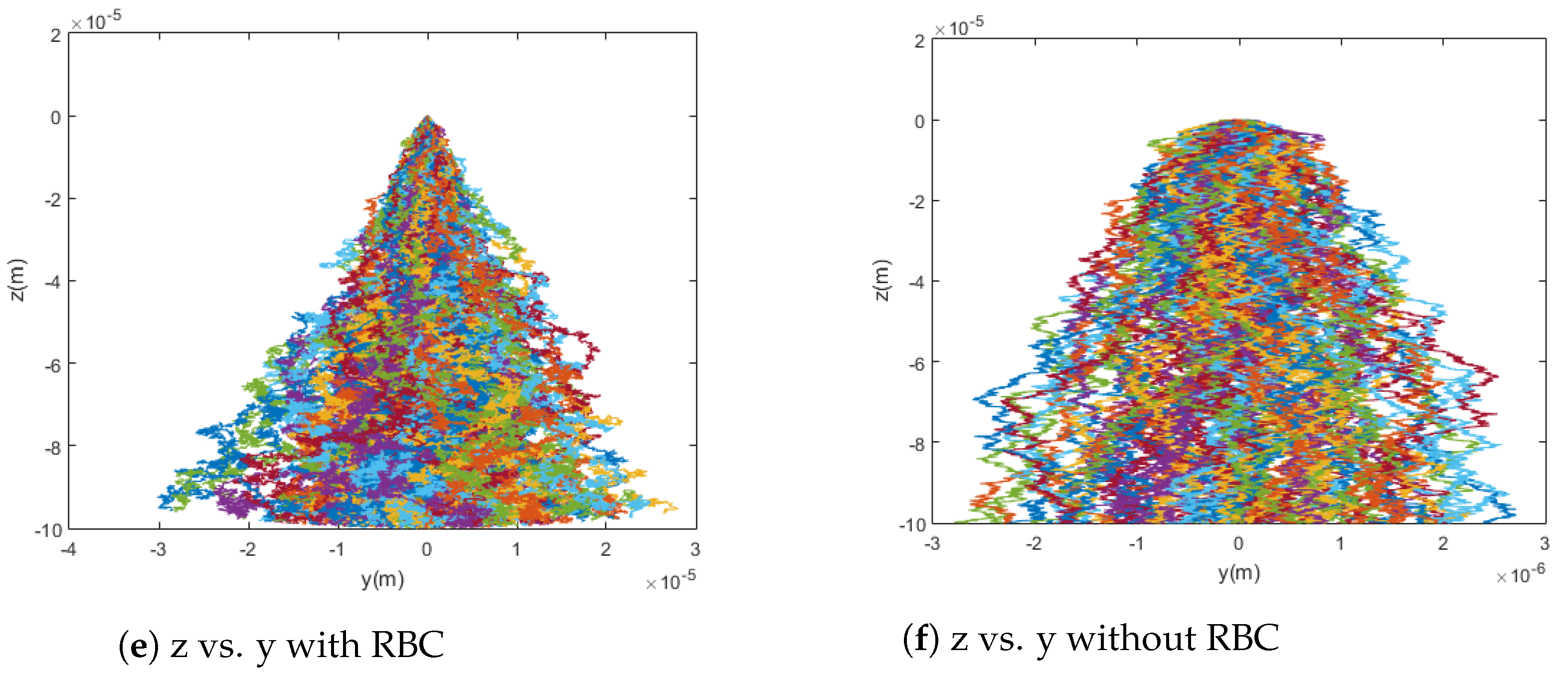
3.4. Red Blood Cell Collisions
By comparing Equations (
19) and (
20), it can be shown that, in a typical case, the diffusion due to collisions with red blood cells (RBC) significantly overpowers standard Brownian motion. This fact is confirmed by the model presented in this paper and shown in
Figure 5. When the particles are simulated without any diffusion, with only Brownian motion, and with only red blood cell collision diffusion, it can easily be seen that the difference in capture rate between the first and third cases is much greater than the difference in capture rate between the first and second cases. That is, the capture rate is much more dramatically affected by the introduction of red blood cell collisions than by that of Brownian motion. Even conceptually, the scale for red blood cell collisions is larger and its effects are much less local as compared to the relevant dimensions for Brownian motion. This highlights the need to consider the effects of red blood cells as sources of diffusion in addition to their impact on the viscosity of blood. That is, the viscosity models implemented in this paper and previous work have been adapted to treat blood as a homogeneous fluid while capturing its shear-thinning behavior, which is dictated largely by the radial distribution of cells across the flow in vessels. However, as can be seen from the trajectories and differences in capture rates shown in
Figure 5—for example, the red blood cells also have significant impact as sources of collisions. For these reasons, though the stochasticity from Brownian motion is incredibly important for the modeling of the trajectories of these particles, it alone is insufficient and, based on the significant effect of the diffusion due to collisions with red blood cells on capture rate, red blood cell collisions must also be taken into account for a model to be considered accurate.