3.1. Scalable Supra-Molecular Setup
In this section, we describe the supra-molecular setup proposed as a quantum simulator, inspired by the platform of [
18]. The elementary unit of the scalable array consists of an
pair of qubits linked by an interposed switch, in which
and
transitions are spectroscopically distinguishable. As a physical implementation of this architecture, we consider a couple of perpendicularly arranged Cr
7Ni rings, connected through a Co
2+ complex, as reported in [
20]. This two-qubit unit can be extended to form the
one-dimensional register schematically shown in
Figure 1. We exploit the anisotropy of the
tensors of the orthogonally arranged Cr
7Ni rings to selectively address
or
transitions. As explained below, in order to get a conditional excitation of odd (even) pairs of qubits, we also require to spectroscopically distinguish the transitions associated with odd (even) switches (see below), labeled S
1 and S
2 in
Figure 1. In the present setup, S
1 and S
2 can be obtained by rotating the same Co
2+ ion, thanks to the large anisotropy of its
tensor (see
Table 1).
The spin Hamiltonian describing the hardware is given by:
where capital (
) and lowercase (
) letters are used to indicate the effective spin 1/2 operators of the logical Cr
7Ni qubits and of the Co
2+ switches, respectively.
qubits and S
1 switches are labeled by odd indices, while
qubits and S
2 switches by even indices. The spectroscopic tensors
,
(
,
) describe the interaction of the qubits (switches) with an external magnetic field
B, and
is the Bohr magneton. Finally,
and
are exchange tensors describing the interaction of the switches with
and
qubits, respectively. The parameters employed in the simulations are listed in
Table 1.
,
, and
were determined by X-, K-, Q-, and W-band electron paramagnetic resonance (EPR) performed on the elementary Cr
7Ni–Co–Cr
7Ni unit [
20], while
and
were reduced by a factor of three with respect to the experimental values of [
20], in order to improve the scalability of the setup (see discussion below). A similar reduction could be achieved chemically by adding an extra phenyl group between the ring and the central node.
3.2. Quantum Gates with Uniform Magnetic Pulses
We describe here a scheme for performing one- and two-qubit gates (which constitute the essential building blocks of digital quantum simulation algorithms) on a scalable platform, based on the ideas of [
19,
20]. As discussed below, this scheme can be exploited for proof-of-principle experiments of quantum simulation on short chains of molecular qubits. The qubit–qubit coupling is switched by a single (Co
2+) ion, interposed between the Cr
7Ni qubits, as in the newly synthesized family of complexes Cr
7Ni–Co–Cr
7Ni. A necessary condition for the scheme to work is that as long as the switch is in the ground state, the effective qubit–qubit interaction (resulting from virtual excitations of the switch) is small enough that the associated unwanted evolution is very slow on the timescale of the quantum gates. On one hand, this condition is fulfilled if the difference between the excitation energies of the qubits and of the switch is much larger than the qubit–switch coupling. On the other hand, to enable conditional dynamics, this coupling must be large enough to make the excitation energy of the switch sufficiently dependent on the state of the qubits. This requires a suitable chemical engineering of the qubit–switch bond. In the present implementation, the feasibility of the scheme relies on a weak Co-ring coupling, if compared to the difference between the Co and ring Zeeman interaction with an applied field.
We first focus on the two-qubit elementary unit, and let
z be the direction of the external field. Since
, in a field of a few Teslas, the eigenstates of the Hamiltonian are factorized and we can define the computational basis within the low-energy subspace corresponding to the Co frozen into its ground state
. Here
, and we associate the logical
and
to the
and
state of each ring. It is therefore possible to implement single-qubit rotations by EPR pulses resonant with the
Cr
7Ni gaps. Notice that the
and
transitions are made significantly inequivalent by the anisotropy of the Cr
7Ni
tensor (
, see
Table 1), combined with the asymmetric coupling to the switch (
). Indeed, the
z component of the exchange interaction yields a renormalization of the magnetic field felt by the qubits:
for qubit
and
for qubit
. This leads to an energy difference
between the
and
transitions and allows us to independently rotate
and
qubits.
Conversely, the entangling two-qubit gate controlled-
(C
) is obtained by exciting and de-exciting the
component of the two-qubit wavefunction to a state outside the computational basis, corresponding to a rotation of the central Co
2+ ion state. This allows us to implement a conditional (two-qubit) dynamics because the energy cost of this rotation depends on the states of the two molecular qubits by an amount of the order of
J. Hence, C
can be implemented by a pulse resonant with the
gap, followed by a repetition of the same pulse that brings the state back to
with an additional phase
. The other two-qubit states are left unaffected by the pulse sequence, as required by the controlled-phase gate [
3]. The value of
is controlled by the phase difference between the first and the second pulse.
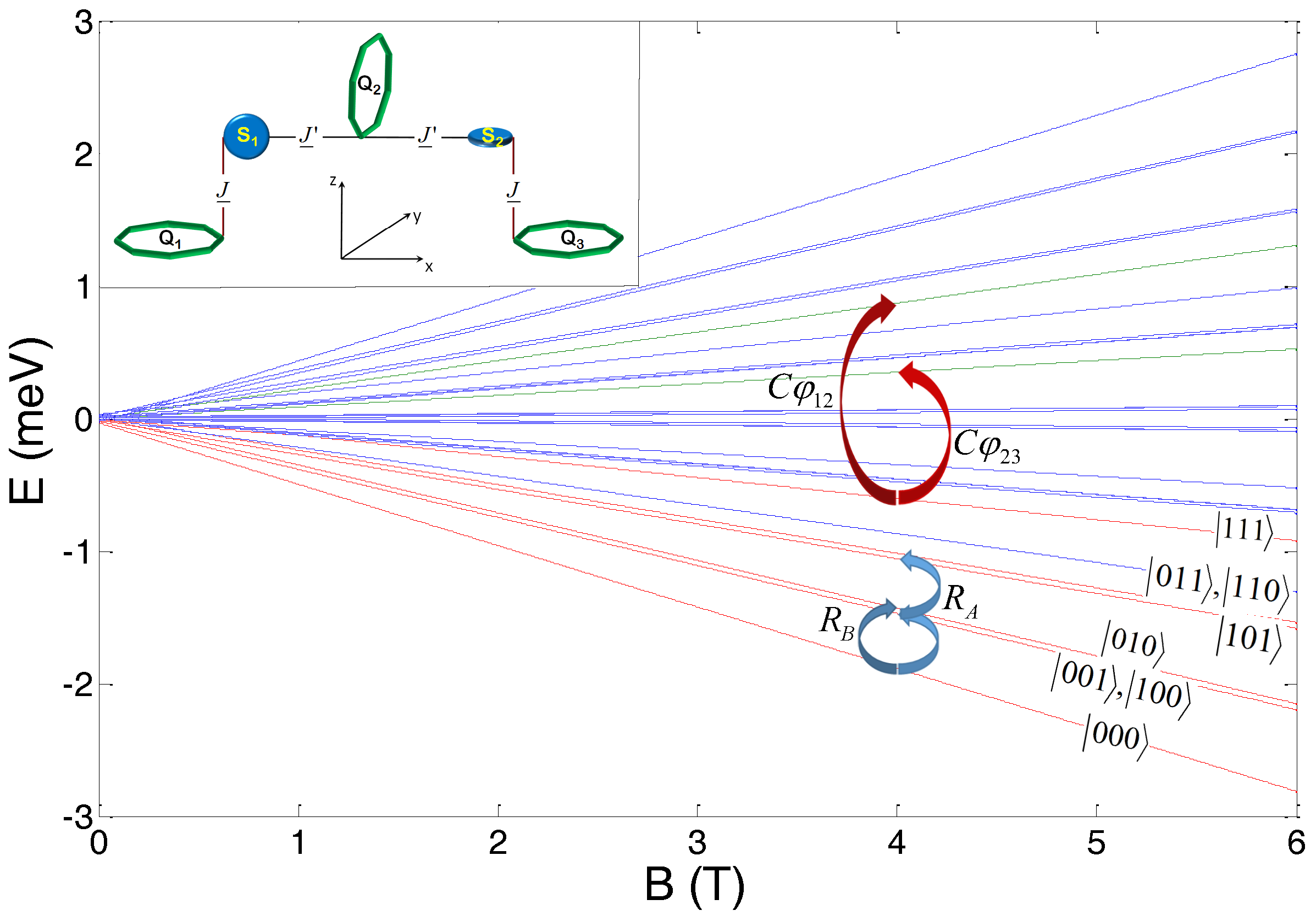
Below we extend this scheme for quantum computation to a chain of three qubits, schematically shown in the inset of
Figure 2. Qubits Q
1 and Q
3 belong to the
sublattice, while Q
2 to the
sublattice. In
Figure 2, we also report the energy level diagram as a function of the applied magnetic field (along the
z-axis). The computational three-qubit basis is defined in the low-energy subspace where both switches S
1 and S
2 are frozen into their
ground state, corresponding to the red lines in
Figure 2. Quantum gates are implemented in a static field
T, by means of gaussian EPR pulses. Single-qubit rotations of
and
qubits are obtained by pulses resonant with the gaps indicated by blue arrows. In this three-qubit setup, the rotation of Q
1 and Q
3 qubits (
sublattice) occurs in two steps via the intermediate excitation of the degenerate
and
states. Conversely, C
(C
) gates on the 12 (23) pair of qubits are implemented by a conditional excitation of the
(
) component of the wave-function (red arrows in
Figure 2) to the excited states (green lines), corresponding to the flip of the switch S
1 (S
2). Notice that if the pulse is applied along the
y direction, the implementation of this gate is fast, owing to the large value of
. Moreover, the exchange interaction in Equation (
3) is sufficiently large to allow us to employ large oscillating fields (50 G), since the desired transition is spectroscopically well resolved from all the others. Consequently, the C
gate can be performed in only about 12 ns.
3.3. Numerical Experiments
In order to quantify the performance of the elementary gates, we compute the fidelity
, which is a well-known figure of merit of the proximity of two quantum states [
3]. Here
is the final state that would result from an ideal implementation of the gates, while
is the actual final state, obtained by numerically simulating the evolution of the wave-function, subject to the static Hamiltonian
3 and to the sequence of pulses required to implement such gates. The fidelities calculated for two and three qubit setups in the implementation of single-qubit rotations, C
gates, as well as in the simulation of spin Hamiltonian terms
are reported in
Table 2. In order to simplify the simulation of the term
—which yields a phase-difference between parallel and anti-parallel spin components—we simultaneously apply two pulses for a conditional excitation/de-excitation of both
and
components of the two-qubit wave-function to a state in which the Co spin is reversed. This directly adds the desired phase to
and
, without requiring additional single-qubit phase-gates.
It is worth noting that the reported fidelities are very high. The small errors are predominantly caused by imperfect operation of the switches. Indeed, the permanent Co-rings couplings (
and
) lead to a small residual qubit–qubit interaction, even when the switch is in the off-state. The analytic form of this residual coupling can be deduced at second-order perturbation theory level. Indeed, since
, the exchange terms in (
3) act as a small perturbation with respect to the energy cost of flipping a pair of neighboring spins. This allows us to eliminate the switch degrees of freedom in the subspace in which
, and to obtain a residual qubit–qubit interaction expressed by:
with
Here, in the limit of small qubit–switch exchange interaction, the leading term is given by a first order correction to the magnetic field felt by the qubits, induced by and . Two-qubit XX and YY interactions emerge as a second-order effect, which induce an unwanted two-qubit evolution—even when the switch is turned off—by mixing states and of the computational basis. To obtain high-fidelity single qubit gates, these interactions should be small, so that the associated dynamics occurs on a time-scale much longer than the gating time (∼10–20 ns). For the here-reported parameters, we have estimated that the time required to reduce the fidelity in an idle evolution of a couple of qubits to 0.9 is of the order of several s. The effect increases by increasing the number n of qubits, but remains negligible for . Remarkably, this timescale is much longer than , since the combination of the perpendicular arrangement of the rings and of the highly anisotropic behavior of Co2+ leads to a significant splitting of the and states, thus effectively suppressing the residual inter-qubit interaction. Hence, the fidelities of the elementary gates for and are very similar and practically unaffected by the unwanted evolution.
Even if the demonstration of the elementary single- and two-qubit gates is in principle sufficient to ensure the implementation of quantum simulation algorithms, the actual feasibility of such simulations needs to be quantitatively assessed by testing whether the complex sequences of gates needed are robust with respect to errors. To demonstrate the effectiveness of the proposed scheme, we have performed numerical experiments in which many gates have been concatenated to implement quantum simulation algorithms on a chain of three qubits. As a paradigmatic example, we report the digital quantum simulation of the transverse field Ising model, described by the target Hamiltonian:
If we exploit the first order expansion
1, simulating the evolution induced by
requires the implementation of three single-qubit rotations and four conditional gates per Trotter step.
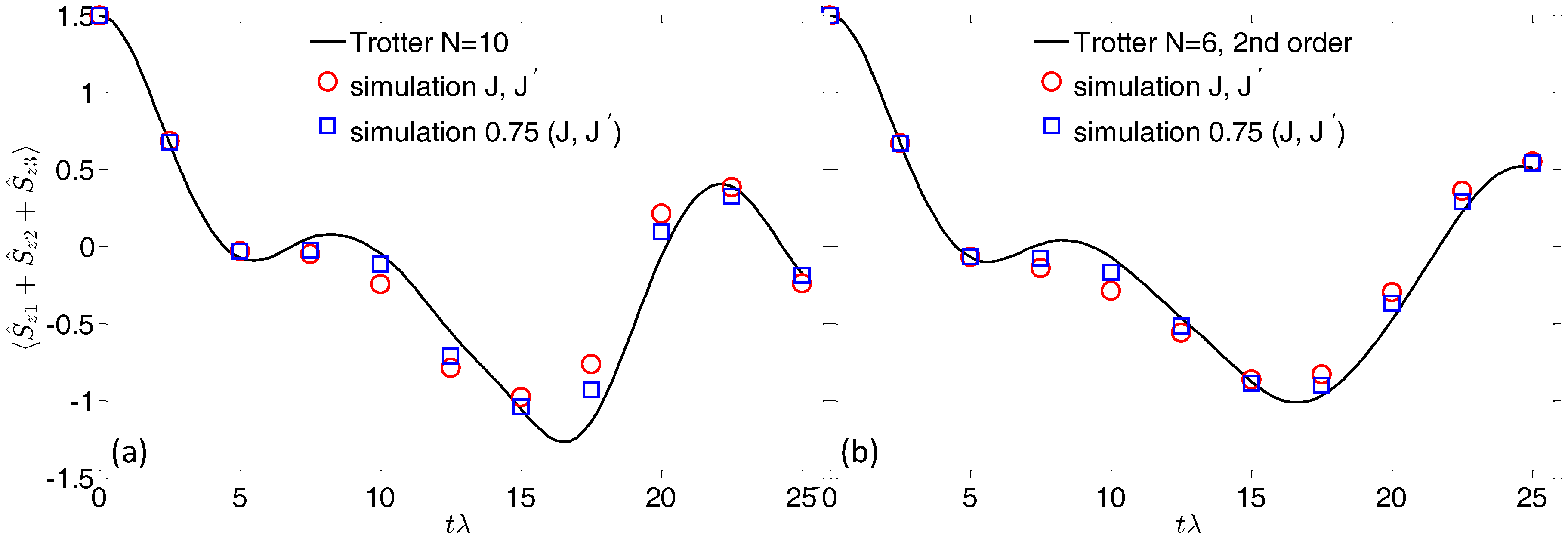
Figure 3a shows the time evolution of the final magnetization of the three qubits, calculated by using
Trotter steps. This is the typical quantity that can be extracted in a pulse-EPR experiment on a bulk crystal of molecular nanomagnets (see, e.g., [
24]). The polarization detectors either measure the entire polarization pattern or selectively record the on-resonance polarization, thus targeting the transitions of each qubit. In the former case, the qubits polarization can be obtained by subtracting the contribution of the Co switches (which are practically frozen into the
ground state) from the entire polarization.
By analyzing
Figure 3, we note that the agreement with the expected evolution (continuous line) is generally good. However, since we are now considering the sequential application of many gates (the total simulation time is about 300 ns), the effect of the residual qubit–qubit interaction is much more pronounced than in the case of a single gate. On the one hand, this is a direct consequence of increasing the computational time; on the other hand, errors accumulated in the implementation of each gate can combine non-linearly, leading (for significantly large errors) to unreliable results.
We can point out different ways to reduce the detrimental effect of the residual coupling. As noted above, with a static field of 4 T, the oscillation induced by
occurs on a timescale of several
s, which is much longer than the time required for the whole simulation. Hence, simulated (blue) points reported in
Figure 3a are in good agreement with the exact evolution (continuous line). The analytic expression (
4) can be exploited to further improve the simulation. Indeed, we note that
and
can be controlled by the strength of the applied field or by the size of the Co-ring exchange. Hence, increasing the magnetic field or reducing
J (red points in
Figure 3) leads to a better agreement between the exact and simulated time evolution.
Alternatively, a strategy to reduce the total number of gates (hence the error associated with the unwanted evolution) is to exploit a second order Trotter–Suzuki expansion [
22]. For instance, we can decompose the target Hamiltonian into four terms:
, with
,
,
,
. Then, we approximate the unitary evolution associated to
by:
This is a second order expansion of the exponential, meaning that the associated error is
, with
. Consequently, Equation (
6) gives a better approximation of the exact evolution for short
t, while expansion
1 is preferable for long times. By exploiting Equation (
6), the total number of gates per step is increased (four rotations and six conditional gates), but we can reduce the number of Trotter steps to
, while keeping (for small
) a digital error similar to that obtained with
steps in the first order decomposition. This reduces the total number of gates required for the simulation and leads to a better agreement between the expected and simulated evolution, reported in panel (b) of
Figure 3.