Cold Atoms in U(3) Gauge Potentials
Abstract
:1. Introduction
2. Review of Artificial Gauge Potentials in Optical Lattices
3. Gauge Potential with Non-Constant Wilson Loop
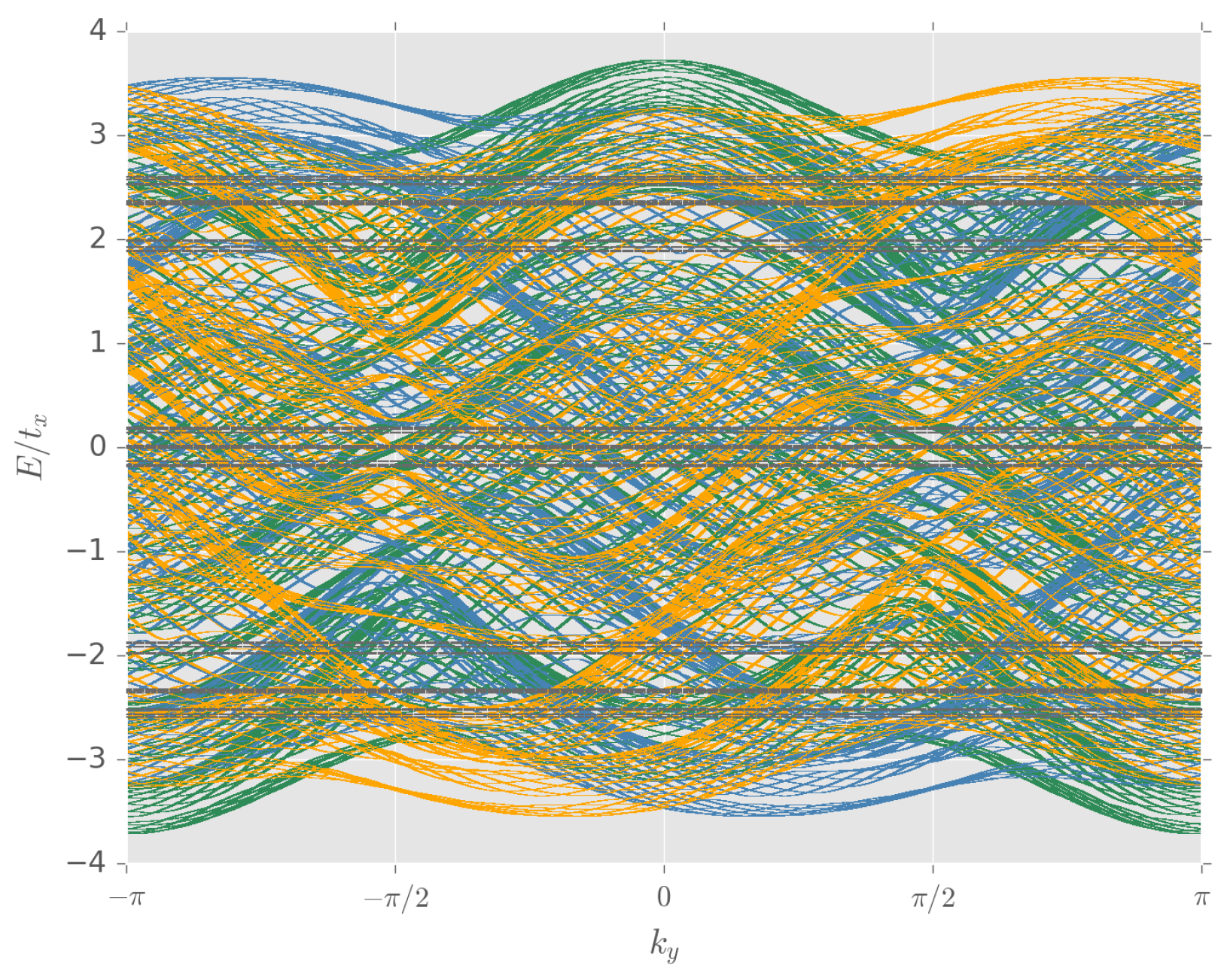
3.1. Spectrum for Rational Fluxes
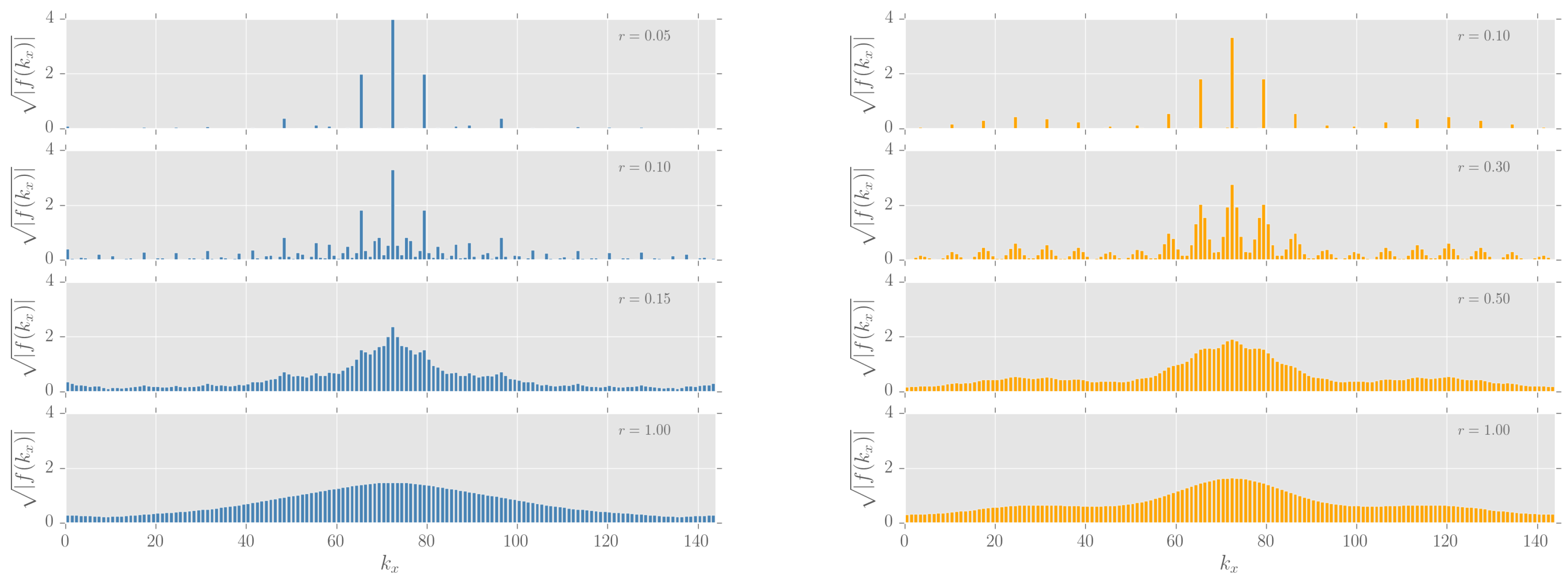
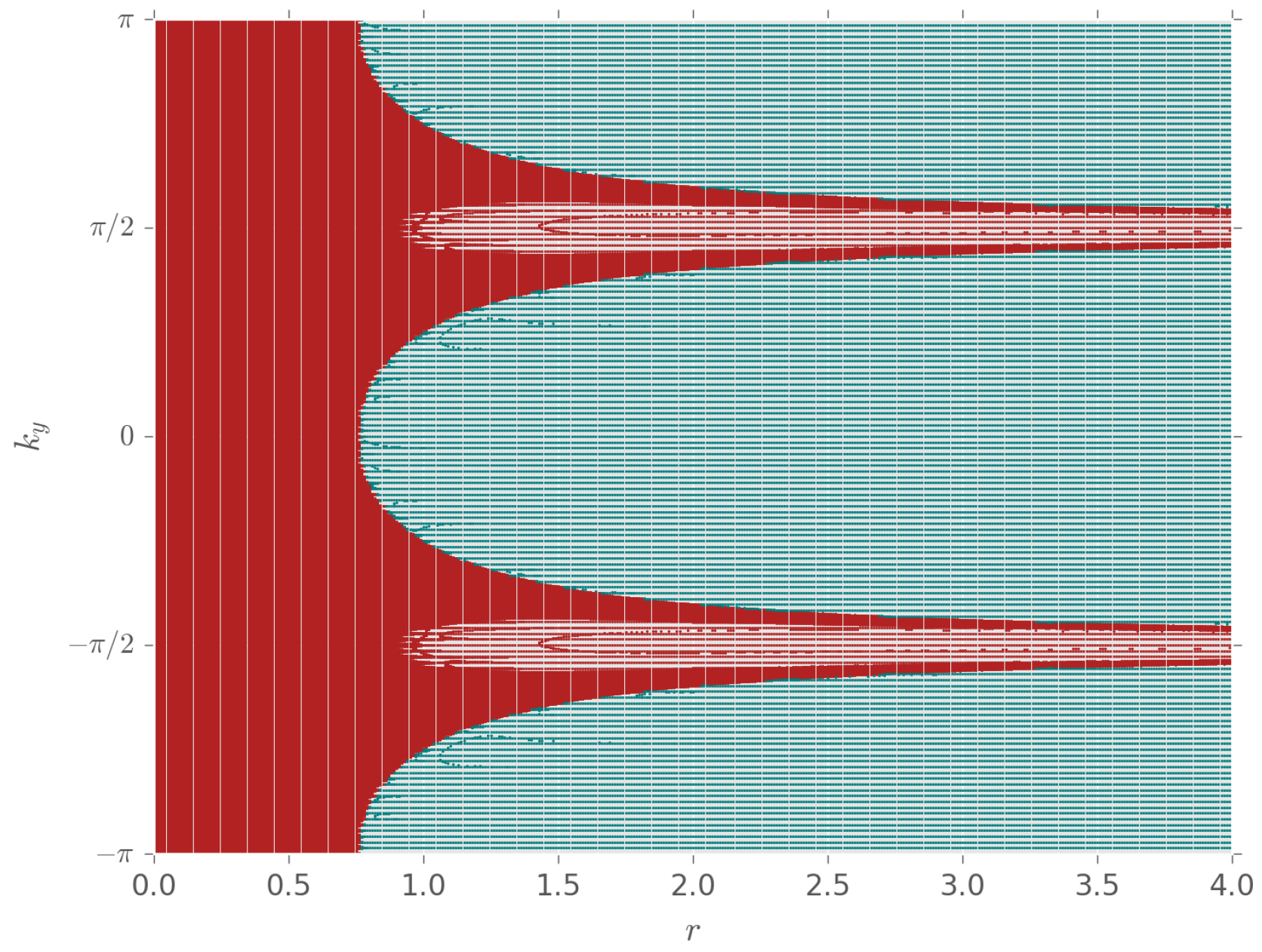
3.2. Metal–Insulator Transition for Irrational Flux
4. Gauge Potential with Constant Wilson Loop
4.1. Spectrum for Rational Flux
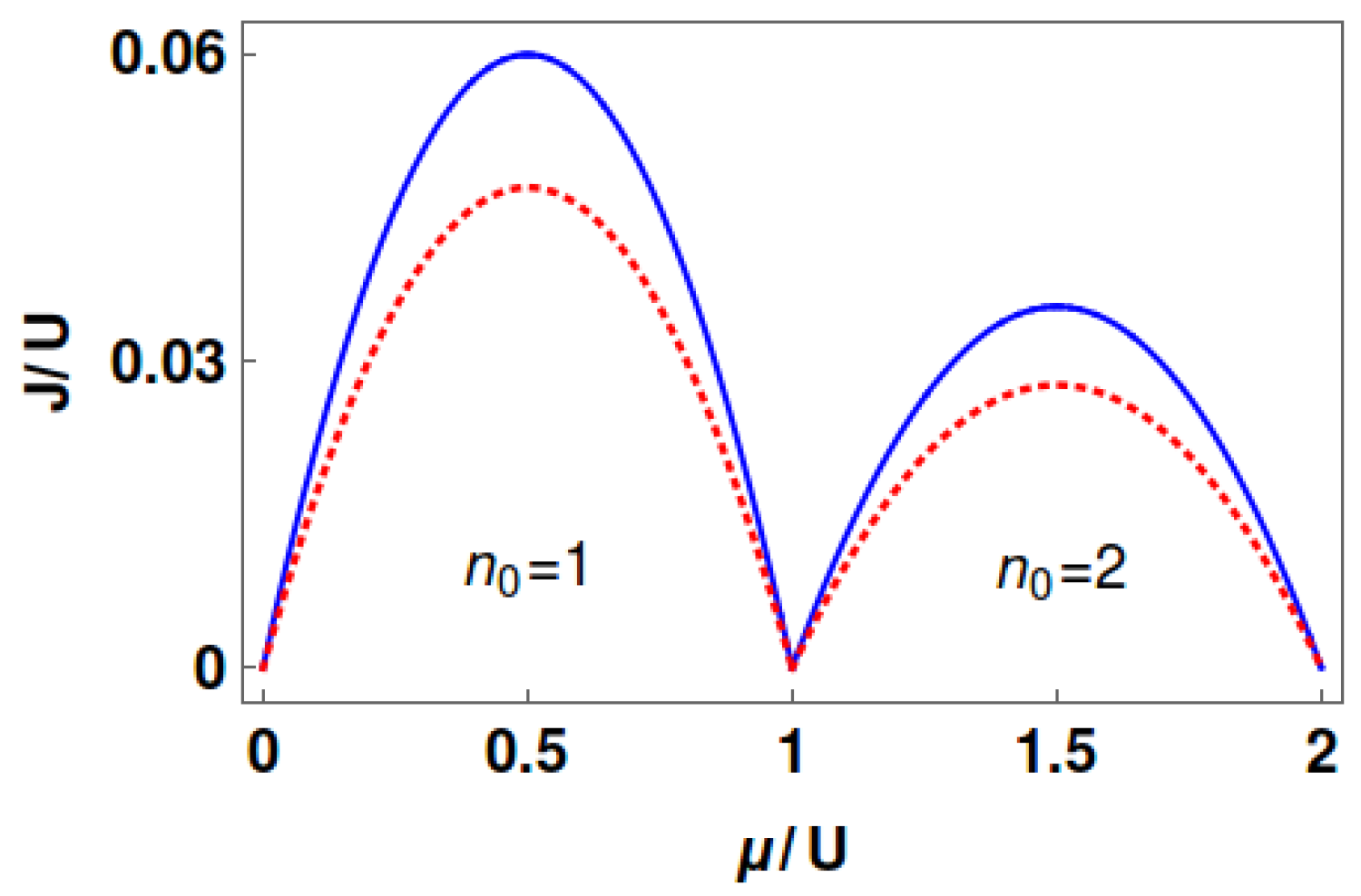
4.2. Superfluid–Insulator Transition of Ultracold Bosons
5. Discussion
Acknowledgments
Author Contributions
References
- Bloch, I.; Dalibard, J.; Zwerger, W. Many-body physics with ultracold gases. Rev. Mod. Phys. 2008, 80, 885–964. [Google Scholar] [CrossRef]
- Lewenstein, M.; Sanpera, A.; Ahufinger, V.; Damski, B.; Sen, A.; Sen, U. Ultracold atomic gases in optical lattices: mimicking condensed matter physics and beyond. Adv. Phys. 2007, 56, 243–379. [Google Scholar] [CrossRef]
- Juzeliūnas, G.; Ruseckas, J.; Dalibard, J. Generalized Rashba-Dresselhaus spin-orbit coupling for cold atoms. Phys. Rev. A 2010, 81, 053403. [Google Scholar] [CrossRef]
- Dalibard, J.; Gerbier, F.; Juzeliūnas, G.; Öhberg, P. Colloquium: Artificial gauge potentials for neutral atoms. Rev. Mod. Phys. 2011, 83, 1523–1543. [Google Scholar] [CrossRef]
- Banerjee, D.; Dalmonte, M.; Müller, M.; Rico, E.; Stebler, P.; Wiese, U.J.; Zoller, P. Atomic Quantum Simulation of Dynamical Gauge Fields Coupled to Fermionic Matter: From String Breaking to Evolution after a Quench. Phys. Rev. Lett. 2012, 109, 175302. [Google Scholar] [CrossRef] [PubMed]
- Goldman, N.; Satija, I.; Nikolic, P.; Bermudez, A.; Martin-Delgado, M.A.; Lewenstein, M.; Spielman, I.B. Realistic Time-Reversal Invariant Topological Insulators with Neutral Atoms. Phys. Rev. Lett. 2010, 105, 255302. [Google Scholar] [CrossRef] [PubMed]
- Bermudez, A.; Mazza, L.; Rizzi, M.; Goldman, N.; Lewenstein, M.; Martin-Delgado, M.A. Wilson Fermions and Axion Electrodynamics in Optical Lattices. Phys. Rev. Lett. 2010, 105, 190404. [Google Scholar] [CrossRef] [PubMed]
- Mazza, L.; Bermudez, A.; Goldman, N.; Rizzi, M.; Martin-Delgado, M.A.; Lewenstein, M. An optical-lattice-based quantum simulator for relativistic field theories and topological insulators. New J. Phys. 2012, 14, 015007. [Google Scholar] [CrossRef]
- Goldman, N.; Kubasiak, A.; Bermudez, A.; Gaspard, P.; Lewenstein, M.; Martin-Delgado, M.A. Non-Abelian Optical Lattices: Anomalous Quantum Hall Effect and Dirac Fermions. Phys. Rev. Lett. 2009, 103, 035301. [Google Scholar] [CrossRef] [PubMed]
- Bermudez, A.; Goldman, N.; Kubasiak, A.; Lewenstein, M.; Martin-Delgado, M.A. Topological phase transitions in the non-Abelian honeycomb lattice. New J. Phys. 2010, 12, 033041. [Google Scholar] [CrossRef]
- Ho, T.L. Bose–Einstein Condensates with Large Number of Vortices. Phys. Rev. Lett. 2001, 87, 060403. [Google Scholar] [CrossRef] [PubMed]
- Jaksch, D.; Zoller, P. Creation of effective magnetic fields in optical lattices: the Hofstadter butterfly for cold neutral atoms. New J. Phys. 2003, 5, 56. [Google Scholar] [CrossRef]
- Mueller, E.J. Artificial electromagnetism for neutral atoms: Escher staircase and Laughlin liquids. Phys. Rev. A 2004, 70, 041603. [Google Scholar] [CrossRef]
- Sørensen, A.S.; Demler, E.; Lukin, M.D. Fractional Quantum Hall States of Atoms in Optical Lattices. Phys. Rev. Lett. 2005, 94, 086803. [Google Scholar] [CrossRef] [PubMed]
- Juzeliūnas, G.; Öhberg, P.; Ruseckas, J.; Klein, A. Effective magnetic fields in degenerate atomic gases induced by light beams with orbital angular momenta. Phys. Rev. A 2005, 71, 053614. [Google Scholar] [CrossRef] [Green Version]
- Juzeliūnas, G.; Öhberg, P. Slow Light in Degenerate Fermi Gases. Phys. Rev. Lett. 2004, 93, 033602. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.J.; Compton, R.L.; Jiménez-García, K.; Porto, J.V.; Spielman, I.B. Synthetic magnetic fields for ultracold neutral atoms. Nature 2009, 462, 628–632. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.J.; Compton, R.L.; Perry, A.R.; Phillips, W.D.; Porto, J.V.; Spielman, I.B. Bose–Einstein Condensate in a Uniform Light-Induced Vector Potential. Phys. Rev. Lett. 2009, 102, 130401. [Google Scholar] [CrossRef] [PubMed]
- Bhat, R.; Holland, M.J.; Carr, L.D. Bose–Einstein Condensates in Rotating Lattices. Phys. Rev. Lett. 2006, 96, 060405. [Google Scholar] [CrossRef] [PubMed]
- Polini, M.; Fazio, R.; MacDonald, A.H.; Tosi, M.P. Realization of Fully Frustrated Josephson-Junction Arrays with Cold Atoms. Phys. Rev. Lett. 2005, 95, 010401. [Google Scholar] [CrossRef] [PubMed]
- Bhat, R.; Krämer, M.; Cooper, J.; Holland, M.J. Hall effects in Bose–Einstein condensates in a rotating optical lattice. Phys. Rev. A 2007, 76, 043601. [Google Scholar] [CrossRef]
- Tung, S.; Schweikhard, V.; Cornell, E.A. Observation of Vortex Pinning in Bose–Einstein Condensates. Phys. Rev. Lett. 2006, 97, 240402. [Google Scholar] [CrossRef] [PubMed]
- Klein, A.; Jaksch, D. Phonon-induced artificial magnetic fields in optical lattices. Europhys. Lett. 2009, 85, 13001. [Google Scholar] [CrossRef]
- Hu, Y.X.; Miniatura, C.; Wilkowski, D.; Grémaud, B. U(3) artificial gauge fields for cold atoms. Phys. Rev. A 2014, 90, 023601. [Google Scholar] [CrossRef]
- Hofstadter, D.R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields. Phys. Rev. B 1976, 14, 2239–2249. [Google Scholar] [CrossRef]
- Goldman, N. Spatial patterns in optical lattices submitted to gauge potentials. Europhys. Lett. 2007, 80, 20001. [Google Scholar] [CrossRef]
- Palmer, R.N.; Jaksch, D. High-Field Fractional Quantum Hall Effect in Optical Lattices. Phys. Rev. Lett. 2006, 96, 180407. [Google Scholar] [CrossRef] [PubMed]
- Goldman, N.; Gaspard, P. Quantum Hall-like effect for cold atoms in non-Abelian gauge potentials. Europhys. Lett. 2007, 78, 60001. [Google Scholar] [CrossRef]
- Hafezi, M.; Sørensen, A.S.; Lukin, M.D.; Demler, E. Characterization of topological states on a lattice with Chern number. Europhys. Lett. 2008, 81, 10005. [Google Scholar] [CrossRef]
- Osterloh, K.; Baig, M.; Santos, L.; Zoller, P.; Lewenstein, M. Cold Atoms in Non-Abelian Gauge Potentials: From the Hofstadter “Moth” to Lattice Gauge Theory. Phys. Rev. Lett. 2005, 95, 010403. [Google Scholar] [CrossRef] [PubMed]
- Ruseckas, J.; Juzeliūnas, G.; Öhberg, P.; Fleischhauer, M. Non-Abelian Gauge Potentials for Ultracold Atoms with Degenerate Dark States. Phys. Rev. Lett. 2005, 95, 010404. [Google Scholar] [CrossRef] [PubMed]
- Satija, I.I.; Dakin, D.C.; Vaishnav, J.Y.; Clark, C.W. Physics of a two-dimensional electron gas with cold atoms in non-Abelian gauge potentials. Phys. Rev. A 2008, 77, 043410. [Google Scholar] [CrossRef]
- Jacob, A.; Öhberg, P.; Juzeliūnas, G.; Santos, L. Landau levels of cold atoms in non-Abelian gauge fields. New J. Phys. 2008, 10, 045022. [Google Scholar] [CrossRef]
- Jacob, A.; Öhberg, P.; Juzeliūnas, G.; Santos, L. Cold atom dynamics in non-Abelian gauge fields. Appl. Phys. B Lasers Opt. 2007, 89, 439–445. [Google Scholar] [CrossRef]
- Juzeliūnas, G.; Ruseckas, J.; Jacob, A.; Santos, L.; Öhberg, P. Double and Negative Reflection of Cold Atoms in Non-Abelian Gauge Potentials. Phys. Rev. Lett. 2008, 100, 200405. [Google Scholar] [CrossRef] [PubMed]
- Barnett, R.; Boyd, G.R.; Galitski, V. SU(3) Spin-Orbit Coupling in Systems of Ultracold Atoms. Phys. Rev. Lett. 2012, 109, 235308. [Google Scholar] [CrossRef] [PubMed]
- Graß, T.; Chhajlany, R.W.; Muschik, C.A.; Lewenstein, M. Spiral spin textures of a bosonic Mott insulator with SU(3) spin-orbit coupling. Phys. Rev. B 2014, 90, 195127. [Google Scholar] [CrossRef]
- Goldman, N.; Kubasiak, A.; Gaspard, P.; Lewenstein, M. Ultracold atomic gases in non-Abelian gauge potentials: The case of constant Wilson loop. Phys. Rev. A 2009, 79, 023624. [Google Scholar] [CrossRef]
- Sengupta, K.; Dupuis, N. Mott-insulator–to–superfluid transition in the Bose–Hubbard model: A strong-coupling approach. Phys. Rev. A 2005, 71, 033629. [Google Scholar] [CrossRef]
- Freericks, J.K.; Krishnamurthy, H.R.; Kato, Y.; Kawashima, N.; Trivedi, N. Strong-coupling expansion for the momentum distribution of the Bose–Hubbard model with benchmarking against exact numerical results. Phys. Rev. A 2009, 79, 053631. [Google Scholar] [CrossRef]
- Sinha, S.; Sengupta, K. Superfluid-insulator transition of ultracold bosons in an optical lattice in the presence of a synthetic magnetic field. Europhys. Lett. 2011, 93, 30005. [Google Scholar] [CrossRef]
- Graß, T.; Saha, K.; Sengupta, K.; Lewenstein, M. Quantum phase transition of ultracold bosons in the presence of a non-Abelian synthetic gauge field. Phys. Rev. A 2011, 84, 053632. [Google Scholar] [CrossRef]


© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mandal, I.; Bhattacharya, A. Cold Atoms in U(3) Gauge Potentials. Condens. Matter 2016, 1, 2. https://doi.org/10.3390/condmat1010002
Mandal I, Bhattacharya A. Cold Atoms in U(3) Gauge Potentials. Condensed Matter. 2016; 1(1):2. https://doi.org/10.3390/condmat1010002
Chicago/Turabian StyleMandal, Ipsita, and Atri Bhattacharya. 2016. "Cold Atoms in U(3) Gauge Potentials" Condensed Matter 1, no. 1: 2. https://doi.org/10.3390/condmat1010002




