A New Observer Design for Fuzzy Bilinear Systems with Unknown Inputs
Abstract
:1. Introduction
2. Fuzzy Bilinear Systems
- 1.
- A and are given. There exists such that:
- 2.
- A and are given. There exist and R such that:
3. Observer Design
3.1. Non-PDO Design
| Algorithm 1: |
|
3.2. Generalization of the Nonlinear Output Equation
- 1.
- ;
- 2.
- is measurable.
3.3. Extension to Observer Design with Unmeasurable Premise Variables
- 1.
- 2.
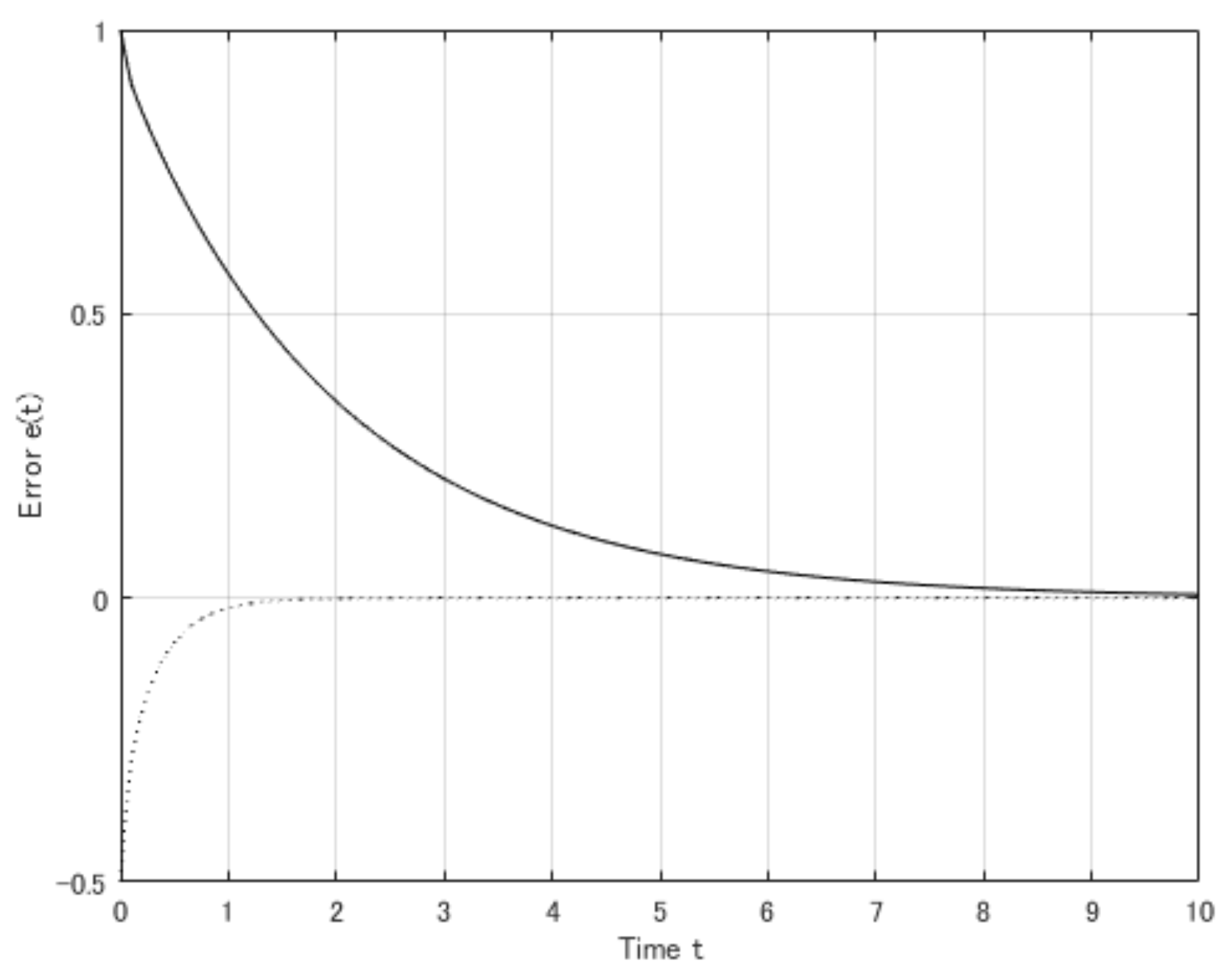
4. Numerical Examples
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Takagi, T.; Sugeno, M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans. Syst. Man Cybern. 1985, 15, 116–132. [Google Scholar] [CrossRef]
- Dong, S.; Wu, Z.-G.; Shi, P.; Su, H.; Lu, R. Reliable control of fuzzy systems with quantization and switched actuator failures. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2198–2208. [Google Scholar] [CrossRef]
- Lendek, Z.; Guerra, T.M.; Babuska, R.; De Schutter, B. Stability Analysis and Nonlinear Observer Design Using Takagi–Sugeno Fuzzy Models; Springer: Berlin, Germany, 2010. [Google Scholar]
- Tanaka, K.; Ohtake, H.; Wang, H.O. A descriptor system approach to fuzzy control system design via fuzzy Lyapunov functions. IEEE Trans. Fuzzy Syst. 2007, 15, 333–341. [Google Scholar] [CrossRef]
- Tanaka, K.; Sugeno, M. Stability analysis and design of fuzzy control systems. Fuzzy Sets Syst. 1992, 45, 135–156. [Google Scholar] [CrossRef]
- Wu, Z.-G.; Dong, S.; Shi, P.; Su, H.; Huang, T.; Lu, R. Fuzzy-model-based non fragile guaranteed cost control of nonlinear Markov jump systems. IEEE Trans. Syst. Man Cybern. Syst. 2017, 47, 2388–2397. [Google Scholar] [CrossRef]
- Yoneyama, J. Nonlinear control design based on generalized Takagi–Sugeno fuzzy systems. J. Frankl. Inst. 2014, 351, 3524–3535. [Google Scholar] [CrossRef]
- Gao, Z.-F.; Chen, J.; Liu, F. Guaranteed cost control for fuzzy bilinear systems with uncertain parameters. In Proceedings of the 2010 International Conference on Electrical Engineering, Computing Science and Automatic Control, Tuxtla Gutierrez, Mexico, 8–10 September 2010; pp. 644–647. [Google Scholar]
- Guo, Z.; Bo, R. Non-fragile static output controller design for fuzzy systems. In Proceedings of the 2000 International Conference on Intelligent System Design and Engineering Application, Changsha, China, 13–14 October 2010; pp. 1017–1020. [Google Scholar]
- Li, T.-H.S.; Tsai, S.-H.; Lee, J.-Z.; Hsiao, M.-Y.; Chao, C.-H. Robust H∞ fuzzy control for a class of uncertain discrete fuzzy nonlinear systems. IEEE Trans. Syst. Man Cybern. Part B 2007, 38, 510–527. [Google Scholar] [CrossRef] [PubMed]
- Li, T.-H.S.; Tsai, S.-H. T–S fuzzy bilinear model and fuzzy controller design for a class of nonlinear systems. IEEE Trans. Fuzzy Syst. 2007, 15, 494–506. [Google Scholar] [CrossRef]
- Takada, R.; Uchida, Y.; Yoneyama, J. Output Feedback Stabilization of Takagi–Sugeno Fuzzy Bilinear Time-Delay Systems. In Proceedings of the 2012 IEEE International Conference on Fuzzy Systems, Brisbane, Australia, 10–15 June 2012; pp. 300–307. [Google Scholar]
- Takada, R.; Uchida, Y.; Yoneyama, J. Output feedback guaranteed cost control for fuzzy bilinear systems. Appl. Math. Sci. 2013, 7, 1303–1318. [Google Scholar]
- Tsai, S.-H.; Li, T.-H.S. Robust fuzzy control of a class of fuzzy bilinear systems with time-delay. Chaos Solitons Fractals 2009, 39, 2028–2040. [Google Scholar] [CrossRef]
- Yoneyama, J. Stabilization of Takagi–Sugeno fuzzy bilinear time-delay systems. In Proceedings of the 2010 IEEE Multi-Conference Systems and Control, Yokohama, Japan, 8–10 September 2010; pp. 111–116. [Google Scholar]
- Yoneyama, J. Output feedback control design for Takagi–Sugeno fuzzy bilinear time-delay systems. In Proceedings of the 2010 IEEE Conference on Systems, Man and Cybernetics, Istanbul, Turkey, 10–13 October 2010; pp. 1671–1677. [Google Scholar]
- Marquez, R.; Guerra, T.M.; Bernal, M.; Kruszewski, A. A non-quadratic Lyapunov functional for H∞ control of nonlinear systems via Takagi–Sugeno models. J. Frankl. Inst. 2016, 353, 781–796. [Google Scholar] [CrossRef]
- Yoneyama, J.; Hoshino, K. A novel non-fragile output feedback controller design for uncertain Takagi–Sugeno fuzzy systems. In Proceedings of the World Congress on Computational Intelligence, Vancouver, BC, Canada, 24–29 July 2016; pp. 2193–2198. [Google Scholar]
- Estrada-Manzo, V.; Guerra, T.M.; Lendek, Z. An LMI approach for observer design for Takagi–Sugeno descriptor models. In Proceedings of the 2014 IEEE International Conference on Automation, Quality and Testing, Robotics, Cluj-Napoca, Romania, 22–24 May 2014. [Google Scholar]
- Shi, P.; Su, X.; Li, F. Dissipativity-based filtering for fuzzy switched systems with stochastic perturbation. IEEE Trans. Autom. Control 2016, 61, 1694–1699. [Google Scholar] [CrossRef]
- Shi, P.; Zhang, Y.; Chadli, M.; Agarwal, R.K. Mixed H-infinity and passive filtering for discrete fuzzy neural networks with stochastic jumps and time delays. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 903–909. [Google Scholar] [CrossRef] [PubMed]
- Yoneyama, J. H∞ Filtering for Fuzzy Systems with Immeasurable Premise Variables: An Uncertain System Approach. Fuzzy Sets Syst. 2009, 160, 1738–1748. [Google Scholar] [CrossRef]
- Yoneyama, J. H∞ Filtering for Sampled-Data Systems. In Proceedings of the 2009 IEEE International Conference on Control and Automation, Christchurch, New Zealand, 9–11 December 2009; pp. 1728–1733. [Google Scholar]
- Yoneyama, J.; Nishikawa, M.; Katayama, H.; Ichikawa, A. Output stabilization of Takagi–Sugeno fuzzy systems. Fuzzy Sets Syst. 2000, 111, 253–266. [Google Scholar] [CrossRef]
- Saoudi, D.; Mechmeche, C.; Braiek, N.B. T-S fuzzy bilinear observer for a class of nonlinear systems. In Proceedings of the 18th Mediterranean Conference on Control and Automation, Marrakech, Morocco, 23–25 June 2010; pp. 1395–1400. [Google Scholar]
- Saoudi, D.; Chadli, M.; Braiek, N.B. State estimation of unknown input fuzzy bilinear systems: Application to fault diagnosis. In Proceedings of the 2013 European Control Conference, Zurich, Switzerland, 17–19 July 2013; pp. 2465–2470. [Google Scholar]
- Saoudi, D.; Chadli, M.; Braiek, N.B. Robust H∞ fault detection for fuzzy bilinear systems via unknown input observer. In Proceedings of the 22nd Mediterranean Conference on Control and Automation, Palermo, Italy, 16–19 June 2014; pp. 281–286. [Google Scholar]
- Tsai, T.H. A global exponential fuzzy observer design for time-delay Takagi–Sugeno uncertain discrete fuzzy bilinear systems with disturbance. IEEE Trans. Fuzzy Syst. 2012, 20, 1063–1075. [Google Scholar] [CrossRef]
- Yoneyama, J.; Nishikawa, M.; Katayama, H.; Ichikawa, A. Design of output feedback controllers for Takagi–Sugeno fuzzy systems. Fuzzy Sets Syst. 2001, 121, 127–148. [Google Scholar] [CrossRef]
- Guerra, T.M.; Marquez, R.; Kruszewski, A.; Bernal, M. H∞ LMI-based observer design for nonlinear systems via Takagi–Sugeno models with unmeasured premise variables. IEEE Trans. Fuzzy Syst. 2017, PP. [Google Scholar] [CrossRef]
- Rotondo, D.; Witczak, M.; Puig, V.; Nejjari, F.; Pazera, M. Robust unknown input observer for state and fault estimation in discrete-time Takagi–Sugeno systems. Int. J. Syst. Sci. 2016, 47, 3409–3424. [Google Scholar] [CrossRef] [Green Version]
- Wang, L.K.; Zhang, H.G.; Liu, X.D. H∞ observer design for continuous-time Takagi–Sugeno fuzzy model with unknown premise variables via nonquadratic Lyapunov function. IEEE Trans. Cybern. 2016, 46, 1986–1996. [Google Scholar] [CrossRef] [PubMed]
- Yoneyama, J.; Ishihara, T. Control Design of Fuzzy Systems with Immeasurable Premise Variables. In Fuzzy Systems; In-Tech: Rijeka, Croatia, 2010. [Google Scholar]
- Yoneyama, J. Robust H∞ Output Feedback Control for Uncertain Fuzzy Systems with Immeasurable Premise Variables. Adv. Fuzzy Sets Syst. 2008, 3, 99–113. [Google Scholar]
- Yoneyama, J. H∞ Output Feedback Control for Fuzzy Systems with Immeasurable Premise Variables: Discrete-Time Case. Appl. Soft Comput. 2008, 8, 949–958. [Google Scholar] [CrossRef]
- Tuan, H.D.; Apkarian, P.; Narikiyo, T.; Yamamoto, Y. Parameterized linear matrix inequality techniques in fuzzy control system design. IEEE Trans. Fuzzy Syst. 2001, 9, 324–332. [Google Scholar] [CrossRef]
- Peaucelle, D.; Arzelier, D.; Bachelier, O.; Bemussou, J. A new robust D-stabiity condition for real convex polytopic uncertainty. Syst. Control Lett. 2000, 40, 21–30. [Google Scholar] [CrossRef]
- Zill, D.G.; Wright, W.S. Calculus: Early Transcendentals; Jones & Bartlett Publishers: Burlington, MA, USA, 2010. [Google Scholar]
- Xie, L.; de Souza, C.E. Robust H∞ control for linear systems with norm-bounded time-varying uncertainty. IEEE Trans. Autom. Control 1992, 37, 1188–1191. [Google Scholar] [CrossRef]
- Tanaka, K.; Wang, H.O. Fuzzy Control Systems Design and Analysis: A Linear Matrix Inequality Approach; Wiley: Hoboken, NJ, USA, 2000. [Google Scholar]
- Saoudi, D.; Chadli, M.; Mechmeche, C.; Braiek, N.B. Unknown input observer design for fuzzy bilinear system: An LMI approach. Math. Probl. Eng. 2012, 2012, 794581. [Google Scholar] [CrossRef]
- Chadli, M.; Karimi, H.R. Robust observer design for unknown inputs Takagi–Sugeno models. IEEE Trans. Fuzzy Syst. 2013, 21, 158–164. [Google Scholar] [CrossRef]
- Li, S.; Wang, H.; Aitouche, A.; Tian, Y.; Christov, N. Robust unknown input observer design for state estimation and fault detection using linear parameter varying model. J. Phys. Conf. Ser. 2017, 783, 012001. [Google Scholar] [CrossRef]
- Perez, H.; Ogunnaike, B.; Devasia, S. Output tracking between operating points for nonlinear processes: Van de Vusse example. IEEE Trans. Control Syst. Technol. 2002, 10, 611–617. [Google Scholar] [CrossRef]

© 2017 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yoneyama, J. A New Observer Design for Fuzzy Bilinear Systems with Unknown Inputs. Designs 2017, 1, 10. https://doi.org/10.3390/designs1020010
Yoneyama J. A New Observer Design for Fuzzy Bilinear Systems with Unknown Inputs. Designs. 2017; 1(2):10. https://doi.org/10.3390/designs1020010
Chicago/Turabian StyleYoneyama, Jun. 2017. "A New Observer Design for Fuzzy Bilinear Systems with Unknown Inputs" Designs 1, no. 2: 10. https://doi.org/10.3390/designs1020010



