Adaptive Sliding Mode Control for High-Frequency Sampled-Data Systems with Actuator Faults
Abstract
:1. Introduction
2. Problem Statement
- (A1)
- , where , are known constants.
- (A2)
- The actuator fault redundancy condition is that .
- (A3)
- The unknown time-varying bounded fault-deviation vector satisfies:where and stand for the unknown upper and lower bounds of , respectively, and we denote
3. Stability Analysis of the Sliding Motion Equation
4. Stability Analysis of the Error Dynamic
5. Section Stabilization of the Overall Closed-Loop Systems
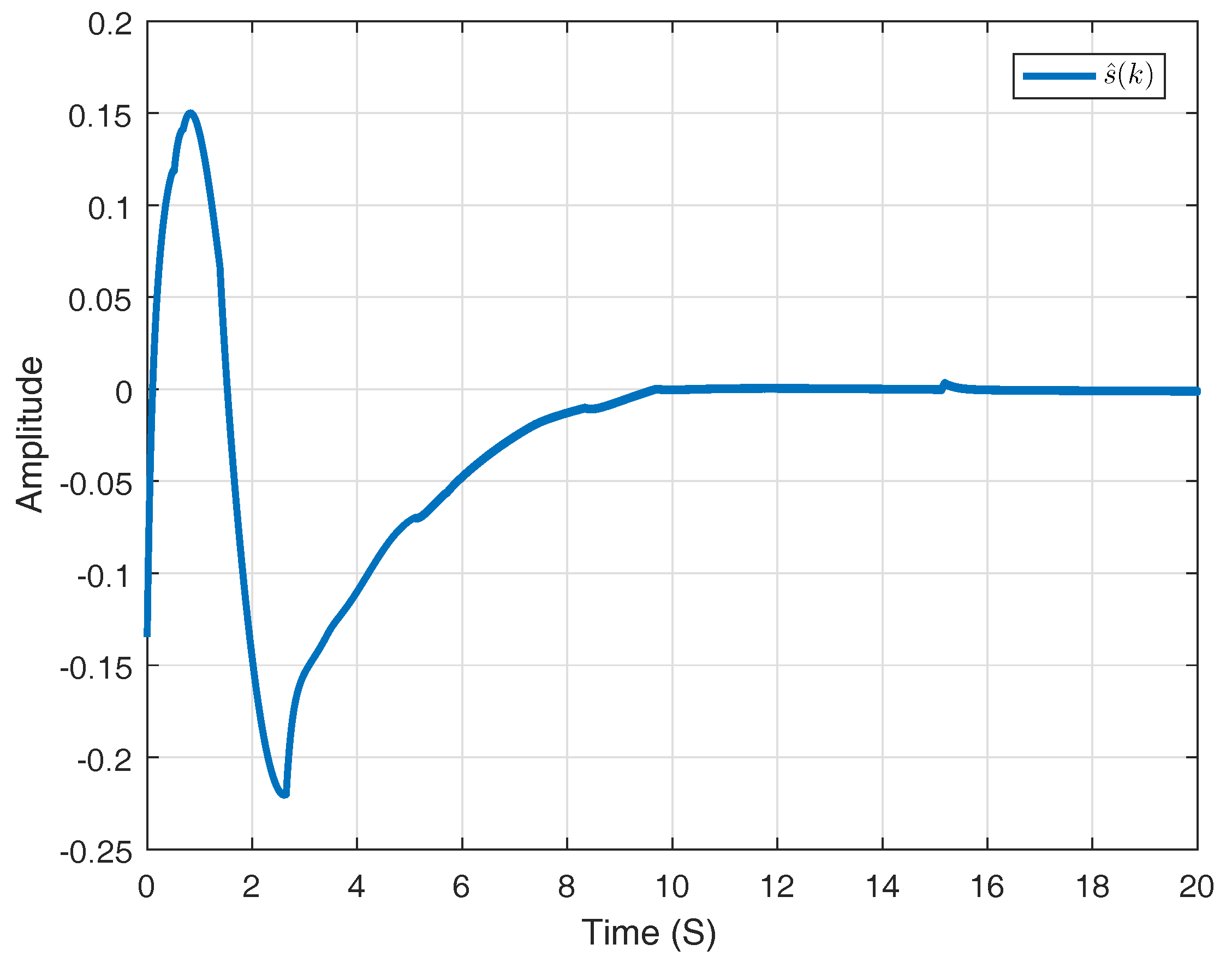
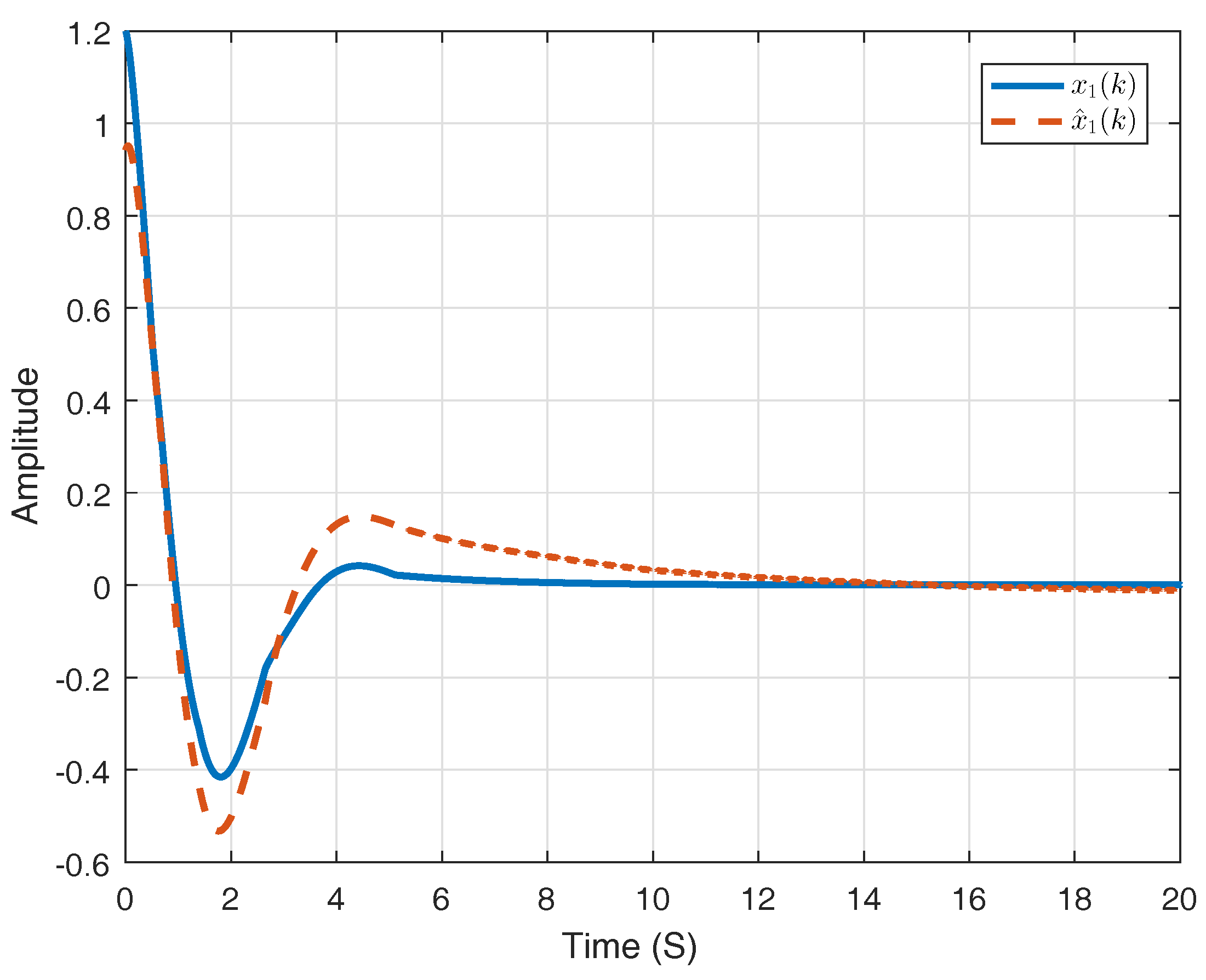
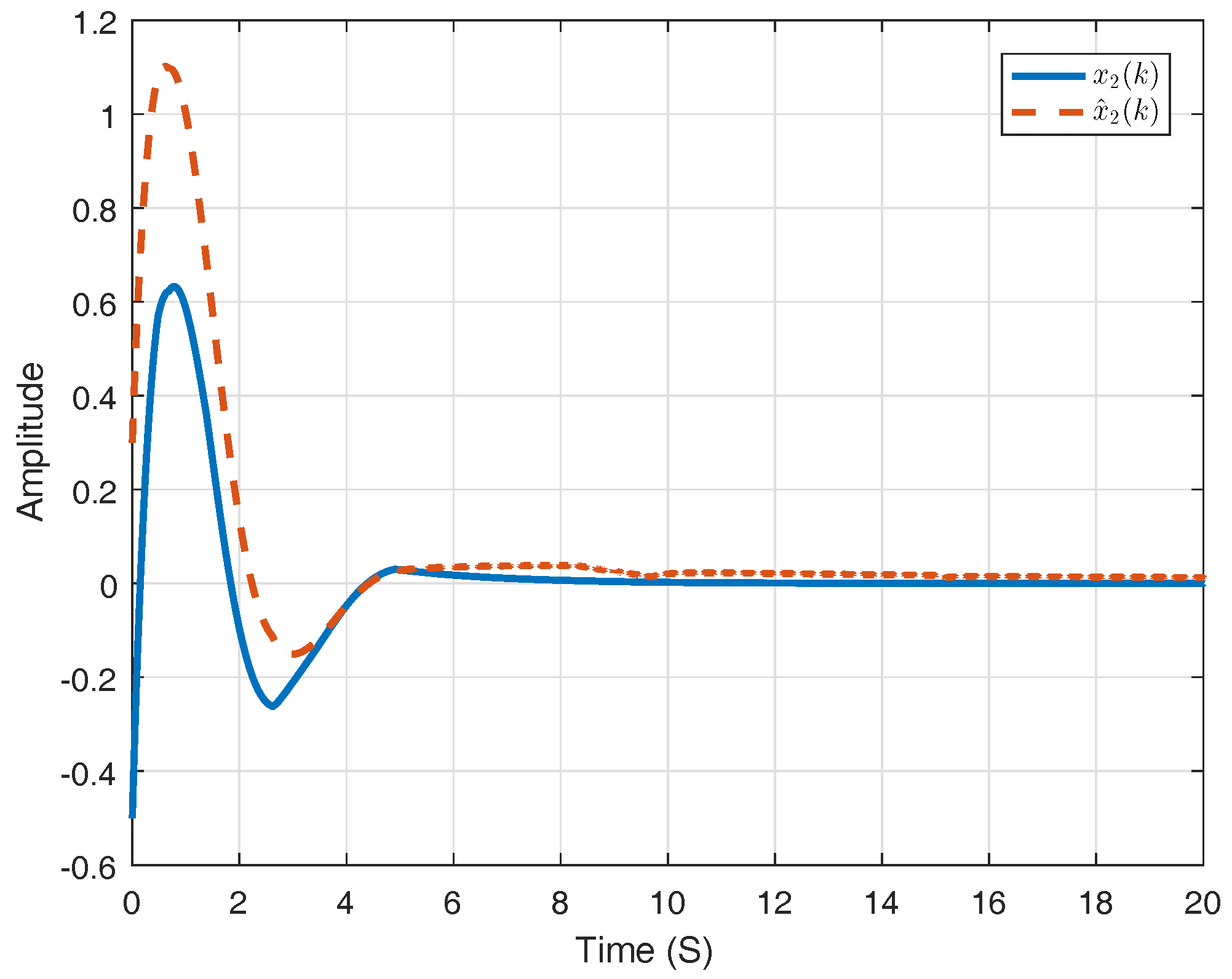
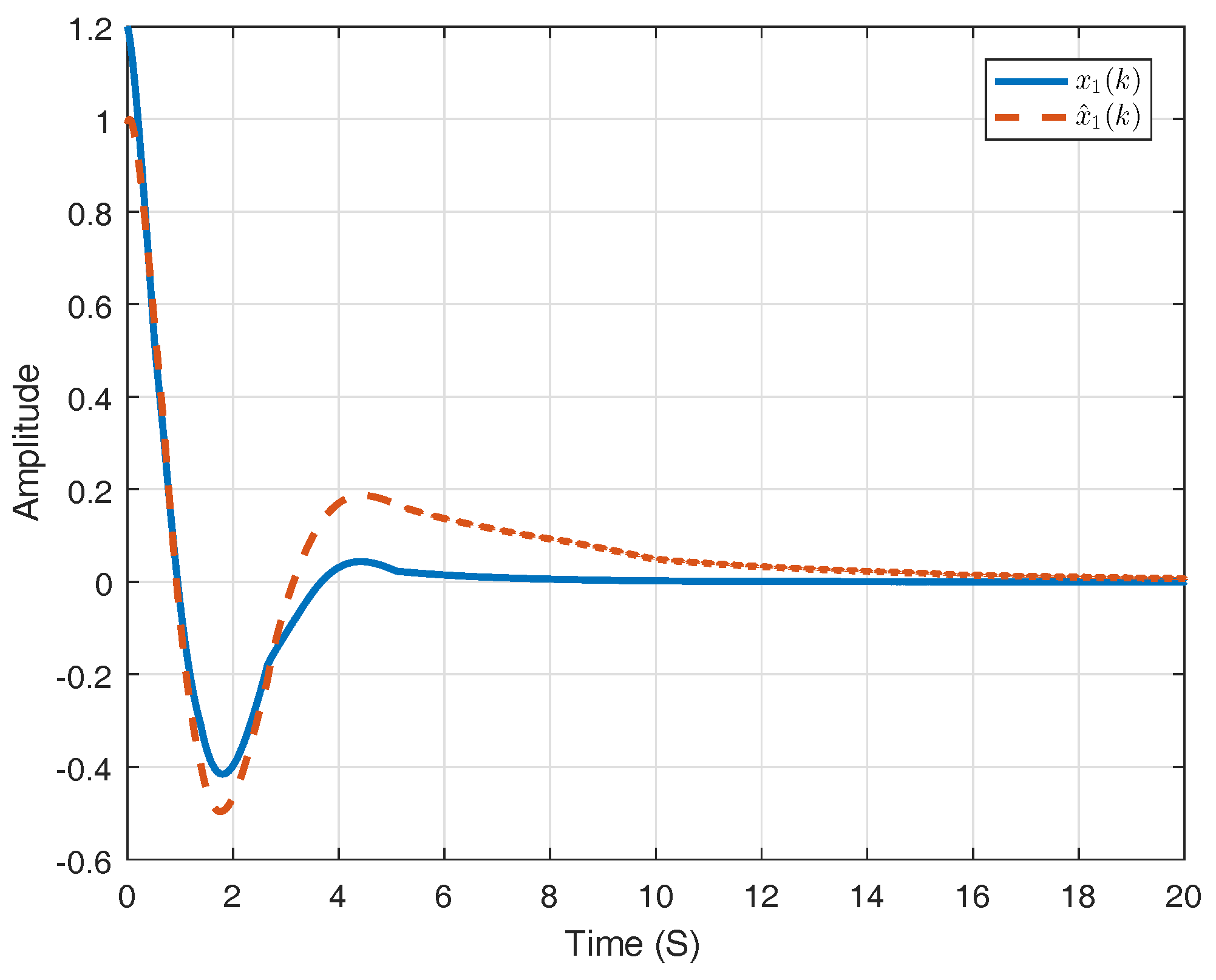
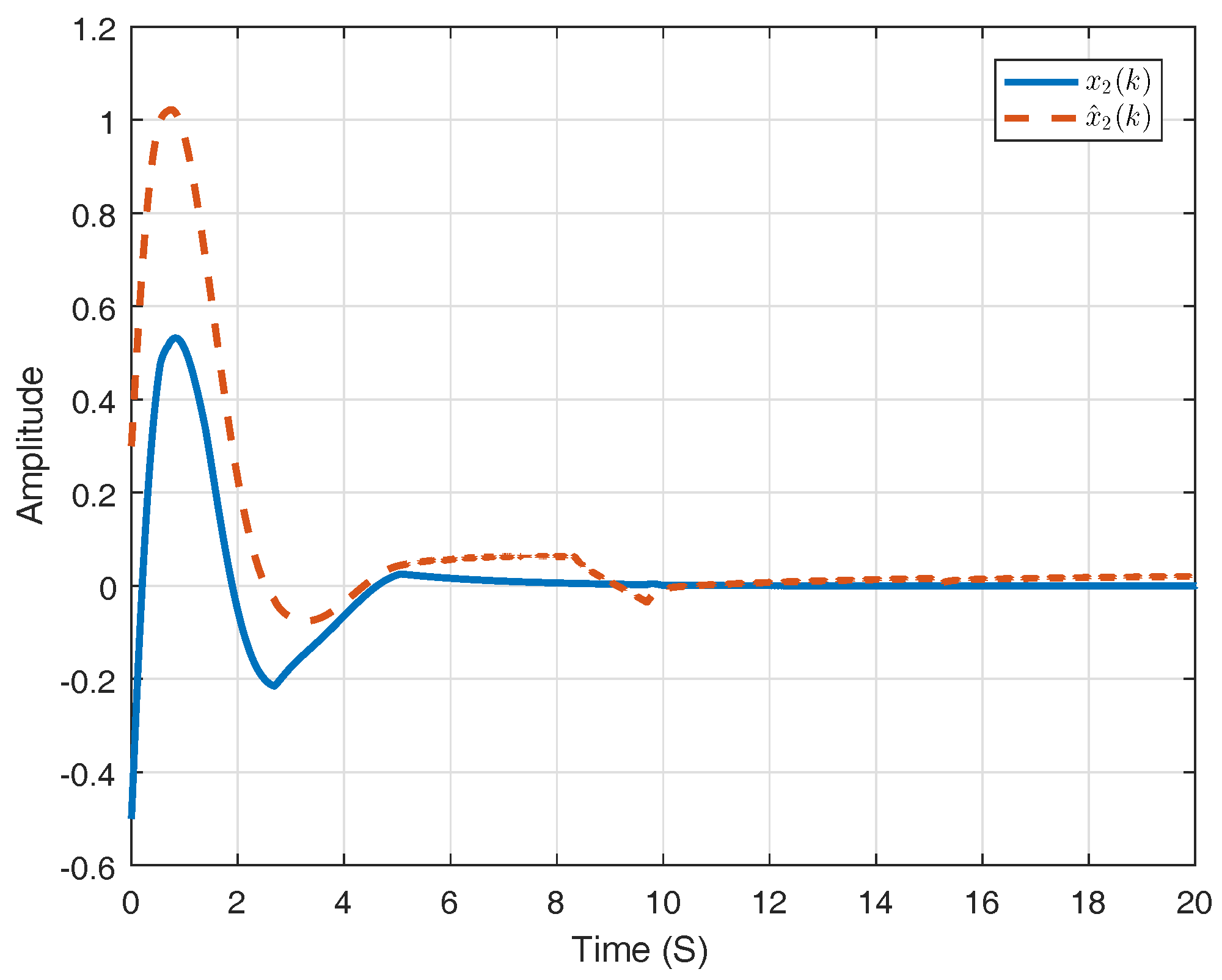
6. Numerical Example
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Liu, H.H.T.; Shi, P.; Jiang, B. Fault detection, diagnosis, and fault tolerant control with flight applications. J. Frankl. Inst. 2013, 350, 2371–2372. [Google Scholar] [CrossRef]
- Jiang, B.; Wang, J.L. Actuator fault diagnosis for a class of bilinear systems with uncertainty. J. Frankl. Inst. 2002, 339, 361–374. [Google Scholar] [CrossRef]
- Li, L.; Chadli, M.; Ding, S.X.; Qiu, J.; Yang, Y. Diagnostic Observer Design for TS Fuzzy Systems: Application to Real-Time Weighted Fault Detection Approach. IEEE Trans. Fuzzy Syst. 2017. [Google Scholar] [CrossRef]
- Hao, L.Y.; Yang, G.H. Robust fault tolerant control based on sliding mode method for uncertain linear systems with quantization. ISA Trans. 2013, 52, 600–610. [Google Scholar] [CrossRef] [PubMed]
- Rios, H.; Kamal, S.; Fridman, L.M.; Zolghadri, A. Fault tolerant control allocation via continuous integral sliding-modes: A HOSM-Observer approach. Automatica 2015, 51, 318–325. [Google Scholar] [CrossRef]
- Youssef, T.; Chadli, M.; Karimi, H.R.; Wagn, R. Actuator and sensor faults estimation based on proportional integral observer for TS fuzzy model. J. Frankl. Inst. 2017, 354, 2524–2542. [Google Scholar] [CrossRef]
- Saifia, D.; Chadli, M.; Labiod, S.; Guerra, T.M. Robust H∞ static output feedback stabilization of TS fuzzy systems subject to actuator saturation. Int. J. Control Autom. Syst. 2012, 10, 613–622. [Google Scholar] [CrossRef]
- Niu, Y.; Ho, D.W.C. Control strategy with adaptive quantizer’s parameters under digital communication channels. Automatica 2014, 50, 2665–2671. [Google Scholar] [CrossRef]
- Li, Y.; Tong, S.; Liu, Y.; Li, T. Adaptive Fuzzy Robust Output Feedback Control of Nonlinear Systems with Unknown Dead Zones Based on a Small-Gain Approach. IEEE Trans. Fuzzy Syst. 2014, 22, 164–176. [Google Scholar] [CrossRef]
- Liu, D.; Wei, Q. Policy iteration adaptive dynamic programming algorithm for discrete-time nonlinear systems. IEEE Trans. Neural Netw. Learn. Syst. 2014, 25, 621. [Google Scholar] [PubMed]
- Su, J.; Chen, W.H. Model-based fault diagnosis system verification using reachability analysis. IEEE Trans. Syst. Man Cybern. Syst. 2017. [Google Scholar] [CrossRef]
- Yu, S.; Yu, X.; Shirinzadeh, B.; Man, Z. Continuous finite-time control for robotic manipulators with terminal sliding mode. Automatica 2005, 41, 1957–1964. [Google Scholar] [CrossRef]
- Shah, D.H.; Mehta, A.J. Multirate output feedback based discrete-time sliding mode control for fractional delay compensation in NCSs. In Proceedings of the IEEE International Conference on Industrial Technology, Toronto, ON, Canada, 22–25 March 2017. [Google Scholar]
- Mathiyalagan, K.; Ju, H.P.; Sakthivel, R. New results on passivity-based H∞ math Container Loading Mathjax, control for networked cascade control systems with application to power plant boiler-turbine system. Nonlinear Anal. Hybrid Syst. 2015, 17, 56–69. [Google Scholar] [CrossRef]
- Du, D.J.; Qi, B.; Wang, Z.X.; Fei, M.R.; Peng, C. Distributed event-triggered hybrid wired-wireless networked control with H2/H∞, filtering. Memet. Comput. 2017, 9, 55–86. [Google Scholar] [CrossRef]
- Wang, H.; Shi, P.; Zhang, J. Event-triggered fuzzy filtering for a class of nonlinear networked control systems. Signal Process. 2015, 113, 159–168. [Google Scholar] [CrossRef]
- Wei, Y.; Park, J.H.; Karimi, H.R.; Tian, Y.C.; Jung, H. Improved Stability and Stabilization Results for Stochastic Synchronization of Continuous-Time Semi-Markovian Jump Neural Networks With Time-Varying Delay. IEEE Trans. Neural Netw. Learn. Syst. 2017, 1–14. [Google Scholar] [CrossRef] [PubMed]
- Niu, Y.; Jia, T.; Wang, X.; Yang, F. Output-feedback control design for NCSs subject to quantization and dropout. Inf. Sci. 2009, 179, 3804–3813. [Google Scholar] [CrossRef]
- Qu, F.L.; Guan, Z.H.; He, D.X.; Chi, M. Event-triggered control for networked control systems with quantization and packet losses. J. Frankl. Inst. 2015, 352, 974–986. [Google Scholar] [CrossRef]
- Tang, X.; Ding, B. Model predictive control of linear systems over networks with data quantizations and packet losses. Automatica 2013, 49, 1333–1339. [Google Scholar] [CrossRef]
- Nguyen, T.; Su W, C.; Gajic, Z. Output feedback sliding mode control for sampled-data systems. IEEE Trans. Autom. Control 2010, 55, 1684–1689. [Google Scholar]
- Bououden, S.; Chadli, M.; Karimi, H.R. Fuzzy sliding mode controller design using Takagi-Sugeno modelled nonlinear systems. Math. Probl. Eng. 2013, 2013, 734094. [Google Scholar] [CrossRef]
- Su, J.; Yang, J.; Li, S. Continuous finite-time anti-disturbance control for a class of uncertain nonlinear systems. Trans. Inst. Meas. Control 2014, 36, 300–311. [Google Scholar] [CrossRef]
- Iwasaki, T.; Skelton, R.E. All Controllers for the General, H∞, Control Problem: LMI Existence Conditions and State Space Formulas; Pergamon Press, Inc.: Oxford, UK, 1994. [Google Scholar]
- Qiu, J.; Xia, Y.; Yang, H.; Zhang, J. Robust stabilisation for a class of discrete-time systems with time-varying delays via delta operators. IET Control Theory Appl. 2008, 2, 87–93. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, D.; Liu, Y.; Liu, M.; Yu, J. Adaptive Sliding Mode Control for High-Frequency Sampled-Data Systems with Actuator Faults. Designs 2018, 2, 3. https://doi.org/10.3390/designs2010003
Zhao D, Liu Y, Liu M, Yu J. Adaptive Sliding Mode Control for High-Frequency Sampled-Data Systems with Actuator Faults. Designs. 2018; 2(1):3. https://doi.org/10.3390/designs2010003
Chicago/Turabian StyleZhao, Dongyang, Yu Liu, Ming Liu, and Jinyong Yu. 2018. "Adaptive Sliding Mode Control for High-Frequency Sampled-Data Systems with Actuator Faults" Designs 2, no. 1: 3. https://doi.org/10.3390/designs2010003




