Monitoring the Path to the Elimination of Infectious Diseases
Abstract
:1. Introduction
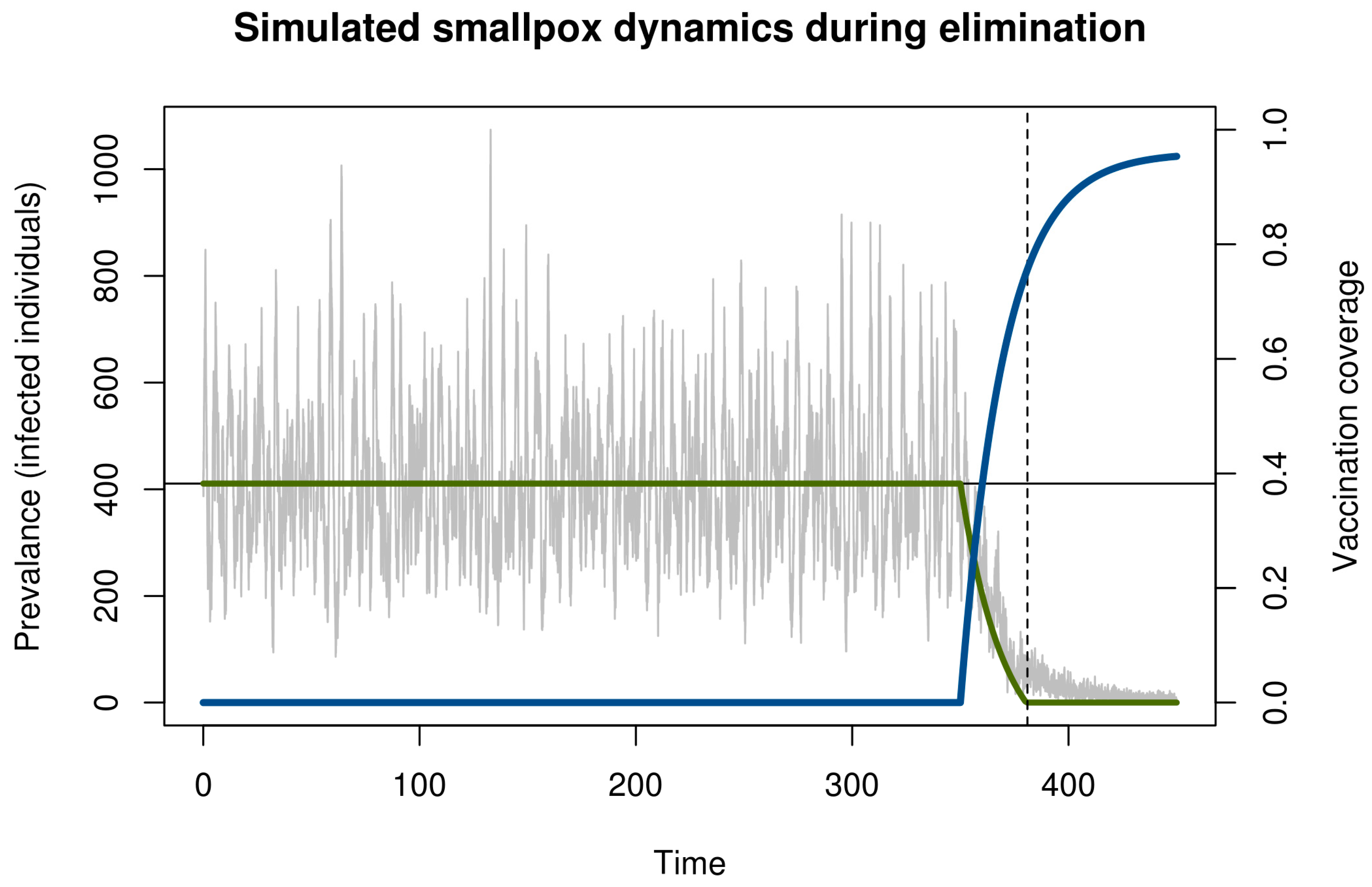
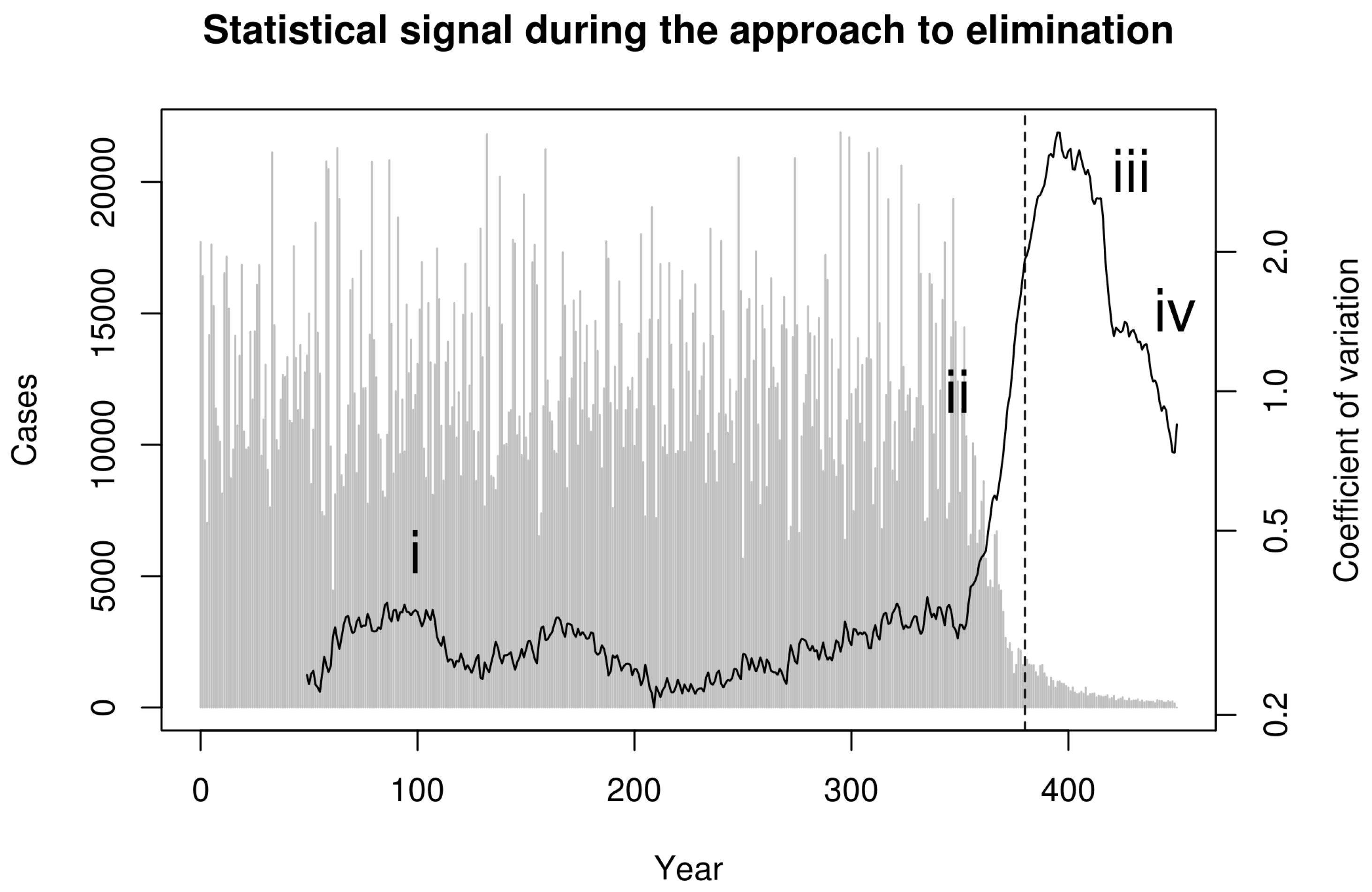
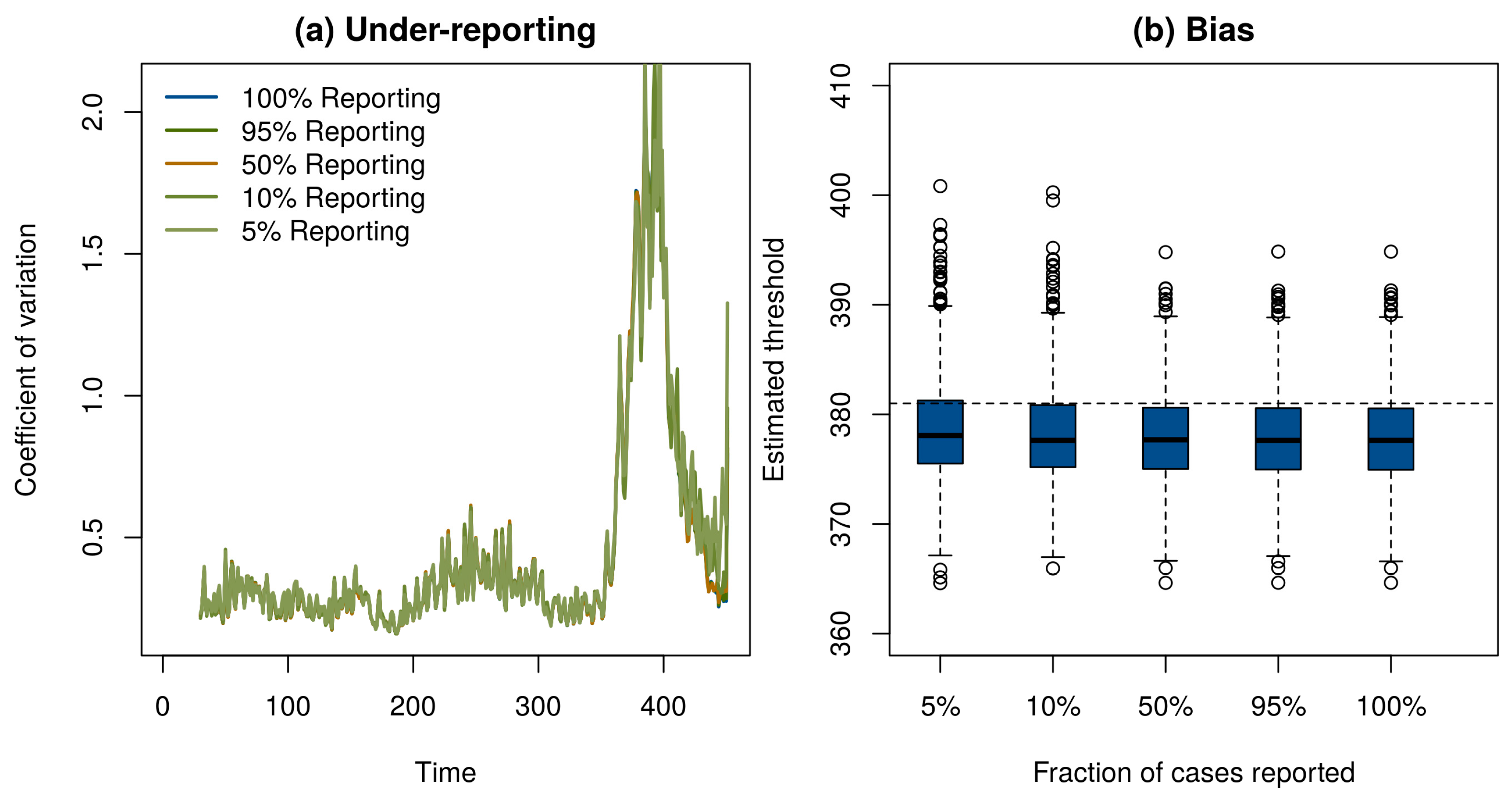
2. Model
3. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hopkins, D.R. Disease eradication. N. Engl. J. Med. 2013, 368, 54–63. [Google Scholar] [CrossRef] [PubMed]
- Fenner, F.; Henderson, D.A.; Arita, I.; Jecek, Z.; Ladnyi, I.D. Smallpox and Its Eradication. History of International Public Health; World Health Organization: Geneva, Switzerland, 1998. [Google Scholar]
- Grassly, N.C. The final stages of the global eradication of poliomyelitis. Philos. Trans. R. Soc. B 2013, 368, 20120140. [Google Scholar] [CrossRef] [PubMed]
- Biswas, G.; Sankara, D.P.; Agua-Agum, J.; Maiga, A. Dracunculiasis (guinea worm disease): Eradication without a drug or a vaccine. Philos. Trans. R. Soc. B 2013, 368, 20120146. [Google Scholar] [CrossRef] [PubMed]
- Rinaldi, A. Yaws eradication: Facing old problems, raising new hopes. PLoS Negl. Trop. Dis. 2012, 6, e1837. [Google Scholar] [CrossRef] [PubMed]
- Global Health Group; Malaria Atlas Project. Atlas of Malaria Eliminating Countries; The Global Health Group, Global Health Sciences, University of California: San Francisco, CA, USA, 2011. [Google Scholar]
- World Health Organization. Global programme to eliminate lymphatic filariasis: Progress report, 2011. Wkly. Epidemiol. Rec. 2012, 37, 345–356. [Google Scholar]
- Brady, M. Global Alliance to Eliminate Lymphatic Filariasis. Seventh meeting of the Global Alliance to Eliminate Lymphatic Filariasis: Reaching the vision by scaling up, scaling down, and reaching out. Parasites Vectors 2014, 7, 46. [Google Scholar] [CrossRef] [PubMed]
- Ferrari, M.J.; Grenfell, B.T.; Strebel, P.M. Think globally, act locally: The role of local demographics and vaccination coverage in the dynamic response of measles infection to control. Philos. Trans. R. Soc. B 2013, 368, 20120141. [Google Scholar] [CrossRef] [PubMed]
- Papania, E.J.; Wallace, G.S.; Rota, P.A.; Icenogle, J.P.; Fiebelkorn, A.P.; Armstrong, G.L.; Reef, S.E.; Redd, S.B.; Abernathy, E.S.; Barskey, A.E.; et al. Elimination of endemic measles, rubella, and congenital rubella syndrome from the Western hemisphere: The US experience. JAMA Pediatr. 2014, 168, 148–155. [Google Scholar] [CrossRef] [PubMed]
- Mackenzie, C.D.; Homeida, M.M.; Hopkins, A.D.; Lawrence, J.C. Elimination of onchocerciasis from Africa: Possible? Trends Parasitol. 2012, 28, 16–22. [Google Scholar] [CrossRef] [PubMed]
- Traore, M.O.; Sarr, M.D.; Badji, A.; Bissan, Y.; Diawara, L.; Doumbia, K.; Goita, S.F.; Konate, L.; Mounkoro, K.; Seck, A.F.; et al. Proof-of-principle of onchocerciasis elimination with ivermectin treatment in endemic foci in Africa: Final results of a study in Mali and Senegal. PLoS Negl. Trop. Dis. 2012, 6, e1825. [Google Scholar] [CrossRef] [PubMed]
- Rollinson, D.; Knopp, S.; Levitz, S.; Stothard, J.R.; Tchuenté, L.-A.T.; Garba, A.; Mohammed, K.A.; Schur, N.; Person, B.; Colley, D.G.; et al. Time to set the agenda for schistosomiasis elimination. Acta Trop. 2013, 128, 423–440. [Google Scholar] [CrossRef] [PubMed]
- Franco, J.R.; Simarro, P.P.; Diarra, A.; Ruiz-Postigo, J.A.; Jannin, J.G. The journey towards elimination of gambiense human African trypanosomiasis: Not far, nor easy. Parasitology 2014, 141, 748–760. [Google Scholar] [CrossRef] [PubMed]
- Klepac, P.; Metcalf, J.E.; McLean, A.R.; Hampson, K. Towards the endgame and beyond: Complexities and challenges for the elimination of infectious diseases. Philos. Trans. R. Soc. B 2013, 368, 20120137. [Google Scholar] [CrossRef] [PubMed]
- Bousema, T.; Griffin, J.T.; Sauerwein, R.W.; Smith, D.L.; Churcher, T.S.; Takken, W.; Ghani, A.; Drakeley, C.; Gosling, R. Hitting hotspots: Spatial targeting of malaria for control and elimination. PLoS Med. 2012, 9, e1001165. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J.M.; Smith, D.L.; Cotter, C.; Ward, A.; Yamey, G.; Sabot, O.J.; Moonen, B. Malaria resurgence: A systematic review and assessment of its causes. Malar. J. 2012, 11, 122. [Google Scholar] [CrossRef] [PubMed]
- Cochi, S.L.; Linkins, R.W. The final phase of polio eradication: New vaccines and complex choices. J. Infect. Dis. 2012, 205, 169–171. [Google Scholar] [CrossRef] [PubMed]
- Kew, O. Reaching the last one per cent: Progress and challenges in global polio eradication. Curr. Opin. Virol. 2012, 2, 188–198. [Google Scholar] [CrossRef] [PubMed]
- Omer, S.B.; Orenstein, W.A.; Koplan, J.P. Go big and go fast—Vaccine refusal and disease eradication. N. Engl. J. Med. 2013, 368, 1374–1376. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, M.; Carpenter, S.R.; Lenton, T.M.; Bascompte, J.; Brock, W.; Dakos, V.; van de Koppel, J.; van de Leemput, I.A.; Levin, S.A.; van Nes, E.H.; et al. Anticipating critical transitions. Science 2012, 338, 344–348. [Google Scholar] [CrossRef] [PubMed]
- O’Regan, S.M.; Drake, J.M. Theory of early warning signals of disease emergence and leading indicators of elimination. Theor. Ecol. 2013, 6, 333–357. [Google Scholar] [CrossRef]
- Boettiger, C.; Ross, N.; Hastings, A. Early warning signals: The charted and uncharted territories. Theor. Ecol. 2013, 6, 255–264. [Google Scholar] [CrossRef]
- O’Regan, S.M.; Lillie, J.W.; Drake, J.M. Leading indicators of mosquito-borne disease elimination. Theor. Ecol. 2016, 9, 269–286. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Gillespie, D.T.; Petzold, L.R. Efficient step size selection for the tau-leaping simulation method. J. Chem. Phys. 2006, 124, 044109. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, N.M.; Keeling, M.J.; Edmunds, W.J.; Gani, R.; Grenfell, B.T.; Anderson, R.M.; Leach, S. Planning for smallpox outbreaks. Nature 2003, 426, 681–685. [Google Scholar] [CrossRef] [PubMed]
- Dibble, C.; O’Dea, E.A.; Park, A.W.; Drake, J.M. Waiting time to infectious disease emergence. J. R. Soc. Interface 2016, 13, 20160540. [Google Scholar] [CrossRef] [PubMed]
- Dakos, V.; Carpenter, S.R.; Brock, W.A.; Ellison, A.M.; Guttal, V.; Ives, A.R.; Kéfi, S.; Livina, V.; Seekell, D.; van Nes, E.H.; et al. Methods for detecting early warnings of critical transitions in time series illustrated using simulated ecological data. PLoS ONE 2012, 7, e41010. [Google Scholar] [CrossRef] [PubMed]
- Guttal, V.; Jayaprakash, C. Spatial variance and spatial skewness: Leading indicators of regime shifts in spatial ecological systems. Theor. Ecol. 2009, 2, 3–12. [Google Scholar] [CrossRef]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Drake, J.M.; Hay, S.I. Monitoring the Path to the Elimination of Infectious Diseases. Trop. Med. Infect. Dis. 2017, 2, 20. https://doi.org/10.3390/tropicalmed2030020
Drake JM, Hay SI. Monitoring the Path to the Elimination of Infectious Diseases. Tropical Medicine and Infectious Disease. 2017; 2(3):20. https://doi.org/10.3390/tropicalmed2030020
Chicago/Turabian StyleDrake, John M., and Simon I. Hay. 2017. "Monitoring the Path to the Elimination of Infectious Diseases" Tropical Medicine and Infectious Disease 2, no. 3: 20. https://doi.org/10.3390/tropicalmed2030020




