Towards a Generalized Beer-Lambert Law

Abstract

Anomalous deviations from the Beer-Lambert law have been observed for a long time in a wide range of application. Despite all the attempts, a reliable and accepted model has not been provided so far. In addition, in some cases the attenuation of radiation seems to follow a hyperbolic more than an exponential extinction law. Starting from a probabilistic interpretation of the Beer-Lambert law based on Poissonian distribution of extinction events, in this paper we consider deviations from the classical exponential extinction introducing a weighted version of the classical law. The generalized law is able to account for both sub or super-exponential extinction of radiation, and can be extended to the case of inhomogeneous media. Focusing on this case, we consider a generalized Beer-Lambert law based on an inhomogeneous weighted Poisson distribution involving a Mittag-Leffler function, and show how it can be directly related to hyperbolic decay laws observed in some applications particularly relevant to microbiology and pharmacology.

1. Introduction

In the last decades, evidences of deviations from the Beer-Lambert law have been reported in many fields and applications, spanning from atmospheric and nuclear physics to microbiology and condensate matter (see e.g., [1,2,3,4,5] and references therein). In order to get a better understanding of such phenomena, different attempts to generalize the classical exponential extinction law in radiative transfer processes have been proposed so far, from both classical [6,7,8] and fractional point of view [9,10,11].

Focusing on the latter approach, a generalization of the Beer-Lambert Law derived from a fractional Poisson process was proposed in [9] and further extended in [11], along with an estimate of the deviation from a classical exponential function. This results was used in [10] to introduce a generalized form of the Beer-Lambert equation by employing fractional operators in the unit disk, i.e., through a generalization of the Srivastava-Owa operators. Very recently, the fractional form of the Beer-Lambert Law was also used to model anomalous transport phenomena and derive a generalized diffusion model on the basis of the fractional radiative transport equation [12,13].

Despite the fact that none of the cited works included experimental data originally, in some cases a certain degree of success has been already achieved. As an example, the fractional approach described in [9] was used in [4] to take into account sub-exponential effects in determining aluminium foil half-value thickness for different beta sources, and in [1] to estimate light attenuation within photosynthetic cultures in photobioreactors.

Nevertheless, a more general model capable of describing all the characteristics observed so far is still lacking, as the current generalization of the fractional Beer-Lambert Law cannot take into account neither the super-exponential extinction, that may, for example, play a relevant role in some atmospheric physics phenomena [14], nor the hyperbolic extinction often observed when measuring light extinction by biomass [15]. Thus, finding a model to describe these three different behaviour would be a significant improvement towards a generalized law of radiation extinction.

As a more general remark, it is worth mentioning that fractional differential equations have also found relevant applications in a wide range of contexts, spanning from neurology [16] to chemistry [17], rheology [18,19] and stochastic processes [20].

In this paper, we introduce a general mathematical approach for the analysis of non-exponential extinction of radiation, starting from the probabilistic derivation of the classical Beer-Lambert law as discussed in previous literature (see e.g., [7]). Our approach includes a wide class of non-exponential extinctions and is based on the application of weighted Poisson distributions [21], leading to a whole family of corresponding processes governed by a generalized weighted Beer-Lambert law, capable of accounting for both sub and super-exponential extinction phenomena. In this general framework, we then include hyperbolic extinction processes considering in more detail an inhomogeneous weighted process that involves the Mittag-Leffler function [22], following an alternative approach to fractional Poisson processes suggested by Beghin and Orsingher [23], and more recently by Herrmann in [24] and by Chakraborty and Ong in [25].

2. Beer-Lambert Law Stochastic Interpretation

Here we briefly recall the heuristic idea for the stochastic interpretation of the classical Beer-Lambert Law, referring to [7,26] and references therein for a more detailed discussion. Let’s consider a uniform, incoherent and parallel photon beam of cross-sectional area A, normally incident on an infinite slab of a dilute random medium of depth x containing randomly positioned obstacles. Assuming the probability distribution of the extinction events to be Poissonian, the number of absorbed photons is given by

$$p_n\left(x\right)={\overline{n\left(x\right)}}^n\frac{exp(-\overline{n\left(x\right)})}{n!},$$

(1)

where $p_n\left(x\right)$ is the probability of having n photons absorbed in a given volume of a layer of depth x, and $\overline{n\left(x\right)}$ is the mean count over many realizations as a function of x. Now, according to the distribution (1), the probability of photon transmission (no extinction, that means setting $n=0$ and holding $\overline{n}$ constant in the previous equation) is given by

$$p_0\left(x\right)=exp(-\overline{n\left(x\right)})=exp(-\beta x),$$

(2)

where $\beta =\sigma c={\mathsf{\Lambda }}^{-1}$, with $\mathsf{\Lambda }$, $\sigma$ and c being the mean free path, the extinction cross section per obstacle and the obstacle concentration, respectively. By means of the large numbers, Kostinski [7] found out that Equation (2) leads to the classical Beer-Lambert law

$$\frac{N_{tr}}{N_{in}}=exp(-\beta x),$$

(3)

where $N_{in}$ and $N_{tr}$ stand for the number of incident and transmitted photons. Hence, assuming the Poissonian distribution of the extinction events we obtain the classical exponential extinction law. Nevertheless, physically speaking such an assumption turns out too restrictive. As discussed in [7] and more briefly in the previous section, assuming a homogeneous Poissonian distribution leads to neglect both correlation between obstacles and spatial memory effects, that may play a relevant role in many real phenomena.

Following this approach, in a previous work [9] we applied the fractional Poisson process (see e.g., [23]) to consider slower than exponential attenuation of radiation in a random medium. The result is the fractional Beer-Lambert law

$$\frac{N_{tr}}{N_{in}}=E_{\alpha }(-\beta x^{\alpha }),\alpha \in (0,1],$$

(4)

where

$$E_{\alpha }(-\beta x^{\alpha })=\sum _{k=0}^{\infty }\frac{{(-\beta x^{\alpha })}^k}{\mathsf{\Gamma }(\alpha k+1)},$$

(5)

is the one parameter Mittag-Leffler function. It is worth noting that for $\alpha =1$ in (5) the exponential function is recovered. In order to highlight the utility of the Mittag-Leffler function for modelling power law decays, we recall that the asymptotic behaviour of the Mittag–Leffler function is given by (see, e.g., [22])

$$E_{\alpha }(-x^{\alpha })=\left\{\begin{array}{c}1-\frac{x^{\alpha }}{\mathsf{\Gamma }(1+\alpha )}\mathrm{for}x\to 0\hfill \\ \frac{x^{-\alpha }}{\mathsf{\Gamma }(1-\alpha )}\mathrm{for}x\to +\infty ,\alpha \in (0,1).\hfill \end{array}\right.$$

(6)

The fractional Beer-Lambert law has been recently, and successfully, applied in [1] to estimate light attenuation within photosynthetic cultures in photobioreactors, and in [4] to determine the half-value thickness of aluminium foils from beta sources.

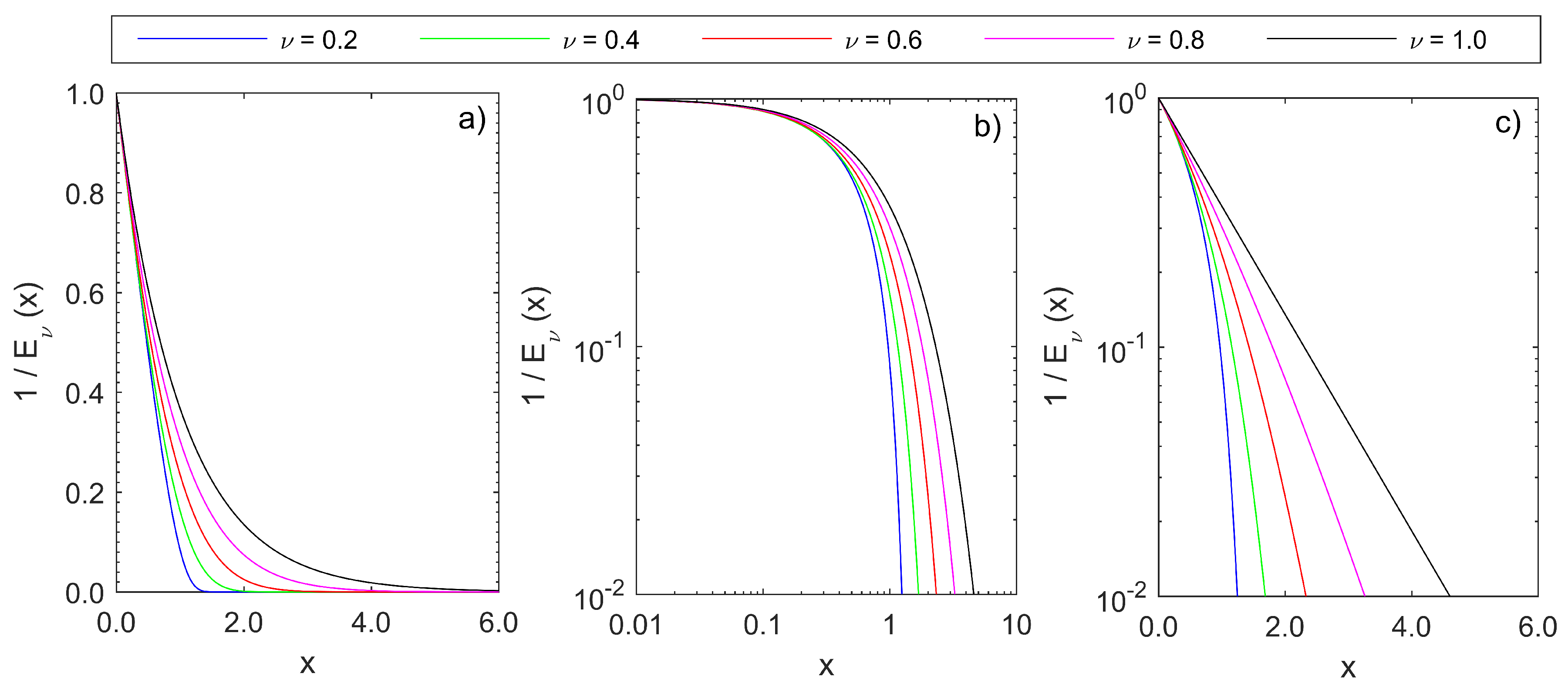
3. Generalizations of the Beer-Lambert Law Based on Weighted Poisson Distributions

As just seen, the assumption of Poissonian distribution of extinction events plays a key role for the stochastic interpretation of the classical (exponential) Beer-Lambert law. In order to take into account deviations from the pure exponential extinction, here we discuss the applications of weighted Poisson distributions [21]. Adopting the notation of [21] and references therein, the probability mass function of a weighted Poisson process is

$$P\{N^w\left(x\right)=n\}=\frac{w\left(n\right)p_n\left(x\right)}{\mathbb{E}\left[w\right(N\left)\right]},n\ge 0,$$

(7)

where N is a random variable with a Poisson distribution $p_n\left(x\right)$, and $w(·)$ a positive weight function with non-zero, finite expectation

$$0<\mathbb{E}\left[w\left(N\right)\right]=\sum _{n=0}^{\infty }w\left(n\right)p_n\left(x\right)<\infty .$$

(8)

According to the previous probabilistic derivation of the Beer-Lambert law, we here assume that the number of absorbed photons is distributed according to the weighted Poisson process (7). In this framework, the probability of transmission $T\left(x\right)$ is then given by

$$T\left(x\right)=P\{N^w\left(x\right)=0\}=\frac{w\left(0\right)}{{\displaystyle \sum _{n=0}^{\infty }w\left(n\right)\frac{{\left(\beta x\right)}^n}{n!}}},$$

(9)

The previous equation leads to a wide class of extinctions laws, including both faster and slower than exponential behaviors. Equation (9) can be considered as a weighted Beer-Lambert law, in the sense that it generalizes the classical exponential law depending on the weight function $w(·)$. The measure of the deviation from Poisson statistics is usually given by the Mandel parameter Q [27], which is positive for super-Poissonian and negative for sub-Poissonian distributions.

It is well-known that Mittag-Leffler functions play a relevant role in the theory of fractional differential equations and also in their applications as, for example, reported in the recent monograph [22]. In the applications we are considering, an interesting example is given by the Mittag-Leffler weighted Beer-Lambert

$$T\left(x\right)=\frac{1}{E_{\nu }\left(\beta x\right)},\nu \in (0,1]$$

(10)

that can be retrieved using the the particular weight $w\left(n\right)=n!/\mathsf{\Gamma }(\nu n+1)$ in Equation (9), and clearly include the classical Beer-Lambert law as a special case ($\nu =1$). It is worth noting that this kind of weighted Beer-Lambert law directly results from one of the fractional Poisson distributions studied by Beghin and Orsingher in [23]. As qualitatively shown in Figure 1, Equation (10) describes a family of super-exponential curves depending on the Mittag-Leffler parameter $\nu$. The more $\nu$ approaches 0, the more the correspondent curve decrease rapidly. Despite super-exponential processes appear to be not very common, such a model may turn out to be useful at least in some physics applications [14,28].

4. Weighted Beer-Lambert Law in Inhomogeneous Media

As pointed out in relatively recent literature, some applications particularly relevant to microbiology and pharmacology seems to follow hyperbolic more than exponential extinction laws. As an example, a hyperbolic equation was proposed in [15] to reproduce solar light attenuation in microalgal cultures grown in outdoor photobioreactors, and later in [5] to model attenuation of both monochromatic and polychromatic light in Chlorella Vulgaris suspensions. Anyway, these results need further confirmations, for the fractional Beer-Lambert Law proposed in [9] was used very recently to successfully model light attenuation profile of different photosynthetic microorganism culture. As the latter result is clearly in contrast to what was previously reported, and this specific topic still needs to be investigated in more detail.

The deviations from the classical Lambert-Beer law, particularly relevant at high microalgal densities, are mostly attributed to scattering effects and selective absorption (i.e., cells absorb radiation at wavelengths closer to their absorption spectra peaks more effectively). We show in the following that a hyperbolic attenuation can be explained relaxing the hypothesis of homogeneous medium, i.e., taking into account the case in which the extinction event distribution is a weighted Poisson distribution with a space varying rate (see e.g., [29]).

Under this assumption, the probability of transmission of the non-homogeneous weighted Beer-Lambert law is generally given by

$$P\{N_N^w\left(x\right)=0\}=\frac{w\left(0\right)}{{\displaystyle \sum _{n=0}^{\infty }w\left(n\right)\frac{\lambda {\left(x\right)}^n}{n!}}},$$

(11)

where $\lambda \left(x\right)$ is a sufficiently regular function. More specifically, we now consider the following case:

$$\left\{\begin{array}{c}\lambda \left(x\right)=ln(x+x_0),x_0\ge 1,\hfill \\ w\left(n\right)=\frac{n!}{\mathsf{\Gamma }(\nu n+1)},\nu \in (0,1].\hfill \end{array}\right.$$

(12)

This choice leads to the following non-homogeneous version of fractional-type Poisson distribution

$$\begin{array}{cc}\hfill P\{N_N^w\left(x\right)=n\}& =\frac{1}{{\displaystyle \sum _{n=0}^{\infty }\frac{{(ln(x+x_0))}^n}{\mathsf{\Gamma }(\nu n+1)}}}\frac{{(ln(x+x_0))}^n}{\mathsf{\Gamma }(\nu n+1)}\hfill \\ \hfill & =\frac{1}{{\displaystyle E_{\nu }\left(ln(x+x_0)\right)}}\frac{{(ln(x+x_0))}^n}{\mathsf{\Gamma }(\nu n+1)}.\hfill \end{array}$$

(13)

The fractionality of the distribution (13) stands in the fact that probability generating function

$$G(u;x)=\sum _{n=0}^{\infty }{u}^{n}P\{N_N^w\left(x\right)=n\}=\frac{E_{\nu }\left(uln(x+x_0)\right)}{E_{\nu }\left(ln(x+x_0)\right)},$$

(14)

satisfies the fractional equation

$$\frac{d^{\nu }}{d{u}^{\nu }}G(u^{\nu },x)=ln(x+x_0)G(u^{\nu },x),$$

(15)

involving the Caputo fractional derivative of order $\nu \in (0,1]$ [22]

$$\frac{d^{\nu }f\left(t\right)}{d{t}^{\nu }}=\frac{1}{\mathsf{\Gamma }(1-\nu )}{\int }_0^t{(t-\tau )}^{-\nu }\frac{df}{d\tau }d\tau .$$

(16)

This result can be simply obtained by direct calculation, observing that the Mittag-Leffler function is an eigenfunction of the Caputo derivative (see e.g., [22]). Therefore, we have that

$$\begin{array}{c}\frac{d^{\nu }}{d{u}^{\nu }}G(u^{\nu },x)=\frac{d^{\nu }}{d{u}^{\nu }}\frac{E_{\nu }\left(u^{\nu }ln(x+x_0)\right)}{E_{\nu }\left(ln(x+x_0)\right)}\hfill \\ =ln(x+x_0)\frac{E_{\nu }\left(u^{\nu }ln(x+x_0)\right)}{E_{\nu }\left(ln(x+x_0)\right)}=ln(x+x_0)G(u^{\nu },x).\hfill \end{array}$$

This specific case given by distribution (13) is of main interest for at least two reasons. First of all, as pointed out before, it is well-known that the Mittag-Leffler function plays a relevant role in the description of power-law-type decay and in the field of anomolous relaxation and extinction processes. In addition, secondly, it is worth noting that with this particular choice of space-dependent rate $\lambda \left(x\right)$ we recover a hyperbolic type decay in the limiting $\nu =1$ (e.g., in the classic case):

$$P\{N_N^w\left(x\right)=0\}=\frac{1}{e^{ln(x+x_0)}}=\frac{1}{x+x_0},$$

(17)

that solves the non-linear equation

$$\frac{dI}{dx}=-I^2$$

(18)

The latter result suggest that hyperbolic extinction can be considered as a special case of a more general weighted Beer-Lambert law, at least when obstacles follow a logarithmic distribution.

We observe that in [7] a hyperbolic Beer-Lambert law (17) was obtained by considering radiation extinction in a spatially correlated random medium, that appears to be the case when solar radiation is attenuated by clouds. We have just shown that the same result can be retrieved as a special case of a more general approach. Finally, according to [7] we want to underline that stronger deviations from the classical Beer-Lambert law are expected as long as absorption dominates, while in the single-scattering regime the deviations are less relevant.