Analytical Solutions to Fractional Fluid Flow and Oscillatory Process Models
Abstract
:1. Introduction
2. Preliminaries
Basic Properties of the Caputo Fractional Derivative
3. Main Results
3.1. Dynamics of a Sphere Immersed in an Incompressible Viscous Fluid
3.2. Oscillatory Process with Fractional Damping
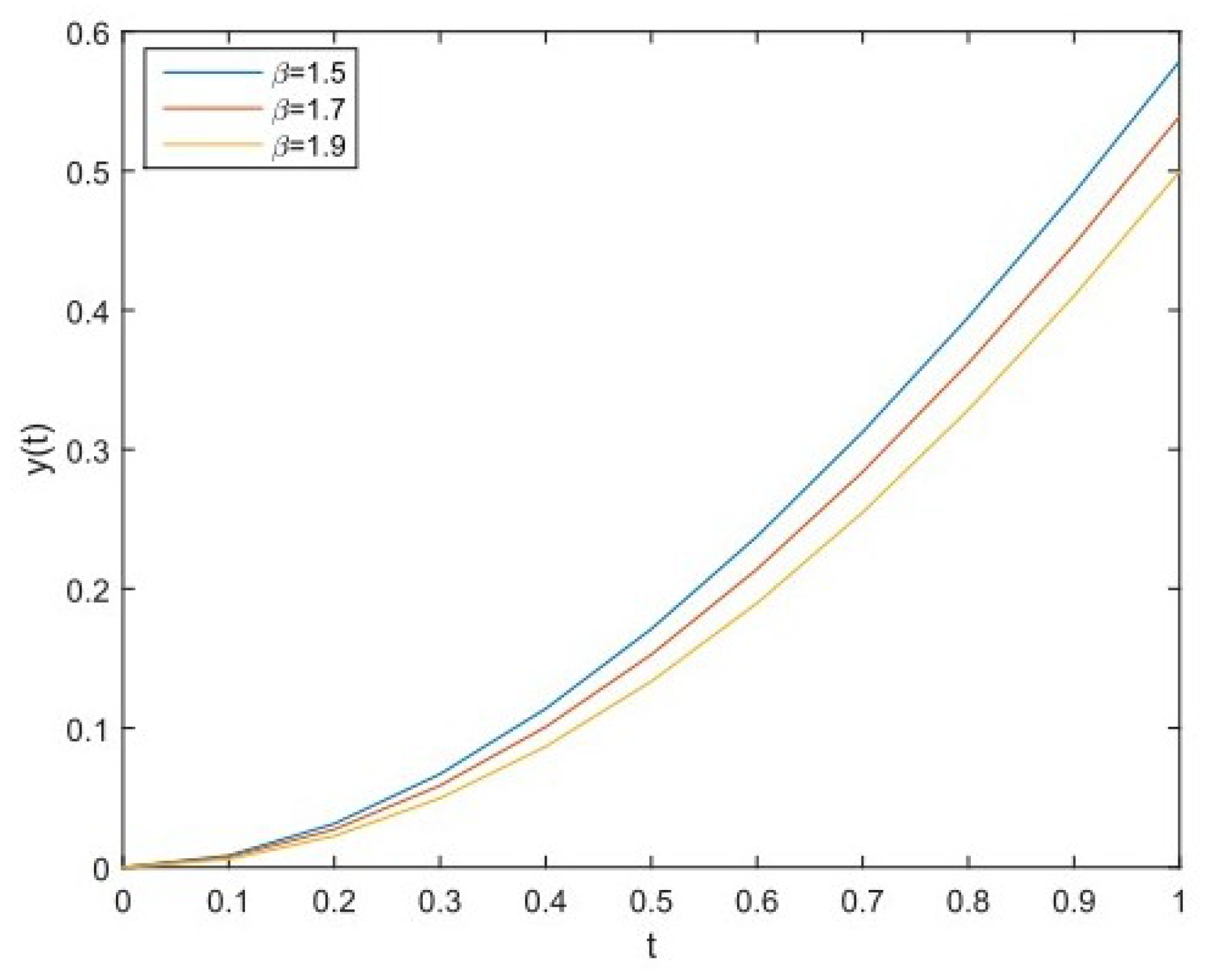
4. Numerical Examples
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Podlubny, I.; Magin, M.; Trymorush, I. Historical survey Niels Henrik Abel and the birth of fractional calculus. Fract. Calc. Appl. Anal. 2017, 20, 1068–1075. [Google Scholar] [CrossRef]
- Sergei, F.; Vladimir, C.; Toshiyuki, H. Application of Fractional Differential Equations for Modeling the Anomalous Diffusion of Contaminant from Fracture into Porous Rock Matrix with Bordering Alteration Zone. Transp. Porous Media 2010, 81, 187–205. [Google Scholar] [CrossRef]
- Hassan, F.; Zolotas, A. Impact of fractional order methods on optimized tilt control for rail vehicles. Fract. Calc. Appl. Anal. 2017, 20, 765–789. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; AlQurashi, M.; Baleanu, D. A Novel Numerical Approach for a Nonlinear Fractional Dynamical Model of Interpersonal and Romantic Relationships. Entropy 2017, 19, 375. [Google Scholar] [CrossRef]
- Fallahgoul, H.A.; Fabozzi, S.M.; Frank, F.J. Fractional partial differential equation and option pricing. In Fractional Calculus and Fractional Processes with Applications to Financial Economics; Fallahgoul, H.A., Focardi, S.M., Fabozzi, F.J., Eds.; Academic Press: Cambridge, MA, USA, 2017; pp. 59–80. [Google Scholar]
- Singh, J.; Kumar, D.; Hammouch, Z.; Atangana, A. A fractional epidemiological model for computer viruses pertaining to a new fractional derivative. Appl. Math. Comput. 2018, 316, 504–515. [Google Scholar] [CrossRef]
- Fouda, M.E.; Elwakil, A.S.; Radwan, A.G.; Maundy, B.J. Fractional-Order Two-Port Networks. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: New York, NY, USA, 2006; Volume 204, pp. 1–523. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D.; Sushila, J. Analysis of regularized long-wave equation associated with a new fractional operator with Mittag-Leffler type kernel. Phys. A Stat. Mech. Its Appl. 2018, 492, 155–167. [Google Scholar] [CrossRef]
- Li, Q.; Zhou, Y.; Zhao, X.; Ge, X. Dynamic Hedging Based on Fractional Order Stochastic Model with Memory Effect. Math. Probl. Eng. 2016, 2016. [Google Scholar] [CrossRef]
- Yanxin, W.; Li, Z. Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method. Adv. Differ. Equ. 2017, 27. [Google Scholar] [CrossRef]
- Kilbas, A.; Trujillo, J. Differential equations of fractional order: Methods results and problem–I. Appl. Anal. 2001, 78, 153–192. [Google Scholar] [CrossRef]
- Mustapha, K.; Abdallah, B.; Furati, K.; Nour, M. A discontinuous Galerkin method for time fractional diffusion equations with variable coefficients. Numer. Algorithms 2016, 73, 517–534. [Google Scholar] [CrossRef]
- Li, Z.; Zhu, W. Fractional series expansion method for fractional differential equations. Int. J. Numer. Methods Heat Fluid Flow 2015, 25, 1525–1530. [Google Scholar] [CrossRef]
- Aghili, A.; Ansari, A. Solving partial fractional differential equations using the FA-transform. Arab J. Math. Sci. 2013, 19, 61–71. [Google Scholar] [CrossRef]
- Klimek, M.; Dziembowski, D. Mellin Transform for Fractional Differential Equations with Variable Potential. In Nonlinear Science and Complexity; Machado, J., Luo, A., Barbosa, R., Silva, M.S., Figueiredo, L., Eds.; Springer: Dordrecht, The Netherlands, 2011; pp. 281–292. [Google Scholar] [CrossRef]
- Li, K.; Peng, J. Laplace transform and fractional differential equations. Appl. Math. Lett. 2011, 24, 2019–2023. [Google Scholar] [CrossRef]
- Zainal, N.H.; Kilicman, A. Solving Fractional Partial Differential Equations with Corrected Fourier Series Method. Abstr. Appl. Anal. 2014. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. A new numerical algorithm for fractional Fitzhugh–Nagumo equation arising in transmission of nerve impulses. Nonlinear Dyn. 2018, 91, 307–317. [Google Scholar] [CrossRef]
- Singh, J.; Rashidi, M.; Sushila, J.; Kumar, D. A hybrid computational approach for Jeffery–Hamel flow in non-parallel walls. Neural Comput. Appl. 2017, 1–7. [Google Scholar] [CrossRef]
- Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos Solitons Fractals 1996, 7, 1461–1477. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Derivatives and Integrals. In Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Podlubny, I., Ed.; Elsevier: New York, NY, USA, 1999; Volume 198, pp. 41–119. [Google Scholar] [CrossRef]
- Gorenflo, R.; Kilbas, A.; Mainardi, F.; Rogosin, S. Mittag-Leffler Functions, Related Topics and Applications; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Jumarie, G. Laplace’s transform of fractional order via the Mittag-Leffler function and modified Riemann-Liouville derivative. Appl. Math. Lett. 2009, 22, 1659–1664. [Google Scholar] [CrossRef]
- Teodoro, G.S.; de Oliveira, E.C. Laplace transform and the Mittag-Leffler function. Int. J. Math. Educ. Sci. Technol. 2014, 45, 595–604. [Google Scholar] [CrossRef]
- Wright, E. On the Coefficients of Power Series Having Exponential Singularities. J. Lond. Math. Soc. 1933, 8, 71–79. [Google Scholar] [CrossRef]
- Wright, E. The asymptotic expansion of the generalized Bessel function. Proc. Lond. Math. Soc. (Ser. II) 1935, 38, 257–270. [Google Scholar] [CrossRef]
- Wright, E. The generalized Bessel function of order greater than one. Q. J. Math. 1940, 11, 36–48. [Google Scholar] [CrossRef]
- Gorenflo, R.; Luchko, Y.; Mainardi, F. Analytic properties and applications of Wright functions. Fract. Calc. Appl. Anal. 1999, 2, 383–414. [Google Scholar]
- Prajapat, J. Certain geometric properties of the Wright function. Integral Transform. Spec. Funct. 2015, 26, 203–212. [Google Scholar] [CrossRef]
- Paneva-Konovska, J. From Bessel to Multi-Index Mittag-Leffler Functions: Enumerable Families, Series in Them and Convergence; World Scientific Publishing Europe: London, UK, 2016; pp. 1–228. [Google Scholar]
- Sandev, T.; Tomovski, Z.; Dubbeldam, J.L. Generalized Langevin equation with a three parameter Mittag-Leffler noise. Phys. A Stat. Mech. Its Appl. 2011, 390, 3627–3636. [Google Scholar] [CrossRef]
- Sandev, T. Generalized Langevin equation and the Prabhakar derivative. Mathematics 2017, 5, 66. [Google Scholar] [CrossRef]
- Sandev, T.; Metzler, R.; Tomovski, Z. Correlation functions for the fractional generalized Langevin equation in the presence of internal and external noise. J. Math. Phys. 2014, 55, 023301. [Google Scholar] [CrossRef]
- Saxena, R.; Mathai, A.; Haubold, H. Unified fractional kinetic equation and a fractional diffusion equation. J. Astrophys. Space Sci. 2004, 209, 299–310. [Google Scholar] [CrossRef]



© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zakariya, Y.F.; Afolabi, Y.O.; Nuruddeen, R.I.; Sarumi, I.O. Analytical Solutions to Fractional Fluid Flow and Oscillatory Process Models. Fractal Fract. 2018, 2, 18. https://doi.org/10.3390/fractalfract2020018
Zakariya YF, Afolabi YO, Nuruddeen RI, Sarumi IO. Analytical Solutions to Fractional Fluid Flow and Oscillatory Process Models. Fractal and Fractional. 2018; 2(2):18. https://doi.org/10.3390/fractalfract2020018
Chicago/Turabian StyleZakariya, Yusuf F., Yusuf O. Afolabi, Rahmatullah I. Nuruddeen, and Ibrahim O. Sarumi. 2018. "Analytical Solutions to Fractional Fluid Flow and Oscillatory Process Models" Fractal and Fractional 2, no. 2: 18. https://doi.org/10.3390/fractalfract2020018




