Recovery of Differential Equations from Impulse Response Time Series Data for Model Identification and Feature Extraction
Abstract
:1. Introduction
- State observation and supervision, especially for quality assurance and human–machine interaction purposes during operation.
- Future state and fault prediction, commonly known as structural health monitoring [5].
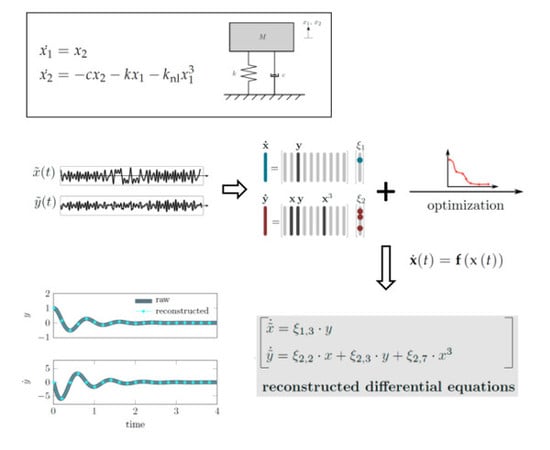
2. Methods
2.1. Sparse Identification of Non-Linear Dynamics—SINDy
2.2. Time-Delay Embedding
2.3. Uncertainty Suppressing Numerical Differentiation
2.4. Time Series Comparison Measures
- Instance-based schemes that compare contemporaneous pairs of time series instances. In the simplest case, sequences are subtracted from each other. Modifications and advanced approaches include warping methods that add more flexibility and the ability to also take into account phase shifts.
- Higher-level features based on transforms, sampling strategies or correlation measures. Examples include statistical moments and linear transforms, such as the Fourier transform. Time series comparison is then performed based on features extracted from the transforms, such as the standard deviation or major periodicities.
- Quantifiers for qualitative behavior, mostly borrowed from nonlinear time series analysis and complexity sciences [29]. Here, the actual shape of the sequence is rather irrelevant. Instead, the qualitative nature of the dynamics encoded in the time series is of interest: dynamical invariants quantify the degree of regularity, entropy, or fractal properties of the sequence when studied in a dynamical framework, cf. [17].
2.5. Constrained Nonlinear Optimization
2.6. Models Used
3. Results
3.1. Instance-Based Error Measure
3.1.1. Providing Full Information: All States and Analytical Derivatives
3.1.2. Providing Less Information: All States and Numerical Derivatives
3.1.3. Providing Less Information: State Space Reconstruction and Numerical Derivatives
3.2. Balancing Reconstruction Error and Model Complexity
3.3. Model Identification Studies
3.3.1. Identification of Parameter Dependencies
3.3.2. Robust Model Parameter Identification
3.3.3. Test for Nonlinearity
3.4. Feature Generation for Unsupervised Time Series Classification Tasks
4. Conclusions
- Reconstruction of dynamic minimal models: The sparse regression reconstructs systems of differential equations from time series data. Hence, these equations can be studied and analyzed by classical methods and provide detailed insight into the governing dynamics underlying an observation.
- Model reconstruction for limited input data: The proposed framework automates and optimizes the model reconstruction procedure while being suited well for accommodating limited data quality resulting from the amount of information, noise contamination, and unknown model dimensions.
- Test for nonlinearity: The qualitative character of the underlying dynamical system can be estimated in terms of linearity and type and degree of nonlinearity by inspecting the set of reconstructed differential equations.
- Model identification and model updating methods: The optimized reconstruction allows for identification of terms that depend explicitly on parameters that are prescribed or measured during experimentation. After identifying those terms in the reconstructed ODEs, uncertainty and bifurcation studies can be used in predictive modeling approaches to design safe and efficient structures without extensive testing.
- Time series feature generation for classification and regression tasks: The reconstructed models represent features that are discriminative and possibly superior to classical time series features for uni-variate, short and highly transient input data.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DOF | Degree Of Freedom |
| NZE | Non-Zero Entries |
| ODE | Ordinary Differential Equation |
| SINDy | Sparse Identification of Nonlinear Dynamics |
| TVRegDiff | Total Variation Regularized Numerical Differentiation |
Appendix A. The Filtering Property of TVRegDiff Numerical Derivation Schemes

References
- Ondra, V.; Sever, I.A.; Schwingshackl, C.W. A method for non-parameteric identification of nonlinear vibration systems with asymmetric restoring forces from a resonant decay response. Mechan. Syst. Signal Process. 2019, 114, 239–258. [Google Scholar] [CrossRef]
- Ondra, V.; Sever, I.A.; Schwingshackl, C.W. A method for detection and characterisation of structural nonlinearities using the Hilbert transform. Mechan. Syst. Signal Process. 2017, 83, 210–227. [Google Scholar] [CrossRef]
- Pesaresi, L.; Stender, M.; Ruffini, V.; Schwingshackl, C.W. DIC Measurement of the Kinematics of a Friction Damper for Turbine Applications. In Dynamics of Coupled Structures, Volume 4, Conference Proceedings of the Society for Experimental Mechanics Series; Springer: Cham, Switzerland, 2017; pp. 93–101. [Google Scholar]
- Kurt, M.; Chen, H.; Lee, Y.; McFarland, M.; Bergman, L.; Vakakis, A. Nonlinear system identification of the dynamics of a vibro-impact beam: Numerical results. Arch. Appl. Mech. 2012, 82, 1461–1479. [Google Scholar] [CrossRef]
- Farrar, C.R.; Worden, K. An introduction to structural health monitoring. Philos. Trans. R. Soc. A 2007, 365, 303–315. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Nuawi, M.Z.; Bahari, A.R.; Abdullah, S.; Ariffin, A.K.; Nopiah, Z.M. Time Domain Analysis Method of the Impulse Vibro-acoustic Signal for Fatigue Strength Characterisation of Metallic Material. Procedia Eng. 2013, 66, 539–548. [Google Scholar] [CrossRef]
- Crutchfield, J.P.; McNamara, B.S. Equations of motion from a data series. Complex Syst. 1987, 1, 121. [Google Scholar]
- Kurt, M.; Eriten, M.; McFarland, M.; Bergman, L.; Vakakis, A. Methodology for model updating of mechanical components with local nonlinearities. J. Sound Vib. 2015, 357, 331–348. [Google Scholar] [CrossRef]
- Moore, K.; Kurt, M.; Eriten, M.; McFarland, M.; Bergman, L.; Vakakis, A. Direct detection of nonlinear modal interactions from time series measurements. Mechan. Syst. Signal Process. 2018. [Google Scholar] [CrossRef]
- González-García, R.; Rico-Martínez, R.; Kevrekidis, I.G. Identification of distributed parameter systems: A neural net based approach. Comput. Chem. Eng. 1998, 22, S965–S968. [Google Scholar] [CrossRef]
- Raissi, M.; Karniadakis, G.E. Hidden physics models: Machine learning of nonlinear partial differential equations. J. Comput. Phys. 2018, 357, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Gouesbet, G.; Letellier, C. Global vector-field reconstruction by using a multivariate polynomial L2 approximation on nets. Phys. Rev. E 1994, 49, 4955–4972. [Google Scholar] [CrossRef]
- Liu, W.-D.; Ren, K.F.; Meunier-Guttin-Cluzel, S.; Gouesbet, G. Global vector-field reconstruction of nonlinear dynamical systems from a time series with SVD method and validation with Lyapunov exponents. Chin. Phys. 2003, 12, 1366. [Google Scholar]
- Wang, W.X.; Yang, R.; Lai, Y.C.; Kovanis, V.; Grebogi, C. Predicting catastrophes in nonlinear dynamical systems by compressive sensing. Phys. Rev. Lett. 2011, 106, 154101. [Google Scholar] [CrossRef] [PubMed]
- Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Discovering governing equations from data by sparse identification of nonlinear dynamical systems. Proc. Natl. Acad. Sci. USA 2016, 113, 3932–3937. [Google Scholar] [CrossRef] [PubMed]
- Rudy, S.H.; Brunton, S.L.; Proctor, J.L.; Kutz, J.N. Data-driven discovery of partial differential equations. Sci. Adv. 2017, 3, e1602614. [Google Scholar] [CrossRef]
- Oberst, S.; Stender, M.; Baetz, J.; Campbell, G.; Lampe, F.; Morlock, M.; Lai, J.C.; Hoffmann, N. Extracting differential equations from measured vibro-acoustic impulse responses in cavity preparation of total hip arthroplasty. In Proceedings of the 15th Experimental Chaos and Complexity Conference, Madrid, Spain, 4–7 June 2018. [Google Scholar]
- Takens, F. Detecting strange attractors in turbulence. In Dynamical Systems and Turbulence; Springer: Berlin/Heidelberg, Germany, 1981; pp. 366–381. [Google Scholar]
- Kantz, H.; Schreiber, T. Nonlinear Time Series Analysis; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Oberst, S.; Lai, J.C. A statistical approach to estimate the Lyapunov spectrum in disc brake squeal. J. Sound Vib. 2015, 334, 120–135. [Google Scholar] [CrossRef]
- Abarbanel, H.D.I.; Brown, R.; Sidorowich, J.J.; Tsimring, L.S. The analysis of observed chaotic data in physical systems. Rev. Mod. Phys. 1993, 65, 1331–1392. [Google Scholar] [CrossRef]
- Kennel, M.B.; Brown, R.; Abarbanel, H.D.I. Determining embedding dimension for phase-space reconstruction using a geometrical construction. Phys. Rev. A 1992, 45, 3403–3411. [Google Scholar] [CrossRef]
- Oberst, S.; Baetz, J.; Campbell, G.; Lampe, F.; Lai, J.C.; Hoffmann, N.; Morlock, M. Vibro-acoustic and nonlinear analysis of cadavric femoral bone impaction in cavity preparations. Int. J. Mech. Sci. 2018, 144, 739–745. [Google Scholar] [CrossRef]
- Gilmore, R.; Lefranc, M.; Tufillaro, N.B. The Topology of Chaos. Am. J. Phys. 2003, 71, 508–510. [Google Scholar] [CrossRef]
- Chartrand, R. Numerical Differentiation of Noisy, Nonsmooth Data. ISRN Appl. Math. 2011, 2011, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Fulcher, B.D.; Jones, N.S. Highly Comparative Feature-Based Time-Series Classification. IEEE Trans. Knowl. Data Eng. 2014, 26, 3026–3037. [Google Scholar] [CrossRef] [Green Version]
- Bagnall, A.; Lines, J.; Hills, J.; Bostrom, A. Time-Series Classification with COTE: The Collective of Transformation-Based Ensembles. IEEE Trans. Knowl. Data Eng. 2015, 27, 2522–2535. [Google Scholar] [CrossRef]
- Fulcher, B.D.; Jones, N.S. hctsa: A Computational Framework for Automated Time-Series Phenotyping Using Massive Feature Extraction. Cell Syst. 2017, 5, 527–531.e3. [Google Scholar] [CrossRef] [PubMed]
- Marwan, N.; Romano, M.C.; Thiel, M.; Kurths, J. Recurrence plots for the analysis of complex systems. Phys. Rep. 2007, 438, 237–329. [Google Scholar] [CrossRef]
- Stender, M.; Papangelo, A.; Allen, M.; Brake, M.; Schwingshackl, C.; Tiedemann, M. Structural Design with Joints for Maximum Dissipation. In Shock & Vibration, Aircraft/Aerospace, Energy Harvesting, Acoustics & Optics; Springer: Cham, Switzerland, 2016; Volume 9, pp. 179–187. [Google Scholar]
- Srivastava, N.; Hinto, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]














| 1 | Other Terms | |||||||
|---|---|---|---|---|---|---|---|---|
| , | 0 | −0.74 | −5.84 | - | - | - | - | |
| −0.008 | 10.60 | −2.45 | - | - | - | - | ||
| , | 0 | −0.75 | −5.82 | −0.06 | - | - | - | |
| −0.007 | 10.62 | −2.45 | 0 | - | - | - | ||
| , | 0 | −0.81 | −5.84 | −0.13 | 0.51 | 0.16 | - | |
| 0 | 10.60 | −2.39 | 0 | 0 | 0 | - | ||
| , | 0 | −0.85 | −5.86 | 0 | 0.7080 | 0 | −0.96 −1.44 | |
| 0 | 10.54 | −2.36 | 0 | 0 | 0 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stender, M.; Oberst, S.; Hoffmann, N. Recovery of Differential Equations from Impulse Response Time Series Data for Model Identification and Feature Extraction. Vibration 2019, 2, 25-46. https://doi.org/10.3390/vibration2010002
Stender M, Oberst S, Hoffmann N. Recovery of Differential Equations from Impulse Response Time Series Data for Model Identification and Feature Extraction. Vibration. 2019; 2(1):25-46. https://doi.org/10.3390/vibration2010002
Chicago/Turabian StyleStender, Merten, Sebastian Oberst, and Norbert Hoffmann. 2019. "Recovery of Differential Equations from Impulse Response Time Series Data for Model Identification and Feature Extraction" Vibration 2, no. 1: 25-46. https://doi.org/10.3390/vibration2010002