Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint
Abstract
:1. Introduction
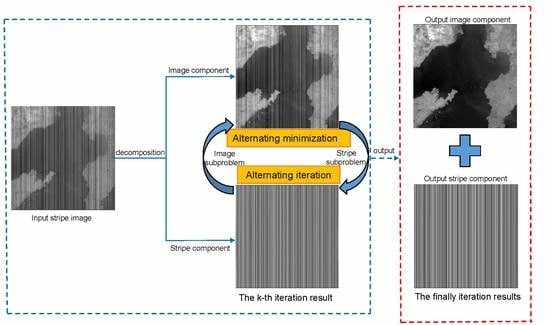
- The image decomposition framework is studied and applied to the stripe noise removal of remote sensing images. From image decomposition perspective, we construct a convex sparse optimization model to remove various of stripes, which can simultaneously estimate the stripe noise and underlying image.
- The directional and structural characteristics of the stripe noise are analyzed in detail via implementing statistical analysis, and we utilize unidirectional TV and group sparsity regularization to depict them, respectively.
- The alternating minimization algorithm is designed to solve the proposed model. Numerical experimental results, including simulated and real experiments, demonstrate that the proposed method outperforms the state-of-the-art results.
2. Problem Formulation and Image Decomposition Framework
3. Image and Stripes Characteristics Analysis
3.1. TV Regularization
3.2. The Characteristic of Stripe Noise
4. Methodology
4.1. The Proposed Model
4.2. Optimization Procedure
- -subproblem is followed by
- Similarly, we solve the -subproblem as follows
- The -subproblem is described as followswhich is a quadratic optimization and differentiability. Thus, by the first derivations to , it is equivalent to the following linear system of equationUnder the periodic boundary conditions for , both and are block circulant matrices with circulant blocks. For the detailed discussion, we refer the reader to [50]. Therefore, they can diagonalization by the 2D discrete Fourier transforms. Using the convolution theorem of Fourier transforms, we can obtain the solution of as followswhere , “*” denotes complex conjugacy, “∘” denotes component-wise multiplication, and the division is component-wise as well, represents the fast Fourier transform and denotes its inverse transform.
- -subproblem is given byIs is easy to obtain the solution by soft-threshold shrinkage
- W-subproblem is described as followsSimple manipulation shows that subproblem (25) is equivalent to
- -subproblem is followed byThis subproblem is similarly with -subproblem optimization, and the solution can be used FFT as follows
| Algorithm 1 The proposed destriping algorithm |
| Input: Stripe image , parameters , , , , and . Output: Image component and stripe component . |
5. Experiment Results
5.1. Simulated Data Experiments
5.2. Real Data Experiments
6. Discussion
6.1. Experimental Results Analysis
6.2. Analysis of the Parameters
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Chen, J.; Shao, Y.; Guo, H.; Wang, W.; Zhu, B. Destriping CMODIS data by power filtering. IEEE Trans. Geosci. Remote Sens. 2003, 41, 2119–2124. [Google Scholar] [CrossRef]
- He, W.; Zhang, H.; Zhang, L.; Shen, H. Total-variation-regularized low-rank matrix factorization for hyperspectral image restoration. IEEE Trans. Geosci. Remote Sens. 2016, 54, 178–188. [Google Scholar] [CrossRef]
- Zhang, H.; He, W.; Zhang, L.; Shen, H.; Yuan, Q. Hyperspectral image restoration using low-rank matrix recovery. IEEE Trans. Geosci. Remote Sens. 2014, 52, 4729–4743. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, L.; Shen, H. Hyperspectral Image denoising employing a spectral-spatial adaptive total variation model. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3660–3677. [Google Scholar] [CrossRef]
- Aggarwal, H. K.; Majumdar, A. Hyperspectral Image denoising using spatio-spectral total variation. IEEE Geosci. Remote Sens. Lett. 2016, 13, 442–446. [Google Scholar] [CrossRef]
- Xu, Y.; Qian, Y. Group sparse nonnegative matrix factorization for hyperspectral image denoising. IGARSS 2016, 6958–6961. [Google Scholar]
- Zhang, H.; Li, J.; Huang, Y.; Zhang, L. A nonlocal weighted joint sparse representation classification method for hyperspectral imagery. IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens. 2014, 7, 2056–2065. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Total variation spatial regularization for Sparse hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2012, 50, 4484–4502. [Google Scholar] [CrossRef]
- Zhao, X.-L.; Wang, F.; Huang, T.-Z.; Ng, M.K.; Plemmons, R.J. Deblurring and sparse unmixing for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4045–4058. [Google Scholar] [CrossRef]
- Iordache, M.D.; Bioucas-Dias, J.M.; Plaza, A. Collaborative sparse regression for hyperspectral unmixing. IEEE Trans. Geosci. Remote Sens. 2014, 52, 341–354. [Google Scholar] [CrossRef]
- Tarabalka, Y.; Chanussot, J.; Benediktsson, J.A. Segmentation and classification of hyperspectral images using watershed transformation. Pattern Recognit. 2010, 43, 2367–2379. [Google Scholar] [CrossRef]
- Stein, D.W.; Beaven, S.G.; Hoff, L.E.; Winter, E.M.; Schaum, A.P.; Stocker, A.D. Anomaly detection from hyperspectral imagery. IEEE Signal Process. Mag. 2002, 19, 58–69. [Google Scholar] [CrossRef]
- Chen, J.; Chang, C. Destriping of Landsat MSS images by filtering techniques. Photogramm. Eng. Remote Sensing 1992, 58, 1417–1423. [Google Scholar]
- Torres, J.; Infante, S.O. Wavelet analysis for the elimination of striping noise in satellite images. Opt. Eng. 2001, 40, 1309–1314. [Google Scholar]
- Chen, J.; Lin, H.; Shao, Y.; Yang, L. Oblique striping removal in remote sensing imagery based on wavelet transform. Int. J. Remote Sens. 2006, 27, 1717–1723. [Google Scholar] [CrossRef]
- Münch, B.; Trtik, P.; Marone, F.; Stampanoni, M. Stripe and ring artifact removal with combined wavelet-Fourier filtering. Opt. Express 2009, 17, 8567–8591. [Google Scholar] [CrossRef] [PubMed]
- Pande-Chhetri, R.; Abd-Elrahman, A. De-striping hyperspectral imagery using wavelet transform and adaptive frequency domain filtering. ISPRS J. Photogramm. Remote Sens. 2011, 66, 620–636. [Google Scholar] [CrossRef]
- Sun, L.; Neville, R.; Staenz, K.; White, H.P. Automatic destriping of Hyperion imagery based on spectral moment matching. Can. J. Remote Sens. 2008, 34, 68–81. [Google Scholar] [CrossRef]
- Rakwatin, P.; Takeuchi, W.; Yasuoka, Y. Stripe noise reduction in MODIS data by combining histogram matching with facet filter. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1844–1856. [Google Scholar] [CrossRef]
- Horn, B.K.; Woodham, R.J. Destriping Landsat MSS images by histogram modification. Comput. Gr. Image Process. 1979, 10, 69–83. [Google Scholar] [CrossRef]
- Wegener, M. Destriping multiple sensor imagery by improved histogram matching. Int. J. Remote Sens. 1990, 11, 859–875. [Google Scholar] [CrossRef]
- Gadallah, F.; Csillag, F.; Smith, E. Destriping multisensor imagery with moment matching. Int. J. Remote Sens. 2000, 21, 2505–2511. [Google Scholar] [CrossRef]
- Carfantan, H.; Idier, J. Statistical linear destriping of satellite-based pushbroom-type images. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1860–1871. [Google Scholar] [CrossRef]
- Shen, H.; Zhang, L. A MAP-based algorithm for destriping and inpainting of remotely sensed images. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1492–1502. [Google Scholar] [CrossRef]
- Bouali, M.; Ladjal, S. Toward optimal destriping of MODIS data using a unidirectional variational model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 2924–2935. [Google Scholar] [CrossRef]
- Chang, Y.; Fang, H.; Yan, L.; Liu, H. Robust destriping method with unidirectional total variation and framelet regularization. Opt. Express 2013, 21, 23307–23323. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhou, G.; Yan, L.; Zhang, T. A destriping algorithm based on TV-Stokes and unidirectional total variation model. Optik-Int. J. Light Electron Opt. 2016, 127, 428–439. [Google Scholar] [CrossRef]
- Zhou, G.; Fang, H.; Lu, C.; Wang, S.; Zuo, Z.; Hu, J. Robust destriping of MODIS and hyperspectral data using a hybrid unidirectional total variation model. Optik-Int. J. Light Electron Opt. 2015, 126, 838–845. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Liu, H. Simultaneous destriping and denoising for remote sensing images with unidirectional total variation and sparse representation. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1051–1055. [Google Scholar] [CrossRef]
- Wang, M.; Zheng, X.; Pan, J.; Wang, B. Unidirectional total variation destriping using difference curvature in MODIS emissive bands. Infrared Phys. Technol. 2016, 75, 1–11. [Google Scholar] [CrossRef]
- Acito, N.; Diani, M.; Corsini, G. Subspace-based striping noise reduction in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1325–1342. [Google Scholar] [CrossRef]
- Lu, X.; Wang, Y.; Yuan, Y. Graph-regularized low-rank representation for destriping of hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4009–4018. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Fang, H.; Luo, C. Anisotropic spectral-spatial total variation model for multispectral remote sensing image destriping. IEEE Trans. Image Process. 2015, 24, 1852–1866. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Lu, X.; Shen, H.; Yuan, Q.; Jiao, Y.; Zhang, L. Stripe noise separation and removal in remote sensing images by consideration of the global sparsity and local variational properties. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3049–3060. [Google Scholar] [CrossRef]
- Chang, Y.; Yan, L.; Wu, T.; Zhong, S. Remote sensing image stripe noise removal: from image decomposition perspective. IEEE Trans. Geosci. Remote Sens. 2016, 54, 7018–7031. [Google Scholar] [CrossRef]
- Liu, J.; Huang, T.-Z.; Selesnick, I.W.; Lv, X.G.; Chen, P. Image restoration using total variation with overlapping group sparsity. Information Sciences 2015, 295, 232–246. [Google Scholar] [CrossRef]
- Liu, G.; Huang, T.-Z.; Liu, J. High-order TVL1-based images restoration and spatially adapted regularization parameter selection. Comput. Math. Appl. 2014, 67, 2015–2026. [Google Scholar] [CrossRef]
- Huang, J.; Huang, T.-Z.; Zhao, X.-L.; Xu, Z.B.; Lv, X.G. Two soft-thresholding based iterative algorithms for image deblurring. Information Sciences 2014, 271, 179–195. [Google Scholar] [CrossRef]
- Huang, J.; Donatelli, M.; Chan, R.H. Nonstationary iterated thresholding algorithms for image deblurring. Inverse Probl. Imaging 2013, 7, 717–736. [Google Scholar]
- Tikhonov, A.; Arsenin, V. Solutions of Ill-Posed Problems; Winston and Sons: Washington, DC, USA, 1977. [Google Scholar]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phy. D: Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Zhao, X.-L.; Wang, F.; Ng, M.K. A new convex optimization model for multiplicative noise and blur removal. SIAM J. Imaging Sci. 2014, 7, 456–475. [Google Scholar] [CrossRef]
- Deng, L.-J.; Guo, H.; Huang, T.-Z. A fast image recovery algorithm based on splitting deblurring and denoising. J. Comput. Appl. Math. 2015, 287, 88–97. [Google Scholar] [CrossRef]
- Ji, T.Y.; Huang, T.-Z.; Zhao, X.-L.; Ma, T.H.; Liu, G. Tensor completion using total variation and low-rank matrix factorization. Inf. Sci. 2016, 326, 243–257. [Google Scholar] [CrossRef]
- Qin, Z.; Goldfarb, D.; Ma, S. An alternating direction method for total variation denoising. Optim. Methods Softw. 2015, 30, 594–615. [Google Scholar] [CrossRef]
- Deng, W.; Yin, W.; Zhang, Y. Group sparse optimization by alternating direction method. Proc. SPIE 2013. [Google Scholar] [CrossRef]
- Eckstein, J.; Bertsekas, D.P. On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Math. Program. 1992, 55, 293–318. [Google Scholar] [CrossRef]
- Boyd, S.; Parikh, N.; Chu, E.; Peleato, B.; Eckstein, J. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 41, 613–627. [Google Scholar] [CrossRef]
- Ng, M.K.; Chan, R.H.; Tang, W.C. A Fast Algorithm for deblurring models with neumann boundary conditions. SIAM J. Sci. Comput. 1999, 21, 851–866. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yu, Y. Robust subspace segmentation by low-rank representation. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 663–670. [Google Scholar]
- Tseng, P. Convergence of a block coordinate descent method for nondifferentiable minimization. J. Optim. Theory Appl. 2001, 109, 475–494. [Google Scholar] [CrossRef]
- Deng, L.-J.; Guo, W.; Huang, T.-Z. Single-image super-resolution via an iterative reproducing kernel hilbert space method. IEEE Trans. Circuits Syst. Video Technol. 2016, 26, 2001–2014. [Google Scholar] [CrossRef]
- A Freeware Multispectral Image Data Analysis System. Available online: https://engineering.purdue.edu/~biehl/MultiSpec/hyperspectral.html (accessed on 7 April 2017).
- LAADS DAAC. Available online: https://ladsweb.nascom.nasa.gov (accessed on 7 April 2017).
- Open Remote Sensing. Available online: https://openremotesensing.net (accessed on 7 April 2017).
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: from error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Index of Hyperspectral Imagedata. Available online: http://compression.jpl.nasa.gov/hyperspectral/imagedata (accessed on 7 April 2017).




















| Image | Method | r = 0.2 | r = 0.4 | r = 0.6 | r = 0.8 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | Intensity | ||||||||||||||
| 10 | 50 | 100 | 0–100 | 10 | 50 | 100 | 0–100 | 10 | 50 | 100 | 0–100 | 10 | 50 | 100 | 0–100 | ||
| Hyperspectral periodic stripes | Degrade | 35.22 | 21.24 | 15.22 | 20.82 | 32.21 | 18.23 | 12.21 | 17.40 | 30.45 | 16.47 | 10.45 | 15.46 | 29.20 | 15.22 | 9.20 | 14.27 |
| WAFT | 41.91 | 37.69 | 37.69 | 30.83 | 38.20 | 32.94 | 32.89 | 27.53 | 33.12 | 32.65 | 32.11 | 25.53 | 35.37 | 32.70 | 32.22 | 24.89 | |
| SLD | 41.73 | 38.82 | 34.87 | 35.44 | 39.66 | 37.61 | 34.77 | 33.94 | 38.84 | 34.49 | 33.84 | 31.73 | 39.11 | 34.51 | 33.84 | 28.86 | |
| GSLV | 35.24 | 29.86 | 31.52 | 29.58 | 32.23 | 30.31 | 31.43 | 29.98 | 31.51 | 30.17 | 31.17 | 29.68 | 31.29 | 31.46 | 31.60 | 27.91 | |
| LRSID | 40.40 | 37.00 | 35.78 | 34.69 | 39.43 | 36.42 | 34.96 | 32.17 | 37.81 | 34.20 | 33.32 | 30.17 | 38.14 | 35.12 | 33.57 | 27.95 | |
| Proposed | 45.02 | 44.66 | 42.29 | 45.66 | 42.79 | 38.34 | 36.54 | 38.90 | 39.74 | 35.94 | 35.60 | 35.42 | 40.33 | 36.17 | 35.25 | 33.73 | |
| Hyperspectral nonperiodic stripes | Degrade | 35.14 | 21.16 | 15.14 | 20.12 | 32.13 | 18.15 | 12.13 | 6.57 | 30.34 | 16.36 | 10.34 | 15.42 | 29.10 | 15.12 | 9.10 | 14.07 |
| WAFT | 37.91 | 28.23 | 24.42 | 27.26 | 35.63 | 26.62 | 24.50 | 25.86 | 34.43 | 25.60 | 24.42 | 25.02 | 33.78 | 25.43 | 24.16 | 25.31 | |
| SLD | 39.79 | 32.33 | 28.61 | 31.99 | 38.34 | 30.77 | 26.17 | 29.77 | 36.80 | 29.52 | 24.58 | 29.49 | 37.08 | 29.68 | 25.12 | 29.98 | |
| GSLV | 35.15 | 29.20 | 27.04 | 28.12 | 32.13 | 28.70 | 24.86 | 28.03 | 30.35 | 29.21 | 24.07 | 28.04 | 31.69 | 30.06 | 23.95 | 28.79 | |
| LRSID | 39.25 | 31.33 | 27.39 | 30.52 | 38.21 | 29.39 | 24.73 | 28.51 | 36.26 | 28.46 | 23.76 | 28.18 | 36.42 | 28.56 | 24.09 | 29.07 | |
| Proposed | 42.52 | 41.43 | 38.78 | 39.89 | 40.79 | 35.37 | 31.81 | 33.30 | 37.03 | 30.45 | 26.54 | 32.91 | 36.98 | 29.76 | 25.94 | 31.61 | |
| MODIS periodic stripes | Degrade | 35.12 | 21.14 | 15.12 | 20.27 | 32.11 | 18.13 | 12.11 | 17.18 | 30.35 | 16.37 | 10.35 | 14.98 | 29.10 | 15.12 | 9.10 | 14.11 |
| WAFT | 49.33 | 45.43 | 41.55 | 37.18 | 44.97 | 42.50 | 38.80 | 35.37 | 49.22 | 44.94 | 36.08 | 29.98 | 49.66 | 48.80 | 45.42 | 31.65 | |
| SLD | 51.90 | 46.42 | 41.11 | 38.33 | 50.47 | 41.53 | 38.81 | 33.40 | 51.22 | 43.24 | 39.56 | 31.25 | 52.20 | 49.88 | 41.64 | 32.92 | |
| GSLV | 42.55 | 38.97 | 38.96 | 38.48 | 42.37 | 37.92 | 37.75 | 36.83 | 38.01 | 37.64 | 37.46 | 32.31 | 39.93 | 40.29 | 39.93 | 32.47 | |
| LRSID | 49.70 | 47.02 | 46.72 | 39.50 | 49.33 | 44.48 | 41.83 | 35.65 | 49.32 | 45.20 | 38.90 | 32.05 | 49.64 | 47.76 | 48.12 | 33.97 | |
| Proposed | 51.28 | 47.66 | 47.76 | 45.94 | 48.10 | 45.11 | 44.06 | 43.91 | 48.35 | 42.70 | 40.42 | 42.71 | 52.31 | 51.13 | 50.53 | 40.99 | |
| MODIS nonperiodics tripes | Degrade | 35.12 | 21.14 | 15.12 | 19.79 | 32.11 | 18.13 | 12.11 | 17.68 | 30.35 | 16.37 | 10.35 | 15.18 | 29.10 | 15.12 | 9.10 | 14.20 |
| WAFT | 44.46 | 35.40 | 31.52 | 36.39 | 42.83 | 34.65 | 31.64 | 34.22 | 41.04 | 31.17 | 28.25 | 31.46 | 38.20 | 30.52 | 27.68 | 30.30 | |
| SLD | 46.81 | 39.40 | 34.36 | 39.26 | 45.69 | 35.25 | 30.82 | 35.03 | 43.25 | 33.70 | 27.75 | 32.56 | 40.42 | 31.07 | 25.22 | 31.31 | |
| GSLV | 39.52 | 38.35 | 33.22 | 38.30 | 39.34 | 35.73 | 32.21 | 35.71 | 39.48 | 33.22 | 26.38 | 31.73 | 39.34 | 30.17 | 21.83 | 29.68 | |
| LRSID | 45.11 | 38.28 | 35.31 | 38.20 | 43.98 | 35.13 | 30.74 | 35.12 | 41.94 | 33.95 | 27.80 | 32.45 | 39.76 | 31.39 | 23.23 | 31.58 | |
| Proposed | 49.66 | 45.84 | 43.00 | 42.88 | 45.02 | 43.60 | 39.56 | 44.77 | 41.44 | 35.45 | 35.20 | 38.30 | 39.98 | 34.27 | 30.89 | 35.48 | |
| Image | Method | r = 0.2 | r = 0.4 | r = 0.6 | r = 0.8 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Intensity | Intensity | Intensity | Intensity | ||||||||||||||
| 10 | 50 | 100 | 0–100 | 10 | 50 | 100 | 0–100 | 10 | 50 | 100 | 0–100 | 10 | 50 | 100 | 0–100 | ||
| Hyperspectral periodic stripes | Degrade | 0.961 | 0.646 | 0.422 | 0.667 | 0.926 | 0.458 | 0.216 | 0.464 | 0.904 | 0.348 | 0.113 | 0.366 | 0.867 | 0.280 | 0.088 | 0.292 |
| WAFT | 0.992 | 0.985 | 0.985 | 0.955 | 0.980 | 0.964 | 0.963 | 0.936 | 0.957 | 0.963 | 0.962 | 0.927 | 0.973 | 0.963 | 0.962 | 0.911 | |
| SLD | 0.993 | 0.992 | 0.989 | 0.987 | 0.988 | 0.989 | 0.988 | 0.987 | 0.993 | 0.988 | 0.986 | 0.984 | 0.993 | 0.988 | 0.987 | 0.977 | |
| GSLV | 0.961 | 0.960 | 0.966 | 0.964 | 0.926 | 0.975 | 0.978 | 0.971 | 0.974 | 0.977 | 0.978 | 0.973 | 0.976 | 0.980 | 0.979 | 0.967 | |
| LRSID | 0.993 | 0.991 | 0.988 | 0.986 | 0.992 | 0.989 | 0.983 | 0.972 | 0.988 | 0.981 | 0.981 | 0.966 | 0.990 | 0.985 | 0.982 | 0.958 | |
| Proposed | 0.997 | 0.997 | 0.995 | 0.997 | 0.997 | 0.994 | 0.990 | 0.992 | 0.994 | 0.989 | 0.987 | 0.987 | 0.994 | 0.990 | 0.985 | 0.980 | |
| Hyperspectral nonperiodic stripes | Degrade | 0.964 | 0.667 | 0.443 | 0.682 | 0.935 | 0.487 | 0.230 | 0.467 | 0.908 | 0.369 | 0.126 | 0.368 | 0.875 | 0.294 | 0.081 | 0.286 |
| WAFT | 0.985 | 0.945 | 0.910 | 0.936 | 0.976 | 0.936 | 0.910 | 0.923 | 0.974 | 0.922 | 0.907 | 0.914 | 0.968 | 0.922 | 0.909 | 0.921 | |
| SLD | 0.992 | 0.986 | 0.975 | 0.985 | 0.994 | 0.984 | 0.968 | 0.982 | 0.992 | 0.978 | 0.950 | 0.977 | 0.992 | 0.980 | 0.950 | 0.981 | |
| GSLV | 0.964 | 0.966 | 0.954 | 0.964 | 0.935 | 0.971 | 0.950 | 0.967 | 0.908 | 0.971 | 0.930 | 0.963 | 0.976 | 0.976 | 0.918 | 0.965 | |
| LRSID | 0.993 | 0.981 | 0.957 | 0.969 | 0.992 | 0.968 | 0.944 | 0.965 | 0.989 | 0.961 | 0.916 | 0.958 | 0.988 | 0.959 | 0.921 | 0.961 | |
| Proposed | 0.997 | 0.996 | 0.986 | 0.994 | 0.996 | 0.992 | 0.985 | 0.990 | 0.993 | 0.971 | 0.956 | 0.980 | 0.992 | 0.974 | 0.945 | 0.978 | |
| MODIS periodic stripes | Degrade | 0.902 | 0.329 | 0.130 | 0.356 | 0.826 | 0.213 | 0.076 | 0.235 | 0.763 | 0.163 | 0.055 | 0.165 | 0.903 | 0.326 | 0.127 | 0.302 |
| WAFT | 0.997 | 0.993 | 0.992 | 0.982 | 0.993 | 0.993 | 0.991 | 0.984 | 0.996 | 0.995 | 0.964 | 0.979 | 0.997 | 0.997 | 0.997 | 0.977 | |
| SLD | 0.998 | 0.994 | 0.982 | 0.986 | 0.998 | 0.979 | 0.977 | 0.949 | 0.998 | 0.979 | 0.984 | 0.986 | 0.998 | 0.998 | 0.997 | 0.989 | |
| GSLV | 0.997 | 0.991 | 0.991 | 0.993 | 0.997 | 0.996 | 0.996 | 0.994 | 0.997 | 0.998 | 0.996 | 0.992 | 0.996 | 0.996 | 0.995 | 0.969 | |
| LRSID | 0.998 | 0.996 | 0.995 | 0.989 | 0.998 | 0.989 | 0.980 | 0.994 | 0.998 | 0.992 | 0.981 | 0.989 | 0.998 | 0.998 | 0.998 | 0.989 | |
| Proposed | 0.999 | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 0.997 | 0.996 | 0.998 | 0.998 | 0.995 | 0.995 | 0.999 | 0.999 | 0.999 | 0.993 | |
| MODIS nonperiodic stripes | Degrade | 0.919 | 0.410 | 0.189 | 0.398 | 0.838 | 0.256 | 0.099 | 0.249 | 0.813 | 0.227 | 0.083 | 0.183 | 0.798 | 0.210 | 0.074 | 0.182 |
| WAFT | 0.994 | 0.985 | 0.980 | 0.986 | 0.992 | 0.982 | 0.978 | 0.983 | 0.989 | 0.977 | 0.972 | 0.979 | 0.987 | 0.974 | 0.970 | 0.975 | |
| SLD | 0.997 | 0.994 | 0.988 | 0.993 | 0.996 | 0.994 | 0.986 | 0.995 | 0.996 | 0.993 | 0.978 | 0.992 | 0.996 | 0.986 | 0.956 | 0.986 | |
| GSLV | 0.993 | 0.993 | 0.987 | 0.993 | 0.994 | 0.994 | 0.936 | 0.993 | 0.996 | 0.992 | 0.925 | 0.988 | 0.997 | 0.985 | 0.830 | 0.983 | |
| LRSID | 0.997 | 0.993 | 0.988 | 0.992 | 0.996 | 0.995 | 0.989 | 0.994 | 0.995 | 0.990 | 0.974 | 0.989 | 0.994 | 0.987 | 0.910 | 0.987 | |
| Proposed | 0.999 | 0.995 | 0.994 | 0.994 | 0.997 | 0.996 | 0.991 | 0.996 | 0.995 | 0.991 | 0.989 | 0.989 | 0.995 | 0.990 | 0.980 | 0.989 | |
| Image | Methods | r = 0.3, intensity = 40 | r = 0.5, intensity = [0, 50] | r = 0.7, intensity = [50, 100] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| = 2.55 | = 5.1 | = 2.55 | = 5.1 | = 2.55 | = 5.1 | ||||||||
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | ||
| IKONOS periodic stripes | Degrade | 21.27 | 0.480 | 21.10 | 0.471 | 22.13 | 0.541 | 21.92 | 0.527 | 12.23 | 0.154 | 12.21 | 0.154 |
| WAFT | 34.21 | 0.962 | 31.70 | 0.894 | 33.28 | 0.959 | 31.15 | 0.892 | 29.74 | 0.939 | 28.68 | 0.874 | |
| SLD | 33.95 | 0.958 | 31.42 | 0.889 | 34.16 | 0.964 | 31.54 | 0.896 | 28.26 | 0.920 | 27.32 | 0.853 | |
| GSLV | 32.68 | 0.961 | 30.88 | 0.894 | 32.36 | 0.951 | 30.24 | 0.884 | 31.55 | 0.960 | 30.48 | 0.890 | |
| LRSID | 33.76 | 0.965 | 32.63 | 0.943 | 34.60 | 0.967 | 33.21 | 0.945 | 29.39 | 0.949 | 28.87 | 0.927 | |
| Proposed | 38.81 | 0.971 | 35.68 | 0.947 | 38.54 | 0.971 | 35.57 | 0.948 | 37.27 | 0.968 | 34.91 | 0.945 | |
| IKONOS nonperiodic stripes | Degrade | 21.28 | 0.527 | 21.11 | 0.514 | 22.69 | 0.585 | 22.46 | 0.566 | 12.03 | 0.152 | 12.01 | 0.152 |
| WAFT | 31.14 | 0.949 | 29.71 | 0.884 | 34.92 | 0.961 | 32.07 | 0.894 | 23.95 | 0.916 | 23.65 | 0.854 | |
| SLD | 32.16 | 0.954 | 30.13 | 0.885 | 34.97 | 0.962 | 30.34 | 0.889 | 26.82 | 0.945 | 25.96 | 0.877 | |
| GSLV | 34.62 | 0.964 | 31.69 | 0.896 | 35.63 | 0.966 | 32.47 | 0.898 | 26.46 | 0.942 | 25.56 | 0.874 | |
| LRSID | 34.75 | 0.965 | 33.25 | 0.943 | 36.56 | 0.969 | 34.26 | 0.945 | 26.76 | 0.828 | 26.56 | 0.819 | |
| Proposed | 38.05 | 0.970 | 35.23 | 0.947 | 38.37 | 0.970 | 35.45 | 0.947 | 28.02 | 0.940 | 26.98 | 0.926 | |
| Image | Index | WAFT | SLD | GSLV | LRSID | Proposed |
|---|---|---|---|---|---|---|
| Terra MODIS band 34 | NR | 1.18 | 1.14 | 1.28 | 1.66 | 1.70 |
| MRD (%) | 1.82 | 1.56 | 4.00 | 2.29 | 1.97 | |
| Hyperion band 211 | NR | 3.69 | 3.45 | 3.97 | 4.65 | 4.00 |
| MRD (%) | 4.93 | 4.14 | 9.22 | 4.16 | 3.90 | |
| Terra MODIS band 33 | NR | 1.17 | 1.21 | 1.49 | 1.74 | 1.97 |
| MRD (%) | 1.15 | 1.21 | 2.21 | 1.28 | 1.44 | |
| Terra MODIS band 30 | NR | 3.04 | 3.02 | 3.19 | 3.87 | 3.97 |
| MRD (%) | 2.44 | 2.25 | 2.09 | 2.73 | 2.07 | |
| Aqua MODIS band 5 | NR | 1.90 | 1.06 | 1.79 | 2.66 | 3.17 |
| MRD (%) | 1.44 | 1.06 | 6.24 | 2.22 | 1.85 | |
| Aqua MODIS band 30 | NR | 7.64 | 4.85 | 7.84 | 8.27 | 8.92 |
| MRD (%) | 3.61 | 3.43 | 4.14 | 3.23 | 2.63 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Huang, T.-Z.; Zhao, X.-L.; Deng, L.-J.; Huang, J. Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint. Remote Sens. 2017, 9, 559. https://doi.org/10.3390/rs9060559
Chen Y, Huang T-Z, Zhao X-L, Deng L-J, Huang J. Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint. Remote Sensing. 2017; 9(6):559. https://doi.org/10.3390/rs9060559
Chicago/Turabian StyleChen, Yong, Ting-Zhu Huang, Xi-Le Zhao, Liang-Jian Deng, and Jie Huang. 2017. "Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint" Remote Sensing 9, no. 6: 559. https://doi.org/10.3390/rs9060559
APA StyleChen, Y., Huang, T. -Z., Zhao, X. -L., Deng, L. -J., & Huang, J. (2017). Stripe noise removal of remote sensing images by total variation regularization and group sparsity constraint. Remote Sensing, 9(6), 559. https://doi.org/10.3390/rs9060559