Specular Reflection Effects Elimination in Terrestrial Laser Scanning Intensity Data Using Phong Model

Abstract

The intensity value recorded by terrestrial laser scanning (TLS) systems is significantly influenced by the incidence angle. The incidence angle effect is an object property, which is mainly related to target scattering properties, surface structures, and even some instrumental effects. Most existing models focus on diffuse reflections of rough surfaces and ignore specular reflections, despite that both reflections simultaneously exist in all natural surfaces. Due to the coincidence of the emitter and receiver in TLS, specular reflections can be ignored at large incidence angles. On the contrary, at small incidence angles, TLS detectors can receive a portion of specular reflections. The received specular reflections can trigger highlight phenomenon (hot-spot effects) in the intensity data of the scanned targets, particularly those with a relatively smooth or highly-reflective surface. In this study, a new method that takes diffuse and specular reflections, as well as the instrumental effects into consideration, is proposed to eliminate the specular reflection effects in TLS intensity data. Diffuse reflections and instrumental effects are modeled by a polynomial based on Lambertian reference targets, whereas specular reflections are modeled by the Phong model. The proposed method is tested and validated on different targets scanned by the Faro Focus^3D 120 terrestrial scanner. Results imply that the coefficient of variation of the intensity data from a homogeneous surface is reduced by approximately 38% when specular reflections are considered. Compared with existing methods, the proposed method exhibits good feasibility and high accuracy in eliminating the specular reflection effects for intensity image interpretation and 3D point cloud representation by intensity.

1. Introduction

Terrestrial laser scanning (TLS) is a powerful technique for the spatial data acquisition and 3D characterization of different targets. This active remote sensing technique allows the direct, illumination-independent measurement of objects in a rapid, contactless, and accurate manner and has been increasingly adopted in various fields in the past two decades. In addition to the conventional precise 3D coordinates, TLS systems simultaneously measure the power of the backscattered laser signal of each scanned point and record it as an intensity value. The intensity value is the momentary amplitude of the return signal, which can be derived from the analog electrical signal output of the photodetector or digitized waveform [1]. Theoretically, surfaces of higher reflectance will reflect a greater portion of the incident laser radiation, thereby increasing the backscattered signal power and further the intensity [1]. Therefore, the intensity is a source of information closely associated with the reflectance properties of the scanned surface [2,3,4]. Intensity, which is insensitive to ambient light and shadowing [5], is initially used to improve point cloud separability. Apart from visualization purposes, intensity data can be used as a major or complementary data source in various studies, such as vegetation and forest investigation [6,7], road traffic marking identification [8,9], water content extraction [6,10,11,12,13], metro tunnel inspection [10,14], and lithological differentiation [5,15,16].

However, many confounding variables distort the capability of the original intensity to directly retrieve the target characteristics, of which the instrumental mechanism, atmospheric conditions, target surface properties, and data acquisition geometry plays a significant and dominant role [17,18]. During one campaign period, instrumental configurations are kept constant and atmospheric attenuation can be ignored. As such, the intensity data recorded by the same TLS system are predominantly influenced by the target reflectance, distance, and incidence angle [19]. In order to utilize the intensity for further applications, all influences not related to the material composing the scanned surface should be corrected [5]. A number of studies have been successfully conducted to derive a corrected intensity that is merely related to the scattering properties of the scanned target by correcting the effects of incidence angle and distance. The irregular TLS distance effect is strongly dominated by instrumental factors (e.g., aperture size, automatic gain control, amplifier for low-reflective surfaces, and a brightness reducer for near distances [1]) and differs significantly among different systems. The distance effect does not completely follow the inverse square range function from the radar range equation [18,19,20]. Empirically, the distance effect was satisfactorily corrected by a polynomial in [21] or based on reference targets in [19]. In this study, the polynomial method was adopted to eliminate the distance effect to obtain the distance-independent intensity value.

In contrast to the distance effect that mainly depends on instrumental properties, the incidence angle effect is related to target scattering properties and surface structure [22,23]. Theoretically, the incidence angle effect should be individually corrected in terms of target surface properties. To simplify the correction of the incidence angle effect, most existing methods assume that scanned surfaces are diffuse reflectors (i.e., Lambertian). Lambert’s cosine law is extensively used to correct the incidence angle effect, regardless of discrepancies in the surface characteristics of various targets [24,25,26]. However, natural surfaces do not behave as perfect Lambertian reflectors and Lambert’s cosine law leads to an over-correction of the intensity values at large incidence angles [5]. A number of reflection models are, therefore, proposed to optimize the Lambertian reflection model. To improve the accuracy of the correction of incidence angle effect, a revised model called the extended Lambertian reflection model was proposed in [22] to modify the contribution of incidence angle by changing the constant exponential value 1 to a parameter which describes the beam divergence. Considering that non-Lambertian behavior occurs in some natural surfaces, a model, which is a linear combination of the Lommel-Seeliger law pertaining to intrinsically dark surfaces and the Lambertian law related to brighter targets, was applied to correct the incidence angle effect in [17,20]. Based on the idea that the surface geometry can be modeled by a relief of multiple micro-facets, the Oren-Nayar model was adopted in [5] to correct the incidence angle effect of different rock outcrops. However, these models mainly take into account the diffuse reflections for matte and rough surfaces.

Theoretically, both diffuse and specular reflections exist in all natural surfaces [22,27]. The type of reflections influence the direction and strength of the backscattered light [26]. Specular reflections can be ignored for rough surfaces. However, for targets with a relatively smooth or glossy surfaces, highlight phenomena (i.e., hot-spot effects in remote sensing [28,29,30,31]) caused by the specular reflections may appear in the intensity data. Highlights are detrimental for 3D visualization of the point cloud and further applications (e.g., target recognition, classification, and feature extraction) based on intensity. In this study, a novel method that considers diffuse and specular reflections, as well as the instrumental effects, is proposed to eliminate the specular reflection effects (i.e., highlight phenomenon). The effects of diffuse reflections and instrumental properties on the incidence angle are the same as that of Lambertian targets and are modeled by a polynomial. Specular reflections are modeled by the Phong model. Compared with existing methods that ignore specular reflections and are only suitable for rough surfaces, the proposed method can be applied to all surfaces. This study specifically aims to:

• Explore the mechanism of the specular reflection effects in TLS intensity;
• Use the Phong model to eliminate the highlight phenomenon caused by specular reflections; and
• Propose a new method to estimate the parameters of the Phong model.

The rest of the study is organized as follows: The proposed method is illustrated in detail in Section 2. Section 3 outlines the experiments. Section 4 and Section 5 present the results and discussion, respectively. The conclusions are provided in Section 6.

2. Methodology

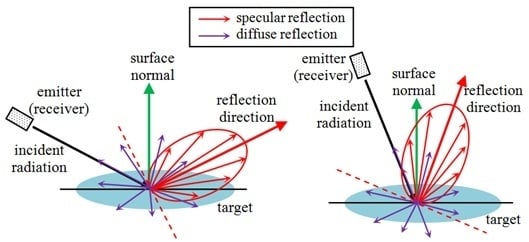
2.1. Specular Reflections and Highlight Phenomenon

The TLS sensor emits laser pulses, illuminates the surface objects, and records the returned laser pulse signals backscattered from the surface objects [32]. TLS backscattered light is significantly influenced by the surface scattering characteristics. If the scanned target is an ideal Lambertian reflector, pure diffuse reflection occurs. The entire surface reflects laser shots by Lambert’s cosine law and the incident ray is uniformly reflected to a hemisphere isotropically. The radiation observed from a Lambertian surface is directly proportional to the cosine of the angle between the observer’s viewing direction and the surface normal. Given that light paths from the emitter to the detector coincide in TLS, the received radiation is proportional to the cosine of the incidence angle $\mathsf{\theta }$ ($0\le \mathsf{\theta }\le \mathsf{\pi }/2$) [26]:

$${\mathrm{L}}_{\mathrm{d}}={\mathrm{L}}_{\mathrm{in}}\cos \mathsf{\theta }$$

(1)

where ${\mathrm{L}}_{\mathrm{d}}$ is the diffuse radiation received by the observer and ${\mathrm{L}}_{\mathrm{in}}$ is the incident radiation.

When a ray of light strikes a plane mirror (i.e., an ideal specular reflector), the incident ray reflects off the mirror. According to the law of reflection, the incidence and reflection angles are equal and are symmetrically distributed on two sides of the surface normal. However, for a generally-smooth surface constituted by multiple micro-facets with different orientations, specular reflections are distributed in the surroundings of the direction of reflection angle. When the viewpoint is within the vicinity of the direction of the reflection angle, strong specular reflection light can be received by the observer. On the contrary, specular light will be weak, or even disappear, when the viewpoint deviates significantly from the reflection direction [33].

The spatial distribution of specular reflections is directional. Specular reflection intensity depends on the intensity of the incident light and the surface material; it is also related with the viewing direction. Generally, the power function is used to simulate the spatial distribution of the specular reflections for a generally smooth surface [33], as shown by Equation (2):

$${\mathrm{L}}_{\mathrm{s}}={\mathrm{L}}_{\mathrm{in}}{\left(\cos \mathsf{\varphi }\right)}^{\mathrm{n}}$$

(2)

where ${\mathrm{L}}_{\mathrm{s}}$ is the specular radiation received by the observer, $\mathsf{\varphi }$ ($0\le \mathsf{\varphi }\le \mathsf{\pi }/2$) is the angle between the directions of specular reflection and observer, and $\mathrm{n}$ is the specular highlight coefficient which is related to the object surface glossiness [27]. Due to the coincidence of the positions of the emitter and detector, the angle between the directions of specular reflection and observer is the sum of the incidence and reflection angles, i.e., $\mathsf{\varphi }=2\mathsf{\theta }$. Therefore, Equation (2) can be written as:

$${\mathrm{L}}_{\mathrm{s}}={\mathrm{L}}_{\mathrm{in}}{\left(\cos 2\mathsf{\theta }\right)}^{\mathrm{n}}, 0\le \mathsf{\theta }\le \mathsf{\pi }/4$$

(3)

Actually, diffuse and specular reflections exist simultaneously on all natural surfaces [22,27]. There are no ideal specular or diffuse targets. Therefore, considering only diffuse reflections is not appropriate when both diffuse and specular reflections exist. The Phong model is a bidirectional reflectance distribution function (BRDF) model [34,35]. It describes the way that a surface reflects light as a combination in both diffuse and specular forms and has found wide application in computer graphics and 3D model rendering. In the study of [27], the Phong model was used to attenuate the effects of strong reflections that typically occur over wet or water-dominated areas scanned by airborne laser scanning. In this study, we adopted the Phong model to eliminate the highlight phenomenon in the TLS intensity data of smooth targets.

According to the Phong model [33], the total reflection radiation ${\mathrm{L}}_{\mathrm{t}}$ is a combination of diffuse and specular reflections for natural targets [22,27], as shown by Equation (4):

$${\mathrm{L}}_{\mathrm{t}}=\left(1-{\mathrm{k}}_{\mathrm{s}}\right)·{\mathrm{L}}_{\mathrm{d}}+{\mathrm{k}}_{\mathrm{s}}·{\mathrm{L}}_{\mathrm{s}}$$

(4)

where ${\mathrm{k}}_{\mathrm{s}}$ ($0\le {\mathrm{k}}_{\mathrm{s}}\le 1$) is the specular reflectance parameter which differs significantly for different targets. If ${\mathrm{k}}_{\mathrm{s}}=0$, the Phong model is completely equivalent to the Lambertian reflection model. On the contrary, the Phong model is exactly the same as the ideal specular reflection model when ${\mathrm{k}}_{\mathrm{s}}=0$. For natural surfaces, $0<{\mathrm{k}}_{\mathrm{s}}<1$.

According to Equation (3), at incidence angles larger than 45°, the laser receiver cannot receive specular reflections though it exists in all natural targets (Figure 1a). Only diffuse reflections reach the receiver. However, at incidence angles smaller than 45°, the received radiations include both diffuse and specular reflections (Figure 1b). The smaller the incidence angle is, more specular reflections can be received by the detector. If specular reflections are dominant over diffuse reflections, then highlight phenomena may exist in the intensity data. Highlight phenomena are those regions with small incidence angles that are brighter in the intensity image than those with large incidence angles where merely diffuse reflections can be received. Strictly, specular reflections should be considered in the intensity correction for all natural targets. ${\mathrm{k}}_{\mathrm{s}}$ is usually small for rough targets. As shown in Figure 2a, the diffuse reflections are nearly the same as the total reflections even at small incidence angles. This explains why Lambertian model can be used to approximately correct the incidence angle effect for rough targets [25]. However, specular reflections of smooth surfaces are much larger than diffuse reflections at incidence angles smaller than 45° and must be considered to eliminate the highlight phenomenon (Figure 2b).

2.2. Physical Background of TLS Intensity

The TLS intensity value is theoretically a function of target reflectance $\mathsf{\rho }$, incidence angle $\mathsf{\theta }$, and distance $\mathrm{R}$. According to the Lambert’s cosine law and radar range equation, the intensity value $\mathrm{I}$ can be expressed as [26]:

$$\mathrm{I}\propto \mathsf{\rho }·\cos \mathsf{\theta }·{\mathrm{R}}^{-2}$$

(5)

However, the scattering behaviors of most natural surfaces do not exhibit Lambertian attributes. Additionally, intensity measurement is generally intended to enhance range determination; the raw values of the intensity signal can be modified to obtain an optimal range value [18,36]. The range-dependent inverse square model from the radar range equation is insufficient to estimate the accurate intensity at the entire range scale. Considering the fact that the incidence angle and distance effects are theoretically independent of each other and can be solved individually [24], the intensity is written as [19,21]:

$$\mathrm{I}={\mathrm{f}}_1\left(\mathsf{\rho }\right)·{\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)·{\mathrm{f}}_3\left(\mathrm{R}\right)$$

(6)

where ${\mathrm{f}}_1\left(\mathsf{\rho }\right)$, ${\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)$, and ${\mathrm{f}}_3\left(\mathrm{R}\right)$ are functions of reflectance, cosine of incidence angle, and distance, respectively. Therefore, the corrected intensity ${\mathrm{I}}_{\mathrm{s}}$ that is merely related to the target reflectance can be expressed as:

$${\mathrm{I}}_{\mathrm{s}}={\mathrm{f}}_1\left(\mathsf{\rho }\right)·{\mathrm{f}}_2\left(\cos {\mathsf{\theta }}_{\mathrm{s}}\right)·{\mathrm{f}}_3\left({\mathrm{R}}_{\mathrm{s}}\right)$$

(7)

where ${\mathsf{\theta }}_{\mathrm{s}}$ and ${\mathrm{R}}_{\mathrm{s}}$ are the reference incidence angle and distance, respectively. ${\mathsf{\theta }}_{\mathrm{s}}$ and ${\mathrm{R}}_{\mathrm{s}}$ can be arbitrarily defined [19].

By dividing Equations (6) and (7), we obtain [3]:

$${\mathrm{I}}_{\mathrm{s}}=\mathrm{I}·\frac{{\mathrm{f}}_2\left(\cos {\mathsf{\theta }}_{\mathrm{s}}\right)·{\mathrm{f}}_3\left({\mathrm{R}}_{\mathrm{s}}\right)}{{\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)·{\mathrm{f}}_3\left(\mathrm{R}\right)}={\mathrm{I}}_{\mathrm{d}}·\frac{{\mathrm{f}}_2\left(\cos {\mathsf{\theta }}_{\mathrm{s}}\right)}{{\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)}={\mathrm{I}}_{\mathrm{a}}·\frac{{\mathrm{f}}_3\left({\mathrm{R}}_{\mathrm{s}}\right)}{{\mathrm{f}}_3\left(\mathrm{R}\right)}$$

(8)

Distance-corrected intensity ${\mathrm{I}}_{\mathrm{d}}$ and incidence angle-corrected intensity ${\mathrm{I}}_{\mathrm{a}}$ are expressed as [3]:

$$\{\begin{array}{l}{\mathrm{I}}_{\mathrm{d}}=\mathrm{I}·\frac{{\mathrm{f}}_3\left({\mathrm{R}}_{\mathrm{s}}\right)}{{\mathrm{f}}_3\left(\mathrm{R}\right)}={\mathrm{f}}_1\left(\mathsf{\rho }\right)·{\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)·{\mathrm{C}}_1\\ {\mathrm{I}}_{\mathrm{a}}=\mathrm{I}·\frac{{\mathrm{f}}_2\left(\cos {\mathsf{\theta }}_{\mathrm{s}}\right)}{{\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)}={\mathrm{f}}_1\left(\mathsf{\rho }\right)·{\mathrm{f}}_3\left(\mathrm{R}\right)·{\mathrm{C}}_2\end{array}$$

(9)

where ${\mathrm{C}}_1={\mathrm{f}}_3\left({\mathrm{R}}_{\mathrm{s}}\right)$ and ${\mathrm{C}}_2={\mathrm{f}}_2\left(\cos {\mathsf{\theta }}_{\mathrm{s}}\right)$ are two constants. Empirically, the distance and incidence angle effects were satisfactorily corrected by polynomials in [21] or by using reference targets in [19]. In this study, we aimed to eliminate the highlight phenomena that are merely related to the incidence angle effect. First of all, the original intensity is corrected by a polynomial, i.e., ${\mathrm{f}}_3\left(\mathrm{R}\right)={\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_3}\left({\mathsf{\beta }}_{\mathrm{i}}·{\mathrm{R}}^{\mathrm{i}}\right)$, where ${\mathsf{\beta }}_{\mathrm{i}}$ and ${\mathrm{N}}_3$ are polynomial coefficients, to eliminate the influence of the distance effect and obtain the distance corrected intensity ${\mathrm{I}}_{\mathrm{d}}=\mathrm{I}·\frac{{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_3}\left({\mathsf{\beta }}_{\mathrm{i}}·{\mathrm{R}}_{\mathrm{s}}^{\mathrm{i}}\right)}{{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_3}\left({\mathsf{\beta }}_{\mathrm{i}}·{\mathrm{R}}^{\mathrm{i}}\right)}$. ${\mathrm{I}}_{\mathrm{d}}$ only depends on the reflectance and incidence angle, as shown by the right part of the first equation of Equation (9).

2.3. Proposed Method

Previous studies [19,21] have indicated that, even for pure Lambertian targets, Lambert’s cosine law cannot be applied to correct the incidence angle effect because some commercial undisclosed instrumental effects may be mixed with the incidence angle effect. For natural surfaces, the incidence angle effect is, therefore, a combination of diffuse reflections, instrumental effects, and specular reflections. According to the first equation of Equation (9), the distance-corrected intensity ${\mathrm{I}}_{\mathrm{d}}$ can be expressed as:

$${\mathrm{I}}_{\mathrm{d}}={\mathrm{C}}_1·{\mathrm{f}}_1\left(\mathsf{\rho }\right)·{\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)={\mathrm{K}}_0·\left({\mathrm{I}}_{\mathrm{diffuse}}+{\mathrm{I}}_{\mathrm{instrument}}+{\mathrm{I}}_{\mathrm{specular}}\right)$$

(10)

where ${\mathrm{K}}_0={\mathrm{C}}_1·{\mathrm{f}}_1\left(\mathsf{\rho }\right)$ is a parameter related to target reflectance; ${\mathrm{I}}_{\mathrm{diffuse}}$, ${\mathrm{I}}_{\mathrm{instrument}}$, and ${\mathrm{I}}_{\mathrm{specular}}$ are intensity values caused by diffuse reflections, instrumental effects, and specular reflections, respectively.

The diffuse reflections of a natural target are the same as that of a Lambertian target. Instrumental effects do not depend on target characteristics and are exactly the same for all scanned targets. Therefore, the former two parts of the right side of Equation (10) can be modeled by using a reference Lambertian target. Unfortunately, the specific instrumental effects are confidential due to commercial purposes and may differ significantly among different scanners. Regardless of what the specific instrumental effects are, a polynomial can be used to approximate the total effects of diffuse reflections and instrumental properties based on the Weierstrass approximation theorem [36]. It should be noted that specular reflections should only be considered when incidence angles are smaller than 45°. Thus, Equation (10) can be further written as:

$${\mathrm{I}}_{\mathrm{d}}=\{\begin{array}{c}{\mathrm{K}}_0·\left[{{\displaystyle \sum }}_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos \mathsf{\theta }\right)}^{\mathrm{i}}+{\mathrm{k}}_{\mathrm{s}}{\cos }^{\mathrm{n}}\left(2\mathsf{\theta }\right)\right],\mathsf{\theta }\le {45}^{°}\\ {\mathrm{K}}_0·\left[{{\displaystyle \sum }}_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos \mathsf{\theta }\right)}^{\mathrm{i}}\right],\mathsf{\theta }>{45}^{°}\end{array}$$

(11)

The polynomial parameters ${\mathsf{\alpha }}_{\mathrm{i}}$, ${\mathsf{\beta }}_{\mathrm{i}}$, ${\mathrm{N}}_2$, and ${\mathrm{N}}_3$ are the same for all targets and can be estimated by some Lambertian targets scanned at various incidence angles and distances. The estimation method is introduced in detail in [36]. On the contrary, specular reflections depend on object surface smoothness and material. Consequently, ${\mathrm{k}}_{\mathrm{s}}$ and $\mathrm{n}$ should be determined individually.

The parameters ${\mathrm{k}}_{\mathrm{s}}$ and $\mathrm{n}$ were iteratively optimized within a homogeneous regions in [22] or empirically determined according to the data itself in [27]. Considering that Equation (11) is a piecewise function and the first equation of Equation (11) is nonlinear, we proposed to estimate the polynomial parameters and specular reflection coefficients separately. Datasets of a certain surface with incidence angles both smaller and larger than 45° should be sampled. According to the second equation of Equation (11), ${\mathrm{K}}_0={\mathrm{I}}_{\mathrm{d}}/[{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos \mathsf{\theta }\right)}^{\mathrm{i}}]$ can be calculated by using the sub-datasets with incidence angles larger than 45° where no specular reflections exist in the intensity data. Then, the intensity value at incidence angles smaller than 45° that is resulted from diffuse reflections and instrumental effects can be determined by the estimated polynomial. By subtracting the distance corrected intensity ${\mathrm{I}}_{\mathrm{d}}$ with the value of the polynomial, ${\mathrm{I}}_{\mathrm{specular}}$ can be estimated, as shown by Equation (12):

$${\mathrm{K}}_0·{\mathrm{k}}_{\mathrm{s}}{\cos }^{\mathrm{n}}\left(2\mathsf{\theta }\right)=\mathrm{M},\mathsf{\theta }\le {45}^{°}$$

(12)

where $\mathrm{M}={\mathrm{I}}_{\mathrm{d}}-{\mathrm{K}}_0·{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos \mathsf{\theta }\right)}^{\mathrm{i}}$.

To estimate the parameters of the Phong model, natural logarithms can be conducted on the two sides of Equation (12). Thus, Equation (12) can be written as:

$${\log }_{\mathrm{e}}\left(\mathrm{K}\right)+\mathrm{n}·{\log }_{\mathrm{e}}\left[\cos \left(2\mathsf{\theta }\right)\right]={\log }_{\mathrm{e}}\left(\mathrm{M}\right)$$

(13)

where $\mathrm{e}$ is the Euler’s number and $\mathrm{K}={\mathrm{K}}_0·{\mathrm{k}}_{\mathrm{s}}$. Equation (13) can be further written as:

$$\left[\begin{array}{cc}1& {\log }_{\mathrm{e}}\left[\cos \left(2\mathsf{\theta }\right)\right]\end{array}\right]·\left[\begin{array}{c}{\log }_{\mathrm{e}}\left(\mathrm{K}\right)\\ \mathrm{n}\end{array}\right]-{\log }_{\mathrm{e}}\left(\mathrm{M}\right)=0$$

(14)

By conducting indirect adjustment of Equation (14) using the sub-datasets with incidence angles smaller than 45°, the parameter ${\mathrm{X}}^{\mathrm{T}}={\left[{\log }_{\mathrm{e}}\left(\mathrm{K}\right),\mathrm{n}\right]}^{\mathrm{T}}={\left({\mathbf{B}}^{\mathrm{T}}·\mathbf{B}\right)}^{-1}·{\mathbf{B}}^{\mathrm{T}}·\mathbf{L}$ can be estimated where $\mathbf{B}$ and $\mathbf{L}$ are the matrix forms of $\left[\begin{array}{cc}1& {\log }_{\mathrm{e}}\left[\cos \left(2\mathsf{\theta }\right)\right]\end{array}\right]$ and ${\log }_{\mathrm{e}}\left(\mathrm{M}\right)$, respectively. Finally, the distance-corrected intensity can be further corrected for the incidence angle effect by the polynomial method according to the third part of Equation (8), as shown by Equation (15):

$${\mathrm{I}}_{\mathrm{s}}=\{\begin{array}{c}\left[{\mathrm{I}}_{\mathrm{d}}-\mathrm{K}{\cos }^{\mathrm{n}}\left(2\mathsf{\theta }\right)\right]·\frac{{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos {\mathsf{\theta }}_{\mathrm{s}}\right)}^{\mathrm{i}}}{{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos \mathsf{\theta }\right)}^{\mathrm{i}}},\mathsf{\theta }\le {45}^{°}\\ {\mathrm{I}}_{\mathrm{d}}·\frac{{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos {\mathsf{\theta }}_{\mathrm{s}}\right)}^{\mathrm{i}}}{{\sum }_{\mathrm{i}=0}^{{\mathrm{N}}_2}{\mathsf{\alpha }}_{\mathrm{i}}{\left(\cos \mathsf{\theta }\right)}^{\mathrm{i}}},\mathsf{\theta }>{45}^{°}\end{array}$$

(15)

The distance is calculated with the original 3D geometric coordinates of the scanned point and the scanner center. The surface normal is estimated by the best-fitting plane to a neighborhood of points surrounding the point of interest, and then the cosine of the incidence angle can be calculated by the incident radiation vector and the surface normal vector [21,36].

3. Experiments

Experiments on a wooden door in a laboratory were designed to validate the proposed method. The door, with a size of approximately 2 m × 1.4 m, is painted dark brown and surrounded by white lime walls. The surface of the door is smooth, whereas that of the wall is relatively rough. Experiments were conducted under indoor conditions through the use of the Faro Focus^3D 120, (FARO Technologies, Inc., Orlando, FL, USA) which delivers geometric information and returns intensity values recorded in 11 bits [0, 2048]. Faro Focus^3D 120 is a continuous-wave 905 nm terrestrial laser scanner. The maximum distance is 120 m and the field-of-view is 360° × 305°. The beam divergence and the circular beam diameter at the exit are 0.009° and 3.8 mm, respectively.

During the scanning period, all lights in the room were turned off and all curtains were pulled down to create a dark environment. This can avoid unnecessary errors from ambient light to make the results convincing and rigorous, although TLS intensity is insensitive to ambient light. The scan quality and scan resolution were set to 4 and 1/4, respectively. The scanner was moved from left to right with a total of five scans. The original intensity data were extracted in a point cloud image created by the standard software Faro SCENE 4.8. In our previous studies [21,36], the polynomial parameters of ${\mathrm{f}}_2\left(\cos \mathsf{\theta }\right)$ and ${\mathrm{f}}_3\left(\mathrm{R}\right)$ for the Faro Focus^3D 120 were calculated by some Lambertian targets scanned at various incidence angles and distances (

Table 1. Polynomial parameters for Faro Focus^3D 120.

${\mathsf{\alpha }}_0$	${\mathsf{\alpha }}_1$	${\mathsf{\alpha }}_2$	${\mathsf{\alpha }}_3$
2.41	2.27	−2.42	1
${\mathsf{\beta }}_0$	${\mathsf{\beta }}_1$	${\mathsf{\beta }}_2$	${\mathsf{\beta }}_3$	${\mathsf{\beta }}_4$
3.71 × 109	−7.23 × 108	2.90 × 108	−5.20 × 107	4.92 × 106
${\mathsf{\beta }}_5$	${\mathsf{\beta }}_6$	${\mathsf{\beta }}_7$	${\mathsf{\beta }}_8$
−2.66 × 105	8.33 × 103	−140.91	1

). In this study, ${\mathsf{\theta }}_{\mathrm{s}}$ and ${\mathrm{R}}_{\mathrm{s}}$ were chosen as 0° and 5 m, respectively.

4. Results

The original intensity images of the five scans created by Faro SCENE are shown in Figure 3. Obviously, Scans 2 and 3 present a significant bright region (highlights) on the door because the incident ray is perpendicular to the bright region and the surface of the door is relatively smooth. On the contrary, Scans 1, 4, and 5 do not have apparent highlight regions because the incident radiation is perpendicular to the white lime wall whose surface is relatively rough. Datasets of the door with incidence angles from 0° to 76° were sampled. Firstly, the original intensity data were corrected for the distance effect by the polynomial method according to Equation (9) and the parameters in Table 1. As shown in Figure 4, the mean distance corrected intensity values for 0.5° bin sizes, were used to estimate the parameters of the proposed method. The sub-datasets with incidence angles larger than 45° were used to estimate ${\mathrm{K}}_0$. ${\mathrm{K}}_0$ was estimated as 484.86. Then, the theoretical intensity values of the polynomial at incidence angles smaller than 45° can be calculated. As shown in Figure 4a, the distance corrected intensity values of the door at incidence angles smaller than 45° (particularly smaller than 15°) deviate significantly from the curve of the polynomial. By subtracting the polynomial values (red line in Figure 4a) with the distance corrected intensities, ${\mathrm{I}}_{\mathrm{specular}}$ can be estimated. Finally, according to Equation (14), $\left[{\log }_{\mathrm{e}}\left(\mathrm{K}\right),\mathrm{n}\right]$ was estimated as [215.06, 16.55] and ${\mathrm{k}}_{\mathrm{s}}$ = 0.44.

With the obtained parameters of the Phong model, the curve of the first equation of Equation (11) (i.e., the curve of the sum of the polynomial and Phong model) can be drawn, as shown in Figure 4a. Apparently, the curve of the sum of the polynomial and Phong model fits optically with the distance corrected intensities at incidence angles smaller than 45°, whereas the curve of the polynomial can fit the intensities at incidence angles larger than 45°. This result proves the feasibility of our proposed method. Similarly, datasets of the white lime wall with incidence angles from 0° to 68° were sampled. The mean distance corrected intensity values for 0.5° bin sizes are shown in Figure 4b. ${\mathrm{K}}_0$ was estimated as 556.12 for the white lime wall. However, the distance-corrected intensity values are distributed closely around the curve of the polynomial at the entire scale of the incidence angles. This result indicates that the specular reflections of the wall are subtle and can be ignored; it also explains why there were no highlight regions when the incident ray was perpendicular to the white wall in Scans 1, 4, and 5.

Door data in Scans 2 and 3 were manually sampled using the polygon selector tool from the planar view in Faro SCENE to test the proposed method. The correction results are shown in Figure 5. The polynomial and reference targets methods were also used to correct the intensities, as shown in Figure 5b,c,f,g. However, the polynomial and reference targets methods failed to eliminate the specular reflection effects both in Scans 2 and 3. On the contrary, the highlight phenomenon was effectively eliminated by the proposed method, as shown in Figure 5d,h. The coefficient of variation ($\mathrm{CV}$), namely, the ratio of the values of standard deviation ($\mathsf{\sigma }$) and mean ($\overline{\mathrm{u}}$) [22,26], can indicate the degree of dispersion of the intensity values from a homogenous target. The variation rate of $\mathrm{CV}$, i.e., $\mathsf{\delta }=\left({\mathrm{CV}}_{\mathrm{ori}}-{\mathrm{CV}}_{\mathrm{cor}}\right)/{\mathrm{CV}}_{\mathrm{ori}}$, where ${\mathrm{CV}}_{\mathrm{ori}}$ and ${\mathrm{CV}}_{\mathrm{cor}}$ are the coefficient of variations of the original and corrected intensities, respectively, was used to quantitatively evaluate the correction results. The statics of the intensities are shown in

Table 2. Statics of intensity values of the door.

Scan 2	$\overline{\mathbf{u}}$	$\mathsf{\sigma }$	$\mathbf{C}\mathbf{V}/\mathsf{\delta } (\%)$	Scan 3	$\overline{\mathbf{u}}$	$\mathsf{\sigma }$	$\mathbf{C}\mathbf{V}/\mathsf{\delta } (\%)$
Original	1499	83.87	5.60/-	Original	1558	85.50	5.49/-
${\mathbf{I}}_{\mathbf{d}}$	1560	89.03	5.71/−1.78	${\mathbf{I}}_{\mathbf{d}}$	1616	90.56	5.60/−2.00
Polynomial	1572	84.07	5.35/4.46	Polynomial	1623	86.60	5.34/2.73
Reference Targets	1570	84.79	5.40/3.57	Reference Targets	1622	87.17	5.37/2.19
Proposed	1541	58.54	3.80/32.14	Proposed	1565	51.14	3.27/40.44

. In Scan 2, $\mathrm{CV}$ is 5.60% for the original intensities. It significantly decreases to 3.80% ($\mathsf{\delta }$ = 32.14%) for the intensities corrected by the proposed method. However, $\mathrm{CV}$ is 5.35% ($\mathsf{\delta }$ = 4.46%) and 5.40% ($\mathsf{\delta }$ = 3.57%) for the intensities corrected by the polynomial and reference targets methods, respectively, which changes slightly compared with that of the original intensities. This result indicates that the polynomial and reference targets methods are invalid for the regions with incidence angles smaller than 45°, i.e., these two methods cannot eliminate the highlight phenomenon caused by specular reflections. Similar results can be obtained for Scan 3, as shown in Table 2.

5. Discussion

Smooth surfaces (e.g., water [27], leaves [7], metal, and rubber products) widely exist in TLS scenarios and, thus, the elimination of specular reflection effects is highly important. To better validate the proposed method, a plastic curtain, a building facade decorated with small square ceramic tiles, a plywood door, a marble wall, an iron bookcase, and a rubber decorative board scanned by the Faro Focus^3D 120 terrestrial scanner were chosen for further analysis (Figure 6). Datasets of these six surfaces were sampled. The distance corrected intensity values of the sampled datasets of these six surfaces are shown in Figure 7. Similar to the parameter estimation of the door, the parameters of the proposed method of these six surfaces were estimated (

Table 3. Parameters of the proposed method for the seven experimental targets.

	${\mathbf{K}}_0$	${\mathbf{k}}_{\mathbf{s}}$	$\mathbf{n}$
Door	484.86	0.44	16.55
Curtain	445.08	0.61	81.74
Building facade	446.32	0.42	22.44
Plywood	516.47	0.37	31.38
Marble	538.41	0.48	117.26
Bookcase	503.28	0.60	62.83
Rubber board	529.56	0.42	108.41

). As expected, parameters of the seven targets differ significantly. This result indicates that parameters of the proposed method for different targets need to be individually estimated. The specular reflectance parameters (${\mathrm{k}}_{\mathrm{s}}$) of the door, curtain, building facade, plywood, marble, bookcase, and rubber are 0.44, 0.61, 0.42, 0.37, 0.48, 0.60, and 0.42, respectively. This means that the specular reflections account for 44%, 61%, 42%, 37%, 48%, 60%, and 42% of the overall reflections for the seven targets. As shown in Figure 7, the distance-corrected intensity values of the six surfaces at incidence angles smaller than 45° deviate significantly from the curves of the polynomials. The curves of the sum of the polynomial and Phong model for the six surfaces fit optically with the distance-corrected intensities at incidence angles smaller than 45°, whereas that of the polynomials fit the intensity values at incidence angles larger than 45°. It is also worth noticing that the thresholds of the incidence angles from which the distance corrected intensities start to deviate significantly from the polynomial differ significantly. The thresholds of the incidence angles are approximately 15°, 5°, 12°, 10°, 8°, 9°, and 6° for the door, curtain, building facade, plywood, marble, bookcase, and rubber, respectively.

The point clouds in the red dotted rectangles in Figure 6 were sampled to test the proposed method. The results are shown in Figure 8. The polynomial and reference targets methods are still invalid for these six surfaces. The mean values of $\mathsf{\delta }$ for the polynomial and reference targets methods for the experimental targets are approximately 3.78% and 3.04%, respectively. Conversely, the proposed method can effectively correct the intensities of the highlight regions on these six surfaces. The values of $\mathsf{\delta }$ when different parameters were used to eliminate the highlight phenomenon are shown in

Table 4. Values of $\mathsf{\delta }$ (%) when parameters of one surface (row) were used to eliminate highlight phenomena of another surface (column).

	Curtain	Building	Plywood	Marble	Bookcase	Rubber
Curtain	4.88	2.85	3.66	4.78	4.27	4.57
Building	14.95	18.64	18.03	15.25	11.86	16.64
Plywood	10.62	10.23	11.00	10.04	9.85	9.46
Marble	60.89	41.94	53.23	61.29	51.21	60.08
Bookcase	69.63	32.23	40.14	64.48	69.98	57.90
Rubber	33.93	44.64	48.21	51.07	10.36	62.50

. The values of $\mathsf{\delta }$ for the proposed method with optimal parameters are 4.88%, 18.64%, 11.00%, 61.29%, 69.98%, and 62.50% for the six surfaces. However, as expected the parameters of one surface are not suitable for another surface, i.e., the values on the diagonal are the largest among each column in Table 4. These results indicate that the parameters of the proposed method for different targets should be individually estimated based on the surface characteristics.

6. Conclusions

This study presents a new method to eliminate the specular reflection effects in the intensity data of smooth surfaces. By considering the effects of diffuse reflections, instrumental properties, and specular reflections, the incidence angle effect can be accurately corrected. The coefficients of variation of the intensity data are reduced by approximately 37.61%, 3.78%, and 3.04% for the proposed, polynomial, and reference targets methods, respectively. Since glossy or highly-reflective surfaces widely exist in TLS scenarios, elimination of specular reflection effects is inevitable and the proposed method can be used for applications (e.g., cultural relics modeling and preservation [20,37,38], point cloud supervision classification, and 3D visualization) based on TLS intensity data. To avoid the influence of specular reflection effects in the intensity data of smooth surfaces, a feasible way is to scan the target at large incidence angles, i.e., perpendicular scanning, is not preferred. However, large incidence angles may lead to poor quality point clouds [39]. Therefore, this topic should be studied further.

Compared with existing methods which do not consider specular reflections, the proposed method is suitable for all natural surfaces. For rough surfaces whose specular reflections are relatively subtle, the second equation of Equation (15) with uniform parameters can be approximately applied to correct the incidence angle effect without considering the differences in surface characteristics. On the contrary, the parameters of the proposed method for glossy targets should be individually estimated based on the surface characteristics. By sampling datasets with incidence angles both smaller and larger than 45°, the parameters of a certain target can be easily determined by two steps as stated in Section 2.

The Faro phase-based scanner was used to test the proposed method in this study. Theoretically, the incidence angle effect on intensity of all targets is a combination of diffuse reflections, specular reflections, and instrumental effects. For different scanners from other manufacturers, or using time-of-flight ranging methods, instrumental effects on intensity may be different. Therefore, the polynomial parameters ${\mathrm{N}}_2$ and ${\mathsf{\alpha }}_{\mathrm{i}}$ may be different. Regardless of the types and manufacturers of the scanners, the proposed method can be applied to other terrestrial laser scanners. However, this should be further tested and validated. Empirically, the scanned data of Faro Focus^3D 120 above 30 m are unreliable in practical applications because of the low accuracy, large amount of noise, and high level of uncertainty, although the theoretical maximum distance is 120 m [3]. The parameters of ${\mathrm{f}}_3\left(\mathrm{R}\right)$ in our previous studies [21,36] were estimated by some Lambertian targets scanned at various distances below 30 m. Therefore, the polynomial parameters of ${\mathrm{f}}_3\left(\mathrm{R}\right)$ in Table 1 are suitable for targets scanned at distances below 30 m. However, it should be noted that the proposed method can be theoretically applied to arbitrary distances if the parameters of ${\mathrm{f}}_3\left(\mathrm{R}\right)$ are estimated by Lambertian targets scanned within the entire scanning range scale.