Towards Systematic Prediction of Urban Heat Islands: Grounding Measurements, Assessing Modeling Techniques

Abstract

While there exists extensive assessment of urban heat, we observe myriad methods for describing thermal distribution, factors that mediate temperatures, and potential impacts on urban populations. In addition, the limited spatial and temporal resolution of satellite-derived heat measurements may limit the capacity of decision makers to take effective actions for reducing mortalities in vulnerable populations whose locations require highly-refined measurements. Needed are high resolution spatial and temporal information for urban heat. In this study, we ask three questions: (1) how do urban heat islands vary throughout the day? (2) what statistical methods best explain the presence of temperatures at sub-meter spatial scales; and (3) what landscape features help to explain variation in urban heat islands? Using vehicle-based temperature measurements at three periods of the day in the Pacific Northwest city of Portland, Oregon (USA), we incorporate LiDAR-derived datasets, and evaluate three statistical techniques for modeling and predicting variation in temperatures during a heat wave. Our results indicate that the random forest technique best predicts temperatures, and that the evening model best explains the variation in temperature. The results suggest that ground-based measurements provide high levels of accuracy for describing the distribution of urban heat, its temporal variation, and specific locations where targeted interventions with communities can reduce mortalities from heat events.

1. Introduction

In the US and many other industrialized countries, heat events account for more than all other natural hazards combined [1,2]. Urban populations are especially susceptible to heat stress due to the high density of human habitation and the spatial variability in temperatures that result in microclimates [3,4]. An increasing urban population [5] and greater heat trapped in the atmosphere make relatively certain that larger populations of people across the wider latitudes will experience extreme heat stress. Indeed, based on the combination of several large-scale climate models, Meehl and Tebaldi (2004) [6] predict that extreme heat events “will become more intense, more frequent, and longer lasting in the second half of the 21st century”. A warming of urban climate has far-reaching implications on the approaches to identifying the hottest areas of cities, and those communities who may suffer fatalities during heat waves.

Urban heat islands (UHIs) are a common phenomenon that have been studied and documented since the early 19th century [7]. Modern advances in data capture and analysis seem to have increased interest in the subject, with calls for greater resolution and direct public action [8,9]. While numerous cities have empirically documented UHIs, the extant literature suggests extensive variation in the processes, descriptions, and measurements for capturing heat data, and their methods of assessment. The most prominent approach is the use of satellite-based methods, which draw on the extensive availability of datasets for virtually every city on the planet [10,11,12]. The satellite platforms provide direct measurement of UHI through specific sensors that are placed on the satellite. The most common sources for satellite-based temperature data are Landsat and Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER). While satellite imagery from Landsat and ASTER provide measures of surface-level temperature at varying resolutions, subsequent statistical analysis with land cover offers insights about the role of urban form that helps to explain the distribution of temperatures across the study region [13,14,15,16].

Integrating satellite imagery with land cover data offers numerous opportunities to diagnose potential contributions of physical landscape features that create UHIs. While abundantly available, and relatively inexpensive, satellite-based approaches to describe UHIs face several challenges. First, they are limited in terms of the spatial and temporal resolution of the datasets. The current Landsat platform, Landsat 8 Operational Land Imager (OLI) and Thermal Infrared Sensor (TIRS), has a spatial resolution of 100 m in its thermal infrared datasets, and a temporal resolution of 16 days; ASTER’s thermal infrared bands have a spatial resolution of 90 m and a temporal resolution of 16 days. UHIs, however, impact vulnerable populations at the parcel level, and with 90 m pixels, these descriptions are often too coarse to take mitigative and/or preventative actions [17]. Second, due to the long time periods between data capture, Landsat and ASTER temperature data are not able to describe changes in a city’s UHI throughout a day, which is necessary for understanding how fast specific areas of the city heat and cool. The 16-day intervals for satellite flights, furthermore, prevent systematic evaluations over a multi-day heat wave in a specific location. Relying on the available data can constrain, indeed, overlook the variations in temperatures throughout each day (i.e., 24-h period), and over a multi-day heat wave. Higher resolution techniques for characterizing UHIs are needed, especially for developing public policies that aim to reduce impacts to the public’s health [8].

Alternative approaches to satellite-based measurements of urban temperatures were first used in the 1960s, and consisted of ground-based collection of temperatures [18]. Ground-based methods offer advantages over satellite-based data collection of urban heat, because they capture temperatures on the ground where people experience the heat waves, as opposed to satellite readings, which reflect the surface temperatures. Surface temperatures based on satellite measurements are often much hotter than the ambient environment, because they reflect readings from roofs of buildings, and the surface of asphalt and roads [19]. The collection of ambient temperatures, on the contrary, uses ‘vehicular-based traverses’ that contain highly sensitive temperature sensors, and can provide accurate readings throughout the day [20,21,22,23,24]. Limitations to traverse-based UHI analysis include data collection only being possible in areas that are accessible by vehicle. Due to this, a continuous surface of temperatures must be modeled based on site variables and predicted, as opposed to the direct measurement available through remote sensing techniques. Aside from potential error introduced during modeling, this ground-based approach provides several advantages that complement publically available satellite data, including: (1) the ability to develop UHI models that describe variation in temperatures throughout the day by location; (2) descriptions of ambient temperature readings that are consistent with human exposure to heat; and (3) the creation of models that describe specific landscape features that help to explain temperatures at highly resolved spatial scales. The emergence of GPS and highly accurate temperature measuring instruments offers an immediate and effective technique for characterizing UHIs and the factors that help to explain variations [21,24].

Currently missing from ground-based approaches, however, is the ability to identify landscape characteristics that are amenable to change and modification, which could be of direct relevance to public policy, urban planning, and public health organizations. Aligning ambient temperature data collection and analysis to support the mitigation of extreme heat is essential for reducing fatalities from urban heat waves. We note that planning organizations often focus on physical design and urban form that can potentially contribute to UHIs, while public health organizations are responsible for outreach and prevention of fatalities during heat events. Together these two agencies are often the front line for reducing excess mortality and morbidity [9].

Our research aims to improve the spatial and temporal resolution of describing variations in urban temperatures, specifically UHI, while identifying landscape features that can be modified for reducing extreme microclimates. We ask three research questions: (1) how do urban heat islands vary in location throughout the day? (2) what statistical methods best explain the presence of temperatures at sub-neighborhood spatial scales; and (3) what landscape features help to explain variation in urban heat islands? We build on the extant traverse-based methods, incorporating high spatial resolution LiDAR-derived datasets to describe the landscape features. We further evaluate three statistical techniques for modeling and predicting variation in temperatures during a heat wave. We begin with a description of our methods, including data and processing, and follow with our results. Since one of the primary purposes of the present study is to provide guidance for reducing excess mortality and morbidity from heat waves, we conclude with a description of opportunities for improving public policy.

2. Materials and Methods

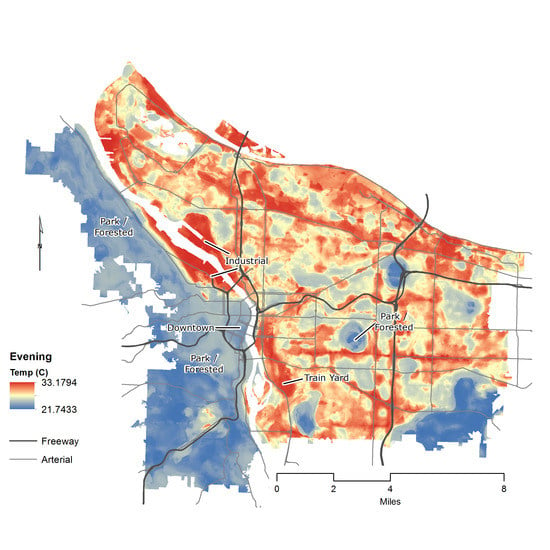
2.1. Study Area

Our study area is the City of Portland, a mid-size city covering approximately 376 km², with a population of ~619,000, located in the Pacific Northwest state of Oregon (USA, Figure 1). The city is in a temperate climate, with rainy winters and warm, increasingly hot and relatively dry summers. The Cascade Mountain Range is located 70 km to the east, and the Pacific Ocean is located 130 km to the west. For purposes of this paper, we use the official city limit boundaries, which were accessed through the Oregon regional government agency, Metro’s, Regional Land Information System (RLIS) [25].

2.2. Data

2.2.1. Temperature Data Collection and Compilation

The initial step in describing the variation in Portland’s temperature extremes was the collection of temperature data during a heat wave. Although we currently do not have a universally acceptable definition of a heat wave [6], for the purposes of this study, we defined it as occurring when temperatures exceed the 90th percentile of the historic average high temperatures for both the month and the day. Our measurements were collected on 25 August 2014, when the temperature exceeded the 90th percentile threshold; August high temperatures in Portland average 23.16 °C over the last 30 years, and this specific date had an average high of 27.65 °C over the last 30 years [26].

Based on existing methods [21,24], we conducted vehicle traverses in six pre-determined sections of the city. The temperature sensors consisted of a Type T fine (30 gauge) thermocouple mounted within a 50 cm long, 2.5 cm diameter white plastic shade tube (Figure 2A–G). The tube was mounted on the passenger-side window approximately 25 cm above the vehicle roof (Figure 2H). These sensors were connected to data loggers, which recorded the temperature to an accuracy level of 0.1 °C once every second. Observations were collected three times a day for one-hour intervals beginning at 6 a.m., 3 p.m., and 7 p.m.. A GPS unit was attached to each vehicle in order to pair the temperature measurements with their corresponding location. Based on time and vehicle, the temperature and location datasets were combined to create a spatial dataset that we integrated into a geographic information system (GIS). In order to reduce error in the model, all points collected during times of non-aspiration (when the vehicle was not moving) were discarded. Additionally, data collected at speeds over 56 kph were discarded to prevent any cooling of the sensors that might occur due to turbulence at higher speeds. Over the three time periods, approximately 50,000 temperature measurements and their corresponding locations were collected on 25 August 2014.

2.2.2. LiDAR Data

We used Light Detection and Ranging (LiDAR) data to characterize the biophysical landscape of the study region. The Oregon Department of Geology and Mineral Industry (DOGAMI) and the Oregon LiDAR Consortium (OLC) provided the 2014 LiDAR data, which was collected with both Leica ALS 70 and Orion H sensors operating at approximately 194 kHz. The flights covered the study area, and a total area of over 3200 km², coinciding with the temperature traverses. The resulting point cloud had an average density of 12.24 points per square meter on flat surfaces, with a vertical accuracy of 0.03 m with an average deviation of 0.003 m. The data was obtained in both point cloud (all points from the scan) and raster formats (split into ‘ground only’ and ‘highest hit’ elevations) from the OLC. With these LiDAR data we are able to characterize the entire study region in terms of feature height and physical structures.

2.2.3. Orthophotography Data

The LiDAR data was next combined with orthorectified aerial imagery to characterize all the biophysical features in the study area. The aerial imagery was collected via a Four-Band Radiometric Image Enhanced Survey (FRIES) along with the aforementioned LiDAR data. The FRIES utilized a charge coupled device (CCD)-based 260 megapixel 4-band (red: 590–720 nm; green: 490–660 nm; blue: 410–590 nm; infrared: 690–990 nm) UltraCam Eagle camera which produced approximately 15 cm resolution imagery. Horizontal accuracy of the imagery has an RMSE of 0.31 m. The orthophotography data can be combined with the LiDAR height and structural data to classify biophysical landscape features known to affect temperatures.

2.2.4. Building Data

Buildings and the built environment have been shown to play a role in UHIs [4,27]. Building polygon data were collected from Metro’s 2014 RLIS [25]. The building polygons contained information on heights, total area, and footprint of each building. To integrate the buildings with other data, we converted them into discrete raster datasets at 1 m resolution, giving each pixel a value corresponding to the specific building’s height. The resulting raster is used to calculate building heights, the standard deviation in heights, and total volume.

2.2.5. Canopied and Non-Canopied Vegetation

The presence of canopied vegetation (i.e., trees) has also been shown to contribute to the reduction in urban heat [28,29]. In addition, non-canopied vegetation (i.e., grasses and shrubs) may mediate observed temperatures [30,31]. From the orthophotography dataset, a 1 m resolution Green Normalized Difference Vegetation Index (gNDVI) was created using the following formula:

$$\mathrm{gNDVI}=\frac{\mathrm{NIR}-\mathrm{G}}{\mathrm{NIR}+\mathrm{G}}$$

where:

NIR = Near Infrared Imagery Band

G = Green Imagery Band

The gNDVI raster contains values between −1 and 1, with higher numbers signifying a higher amount of aboveground biomass [32]. In our approach, we used a gNDVI value of 0.02 and greater as a means for determining living plants from all other features. The gNDVI is similar to the more standard NDVI in terms of identifying vegetation [33]; however, we note the ability of gNDVI to perform especially well in vegetation classification in urban environments [34].

We also created a one-meter digital height model (DHM) by calculating the difference between two other datasets: a Digital Surface Model (DSM) and a Digital Elevation Model (DEM). To characterize canopied vegetation, we deployed a conditional equation to determine areas where gNDVI was greater or equal to 0.02 (heuristically determined to be a suitable threshold for vegetation representation) and DHM was greater than or equal to 3.048 m:

$$\mathrm{Canopied} \mathrm{Vegetation}=\mathrm{DHM}\ge 3.048 \mathrm{and} \mathrm{gNDVI}\ge 0.02$$

Alternately, non-canopied vegetation was calculated using the DHM where it was less than 3.048 m:

$$\mathrm{Non} \mathrm{Canopied} \mathrm{Vegetation}=\mathrm{DHM}<3.048 \mathrm{and} \mathrm{gNDVI}\ge 0.02$$

We note that these specific thresholds can be changed depending on the context.

2.2.6. Canopy Density Metric

The canopy dataset we created is a 2-dimensional top-down presence/absence representation of canopy; however, we endeavored to characterize a canopy density metric (CDM) that accounts for the volume of each tree in the city. All point clouds, in LAS file format, were sent through ENVI LiDAR’s automatic classification routine. This process classified points into four categories based on structure and planar continuity: (1) ground; (2) canopied vegetation; (3) buildings; and (4) other. The classified point clouds were next exported to two separate 1 m raster format datasets. The first dataset’s cell values represented the count of all LiDAR returns classified by the software as ‘canopied vegetation’, whereas the second dataset’s cell values represented the count of all LiDAR returns classified as ‘ground/building’. A canopy density ratio raster was created by dividing the ‘canopied vegetation’ raster by the sum of the ‘canopied vegetation’ and ‘ground/building’ rasters. Finally, the density ratio was multiplied by the DHM, resulting in a density-adjusted canopy height metric. A standard CDM equation includes an argument for filtering vegetation within a specified distance of the ground in order to define ‘canopy’ [35]. We use our definition of canopy, which incorporates this low-height filtering during classification, to generate a CDM equation for the present study:

$$\mathrm{CDM}=\mathrm{h}(\frac{\mathrm{Lt}}{\mathrm{Lt}+\mathrm{Lg}})$$

where:

CDM = Canopy Density Metric per cell

h = height from DHM

Lt = ‘canopied vegetation’ classified LiDAR return count raster

Lg = ‘ground/building’ classified LiDAR return count raster

2.2.7. Elevation

Given the role of elevation in affecting temperatures, we include elevation though the use of the LiDAR data. The LiDAR data provides a high resolution and accurate measurement of ground elevation, which we have chosen to omit this from our modeling for two primary reasons. First, in exploratory analysis we found a high correlation between elevation and canopy cover. Using 4000 randomly generated points within the study region, we evaluated the correlation between canopy cover and elevation resulting a statistical significant and strong multi-collinearity (r² = 0.6267, p < 0.001). Second, our aims for this analysis are to assess the role of land use/land cover in amplifying or mitigating urban heat to inform mitigation opportunities. Though elevation will undoubtedly play a role in temperatures due to the adiabatic lapse rate, it is not easily altered, while arguably, vegetation (i.e., canopy cover) can be modified relatively easily.

2.3. Modeling

2.3.1. Effective Distances

In order to understand the role of the biophysical landscape in explaining variations in temperature, we evaluated a series of distances from each of the measurement points. For this study, the following fifteen distances were chosen to search for patterns that could potentially occur both locally and at larger neighborhood scales: 50 m, 100 m, 150 m, 200 m, 250 m, 300 m, 350 m, 400 m, 450 m, 500 m, 600 m, 700 m, 800 m, 900 m, and 1000 m. We combined each of the landscape features described above with each of these distances from the temperature measurement points to determine which variable at what distance best explains the variation in temperatures. To calculate statistics (e.g., mean, sum) for each variable at each distance we employed a moving window analysis. This process creates new raster data by assigning the value of the specific measurement statistic from all cells that fall within a specified distance (i.e., “window”, Figure 3).

The resulting raster datasets were merged to the vehicle traverse temperature observation data based on the raster value and geographic location. The merging results in a single table (henceforth known as the Master List) consisting of approximately 50,000 locations with observed temperatures, and a summary of each land use variable within each buffer distance from that point. For each modeling method, the Master List is split into three separate tables for each observation, creating three independent models for the morning, afternoon, and evening.

2.3.2. Model Validity

To assess the strength of our models, we used a 70/30 holdout cross-validation method, which consists of predicting 30% of the data with 70% of the observed data, selected randomly and without replacement from the Master List. The 70% is used to create a model of temperatures for the study area, which is then tested against the 30% of the data to evaluate the effectiveness of our model through three types of statistical predictive methods.

2.3.3. Multiple Linear Regression (MLR)

The first modeling method applied was multiple linear regression (MLR). For each time period, the respective table of temperatures vs. land uses was run through stepwise regression modeling in SPSS. We expected high multicollinearity in our dataset resulting from the inclusion of multiple effective distance variables, many of which would be only slightly different from one another. Multicollinearity and its effect on our model is addressed by calculating the variance inflation factor (VIF), which, if greater than ten, indicates an invalid model [36]. Other literature suggests that lowering the maximum allowable VIF limit to three is a more appropriate threshold [37]. Due to our large quantity of highly similar variables and expected high multicollinearity through these variables, a maximum allowable VIF between any two variables in any time-period model was capped at two. MLR and all subsequent techniques were performed in R statistical software [38] and the Master List, leveraging the “raster” package to allow for modeling temperatures directly from the effective distance raster datasets [39].

2.3.4. Classification and Regression Tree/Multiple Linear Regression Hybrid

In addition to MLR, we created a combination of machine learning/clustering techniques and MLR. By combining Classification and Regression Tree (CART) analysis with MLR, we are able to increase the overall predictive power of a model [21,40,41]. CART analysis involves a recursive partitioning of data in order to separate it into more homogenous subsets [42]. This separation into like cluster was applied to the land use-based Effective Distance rasters to separate our study area into eight sections of similar urban form. Once a full CART tree was constructed, it was pruned back into six terminating nodes in order to prevent errors due to overfitting the model [43]. Next, the training dataset of observation points was put through the CART model to determine the classification scheme. Stepwise regression modeling was performed for each of these subsets of observation points in order to create a cluster-specific mode. CART analyses and functions were performed in R statistical software using the “rpart” package [44].

2.3.5. Random Forest Analysis

Finally, we evaluated the strength of a random forest (RF) model. The RF model is built from a collection of individual CART analyses. At an individual level, the CARTs are created randomly: a random independent variable is selected to start the analysis, and each subsequent fork in the tree is selected from a random subset of variables. By building CARTs in this random fashion, they can be assumed to be unbiased and have a reduced variance [43]. Once a predetermined number of randomized CART trees are created, a bootstrap aggregation technique averages out their results into one defined model. The final RF model can be used to predict new values based on new inputs. In this study we developed a model using 1000 individual and randomized CART trees built from the Master List. The model was next applied to all of the effective distance rasters in order to predict a new raster file representing temperature values across the study area. Random forest modeling was performed in R statistical software using the “randomForest” package [45].

3. Results

We describe our results in three sections. First we use the 70/30 hold out method to evaluate the strength of each of the three statistical models in terms of their predictive power across the three vehicle-based traverses (

Table 1. Overall Model Performance. Correlation and RMSE values calculated from the 70/30 holdout method for consistency across the three modelling methods.

Time	Rank	Model	r2	RMSE
6 a.m.	3	MLR	0.5912	0.6575
	2	CART/MLR	0.8595	0.3758
	1	Random Forest	0.9793	0.1479
3 p.m.	3	MLR	0.4554	0.8406
	2	CART/MLR	0.5681	0.7633
	1	Random Forest	0.8199	0.4798
7 p.m.	3	MLR	0.4290	0.9011
	2	CART/MLR	0.6638	0.7086
	1	Random Forest	0.9715	0.2078

). While all three models perform well (e.g., greater than 50% predictive power in almost all trials), we observe that across all three time periods, the RF model performs the best in predicting temperatures.

3.1. Multiple Linear Regression (MLR)

The MLR models for each of the three time periods were compared with the 30% holdout data and had relatively poor performance. The 6 a.m. model indicated the strongest performance with an r² of 0.591 and an RMSE of 0.658 °C. The stepwise regression revealed that three landscape factors helped to predict over 50% of the temperatures: the percent of land cover classified as vegetation within 700 m, the percent of land cover classified as canopy within 450 m, and the sum of CDM within 900 m. The 3 p.m. model had an r² of 0.455 and an RMSE of 0.841 °C. This afternoon model indicated that four landscape variables were the strongest predictors of temperatures: sum of CDM within 1 km, the sum of building volume within 800 m, mean building height within 350 m, and the sum of CDM within 50 m. The 7 p.m. model had even lower predictive power (an r² of 0.429 and an RMSE of 0.901 °C), and had a different set of predictors: percent of land cover classified as canopy within 150 m, the sum of CDM within 600 m, the sum of building volume within 900 m, and the percent of land cover classified as vegetation within 400 m.

3.2. Classification and Regression Tree/Multiple Linear Regression Hybrid

The CART/MLR hybrid method outperformed the standard MLR model. The ability to define homogenous subsets allowed for a notable increase in predictive power and reduction in RMSE over a single MLR model applied across the study area. Similar to MLR, the CART/MLR hybrid has optimum performance modeling during the 6 a.m. period with an increase in predictive power (r²) over MLR of 0.268 (to 0.859) and a decrease in RMSE of 0.282 °C (to 0.376 °C). CART/MLR only saw a slight increase over MLR during the afternoon traverse with an increase in r² of 0.113 (to 0.568) and a decrease in RMSE of 0.077 °C (to 0.763 °C). Finally, the 7 p.m. evening traverse increased the performance of the model more so than the afternoon model with an increase in r² of 0.235 (to 0.664) and a decrease in RMSE of 0.193 °C (to 0.709 °C).

3.3. Classification and Regression Tree/Multiple Linear Regression Hybrid

Lastly the RF models performed the best of the three models. We note the top five most influential variables for each data collection time period RF model below (

Table 2. MLR variables selected with stepwise linear regression. Standardized (Beta) coefficients provided for comparison of variable influence.

Time	r2	RMSE (°C)	Variables	Beta
6 a.m.	0.5912	0.6575	Vegetation cover within 700 m	−0.6664
			Canopy cover within 450 m	−0.3925
			Sum of CDM within 900 m	−0.2710
3 p.m.	0.4554	0.8406	Sum of CDM within 1000 m	−0.5483
			Building volume within 800 m	−0.5128
			Mean building height within 350 m	−0.3541
			Sum of CDM within 50 m	−0.1652
7 p.m.	0.4290	0.9011	Building volume within 900 m	−0.5446
			Sum of CDM within 600 m	−0.4589
			Vegetation cover within 400 m	−0.2392
			Canopy cover within 150 m	−0.1673

), however the model takes into account all independent variables and buffer distances when predicting temperatures. Variable rank (i.e., importance) is determined by taking the average of model MSE change when each variable is randomized (denoted by “%IncMSE” in

Table 3. The five most important landscape features using the RF model (determined by the %IncMSE) by time period.

Model	Variable Rank	Variable	%IncMSE
6 a.m.	1	Vegetation cover within 50 m	42.48
	2	Vegetation cover within 800 m	38.72
	3	Building volume within 900 m	33.90
	4	Sum of CDM within 1000 m	32.98
	5	Mean building height 100 m	32.69
3 p.m.	1	Standard deviation of building height within 1000 m	40.83
	2	Standard deviation of building height within 300 m	39.12
	3	Sum of CDM within 50 m	38.94
	4	Standard deviation of building height within 150 m	38.66
	5	Standard deviation of building height within 200 m	38.54
7 p.m.	1	Standard deviation of building height within 1000 m	39.95
	2	Vegetation cover within 100 m	32.53
	3	Building volume within 1000 m	30.93
	4	Canopy cover within 800 m	30.91
	5	Building volume within 900 m	30.58

) in the tree-growing stage of the random forest model [43].

3.3.1. Random Forest: Morning Results

Based the above variables, the RF model provides spatially explicit descriptions of the distribution of urban heat throughout the city and by each of the time periods. Morning temperatures are derived by percent of land cover classified as vegetation at a local and broad scale (50 m and 800 m respectively), total building volume within 900 m, sum of CDM at broad scale (1 km), and the mean building height within a localize area (100 m) (Figure 4). Temperatures of the output raster surface model representation depict temperatures from 13.04 °C to 18.20 °C, with a mean of 15.79 °C and standard deviation of 0.94 °C. We observe a pattern of heat distribution wherein downtown Portland, along with the inner-eastside industrial area, NW industrial area, and Swan Island Industrial area all exhibit the highest levels of heat. Temperatures in these areas can be over 5 °C hotter than areas of the city such as those to the east and southwest.

3.3.2. Random Forest: Afternoon Results

Afternoon temperatures depend on the standard deviation of building height at 1 km, 300 m, 150 m, and 200 m. Also included in the top five most important variables is the sum of CDM at 50 m. Temperatures of the output raster surface model representation depict temperatures from 25.21 °C to 34.87 °C with a mean of 30.98 °C and standard deviation of 1.43 °C (Figure 5). Distribution of relative hot/cold temperatures through the city show a pattern that is quite different than that of the morning model. Unlike the morning model, the downtown area has shifted from being the hottest area in the city to one of the cooler ones. Heavily forested areas (including major parks, in addition to certain residential areas) show a tendency towards cooler temperatures. Areas with lower canopy cover, such as those at the northern edge of the city (industrial, port, and airport areas), eastern freeway corridors, and train yards, consistently appear hotter in the afternoon model. Additionally, areas around freeways and arterial roadways show small and localized ‘pockets’ of heat within close proximity.

3.3.3. Random Forest: Evening Results

Evening temperatures exhibit the greatest diversity in terms of the top five most important variables that predict temperatures (Figure 6). The most important factors during this time period consisted of: standard deviation of building heights within 1 km, localized percent of land cover classified as vegetation within 100 m, total building volume within 1 km, percent of land cover classified as canopy within 800 m, and total building volume within 900 m. The evening model raster surface displays strong similarities to areas of relative heat and major freeways and arterial roads. Similar to the afternoon model, the major parks and forested areas are relatively cool and industrial areas (including train yards) are quite hot. Downtown Portland, which is hottest in the morning, appears relatively cooler in the evening.

4. Discussion

Our results suggest that the RF model helps to explain the greatest variation in temperatures across the city. While others have observed similar results (e.g., Makido et al., 2016 [24]), these results go further to suggest that in comparison to other models—including MLR and CART, which are often applied to urban heat assessments—RF models provide greater certainty for understanding the distribution of UHIs. Although we evaluate the strength of these different models in one city, the strength of these models (e.g., an r² of 0.97) suggests that RF will likely be applicable in other cities with similar predictive power. Although the RF is a far stronger predictor, this is not to say that MLR and CART analysis are not useful. They do offer alternatives to conducting citywide assessments of urban heat, and indicate that similar landscape variables help to explain variations in urban heat. In the policy context, where certainty and resolution are essential, the RF model may provide greater value in making decisions about specific mitigation efforts.

The variation in temperatures throughout the day also offers new insights about the dynamic nature of urban heat events. Afternoon temperatures were consistently more difficult to predict, which we speculate may be due to the non-land use variables (e.g., wind speed, albedo, urban canyons, etc.) that are left out of our models. Satellite-derived UHI studies commonly include variables such as albedo in their models which, if included in our research, could improve our predictive power for the afternoon periods. Henry and Dicks (1987) [3] predict that the placement, clustering, and contiguity of the urban forest throughout a city may be the dominant driver of the distribution of urban heat during midday. In addition to the form, we draw on earlier research [46] to further speculate that a difference in tree functional type (coniferous or deciduous) could help to explain differences in temperature during the afternoons. The evening temperatures have the strongest predictive power, and high-heat distribution is concentrated along major paved areas, including the industrial and roadways. These findings are consistent with thermodynamics literature, which suggests that building materials absorb heat throughout the day, and release through the night [4,21]. At the same time the forested areas are the coolest in the city, likely due to the evapotranspiration that occurs [11]. Many of the explanatory land uses were significant at multiple distances; this local vs. regional cooling effect of trees is noted in other studies [47,48]. We attributed this result to site-specific (e.g., a tree directly shading the ground beneath it) and background effects (e.g., a high canopy cover neighborhood will provide a more broad-scale reduction in ambient temperatures) of land use/cover configurations [49].

Essential to understand is that our approach offers the ability to track the distribution of temperature across an entire city (or metropolitan region) throughout the day. While we used three time periods for assessing differences in temperature, we are also able to describe those areas that have cooled the fastest and conversely also amplify heat. We note that certain areas such as train depots/yards, heavy industry zones, ports, and transit corridors have consistently higher temperatures throughout morning, afternoon and evening. The city’s downtown area, often thought of as the hottest part of the city due to the highest amount of concrete, suggests a different pattern when compared to the rest of the diurnal period: though relatively hot in the morning, it does not warm as rapidly as, or to the maximum temperature of, many other areas. We speculate that the downtown area is cooler due to two interacting factors: (1) the orientation of the buildings and streets that provide shade to most streets during the hottest parts of the day [50,51]; and (2) the high variation in building heights (accounted for in the model with “standard deviation of building height”), which can generate turbulence in air flowing across the city, cooling it through increased heat transfer [52,53]. Other regions have found similar results [24,54].

Our method, though capable of producing high-accuracy models of intra-urban heat, does have several limitations. First, with 90 moving window rasters (6 land use/cover variables as 15 distance) and an average file size of approximately 5.5 GB, this analysis required a large amount of computer memory, which was computationally large and complex. Even when running the analysis on a high-performance computational server, the time requirements for training and predicting a random forest UHI model limits the widespread adoption of these methods outside of research environments. As a result, practitioners may not be able to readily replicate our analysis. Second, the random forest model does not produce coefficients—much like the OLS model—making ascribing the contribution of each input variable difficult to interpret. Admittedly, we traded prediction accuracy for the interpretability of the model because the use of random forest modeling offers many advantages in terms of improving prediction accuracy, yet comes at a cost of not knowing the exact effects of explanatory variables (e.g. beta-coefficient). In addition, this method does not fit all of the use cases of more complex climate models. Unlike mesoscale and microscale climate models, our urban heat island models do not attempt to simulate complex climate or weather system interactions for the creation of long-term forecasting models. Often, these climate models point to areas where further non-simulated investigation (such as our on-ground empirical temperature measurements) is needed, as climate model performance can often vary at different locations or scales [55,56].

The temporal resolution of this study allows for a deeper understanding of temperature changes that can occur throughout the city, whereas the high spatial resolution allows for a more accurate measurement of temperatures in specific areas. With a 1 m resolution, the UHI surfaces allow for temperature analyses at the household-level for the entire study area without any resampling of the data (which, inherently, would introduce additional error). High spatial resolution also increases the ability to detect subtle changes in temperatures. Nowhere is this more important than in the smooth gradients of temperature surrounding heat-reducing landscapes (major parks and natural areas), where many suburban land uses develop. The edge effect of major cooling/heating landforms is accurately described only with high-resolution data, as coarse resolution pixels would obscure these subtleties.

5. Conclusions

This study created descriptions of the distribution of Portland, Oregon’s urban temperatures throughout the day with extremely high spatial resolution and accuracy. For three separate time periods in the morning, afternoon, and evening, we collected GPS-located temperature measurements. These measurements were used in a variety of modeling methods, of which random forest produced the highest predictive power (r² = 0.9793, r² = 0.8199, and r² = 0.9715 for morning, afternoon, and evening models, respectively). The applications of this research’s results to land use planning could prove helpful in shaping building, zoning, and general urban growth policies. We posit that our study contributes to the literature and practice of managing urban heat in two ways. First, urban planners are able to examine the drivers of heat within the city in terms of land cover and land use (i.e., built form). With greater detail in understanding the relationships between urban form and UHI, we can more effectively shape them, such that city design can reduce extreme heat impacts on the most vulnerable populations. Potential planning policies could include, for example, specific requirements for varied building heights within an area, to ensure that turbulent airflow will aid in cooling (as observed in downtown Portland, Oregon), or stricter stipulations on construction-related tree removals. Second, municipal decision makers could develop responsive building designs that ameliorate the presence of extreme heat. Though it may be far-fetched to alter building heights after they are built, tree planting campaigns in specific sections of the city could prove to reduce extreme heat [12,46].

Beyond urban planning work, the results of this study can be used to inform public health programs. These multi-temporal, high-accuracy, and high spatial resolution results provide an unparalleled description of potential heat exposure within the city. Locations in which the heat is ‘trapped’ and does not dissipate are especially important to identify, as populations residing within them will potentially have longer exposure to extreme heat throughout the day. Extensive epidemiological evidence suggests that prolonged exposure to high temperatures can lead to heat-related illness such as heat stroke, which has the potential to be fatal [1,57,58]. By coupling an understanding of exposure data with demographic information specific to sensitivity populations (i.e., older adults, pre-existing health conditions), and coping capacities (i.e., lower income, isolated individuals or communities), public health practitioners can specify residents who may face fatal impacts during extreme heat events [59]. Due to the high spatial resolution of the UHI surfaces, it is conceivable that a heat/health mitigation strategy could be enacted at a household scale, which could be conducted through information dissemination (e.g., pamphlets on cooling center locations). Highly accurate and spatially precise exposure information increases the likelihood of a successful overall health outcome for urban populations [8].

Climate change and destabilization will likely create impacts beyond our ability to respond effectively; indeed, it already has. An emerging body of research describes an increase in duration, intensity, and frequency of extreme weather events [6]; however, we have yet to understand local opportunities for evaluating the intensity and distribution of urban heat. Our study offers a timely and effective approach for addressing localized impacts before they occur. Although only for one city, we believe that our methods and approach are transferable to other metropolitan regions, and applications are currently underway [24]. Through systematic evaluation across multiple cities in different biophysical environments, and using similar ground-based techniques, we will be able to equip decision makers with highly resolved data for taking proactive action, ultimately reducing vulnerability to infrastructure, ecologies, and communities.