A Modified Enthalpic Lattice Boltzmann Method for Simulating Conjugate Heat Transfer Problems in Non-Homogeneous Media
Abstract
:1. Introduction
2. Materials and Methods
2.1. Lattice Boltzmann Method for Fluid Flow
2.2. Boussinesq Approach for Natural Convection
2.3. Lattice Boltzmann Method for Conjugate Heat-Transfer
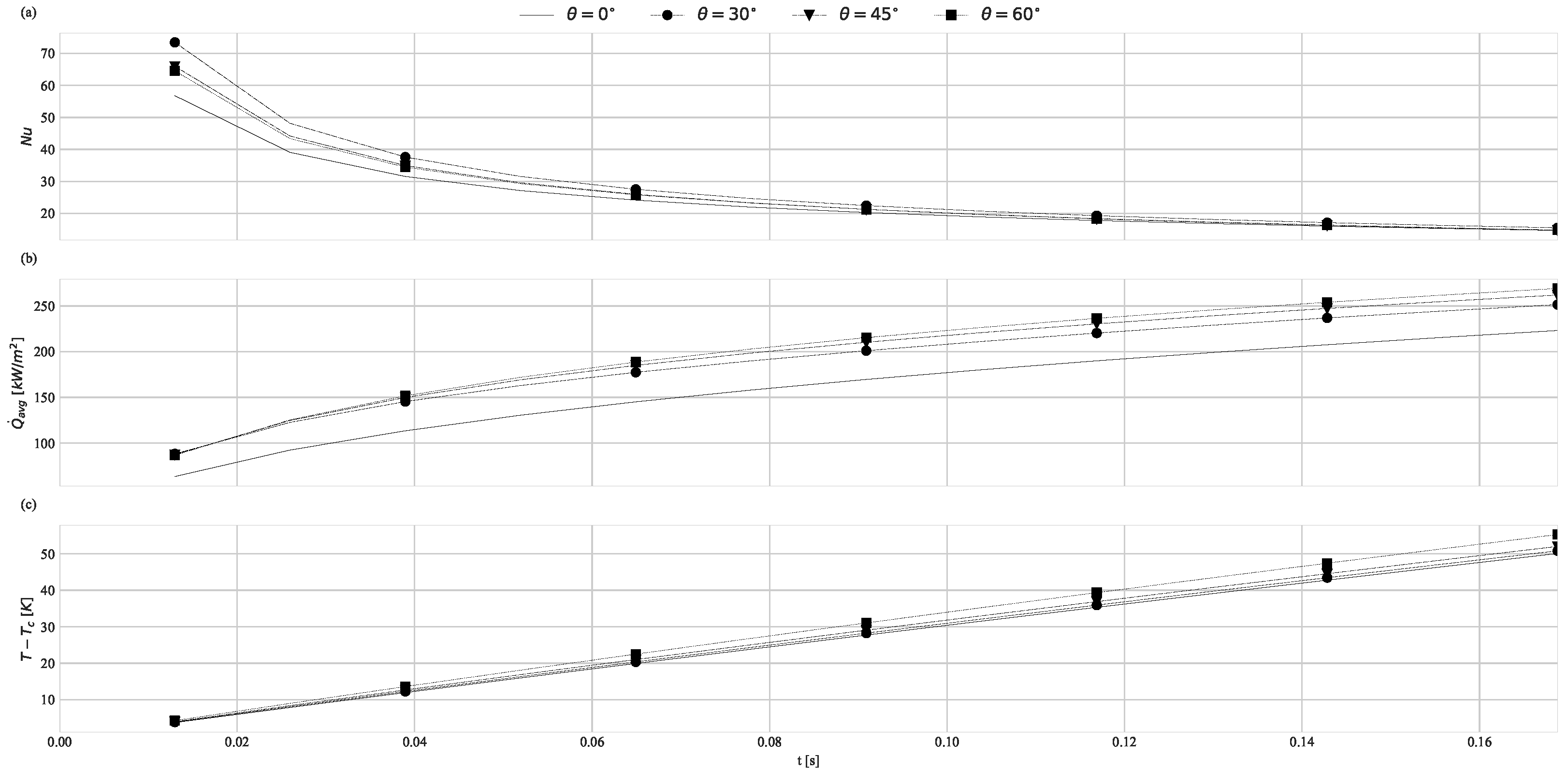
3. Results and Discussion
3.1. Benchmark Tests
3.1.1. Heat Diffusion between Three Solids
3.1.2. Convection–Diffusion with a Flat Interface
3.1.3. Natural Convection with a Fixed Heat Flux
3.2. Results for Natural Convection with Structured Cavities
3.2.1. Geometry Impact on Natural Convection with Imposed Heat Flux
3.2.2. Natural Convection with Fixed Base Temperature
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Chapman–Enskog Analysis
Appendix B. Analytical Solution Heat Diffusion between Three Solids
Appendix C. Analytical Solution Convection–Diffusion with a Flat Interface
Appendix D. Nusselt Number Calculation
References
- Bejan, A.; Kraus, A. Heat Transfer Handbook; Wiley: Hoboken, NJ, USA, 2003; Volume 1. [Google Scholar]
- Aneesh, A.; Sharma, A.; Srivastava, A.; Vyas, K.; Chaudhuri, P. Thermal-hydraulic characteristics and performance of 3D straight channel based printed circuit heat exchanger. Appl. Therm. Eng. 2016, 98, 474–482. [Google Scholar] [CrossRef]
- Buchberg, H.; Catton, I.; Edwards, D.K. Natural Convection in Enclosed Spaces—A Review of Application to Solar Energy Collection. J. Heat Transf. 1976, 98, 182–188. [Google Scholar] [CrossRef]
- Baïri, A.; Zarco-Pernia, E.; De María, J.M.G. A review on natural convection in enclosures for engineering applications. The particular case of the parallelogrammic diode cavity. Appl. Therm. Eng. 2014, 63, 304–322. [Google Scholar] [CrossRef]
- Pretot, S.; Zeghmati, B.; Caminat, P. Influence of surface roughness on natural convection above a horizontal plate. Adv. Eng. Softw. 2000, 31, 793–801. [Google Scholar] [CrossRef]
- Oosthuizen, P.H. A numerical study of laminar and turbulent natural convective heat transfer from an isothermal vertical plate with a wavy surface. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Vancouver, BC, Canada, 12–18 November 2010; Volume 44441, pp. 1481–1486. [Google Scholar]
- Oosthuizen, P. Natural convective heat transfer from an inclined isothermal plate with a wavy surface. In Proceedings of the 42nd AIAA Thermophysics Conference, Honolulu, HI, USA, 27–30 June 2011; p. 3943. [Google Scholar]
- Oosthuizen, P.H.; Kalendar, A. A numerical study of the effect of spaced triangular surface waves on natural convective heat transfer from an upward facing heated horizontal isothermal surface. In Proceedings of the 5th Thermal and Fluids Engineering Conference (TFEC), New Orleans, LA, USA, 5–8 April 2020. [Google Scholar]
- Hussain, S.; Kalendar, A.; Rafique, M.Z.; Oosthuizen, P.H. Assessment of thermal characteristics of square wavy plates. Heat Transf. 2020, 49, 3742–3757. [Google Scholar] [CrossRef]
- Hossain, M.; Rees, D.A.S. Combined heat and mass transfer in natural convection flow from a vertical wavy surface. Acta Mech. 1999, 136, 133–141. [Google Scholar] [CrossRef]
- Siddiqa, S.; Hossain, M.; Saha, S.C. The effect of thermal radiation on the natural convection boundary layer flow over a wavy horizontal surface. Int. J. Therm. Sci. 2014, 84, 143–150. [Google Scholar] [CrossRef]
- Siddiqa, S.; Hossain, M.A.; Gorla, R.S.R. Natural convection flow of viscous fluid over triangular wavy horizontal surface. Comput. Fluids 2015, 106, 130–134. [Google Scholar] [CrossRef]
- Oosthuizen, P.H.; Paul, J.T. A numerical study of natural convective heat transfer from an inclined isothermal plate having a square wave surface. In Proceedings of the ASME International Mechanical Engineering Congress and Exposition, Denver, CO, USA, 11–17 November 2011; Volume 54969, pp. 445–450. [Google Scholar]
- Perelman, T. On conjugated problems of heat transfer. Int. J. Heat Mass Transf. 1961, 3, 293–303. [Google Scholar] [CrossRef]
- Armero, F.; Simo, J. A new unconditionally stable fractional step method for non-linear coupled thermomechanical problems. Int. J. Numer. Methods Eng. 1992, 35, 737–766. [Google Scholar] [CrossRef]
- Giles, M.B. Stability analysis of numerical interface conditions in fluid–structure thermal analysis. Int. J. Numer. Methods Fluids 1997, 25, 421–436. [Google Scholar] [CrossRef]
- Roe, B.; Jaiman, R.; Haselbacher, A.; Geubelle, P. Combined interface boundary condition method for coupled thermal simulations. Int. J. Numer. Methods Fluids 2008, 57, 329–354. [Google Scholar] [CrossRef]
- Zhang, J.; Yang, C.; Mao, Z.S. Unsteady conjugate mass transfer from a spherical drop in simple extensional creeping flow. Chem. Eng. Sci. 2012, 79, 29–40. [Google Scholar] [CrossRef]
- Succi, S. The Lattice Boltzmann Equation: For Fluid Dynamics and Beyond; Oxford University Press: Oxford, UK, 2001. [Google Scholar]
- Korba, D.; Wang, N.; Li, L. Accuracy of interface schemes for conjugate heat and mass transfer in the lattice Boltzmann method. Int. J. Heat Mass Transf. 2020, 156, 119694. [Google Scholar] [CrossRef]
- Li, L.; Chen, C.; Mei, R.; Klausner, J.F. Conjugate heat and mass transfer in the lattice Boltzmann equation method. Phys. Rev. E 2014, 89, 043308. [Google Scholar] [CrossRef]
- Karani, H.; Huber, C. Lattice Boltzmann formulation for conjugate heat transfer in heterogeneous media. Phys. Rev. E 2015, 91, 023304. [Google Scholar] [CrossRef] [PubMed]
- Rihab, H.; Moudhaffar, N.; Sassi, B.N.; Patrick, P. Enthalpic lattice Boltzmann formulation for unsteady heat conduction in heterogeneous media. Int. J. Heat Mass Transf. 2016, 100, 728–736. [Google Scholar] [CrossRef]
- Chen, S.; Yan, Y.; Gong, W. A simple lattice Boltzmann model for conjugate heat transfer research. Int. J. Heat Mass Transf. 2017, 107, 862–870. [Google Scholar] [CrossRef]
- Hosseini, S.; Darabiha, N.; Thévenin, D. Lattice Boltzmann advection-diffusion model for conjugate heat transfer in heterogeneous media. Int. J. Heat Mass Transf. 2019, 132, 906–919. [Google Scholar] [CrossRef]
- Yang, L.; Shu, C.; Yang, W.; Wu, J. Simulation of conjugate heat transfer problems by lattice Boltzmann flux solver. Int. J. Heat Mass Transf. 2019, 137, 895–907. [Google Scholar] [CrossRef]
- Kiani-Oshtorjani, M.; Kiani-Oshtorjani, M.; Mikkola, A.; Jalali, P. Conjugate heat transfer in isolated granular clusters with interstitial fluid using lattice Boltzmann method. Int. J. Heat Mass Transf. 2022, 187, 122539. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2002. [Google Scholar]
- Martins, I.T.; Alvariño, P.F.; Cabezas-Gómez, L. Lattice Boltzmann method for simulating transport phenomena avoiding the use of lattice units. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 333. [Google Scholar] [CrossRef]
- Bhatnagar, P.L.; Gross, E.P.; Krook, M. A Model for Collision Processes in Gases. I. Small Amplitude Processes in Charged and Neutral One-Component Systems. Phys. Rev. 1954, 94, 511–525. [Google Scholar] [CrossRef]
- Krüger, T.; Kusumaatmaja, H.; Kuzmin, A.; Shardt, O.; Silva, G.; Viggen, E. The Lattice Boltzmann Method: Principles and Practice; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Qian, Y.H.; D’Humieres, D.; Lalleman, P. Lattice BGK Models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479–484. [Google Scholar] [CrossRef]
- Guo, Z.; Shu, C. Lattice Boltzmann Method and Its Applications in Engineering; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2013. [Google Scholar]
- Guo, Z.; Zheng, C.; Shi, B. Discrete lattice effects on the forcing term in the lattice Boltzmann method. Phys. Rev. E 2002, 65, 046308. [Google Scholar] [CrossRef] [PubMed]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases, 2nd ed.; Cambridge University Press: Cambridge, UK, 1952. [Google Scholar]
- Klein, S.A. EES – Engineering Equation Solver, Version 11.444 (2022-09-29); Computer Software; F-Chart Software: Madison, WI, USA, 2022. [Google Scholar]
- Seta, T. Implicit temperature correction-based immersed boundary-thermal lattice Boltzmannmethod for the simulation of natural convection. Phys. Rev. E 2013, 87, 063304. [Google Scholar] [CrossRef]
- Chai, Z.; Zhao, T.S. Nonequilibrium scheme for computing the flux of the convection-diffusion equation in theframework of the lattice Boltzmann method. Phys. Rev. E 2014, 90, 013305. [Google Scholar] [CrossRef] [PubMed]
- Martins, I.T.; Matsuda, V.A.; Cabezas-Gómez, L. A new Neumann boundary condition scheme for the thermal lattice Boltzmann method. J. Int. Commun. Heat Mass Transf. 2023, preprint. [Google Scholar]
- Sun, Y.; Wichman, I.S. On transient heat conduction in a one-dimensional composite slab. Int. J. Heat Mass Transf. 2004, 47, 1555–1559. [Google Scholar] [CrossRef]
- Cheikh, N.B.; Beya, B.B.; Lili, T. Influence of thermal boundary conditions on natural convection in a square enclosure partially heated from below. Int. Commun. Heat Mass Transf. 2007, 34, 369–379. [Google Scholar] [CrossRef]
- Moreira, D.C.; Nascimento, V.; Ribatski, G.; Kandlikar, S. Combining liquid inertia and evaporation momentum forces to achieve flow boiling inversion and performance enhancement in asymmetric Dual V-groove microchannels. Int. J. Heat Mass Transf. 2022, 194, 123009. [Google Scholar] [CrossRef]
- Kakac, S.; Bergles, A.; Mayinger, F.; Yuncu, H. Heat transfer enhancement of heat exchangers. Dry. Technol. 2000, 18, 837–838. [Google Scholar]
- Lienhard, J.H., IV; Lienhard, J.H., V. A Heat Transfer Textbook, 5th ed.; Phlogiston Press: Cambridge, MA, USA, 2020; Version 5.10. [Google Scholar]













| t | Global Errors | t | Global Errors |
|---|---|---|---|
| Global Errors | Global Errors | ||
|---|---|---|---|
| Reference Nusselt Number: | ||
|---|---|---|
| [m] | Errors [%] | |
| θ ° | 30 | 45 | 60 | 30 | 45 | 60 |
| C | C | C | C | C | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| θ ° | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 | 0 | 30 | 45 | 60 |
| 1.03 | 0.94 | 0.84 | 0.8 | 1.03 | 0.94 | 0.84 | 0.8 | 1.86 | 1.74 | 1.55 | 1.43 | 2.75 | 2.56 | 2.28 | 2.1 | 3.04 | 2.84 | 2.52 | 2.32 | |
| 3.14 | 3.01 | 2.89 | 2.63 | 6.36 | 6.1 | 5.86 | 5.33 | 23.29 | 23.0 | 21.97 | 19.41 | 52.46 | 51.86 | 49.4 | 43.75 | 68.25 | 67.46 | 64.25 | 56.83 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsuda, V.A.; Martins, I.T.; Moreira, D.C.; Cabezas-Gómez, L.; Bandarra Filho, E.P. A Modified Enthalpic Lattice Boltzmann Method for Simulating Conjugate Heat Transfer Problems in Non-Homogeneous Media. Inventions 2024, 9, 57. https://doi.org/10.3390/inventions9030057
Matsuda VA, Martins IT, Moreira DC, Cabezas-Gómez L, Bandarra Filho EP. A Modified Enthalpic Lattice Boltzmann Method for Simulating Conjugate Heat Transfer Problems in Non-Homogeneous Media. Inventions. 2024; 9(3):57. https://doi.org/10.3390/inventions9030057
Chicago/Turabian StyleMatsuda, Vinicius Akyo, Ivan Talão Martins, Debora Carneiro Moreira, Luben Cabezas-Gómez, and Enio Pedone Bandarra Filho. 2024. "A Modified Enthalpic Lattice Boltzmann Method for Simulating Conjugate Heat Transfer Problems in Non-Homogeneous Media" Inventions 9, no. 3: 57. https://doi.org/10.3390/inventions9030057





